Finite Platelet Size Could Be Responsible for Platelet Margination Effect

Abstract

Blood flows through vessels as a segregated suspension. Erythrocytes distribute closer to the vessel axis, whereas platelets accumulate near vessel walls. Directed platelet migration to the vessel walls promotes their hemostatic function. The mechanisms underlying this migration remain poorly understood, although various hypotheses have been proposed to explain this phenomenon (e.g., the available volume model and the drift-flux model). To study this issue, we constructed a mathematical model that predicts the platelet distribution profile across the flow in the presence of erythrocytes. This model considers platelet and erythrocyte dimensions and assumes an even platelet distribution between erythrocytes. The model predictions agree with available experimental data for near-wall layer margination using platelets and platelet-modeling particles and the lateral migration rate for these particles. Our analysis shows that the strong expulsion of the platelets from the core to the periphery of the blood vessel may mainly arise from the finite size of the platelets, which impedes their positioning in between the densely packed erythrocytes in the core. This result provides what we believe is a new insight into the rheological control of platelet hemostasis by erythrocytes.

Introduction

Platelet aggregation is one of the first physiological reactions to vessel wall injury (1,2). A few seconds after injury, the damaged site is covered with a plug of aggregated platelets. For this process to occur efficiently, platelets must be delivered to the vessel wall and collide with either the damaged site or previously adhered platelets. The lateral migration of cells in flowing blood has been the subject of extensive experiments (3–6). Results from these studies have led to the recognition that lateral platelet movement is caused by continuous rebounding collisions between erythrocytes (7). These net collisions produce shear-induced diffusion (dispersion), which locally mixes the plasma and platelets near erythrocytes. The intensity of this dispersion is proportional to the hematocrit, shear rate, and squared radius of the erythrocyte (8,9). The Brownian diffusion of platelets is 2–3 orders-of-magnitude smaller than shear-induced diffusion and, therefore, has a negligible contribution to platelet motion under physiological conditions (7).

In addition to moving randomly across the flow, platelets gradually migrate from the flow core to the periphery (3,7). As a result, the platelet concentration near the vessel wall in vivo is 2–3 times greater than at the vessel core (10–12). In vitro, this nonuniformity is 3- to 18-fold compounded and increases with higher hematocrits and shear rates (13–23). This near-wall excess (NWE) augments the frequency of platelet-wall collision, which aids in the hemostatic function of platelets. Therefore, the nonuniformity of platelet distribution across the flow is physiologically significant.

The mechanism underlying this nonuniformity is not well understood. Alone, the aforementioned shear-induced diffusion cannot lead to spatial nonuniformity. However, many aspects of blood flow are spatially nonuniform; velocity and shear rate (24–27), shear stress and viscosity (28), and concentration and aggregation of erythrocytes (20,27,29–32) are considerably nonuniform across the flow. The first hypothesis that aimed to explain the origin of nonuniform platelet distribution across blood flow was the available-volume model (33). It proposes that the distribution of platelets results from erythrocytes physically preventing them from remaining in the flow core, where the local hematocrit is high, which forces platelets to the erythrocyte-free near-wall region. Further, platelets evenly distribute themselves in the space between erythrocytes and, as the platelets have a finite size, the distribution of platelets is more nonuniform than the distribution of intererythrocyte space. A more general hypothesis, the drift-flux model, assumes the existence of an active laterally directed platelet drift that arises from the differences in the hydrodynamic properties of platelets and erythrocytes (14,18,34). To describe this drift, it was proposed that a “rheological potential” drives platelets to the vessel walls. Neither of these hypotheses has been experimentally or theoretically validated.

Here, we have generated a quantitative mathematical model for lateral platelet migration in blood flow. This model is based on the available volume model and accounts for platelet and erythrocyte dimensions as well as the erythrocyte distribution profile across the flow. Our approach can predict the platelet migration velocity toward the wall as a function of the available volume fraction gradient for platelets and the shear-induced dispersion coefficient. The calculations for the steady and transient cases agree with the available experimental data on the nonuniform distribution of platelets and platelet-modeling particles and on the rate of redistribution, respectively. Thus, simple, physical erythrocyte exclusion of platelets from the flow core may explain the platelet NWE phenomenon. We conclude that the “rheological potential” and drift velocity may primarily be produced by the available volume gradient in flowing blood.

Mathematical Model

Model assumptions. The “excluded and available volumes”

Our model considers the distribution and migration of platelets in blood flow and is based on the following assumptions:

• Assumption 1.

  The erythrocyte distribution across the flow is independent of platelets, and this distribution has previously been either experimentally or theoretically established.

• Assumption 2.

  Platelets cannot penetrate individual erythrocytes but can evenly distribute themselves between erythrocytes.

• Assumption 3.

  The migration of platelets across the blood flow is exclusively due to shear-induced dispersion.

Below, we provide a short explanation for these assumptions.

Assumption 1: Fixed erythrocyte distribution

Erythrocytes occupy ∼40% of the blood volume and completely determine the character of the flow. In contrast, platelets constitute a small percentage of blood cellular mass (∼0.7% of the volume) and, thus, practically do not influence blood flow (7). Given these properties, we can uncouple descriptions for erythrocyte and platelet distribution. Here, the erythrocyte distribution is considered predetermined.

Assumption 2: Spatial distribution of platelets in the presence of erythrocytes

The distribution of platelets between erythrocytes is considered to be random. In other words, platelets are supposed to be evenly distributed throughout the space that is available to them (33). As platelet size has a finite value (a few micrometers), not all of the space between erythrocytes is available (Fig. 1). When the space between two erythrocytes is smaller than the minimal platelet dimension, a platelet cannot occupy this space, whereas blood plasma fills it completely. In addition, the platelet center cannot approach an erythrocyte surface at a distance less than one-half of the platelet thickness (33). Thus, each erythrocyte has a surrounding excluded volume layer. If one designates a volume fraction of these layers (in some microvolume) as Φ_ex and an erythrocyte volume fraction as Φ_RBC, then the intererythrocyte volume fraction equals 1 − Φ_RBC, and the fraction of available to platelets volume equals

$${\Phi }_a=1-{\Phi }_{RBC}-{\Phi }_{ex}.$$

As Φ_RBC increases, Φ_a decreases more rapidly than 1 − Φ_RBC.

Figure 1.

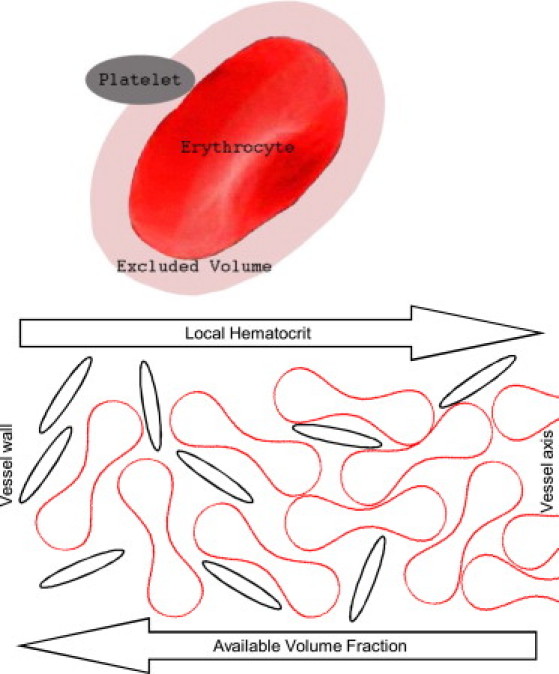
Illustration of the concept of the “excluded and available volumes”. Further away from the wall (from left to right), the erythrocyte volume fraction increases, causing a rapid decrease in the volume fraction that is available to the platelets.

Assumption 3: Dispersive platelet motion

The platelet migration between erythrocytes in laminar shear blood flow is a consequence of dispersion, which arises from continuous collisions between erythrocytes (3,7). Because they completely dominate blood flow behavior, erythrocytes also set the intensity of dispersive motion for all other blood cells and plasma (8,9). This intensity is 2–3 orders-of- magnitude greater than the Brownian diffusion of blood cells (7). Direct measurements (3) and theory (8,35) have shown that the platelet shear-induced dispersion coefficient is close or equal to that of erythrocytes. Therefore, this coefficient is assigned by the analytical formula that approximates the results from numerous observations of the lateral migration of erythrocytes and other deformable particles in shear flow (see Eq. 5). The nonuniform available volume distribution (Fig. 1) leads to a difference in the probability that the platelet is displaced up as compared to when it is displaced down the gradient of Φ_a. This difference leads to a modified Fick's equation (see Eq. 6). At a micro level, this equation describes the tendency of platelets to distribute evenly throughout the volume that is available to them. At a macro level, it describes the redistribution of platelets from regions of lower to higher available volumes.

Equations of the model

Steady conditions

Platelets or platelet-modeling spheres with a radius a_P were assumed to be evenly distributed in the available volume between erythrocytes. The relative concentration of platelets (or spheres) at the given radial position is proportional to the local available volume fraction as follows:

$$\frac{P\left(r\right)}{\langle P\rangle }=\frac{{\Phi }_a\left({\Phi }_{\text{RBC}}\left(r\right)\right)}{\langle {\Phi }_a\rangle }.$$ (1)

Here, 〈·〉 indicates the value averaged over the cross section of a tube, i.e., $\langle F\rangle ={\int }_{-1}^{1}F\left(r\right)\cdot rdr$, where r ∈ [−1,1] is a nondimensional radial coordinate. Direct stochastic calculations have shown that Φ_a rapidly decreases as Φ_RBC increases, and the rate of this drop depends on a_P (see Fig. 2). The analytical formula

$${\Phi }_a\left({\Phi }_{\text{RBC}}\right)=\frac{\text{exp}\left(-p{\Phi }_{\text{RBC}}·\left(2{\Phi }_{\text{RBC}}+1\right)\right)+f}{1+f},$$ (2)

where p ≈ exp(a_P), approximates results of these stochastic calculations when f = 0. At a large Φ_RBC, however, flow-mediated erythrocyte ordering and deformation are expected to increase Φ_a compared with calculated values. Therefore, the parameter f (0 < f << 1) was introduced into Eq. 2, so that ${\Phi }_a\approx f/\left(1+f\right)\approx f$ at a large Φ_RBC. The erythrocyte volume fraction distribution was modeled from an analytical interpolation of the experimental data of Aarts et al. (20) on erythrocyte ghost distribution in glass tubes in vitro as follows (see the Supporting Material):

$${\Phi }_{RBC}\left(r\right)={\Phi }_m·{\left[1-\text{exp}\left(a-b{\Phi }_m\right)+\text{exp}\left(a-b{\Phi }_m·\left(1-r^2\right)\right)\right]}^{-1},$$ (3a)

$${\Phi }_m=\frac{1.45{\Phi }_0}{0.5+{\Phi }_0}.$$ (3b)

Here, Φ_m = Φ_RBC (0) is an erythrocyte volume fraction on the flow axis; Φ₀ = hematocrit/100% is an inflow erythrocyte volume fraction; a = 3.5; and b = 9.

Figure 2.

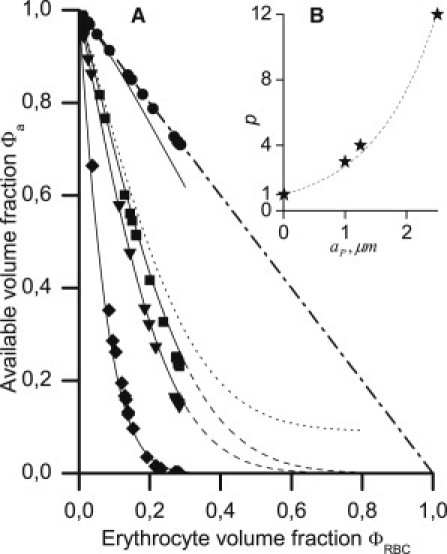
(A) Dependence of the available volume fraction for platelet-modeling spheres on the erythrocyte volume fraction at a_P = 0.01 (●), 1 (■), 1.25 (▾), and 2.5 μm (♦). (Solid and dashed lines) Plotted according to Eq. 2 with p = 1, 3, 4, and 12, respectively, and f = 0. (Dotted line) Plotted with p = 4, f = 0.1. (Dash-dotted line) Intererythrocyte volume fraction 1 − Φ_RBC. (B) Dependence p(a_P) and its approximation by the function p = exp(a_P).

The margination level (i.e., NWE) of platelets and platelet-modeling particles has been defined as the ratio of the near-wall/flow-core concentration (13,15). According to Eq. 1, this ratio is given by

$$\frac{P_{wall}}{P_{axis}}=\frac{{\Phi }_a\left({\Phi }_{RBC}\left(1\right)\right)}{{\Phi }_a\left({\Phi }_m\right)}\approx \frac{1}{{\Phi }_a\left({\Phi }_m\right)}.$$ (4)

The last approximation is from the value of the erythrocyte near-wall volume fraction Φ_RBC (1). This fraction does not exceed several percent values for all of the inflow hematocrits studied (up to 40%) (20). Equation 4 in combination with Eq. 3b was used to calculate the NWE later in Fig. 4 B.

Figure 4.

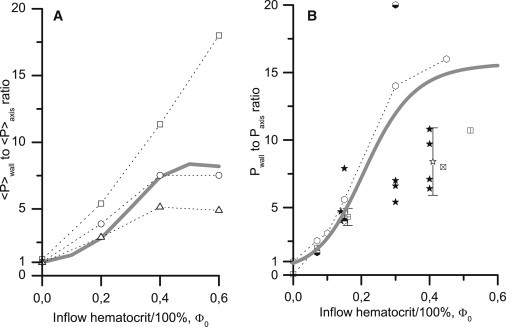
Hematocrit dependence for the NWE of platelets (A) and platelet-modeling particles (B) calculated at p = 3.5, f = 0.06 (lines) and from in vitro experiments (markers). (A) The distributions of OsO₄-fixed platelets in the presence of erythrocyte ghosts were detected using the laser-Doppler velocimetry method in glass tubes of 3 mm internal diameter and averaged over the near-wall and central zones (20), as described in Mathematical Model (see main text). Wall shear rates were 240 s⁻¹ (open triangle), 760 s⁻¹ (open circle), and 1200 s⁻¹ (open square). Fixing the platelets did not change their behavior in the flow. Theoretical calculations used Eqs. 1–3; the calculated platelet profiles were averaged similarly to the experimental profiles. (B) The distributions of platelet-sized particles (2a_P = 2.2 ÷ 2.5 μm) in the presence of washed erythrocytes were obtained by stroboscopic epifluorescence microscopy in Tilles and Eckstein (13) (open hexagon), Eckstein et al. (14) (white and black hexagon), and Eckstein et al. (15) (black and white hexagon) at ${\dot{\gamma }}_w$ = 1630 s⁻¹ and by using the freeze-capture method in Bilsker et al. (16) (crossed box, vertically divided box, quartered box, and horizontally divided box at ${\dot{\gamma }}_w$ = 400, 410, 500, and 900 s⁻¹, respectively), Koleski and Eckstein (17) (solid star, ${\dot{\gamma }}_w$ = 400 s⁻¹) and Yeh et al. (18) (open star, ${\dot{\gamma }}_w$ = 555 s⁻¹; and white and black star, 700 ÷ 900 s⁻¹). The errors are indicated if they were reported in the original studies. At Φ₀ = 0.15 and 0.4, the markers are shifted by ±0.01 to reduce overlapping. Eq. 4 (with Eqs. 2 and 3b) were used for the theoretical calculations.

In previous work (20), NWE values were presented as the percentage of platelets (A%) in the near-wall layer (2/3 ≤ |r| ≤ 1) divided by the diameter-averaged (0 ≤ |r| ≤ 1) value. We converted these percentages into ratios of the mean platelet concentration in the near-wall layer 〈P〉_wall to the mean concentration in the core (|r| ≤ 2/3) of the flow 〈P〉_axis. Note that in Aarts et al. (20), the core is twofold wider than the near-wall layer, and the platelet concentration in the core is uniform. Therefore,

$$A\%\approx \frac{{\langle P\rangle }_{wall}}{{\langle P\rangle }_{wall}+2{\langle P\rangle }_{axis}}·100\%\text{and}\frac{{\langle P\rangle }_{wall}}{{\langle P\rangle }_{axis}}\approx \frac{2A\%}{100\%-A\%}$$

(Fig. 4 A, markers). To calculate the theoretical ${\langle P\rangle }_{wall}/{\langle P\rangle }_{axis}$ ratios, the distribution of the available volume fraction, Φ_a(r), was calculated from Eqs. 2 and 3 at various values of Φ₀. Next, each Φ_a(r) profile was averaged over two near-wall and near-axis regions, and the ratio of these average values was calculated (Fig. 4 A, line).

Redistribution in a flow

Because the platelet shear-induced dispersion coefficient is close or equal to that of erythrocytes (3,8,35), it was taken from the empirical-based dependence proposed by Zydney and Colton (8) for erythrocytes and other deformable particles:

$$D_{\text{ZC}}=k{R}_{RBC}^2·\dot{\gamma }·{\Phi }_{RBC}·{\left(1-{\Phi }_{RBC}\right)}^n.$$ (5)

Here, R_RBC is the major erythrocyte radius; $\dot{\gamma }$ is a local shear rate (s⁻¹); Φ_RBC is the local erythrocyte volume fraction; ${kR}_{RBC}^2=2.646{\mu \mathrm{m}}^2$; and n = 0.8. Brownian diffusion was neglected. The dependence in Eq. 5 was established for lateral shear-induced dispersion; nevertheless, herein, it is also prescribed for axial dispersion. First, shear-induced dispersion coefficients are of the same order in different directions (36). Second, the precise value of the axial dispersion coefficient is of low importance because platelet transport in this direction is convection-dominated (at tube radius R₀ = 100 μm and Ф_RBC = 0.5 R₀U/D_ZC ∼ 10⁴, where U is an average flow velocity) (37). Accounting for the nonuniform distribution of the available volume fraction, the expression for the dispersive particle flux has the following form (see the Supporting Material):

$$N=-D_{ZC}·gradP+P·D_{ZC}·\frac{grad{\Phi }_a}{{\Phi }_a}=-{\Phi }_a·D_{ZC}·grad\frac{P}{{\Phi }_a}.$$ (6)

For the stationary case, this expression reduces to Eq. 1.

To simulate transient lateral migration of an individual particle across the flow under the conditions used in Goldsmith (3), the probability density of finding a particle at a given radial position and time was found by solving the following equation:

$$\frac{d}{dt}p=-\left(\frac{\partial }{\partial r}+\frac{1}{r}\right)N_r.$$ (7)

Here, the probability flux $N_r=-{\Phi }_a\cdot D_r\cdot \partial /\partial r(p/{\Phi }_a)$ corresponds to Eq. 6 by substituting the concentration P with the probability density p (34,38,39). This one-dimensional treatment is possible by the fact that a single particle in steady flow experiences lateral forces that are independent of the axial coordinate. In Eq. 7, r is nondimensionalized by the tube radius R₀; t is nondimensionalized by the characteristic time of the migration of the particle from r ∼ 0.5 to r ∼ 1, t₀; $D_r=D_{ZC}·t_0/R_0^2$. This equation was solved on the segment r ∈ [0,1]. The initial condition was p(r)_{t = 0} = 1, which corresponds to a uniform probability distribution; the boundary conditions were N_r |_{r = 0,1} = 0.

To simulate particle redistribution dynamics in a suspension that is flowing through a tube under the conditions used in Yeh and Eckstein (19), the concentration of particles was determined by solving the following equation:

$$\frac{\partial }{\partial t}P+u\frac{\partial }{\partial x}P=-\left(\frac{\partial }{\partial r}+\frac{1}{r}\right)N_r-\frac{\partial }{\partial x}{N}_x.$$ (8)

In this equation, $N_r=-{\Phi }_a·D_r·\partial /\partial r(P/{\Phi }_a)$, $N_x=-{\Phi }_a·D_x·\partial /\partial x(P/{\Phi }_a)$; P is nondimensionalized by the inflow concentration P₀; the axial coordinate x is nondimensionalized by the axial path of the particle-containing suspension between switching and freezing, L₀; and the velocity u is nondimensionalized by the axial velocity $u_0={\dot{\gamma }}_w{R}_0/2,$ t – by $L_0/u_0$. The dimensionless dispersion coefficients in the x and r directions are $D_x=2D_{ZC}/\left({\dot{\gamma }}_w{R}_0{L}_0\right)$ and $D_r=D_x\cdot {\left(L_0/R_0\right)}^2$, respectively.

Equation 8 was solved in the rectangle [0 ≤ x ≤ 1.1] × [0 ≤ r ≤ 1] using the initial condition P(x,r) _{t = 0} = 0, inflow condition P(r) _{x = 0} = 1, and remaining boundary conditions N_r |_{r = 0,1} = 0, N_x |_{x = 1.1} = 0. The velocity profile was assumed to be parabolic, and the corresponding shear rate profile was assumed to be linear in Eqs. 7 and 8.

Numerical methods

Direct simulations at the level of distinct particles were performed to find the dependence Φ_a (Φ_RBC) while varying Φ_RBC and a_P (see the Supporting Material). In short, a cube with edge L represented the microvolume containing randomly located and oriented erythrocytes with a total volume fraction Φ_RBC. The shape of each erythrocyte in the local coordinates (x, y, z) satisfied the equation

$${\left(\frac{z}{c·g\left(r_1\right)}\right)}^2+r_1^2=1,$$ (9)

which approximates the real shape of a human erythrocyte (40,41). Here, $r_1^2=(x^2+y^2)/R_{RBC}^2$, $g\left(r_1\right)=1+g_2{r}_1^2+g_4{r}_1^4$, g₂ = 9.66, g₄ = −5.43, c = 0.405 μm, and R_RBC = 3.91 μm. The simulations consisted of multiple, random positions for the test sphere with radius a_P in this cube. The fraction of the available volume was calculated as the ratio of the number of times that the test sphere was positioned between erythrocytes (without intersecting either the cube or their borders) to the total number of attempts M. The parameters L and M were sufficiently large (L = 50 μm, M = L³/1 μm³) such that they would not influence the results. This method was verified by comparing the results with analytical estimates at either a_P << c or g = 1 (see Fig. S5 in the Supporting Material). In the first case, Φ_a ≈ 1 − Φ_RBC. In the second case, the initial decline of the Φ_a (Φ_RBC) dependence was obtained from the volumes of the erythrocyte and surrounding layer of a thickness a_P. Erythrocyte aggregation was not considered in these direct simulations because 1), erythrocytes did not aggregate in the experiments (3,13–20) that were used for a comparison with the model results; 2), rouleaux form at shear rates that are ∼50 1/s and below (7), but NWE occurs above ∼200 s⁻¹ (13,14); and 3), there are no conclusive experimental data on the influence of erythrocyte aggregation on platelet NWE (42).

Equations 7 and 8 were solved numerically with the COMSOL 3.2a software package (http://www.scientificcomputing.com/comsol-multiphysics-3-2a.aspx) using the finite element method with second-order Lagrangian elements. The relative tolerance was 0.1%; the maximum element size was 0.008 and 0.02, respectively.

Results

The finite size of platelets reduces the available volume fraction

We first examined the hypothesis that the finite size of the platelets reduces the available volume fraction relative to the total intererythrocyte volume fraction (33). We substituted spheres with a radius a_P for platelets and calculated the dependence Φ_a(Φ_RBC) at various values of a_P using direct numerical simulations. With increasing Φ_RBC, the Φ_a values decreased more rapidly than 1 − Φ_RBC (Fig. 2 A, markers); the slope increased with increasing a_P. These results were interpolated using an analytical formula, Eq. 2, with f = 0 (solid lines). The p(a_P) dependence appears to be close to exponential (Fig. 2 B). Microspheres with an ∼1.25-μm radius were used as platelet substitutes in the majority of the in vitro nonuniform platelet distribution studies (13–19,22,23); twice this value is 2.5 μm, which is the intermediate value between the platelet length and thickness. Thus, for comparison with experimental data, we set p = exp(1.25) = 3.5.

The limitation of our direct simulations is that the erythrocytes are considered solid and fixed in space. Thus, we could not generate a hematocrit above ∼30% because it would require erythrocyte deformation or/and reorientation. Therefore, it is not entirely valid to extrapolate the Φ_a(Φ_RBC) curves to higher hematocrits. We expect that, at high hematocrit values, the available volume fraction is slightly larger than that predicted by the extrapolation of the curves plotted at f = 0 (dashed lines). We believe that this is the case because erythrocytes can be ordered, even in the absence of aggregation, or deformed when they are densely packed in the flow core (4,5,7). Under such conditions, some particles could be placed even between erythrocytes that are spaced smaller than 2a_P. Therefore, it should be expected that f > 0 (in Fig. 2 A, dotted line corresponds to f = 0.1). In the next two sections, we show that the near-wall platelet concentration has a relatively small sensitivity to f, and for agreement with the NWE experimental data, one should assume that f is approximately several percent values, i.e., f < 0.1.

A nonuniform platelet distribution may primarily originate from the excluded-and-available-volumes effect

We qualitatively examined the impact of the excluded-and-available-volumes effect on the nonuniformity of the platelet distribution across the flow and its relative dependence on p and f. We calculated the platelet concentration profiles at a fixed erythrocyte distribution for several sets of p- and f-values (Fig. 3). Increasing p leads to a considerable increase in platelet displacement from the core of the flow to the walls (Fig. 3 A). The general profile shapes agree with all known NWE studies on platelets and their analogs (10–23): the near-wall layer is strongly enriched, and the central region is depleted of particles. The influence of the f-value on the profile shape is shown in Fig. 3 B. As f increases, the particle distribution becomes slightly more uniform. The platelet near-wall concentration is much less influenced by f than by p, and f has greater influence on the near-axial than on the near-wall concentration. Thus, the excluded-and-available-volumes effect could be responsible for the near-wall layer margination, and the magnitude of this effect is primarily determined by particle size (defining the p-value).

Figure 3.

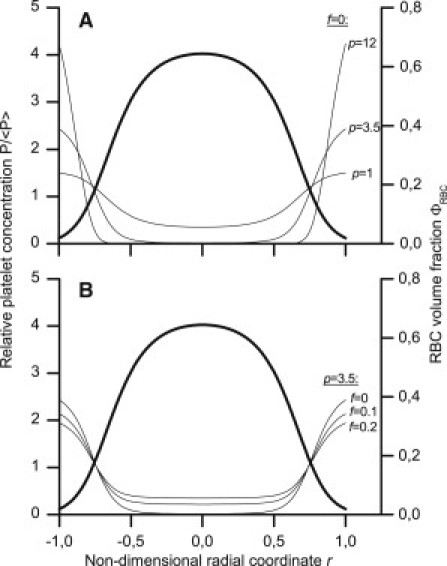
Lateral platelet distribution (thin lines, left axes) calculated using Eqs. 1 and 2 at various values of the parameters p (A) and f (B). The erythrocyte volume fraction distribution (thick curves, right axes) was assigned using Eq. 3 with Φ₀ = 0.4.

The hematocrit dependence of NWE

In Fig. 4 we present a quantitative comparison of the theoretical (lines, f = 0.06) and experimental NWE levels (markers) at various inflow hematocrits. The study from Sixma's group (20), Fig. 4 A, presents unique simultaneous measurements for both erythrocyte and platelet lateral distributions. Because the tube diameter was 3 mm, erythrocyte ghosts were used; earlier studies have shown that the flow behavior of erythrocytes and their ghosts are essentially alike and that ghosts are good physical analogs of erythrocytes in flow (5,43). The conditions in the studies from Eckstein's group (13–18), Fig. 4 B, were more physiological; the tube diameters and channel heights were 50–220 μm, and the erythrocytes were washed but intact (not lysed). However, erythrocyte distributions were not measured in these studies. Thus, NWE was calculated from the erythrocyte distribution profiles (Fig. 4 A) and from the dependence Φ_m(Φ₀) taken from Aarts et al. (20) (Fig. 4 B).

The model predictions in Fig. 4 agree with the experimental NWE growth as the hematocrit increases. This growth begins at 1 (no excess) with Φ_RBC = 0 and is sigmoidal. The theoretical curve differences shown in Fig. 4, A and B, are from the different NWE calculation methods, which reproduced the different methods of treatment of the experimental data. The agreement on a NWE hematocrit dependence confirms that the excluded volume gradient in flowing blood is sufficient to produce a strong NWE in platelets. Nevertheless, experimental data also show a shear rate influence on NWE (Fig. 4 A). Although this behavior can be described by assuming that f has a monotonically decreasing dependence on shear rate (not shown), a detailed investigation of this dependence mechanism is a subject of future work.

Transient lateral transport in a gradient of available volume fraction

The above steady-state calculations and Eq. 6 show that the available volume fraction gradient may be the primary origin of “rheological potential”, which has been proposed by Eckstein to describe nonuniform platelet distribution (14,18,34). To address this issue for transient platelet distribution, we performed calculations to simulate the platelet redistribution process. Fig. 5 A shows the trajectories of individual platelet-modeling spheres in a moving erythrocyte ghost suspension recorded by Goldsmith (3). The spheres undergo frequent, random changes in the direction of radial movement and gradually migrate toward the flow periphery. Fig. 5 B shows the calculated radial distributions of a probability density for the location of a sphere at successive instants if at time 0 its location is equally probable everywhere. Over time, the probability that the sphere is located in a near-wall region increases and the probability that it is in a near-axial region decreases, in accordance with experimental data.

Figure 5.

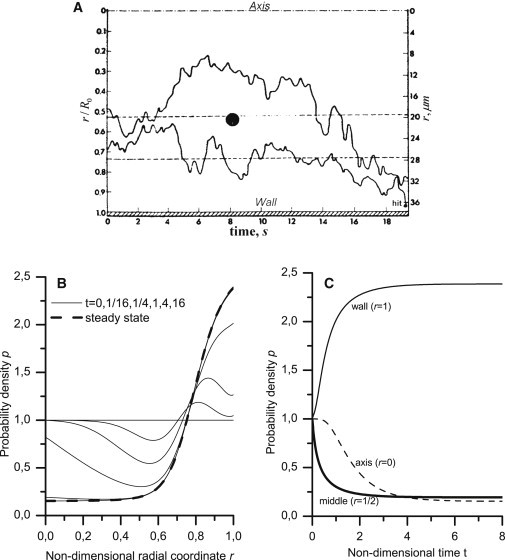
Migration of a individual platelet-modeling sphere across the flow. (A) The experimental paths for two latex spheres with a 2-μm diameter in a erythrocyte ghost suspension that flows through a tube with a radius R₀ = 38.25 μm (3). (Upper bound) Flow axis; (bottom bound) tube wall. The erythrocyte volume fraction at the inflow was Φ₀ = 0.44, and the wall shear rate was 16 s⁻¹. (B) The radial distribution of the probability density was calculated using Eq. 7 (with Eqs. 2, 3, 5, and 6) at successive time points (solid lines). The tube radius, wall shear rate, and hematocrit corresponded to the experimental conditions; p- and f-values were the same as in Fig. 4, and t₀ was set to 20 s. The steady-state profile was calculated using Eq. 1 and is shown (dashed line). (C) Time dependence of the probability density at r = 0, 1/2, and 1. The characteristic times for the change in probability density (0.37 and 0.78 for r = 1/2 and 1, respectively) were determined from the decrease in $\left(p-p_{t\to \infty }/1-p_{t\to \infty }\right)$ values by a factor of e.

We could only approximately compare the redistribution times, as the data for two particles are statistically insufficient to extract an exact value for characteristic migration time. The migration time for a sphere from a point that is midway between the wall and the axis to the wall is ∼20 s (Fig. 5 A). Because the diffusion/dispersion time is proportional to the square of the distance, the time required to fully redistribute the spheres across the flow can be estimated to be of ∼2² · 20 s = 80 s. In the calculations, the characteristic times for the change in probability density at r = 1/2 and r = 1 were ∼0.37 · t₀ = 7.4 s and 0.78 · t₀ ≈ 16 s, respectively (Fig. 5 C, solid lines). The full redistribution time was (3 ÷ 5) · t₀ = 60 ÷ 100 s (Fig. 5 C, all lines). These values agree with the estimated experimental values.

The transient process of the formation of the nonuniform distribution of platelet-modeling spheres in the flow of a suspension of washed erythrocytes was studied in Yeh and Eckstein (19). The particle distribution profiles across the flow were measured a short time after switching the flow source from a reservoir without spheres to a sphere-containing reservoir. Fig. 6 shows the experimental (Fig. 6 A) and calculated particle distribution profiles for these conditions (Fig. 6 B). Both in theory and empirically, the greatest near-wall region margination occurs in the section closest to the inflow point (solid lines); margination in the more distant section was smaller (dashed lines); and margination was almost absent in the most distant section (dotted lines). The experimental and calculated profiles were qualitatively similar. As discussed below, quantitative discrepancies could be caused by uncertainties in the distribution of the erythrocyte volume fraction, flow velocity, and shear rate.

Figure 6.

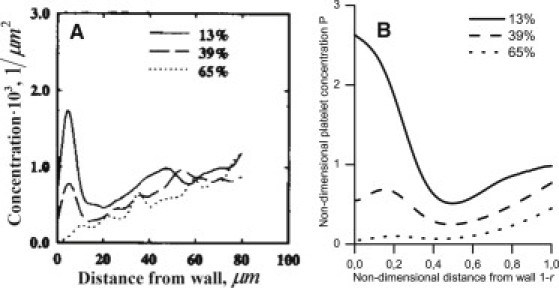
Radial distribution of the platelet-modeling spheres that are 2.5 μm in diameter from experiment (A) and the calculated result (B) at various distances from the tube entrance. (A) The steady-state erythrocyte distribution was established at the beginning of each experiment (19). Next, the flow source was switched to a similar erythrocyte-containing reservoir with a small added mix of spheres. After a few seconds, the flow was rapidly frozen, and the radial profiles for the sphere distribution (spheres/μm²) were measured using fluorescence microscopy. The profiles from a few separate trials were averaged. The axial coordinates for the cross sections are presented as a percentage of the length of an ideal paraboloid that contains spheres at any given time. This length was L₀ = 40 μm; the tube length was 50 μm; the tube radius was R₀ = 110 μm; and the hematocrit was 40%. (B) The calculation was performed using Eq. 8 (with Eqs. 2, 3, 5, and 6) at Φ₀ = 0.4; the p- and f-values were the same as in Fig. 4.

Discussion

This work explores the influence of the finite size of platelets on the nonuniformity of their distribution across blood flow. More then 30 years ago, Blackshear et al. (33) proposed that platelets evenly distribute themselves between erythrocytes and that the finite size of the platelets favors their expulsion from a region of high local hematocrit (i.e., flow core) to a region of low local hematocrit (i.e., near-wall zone). Our mathematical formalization of this hypothesis uses the concept of the available volume (Eqs. 1 and 6). Away from the wall, the local hematocrit increases, which leads to a rapid decrease in the available volume fraction (Fig. 1). This decrease is much stronger than the decrease in the intererythrocyte volume fraction 1 − Φ_RBC (Fig. 2 A). Without invoking the influence of finite platelet size on platelet distribution, assuming that the platelet concentration is simply proportional to 1 − Φ_RBC, it is possible to explain a value of no more than 2.5 for NWE at a normal average hematocrit (40%). This estimation assumes that the hematocrit is zero at the walls and is 60% along the axis (20,27):

$$\frac{P_{wall}}{P_{axis}}\approx \frac{1-{\Phi }_{RBC,wall}}{1-{\Phi }_{RBC,axis}}\approx \frac{1}{1-\frac{60\%}{100\%}}=2.5.$$

The available-volume hypothesis was doubted by Eckstein, mainly due to complexity of its testing and specifically due to difficulties in the calculation of Φ_a at high values of Φ_RBC (14,18,34). In his studies, he proposed an alternative hypothesis, a “rheological potential”, which drives platelets to the walls. However, the mechanism for the origin of this potential remained poorly understood. The study herein shows that these two hypotheses are not strictly contradictory. In particular, Eq. 6 is in drift-flux form, and the drift velocity is given by $D_{ZC}·grad{\Phi }_a/{\Phi }_a$. Thus, a nonuniform Φ_a distribution may be the primary origin for “rheological potential”. Results from recent, direct numerical blood motion simulations in a periodic channel support this conclusion, in general (35). However, in addition to the excluded volume effect, platelet drift may be influenced by other factors; for example, platelet-erythrocyte collisions near walls (35,44).

In this study, we aimed to answer the following two primary questions: whether the available volume effect can produce the empirically observed increase in near-wall platelet concentration, and, if so, how do the results depend on different parameters that can be varied in the theoretical model?

We answered the first question in the affirmative using our model (Figs. 3–6). Figs. 3 and 4 show that platelet size (which determines the model p-value) and hematocrit level have the strongest influence on platelet drift. For quantitative agreement between theoretical and experimental NWE values (Fig. 4), the f-value should be equal to several percent values. The value f indicates the fraction of available volume in the core of the flow and has a very weak influence on the near-wall concentration, P_wall, of the platelets (Fig. 3 B).

According to experimental data in Aarts et al. (20), the NWE gradually increases with shear rate in the range 240–1200 s⁻¹ (Fig. 4 A). In other studies, this increase differs; the margination effect either switched itself on when the shear rate was in the range 210–430 s⁻¹ (13) or increased gradually to ∼400 s⁻¹ (45). In both of these studies, a further increase in shear rate had no effect. NWE growth with increasing shear rate is consistent with an early proposal by Blackshear et al. (33) that at sufficiently high hematocrit, shear rate increase results in decrease in the available volume fraction. Currently, we cannot conclusively prove or reject this proposal, as shear flow was not accounted for in our stochastic simulations.

We suggest that a decrease in Φ_a with increasing ${\dot{\gamma }}_w$ may result from an increase in erythrocyte random motion. Frequent random motions force erythrocytes to sweep up more volume in each unit of time, increasing the effective width of the excluded volume layer that surrounds each erythrocyte. In addition, random motions force erythrocytes to spend less time in dense contact and become more spaced apart, reducing the overlap in the excluded volume layers surrounding neighboring erythrocytes. Both mechanisms increase the total excluded volume fraction Φ_ex and reduce Φ_a. Therefore, the growth of the NWE with increasing shear rate, which has been observed in a number of studies (13–15,20,45), may be explained by a reduction in the fraction of the available volume between erythrocytes.

It was impossible to quantitatively reproduce all of the experimental data, perhaps due to limitations in the experiments. In the experimental observations, the particle distribution profiles are very steep; thus, their measurement and analysis are subject to large errors. The majority of the empirical studies do not include error estimates, and the published errors are quite large (Fig. 4, A and B). In addition, all of the studies, except for Aarts et al. (20), fail to report the erythrocyte distribution. Therefore, in simulations of these experiments (conducted in capillaries of 80–220 μm in diameter), the Φ_m(Φ₀) dependence (Fig. 4 B) and erythrocyte distribution (Figs. 5 and 6) were assumed to be similar to that reported in Aarts et al. (20) (measured in 3-mm-diameter tubes). The qualitative acceptability of this approach is confirmed by the essential similarity of the latter distribution and the distribution obtained in vivo (27) in a 40-μm frog arteriole (see Fig. S1 B).

The greatest empirical and theoretical discrepancy is apparent in the transient profiles for the platelet-modeling particle distribution (Fig. 6). Compared with the experimental data, the theoretical distributions are 1), wider with a lower slope in the near-wall zone and 2), vary more strongly between the cross sections in the near-axial zone. The first distinction may result from a slightly lower slope of the near-wall erythrocyte distribution in the model than what actually existed in the experiment. Due to the strong dependence Φ_a(Φ_RBC) (Fig. 2 A), even small differences in the steepness of the Φ_RBC(r) distribution could lead to major changes in the Φ_a(r) distribution. The second distinction is most likely due to the neglected difference between the velocity distribution and the parabolic distribution used in the model. This difference exists both in the blood and in a suspension of washed erythrocytes (4,7) and leads to a low value of shear rate in a substantial part of the near-axial zone (far from the walls) (28). According to Eqs. 5 and 6, the smaller the shear rate, the smaller the local rate of radial redistribution. Fig. 6 A supports this conclusion. In the model, the shear rate deviates appreciably from zero in the greater part of the cross section, and the particles are removed from the near-axial zone more quickly than they are in the experiment.

In summary, our study does not provide a final answer to the question of what causes the platelet margination phenomenon. However, it justifies the possibility that the main contributor toward the origin of this phenomenon may be the excluded-and-available-volumes effect.