Abstract
Blood coagulation is triggered not only by surface tissue factor (TF) density but also by surface TF distribution. We investigated recognition of surface TF distribution patterns during blood coagulation and identified the underlying molecular mechanisms. For these investigations, we employed 1), an in vitro reaction-diffusion experimental model of coagulation; and 2), numerical simulations using a mathematical model of coagulation in a three-dimensional space. When TF was uniformly immobilized over the activating surface, the clotting initiation time in normal plasma increased from 4 min to >120 min, with a decrease in TF density from 100 to 0.7 pmol/m2. In contrast, surface-immobilized fibroblasts initiated clotting within 3–7 min, independently of fibroblast quantity and despite a change in average surface TF density from 0.5 to 130 pmol/m2. Experiments using factor V-, VII-, and VIII-deficient plasma and computer simulations demonstrated that different responses to these two TF distributions are caused by two positive feedback loops in the blood coagulation network: activation of the TF–VII complex by factor Xa, and activation of factor V by thrombin. This finding suggests a new role for these reactions: to supply sensitivity to local TF density during blood coagulation.
Introduction
Blood coagulation is activated upon vessel wall injury from the contact of blood with the transmembrane glycoprotein tissue factor (TF) that is exposed on almost all extravascular cells. TF can also be expressed on endothelial or immune cells during certain pathological processes, such as inflammation (1). This contact leads to the formation of the extrinsic tenase complex between TF and the circulating activated factor VII (fVIIa), which can activate factor X (fX) and begin the blood coagulation reaction cascade. Clotting initiation is tightly regulated by a complex mechanism: fVIIa initially accounts for only 1% of the fVII that is activated in a feedback loop by the fXa and fIIa produced during coagulation (2).
Although many well-established in vitro experimental coagulation models predominantly employ TF homogeneously distributed throughout the reaction volume (3,4), both physiological and pathological coagulation processes in vivo are likely often activated by TF-expressing cell layers (5,6). The size of the activating region can vary greatly, from a single TF-expressing cell to a monolayer that is several centimeters wide, and the same is true for TF density within this region. Reported physiological TF densities range from <1 molecule/μm2 on endothelial cells in culture (approximated from previous studies (7,8)) to ∼5 molecules/μm2 in vivo underneath atherosclerotic plaques (9,10) and ∼100 molecules/μm2 on fibroblasts (7). For investigations in basic research, pharmacology, diagnostics, and clinical treatment of blood coagulation, it is critical to understand how clotting is regulated depending on the density and distribution of the activator.
The coagulation system's response to TF exposure is known to depend in a trigger-like manner on either surface TF density (10) or concentration (11). Density and TF distribution appear to be critical. Clotting is initiated in plasma only when the TF-exposed region exceeds a threshold size (12). Curiously, clotting was also reported to depend on the shape of the activating region: although a narrow rectangular or star-shaped patch of TF does not activate plasma clotting, a circle with the same area and TF density does (13). Furthermore, our previous report (14) showed that confluent cell monolayers with varying TF expression levels activate coagulation differently. Interestingly, in the same experimental system, no difference was observed for clotting in normal plasma activated by fibroblast monolayers with cell densities of 2 or 1000 cells/mm2 (6).
The molecular mechanisms that control the surface TF density threshold and are responsible for recognition of the activating patch size and/or shape remain unclear. Certain mathematical models suggest that positive feedback loops (activation of the top factors in the cascade by the enzymes that occupy the bottom positions) might be responsible for providing a simple cascade system with a trigger-like dependence on activator density and patch size (12,15–17). The critical role of factor V in feedback activation by thrombin for triggering homogeneous coagulation was recently demonstrated experimentally (11).
To investigate how coagulation depends on surface TF density and distribution, and identify the mechanisms of this regulation, we used two different patterns of clotting activation: TF-expressing cells and uniformly distributed surface-immobilized TF (Fig. 1). For both experimental designs, the average surface TF density varied by two orders of magnitude. Experiments in normal plasma and fV-, fVII-, and fVIII-deficient plasma, using a reaction-diffusion in vitro experimental model, were performed with computer simulations that employed a detailed three-dimensional (3D) mathematical model of blood coagulation. Clot formation was controlled by local, small-scale TF density; for example, highly procoagulant fibroblasts rapidly activated clotting independently of the average surface TF density. This sensitivity to TF density was controlled by two positive feedback loops: activation of the TF-VII complex by fXa, and activation of fV by thrombin.
Figure 1.
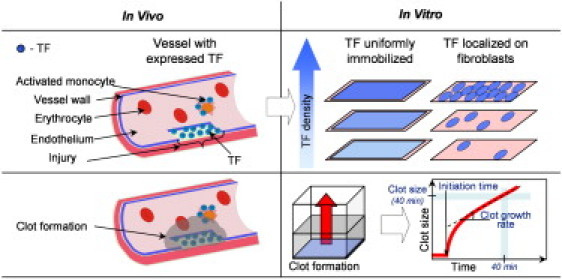
Blood clotting activation on TF-expressing surfaces in a vessel (in vivo) and in a reaction-diffusion experimental model (in vitro). Under normal conditions, TF is expressed by subendothelial cells only. In many pathological conditions, such as inflammation and cancer, TF can also appear on the surface of blood cells and endothelial cells, either isolated or in monolayers. TF density varies over a wide range. By analogy, coagulation in the in vitro model system used herein was activated by films with either uniformly distributed TF or TF-bearing cells. In both cases, the average surface TF density varied over two orders of magnitude. Spatial clot growth was recorded by means of light scattering. Initiation times, clot growth rates, and clot sizes after 40 min were determined as shown.
Materials and Methods
Proteins
The following materials were purchased from the sources shown in parentheses: human fVa, fV, fIXa, thrombin, and RVV-V activator (Haematologic Technologies, Essex Junction, VT); recombinant factor VIIa and NovoSeven (Novo Nordisk, Copenhagen, Denmark); human fVIII (Hemophil M, Baxter Russia, Moscow, Russia); EDTA (Helicon, Moscow, Russia); PPACK (Calbiochem, Darmstadt, Germany); fXa-specific chromogenic substrate S2765 (Chromogenix, Milano, Italy); and human prothrombin and fXa (Enzyme Research Laboratories, South Bend, IN). The thrombin-specific chromogenic substrate, Gly-Pro-Arg-NA, was synthesized in the Russian Cardiology Research and Production Complex of Ministry of Health Care and Social Development (Moscow, Russia). The specific fXIIa inhibitor, corn trypsin inhibitor (CTI), was prepared from corn seeds as described previously (18). Phospholipid (PL) vesicles were prepared by extrusion from phosphatidylcholine and phosphatidylserine (Avanti, Alabaster, AL) at a molar ratio of 7:3, as described previously (19).
Plasma preparation
Normal plasma was prepared from the whole blood of healthy volunteers and collected with the approval of the ethics committees of the Center for Theoretical Problems of Physicochemical Pharmacology and the National Research Center for Hematology. Blood was drawn into 3.8% sodium citrate (pH 5.5) at a 9:1 blood/anticoagulant volume ratio and supplemented with CTI at a 0.2 mg/ml final concentration to inhibit contact activation. A routine protocol was used to obtain plasma with stable and reproducible procoagulant lipid content. Blood was centrifuged at 1600 × g for 15 min, and the supernatant was collected and centrifuged again at 10,000 × g for 5 min to obtain platelet-free plasma, which was lactate-treated to stabilize the pH at 7.2–7.4 (6). fV-, fVII-, and fVIII-deficient plasma (George King Bio-Medical, Overland Park, KS) was thawed in a 37°C water bath, supplemented with CTI, incubated at room temperature for 4 h to inhibit the enzymes formed from cold-promoted activation (14), and then processed as normal plasma.
Preparation of the fibroblast films
A human fetal lung fibroblast line was obtained from the Ivanovskii Research Institute of Virology (Moscow, Russia). The films were prepared as described previously (6). A detailed description is available in the Supporting Material.
TF immobilization on the films
TF was biotinylated and immobilized on films with covalently bound streptavidin (SAM2 Biotin Capture Membrane, Promega, Madison, WI). A detailed description is available in the Supporting Material.
Assembly of intrinsic tenase on films with immobilized TF or fibroblasts
The ability of the TF-bearing films to provide binding sites for the intrinsic tenase was evaluated based on their acceleration of fX activation. A mixture with TF-bearing films, fIXa, fVIIIa (prepared immediately), and fX was used. We evaluated fXa activity using the rate of S2765 hydrolysis as measured by absorbance at 405 nm using a Thermomax microplate reader (Molecular Devices, Sunnyvale, CA). A detailed description is available in the Supporting Material.
Assembly of prothrombinase on films with immobilized TF or fibroblasts
To evaluate prothrombinase-supporting activity, we prepared a mixture of TF-bearing films, fXa, RVV-V activated fV, and prothrombin. We evaluated thrombin activity using the rate of Gly-Pro-Arg-NA hydrolysis as measured with a Thermomax reader. A detailed description is available in the Supporting Material.
Spatial clot growth in the reaction-diffusion system and image processing
We studied spatial fibrin clot formation using a light-scattering videomicroscopy system, and determined the parameters of spatial clot formation from the experimental image series as described previously (6). The initiation time for clot formation was defined as the time interval required for the mean light-scattering intensity near the activator to reach the half-maximum value for a clot activated by the film with the maximum TF density. For each frame, the clot size was determined as the distance between the activation film and the edge of the clot (the clot edge was defined as the point where the light-scattering intensity is equal to the half-maximum value for a clot activated by the film with the maximum TF density). The rate of clot growth was derived from the clot size versus time curve as a mean rate within the range of 10–40 min after the onset of clotting (Fig. 1). The clot size after 40 min from the beginning of clot activation was also registered. A detailed description is available in the Supporting Material.
Computer simulations
We performed computer simulations of blood clotting using a detailed mechanism-driven mathematical clotting model in a 3D reaction-diffusion system. The model was based on another model that was developed earlier by our group (11,20,21). The reaction kinetics was described by a set of partial differential equations. All model constants were taken from the experimental reports without adjustment. The 3D equation system was solved using finite element method software (COMSOL Multiphysics, Comsol, Burlington, MA). The model was biphasic, i.e., reactions took place both at the surface with TF and in the plasma volume. The activator was located on the bottom surface as uniformly distributed TF or TF spots (see Fig. S1, A and B, in the Supporting Material). Clotting parameters were calculated from fibrin concentrations based on the assumption that the fibrin concentration is proportional to light scattering (14), as an average fibrin concentration across the surface corresponds better to the spatial experiments. The average fibrin concentration was calculated as the mean concentration at some distance from the surface and treated as a light-scattering profile. A detailed description of the model is provided in Fig. S1.
Results
Clot formation as a function of surface TF density
To investigate clotting regulation by TF density, we activated coagulation in plasma by TFs that were uniformly immobilized on films at densities from 0.7 to 107 pmol/m2. Fig. 2 A shows pictures that are typical of clots formed upon activation with 96 and 6 pmol/m2 TF density at 5 and 50 min from the beginning of the experiment. A comparison of light-scattering profiles showed that clot structure depended on TF density. The clots growing from the films with high TF densities (30–107 pmol/m2) had steep fronts (Fig. 2 B, top, and Fig. S6) and propagated into plasma without changing shape. Light-scattering intensity was proportional to fibrin concentration (14), and thus one can conclude that fibrin density remained constant within these clots. With a decrease in TF density, light-scattering profiles became diffusive; there was neither a steep front nor a plateau (Fig. 2 B, bottom).
Figure 2.
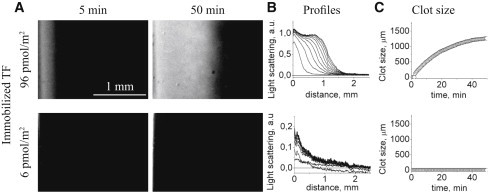
Effect of uniformly immobilized TF on fibrin clot growth in normal plasma depends on the TF density. Typical experimental results for platelet-free plasma coagulation activated by TF at 96 and 6 pmol/m2 are shown. (A) Images of fibrin clots for different TF densities as registered by light scattering are shown. Clotting was performed in thin layers of plasma from healthy donors. The activating surface was located on the vertical wall of the experimental chamber and is shown as a vertical stripe at the left end of each image. During the experiment (2 h), large fibrin clots were formed on the films with high TF densities, but no clot formation was detected with the lowest TF density. For lower TF densities, clot formation was delayed and clot size was smaller. (B) Corresponding profiles of clot growth (note the different scales). Each curve (profile) corresponds to a different time point during clot growth; the left and lowest curve corresponds to 5 min after recalcification, and the subsequent curves are separated by 5-min intervals. As the clot grows and increases in size, the curves shift upward (implying that the clot becomes denser) and to the right (the clot becomes larger). The first 50 min are shown. (C) Clot size as a function of time. The plots were obtained using the series of profiles shown in panel B.
The parameters for clot growth were determined for the entire range of TF densities. We found that the initiation time dramatically depended on TF density and steadily decreased with an increase in TF density (Fig. 3 A). For TF densities below 1.4 pmol/m2, clots did not form for at least 2 h. Differences in initiation time values were up to 30-fold within the experimental range of TF densities. The clot growth rate decreased with a decrease in TF density (Fig. 3 B). Clot growth rate decreased ∼2-fold for a TF density decrease from 107 to 5 pmol/m2. An initiation time increase with a clot growth rate decrease led to a dramatic clot-size dependence on activator density (Fig. 3 C).
Figure 3.
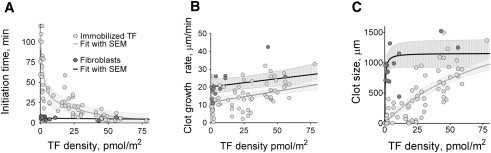
Clotting activation by fibroblasts was independent of their density, whereas clot formation by uniformly immobilized activators was sensitive to TF density. Initiation time (A), clot growth rate (B), and clot size after 40 min (C) are plotted as functions of average TF density for uniformly distributed TF (solid gray circles) and TF-expressing cells (solid dark gray circles). Normal plasma from 23 donors was used. For data approximation, the mathematical functions used were a second-order exponential (A), hyperbolic (B), and hyperbolic plus linear (C). Approximation curves are supplemented with the corresponding mean ± SE.
Thus, throughout the experiment, large fibrin clots were formed on the films with high TF densities, but no clot formation was detected for those with the smallest TF densities. With lower TF densities, delayed clot formation and smaller clot sizes were observed. Thus, clotting is highly sensitive to changes in the density of TF that is uniformly distributed on a surface. We also sought to determine whether the behavior of the clotting system changes when the same quantity of TF is redistributed nonuniformly on a surface as localized spots.
A single fibroblast is sufficient to activate clotting
We investigated how the density of TF-expressing cells influences blood-clotting activation. Films with cell densities ranging from 10 to 1000 cells/mm2 were used. This range of cell densities included both dense fibroblast monolayers and sparsely distributed cells (Fig. S8). Using films with extremely low cell densities, we can study how single cells activate clotting. The maximal distance between adjacent cells was 300 μm, and cell size was 71 × 11 μm. Thus, clots were formed by individual cells.
Average TF densities for fibroblast-containing films ranged by two orders of magnitude, from 0.5 to 135 pmol/m2, and overlapped with the corresponding range of TF densities for uniformly distributed TF.
In contrast to experiments with uniformly distributed TF, clot formation activated with TF-expressing cells mostly did not depend on the average TF density throughout the entire TF density range. Initiation times and clot growth rates had only a weak dependence on average TF density. Initiation time increased only twofold when the average TF density was decreased by two orders of magnitude (Fig. 3 A). A slight decrease in clot growth rate was observed, although it was smaller than in experiments with TFs that were uniformly immobilized on a surface (Fig. 3 B). Clots propagated from films with cells, and after 40 min, the clot size was >700 μm in all experiments (Fig. 3 C).
We controlled the activity of the TF-VIIa complex on films with both immobilized thromboplastin and fibroblasts using a functional assay. This result suggests that the experimentally observed differences in clot formation parameters were not caused by differences in the TF source but by the TF distribution. Thus, the process of clot activation using the same TF quantities dramatically depends on TF presentation on the surface. Clotting is initiated quickly, and the clot grows rapidly upon activation with fibroblasts throughout the entire range of TF densities.
Model design
Thus far, we have discussed two effects: 1), the trigger-like dependence of blood plasma clotting initiation time on the density of the TF uniformly distributed over a surface; and 2), the independence of initiation time on average TF density over the same density range for fibroblasts. To test whether these results can be explained by differences in TF distribution only, and propose hypotheses that explain such results, we used a mathematical model. We performed computer simulations of blood clotting using a mathematical clotting model in a reaction-diffusion system (see Supporting Material for details). The principal equation scheme is shown in Fig. 4 A. The reaction kinetics was described by a set of differential equations.
Figure 4.
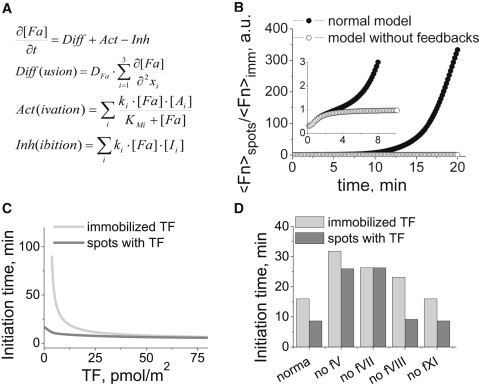
fV activation by thrombin and fVII activation by fXa are essential for clotting system recognition of the local TF concentration. A detailed mechanism-driven mathematical model was used. (A) General equations (F, factor; A, activator; I, inhibitor; t, time; x, spatial coordinate). (B) The ratio of total fibrin generated upon clotting activation by spotted TF to that generated upon stimulation with the same quantity of uniformly distributed TF in the models with and without feedback loops. (C) Dependence of the initiation time on the average surface TF density. Clotting was activated by uniformly distributed TF (gray lines) or by rectangular spots (dark gray lines) with a high TF density (60 × 15 μm size and 500 pmol/m2 TF density) in a 3D region. To evaluate the role of feedback loops in clotting sensitivity to TF distribution, we individually switched off positive feedback loops for fV, fVII, fVIII, and fXI activation by setting the rates of these reactions to zero in our computer simulations (D). The average TF density for this series of simulations was 12.5 pmol/m2.
A simple cascade of enzymatic reactions without feedback loops does not sense surface activator distribution
We wanted to ascertain whether TF distribution on the surface is necessary and sufficient for experiments with both uniformly distributed TFs and cells. Thus, we calculated the initiation times using a model and the same range of average TF densities that was used in the experiments. Two conditions were simulated: uniformly distributed surface-bound TFs and uniformly distributed rectangular spots of bound TFs with a size and density similar to those of fibroblasts. In both cases, average TF density was varied over a wide range. TF density at the spots was not changed, but distance between the spots was altered. Local TF sensitivity was not observed in a simple cascade system without feedback loops because, in that case, fibrin quantity was proportional to the average density of the activator (Fig. 4 B, open circles).
The system becomes sensitive to local TF density when positive feedback loops are introduced
In contrast, there was a difference between two types of activation in the model with positive feedback loops (Fig. 4 B, solid circles). Initiation time plots over average TF densities qualitatively corresponded with the experimental data in both cases (Fig. 4 C). Initiation time was mostly independent of average TF density for the modeled spot-activated clotting with high TF density. In contrast, TF uniformly immobilized on the surface dramatically enhanced the TF-density dependence of the clotting process. Initiation times at low average TF densities were substantially different between activation by uniformly distributed TFs and TF-bearing spots. Thus, the same TF quantities yielded the formation of different fibrin quantities depending on TF distribution at the surface. To study the roles of individual feedback loops, the rates for fV, fVII, fVIII, and fXI activation were each set to zero (Fig. 4 D). Only two positive feedback loops, for fV activation by thrombin and fVII activation by fXa, led to a difference in the two types of TF localization (Fig. S3). This result suggests that the absence of these reactions led to a loss of sensitivity to the surface distribution of the activator. For the activation of fVIII and fXI by thrombin, the influence was minimal; these feedback loops only slightly increased the difference between types of TF localization. A severalfold difference in the binding ability of uniformly immobilized TF and TF spots did not affect the phenomena (Fig. S2).
Roles of factors V and VII in feedback activation: acceleration of clotting initiation
We calculated the contributions from fV and fVII activation using the model system to clarify why fV and fVII activation is essential for the clotting system's sensitivity to surface TF distribution. We simulated two cases: homogenous clotting activation and activation at a surface with uniformly distributed TFs (Fig. 5, left and middle). The fVII activation by fXa was important for clotting initiation only when the activator was localized to the surface. What changes in the system during translocation of TF from the entire volume to the surface? We suggest that, in the latter case, diffusion of all the clotting system components is essential. When we analyzed the contribution from diffusion of individual components, we found that fXa diffusion was the only essential activity (data not shown). When the fXa diffusion coefficient was increased, the initiation time curves for the system, with and without fVII activation, were the same as for homogeneous TF activation (Fig. 5 right).
Figure 5.
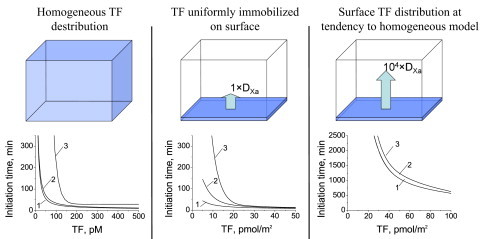
Spatial TF distribution defines the role of positive feedback for fVII activation in clotting. To compare the roles of fV and fVII feedback loops, initiation time dependencies on TF concentration and density were calculated for normal plasma and plasma without either fVII or fV activation. A detailed, mechanism-driven mathematical model was used. (Left) When TF was distributed homogeneously, only the fV activation feedback loop was essential for clotting. (Middle) When immobilized TF was uniformly distributed over the surface in 3D computer simulations, the feedback loops for both fV and fVII activation influenced the initiation time. (Right) TF was uniformly immobilized at the surface, and the fXa diffusion coefficient was increased by 104 to mimic homogeneous TF distribution. The role of positive feedback in the fVII activation of clotting disappeared, suggesting that fVII activation by fXa is important for the clotting process only when fXa is removed by diffusion; thus, additional fVIIa activated fXa and compensated for its diffusion.
To summarize, the mathematical model showed that the positive feedback loops for fV and fVII activation were necessary and likely sufficient to supply clotting activation sensitivity to high TF density at individual spots and the same quantity of TF uniformly distributed on the surface.
Feedback loops for activation of factors V and VII supply clotting system sensitivity to TF distribution at the surface
To test the prediction that fV and fVII activation feedback loops render blood coagulation sensitive to the spatial distribution of TF, we performed experiments using fV-, fVII-, and fVIII-deficient plasma (Fig. S9). To shorten initiation times, fVII- and fV-deficient plasma was supplemented with small quantities of fVIIa and fVa, respectively. As a control, a mixture of fV- and fVII-deficient plasma at a 1:1 volume ratio was used. In agreement with the computer simulations, the difference in initiation times for activation by immobilized TF and cells almost disappeared in the fV- and fVII-deficient plasma. For fVIII-deficient plasma, the difference remained the same as in normal plasma. This result confirms the model prediction that positive feedback loops for fV and fVII activation are essential for clotting system sensitivity to surface TF distribution and its local density (Fig. 6).
Figure 6.
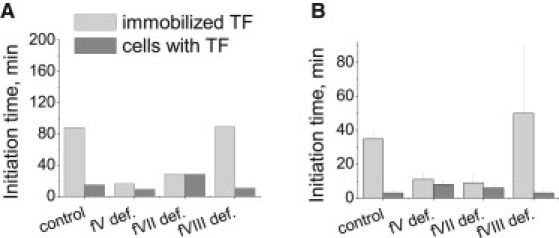
Positive feedback loops for fV and fVII activation render clotting sensitive to surface TF distribution. To validate the mathematical model prediction that the clotting system can recognize local TF concentration only after fV and fVII activation, we performed experiments with fV-, fVII-, and fVIII-deficient plasma. The mathematical model (A) and experimental data (B) are shown. The average TF density was 6.25 pmol/m2 for the mathematical model and 8 pmol/m2 for the experiments. Plots show the initiation times for the control plasma and the fV-, fVII-, and fVIII-deficient plasmas. Immobilized TF and TF-bearing cells were used to activate clotting. For the control plasma, a mixture of fV- and fVII-deficient plasma at a 1:1 volume ratio was used. To enhance clot activation, fV-deficient plasma (<1%) was supplemented with fVa (0.1% of the normal experimental fV concentration and 1% for the model), and fVII-deficient plasma was supplemented with <1% VIIa (1% of the normal fVII concentration). Control and fVIII-deficient plasmas were sensitive to TF distribution in the clotting process, whereas fV- and fVII-deficient plasma showed only small differences between activation by uniform immobilized TFs and fibroblasts. Experimental data are shown with the corresponding SD (n = 3÷5).
In contrast to normal plasma, the clot growth rates in fV- and fVII-deficient plasma were similar for clotting activation with either uniformly distributed or spotted TF, and the clot sizes 40 min after the beginning of the experiment were also similar (Fig. S10). Without fVIII, however, differences in clot growth rates and clot sizes for these two cases of surface TF distribution increased, even compared with normal plasma. This result indicates that the feedback loops for fV activation by thrombin and TF-fVII complex activation by fXa are essential for fast clot growth with a concentrated activator and slow clot growth with uniformly distributed surface TFs. Clots growing in fV- and fVIII-deficient plasma had more diffuse profiles than normal and fVII-deficient plasma, and did not have a distinct boundary between the fibrin clot and liquid plasma, in contrast to the control and fVII-deficient plasma (Fig. S11). Thus, the feedback loops for fV and fVIII activation by thrombin abruptly switched between fibrin clots and liquid plasma.
Effect of plasma and cell surface lipids on the ability of the coagulation system to sense local TF density
To ensure that the difference between fibroblasts and immobilized TF was not caused by factors other than the TF distribution (for example, a difference in tenase and prothrombinase activity), we performed control experiments to evaluate their procoagulant activity. The ability of the films to support prothrombinase was both low and identical (Fig. 7 A). Immobilized TF had higher procoagulant activity compared with intrinsic tenase in fibroblasts (Fig. 7 B). However, the effects were also small (films with the maximum density, at 4 mm2/60 μl, were similar to PL at 200 nM). Thus, a higher procoagulant activity in immobilized TF cannot support the enhanced fibroblast clotting observed in this study.
Figure 7.
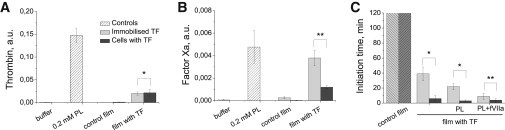
Effect of plasma and cell surface lipids on the sensitivity to local TF density during coagulation. (A) Thrombin production by prothrombinase assembled on PL, films with fibroblasts, or films with immobilized TFs. Shown are the mean ± SD, n = 8÷16. (B) fXa production by intrinsic tenase assembled on either PL, films with fibroblasts, or films with immobilized TFs. Shown are the means ± SD, n = 4÷6. (C) Effect of PL (0 and 10 μM) and fVIIa (0 and 10 nM) on the clotting initiation time. Clot formation was initiated by films with fibroblasts or immobilized TFs, both with an average surface density of 8 pmol/m2. Control films are films without TFs. Shown are the means ± SD, n = 3÷7. Asterisks show a significant difference, and double asterisks show a lack thereof, as calculated using an unpaired, two-sample t-test at p = 0.05.
To test whether the phenomena observed in this study depend on plasma lipid concentration, and to exclude the possibility of artifacts from insufficient surface binding for factors such as Xa, Va, and VIIa, we performed control experiments in plasma supplemented with PL at 10 μM. These data, presented in Fig. 7 C, show that PLs shortened the clotting initiation times by ∼2-fold in all cases but had no effect on the phenomenon itself; fibroblast clotting was still activated more rapidly than uniformly immobilized TF of the same surface density by an order of magnitude. As an additional control, we added both fVIIa (10 nM) and PL (10 μM) to normal plasma activated with either fibroblasts or immobilized TF, and the difference between the activators was greatly decreased (Fig. 7 C). These data confirm that it is the positive feedback loops, not lipid (un)availability, that determine coagulation sensitivity to local TF density independently of other conditions used in this study.
Discussion
The purpose of the study was to investigate the dependence of spatial clot formation on surface TF density and distribution. The principal results were as follows: 1), the clotting system is sensitive to the density of uniformly distributed TF, as clotting initiation time increased with a decrease in TF density; 2), in contrast, immobilized fibroblast cells always activated clotting rapidly, independently of their monolayer density; and 3), the distinction in the clotting response to surface TF distribution was determined by two positive feedback loops, TF-fVII complex activation by fXa and fV activation by thrombin.
These results confirm the concept that the blood clotting system can, in a way, recognize patterns (13). For our experiments, it recognized regions with high local TF density and rapidly generated a fibrin clot proximal to these spots. When the same TF quantity was uniformly distributed across a larger surface, the clotting system was activated slowly and clots did not form. When the activator was a high-density TF spot, the clots always grew rapidly and did not depend on the average nonlocal TF density.
Previous theoretical studies (16,22–24) predicted that in enzyme cascades with positive feedback loops, activation thresholds and sensitivities to local concentration and surface density can arise. A previous experimental study (13) demonstrated that clotting can depend not only on the area of a TF-containing spot but also on its shape. The principal new results from our study are identification of specific coagulation factors and feedback loops that are important for recognizing regions with high local TF density. This ability is controlled by two positive feedback loops: fV activation by thrombin and TF-fVII complex activation by fXa. Our simulations suggest that all of the thresholds for coagulation (i.e., thresholds for TF density, TF-bearing spot size, and blood flow rate (21)) in this reaction-diffusion system are determined by these two feedback loops. Two additional positive feedback loops, fVIII and fXI activation by thrombin, do not affect clotting system sensitivity to TF distribution.
Our conclusions from this study are based on a comparison of two types of activators: TF-expressing cells and uniformly distributed TF. Although the use of native cells renders the experimental conditions more physiological, and we quantitatively determined TF density in all cases, one cannot rule out differences between cells and noncell TF in addition to surface distribution. We performed the following additional control experiments to test this possibility: First, we determined the ability of the cells and noncell TF to support intrinsic tenase and prothrombinase activity. Second, we performed 3D computer simulations of clotting activation by uniform and spotted TF. Finally, we tested the effects of Kd differences between cells and noncell TFs. These results support the conclusion that the principal cause of the difference between cells and noncell TF activation is a difference in surface distribution. Contributions from additional factors were detectable and likely do not affect our conclusions.
Feedback from fV activation aids the clotting system in forming a clear boundary between fibrin clots and liquid plasma. Clots with a wide range of unstable states, between solid fibrin polymer and liquid plasma, were formed in fV-deficient plasma. In a previous study (11), we showed that for homogeneous clotting activation, this reaction functions similarly: fV activation feedback minimizes the temporal and parametric (TF concentration) intervals of clot instability. Patients with an fV deficiency were previously reported to experience thromboembolisms (25). That report may be consistent with our results, which show a role for fV-activation feedback. One can speculate that blood flow detaches unstable clot portions and causes the embolism.
The role of fVII activation by fXa was previously unclear. Its participation in activation threshold formation has been suggested (22), but it has not been observed in a mechanism-driven clotting model for a homogeneous system (11). FVII activation has also been suggested as a trigger for kinetic changes in coagulation during blood flow along the activation region (21), as fXa is removed from the generation region by flow. Here, we propose a novel (to our knowledge) role for this reaction in the regulation of spatial clotting with low surface TF density (Fig. 8). FXa removal through diffusion is essential in the clotting system, because it is slowly generated. The special role of the fVII activation feedback loop is to enhance the rate of clot growth at spots with high local TF density. Using a mathematical model, we demonstrated that this reaction is only essential in the reaction-diffusion system. The component that is sensitive to spatial heterogeneity is fXa. The influence of the feedback increases as the contribution from diffusion increases. Thus, fXa accumulation near a TF-bearing surface enhances the influence of fVII feedback activation on the clotting system compared with uniform surface TF distribution. When the same quantity of fXa was uniformly distributed throughout the volume, fV and fVII activation played the same role in clotting as it did in homogeneous distribution. The role of fV activation was retained, whereas the role of fVII activation disappeared. Thus, our study shows that fVII feedback activation is not important at a high TF density, but is critical at low TF density. Previous studies showed that flow can enhance the influence of this feedback loop even at high TF density (21), whereas this feedback loop had no effect on homogeneous clotting activation (11). These three findings parallel one another, i.e., they indicate that fVII feedback during coagulation forms additional thresholds under unfavorable, spatially nonuniform activation conditions (when TF is low or rapidly removed by flow).
Figure 8.
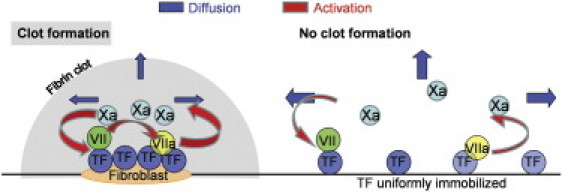
Positive feedback loops supply sensitivity to surface TF distribution during coagulation. (Left) When clotting is activated by cells with a high surface TF density, fX activation is more important than the removal of fXa due to diffusion and inhibition. This result is reinforced by the feedback loop for fVII activation, and the clot rapidly forms near the cells and propagates from them. (Right) In contrast, if the same quantity of TF is distributed uniformly across the surface, then fXa removal and inactivation predominate, and clot formation is prevented.
These results supplement earlier work on the function of the clot system. We can assume that the complicated reaction system for clotting can be decomposed into functional modules with unique roles (11). Currently identified roles include fibrin polymerization, activation triggered by the positive feedback loops for fV and fVII activation, spatial propagation by positive feedback loops for fVIII and fXI activation, and termination of spatial propagation by a negative feedback loop in the protein C pathway (20).
The practical significance of the results obtained in this study is the potential for selectively regulating various processes and properties in the coagulation response. When clotting is activated in vivo, the activation signal (i.e., TF density and distribution, and activating region size) can vary greatly. TF is expressed by endothelial cells and monocytes upon the action of toxins, cytokines, lipids, TFN-6, immune complexes, and other signals (26–30). Thus, at a low density of uniformly distributed activators, clotting begins after tens and even hundreds of minutes. This amount of time is sufficient for the removal of activated enzymes by blood flow and the blood clearance system. Thus, clots are not formed at all when the cells begin expressing TF at low densities, even on a large region. In contrast, a single cell with high TF expression can effectively cause clot formation. Information regarding each reaction's role during clotting formation may aid in specifically influencing the system during pathological conditions. For example, inhibition or stimulation of fV and fVII activation can modulate the clotting system's sensitivity to activator distribution.
Acknowledgments
We thank Dr. Ljudmila I. Ulyanova (Institute of Immunology, Moscow, Russia) for her help with fibroblast cell culture, Prof. Vitaly Volpert (University of Lyon 1, Lyon, France) for providing access to computational facilities and software, and Alexey Tokarev (National Research Center for Hematology) for his advice on numerical simulations in COMSOL.
This work was supported by the Russian Academy of Sciences Presidium basic research programs Molecular and Cellular Biology, and Basic Sciences for Medicine; the Russian Foundation for Basic Research (grants 09-04-00232, 09-04-00357, 09-02-00018, 10-01-91055, 11-04-00303); and a Russian Federation President Grant for Young Scientists (MK-155.2010.4). The authors declare no financial conflicts of interest.
Supporting Material
References
- 1.Monroe D.M., Key N.S. The tissue factor-factor VIIa complex: procoagulant activity, regulation, and multitasking. J. Thromb. Haemost. 2007;5:1097–1105. doi: 10.1111/j.1538-7836.2007.02435.x. [DOI] [PubMed] [Google Scholar]
- 2.Butenas S., Mann K.G. Kinetics of human factor VII activation. Biochemistry. 1996;35:1904–1910. doi: 10.1021/bi951768c. [DOI] [PubMed] [Google Scholar]
- 3.Hemker H.C., Al Dieri R., Béguin S. Thrombin generation, a function test of the haemostatic-thrombotic system. Thromb. Haemost. 2006;96:553–561. [PubMed] [Google Scholar]
- 4.Rand M.D., Lock J.B., Mann K.G. Blood clotting in minimally altered whole blood. Blood. 1996;88:3432–3445. [PubMed] [Google Scholar]
- 5.Monroe D.M., Hoffman M., Roberts H.R. Transmission of a procoagulant signal from tissue factor-bearing cell to platelets. Blood Coagul. Fibrinolysis. 1996;7:459–464. doi: 10.1097/00001721-199606000-00005. [DOI] [PubMed] [Google Scholar]
- 6.Ovanesov M.V., Krasotkina J.V., Ataullakhanov F.I. Hemophilia A and B are associated with abnormal spatial dynamics of clot growth. Biochim. Biophys. Acta. 2002;1572:45–57. doi: 10.1016/s0304-4165(02)00278-7. [DOI] [PubMed] [Google Scholar]
- 7.Bach R., Rifkin D.B. Expression of tissue factor procoagulant activity: regulation by cytosolic calcium. Proc. Natl. Acad. Sci. USA. 1990;87:6995–6999. doi: 10.1073/pnas.87.18.6995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zwaginga J.J., de Boer H.C., de Groot P.G. Thrombogenicity of vascular cells. Comparison between endothelial cells isolated from different sources and smooth muscle cells and fibroblasts. Arteriosclerosis. 1990;10:437–448. doi: 10.1161/01.atv.10.3.437. [DOI] [PubMed] [Google Scholar]
- 9.Hatakeyama K., Asada Y., Sumiyoshi A. Localization and activity of tissue factor in human aortic atherosclerotic lesions. Atherosclerosis. 1997;133:213–219. doi: 10.1016/s0021-9150(97)00132-9. [DOI] [PubMed] [Google Scholar]
- 10.Okorie U.M., Denney W.S., Diamond S.L. Determination of surface tissue factor thresholds that trigger coagulation at venous and arterial shear rates: amplification of 100 fM circulating tissue factor requires flow. Blood. 2008;111:3507–3513. doi: 10.1182/blood-2007-08-106229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Panteleev M.A., Balandina A.N., Ataullakhanov F.I. Task-oriented modular decomposition of biological networks: trigger mechanism in blood coagulation. Biophys. J. 2010;98:1751–1761. doi: 10.1016/j.bpj.2010.01.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kastrup C.J., Shen F., Ismagilov R.F. Characterization of the threshold response of initiation of blood clotting to stimulus patch size. Biophys. J. 2007;93:2969–2977. doi: 10.1529/biophysj.107.109009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kastrup C.J., Shen F., Ismagilov R.F. Response to shape emerges in a complex biochemical network and its simple chemical analogue. Angew. Chem. Int. Ed. Engl. 2007;46:3660–3662. doi: 10.1002/anie.200604995. [DOI] [PubMed] [Google Scholar]
- 14.Ovanesov M.V., Ananyeva N.M., Saenko E.L. Initiation and propagation of coagulation from tissue factor-bearing cell monolayers to plasma: initiator cells do not regulate spatial growth rate. J. Thromb. Haemost. 2005;3:321–331. doi: 10.1111/j.1538-7836.2005.01128.x. [DOI] [PubMed] [Google Scholar]
- 15.Anand M., Rajagopal K., Rajagopal K.R. A model incorporating some of the mechanical and biochemical factors underlying clot formation and dissolution in flowing blood. J. Theor. Med. 2004;6:183–218. [Google Scholar]
- 16.Beltrami E., Jesty J. The role of membrane patch size and flow in regulating a proteolytic feedback threshold on a membrane: possible application in blood coagulation. Math. Biosci. 2001;172:1–13. doi: 10.1016/s0025-5564(01)00064-5. [DOI] [PubMed] [Google Scholar]
- 17.Kuharsky A.L., Fogelson A.L. Surface-mediated control of blood coagulation: the role of binding site densities and platelet deposition. Biophys. J. 2001;80:1050–1074. doi: 10.1016/S0006-3495(01)76085-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hojima Y., Pierce J.V., Pisano J.J. Hageman factor fragment inhibitor in corn seeds: purification and characterization. Thromb. Res. 1980;20:149–162. doi: 10.1016/0049-3848(80)90381-3. [DOI] [PubMed] [Google Scholar]
- 19.Panteleev M.A., Ananyeva N.M., Saenko E.L. Factor VIIIa regulates substrate delivery to the intrinsic factor X-activating complex. FEBS J. 2006;273:374–387. doi: 10.1111/j.1742-4658.2005.05070.x. [DOI] [PubMed] [Google Scholar]
- 20.Panteleev M.A., Ovanesov M.V., Ataullakhanov F.I. Spatial propagation and localization of blood coagulation are regulated by intrinsic and protein C pathways, respectively. Biophys. J. 2006;90:1489–1500. doi: 10.1529/biophysj.105.069062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Shibeko A.M., Lobanova E.S., Ataullakhanov F.I. Blood flow controls coagulation onset via the positive feedback of factor VII activation by factor Xa. BMC Syst. Biol. 2010;4:5. doi: 10.1186/1752-0509-4-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Beltrami E., Jesty J. Mathematical analysis of activation thresholds in enzyme-catalyzed positive feedbacks: application to the feedbacks of blood coagulation. Proc. Natl. Acad. Sci. USA. 1995;92:8744–8748. doi: 10.1073/pnas.92.19.8744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Jesty J., Beltrami E. Positive feedbacks of coagulation: their role in threshold regulation. Arterioscler. Thromb. Vasc. Biol. 2005;25:2463–2469. doi: 10.1161/01.ATV.0000187463.91403.b2. [DOI] [PubMed] [Google Scholar]
- 24.Khanin M.A., Semenov V.V. A mathematical model of the kinetics of blood coagulation. J. Theor. Biol. 1989;136:127–134. doi: 10.1016/s0022-5193(89)80220-6. [DOI] [PubMed] [Google Scholar]
- 25.Reich N.E., Hoffman G.C., Van Ordstrand H.S. Recurrent thrombophlebitis and pulmonary emboli in congenital factor 5 deficiency. Chest. 1976;69:113–114. doi: 10.1378/chest.69.1.113. [DOI] [PubMed] [Google Scholar]
- 26.Ahamed J., Niessen F., Ruf W. Regulation of macrophage procoagulant responses by the tissue factor cytoplasmic domain in endotoxemia. Blood. 2007;109:5251–5259. doi: 10.1182/blood-2006-10-051334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bryant A.E., Hayes-Schroer S.M., Stevens D.L. M type 1 and 3 group A streptococci stimulate tissue factor-mediated procoagulant activity in human monocytes and endothelial cells. Infect. Immun. 2003;71:1903–1910. doi: 10.1128/IAI.71.4.1903-1910.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Drake T.A., Hannani K., Berliner J.A. Minimally oxidized low-density lipoprotein induces tissue factor expression in cultured human endothelial cells. Am. J. Pathol. 1991;138:601–607. [PMC free article] [PubMed] [Google Scholar]
- 29.Haubitz M., Gerlach M., Brunkhorst R. Endothelial tissue factor stimulation by proteinase 3 and elastase. Clin. Exp. Immunol. 2001;126:584–588. doi: 10.1046/j.1365-2249.2001.01587.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Riewald M., Ruf W. Science review: role of coagulation protease cascades in sepsis. Crit. Care. 2003;7:123–129. doi: 10.1186/cc1825. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


