Abstract
Catch-binding is a counterintuitive phenomenon in which the lifetime of a receptor/ligand bond increases when a force is applied to break the bond. Several mechanisms have been proposed to rationalize catch-binding. In the two-pathway model, the force drives the system away from its native dissociation pathway into an alternative pathway involving a higher energy barrier. Here, we analyze an allosteric model suggesting that a force applied to the complex alters the distribution of receptor conformations, and as a result, induces changes in the ligand-binding site. The model assumes explicitly that the allosteric transitions govern the properties of the ligand site. We demonstrate that the dynamics of the ligand is described by two relaxation times, one of which arises from the allosteric site. Therefore, we argue that one can characterize the allosteric transitions by studying the receptor/ligand binding. We show that the allosteric description reduces to the two-pathway model in the limit when the allosteric transitions are faster than the bond dissociation. The formal results are illustrated with two systems, P-selectin/PSGL-1 and FimH/mannose, subjected to both constant and time-dependent forces. The report advances our understanding of catch-binding by combining alternative physical models into a unified description and makes the problem more tractable for the bond mechanics community.
Introduction
Recent years have witnessed increased interest in the biophysics of receptor/ligand complexes, such as FimH/mannose, P,L,E-selectin/PSGL-1, and others (1–7), showing an unusual dependence of the complex lifetime on the magnitude of an external force applied to rupture the bond. For a constant force, the lifetime of the complex grows initially with increasing force magnitude, contradicting the common expectation. Only at a certain force threshold does the lifetime reaches a maximum and start decreasing. In the jump/ramp experiments when the force grows linearly with time, such receptor/ligand complexes exhibit an anomaly in the probability distribution for the rupture force. Namely, for sufficiently slow force ramping, there exists an unusually high probability of bond rupture at small forces.
Several theoretical models (8–21) have been proposed to explain the observed phenomenon. This article focuses on the two-pathway (12) and allosteric (19) models that provide seemingly different physical interpretations of the catch-binding phenomenon. This article establishes a direct connection between the two descriptions. Fig. 1 illustrates, in schematic fashion, creation of the receptor/ligand complex and its dissociation that is coupled to the force-induced allosteric transition between the two conformations of the receptor protein. The diagram also illustrates how the two protein conformations lead to the catch- and slip-pathways of the two-pathway model. Fig. 2 shows the corresponding free energy profiles for the conformational change in the receptor protein and for the receptor/ligand interaction. It should be emphasized that the two-state potential for the allosteric site is separated from the single-state potential describing the receptor/ligand binding, as clearly seen in Fig. 2 a. This creates important distinctions between the current allosteric model and other multiparameter models (10,11,13).
Figure 1.
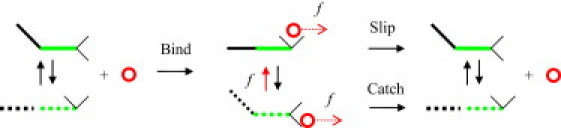
Binding and dissociation of a receptor/ligand catch-bond complex. The diagram is based most directly on the FimH/mannose system (27,44); however, it also represents other catch-bonds. The two-domain fragment of the receptor protein, composed of the pilin (black) and lectin (green) domains, exists in either bent or extended state. (Solid lines) More stable conformation; (dashes) less stable conformation. The bent state is more favorable in the free receptor. Binding to mannose (circle) shifts the conformational equilibrium toward the extended state. The interaction between lectin's binding site (angle made of two thin black lines) and mannose is stronger for the extended state (angle holding the circle) than the bent state (angle releasing the circle). The applied force (red arrows) lowers the bond dissociation barrier and favors the extended conformation. The control of the receptor conformation by force, combined with the correlation between the receptor conformation and the receptor/ligand binding strength, forms the basis for the allosteric model (19); see also Fig. 2a. The bond dissociations via the bent and extended channels represent the catch- and slip-pathways in the two-pathway model (12); see also Fig. 2b.
Figure 2.
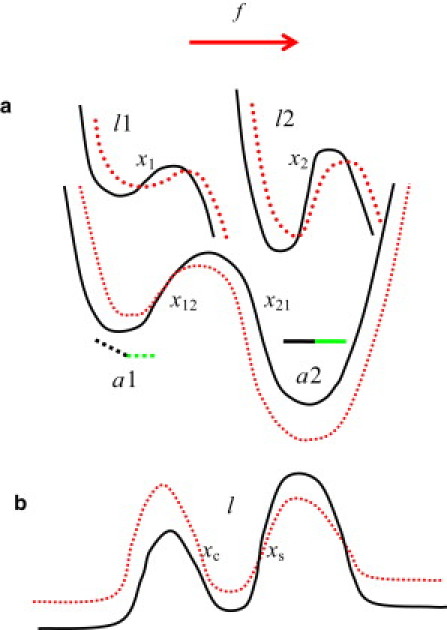
Energy profiles in the bound receptor/ligand complex for (a) allosteric (19) and (b) two-pathway (12) models of catch-binding. Minima a1 and a2 in panel a describe the bent and extended states of the two-domain receptor fragment, in accordance with the central part of Fig. 1. States a1 and a2 of the receptor allosteric fragment correlate with the free energy profiles l1 and l2 characterizing the ligand binding site. For a certain relationship between the model parameters, the allosteric model of panel a transforms into the two-pathway model of panel b, in which the ligand escapes from the binding site l via either the catch-barrier (left) or the slip-barrier (right). Application of the force (vector arrow) modifies the energy profiles for the allosteric and ligand interactions in panels a and b (from solid to dashed curves). All barriers are characterized by their widths x, as labeled in the figure. The barrier width is defined as the distance from the minimum to the maximum.
The two-pathway model (12) provides the simplest mathematical description of the catch-slip transition, leading to many useful analytical results and predictions (22–25). It assumes that the free energy profile for the receptor/ligand interaction (Fig. 2 b) contains one minimum l, describing the bound state, and two alternative pathways of escape from the minimum, describing the catch and slip mechanisms of the bond dissociation. In this model, the dependence of the bond dissociation rate constant k(f) on the applied force f has the simple expression:
| (1) |
Here, ks0 and kc0 are the rate coefficients for the bond dissociation via the slip (s) and catch (c) pathways in the absence of force. For brevity, we use T in Eq. 1 and below to denote the product of the Kelvin temperature and the Boltzmann constant kB. The force dependence of the Kramer's rate coefficient in Eq. 1 is introduced according to Bell (26). The parameters xs and xc are the distances from the minimum to the corresponding maxima of the potential (Fig. 2 b). According to Eq. 1, an increasing force accelerates the bond dissociation via the slip pathway and decelerates the dissociation via the catch pathway. Within a certain range of the model parameters (12), the competition between the two dissociation pathways leads to the catch-slip transition in the bond lifetime as a function of force.
The analysis of the catch-slip transition using the two-pathway model shows (25) that the depth of the free energy minimum describing the bound state of the receptor/ligand complex grows with force within a certain range of forces. Approaching the catch-slip phenomenon from this point of view, the concept of bond deformation was introduced in Pereverzev and Prezhdo (16). According to the deformation model, the receptor/ligand interaction strengthens as a result of a force-induced conformational change in the protein system.
The mathematical simplicity of the two-pathway model of the catch-slip transition, shown by Eq. 1, has led to a number of useful analytical results (12,22–25). At the same time, its direct physical interpretation requires understanding of the two distinct bond dissociation pathways, which are not trivial to establish for a given biological bond. This article shows that the mathematical form of the two-pathway model can be achieved within an alternative physical interpretation of catch-binding that is based on the concept of force-induced allostery (13,19,27) (see Figs. 1 and 2). The allosteric view on the two-pathway model of catch-binding provides a specific prescription to the catch and slip mechanisms of bond dissociation.
Proteins and other biological molecules are flexible objects that exhibit an ensemble of conformations at ambient temperatures. The ensemble perspective on protein properties is being actively explored by the biophysical community (28–41). In thermodynamics equilibrium, each conformation is present with some probability, whose value depends on external parameters, e.g., temperature. Local interactions, including receptor/ligand binding and external forces, can also have a profound effect on the ensemble distribution. Often, the overall conformation of the receptor protein is governed by the state of a local site, known as the allosteric site. Transitions of the allosteric site between different states propagate throughout the protein, changing its global conformation. During allosteric regulation an effector, such as a ligand or a pulling force, acting on the allosteric site in one part of a protein, induces changes in another, distant part of the protein, known as the active site.
After binding to the active site of the protein, the ligand moves in the potential, the structure of which is changing when the protein passes from one state to another. Allosteric regulation modifies the distribution of the binding potentials, and thereby affects the receptor/ligand binding. In turn, the receptor/ligand binding can shift the thermodynamic distribution of protein conformations relative to that for the free protein. The change in the ensemble of protein conformation affecting the receptor/ligand binding can occur via allosteric regulation induced not only by another protein (42,43), but also by force applied to the allosteric site (13,43,44).
Frequently, a protein fragment composed of two domains (Fig. 1) transduces allosteric regulation. Application of an external force changes the two-domain structure, which for simplicity can be characterized by the angle between the domains. The allosteric fragment of the FimH/mannose complex involves the lectin and pilin domains (44). The domains in the P-selectin/PSGL-1 complex are lectin and EGF (43). Following Pereverzev et al. (19), we will assume that the full distribution of the interdomain angles can be represented sufficiently by two angles describing bent and extended protein conformations (Figs. 1 and 2 a).
The article is constructed as follows. In the next section we derive the connection between the allosteric and two-pathway model. Next, we illustrate the derived mapping with the P-selectin/PSGL-1 and FimH/mannose bonds, including both constant force and jump/ramp experiments. Then, we analyze in detail the dynamics of the ligand subjected to a constant pulling force. We show that such analysis of the ligand dynamics can be used to extract information about the properties of the allosteric site, and to establish more rigorously the relationships between the rate coefficients needed for the transition from the allosteric to the two-pathway model. We conclude by discussing how the established connection can be used to unify the various models developed for the description of the catch-slip transition and to facilitate the analysis of the experimental data.
Review of the Allosteric Model
The dissociation of the receptor/ligand complex is described using three probabilities P1(t, f), P2(t, f), and P(t, f) that depend on both time and force. P1(t, f) and P2(t, f) are the probabilities to find the allosteric site in the bound complex in states a1 and a2 (Fig. 2 a) at time t for the complex subjected to force f. States a1 and a2 of the allosteric site in Fig. 2 a correspond to the bent and extended conformations of the receptor protein provided that the ligand is bound to the receptor. P(t, f) is the probability to find the ligand bound to the receptor at time t for force f. This approach differs in an important way from the models of Evans et al. (10), Barsegov and Thirumalai (11), and Thomas et al. (13), where the system is described, but using only two probabilities corresponding to two states of the whole receptor/ligand system. Evans et al. (10), Barsegov and Thirumalai (11), and Thomas et al. (13) do not make an explicit distinction between the probabilities in describing the allosteric and binding sites, and the sum of P1(t, f) and P2(t, f) in these models decreases to zero at long times. In contrast, in our model,
| (2) |
at all times. The evolution of the probabilities P1(t, f) and P2(t, f) is given by (19,45)
| (3) |
where k12(f) and k21(f) are the rate constants for transitions from state a1 to state a2 and back. The force dependence of these coefficients is introduced using the Bell approximation (26,46),
where k012 and k021 are the rate constants in the absence of force, and x12 and x21 are the distances from the first and second minima, respectively, to the top of the barrier (Fig. 2 a). Note the difference in the signs in the two exponents. The signs depend on the direction of the applied force and represent the fact that the force promotes transitions from a1 to a2 and obstructs transitions from a2 to a1. A time-dependent force will be denoted by the explicit notation f(t). In accordance with Eqs. 2 and 3, the receptor fluctuates only between two states (Fig. 2 a) and in contrast to the assumptions made in Evans et al. (10), Barsegov and Thirumalai (11), and Thomas et al. (13), there exist no bond dissociation pathways out of this two-state potential.
In the case of the P-selectin/PSGL-1 and FimH/mannose systems considered in detail below, the allosteric fragments include two protein domains that move with respect to each other. Then, states a1 and a2 of the allosteric model correspond to the bent and extended conformations of the two-domain fragment. The force applied to the ends of the fragment stretches the protein, promoting the transition from the bent to the extended state and obstructing the reverse process (Figs. 1 and 2 a).
It is logical to associate each allosteric state of the receptor protein with a different state of the active site (Fig. 2 a). Each state of the allosteric sites a1 and a2, or in other words, each conformation of the receptor protein, creates its own potential for interaction with the ligands l1 and l2. According to our assumption about the governing role of the allosteric site, the ligand interacting with the receptor moves in the potential that is controlled by the receptor conformation. As a result, one is led to introduce two rate constants for the receptor/ligand bond dissociation,
where k01 and k02 are the rate constants for f = 0, and x1 and x2 are the widths of the barriers associated with each well (Fig. 2 a).
Note that the exponents describing the force dependence of k1(f) and k2(f) above have the same sign, in contrast to the rate constants for the transitions between the two states of the allosteric site (Eq. 3). The bond dissociation rate constants of the two-pathway model (Eq. 1) also have different signs. In contrast to the two-pathway model (12), bond dissociation in the allosteric model (19,45) occurs via a single pathway.
As the allosteric site of the receptor protein fluctuates between two conformations, the active site also fluctuates between two states. The overall rate for the bond dissociation is given by the weighted average of the rates corresponding to each state of the active state,
| (4) |
with the weights given by the probabilities from Eqs. 2 and 3. The probability P(t, f) of finding the receptor/ligand bond intact is given by
| (5) |
To describe the experimental data, one needs to solve Eqs. 2 and 3 to obtain P1(t, f) and P2(t, f). Then, one can solve Eq. 5 with the rate coefficient defined in Eq. 4 and obtain P(t, f) as a function of t and f. Generally, it is hard to solve the problem analytically, especially if the force varies with time. The problem can be simplified significantly using the separation of the timescale for the allosteric transition and bond dissociation.
Timescale Separation and Transformation to the Two-Pathway Model
Small proteins typically fold within microseconds, whereas folding of larger proteins takes milliseconds (47–49). One can expect that large-scale structural transitions in proteins occur on similar or faster timescales. In comparison, the lifetimes of receptor/ligand bonds in the systems under consideration are much longer, ranging from fractions of seconds to several seconds. Further, in experiments with time-dependent forces, the force changes on the timescale of 0.01–0.1 s. Therefore, it is reasonable to assume that allosteric transitions are much faster than dissociation of the receptor/ligand bond, and that on the timescale of the experiment, the allosteric subsystem always remains in thermodynamic equilibrium.
This assumption eliminates the need to solve Eqs. 2 and 3 explicitly, because the experimental timescale corresponds to the long-time limit of these equations, and the solution at long times is given by the equilibrium probabilities (10) that are obtained by setting the left-hand-sides of the expressions in Eq. 3 to zero,
| (6) |
where β = k012/k021 is the ratio of the rate constants for the forward and backward transitions between the two states of the allosteric site, and xd + x12 + x21. The probabilities in Eq. 6 vary with time only if the force itself is time-dependent.
The simplified model given by Eqs. 4–6 contains six independent parameters, instead of the eight parameters in the original model as represented by Eqs. 2–5. To map the allosteric model onto the two-pathway model, the problem should be simplified further, because the two-pathway model contains only four parameters (12).
Recent experiments with FimH/mannose and P-selectin/PSGL-1 have shown (43,44) that upon ligand binding (the first step, refer to Fig. 1), the distribution of conformations of the receptor protein changes to significantly increase the population of the extended state, i.e., state a2 in Fig. 2 a. This implies that the ratio of the rate constants describing transitions between states a1 and a2 of the allosteric site is β = k012/k021 >> 1. Hence, approximately, P1(f) ≈ β−1 exp[−xdf/T] and P2(f) ≈ 1. Taking this into account allows us to express the rate constant for the receptor/ligand bond dissociation from Eq. 4 as
| (7) |
By redefining the parameters of the above expression,
| (8) |
we obtain the two-pathway expression for the bond dissociate rate constant (Eq. 1). To achieve the catch-behavior it is essential that xd > x1, such that xc > 0. Thus, the separation of the timescales of the allosteric transition and bond dissociation, together with the assumption that the allosteric fragment of the receptor protein in the bound receptor/ligand complex exists primarily in state a2 (the extended state), reduce the full allosteric model to the two-pathway model (12).
The mapping of the allosteric model onto the two-pathway model gives an explicit meaning to the catch-dissociation pathway. Namely, the catch-regime of bond dissociation is related to the transition of the allosteric site from the extended (a2) to the bent (a1) conformation, followed by escape of the ligand from the shallower state l2 (see Fig. 2 a). The parameters of the catch pathway barrier (k0c, xc) depend on the properties of both active (k01, x1) and allosteric (β = k012/k021, xd = x12 + x21) sites.
The mapping between the two-pathway and allosteric descriptions leads to the following physical picture of the catch-binding phenomenon (see Figs. 1 and 2): The receptor protein contains an allosteric fragment involving two protein domains. In thermodynamic equilibrium, the two-domain fragment fluctuates between the bent and extended states. The bent state is more stable in the free receptor. However, ligand binding shifts the equilibrium between the bent and extended states of the allosteric fragment toward the extended state (44), because the extended state facilitates much stronger receptor/ligand binding compared to the bent state (Fig. 2 a). Nevertheless, in the absence of force, the receptor/ligand bond dissociates primarily by making a transition to the bent state of the allosteric fragment, which provides a much weaker receptor/ligand binding. This allosteric mechanism of bond dissociation corresponds to the catch pathway in the two-pathway model (Fig. 2 b). The applied force prevents the transition of the allosteric fragment into the bent state, keeping it extended. In the extended state, the receptor/ligand bond dissociates via the typical slip mechanism.
The P-selectin/PSGL-1 Complex
In this and the following sections we will apply the formal results obtained above to the two best studied catch-bond systems (2,3,10,50). Both constant force and jump/ramp experimental scenarios will be considered. It should be noted that the experimental ramp rates are significantly smaller than the rates of transitions between the two states of the allosteric fragment. Therefore, the equilibrium assumption for the allosteric site can be applied to both constant force and jump/ramp scenarios. In addition to fitting the experimental data we will test the validity of the approximations taken in mapping the allosteric model (19) of catch-binding onto the two-pathway model (12).
Constant force experiments
P-selectin is an allosteric protein (see Springer (43) and references therein). The connection between the allosteric and two-pathway models given by Eq. 8, together with the earlier analysis of the P-selectin/PSGL-1 system performed within the limits of the two-pathway model (12), allows us to analyze the system using the allosteric interpretation. The analysis of the experimental lifetime
| (9) |
of the P-selectin/PSGL-1 bond subjected to a constant force has led to the following values of the parameters for the two-pathway model: k0s = 0.25 s−1, xs = 5.1 Å, k0c = 120 s−1, and xc = 21.7 Å (12).
As shown above in Eq. 8, the slip-pathway of the two-pathway model (Fig. 2 b) corresponds directly to the bond dissociation pathway from state 2 of the active site of the allosteric model (Fig. 2 a). Hence, the parameters for state 2 are k02 = 0.25 s−1 and x2 = 5.1 Å. Assuming that the allosteric transition changes only the strength of the receptor/ligand interaction, i.e., the well-depth, but not the width of the free energy barrier, we obtain x1 = x2 = 5.1 Å. Then, the relationship xc = xd – x1 leads to the following value for the distance between the two minima in the free energy profile for the allosteric site: xd = 26.8 Å. This value indicates that the allosteric transition involves significantly larger distances than bond dissociation, as expected.
The dissociation rate constant k0c for the catch-pathway of the two-pathway model corresponds to a combination of the two parameters, k01, β, of the allosteric model, seen in Eq. 8. To establish both parameters, we need to consider the more general version of the allosteric description, from Eqs. 4–6, which treats k01 and β independently. Using Eqs. 4–6 to fit the experimental data (12), we obtain β = 25.1. Indeed, β >> 1, confirming that the reduction of the allosteric model to the two-pathway model is valid for the P-selectin/PSGL-1 complex. Given β and k0c, we determine k01 = 3012 s−1.
The interpretation of the catch-binding phenomenon that follows from the allosteric model, together with the values of the model parameters for the P-selectin/PSGL-1 system established above, lead us to the following biophysical rationalization of the catch-slip dependence of the bond lifetime: In the absence of force, the allosteric site exists in the extended state a2 with high probability, P2 ≈ 0.96 (derived with Eq. 6). The lower-energy, extended state of the allosteric fragment of the receptor protein generates a deep minimum for the binding site, which exists in state l2 with the same high probability, P2 ≈ 0.96. The dissociation rate of the ligand in state l2 is small, k02 = 0.25 s−1. In contrast, the probability for the ligand to be in state l1 of the active site is small, P1 ≈ 0.04. However, state l1 is shallow, and the ligand dissociation rate for this state is high, k01 = 3012 s−1. Because of the high dissociation rate, the ligand leaves the binding pocket primarily with the route involving state l1 corresponding to the bent conformation a1 of the receptor protein, even though the population of state l1 is small. In particular, according to Eqs. 4 and 7, k01P1 ≈ 120.5 s−1, whereas k02P2 ≈ 0.24 s−1.
In the presence of the external force, the rate coefficient for the ligand dissociation from well l1 grows exponentially with force, ∼exp(x1,f). At the same time the probability P1(f) to find the ligand is state l1 decreases exponentially also, ∼exp(−xd,f) (see Eq. 6). Because the dimension xd associated with the conformational change in the allosteric site is significantly larger than the change x1 in the receptor/ligand bond length needed to reach the barrier top, the overall rate coefficient for the bond dissociation changes with applied force as k1(f)P1(f) ∼ exp(−xdf), according to Eqs. 4 and 7. Hence, the bond lifetime increases, resulting in the catch behavior. The lifetime growth will continue as long as the ligand dissociates primarily via well l1. At a certain value of the force, the second term in Eqs. 4 and 7 will become larger than the first term, and the ligand will start dissociating via the channel associated with well l2. At this point, the probability for the ligand to exist in state l2 will be close to unity, and the bond-dissociation rate-coefficient will grow exponentially according to the second term in Eq. 7. Such switch between the two dissociation channels associated with the two conformations of the receptor protein in the allosteric model creates a one-to-one correspondence with the transition between the two pathways in the two-pathway model.
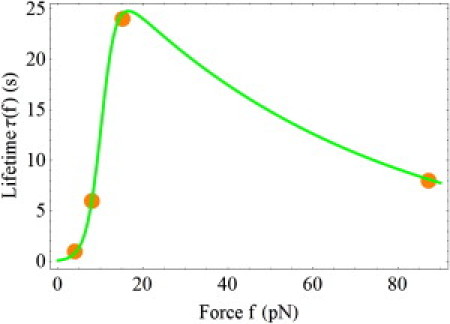
Fig. 3 shows the force dependence of the bond lifetime, represented in Eq. 9, for the P-selectin/PSGL-1 complex in the constant force experiments. The experimental data are taken from Marshall et al. (2) in the representation used in Pereverzev et al. (12). The theoretical curve represents two separate calculations of k(f), using the more general formulation of the allosteric model from Eqs. 4 and 6, in addition to the mapping between the allosteric and two-pathway descriptions given by Eqs. 7 and 8. The two theoretical results coincide, because β >> 1, and Eqs. 7 and 8 provide an excellent approximation to Eqs. 4 and 6.
Figure 3.
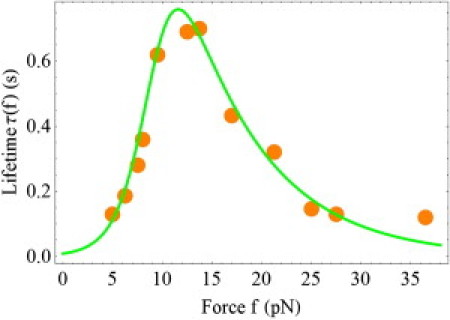
Lifetime of the P-selectin/PSGL-1 complex as a function of force in the constant force experiments. (Dots) Experimental data (2). (Curve) Theoretical results for the allosteric and two-pathway models, Eqs. 4, 5, and 6 and Eq. 1, respectively, with the parameters presented in the text.
Fig. 4 shows the force dependence of the probability P1(f)for the allosteric site to exist in state a1 (see Fig. 2 a). The black-solid line corresponds to P-selectin/PSGL-1, while the red-dashed line describes FimH/mannose. In both cases the probability is small initially and decreases further with increasing force. It is this decrease of P1(f) that is responsible for the catch-behavior of the receptor/ligand bonds.
Figure 4.
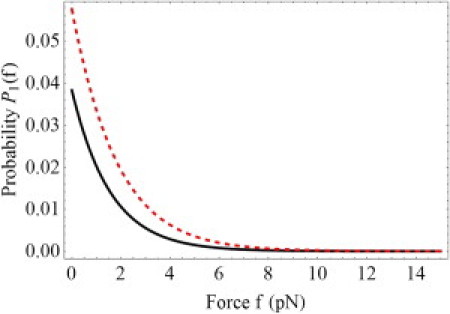
Dependence of the probability P1(f) (see Eq. 6) to find the allosteric fragment in the bent state a1 (see Fig 2b) as a function of force for P-selectin/PSGL-1 (solid line) and FimH/mannose (dashes). Ligand binding favors the extended state (44), defining the initial value P1(0). The applied force stabilizes the extended state further. The small values of P1(f) justify the approximation leading to Eq. 7.
Jump/ramp experiments
Next, consider the mapping of the allosteric model onto the two-pathway model for the case of the applied force that grows linearly with time, as in the jump/ramp experiments (10) (r is the ramp-rate):
| (10) |
If relaxation of the allosteric site occurs much faster than bond dissociation and the receptor protein in the receptor/ligand complex exists primarily in the extended conformation, i.e., β >> 1, then the parameters of the two-pathway and allosteric models are related by Eq. 8. According to the two-pathway model applied to the jump/ramp regime (22), the probability density of the rupture force is given by
| (11) |
where
and
The parameters corresponding to the experimental data of Evans et al. (10) were determined in Pereverzev et al. (12):
To reconstruct parameter β, one needs to consider the allosteric model explicitly and compute p(f), using Eq. 5, with the rate coefficient defined in Eq. 4 and probabilities given in Eq. 6. The resulting expression for the rupture force probability density is more complicated,
| (12) |
where
and
The orange dots in Fig. 5 show the experimental data (10) for the ramp rate r = 1400 pN s−1. The data are presented by the ratio of the number of force rupture events measured within each of the 20-pN force intervals, to the length of the interval, i.e., as Pulls/pN. To fit the experimental data, we used the unnormalized version of Eq. 12, pm(f) = mp(f), where m is the normalization constant. The following values of the parameters were obtained: m = 559.4, β = 131.5, k01 = 2630 s−1, k02 = 0.34 s−1, x1 = x2 = 2.1 Å, and xd = 5.9 Å. These values agree with the parameters of the two-state model (22) reported above. This is not surprising, because β >> 1. The results of both the more general version of the allosteric model, depicted in Eq. 12, and the two-pathway model, depicted in Eq. 11, are represented by the same theoretical curve in Fig. 5.
Figure 5.
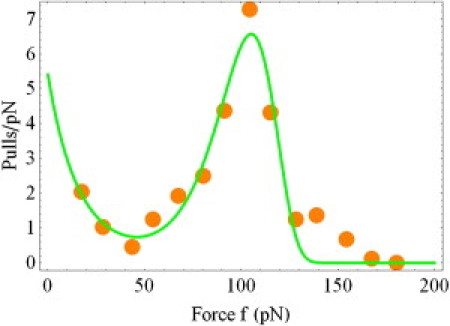
Probability density of the bond rupture force for the P-selectin/PSGL-1 complex, normalized to the total number of pulls for the ramp rate r = 1400 pN s−1. (Dots) Experimental data (10). (Curve) Theoretical results from Eqs. 11 and 12 with the model parameters presented in the text.
The analysis of the experimental data for the P-selectin/PSGL-1 system obtained in the constant force and jump/ramp regimes indicate that the approximations taken in transforming the allosteric model into the two-pathway model are highly accurate.
The FimH/mannose Complex
Constant force experiments
Le Trong et al. (44) clearly showed that FimH bound to mannose exists preferentially in the extended conformation. The angle between the lectin and pilin domains in the allosteric fragment of FimH increases upon binding, and the allosteric model (19) suggests that the allosteric site occupies state a2 with probability close to 1 (see Fig. 2 a). The extension of the allosteric fragment favors strong binding of mannose to FimH.
Similarly to the P-selectin/PSGL-1 case, we assume that there is a small probability for the allosteric site to exist in state a1, corresponding to the bent conformation of FimH (see Fig. 2 a). In this conformation, the binding of mannose to FimH is weak, and in the absence of force the bond dissociates via this pathway.
Fig. 6 shows the experimental data for the constant force experiments on the FimH/mannose complex (13,27), together with the theoretical fits using the two-pathway model from Eq. 7, and the more detailed allosteric model, seen in Eqs. 4–6. The latter description gives the following parameters: x1 = x2 = 0.66 Å, xd = 23.2 Å, k01 = 179.54 Å, k02 = 0.03 s−1, and β = 16.36. The large value of β >> 1 implies that the allosteric description of the FimH/mannose complex can be reduced to the two-pathway description seen in Eq. 1. Using Eq. 8, we obtain the following values for the parameters of the two-pathway model: xs = 0.66 Å, xc = 22.54 Å, k0s = 0.03 s−1, and k0c = 10.97 s−1. The theoretical results obtained with both models coincide on the scale of Fig. 6. They are shown by the green-solid line.
Figure 6.
Same as Fig. 3, but for the FimH/mannose complex. The experimental data are taken from Thomas et al. (13,27).
The red-dashed line presented earlier in Fig. 4 demonstrates that, indeed, the probability of finding the allosteric fragment of FimH in the bent conformation corresponding to state a1 in Fig. 2 a is small, and that it decreases rapidly with increasing force. At small forces, the FimH/mannose bond dissociation occurs primarily through this channel, which is responsible for catch-binding.
Jump/ramp experiments
In this section we apply the two-pathway formulation of the allosteric model to the analysis of the experimental data on the lifetime of the FimH/mannose complex subjected to the time-dependent force (51). Similarly to the P-selectin/PSGL-1 case, we will use both the more detailed allosteric model shown in Eq. 12, and using Eq. 11 that proceeds to Eq. 12 in the limit of large β. Focusing-in on the ramp rate r = 2500 pN/s (see Eq. 10), we will obtain the parameters of our models. The experimental data for this ramp rate were reported in Fig. 3a of Yakovenko et al. (51). The figure characterized bond rupture events that occurred within each of the 20-pN force intervals. In agreement with the data of Yakovenko et al. (51), the studies reported in Pereverzev et al. (22) showed high probability density of rupture force at small force values. The experimental data were fit with the unnormalized version of Eq. 11, pm(f) = mp(f), where m is the normalization constant.
Fig. 7 presents the experimental data (51) together with the theoretical curve corresponding to unnormalized version of Eq. 11 for the following parameter values: m = 395.8, k0s = 0.03 s−1, xs = 2.28 Å, k0c = 48.02 s−1, and xc = 1.56 Å. The number of pulls shown on the y-axis was divided by a factor of 20. To reconstruct the value of β, we used the more detailed allosteric model seen in Eq. 12, and the relationship between the parameters of the two models, as seen in Eq. 8. The analysis gave β = 10.8. The remaining parameters are k01 = 480.2 s−1, k02 = 0.03 s−1, x1 = x2 = 2.28 Å, and xd = 3.84 Å. Just as in the earlier examples, β is large, and the theoretical curves corresponding to Eqs. 11 and 12 coincide on the scale of Fig. 7.
Figure 7.
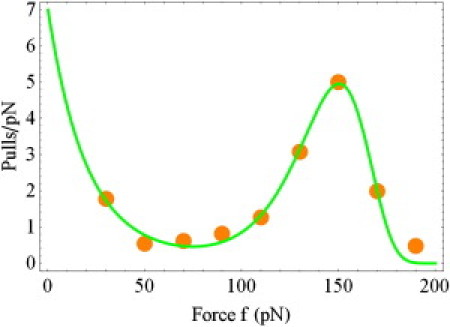
Same as Fig. 5, but for the FimH/mannose complex with the ramp-rate r = 2500 pN s−1. The experimental data are taken from Yakovenko et al. (51).
The low-force region in Fig. 7 is represented only by one point, because of the difficulties in obtaining accurate experimental data at small forces. Using our models, we can estimate the contribution of the low force region into the overall bond rupture. Integration of the bond rupture probability given by Eqs. 11 and 12 over the low force region f < 30 pN gives . Thus, ∼30% of all bond dissociations occur at low forces corresponding to catch binding. This conclusion was obtained for the high ramp rate of r = 2500 pN s−1. The corresponding estimate for r = 250 pN s−1, which is 10-times slower, gives a 97% probability of bond dissociation by the catch-binding mechanism. The above result indicates that low force data are particularly important for characterization of catch-binding at small values of r. Otherwise, one can expect large error-bars in the model parameters.
Allosteric Relaxation Timescale
The results presented above were obtained under the assumption that relaxation of the allosteric fragment subjected to the external force occurs much faster than dissociation of the receptor/ligand bond. This assumption allowed us to eliminate one of the eight parameters of the full allosteric model, seen in Eqs. 2–5, and to introduce the ratio of the rate coefficients for the forward and backward transitions between the two states of the allosteric site, β = k012/k021. To estimate the timescale of allosteric relaxation and to evaluate the validity of this assumption, we need to consider the most detailed level of the allosteric description, as represented in Eqs. 2–5. In this section, we obtain analytic solutions of these equations for the case of constant force.
All information about the dynamics of the force-induced bond dissociation is contained in the time-dependent bond survival probability P(t, f) for a given magnitude of applied force. The model presented in Eqs. 2–5 gives the second-order differential equation for the bond survival probability,
| (13) |
where
| (14) |
The two parameters, va(f) and vl(f), characterize the relaxation rates for the allosteric site and for the ligand in the active site. The force dependence of the rate constants encountered in Eq. 14 has been defined above in Review of the Allosteric Model.
Solving Eq. 13 subject to the initial conditions in
| (15) |
we obtain
| (16) |
The relaxation rate va(f) depends only on the parameters of the allosteric site (Eq. 14). Therefore, it characterizes this site alone. The relaxation rate vl(f) depends on the parameters of both allosteric and active (ligand) sites. If the relaxation of the allosteric site occurs much faster than that of the ligand site, then
| (17) |
Equation 16 reduces to ln P(t, f) ≈ −vl(f)t, and the bond lifetime attains the simple form τ(f) = 1/vl(f). This result coincides with the result derived from Eqs. 4–6 (see also Eq. 9). Further approximation, β >> 1, reduces the allosteric model to the two-pathway model (Eqs. 7 and 8).
To investigate the validity of Eq. 17, we will consider the FimH/mannose example. The parameters obtained earlier for this complex in the subsection entitled Constant Force Experiments are not sufficient for our purpose. Assuming that distances from the each minimum to the top of the barrier for the allosteric site are the same, x12 = x21 = xd/2, we need to define one more parameter: e.g., k021. Assuming that k021 = 5 s−1, representing a reasonable order-of-magnitude estimate, we obtain vl(0)/va(0) ≈ 0.12 for f = 0. As the force increases, this ratio rapidly decreases (see Fig. 8).
Figure 8.
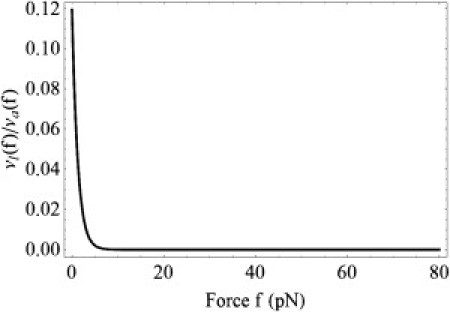
Force dependence of the ratio of the relaxation rates vl(f)/va(f) from Eq. 14, obtained using the model parameters for the FimH/mannose complex and k021 = 5 s−1.
Analysis of the FimH/mannose complex subjected to a constant force shows that if k021 ≥ 5 s−1, Eq. 17 holds for all forces. If k021 < 5 s−1, the inequality from Eq. 17 is true for all but the weakest forces, f < 2 ÷ 3 pN. If the condition in Eq. 17 is valid, ln P(t, f) drops exponentially fast to the value of . The drop happens within a very short time, on the order of 1/va(f). After the initial rapid exponential drop, ln P(t, f) continues to decrease linearly with time. The threshold value d(f) shows anomalous force dependence. Such anomalies in the time and force dependence of the logarithm of the bond survival probability ln P(t, f) were seen in a number of experiments (5,13,51).
Finally, we would like to point out that the expression for the lifetime in combination with Eq. 16 for P(t, f) leads to
| (18) |
where Γ(z) is the Euler γ-function and Γ(z,a) is the generalized incomplete γ-function. The curve plotted using Eq. 18 with the parameters obtained above for the FimH/mannose complex and k021 = 5 s−1 coincides with the theoretical curve shown in Fig. 5. This fact supports the conclusion that if va(f) >> vl(f), the full allosteric model given by Eqs. 2–5 simplifies to Eqs. 4–6, and that, in the limit of β >> 1, the allosteric model reduces to the two-pathway model.
Discussion and Conclusions
A number of authors have developed eight-parameter, two-state models for the description of the catch-slip anomaly observed in the lifetimes of receptor/ligand bonds (10,11,13). Such models agree with the notion of allostery (13). The model of Pereverzev et al. (19) differs from those of Evans et al. (10), Barsegov and Thirumalai (11), and Thomas et al. (13), as it explicitly identifies the governing role of the allosteric fragment in the catch-slip transition.
A multiparameter mathematical model can be given different physical interpretations. For example, the allosteric model (13) applied to the FimH/mannose complex led to two alternative rationalizations. In one case (13), the model parameters were chosen such that in the absence of force, the strongly bound state of the ligand site was more stable than the weakly bound state. With increasing force, the strongly bound state became even more stable. In the other case (51), the model was interpreted such that the strongly bound state was less stable than the weakly bound state, in the absence of force. Only at large forces did the stability of the states revert to the initial interpretation.
Within the limits of an eight-parameter model, several parameter sets can give good description of the catch-slip transition in the FimH/mannose complex. Similar ambiguities can be expected for the P-selectin/PSGL-1 complex. Only additional structural data (43,44) have helped to choose a unique interpretation. These studies showed that in the absence of force, the strongly bound state of the ligand is more stable.
Following the guidance provided by the studies of the receptor protein structure, we were able to show that an eight-parameter allosteric model of the catch/slip transition (19) can be reduced to the simplest four-parameter two-pathway model (12). The reduction was tested with the two complexes, P-selectin/PSGL-1 and FimH/mannose, and gave good results for both constant and time-dependent forces.
The analysis of the experimental data performed within the allosteric model provides a rationalization for the observed force history dependence of the catch-bond dissociation (52). According to our model, the low population of the bent conformation of the allosteric fragment of the receptor protein plays a particularly important role in the dissociation of the receptor/ligand catch-bonds. The bent conformation is responsible for the catch dissociation mechanism. Because the ligand-binding potential corresponding to the bent conformation of the receptor is very shallow and the population of the bent conformation of the allosteric fragment is small, weak perturbations to the receptor/ligand complex may have a strong effect on the depth and population of this binding potential. Depending on the history of the applied force, the protein structure may easily change in a manner that drastically alters or even eliminates this potential well, thereby dramatically modifying the catch-behavior or removing it altogether.
The reduction of the full allosteric model to the four-parameter, two-pathway model relies on the following two approximations: 1), the relaxation of the allosteric fragment in response to the external perturbation is rapid compared to the timescale of bond dissociation, and 2), the receptor/ligand complex has the highest probability to exist in the allosteric conformation that corresponds to strong receptor/ligand binding. The less probable allosteric conformation of the receptor protein gives weaker binding. In the cases when only the first condition is satisfied, the full allosteric model reduces to a six-parameter model.
To recapitulate, the allosteric model (19) provides three levels of description of the catch-slip transition. At the simplest level, Eqs. 7 and 8 correspond directly to the two-pathway model (12), which is shown in Eq. 1, and involves only four independent parameters. This approximation captures the most important features of catch-binding, including the key anomalies observed with the bond lifetime in constant force experiments and with the rupture force probability-density in jump/ramp experiments. The intermediate six-parameter version, presented in Eqs. 4–6, is required to establish the timescale of transitions between different states of the allosteric fragment. The full eight-parameter model represented with Eqs. 2–5 is capable of describing fine features of the experimental data, such as the rapid decay of the bond rupture probability at short times.
Acknowledgments
The research was supported by National Science Foundation grant No. CHE-1050405 and National Institutes of Health grant No. R01 AI50940.
References
- 1.Thomas W.E., Trintchina E., Sokurenko E.V. Bacterial adhesion to target cells enhanced by shear force. Cell. 2002;109:913–923. doi: 10.1016/s0092-8674(02)00796-1. [DOI] [PubMed] [Google Scholar]
- 2.Marshall B.T., Long M., Zhu C. Direct observation of catch bonds involving cell-adhesion molecules. Nature. 2003;423:190–193. doi: 10.1038/nature01605. [DOI] [PubMed] [Google Scholar]
- 3.Sarangapani K.K., Yago T., Zhu C. Low force decelerates L-selectin dissociation from P-selectin glycoprotein ligand-1 and endoglycan. J. Biol. Chem. 2004;279:2291–2298. doi: 10.1074/jbc.M310396200. [DOI] [PubMed] [Google Scholar]
- 4.Guo B., Guilford W.H. Mechanics of actomyosin bonds in different nucleotide states are tuned to muscle contraction. Proc. Natl. Acad. Sci. USA. 2006;103:9844–9849. doi: 10.1073/pnas.0601255103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kong F., García A.J., Zhu C. Demonstration of catch bonds between an integrin and its ligand. J. Cell Biol. 2009;185:1275–1284. doi: 10.1083/jcb.200810002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yago T., Lou J., Zhu C. Platelet glycoprotein Ibα forms catch bonds with human WT vWF but not with type 2B von Willebrand disease vWF. J. Clin. Invest. 2008;118:3195–3207. doi: 10.1172/JCI35754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Snook J.H., Guilford W.H. The effects of load on E-selectin bond rupture and bond formation. Cell. Mol. Bioeng. 2010;3:128–138. doi: 10.1007/s12195-010-0110-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dembo M., Torney D.C., Hammer D. The reaction-limited kinetics of membrane-to-surface adhesion and detachment. Proc. Royal Soc. (Lond) B Biol. Sci. 1988;234:55–83. doi: 10.1098/rspb.1988.0038. [DOI] [PubMed] [Google Scholar]
- 9.Bartolo D., Derényi I., Ajdari A. Dynamic response of adhesion complexes: beyond the single-path picture. Phys. Rev. E. 2002;65:051910. doi: 10.1103/PhysRevE.65.051910. [DOI] [PubMed] [Google Scholar]
- 10.Evans E., Leung A., Zhu C. Mechanical switching and coupling between two dissociation pathways in a P-selectin adhesion bond. Proc. Natl. Acad. Sci. USA. 2004;101:11281–11286. doi: 10.1073/pnas.0401870101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Barsegov V., Thirumalai D. Dynamics of unbinding of cell adhesion molecules: transition from catch to slip bonds. Proc. Natl. Acad. Sci. USA. 2005;102:1835–1839. doi: 10.1073/pnas.0406938102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Pereverzev Y.V., Prezhdo O.V., Thomas W.E. The two-pathway model for the catch-slip transition in biological adhesion. Biophys. J. 2005;89:1446–1454. doi: 10.1529/biophysj.105.062158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Thomas W., Forero M., Vogel V. Catch-bond model derived from allostery explains force-activated bacterial adhesion. Biophys. J. 2006;90:753–764. doi: 10.1529/biophysj.105.066548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zhu C., Lou J.Z., McEver R.P. Catch bonds: physical models, structural bases, biological function and rheological relevance. Biorheology. 2005;42:443–462. [PubMed] [Google Scholar]
- 15.Liu F., Ou-Yang Z.C., Iwamoto M. Dynamic disorder in receptor-ligand forced dissociation experiments. Phys. Rev. E. 2006;73:010901. doi: 10.1103/PhysRevE.73.010901. [DOI] [PubMed] [Google Scholar]
- 16.Pereverzev Y.V., Prezhdo O.V. Force-induced deformations and stability of biological bonds. Phys. Rev. E. 2006;73:050902. doi: 10.1103/PhysRevE.73.050902. [DOI] [PubMed] [Google Scholar]
- 17.Liu F., Ou-Yang Z.C. Force modulating dynamic disorder: a physical model of catch-slip bond transitions in receptor-ligand forced dissociation experiments. Phys. Rev. E. 2006;74:051904. doi: 10.1103/PhysRevE.74.051904. [DOI] [PubMed] [Google Scholar]
- 18.Beste M.T., Hammer D.A. Selectin catch-slip kinetics encode shear threshold adhesive behavior of rolling leukocytes. Proc. Natl. Acad. Sci. USA. 2008;105:20716–20721. doi: 10.1073/pnas.0808213105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Pereverzev Y.V., Prezhdo O.V., Sokurenko E.V. Allosteric role of the large-scale domain opening in biological catch-binding. Phys. Rev. E. 2009;79:051913. doi: 10.1103/PhysRevE.79.051913. [DOI] [PubMed] [Google Scholar]
- 20.Pereverzev Y.V., Prezhdo O.V., Sokurenko E.V. Anomalously increased lifetimes of biological complexes at zero force due to the protein-water interface. J. Phys. Chem. B. 2008;112:11440–11445. doi: 10.1021/jp803819a. [DOI] [PubMed] [Google Scholar]
- 21.Suzuki Y., Dudko O.K. Single-molecule rupture dynamics on multidimensional landscapes. Phys. Rev. Lett. 2010;104:048101. doi: 10.1103/PhysRevLett.104.048101. [DOI] [PubMed] [Google Scholar]
- 22.Pereverzev Y.V., Prezhdo O.V., Sokurenko E.V. Distinctive features of the biological catch bond in the jump-ramp force regime predicted by the two-pathway model. Phys. Rev. E. 2005;72:010903. doi: 10.1103/PhysRevE.72.010903. [DOI] [PubMed] [Google Scholar]
- 23.Pereverzev Y.V., Prezhdo O.V. Dissociation of biological catch-bond by periodic perturbation. Biophys. J. 2006;91:L19–L21. doi: 10.1529/biophysj.106.087288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Pereverzev Y.V., Prezhdo O.V. Universal laws in the force-induced unraveling of biological bonds. Phys. Rev. E. 2007;75:011905. doi: 10.1103/PhysRevE.75.011905. [DOI] [PubMed] [Google Scholar]
- 25.Prezhdo O.V., Pereverzev Y.V. Theoretical aspects of the biological catch bond. Acc. Chem. Res. 2009;42:693–703. doi: 10.1021/ar800202z. [DOI] [PubMed] [Google Scholar]
- 26.Bell G.I. Models for the specific adhesion of cells to cells. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 27.Thomas W.E., Vogel V., Sokurenko E. Biophysics of catch bonds. Annu. Rev. Biophys. 2008;37:399–416. doi: 10.1146/annurev.biophys.37.032807.125804. [DOI] [PubMed] [Google Scholar]
- 28.Gunasekaran K., Ma B., Nussinov R. Is allostery an intrinsic property of all dynamic proteins? Proteins. 2004;57:433–443. doi: 10.1002/prot.20232. [DOI] [PubMed] [Google Scholar]
- 29.Hilser V.J., García-Moreno E B., Whitten S.T. A statistical thermodynamic model of the protein ensemble. Chem. Rev. 2006;106:1545–1558. doi: 10.1021/cr040423+. [DOI] [PubMed] [Google Scholar]
- 30.Henzler-Wildman K., Kern D. Dynamic personalities of proteins. Nature. 2007;450:964–972. doi: 10.1038/nature06522. [DOI] [PubMed] [Google Scholar]
- 31.Bahar I., Chennubhotla C., Tobi D. Intrinsic dynamics of enzymes in the unbound state and relation to allosteric regulation. Curr. Opin. Struct. Biol. 2007;17:633–640. doi: 10.1016/j.sbi.2007.09.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tobi D., Bahar I. Structural changes involved in protein binding correlate with intrinsic motions of proteins in the unbound state. Proc. Natl. Acad. Sci. USA. 2005;102:18908–18913. doi: 10.1073/pnas.0507603102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Whitten S.T., García-Moreno E B., Hilser V.J. Local conformational fluctuations can modulate the coupling between proton binding and global structural transitions in proteins. Proc. Natl. Acad. Sci. USA. 2005;102:4282–4287. doi: 10.1073/pnas.0407499102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ming D., Wall M.E. Allostery in a coarse-grained model of protein dynamics. Phys. Rev. Lett. 2005;95:198103. doi: 10.1103/PhysRevLett.95.198103. [DOI] [PubMed] [Google Scholar]
- 35.Choi B., Zocchi G., Jeanne Perry L. Allosteric control through mechanical tension. Phys. Rev. Lett. 2005;95:078102. doi: 10.1103/PhysRevLett.95.078102. [DOI] [PubMed] [Google Scholar]
- 36.Chodera J.D., Singhal N., Swope W.C. Automatic discovery of metastable states for the construction of Markov models of macromolecular conformational dynamics. J. Chem. Phys. 2007;126:155101. doi: 10.1063/1.2714538. [DOI] [PubMed] [Google Scholar]
- 37.Kidd B.A., Baker D., Thomas W.E. Computation of conformational coupling in allosteric proteins. PLOS Comput. Biol. 2009;5:e1000484. doi: 10.1371/journal.pcbi.1000484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Zuckerman D.M. Simulation of an ensemble of conformational transitions in a united-residue model of calmodulin. J. Phys. Chem. B. 2004;108:5127–5137. [Google Scholar]
- 39.Miyashita O., Wolynes P.G., Onuchic J.N. Simple energy landscape model for the kinetics of functional transitions in proteins. J. Phys. Chem. B. 2005;109:1959–1969. doi: 10.1021/jp046736q. [DOI] [PubMed] [Google Scholar]
- 40.Pereverzev Y.V., Prezhdo O.V. Deformation model for thioredoxin catalysis of disulfide bond dissociation by force. Cell. Mol. Bioeng. 2009;2:255–263. [Google Scholar]
- 41.Krishna V., Ayton G.S., Voth G.A. Role of protein interactions in defining HIV-1 viral capsid shape and stability: a coarse-grained analysis. Biophys. J. 2010;98:18–26. doi: 10.1016/j.bpj.2009.09.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Tchesnokova V., Aprikian P., Sokurenko E. Integrin-like allosteric properties of the catch bond-forming FimH adhesin of Escherichia coli. J. Biol. Chem. 2008;283:7823–7833. doi: 10.1074/jbc.M707804200. [DOI] [PubMed] [Google Scholar]
- 43.Springer T.A. Structural basis for selectin mechanochemistry. Proc. Natl. Acad. Sci. USA. 2009;106:91–96. doi: 10.1073/pnas.0810784105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Le Trong I., Aprikian P., Thomas W.E. Structural basis for mechanical force regulation of the adhesin FimH via finger trap-like β-sheet twisting. Cell. 2010;141:645–655. doi: 10.1016/j.cell.2010.03.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Pereverzev Y.V., Prezhdo O.V., Sokurenko E.V. Regulation of catch binding by allosteric transitions. J. Phys. Chem. B. 2010;114:11866–11874. doi: 10.1021/jp1031459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Dudko O.K., Hummer G., Szabo A. Theory, analysis, and interpretation of single-molecule force spectroscopy experiments. Proc. Natl. Acad. Sci. USA. 2008;105:15755–15760. doi: 10.1073/pnas.0806085105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Lee J.C., Chang I.J., Winkler J.R. The cytochrome c folding landscape revealed by electron-transfer kinetics. J. Mol. Biol. 2002;320:159–164. doi: 10.1016/S0022-2836(02)00466-7. [DOI] [PubMed] [Google Scholar]
- 48.Yang W.Y., Gruebele M. Folding at the speed limit. Nature. 2003;423:193–197. doi: 10.1038/nature01609. [DOI] [PubMed] [Google Scholar]
- 49.Klepeis J.L., Lindorff-Larsen K., Shaw D.E. Long-timescale molecular dynamics simulations of protein structure and function. Curr. Opin. Struct. Biol. 2009;19:120–127. doi: 10.1016/j.sbi.2009.03.004. [DOI] [PubMed] [Google Scholar]
- 50.Gunnerson K.N., Pereverzev Y.V., Prezhdo O.V. Atomistic simulation combined with analytic theory to study the response of the P-selectin/PSGL-1 complex to an external force. J. Phys. Chem. B. 2009;113:2090–2100. doi: 10.1021/jp803955u. [DOI] [PubMed] [Google Scholar]
- 51.Yakovenko O., Sharma S., Thomas W.E. FimH forms catch bonds that are enhanced by mechanical force due to allosteric regulation. J. Biol. Chem. 2008;283:11596–11605. doi: 10.1074/jbc.M707815200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Marshall B.T., Sarangapani K.K., Zhu C. Force history dependence of receptor-ligand dissociation. Biophys. J. 2005;88:1458–1466. doi: 10.1529/biophysj.104.050567. [DOI] [PMC free article] [PubMed] [Google Scholar]


