Kinetic Asymmetry of Subunit Exchange of Homooligomeric Protein as Revealed by Deuteration-Assisted Small-Angle Neutron Scattering

Abstract

We developed a novel, to our knowledge, technique for real-time monitoring of subunit exchange in homooligomeric proteins, using deuteration-assisted small-angle neutron scattering (SANS), and applied it to the tetradecamer of the proteasome α7 subunit. Isotopically normal and deuterated tetradecamers exhibited identical SANS profiles in 81% D₂O solution. After mixing these solutions, the isotope sensitive SANS intensity in the low-q region gradually decreased, indicating subunit exchange, whereas the small-angle x-ray scattering profile remained unchanged confirming the structural integrity of the tetradecamer particles during the exchange. Kinetic analysis of zero-angle scattering intensity indicated that 1), only two of the 14 subunits were exchanged in each tetradecamer and 2), the exchange process involves at least two steps. This study underscores the usefulness of deuteration-assisted SANS, which can provide quantitative information not only on the molecular sizes and shapes of homooligomeric proteins, but also on their kinetic properties.

Introduction

Elucidation of the mechanisms underlying the structural kinetics of proteins is one of the fundamental issues to be addressed in biophysics. Kinetic analyses of hydrogen-deuterium exchange observed by spectroscopic and mass spectrometric methods have provided detailed information on secondary structure formation during folding processes and local and global conformational fluctuations of tertiary structures (1,2). However, because of the lack of appropriate methodology, the detailed formation mechanisms and kinetics of quaternary structures remain largely unknown, particularly in the case of homooligomeric proteins, which are the major forms of proteins in living systems (3,4). Here, we addressed this issue by complementary use of small-angle x-ray scattering (SAXS) and deuteration-assisted small-angle neutron scattering (SANS) focusing on the subunit exchange kinetics of a homooligomeric protein.

SANS is a powerful method to describe protein quaternary structures in solution (5–7). A fascinating property of this method is its ability to distinguish deuterium from hydrogen because of the difference in their neutron scattering lengths (b_D = 6.671 fm for deuterium and b_H = −3.7406 fm for hydrogen). This offers unique opportunities for contrast variation by H₂O/D₂O exchange (8,9) as well as for subunit labeling in complex or oligomeric particles. Labeling of subunits in a homooligomer by selective deuteration for a SANS study is noninvasive, and presents significant advantages in comparison to other subunit-marking methods such as chemical modifications, site-directed mutations, and peptide/protein tagging (10–13). A quantitative analysis of SANS profiles assisted by H₂O/D₂O contrast variation has been applied to unravel the formation and conformational changes of different protein-protein and protein-tRNA complexes between amino-acyl tRNA synthetases and tRNA (14), and, by using selective deuteration, to examine subunit exchange (15). Because of the recent progress in amplification of neutron beam intensity and computer-assisted simulation technique, the SANS method can now be applied to monitor subunit exchange processes in a homooligomer, as the time-dependent changes in the scattering profiles from a mixed solution of deuterated and nondeuterated proteins can be measured in real time. Herein, we developed the quantitative and experimental aspects of this approach and apply it to a model system consisting of the homotetradecamer of the proteasome α7 subunits.

The proteasome is a huge oligomeric protein operating as a proteolytic machine in the ubiquitin-dependent protein degradation pathway in eukaryotic cells (16,17). This large machine consists of a proteolytically active 20S core particle and one or two regulatory particles. The 20S core particle is composed of 28 subunits, i.e., two sets of α1, α2, α3, α4, α5, α6, and α7 and two sets of β1, β2, β3, β4, β5, β6, and β7, which are arranged in a cylindrical shape of four heteroheptameric rings, ${\alpha }_{1-7}{\beta }_{1-7}{\beta }_{1-7}{\alpha }_{1-7}$ (18,19). It has recently been revealed that assembly of the proteasome subunit is a chaperone-assisted and ordered process and not a spontaneous self-organization (20,21). However, among the proteasomal subunits, the α7 subunits spontaneously form a homotetradecamer in the absence of the other subunits (22).

In a previous study, we have characterized the quaternary structure of the α7 homo-tetradecamer in aqueous solution by SANS (23). The analysis indicated a structure made up of two homoheptameric rings stacked back-to-back to form a double ring structure (Fig. 1 A). This suggested that proteasome assembly involves some scrap-and-build processes from homoheptameric α7 rings to the heteroheptameric ring composed of seven different subunits. To provide insights into the mechanisms underlying these processes, it is essential to understand the dynamics and stabilities of the quaternary structure of this homooligomer. Therefore, herein we assess the dynamic properties of the homotetradecamer of proteasome α7 subunits with an attempt to observe subunit exchange by using deuteration-assisted SANS in conjunction with SAXS.

Figure 1.

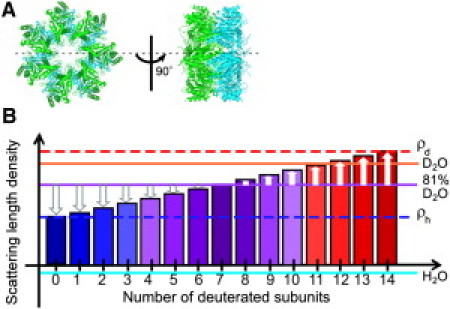
Three-dimensional (3D) structural model and neutron scattering length densities of the tetradecamer of proteasomal α7 subunit computed from the 3D structural model. (A) Top and side views of the double-ring structure of the α7 tetradecamer derived from the SANS data in conjunction with the crystal structure of the 20S core particle (19,23). Each α7 heptameric ring with sevenfold symmetry is drawn in green or cyan. The diameter and thickness are ∼120 Å and 50 Å, respectively. (B) Neutron scattering length densities of tetradecamers of proteasomal α7 composed of different numbers of h-α7 and d-α7 subunits computed from its 3D structural model, shown with bars having color gradient. Blue and red broken lines express the scattering length densities of h-α7 (ρ_h) and d-α7 (ρ_d) tetradecamers, respectively, whereas cyan, orange, and purple solid lines express the scattering length densities of H₂O, D₂O, and 81% D₂O, respectively. The arrows indicate the scattering contrasts of tetradecamers in 81% D₂O solution.

To observe a possible subunit exchange, we prepared two isotopically distinct α7 tetradecamers: one consisted only of deuterated α7 (d-α7) subunits and the other was composed only of nondeuterated (natural abundance) α7 (h-α7) subunits. These tetradecamers show large difference in their neutron scattering length densities: ρ_d = 0.76 fm·Å⁻³ for the d-α7 tetradecamer and ρ_h = 0.308 fm·Å⁻³ for the h-α7 tetradecamer in D₂O solution. Given that the mixture of d-α7 and h-α7 tetradecamers results in subunit exchange giving rise to isotopically mixed tetradecamers, they are expected to exhibit scattering length densities between ρ_h and ρ_d depending upon the ratio of d-α7 and h-α7 subunits (bars in Fig. 1 B). Accordingly, in 81% D₂O solution, of which scattering length density is an intermediate value between those of d-α7 and h-α7 tetradecamers, the scattering contrasts of the h-α7 and d-α7 tetradecamers (defined as the difference in scattering length density between solute and solvent) are equal in absolute value but are opposite in sign, and any subunit exchange causes a reduction in this absolute value (arrows in Fig. 1 B). Therefore, when subunit exchange proceeds in the mixture of both isotopic forms, the SANS intensity (proportional to the square of the scattering contrast) decreases in the low q-region by producing the tetradecamers with a lower scattering contrast, while SAXS (which is not isotope sensitive) is unchanged if the tetradecamer quaternary structure is maintained.

Materials and Methods

Protein samples

The h-α7 and d-α7 subunits were separately produced as recombinant proteins in Escherichia coli grown in H₂O- and D₂O-based minimal media and assembled into tetradecamers. A detailed protocol for preparation of the tetradecamer solutions used in SANS and SAXS experiments are provided in the Supporting Material.

SANS experiments

SANS experiments were performed using the D22 instrument installed at the Institut Laue-Langevin (ILL), Grenoble, France (24) and the SANS-U instrument of the Institute for Solid State Physics (ISSP), University of Tokyo, installed at the JRR-3M, Japan Atomic Energy Agency, Tokai, Japan (25). The SANS intensities measured in the q-range 0.0085–0.13 Å⁻¹ were accumulated at 15 min intervals for 12 h at a constant temperature of 25°C. The observed SANS intensity was corrected for background, empty cell, and buffer scatterings, and transmission factors, and then converted to the absolute scale by dividing by the SANS intensity of H₂O (26).

SAXS experiments

SAXS experiments were performed on the small- and wide-angle x-ray scattering instrument installed at the BL40B2 beamline of SPring-8, Hyogo, Japan (27). The SAXS intensities in the q-range 0.005–2.2 Å⁻¹ were measured for 1 s at eight time points in 12 h at a constant temperature of 25°C. The observed SAXS intensity was corrected for background, cell, buffer scattering, and transmission factors. The data correction details are described elsewhere (28,29).

Results and Analysis

Detection of subunit exchange

Before time-resolved SANS experiments, we checked the structural stability of the α7 tetradecamers in 81% D₂O solution. The SANS profiles of h-α7 and d-α7 tetradecamers before and after 12 h of incubation at 25°C were in excellent agreement (Fig. 2 A), confirming that 1), the h-α7 and the d-α7 tetradecamers have the same absolute value of scattering contrast in 81% D₂O solution and 2), they are structurally stable in this solution at least for 12 h. The structural stability of the α7 tetradecamers in the mixture of both isotopic forms was also confirmed by the time evolution of the SAXS profile, which was unchanged for 12 h after mixing under identical conditions (Fig. 2 B).

Figure 2.

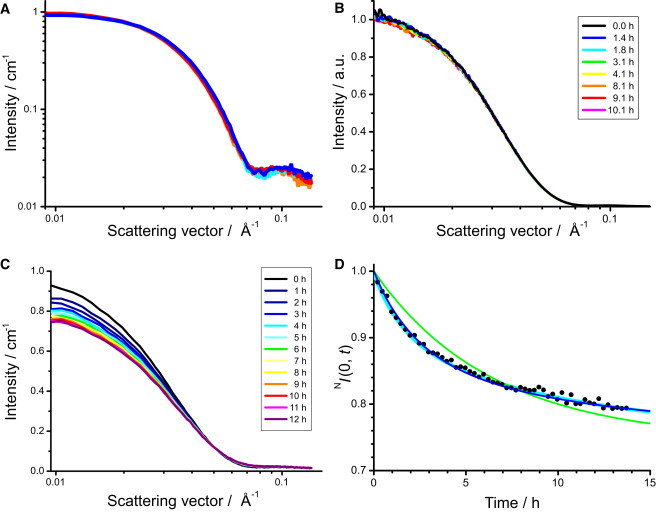
Time evolution of scattering profiles. (A) SANS profiles just after dissolving into 81% D₂O solutions (blue and red for h-α7 and d-α7 tetradecamers, respectively) and after 12 h (cyan and orange for h-α7 and d-α7 tetradecamers, respectively). (B) Time evolution of SAXS profile after mixing the h-α7 tetradecamers with the d-α7 tetradecamers in 81% D₂O solution. (C) Time evolution of SANS profile after mixing the h-α7 tetradecamers with the d-α7 tetradecamers in 81% D₂O solution. (D) Time evolution of normalized zero-angle scattering intensity, ${}^{N}I\left(0,t\right)$. Solid circles show the experimental result calculated with the Guinier formula. Cyan line represents the result of the least-square fitting of the biexponential decay function, Eq. 1 (see text), whereas green and blue lines show the best simulated results using the two-subunit-swapping model with (blue) and without (green) the assumption that the swappable subunits are in equilibrium between active and inactive states (Fig. 3B and see text).

The SANS intensity in the low q-region gradually decreased after mixing the h-α7 tetradecamer with the d-α7 tetradecamer in 81% D₂O solution (Fig. 2 C). As demonstrated by the results of the SAXS experiment, the observed change in SANS profile cannot be attributed to a structural change of the tetradecamers but is ascribed to the subunit exchange between the h-α7 and the d-α7 tetradecamers.

We further analyzed the subunit exchange kinetics, focusing on the time evolution of the zero-angle SANS intensity $I\left(0,t\right)$, which is directly proportional to the sum of the square of scattering contrasts of tetradecamers in the solution. The time evolution of the normalized zero-angle SANS intensity, ${}^{N}I\left(0,t\right)$, which is defined as $I\left(0,t\right)$ against that at the starting point of the time-course, ${}^{N}I\left(0,t\right)\equiv I\left(0,t\right)/I\left(0,0\right)$, could not be expressed with a monoexponential decay function, but was well reproduced with the biexponential decay function:

$${}^{N}I\left(0,t\right)={}^{N}I\left(0,\infty \right)+k_a\text{exp}\left(-\frac{t}{t_a}\right)+k_b\text{exp}\left(-\frac{t}{t_b}\right).$$ (1)

The best result of the least-square fitting (cyan line in Fig. 2 D) was obtained with the parameters, ${}^{N}I\left(0,\infty \right)=0.76\pm 0.02$, $k_a=0.09\pm 0.02$, k_b ($=1-k_a-{}^{N}I\left(0,\infty \right)$) $=0.15\pm 0.03$, $t_a=1.5\pm 0.3$ h, and $t_b=9.1\pm 3.3$ h, and the normalized zero-angle SANS intensity reaches a nonzero value of $0.76\pm 0.02$.

Number of exchangeable subunits

For a quantitative interpretation of the previously mentioned results, we first assumed that all subunits in the α7 tetradecamer had equal probability to exchange randomly with any subunit in another tetradecamer. Under this assumption, the mixture of h-α7 and d-α7 tetradecamers eventually reaches equilibrium between the isotopically mixed tetradecamers with different numbers of the deuterated subunits. Considering the incidence of the individual isotopic forms of tetradecamer, ${}^{N}I\left(0,\infty \right)$was calculated to be 0.0714 (Table 1), which is considerably smaller than the experimentally estimated value of $0.76\pm 0.02$. This raises the idea that the number of exchangeable subunits in one α7 tetradecamer is limited. Hence, under the constrain of the number of the swappable subunits n, we calculated the number ratio with x deuterated subunits $r_n\left(x,\infty \right)$ and the corresponding normalized zero-angle scattering intensities in the equilibrium states ($t=\infty$) as follows:

$$r_n\left(x,\infty \right)={\left(\frac{1}{2}\right)}^{\left(n+1\right)}\left({}_{n}C_x+{}_{n}C_{x-(14-n)}\right),$$ (2)

$${}_{a}C_b=0\left(a<borb<0\right),$$ (3)

$${}^{N}I_n\left(0,\infty \right)=\sum _{x=0}^{14}{r}_n\left(x,\infty \right)\times {\left(\frac{7-x}{7}\right)}^2.$$ (4)

Table 1.

Normalized zero-angle scattering intensity in the equilibrium state ^NI_n (0,∞) calculated for varying numbers of swappable subunits, n

n	0	1	2	3	4
${}^{N}I_n\left(0,\infty \right)$	1	0.867	0.745	0.633	0.531
n	5	6	7	8	9
${}^{N}I_n\left(0,\infty \right)$	0.439	0.357	0.286	0.224	0.173
n	10	11	12	13	14
${}^{N}I_n\left(0,\infty \right)$	0.133	0.102	0.0816	0.0714	0.0714

By inspection of the calculated ${}^{N}I_n\left(0,\infty \right)$ values (Table 1), we concluded that the number of the swappable subunits is two in one α7 tetradecamer; ${}^{N}I_2\left(0,\infty \right)=0.745$, which is in good agreement with the experimental value of $0.76\pm 0.02$. This strongly suggests that one subunit could be swappable in one heptameric ring. No more extensive subunit-swapping was observed at least for 48 h (data not shown).

Kinetics of subunit exchange

Given that the subunit exchange process can be described as a simple bimolecular exchange model (Fig. 3 A), every two swappable subunits in every tetradecamer have an equal exchange probability meaning that every reaction has four subreactions with an equal reaction probability. For example, an exchange reaction between Hhd and Dhd (at  the center of the middle line in Fig. 3 A) includes the following four subreactions with equal reaction probabilities:

$$\text{H}h\text{d}+\text{D}h\text{d}\to \text{H}h\text{d}+\text{D}h\text{d},$$ (5)

$$\text{H}h\text{d}+\text{Dh}d\stackrel{k_2}{\to }\text{H}d\text{d}+\text{Dh}h,$$ (6)

$$\text{Hh}d+\text{D}h\text{d}\stackrel{k_3}{\to }\text{Hh}h+\text{D}d\text{d},$$ (7)

$$\text{Hh}d+\text{Dh}d\to \text{Hh}d+\text{Dh}d,$$ (8)

where H and D represent 12 unswappable subunits, and h, (h) and d, (d) represent the exchangeable (exchanging) subunits. Here, subreaction 6 yields Hdd and Dhh tetradecamers with probability k₂, while subreaction 7 yields Hhh and Ddd tetradecamers with probability $k_3\left(=k_2\right)$. The remaining two subreactions 5 and 8 can be ignored because they do not affect the number ratio of the tetradecamers. On the other hand, the reaction of (Hhh + Ddd) with k₁ or (Hdd + Dhh) with k₄ (at the top and bottom of the middle line in Fig. 3 A, respectively) makes four sets of (Hhd + Dhd) without any branches. This means that the probabilities of the subreactions 6 and 7 are one-quarter of that of the reaction of (Hhh + Ddd) or (Hdd + Dhh). Therefore, the exchange probabilities for the reactions in Fig. 3 A are k₁ = k₄ = 4k₂ = 4k₃. In the same manner, we obtain k₁ = k₄ = k₉ = k₁₁ = 2k₅ = 2k₆ = 2k₇ = 2k₈ = 4k₂ = 4k₃ = 4k₁₀ = 4k₁₂.

Figure 3.

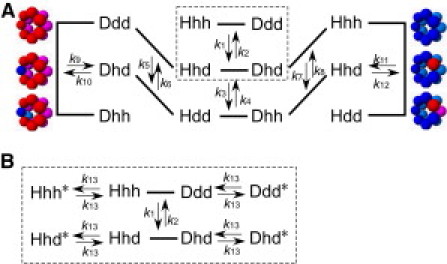
Subunit exchange schemes of two kinetics models. (A) Scheme of simple bimolecular exchange model. The tetradecamer constitution is expressed by H and D for 12 unswappable subunits, and h and d for two swappable subunits. For simplicity, the exchange reactions, which do not cause intensity change, such as Hhh + Dhh↔f Hhh + Dhh (an italic letter means an exchanging subunit), are not shown. Top, middle, and bottom rows correspond to the α7 tetradecamers with zero, one, and two differently labeled subunit(s), respectively. Typical α7 tetradecamers are drawn on the left and right sides, where the blue and red spheres show h-α7 and d-α7 subunits, respectively. $k_1-k_{12}$ denotes the exchange probabilities in the reactions, where $k_1=k_4=k_9=k_{11}=2k_5=2k_6=2k_7=2k_8=4k_2=4k_3=4k_{10}=4k_{12}$ (see text). (B) Extended exchange scheme by the two-step exchange model assuming the transition between active and inactive (^∗) states of the swappable α7 subunit. It is a modification of the reaction scheme Hhh + DddH ⇌Hhd + Dhd (boxed with dashed line in panel A) and exemplifies the extension of the model. k₁₃ is the rate constant of the transition.

Here, the time evolution of the number ratio of each tetradecamer is given as the solutions of a system of differential equations: in the following, as an example, the differential equation of [Hhd(t)] is shown,

$$\begin{array}{c}\frac{d\left[\text{Hhd}\left(t\right)\right]}{dt}=k_1\left[\text{Hhh}\left(t\right)\right]\left[\text{Ddd}\left(t\right)\right]\\ -\left(k_2+k_3\right)\left[\text{Hhd}\left(t\right)\right]\left[\text{Dhd}\left(t\right)\right]\\ +k_4\left[\text{Hdd}\left(t\right)\right]\left[\text{Dhh}\left(t\right)\right]-k_5\left[\text{Hhd}\left(t\right)\right]\left[\text{Ddd}\left(t\right)\right]\\ +k_6\left[\text{Dhd}\left(t\right)\right]\left[\text{Hdd}\left(t\right)\right]+k_7\left[\text{Dhd}\left(t\right)\right]\left[\text{Hhh}\left(t\right)\right]\\ -k_8\left[\text{Dhh}\left(t\right)\right]\left[\text{Hhd}\left(t\right)\right]+k_{11}\left[\text{Hhh}\left(t\right)\right]\left[\text{Hdd}\left(t\right)\right]\\ -k_{12}{\left[\text{Hhd}\left(t\right)\right]}^2.\end{array}$$ (9)

The differential equations of the number ratio of the other tetradecamers are given in the same manner. The equations were numerically solved starting from the initial state, [Hhh(0)] = [Ddd(0)] = 0.5 and [Hhd(0)] = [Hdd(0)] = [Dhd(0)] = [Dhh(0)] = 0. In addition, ${}^{N}I_2\left(0,t\right)$ is also given as follows (Eq. 4).

$$\begin{array}{c}{}^{N}I_2\left(0,t\right)=\left(\left[\text{Hhh}\left(t\right)\right]+\left[\text{Ddd}\left(t\right)\right]\right){\left(\frac{7}{7}\right)}^2\\ +\left(\left[\text{Hhd}\left(t\right)\right]+\left[\text{Dhd}\left(t\right)\right]\right){\left(\frac{6}{7}\right)}^2\\ +\left(\left[\text{Hdd}\left(t\right)\right]+\left[\text{Dhh}\left(t\right)\right]\right){\left(\frac{5}{7}\right)}^2.\end{array}$$ (10)

By substituting the numerical solutions of the six tetradecamers in Eq. 10, we obtained the simulated ${}^{N}I_2\left(0,t\right)$. This time evolution is expressed with monoexponential decay function (green line in Fig. 2 D), which does not reproduce the experimental results, suggesting that the exchange process involves at least two steps.

In general, proteins undergo conformational change to express biological functions such as enzymatic reactions and molecular recognition events. A typical example is the induced-fit mechanism in enzymatic reactions, in which enzymes change their conformations upon binding to substrates to facilitate catalysis (30). In addition, growing evidence indicates that proteins exhibit multiple conformations including those involved in the ligand-binding states even in the absence of the ligands (31). In these cases, ligand-binding processes cannot be expressed as a single exponential process (31).

Such concepts may be applicable to the subunit exchange process of homooligomeric proteins: in the two-step exchange system, the swappable subunits are in equilibrium between the active (or exchangeable) and inactive (or resting) states as follows,

$$\text{Xyz}\stackrel{k_{13}}{\underset{k_{13}}{\rightleftharpoons }}{\text{Xyz}}^{\ast },$$ (11)

where ^∗ indicates an inactive state. The exchange occurs when two homooligomers each containing the active subunit(s) meet. Therefore, the interconversion given in Eq. 11 is introduced to every exchange reaction with the equal rate constant k₁₃ as shown in Fig. 3 B. To obtain the time evolution of the number ratios of tetradecamers in this model, we improved our numerical calculation approach in the iteration. That is, in every iteration we recalculated the number ratios of active tetradecamer for every tetradecamer and then calculated the system of differential equations. For example, the active tetradecamer ratio of Hhh is calculated using the following differential equation,

$$\frac{d\left[\text{Hhh}\left(t\right)\right]}{dt}=-k_{13}\left(\left[\text{Hhh}\left(t\right)\right]-\left[{\text{Hhh}}^{\ast }\left(t\right)\right]\right).$$ (12)

Subsequently, we preformed the calculation as indicated in the simple bimolecular exchange model.

Thus, ${}^{N}I_2\left(0,t\right)$ is expressed with a biexponential decay function, where the ratio of time constants depends upon the ratio of k₁ and k₁₃. The best biexponential function for ${}^{N}I_2\left(0,t\right)$ with $k_1/k_{13}=5.5$ well reproduces the experimental data (blue line in Fig. 2 D). According to this model, the conformational transition can be a rate-limiting step in the subunit exchange process.

In perspectives for future work to validate this model, the subunit exchange rates should be measured at various protein concentrations. The exchange reaction rate with a bimolecular step must depend on the concentration of the α7 tetradecamer while the conformational transition rates do not. These experiments can be performed by using a SANS spectrometer with a higher flux neutron beam.

In conclusion, the study demonstrated that only one subunit is exchangeable among the seven α7 subunits constituting one heptameric ring. This means that the α7 heptameric ring is probably not sevenfold symmetric, although the previous structural studies could not predict such an asymmetric property because of low spatial resolution (22,23). The kinetic asymmetry of subunit exchange of the α7 tetradecamer not only provides important clues to the underlying mechanisms of proteasome subunit assembly but also offers general insights into the formation and dynamics of quaternary structures of homooligomeric proteins. Deuteration-assisted, time-resolved SANS has opened up new opportunities for this unexplored field of research.