GB1 Is Not a Two-State Folder: Identification and Characterization of an On-Pathway Intermediate

Abstract

The folding pathway of the small α/β protein GB1 has been extensively studied during the past two decades using both theoretical and experimental approaches. These studies provided a consensus view that the protein folds in a two-state manner. Here, we reassessed the folding of GB1, both by experiments and simulations, and detected the presence of an on-pathway intermediate. This intermediate has eluded earlier experimental characterization and is distinct from the collapsed state previously identified using ultrarapid mixing. Failure to identify the presence of an intermediate affects some of the conclusions that have been drawn for GB1, a popular model for protein folding studies.

Introduction

Understanding the role and structure of partially folded intermediates is of fundamental mechanistic importance for protein folding studies. Earlier work suggested that the folding of small single domain proteins generally conforms to an all-or-none behavior (1), involving simultaneous formation of secondary and tertiary structure (2). Following this view, folding occurs in a two-state fashion, via condensation around a marginally stable nucleus, and intermediates tend to be avoided (3). When the inherent stability of folding nuclei is increased, however, even very simple protein systems appear to fold in a more complex fashion (4), with population of partially folded intermediates, which may either transiently accumulate leading to multiphasic kinetics, or be a high energy species en route to the native state (5). The presence of such local minima in the landscape is very difficult to address experimentally (6) and intermediates may sometimes escape detection.

The B1 IgG-binding domain of streptococcal protein G, generally called GB1, has played a central role in protein folding studies being the system of choice in more than 200 publications carried out using a wide variety of experimental and theoretical approaches; see for example (7–19). Because of its small size and its simple and highly symmetrical topology, this small protein domain has represented an ideal candidate for a vast number of different studies. Over-and-above contrasting views on the presence of a low energy early collapsed state as detected by ultrarapid mixing (13,15,16), experimental work has been taken to indicate that GB1 folds in a canonical two-state process (20), via a polarized folding transition state with native-like structure localized in the C-terminal β-hairpin (14). On the other hand, despite the evidence arising from experiments, some theoreticians have predicted the presence of intermediates and heterogeneous pathways for the folding of GB1 (19), raising some doubts about the applicability of a bona fide two-state mechanism. In this study, we have undertaken an extensive characterization of the folding of GB1 by experiments and simulations that provide evidence for a folding intermediate. This partially structured state is an on-pathway species that, despite two decades of studies, escaped detection and characterization.

Materials and Methods

The buffers used were 50 mM Glycine/NaOH from pH 9.6 to 9.0, 50 mM Tris/HCl from pH 9.0 to 7.2, 50 mM Bis-Tris/HCl from pH 7.0 to 6.0, 50 mM sodium acetate from pH 5.5 to 3.8, 50 mM sodium formate from pH 3.4 to 3.0, and 50 mM sodium phosphate/phosphoric acid from pH 2.8 to 2.0. All reagents were of analytical grade.

Protein expression and purification

GB1 gene was cloned into the vector pG58, which encodes an engineered subtilisin prosequence as the N-terminus of the fusion protein. Proteins were purified employing an affinity chromatography previously developed (21). Soluble cell extract of prodomain fusion proteins was injected onto a 5-ml Bio-Scale Mini Profinity eXact cartridge (Bio-Rad, Hercules, CA) at 5 ml/min to allow binding and then washed with 10-column volumes of 100 mM NaPO₄ (pH 7.2) to remove impurities. To cleave and elute the purified target proteins, 15 ml of 100 mM NaF in the presence of 100 mM NaPO₄ (pH 7.2) were injected at 5 ml/min. After the first 10 ml, the flow was stopped and the column incubated for 30 min to allow complete cleavage. After elution, the purified proteins were then dialyzed to remove sodium fluoride.

Equilibrium unfolding

Equilibrium denaturations were carried out on a Fluoromax single photon counting spectrofluorometer (Jobin-Yvon, Edison, NJ). Tryptophan fluorescence emission spectra were recorded in a cuvette (1-cm light path) between 300 and 400 nm. The excitation wavelength was 280 nm. Protein concentrations were typically 3 μM.

Stopped-flow measurements

Single mixing kinetic folding experiments were carried out on a Pi-star or on an SX-18 stopped-flow instrument (Applied Photophysics, Leatherhead, UK); the excitation wavelength was 280 nm and the fluorescence emission was measured using a 320 nm cut-off glass filter. In all experiments, performed at 25°C, refolding and unfolding were initiated by an 11-fold dilution of the denatured or the native protein with the appropriate buffer. Final protein concentrations were typically 1 μM. The observed kinetics were always independent of protein concentration (from 0.5 to 5 μM after mixing protein concentration), as expected from monomolecular reactions without effects due to transient aggregation (22).

Data analysis

Equilibrium experiments

Assuming a standard two-state model, the guanidine-induced denaturation transitions were fitted to the following equation:

$$\Delta {\text{G}}_{\text{d}}=m_{\text{D}-\text{N}}\left(\text{D}-{\text{D}}_{50}\right),$$

where m_D–N is the slope of the transition (proportional to the increase in solvent-accessible surface area on going from the native to the denatured state) and D₅₀ is the midpoint of the denaturation transition. An equation, which takes into account the pre- and post-transition baselines, was used to fit the observed unfolding transition (23). Equilibrium folding stabilities calculated at different pH conditions are listed in Table 1.

Table 1.

Folding parameters of GB1 as a function of pH

pH	kDI (s−1)	kNI/(1 + Kpart) (s−1)	Kpart	ΔGD-N∗ (kcal mol−1)	ΔGD-N† (kcal mol−1)
2.0	1000 ± 90	11.0 ± 3.0	1.7 ± 0.2	2.7 ± 0.3	3.9 ± 0.8
2.5	1000 ± 90	19.2 ± 4.8	3.0 ± 0.4	2.3 ± 0.2	3.0 ± 0.7
3.0	1050 ± 95	5.2 ±1.3	0.9 ±0.1	3.1 ± 0.4	3.8 ± 0.4
3.5	1200 ± 120	5.1 ±1.3	1.2 ±0.1	3.2 ± 0.2	3.9 ± 0.4
4.0	1400 ± 120	1.3 ± 0.3	0.42 ± 0.09	4.1± 0.2	4.5 ± 0.4
4.5	1800 ± 170	0.4 ± 0.1	0.20 ± 0.04	5.0 ± 0.2	4.2 ± 0.4
5.0	1300 ± 120	0.15 ± 0.04	0.09 ± 0.02	5.3 ± 0.2	4.9 ± 0.5
5.5	1370 ± 100	0.15 ± 0.04	0.13 ± 0.03	5.4 ± 0.1	4.6 ± 0.5
6.0	720 ± 70	0.12 ± 0.03	0.09 ± 0.02	5.1 ± 0.1	5.2 ± 0.5
6.5	830 ± 70	0.14 ± 0.04	0.10 ± 0.02	5.1 ± 0.2	4.7 ± 0.5
7.0	670 ± 70	0.19 ± 0.05	0.12 ± 0.02	4.8 ± 0.2	5.3 ± 0.5
7.5	630 ± 70	0.27 ± 0.07	0.11 ± 0.02	4.6 ± 0.2	4.3 ± 0.4
8.0	600 ± 60	0.4 ± 0.1	0.12 ± 0.03	4.3 ± 0.3	4.3 ± 0.4
8.5	500 ± 40	0.6 ± 0.2	0.11 ± 0.02	3.9 ± 0.2	3.8 ± 0.4
9.0	390 ± 40	0.9 ± 0.2	0.13 ± 0.03	3.6 ± 0.2	3.3 ± 0.3
9.6	220 ± 25	1.3 ± 0.3	0.11 ± 0.02	3.0 ± 0.2	3.0 ± 0.3

^∗Calculated from chevron plot analysis. The Chevron plots were fitted globally to a three-state model with shared m-values. k_DI is the microscopic rate constant for the formation of the intermediate from the denatured state; k_NI is the microscopic rate constant for the unfolding of the native state to the intermediate state; K_part is the partitioning factor k_ID/k_IN reflecting the difference between the activation barriers for the intermediate to revert to the reagents rather than proceeding to the products. The analysis returned a total m_D-N = 1.95 ± 0.2 kcal mol⁻¹ M⁻¹. The Tanford β-values for the two transition states were β_TS1 = 0.76 ± 0.04 and β_TS2 = 0.93 ± 0.04.

^†Calculated from equilibrium denaturation. Equilibrium denaturations were fitted both individually and globally with shared m_D-N value. The global analysis returned m_D-N = 1.75 ± 0.2 kcal mol⁻¹ M⁻¹. This value was consistent within error with the values obtained by fitting individually each independent equilibrium experiments, as well as with the value calculated from kinetic experiments.

Kinetic experiments

Analysis was performed by nonlinear least-squares fitting of single exponential phases using the fitting procedures provided in the Applied Photophysics software. The chevron plots were fitted globally by numerical analysis based on a three-state model as discussed in the Results section. The global fit of chevron plots at different pH was obtained with Prism software (Graphpad).

Molecular dynamics simulation methods

All-atom explicit solvent molecular dynamics (MD) simulations were performed for protein GB1 by starting with the NMR structure (PDB 3GB1 (24)). Simulations included one native state simulation at 25°C (21 ns) and five unfolding simulations at 225°C (1 × 41 ns, 1 × 38, 3 × 2 ns) resulting in a total of 106 ns of simulation time. All simulations were performed using our in-house MD software, in lucem molecular mechanics (25) with the Levitt et al. (26) all-atom force field. The microcanonical ensemble was used, where the number of atoms, unit cell volume, total energy, and linear momentum were conserved. The protein was solvated in a periodic box of flexible F3C water molecules (27). For a more in-depth discussion of the simulation protocols please see (28).

One-dimensional reaction coordinate

To identify the transition and intermediate states, we calculated a multidimensional property space derived from 15 physical properties of the protein and then calculated a one-dimensional (1D) reaction coordinate based on these 15 properties (29). The 15 properties were native contacts, nonnative contacts, radius of gyration, end-to-end distance, main-chain solvent accessible surface area (SASA) (30) side-chain SASA, polar SASA, nonpolar SASA, main-chain polar SASA, main-chain nonpolar SASA, side-chain polar, side-chain nonpolar SASA, total SASA, fraction of helix, and fraction of β-structure. The distance between two structures in property space is calculated as the average Euclidean distance between the 15-dimensional points. The mean distance in property space was calculated for each time point in a simulation of interest to the native state reference, which contained all the structures of the native state simulation excluding the first nanosecond. The 1D reaction coordinate was created from a histogram of the mean distance to reference for all structures. To compare with experimental Tanford β-values, we calculated the ratio of the average total (SASA) for the transition state ensemble and the average total SASA for the native state simulation.

To investigate the unfolding pathway of GB1 we calculated contact matrices, for each state identified, based on the fraction of time that the residues were in contact. A pair of residues was considered in contact if it contained carbon atoms that were <5.4 Å apart or one carbon atom or any other atoms <4.6 Å.

Results

Equilibrium denaturation of GB1

To study the folding mechanism of GB1, we carried out both equilibrium and kinetic experiments. Guanidine-induced equilibrium denaturation of GB1, monitored by fluorescence spectroscopy, was investigated at 25°C exploring a wide range of pH values, from 2.0 to 9.6 (data not shown). Equilibrium denaturation curves were fitted both individually and globally with a shared m_D-N value. Parameters obtained from global analysis, listed in Table 1, were consistent within error with the values obtained by fitting each independent equilibrium experiment individually, as well as with the values calculated from kinetic experiments, confirming the two-state nature of the equilibrium unfolding transition of GB1. The denaturation profiles were all consistent with two-state unfolding and yielded an m-value of 1.75 ± 0.2 kcal mol⁻¹ M⁻¹.

Kinetic experiments

The folding and unfolding kinetics of GB1 were investigated at several pH values, ranging from 2.0 to 9.6. In all cases, folding and unfolding time courses were fitted satisfactorily to a single exponential decay at any final guanidine concentration. Each rate constant was obtained from the average of at least five independent shots in stopped-flow experiments. Semilogarithmic plots of the observed folding/unfolding rate constant of GB1 versus denaturant concentration (chevron plot) at the different pH values are presented in Fig. 1. Surprisingly, the unfolding arm of the chevron plots at pH values higher than 6.0 shows a deviation from linearity that becomes evident at high guanidine concentrations (rollover effect). This deviation is highlighted in Fig. 2 where the chevron plot of GB1 measured at pH 9.0 is reported together with the residuals of the fit, showing a clear systematic deviation from the expected values for a two-state behavior. This effect escaped previous studies probably because of the restricted range of experimental conditions, limited to [GdnHCl] < 5.5 M (14,15). Indeed, if we were to ignore the data we recorded for [GdnHCl] > 5.5 M, the unfolding arm of the chevron plots would appear essentially linear but would display a puzzling change in slope with the different experimental conditions.

Figure 1.

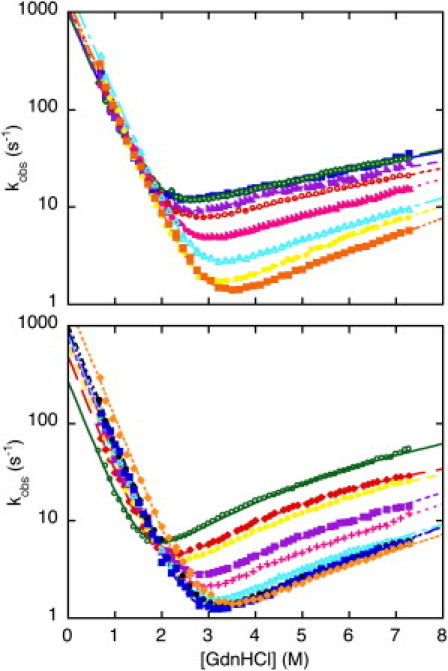
Folding kinetics of GB1. Top panel: Chevron plots measured from pH 2.0 to pH 5.5 at 25°C (blue, pH 2.0; green, pH 2.5; violet, pH 3.0; red, pH 3.5; magenta, pH 4.0; cyan, pH 4.5; yellow, pH 5.0; orange, pH 5.5). Bottom panel: Chevron plots measured from pH 5.5 to pH 9.6 at 25°C (orange, pH 5.5; blue, pH 6.0; black, pH 6.5; cyan, pH 7.0; magenta, pH 7.5; violet, pH 8.0; yellow, pH 8.5; red, pH 9.0; green, pH 9.6). Lines are the best global fit to a three-state equation with shared m-values. If data at [GdnHCl] > 5.5 M were to be ignored, a quasilinear unfolding arm with an apparent change in unfolding m-values would be seen.

Figure 2.

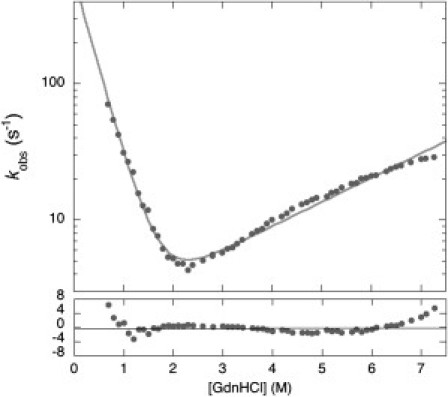
Chevron plot of wild-type GB1 measured at pH 9.0. The gray line is the best fit to a two-state equation; the residuals of the fit below show a clear systematic deviation from the expected values for a two-state behavior. Therefore, data at [GdnHCl] > 5.5 M are critical to detect the rollover effect.

Analysis of chevron plots is a common and powerful tool for detecting protein folding intermediates (31). In fact, if there is only one rate-limiting energy barrier, the logarithm of the observed folding and unfolding kinetics is expected to comply with a V-shaped dependence (32). Therefore, a deviation from linearity in either the folding or the unfolding branches of the curve may be considered of diagnostic value for the identification of intermediates (33,34). If a partially folded intermediate is present, the folding kinetics can be described by a three-state mechanism:

$$\text{D}\begin{array}{c}\stackrel{k_{\text{DI}}}{\to }\\ \underset{k_{\text{ID}}}{\leftarrow }\end{array}\text{I}\begin{array}{c}\stackrel{k_{\text{IN}}}{\to }\\ \underset{k_{\text{NI}}}{\leftarrow }\end{array}\text{N},$$ (Scheme 1)

where k_DI is the microscopic rate constant for the formation of the intermediate from the denatured state, k_ID is the microscopic rate constant for the unfolding of the intermediate to the denatured state, k_IN is the microscopic rate constant for the formation of the native state from the intermediate, and k_NI is the microscopic rate constant for the unfolding of the native to the intermediate state. Two approximations have been introduced to describe the folding pathway of three-state systems. The intermediate may be assumed to be in a fast preequilibrium with one of the ground states, the curvature in the chevron plot being caused by accumulation of the intermediate (33). Alternatively, if the intermediate is assumed to be at steady state and at negligible concentration, the curvature in the observed (un)folding kinetics arises from a change in the rate-limiting step with changing denaturant concentration (34–38). Both approximations lead to nearly identical numerical solutions and are thus indistinguishable based only on analysis of the rate constants. In theory, however, accumulation of the intermediate should lead to multiphasic observed kinetics and more than one relaxation rate constant should be observed. In the case of GB1, because we observed single exponential folding kinetics under all conditions explored, we favored a model involving a high-energy on-pathway intermediate and the observed chevron plots were fitted to the following equation:

$$k_{\text{obs}}=k_{\text{DI}}+\frac{k_{\text{NI}}}{1+K_{\text{part}}},$$

where K_part is the partition factor k_ID/k_IN proportional to the difference between the activation barriers for the intermediate state to revert to the reagents rather than proceeding to the products. The logarithm of each microscopic rate constant was assumed to vary linearly with denaturant concentration (the slope of each dependence yielding the corresponding m-value). The observed chevron plots were fitted globally with shared m-values. Parameters calculated from global analysis (listed in Table 1) allow the identification of the relative positions of the two activation barriers along the reaction coordinate in terms of their relative accessible surface area (Tanford β-value), resulting in β_T-values of 0.76 ± 0.04 for the transition state TS1 and of 0.93 ± 0.04 for the native-like activation barrier TS2. The excellent statistical parameters of the global analysis indicate that the two activation barriers are robust to changes in pH conditions and display a conserved solvent accessible surface area when pH and protein stability are altered.

The effect of pH on the folding kinetics of GB1

The analysis of the chevron plots reported in Fig. 1 allowed determination of the folding and unfolding rate constants of GB1 over a very wide range of pH. The folding rate constants display a negligible dependence on pH (data not shown). A plot of the logarithm of the apparent unfolding rate constants from the native state to TS2 (k_NI) and TS1 (formally equivalent to k_NI/(1 + K_part)) as a function of pH are reported in Fig. 3. Interestingly, both TS1 and TS2 display sigmoidal transitions at acidic and alkaline pH consistent with protonation of at least two groups in the native state with apparent pK_a values of ∼4 and ∼8. Importantly, the acid transition for the unfolding rate constant of TS1 (changing by almost two orders of magnitude) is more pronounced than that for the unfolding rate constant of TS2 (changing by less than an order of magnitude), suggesting the contribution of a salt bridge that is weak or not formed in TS1, but is consolidated in TS2. As detailed in the Discussion section, inspection of the three-dimensional structure of GB1 and the unfolding profiles obtained by MD simulations suggest the acidic group to be either Glu-15 or Glu-56.

Figure 3.

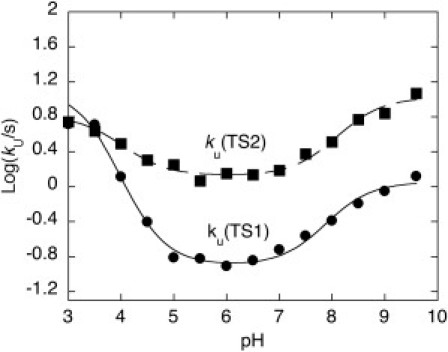
Unfolding rate constants versus pH. Logarithm of the calculated unfolding rate constants from the native state N to the first transition state k_u(TS1), and from the native state to the second transition state k_u(TS2) as a function of pH. The lines are the best fit to a model involving the protonation of two groups. In both cases, we obtained approximately the same pK_a of ∼4 and ∼8.

MD simulations

To further explore the putative intermediate state, all-atom explicit solvent MD simulations of GB1 were carried out. Multiple simulations were performed to model thermal unfolding (at 225°C) as well as native-state behavior at 25°C (control). The transition and intermediate states were identified by calculating a multidimensional property space derived from 15 physical properties of the protein and then embedding this within a 1D reaction coordinate based on the 15 properties (as detailed in Materials and Methods) (Fig. 4). Five independent thermal unfolding simulations were performed; all simulations passed through the intermediate state (Fig. 5) however only two of them (runs 2 and 4) showed the buildup of an intermediate as defined by the 1D reaction coordinate in Fig. 4 and thus warranted further analysis. The native, transition, intermediate and denatured states were identified for the two simulations displaying buildup of the intermediate. The calculated Tanford β_T-values based on simulations, in particular on total SASA, were 0.94 and 0.92 for TS2 in simulations 2 and 4, respectively, in agreement with the experimentally derived value of 0.93 ± 0.04. For TS1 the calculated β_T-values were 0.73 and 0.75 for runs 2 and 4, respectively, in agreement with the experimental value of 0.76 ± 0.04.

Figure 4.

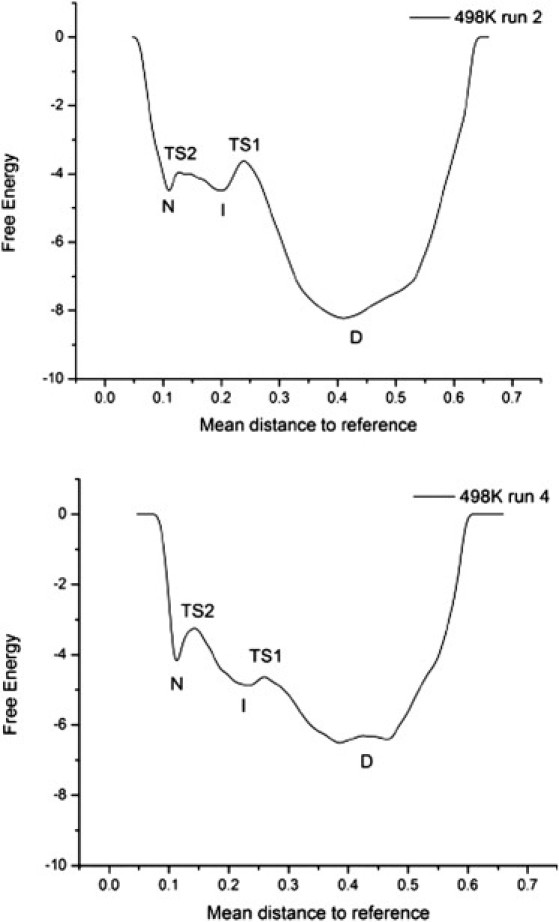
Free energy reaction coordinate for two unfolding simulations of GB1. A 1D reaction coordinate is created by calculating the mean distance to reference in a 15-dimensional property space for all structures in an unfolding simulation. The free energy reaction coordinates are calculated by taking the negative log of the counts in a mean distance to the reference histogram. Each 498 K simulation is shown with a black line. The location of unfolding state D is indicated on each free energy reaction coordinate. Top: Run 2 shows three-state unfolding with TS2 located between 0.12 and 0.13 mean distance to reference and TS1 located between 0.23 and 0.25 mean distance to reference. Bottom: Run 4 also shows three-state unfolding with TS2 located between 0.135 and 0.15 mean distance to reference and TS1 located between 0.25 and 0.265 mean distance to reference.

Figure 5.

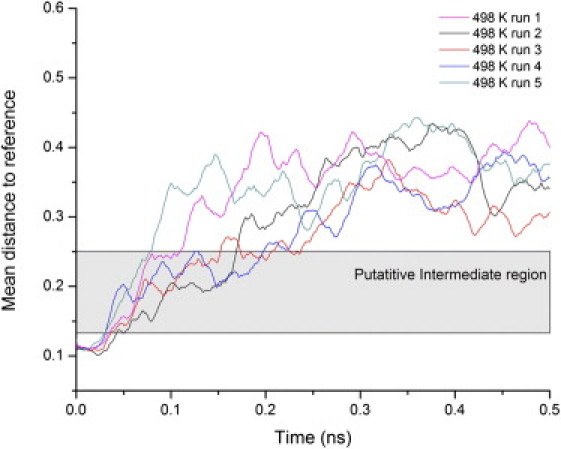
Mean distance to reference versus time for each unfolding simulation at 498 K. Lines have been smoothed using adjacent averaging to remove noise. The intermediate state region (0.135 to 0.15) in property space was determined from the positions of TS1 and TS2 in the free energy reaction coordinates from Fig. 4 for runs 2 and 4. It is clear that runs 2 and 4 populate this region significantly while the others pass through the intermediate more rapidly.

Considering the unfolding runs in reverse, the simulated folding pathways were largely conserved in the different runs (Fig. 6), the main difference originating from formation of nonnative contacts in the loop between strands A and B. Starting in the denatured state, nonnative contacts dominated the contact matrix and there was residual helix, which gave rise to native contacts. Considering TS1, contacts began to form between strands A and B, strands A and D, and strands C and D; the helix was nearly fully formed. The intermediate contained also contacts between strand B and the helix. There were still native contacts between strands A and B. The N-terminal ends of strand A formed contacts with strand D, although many were short-term nonnative contacts. Contacts also formed between strand C and the helix as the latter began to move toward the protein core. Contacts between strands C and D were present and almost fully formed. From I to TS2 the protein gained native contacts between the helix and strand A that allowed the helix to dock to the core. Contacts between strands A and B, strands C and D, and strands A and D became almost fully native-like. In moving from TS2 to the native state, the helix docked to the core of the protein making contacts with strands A, B, and C. The contacts between strands A and B, strands C and D, and strands A and D became fully formed.

Figure 6.

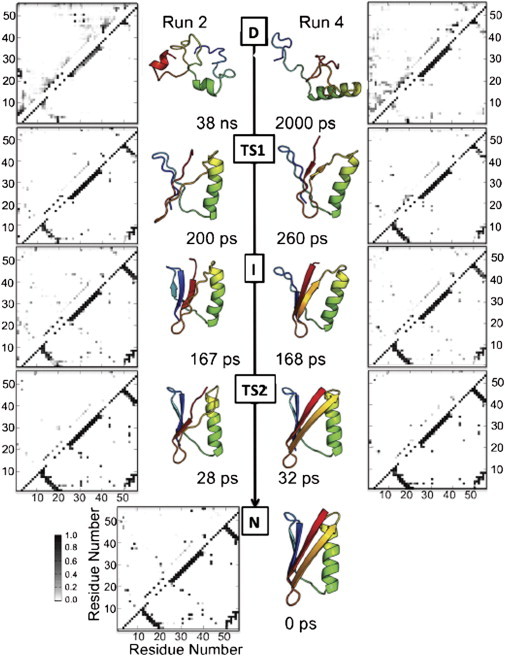
Folding pathway and contact maps for two unfolding simulations of GB1. Representative structures from each state are colored in rainbow from red to blue. The native structure of GB1 contains four β-strands (A = red, B = orange, C = cyan, and D = blue) and a helix. Contact maps show the fraction of time residues were in contact with nonnative interactions (above the diagonal) or with native contacts (below). Contacts are colored in a grayscale from white to black, where white indicates that the residues were never in contact and black those that were in contact 100% of the time. Native contacts are reported over the full 498 K simulation (n = 20,000). TS, I and D contacts are reported for the time points constituting the ensemble of structures as determined by the free energy reaction coordinate (Fig. 5).

Discussion

We have carried out an extensive characterization of the folding pathway of GB1 by experiments and MD simulations. The kinetic experiments, carried out over a wide range of pH values (from 2.0 to 9.6), highlighted the presence of a rollover effect in the chevron plots, which is typically diagnostic of the presence of a folding intermediate. An intermediate was detected also by unfolding MD simulations, which allowed us to present a structural characterization of the (un)folding pathway.

The existence of an intermediate in the folding of GB1 has been previously proposed by Roder and co-workers (15,16), who suggested the presence of a collapsed state accumulating in the μs time range, as observed by continuous-flow ultrarapid mixing experiments. This low-energy intermediate (which later was questioned by Sosnick and co-workers (13)) was also consistent with a detailed ab initio simulation reported by Kmiecik and Kolinski (39). Importantly, however, the partially folded state identified in our work is distinct from that previously suggested, being a high energy species that never accumulates; nevertheless, its existence suggests that GB1 folds via a complex and rough energy barrier with at least two discrete major transition states. Thus, while the equilibrium unfolding is consistent with a simple two-state model (7,8,20), the folding and unfolding kinetics are more complex.

When folding is characterized by a complex chevron plot, the deviation from linearity observed may have different origins: i), the curvature may be due to a movement of the position of the transition state along a single broad barrier (40,41); or ii), it may reflect a change in the rate-limiting step suggestive of a multistate process (34,35,37,38). In the case of GB1, the curved chevron plots are observed only above pH 6 (Fig. 1), making the broad transition state model less likely because it would imply that it is possible to drastically distort the folding free energy profile and to switch between a narrow energy maximum (linear chevron plot) to a broad energy maximum (curved chevron plot) by changing pH. Furthermore, in analogy to what has been observed previously for other proteins (35,42,43), detection of a rollover effect only under some solvent conditions seems more consistent with a multistep folding pathway. The unbiased unfolding MD simulations reported in this work, which identified a folding intermediate, also support this interpretation. The excellent statistical parameters of the global fit suggest that the two transition states surrounding the intermediate are relatively robust and maintain their overall structural features when solvent conditions are varied. This observation is in stark contrast with previous experimental work, which suggested the unfolding m-value to depend strongly on experimental conditions (14–16). We conclude that both TS1 and TS2 display a robust structure that is by and large maintained when solvent and/or sequence composition is altered.

It is of interest to analyze the dependence on pH of the unfolding rate constants measured for the two transition states (Fig. 3). Both energy barriers appear to display a monotonic transition at acidic and alkaline pH values. Both profiles are consistent with a model involving the protonation of two different groups with apparent pK_a values of ∼4 and ∼8 (Fig. 3). While in the alkaline region the total change in activation free energy is approximately the same for TS1 and TS2, the acidic transition is more pronounced in TS1, suggesting the presence of a charged interaction that is weak or not formed in TS1 but consolidated in TS2. Inspection of the three-dimensional structure of GB1 suggests that such a salt bridge may be either Lys-4-Glu-15 (located at the N-terminal β-hairpin, strands A and B) or Lys-10-Glu-56 (between the N-terminal turn and the C terminus of the protein). Both interactions would be consistent with MD simulations, suggesting that the contacts between strands A and B, strands C and D, and strands A and D are just incipient in TS1, whereas they are almost fully formed in TS2.

The thermal unfolding simulations are in good agreement with the experiments and reveal an on-pathway intermediate. The β_T-values for the transition states on either side of the intermediate ensemble are in excellent agreement with the experimentally determined ones. The structure of the intermediate is very native-like with reduced native contacts between β-strands and loss of contacts between the helix and the core of the protein, which facilitates undocking (Fig. 6). Importantly, although some studies have proposed that GB1 folds via a polarized transition state, with native-like structure located in the C-terminal hairpin (14,44), our simulations suggest folding occurs via a slightly different mechanism. In fact, structure formation appears to involve a more extended nucleus, which is stabilized by both the N- and C-terminal β-hairpins, as well as by contacts between the N- and C-terminal strands. This scenario suggests the presence of multiple overlapping folding nuclei (or a diffuse, rather than polarized, nucleus).

To conclude, we have reassessed the folding of GB1 by kinetic experiments and MD simulations and show that, while its equilibrium unfolding conforms to a two-state mechanism, folding and unfolding kinetics are more complex and involve the presence of an energy barrier with at least two discrete transition states and one on-pathway intermediate. The structures of these transition states, which we have assessed by MD simulations, appear robust to changes in pH and are characterized by an extended nucleus, which is stabilized by both the N- and C-terminal β-hairpins, as well as by contacts between the N- and C-terminal strands.