Automated Probabilistic Reconstruction of White-Matter Pathways in Health and Disease Using an Atlas of the Underlying Anatomy

Abstract

We have developed a method for automated probabilistic reconstruction of a set of major white-matter pathways from diffusion-weighted MR images. Our method is called TRACULA (TRActs Constrained by UnderLying Anatomy) and utilizes prior information on the anatomy of the pathways from a set of training subjects. By incorporating this prior knowledge in the reconstruction procedure, our method obviates the need for manual interaction with the tract solutions at a later stage and thus facilitates the application of tractography to large studies. In this paper we illustrate the application of the method on data from a schizophrenia study and investigate whether the inclusion of both patients and healthy subjects in the training set affects our ability to reconstruct the pathways reliably. We show that, since our method does not constrain the exact spatial location or shape of the pathways but only their trajectory relative to the surrounding anatomical structures, a set a of healthy training subjects can be used to reconstruct the pathways accurately in patients as well as in controls.

1. Introduction

Diffusion MRI has become an important tool in the study of a wide range of diseases affecting the brain, as it allows us to probe the shape and integrity of the white-matter pathways that connect functionally related cortical and subcortical regions. Although it is possible to compare diffusion measures between populations on a voxel-by-voxel basis, more specific hypotheses on disease progression can be tested if aggregate measures can be computed for specific pathways that are known or assumed to serve different brain networks.

Several diffusion tractography methods have been proposed over the years to reconstruct white-matter pathways. Most early methods were deterministic and followed the streamline approach, which modeled a path as a one-dimensional curve. The curve was grown from a starting point by taking steps in directions that were determined by the diffusion orientation in the underlying voxels (Conturo et al., 1999; Mori et al., 1999; Basser et al., 2000; Poupon et al., 2000; Lazar et al., 2003). Other deterministic methods were volumetric, modeling the path as a volume, and allowing it to grow in three dimensions (Jones et al., 1999; O’Donnell et al., 2002; Parker et al., 2002; Jackowski et al., 2005; Pichon et al., 2005). Both streamline and volumetric approaches were local, in the sense that the algorithm considered the image data at a single location to determine how to grow the path at each step. Statistical extensions to local streamline tractography were introduced to model uncertainty in the image data by drawing samples from an assumed local distribution of diffusion directions at each voxel (Behrens et al., 2003; Hagmann et al., 2003; Cook et al., 2005; Parker and Alexander, 2005; Friman et al., 2006) or by boot-strapping (Jones and Pierpaoli, 2005; Lazar and Alexander, 2005).

Local tractography algorithms, whether deterministic or probabilistic, are best suited for exploring all possible connections from one brain region, which is used as the tractography seed, to any other region. However, if the goal is to isolate specific white-matter pathways, the required post-processing of the streamlines poses various challenges. Typically a user with substantial neuroanatomical expertise needs to interact manually with the data on a pathway-by-pathway and subject-by-subject basis. For example, thresholds on the curvature of each pathway need to be adjusted by trial-and-error and regions that each pathway does or does not intersect need to be defined. This makes tractography studies time-consuming and compromises their robustness and reliability. Even if an automated method is used to cluster the streamlines into larger bundles a posteriori (O’Donnell and Westin, 2007; Maddah et al., 2008; Wassermann et al., 2010), the results are largely dependent on the quality of the original streamlines. For example streamline tractography might miss a sparser pathway if it is dominated by other, denser pathways that intersect it or that originate in the same region.

Global tractography methods were suggested as an alternative approach to address the problem of identifying specific white-matter pathways (Fletcher et al., 2007; Jbabdi et al., 2007; Melonakos et al., 2007). The global approach defines both end regions where the pathway is thought to terminate and searches the space of all possible connections between these two regions for the connection that best fits the data. Thus the entire pathway is estimated at once, rather than step-by-step. The solution is symmetric with respect to the two end regions, instead of treating one as the “seed” and the other as the “target.” Since global optimization integrates along the length of the pathway, it is less sensitive to localized regions of high uncertainty (e.g., pathway crossings) than the streamline approach. A challenge with global tractography is the size of the solution space, which consists of all possible connections between two regions. Although the pathway is typically parameterized in some way to contain the size of this space, searching through it remains cumbersome and sensitive to initialization, especially for large end regions.

To address these issues, we have developed TRACULA (TRActs Constrained by UnderLying Anatomy), a method for automated reconstruction of major white-matter pathways that is based on the global probabilistic approach of Jbabdi et al. (2007) and utilizes prior information on the anatomy of the pathways from a set of training subjects. Once the pathways have been labeled manually in the training set, their trajectories are combined with an automatic anatomical segmentation of the same subject (Dale et al., 1999; Fischl et al., 1999a,b, 2002, 2004a,b; Fischl and Dale, 2000) to derive a description of the pathways in terms of the structures that they intersect and neighbor. The knowledge on path anatomy that is extracted from the training set is then used to initialize a global probabilistic tractography algorithm and also to constrain its search space by penalizing connections that do not match our prior anatomical knowledge. This allows the algorithm to reconstruct the pathways reliably in a novel subject with no manual intervention, facilitating the analysis of large data sets.

An important question regarding our method is whether a training set consisting entirely of healthy subjects can be used to reconstruct pathways in a diseased population. As a test case, we applied our method to a schizophrenia study, using training sets with different proportions of patients and healthy controls. Several studies of schizophrenia using diffusion MRI have been published to date (see, e.g., Kubicki et al., 2007 for a review). Although several early region-based studies showed anisotropy decreases in patients compared to controls (Lim et al., 1999; Foong et al., 2000; Agartz et al., 2001; Ardekani et al., 2003), others did not find such a decrease (Steel et al., 2001; Kubicki et al., 2002, 2003; Begré et al., 2003). Studies of how white-matter integrity relates to age in schizophrenia patients vs. controls have yielded contradictory results (Jones et al., 2006; Mori et al., 2007; Rosenberger et al., 2008; Voineskos et al., 2010). Although any discrepancies between studies are likely partly due to differences in data acquisition and variability in disease subtypes, part of the challenge has also been defining the regions of interest in a manner that is accurate and repeatable across subjects and studies. Thus investigators have been turning increasingly to tractography for better localization of the effects of schizophrenia in specific pathways (e.g., Buchsbaum et al., 2006; Price et al., 2008; Jeong et al., 2009; Kubicki et al., 2009, 2011; Oh et al., 2009; Skudlarski et al., 2010; Whitford et al., 2010). In this work we show that our automated method for reconstructing white-matter fascicles can be applied to data from schizophrenia patients, even if the training subjects are healthy. This development should allow automatic tractography analyses of even larger data sets to investigate subtle changes in specific fascicles, not only in schizophrenia but in a wide variety of neurological disorders, as well as brain development and aging.

2. Materials and Methods

2.1. Image data

We used image data from 34 schizophrenia patients (ages 37 ± 10, 9 female) and 33 healthy controls (ages 42 ± 10, 14 female). The data was all collected at MGH as part of a multi-site MIND Clinical Imaging Consortium (Magnotta et al., 2008; Roffman et al., 2008; Ehrlich et al., 2010; White et al., 2011). Patients had to meet DSM-IV diagnostic criteria for schizophrenia. Information on their average duration of illness, symptoms, and antipsychotic medication history is given in Table 1. More details on the multi-site patient population that this data set is part of can be found in Ehrlich et al. (2010). Healthy controls had no history of psychiatric diagnosis and were matched to the patient cohort for age, gender, and parental education. Exclusion criteria for both patients and controls were IQ lower than 70 based on a standardized IQ test, history of a head injury resulting in prolonged loss of consciousness, neurosurgical procedure, neurological disease, history of skull fracture, severe or disabling medical conditions, or any contraindication for MRI scanning. All subjects spoke English as their native language. They provided informed consent to participate in the study in accordance with MGH Internal Review Board regulations.

Table 1.

Details on symptoms and medication history of schizophrenia patient population.

	Mean and standard deviation
Duration of illness [years]	14 ± 12
Positive symptom composite score	4.82 ± 3.29
Negative symptom composite score	7.03 ± 4.48
Disorganized symptom composite score	1.26 ± 1.68
Lifetime antipsychotic exposure [CPZ dose years]	78.80 ± 180.16
Current antipsychotic dose [CPZ units]	539.53 ± 497.79

Positive symptom composite score: Sum of the global rating of severity of delusions and the global rating of severity of hallucinations from the scale for the assessment of positive symptoms SAPS; (Andreasen, 1984). Negative symptom composite score: Sum of the values from the global rating of affective flattening, the global rating of alogia, the global rating of avolition-apathy, and the global rating of anhedonia-asociality from the scale for the assessment of negative symptoms SANS; (Andreasen, 1983). Disorganized symptom composite score: Sum of the values from the global rating of severity of bizarre behavior and the global rating of positive formal thought disorder from the scale for the assessment of positive symptoms SAPS; (Andreasen, 1984). Cumulative antipsychotic drug exposures: Given in chlorpromazine dose years, where 1 dose year = 100 chlorpromazine equivalents per day for 1 year. Current antipsychotic drug dose: Given in chlorpromazine units. Antipsychotic history was collected as part of the psychiatric assessment using the PSYCH instrument (Andreasen, 1987). Cumulative and current antipsychotic exposure was calculated using the chlorpromazine (CPZ) conversion factors of Andreasen et al. (2010).

The subjects were scanned in a 1.5 T Siemens scanner with an 8-channel head coil. Diffusion-weighted images were acquired with axial in-plane isotropic resolution 2 mm, slice thickness 2 mm, 128 × 128 × 60 image matrix, TR= 8900 ms, TE = 80 ms, NEX = 1, BW = 1860 Hz/pixel, GRAPPA acceleration factor 2. The series included images acquired with diffusion weighting along 60 non-collinear directions (b = 700 sm⁻²), and 10 images acquired without diffusion weighting (b = 0). T₁-weighted images were acquired in the same session with an oblique axial GRE sequence, in-plane isotropic resolution 0.625 mm, slice thickness 1.5 mm, 256 × 256 × 144 image matrix, TR = 12 ms, TE = 4.76 ms, FA = 20, NEX = 3, BW = 110 Hz/pixel.

2.2. Image preprocessing

We used a standard method, available in FSL¹, for mitigating distortions induced by eddy currents and motion by registering the diffusion-weighted to the b = 0 images. For each subject, we registered the b = 0 image to the T₁-weighted image by an affine registration method that seeks to maximize the intensity contrast of the b = 0 image across the cortical gray/white boundary, which is obtained from the T₁ scan (Greve and Fischl, 2009). We registered each individual’s T₁-weighted image to the 1 mm-resolution MNI-152 atlas (Talairach and Tournoux, 1988), using affine registration (Jenkinson et al., 2002). We used the automated tools in FreeSurfer² to obtain a cortical parcellation and subcortical segmentation for each subject from its T₁-weighted image (Dale et al., 1999; Fischl et al., 1999a,b, 2002, 2004a,b; Fischl and Dale, 2000).

2.3. Manual labeling

Our automated tractography method relies on prior anatomical information derived from a set of training subjects. We obtained this training data by labeling a set of major white-matter pathways manually in each subject from our cohort. The manual labeling was performed on the eddy-current corrected diffusion images in Trackvis³. Conventional deterministic streamline tractography was performed on the whole brain using the FACT method (Mori et al., 1999). Then an expert interacted with the streamlines in Trackvis to isolate the ones belonging to specific white-matter pathways. For each pathway the expert drew at least two regions of interest (ROIs) in anatomical locations that the pathway is known to traverse. We followed an established protocol for identifying these locations and drawing the ROIs (Wakana et al., 2007). Additional ROIs were placed as needed to eliminate streamlines that did not belong to the pathway of interest or to cut streamlines where they merged erroneously with other pathways. Most ROIs were hand-drawn on single slices of the individual’s fractional anisotropy (FA) map, except for the end ROIs for the CST, which came from the FreeSurfer anatomical segmentation.

This was done for all the pathways listed in Wakana et al. (2007) except for the inferior fronto-occipital fasciculus, which we chose not to label due to the controversy surrounding its existence as a separate fascicle (Schmahmann and Pandya, 2007). The pathways that we did label were:

• Corticospinal tract (CST)

• Inferior longitudinal fasciculus (ILF)

• Uncinate fasciculus (UNC)

• Anterior thalamic radiation (ATR)

• Cingulum – cingulate gyrus (supracallosal) bundle (CCG)

• Cingulum – angular (infracallosal) bundle (CAB)

• Superior longitudinal fasciculus – parietal bundle (SLFP)

• Superior longitudinal fasciculus – temporal bundle (SLFT)

• Corpus callosum – forceps major (FMAJ)

• Corpus callosum – forceps minor (FMIN)

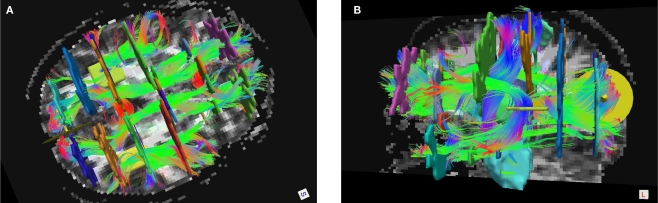
Based on the subdivision of the SLF that has been suggested in the literature (Makris et al., 2005), the SLFP and SLFT above correspond most closely to SLF III and the arcuate fasciculus, respectively. Except for FMAJ and FMIN, which are interhemispheric connections, all other pathways were labeled on the left and right hemisphere. Thus we ended up with a total of 18 pathways per subject. Figure 1 shows an example of a full set of manually labeled pathways and all the ROIs that were drawn for the labeling.

Figure 1.

Manual labeling of all 18 pathways in a single subject, shown in Trackvis with the disks and manually drawn ROIs that were used to define the pathways. An axial (A) and sagittal (B) view is shown, with some ROIs hidden in each case to provide an unobstructed view.

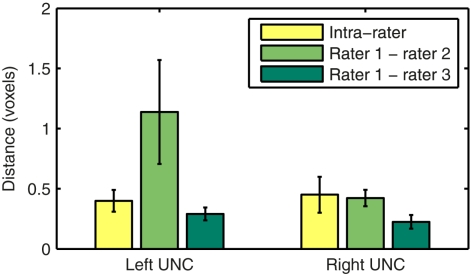
We assessed the intra- and inter-rater reliability of the manual labeling method in the left and right uncinate. The uncinate was labeled twice by rater 1 and once each by raters 2 and 3 in 10 healthy subjects. Intra-rater reliability was quantified as the modified Hausdorff distance between the two labels of the same pathway produced by rater 1. Inter-rater reliability was quantified as the modified Hausdorff distance between labels of the same pathway produced by raters 1 and 2 or raters 1 and 3. We define the modified Hausdorff distance between two labels as the minimum distance of each point on one label from the other label, averaged over all points on the two labels. The means and standard errors of the distances over the 10 subjects are shown in Figure 2.

Figure 2.

Intra- and inter-rater reliability of the manual labeling of the left and right uncinate. Reliability is quantified as the modified Hausdorff distance between two labels of the same pathway produced by the same rater or by two different raters.

2.4. Automated tractography

Our method for automated reconstruction of white-matter pathways is based on the Bayesian framework for global tractography proposed in Jbabdi et al. (2007). In this framework the unknown pathway 𝓕 in any new test subject is estimated from the diffusion-weighted images Y of that subject via the posterior probability distribution of 𝓕 given Y,

$$p\left(\mathcal{F}|Y\right)\propto p\left(Y|\mathcal{F}\right)p\left(\mathcal{F}\right).$$ (1)

We can think of the likelihood p(Y | 𝓕) as the variability in the measured data given the shape of the pathway in the specific subject and the prior distribution p(𝓕) as the variability in the pathway shape from subject to subject. Therefore the likelihood represents uncertainty in the data due to measurement noise and the prior represents uncertainty due to individual anatomical variation.

In our approach we use the same formulation for the likelihood p(Y | 𝓕) as Jbabdi et al. (2007), which assumes Gaussian noise and uses the “ball-and-stick” model of diffusion (Behrens et al., 2003). This model allows for multiple compartments of anisotropic diffusion and one compartment of isotropic diffusion per voxel, expressing the diffusion image data at that voxel as a function of the volumes and orientations of these compartments (Behrens et al., 2007). We used the bedpostx tool in FSL to estimate the distributions of the ball-and-stick model parameters at each voxel from the diffusion data, assuming up to two anisotropic compartments per voxel.

Our departure from Jbabdi et al. (2007) is that, instead of assuming equal prior probability for all possible paths connecting two regions of interest, we use a prior of the form:

$$p\left(\mathcal{F}\right)=p\left(\mathcal{F}|A,{\left\{{\mathcal{F}}_k\right\}}_{k=1}^{N_t},{\left\{A_K\right\}}_{k=1}^{N_t}\right),$$ (2)

where A is the anatomical segmentation map of the test subject, 𝓕_k, k = 1,…, N_t, is the pathway of interest in each of the N_t training subjects, and A_k, k = 1,…, N_t the anatomical segmentation map of each training subject. Thus we allow our prior knowledge on the anatomy of the pathway in the training subjects to inform our belief on the anatomy of the pathway in the test subject.

Specifically, the information that we glean from the training set is which anatomical regions the pathway intersects and neighbors along its trajectory. For each training subject, the anatomical segmentation map A_k, obtained from the T₁ image using FreeSurfer, and the pathway 𝓕_k, obtained from the manual labeling of streamlines in Trackvis, are coregistered using the intra- and inter-subject registration methods described in section 2.2. Once they have been mapped to the common space (here MNI space), the streamlines from the manual labeling of the training subjects are divided into N_s segments along their arc length. The number of segments N_s is chosen separately for each of the 18 pathways so that every training streamline has at least 3 voxels in each segment. For each segment i = 1,…, N_s along the streamlines of 𝓕_k we compute histograms of how often each segmentation label a occurs in the anatomical segmentation map A_k at the voxels that the streamlines traverse, or at the nearest neighboring structures of the streamlines in the left, right, anterior, posterior, superior, and inferior directions. This yields estimates of the a priori probability $p_i^0\left(a\right)$ that a voxel in the pathway’s i-th segment intersects a segmentation label a, and of the a priori probabilities $p_i^L\left(a\right)$, $p_i^R\left(a\right)$, $p_i^A\left(a\right)$, $p_i^P\left(a\right)$, $p_i^I\left(a\right)$, $p_i^S\left(a\right)$ that the nearest neighboring segmentation label to a voxel in the pathway’s i-th segment in the left, right, anterior, posterior, superior, and inferior directions, respectively, is label a. These probabilities form a statistical framework for introducing into the tractography algorithm the same type of anatomical knowledge that an expert would use to label the pathways manually.

The prior probability $p\left(\mathcal{F}|A,{\left\{{\mathcal{F}}_k\right\}}_{k=1}^{N_t},{\left\{A_k\right\}}_{k=1}^{N_t}\right)$ of a path in the test subject given the training data is computed by splitting the path into the same number of segments N_v as the training paths. Let the test path 𝓕 go through N_v voxels in the common space and i(j), j = 1,…, N_v be the segment along the path that the j-th voxel belongs to, where i ∈ {1,…, N_s}. From the test subject’s segmentation map A we obtain the segmentation label $a_j^0$ that the j-th voxel intersects and its nearest neighboring segmentation labels $a_j^L$, $a_j^R$, $a_j^A$, $a_j^P$, $a_j^I$, $a_j^S$ in the left, right, anterior, posterior, superior, and inferior directions, respectively. The prior probability of the path is assumed to be the product of the prior probabilities of each voxel along the path:

$$\begin{array}{rcll}& p\left(\mathcal{F}|A,{\left\{{\mathcal{F}}_k\right\}}_{k=1}^n,{\left\{A_k\right\}}_{k=1}^n\right)=\prod _{j=1}^{N_v}{p}_{i\left(j\right)}^0\left(a_j^0\right)p_{i\left(j\right)}^L\left(a_j^L\right)p_{i\left(j\right)}^R\left(a_j^R\right)& & \\ & \times p_{i\left(j\right)}^A\left(a_j^A\right)p_{i\left(j\right)}^P\left(a_j^P\right)p_{i\left(j\right)}^I\left(a_j^I\right)p_{i\left(j\right)}^S\left(a_j^S\right)& & \text{(3)}\end{array}$$

We estimate the posterior distribution p(𝓕 | Y) for the test subject via a Markov Chain Monte Carlo (MCMC) algorithm. The pathway 𝓕 is modeled as a cubic spline with a fixed number of control points. For the results shown here we used 5 control points to model all pathways. Further investigation is needed to determine the optimal number of control points, as it is possible that increasing it could yield better results for higher-curvature paths such as the corpus callosum. In addition to the estimation of anatomical priors, the training data is also used to derive the initialization of the control points and the end ROIs that are used to constrain the two end points of each pathway. The initialization is obtained by fitting a spline to the median of the training set of streamlines. The end ROIs are obtained by dilating the end points of the training streamlines and finding their intersection with the cortex of the test subject.

The MCMC algorithm generates samples from the posterior distribution p(𝓕 | Y) of the path by perturbing the control points, thus changing the shape of the spline, and computing the likelihood and prior probability of the new spline. The likelihood expresses how well the spline fits the diffusion data, that is, how closely the orientation of the spline at each voxel that the spline goes through matches the orientation of the anisotropic diffusion compartments of the ball-and-stick model at the same voxel. The prior expresses how well the spline fits the training set, that is, how well the anatomical regions that the spline goes through or passes next to in the test subject match those found in the training subjects. In each iteration of the algorithm the control points are perturbed in random order. If the perturbed control point is one of the two end points of the path and the perturbation has placed it outside the end ROI obtained from the training set, it is rejected. Otherwise, every time a control point is perturbed, the likelihood and prior distribution is computed for every voxel along the spline. The control point perturbation and likelihood computation is performed in the native diffusion space, so that the DWI data itself does not need to be mapped to another space. However, the anatomical prior computation requires that each voxel on the spline is mapped to the common coordinate system where all training subjects and the corresponding anatomical segmentations have been normalized (here MNI space). The likelihood and prior are integrated over all voxels along the spline to compute its posterior probability, which is then compared to the posterior probability of the spline from the previous iteration to determine if the new spline will be accepted or rejected. A number of “burn-in” iterations (200 in this experiment) are performed in the beginning of the algorithm. The splines sampled during the burn-in period are discarded to ensure that the spline is initialized close to the center of the distribution. Then the main set of iterations (5000 in this experiment) are run. The splines that are sampled and accepted during this set of iterations are summed to yield an estimate of the posterior distribution of the pathway in the test subject. The optimal number of burn-in and sampling iterations that are needed to ensure convergence for each pathway is a topic for future investigation.

For this paper we investigated how the inclusion of both patients and healthy subjects in the training set affected our ability to reconstruct the pathways reliably in either population. We tested our method by a leave-N-out approach, where we performed automated tractography in each subject using the manual labels from a set of the remaining subjects as training data. We repeated this three times per subject, each time using a different combination of 30 training subjects: (i) all 30 healthy, (ii) 15 healthy and 15 diseased, and (iii) all 30 diseased. Training subjects were selected randomly from the healthy and diseased groups. We also performed the reconstruction using the healthy training data only to initialize the algorithm but not in the pathway prior. This was equivalent to assuming a uniform prior probability and relying on the likelihood term alone for estimating the pathway posterior. We compared the results by computing the distance of an automatically reconstructed pathway in the test subject to the respective manually labeled pathway for the same subject, which had been excluded from the training set.

3. Results

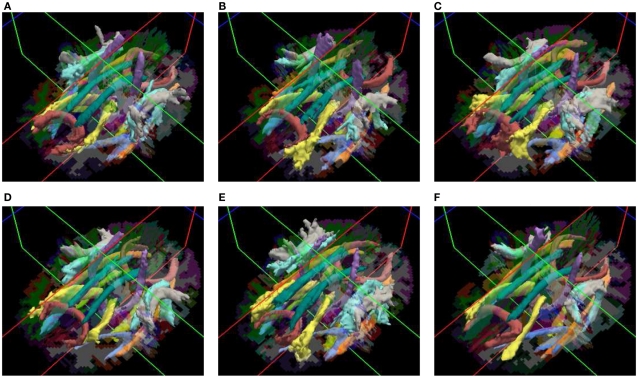
Our method yields volumetric distributions of the pathways. As an example, Figure 3 shows the estimated pathway distributions in three healthy controls and three schizophrenia patients, displayed as isosurfaces at 20% of the maximum value of each distribution.

Figure 3.

Pathways reconstructed automatically with TRACULA in three healthy controls (A–C) and three schizophrenia patients (D–F). The posterior distribution of each pathway, estimated using 30 healthy subjects as the training set and thresholded at 20% of its maximum, is displayed as an isosurface over each individual’s FreeSurfer segmentation.

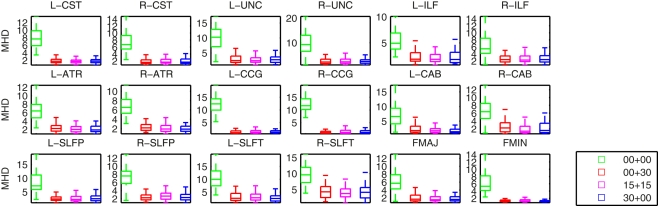
Figure 4 shows plots of the distances between the manually labeled pathways and automatically reconstructed pathways that were estimated with different sets of training subjects. In each case we computed a modified Hausdorff distance between the automatically reconstructed pathway and the manually defined pathway. Before computing the modified Hausdorff distance, the distribution estimates were thresholded by masking out all values below 20% of the maximum. Thus the comparison is based on the center of the distribution and not its tails, as we expect the center and not the tails to overlap with the manual labels. In all cases, the paths reconstructed with the anatomical priors were closer to the manual labels than the ones reconstructed without prior information. The priors reduced both the mean distance and the variance of the distance from the manual labels, thus improving accuracy and robustness.

Figure 4.

Modified Hausdorff distances (MHD) between the manually labeled pathways and automatically reconstructed pathways. Pathway posteriors were estimated without an anatomical prior (green) and with anatomical priors derived from 3 different sets of training subjects: 30 healthy training subjects (red), 15 healthy and 15 patients (magenta), and 30 patients (blue).

Changing the make-up of our training set did not affect this result significantly. In particular our results indicate that it is possible to reconstruct the pathways accurately in the entire study cohort using a training set consisting of healthy subjects only. We computed uncorrected p-values from T-tests on the difference in the modified Hausdorff distances between the case where a healthy-only training set was used and the other three cases. The differences between the cases using a healthy-only training set and no anatomical priors were significant (p < 0.01) for all pathways except for the left ILF. The differences between the cases using a healthy-only and a mixed or patient-only training set were not significant.

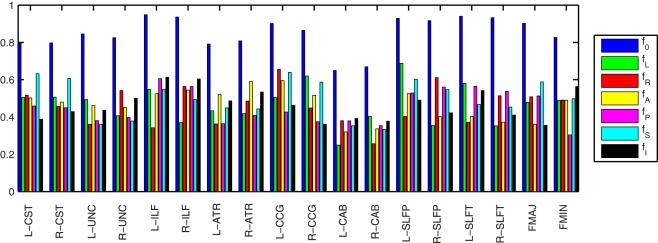
Figure 5 illustrates the amount of anatomical variability that is captured by the priors for an example training set consisting of 30 healthy subjects. To quantify this variability we found the maximum fraction of training samples that corresponded to a single label, i.e., the fraction of training samples corresponding to the most commonly encountered label. The higher this fraction, the lower the variability in the segmentation labels encountered across the samples. We averaged the fraction over all segments along the length of a pathway. We calculated this average maximum fraction for the labels that intersect the pathway (f₀) and for the nearest neighboring labels in the left, right, anterior, posterior, superior, and inferior directions (f_L, f_R, f_A, f_P, f_S, and f_I, respectively). The segmentation labels intersected by the pathways were the least variable (f₀ was 0.8 on average), as these are most commonly white matter. The fractions for the neighboring segmentation labels were 0.5 on average. The left and right CAB were the pathways with the most anatomical variability.

Figure 5.

Anatomical variability captured by the priors in an example training set of 30 healthy subjects. The plots show the fraction of training samples corresponding to the most commonly encountered label, averaged over all segments along the length of each pathway. This was computed for the labels that intersect the pathway (f₀) and for the nearest neighboring labels in the left, right, anterior, posterior, superior, and inferior directions (f_L, f_R, f_A, f_P, f_S, and f_I, respectively). The higher the fraction, the lower the variability of the labels across training samples.

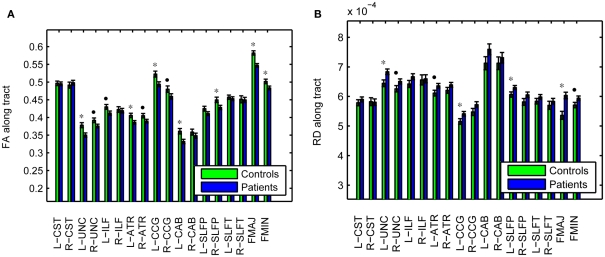
As an illustration of the utility of the tract-based approach in localizing white-matter degeneration in schizophrenia, and to confirm that our data set is consistent with prior findings from the literature, Figure 6 shows group averages and corresponding standard errors of the average fractional anisotropy (FA) in each pathway. Based on uncorrected p-values from a T-test on the difference between groups, we found average FA to be significantly lower in patients compared to controls in the left UNC (p = 0.005), left ATR (p = 0.019), left CCG (p = 0.011), left CAB (p = 0.006), right SLFP (p = 0.033), FMAJ (p = 0.00005), and FMIN (p = 0.034), with trend toward significance in the FA reductions that were observed in the right UNC (p = 0.067), left ILF (p = 0.059), right ATR (p = 0.061), and right CCG (p = 0.088). The average FA over the entire white matter (based on white-matter masks obtained from the FreeSurfer segmentations) was also significantly reduced in patients vs. controls (p = 0.006). We performed similar tests on the average radial diffusivity (RD) and axial diffusivity (AD) in each pathway. Pathways with significantly reduced FA also exhibited increased RD in the patients compared to the controls. More specifically, significant increases of RD in patients were found in the left UNC (p = 0.010), left CCG (p = 0.042), left SLFP (p = 0.044), and FMAJ (p = 0.0003), with trend toward significance in the right UNC (p = 0.080), left ATR (p = 0.057), and FMIN (p = 0.054). The average RD over the whole white matter was also higher in the patients (p = 0.014). In contrast we found no significant changes in the average AD over individual pathways or over the entire white matter.

Figure 6.

Fractional anisotropy (A) and radial diffusivity (B), averaged over individual pathways in schizophrenia patients and healthy controls. *p < 0.05, ^•p < 0.1.

4. Discussion

We have evaluated TRACULA, a method for automated global probabilistic tractography, on a population of schizophrenia patients and healthy controls. Our method yields volumetric distributions of major pathways in a novel subject without the need for manual intervention, thus facilitating clinical studies where large populations need to be analyzed to detect subtle changes in white-matter integrity. Our experiments showed that this approach produced results very close to those of conventional, manually assisted tractography, but without the manual editing. Further investigation is needed to determine the optimal number of subjects that should be included in the training set.

Including patients in the training set did not improve the accuracy of our results. That is, despite the relative clinical heterogeneity of our patients (Table 1), we were able to reconstruct pathways in this population using only healthy training subjects without a decrease in accuracy. This is not entirely surprising as our method does not constrain the exact spatial location or shape of the pathways and is thus impervious to changes in these features between populations. Our priors use only the trajectory of the training paths relative to the surrounding anatomical structures. As long as the disease that we are studying does not cause a radical reorganization of the brain and rerouting of white-matter connections, healthy training subjects could be used to reconstruct the pathways accurately in patients as well as in controls.

Several aspects of the anatomical prior computation can have an impact on the validity of our method. These include the accuracy of the automated segmentation of the T₁-weighted images, the registration of each individual’s T₁-weighted and diffusion-weighted images, and the registration across individuals. The accuracy of the automated anatomical segmentation has been addressed elsewhere (Fischl et al., 2002, 2004b). The intra-subject registration method that we used here benefits from information on the gray/white-matter boundary to improve the alignment of the diffusion and T₁-weighted image. However, this alignment remains a difficult problem, most notably due to susceptibility artifacts that cause distortions in the DWIs. Thus care should be taken to minimize such distortions to improve the accuracy of the reconstructed pathways. Nevertheless it is worth noting that the range of misregistration between the T₁-weighted and DW images across the training subjects will be reflected in the anatomical priors as blurring. If any potential misregistration in the test subject is within the range present in the training set, this misregistration should be less of a problem for pathway reconstruction.

The inter-subject alignment for this study was performed by registering the subjects’ T₁-weighted images to the MNI template. However, recent work from our group has shown that aligning the T₁-weighted images to each other by a combined volume- and surface-based non-linear registration can lead to improved inter-subject alignment of streamlines from deterministic tractography, when compared to affine registration (Zöllei et al., 2010). We are currently investigating the incorporation of this common coordinate system in our tractography framework to replace the MNI template. We expect that improved spatial normalization will be particularly beneficial for the initialization of the control points and for the definition of the end ROIs, as these aspects of the algorithm rely on good spatial correspondence between the training subjects and the test subject. Beyond that, however, we expect that our tractography method would be less sensitive to small misregistrations between subjects than, for example, a voxel-based comparison, since our priors use information on the surrounding anatomical structures of the pathways and not on their exact spatial location.

In the experiments presented here we evaluated the accuracy of the automated tractography by comparing it to the respective manual labels. Of course, the manual labels cannot be considered ground truth, as they are limited by the inability of the deterministic streamline tractography to reach some parts of certain pathways. For example, the more lateral terminations of the CST in the motor cortex, e.g., those corresponding to the hand region, are more challenging to trace than the more medial ones due to intersecting pathways. Similarly the frontal terminations of the SLF are longer and thus more challenging to trace than the prefrontal and premotor ones. Using a high angular-resolution model (Q-ball) instead of the tensor model to obtain the streamlines used for labeling did not yield improvements, since our data acquisition (b = 700 sm⁻², 60 directions) was suboptimal for this purpose.

However, we expect the global probabilistic approach to explore areas of lower anisotropy and tract crossings that are unreachable by deterministic tensor tractography, as long as these areas lie within the same anatomical neighborhood as the training streamlines. One reason for this is that the multi-fiber ball-and-stick model can model more than one tract orientation per voxel. Another reason is that global tractography integrates along the length of the path and would be less sensitive to a low-anisotropy crossing somewhere on that trajectory that could cause streamline tractography to terminate prematurely. Ultimately the availability of high-quality training data will be very beneficial to our method and each tractography approach, manually assisted or automatic, should be validated further by comparing it to tracer studies.

The data likelihood model that is used by our method assumes a Gaussian distribution for the DWI intensity values. This is a good approximation for magnitude images when the SNR is sufficiently high but breaks down at low SNR. To test the Gaussianity of the noise in our data, we used the DWI values in each voxel in the ventricles, where the intensity is independent of gradient direction due to isotropic diffusion. For each of these voxels we used the 60 DWI values available from the 60-direction data to estimate the SNR and test for Gaussianity using a Kolmogorov-Smirnov test. A total of 147781 voxels were tested over all subjects. The null hypothesis of Gaussianity was rejected in only 0.1% of these tests. The average SNR was 5.5.

The data set that we chose to both train and test our method in this work was acquired with the standard DWI sequence that is used routinely to collect data for research studies at MGH. This included using the default choices for b-value, gradient directions, and spatial resolution. It will be important to evaluate our method further on data acquired with different acquisition parameters. Beyond the quality of the test data, the quality of the training data is crucial to our method, since the accuracy of the reconstructed pathways is strongly dependent on the accuracy of the prior information used by the algorithm. In the future, as improved acquisition methods and hardware become available, training data of higher quality can be collected and used to increase automated reconstruction accuracy in data sets of routine quality.

Tractography can be used to qualify white-matter differences between populations in much greater detail than it is possible with a voxel-based or ROI-based approach. Local tractography can handle exploratory analyses, where the anatomy of a connection is not known or the connection may not be present in all subjects. Global tractography is geared toward the reconstruction of a known connection between two end regions. A feature of the global approach is that, by constraining both end points of the pathway, it provides us with a straightforward way to parameterize the pathway by arc length. With such a parameterization one could localize effects further by comparing diffusion measures, such as FA, not only in terms of their averages over a pathway, but also as a function of position along the length of the pathway. With global tractography, in particular, we estimate the posterior distribution of each pathway, from which it is straightforward to calculate the posterior mean or maximum a posteriori pathway for each subject and compare FA or other measures at different locations along the arc length. Since differences may be more pronounced in a particular portion of a pathway, e.g., due to greater disorganization of connections in that portion or more crossings with another pathway, such analyses may be helpful for further interpretation of population differences.

To illustrate the validity of the data set used here, we have also presented results from a tract-based comparison of FA between the schizophrenia patients and matched controls in our cohort. A superset of this cohort, including data acquired at three additional sites, was studied previously with an ROI-based approach. FA was found to be lower in patients than controls when averaged over large regions (whole brain, frontal, parietal, occipital, and temporal lobes) (White et al., 2011). We were able to replicate this result in this much smaller data set and show significant FA reductions localized in specific pathways, as seen in Figure 6. Our results are consistent with prior studies on white-matter integrity in schizophrenia that have sought to localize effects in specific fascicles. In agreement to what we have found, anterior thalamic radiations (Buchsbaum et al., 2006; Oh et al., 2009), cingulum (Kubicki et al., 2003, 2005; Manoach et al., 2007; Mori et al., 2007; Nestor et al., 2007), corpus callosum (Foong et al., 2000; Agartz et al., 2001; Hubl et al., 2004; Kubicki et al., 2005; Douaud et al., 2007a; Whitford et al., 2010), inferior longitudinal fasciculus (Hubl et al., 2004; Jeong et al., 2009), superior longitudinal fasciculus (Hubl et al., 2004; Kubicki et al., 2005; Jones et al., 2006; Karlsgodt et al., 2008; Jeong et al., 2009), and uncinate (Kubicki et al., 2002; Burns et al., 2003; Mori et al., 2007; Price et al., 2008; Szeszko et al., 2008; Voineskos et al., 2010) are major sites where alterations have been reported.

Common limitations of diffusion MRI studies, including our own, are our inability to determine the exact biological causes of diffusion anisotropy changes, our difficulty in distinguishing the effects of the disease from those of medication, and the potentially increased subject motion in patients as compared to controls. Histological studies have shown several changes in the white matter of schizophrenia patients when compared to healthy subjects, including differences in myelination and neuronal arborization patterns (Davis et al., 2003; Flynn et al., 2003). Distinguishing between potential neurobiological causes based on FA changes alone is not possible. However, in combination with other measures extracted from DWIs, such as mean, radial, and axial diffusivity (Kubicki et al., 2003; Douaud et al., 2007b; Whitford et al., 2010), length of tractography streamlines (Buchsbaum et al., 2006), or even measures from magnetization transfer imaging (Kubicki et al., 2005), these findings have been hypothesized to support either demyelination or geometric disorganization as their underlying etiology. Similarly to Whitford et al. (2010), our results show increased radial but unchanged axial diffusivity in the patients, which has been interpreted as evidence of myelin abnormalities (Song et al., 2002).

Whichever the biological cause of changes in white-matter integrity measures derived from diffusion MRI, several studies have found these changes to be associated with cognitive deficits in schizophrenia patients. This includes associations with performance in attention and memory tasks (Kubicki et al., 2002, 2003, 2009, 2011; Nestor et al., 2007; Karlsgodt et al., 2008; Szeszko et al., 2008), with fMRI activation in working memory-related areas (Schlösser et al., 2007), and with fMRI time course correlations within the semantic network (Jeong et al., 2009). Such findings illustrate the potential of diffusion MRI to improve our understanding of the mechanisms of schizophrenia but they also underline the need for extracting diffusion measures specific to each affected network. Our tractography method allows the automatic extraction of such measures and can thus facilitate pathway-specific studies on larger populations than what has been possible with manually assisted tractography.

Conclusion

We have developed TRACULA, a method for automated tractography that uses prior information on the anatomy of white-matter pathways from a set of training subjects. We have evaluated the accuracy of the method on a population of schizophrenia patients and healthy volunteers, to determine how it is affected by the inclusion of patients in the training set. We have found that a training set consisting entirely of healthy subjects could be used to reconstruct white-matter pathways in both patients and healthy controls without compromising accuracy. Of course this conclusion cannot be generalized to every clinical population and further evaluation on other populations is warranted to determine if the training set should be tailored to specific studies.

TRACULA is available for download as part of FreeSurfer 5.1.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.