Abstract
Cognitive development and learning are characterized by diminished reliance on effortful procedures and increased use of memory-based problem solving. Here we identify the neural correlates of this strategy shift in 7–9-year-old children at an important developmental period for arithmetic skill acquisition. Univariate and multivariate approaches were used to contrast brain responses between two groups of children who relied primarily on either retrieval or procedural counting strategies. Children who used retrieval strategies showed greater responses in the left ventrolateral prefrontal cortex; notably, this was the only brain region which showed univariate differences in signal intensity between the two groups. In contrast, multivariate analysis revealed distinct multivoxel activity patterns in bilateral hippocampus, posterior parietal cortex and left ventrolateral prefrontal cortex regions between the two groups. Our results demonstrate that retrieval and counting strategies during early learning are characterized by distinct patterns of activity in a distributed network of brain regions involved in arithmetic problem solving and controlled retrieval of arithmetic facts. Our findings suggest that the reorganization and refinement of neural activity patterns in multiple brain regions plays a dominant role in the transition to memory-based arithmetic problem solving. Our findings further demonstrate how multivariate approaches can provide novel insights into fine-scale developmental changes in the brain. More generally, our study illustrates how brain imaging and developmental research can be integrated to investigate fundamental aspects of neurocognitive development.
Introduction
Behavioral studies have shown that strategy shifts in children’s problem solving are characterized by reduced use of effortful procedures and increased use of efficient retrieval-based processes (Siegler, 1996). Despite considerable advances in our understanding of the behavioral and cognitive mechanisms characterizing these shifts (Siegler & Svetina, 2006), little is known about the underlying brain mechanisms. Children’s arithmetical problem solving provides an ideal domain for studying the brain mechanisms that underlie this cardinal feature of children’s cognitive development because the underlying behavioral characteristics and cognitive processes are particularly well known (Geary, 1994; Shrager & Siegler, 1998).
Children primarily use four strategies to solve addition problems: (a) counting fingers, (b) verbal counting, (c) retrieval, and (d) decomposition (e.g. 6 + 7 = 6 + (6 + 1) = (6 + 6) + 1 = 12 + 1 = 13) (Ashcraft, 1982; Siegler & Shrager, 1984; Siegler, 1986; Geary & Burlingham-Dupree, 1989; Geary, Hoard, Byrd-Craven, Nugent & Numtee, 2007). When first learning to solve addition problems, children rely heavily on effortful and time consuming counting procedures (Geary & Brown, 1991; Geary, Hoard, Byrd-Craven & DeSoto, 2004; Wu, Meyer, Maeda, Salimpoor, Tomiyama, Geary & Menon, 2008). Repeated use of counting results in the formation of associations between problem stems (e.g. 5 + 7) and answers (e.g. 12) such that presenting the stem will eventually trigger retrieval of the correct answer (Siegler & Shrager, 1984). This developmental shift in strategy is most evident during second and third grades in typically achieving children (Ashcraft & Fierman, 1982; Kaye, Post, Hall & Dineen, 1986; Geary, Widaman, Little & Cormier, 1987). In behavioral studies assessing the mix of strategies young children use to solve arithmetic problems, a variety of methods have been employed, ranging from verbal report (Carpenter & Moser, 1984) to mathematical modeling of problem solving RTs (Groen & Parkman, 1972; Ashcraft, 1982). Concerns were initially raised regarding the validity of child reports (Hamann & Ashcraft, 1985), but subsequent studies showed that self-reported strategies were aligned with associated mean RT patterns, Receiver-Operator Characteristic (ROC) of RTs and experimenter observation (Groen & Parkman, 1972; Siegler, 1987; Geary, 1990; Wu et al., 2008).
Developmental neuroimaging studies of arithmetic problem solving have revealed that, compared to adults, children rely more on the hippocampus and ventrolateral and dorsolateral prefrontal cortex (VLPFC and DLPFC), whereas adults depend more on the intraparietal sulcus (IPS) and supramarginal gyrus (SMG) regions of the posterior parietal cortex (PPC) (Rivera, Reiss, Eckert & Menon, 2005). Other cross-sectional studies contrasted brain regions associated with the development of arithmetic skills comparing groups that differed in age by one or more decades (Kawashima, Taira, Okita, Inoue, Tajima, Yoshida, Sasaki, Sugiura, Watanabe & Fukuda, 2004; Kucian, von Aster, Loenneker, Dietrich & Martin, 2008). However, almost nothing is known about brain changes that accompany the transition from the use of procedural counting to direct retrieval which is a critical aspect of children’s early arithmetic development. Grabner, Ansari, Koschutnig, Reishofer, Ebner and Neuper (2009a) asked adults to solve arithmetic problems and then report on their use of procedures or retrieval during problem solving. They found that self-reported retrieval use was associated with greater response in the left AG, whereas self-reported procedural use was associated with responses in IPS and superior parietal lobule regions of the PPC as well as widespread regions of the PFC, occipital cortex, and basal ganglia.
A different approach was taken by Ischebeck and colleagues who examined changes in brain responses associated with adults’ learning of multi-digit arithmetic problems. They reported that increased proficiency with recently learned arithmetic facts was associated with reduced responses in the PFC and IPS and increased activation in the left and right AG (Delazer, Domahs, Bartha, Brenneis, Lochy, Trieb & Benke, 2003; Delazer, Ischebeck, Domahs, Zamarian, Koppelstaetter, Siedentopf, Kaufmann, Benke & Felber, 2005; Ischebeck, Zamarian, Egger, Schocke & Delazer, 2007). However, it is unclear whether this same pattern of strategy-related changes will also apply to young children. It cannot be assumed that learning in adults or contrasts between children and adults is comparable to learning in the developing brain (Karmiloff-Smith, 1981, 2010). Critically, previous studies in adults have not examined the involvement of medial temporal lobe (MTL) memory systems (Squire, Stark & Clark, 2004; Suzuki, 2007; Wang & Morris, 2010) in arithmetic fact learning and memory-based retrieval strategies. To address this gap, we focus here on the transition from greater use of counting to retrieval in 7–9-year-old children at an important period for acquiring knowledge of arithmetic facts.
We used functional magnetic resonance imaging (fMRI) and univariate and multivariate approaches to compare both activation levels and multivoxel activation patterns related to strategy use. The conventional approach in fMRI data analysis is to detect brain regions involved in specific cognitive processes using voxel-wise univariate methods. In this approach, differences in clusters of individual voxels’ signal intensity are used to make inferences about the differential involvement of specific brain regions associated with distinct stimulus types or participant groups. Multivariate pattern analysis (MPA) approaches, on the other hand, examine differences in fine-scale neuronal activity patterns. These patterns are thought to reflect neuronal population codes underlying the representational content of information processing (Kriegeskorte, 2009; Mur, Bandettini & Kriegeskorte, 2009). Furthermore, computer simulations have shown that MPA has higher sensitivity for detecting differences in the spatial pattern of brain activity (Ryali, Supekar, Abrams & Menon, 2010). MPA therefore has the potential to reveal novel information about distinct neural representations underlying differential strategy use in children, independent of overall differences in signal amplitude (Raizada, Tsao, Liu, Holloway, Ansari & Kuhl, 2010; Abrams, Bhatara, Ryali, Balaban, Levitin & Menon, 2010). To our knowledge, this is the first study to apply these methods to better understand the shift in cognitive strategy for problem solving which is an important developmental milestone.
Based on previous literature, we hypothesized that counting and retrieval would be associated with distinct activity patterns in three key brain areas: (1) the MTL which is known to be critical for memory formation (Squire et al., 2004; Suzuki, 2007; Wang & Morris, 2010), (2) the IPS and AG regions of the PPC known to support numerical cognition (Menon, Rivera, White, Glover & Reiss, 2000; Zago, Pesenti, Mellet, Crivello, Mazoyer & Tzourio-Mazoyer, 2001; Dehaene, Piazza, Pinel & Cohen, 2003; Ischebeck et al., 2007; Zago, Petit, Turbelin, Andersson, Vigneau & Tzourio-Mazoyer, 2008; Grabner, Ischebeck, Reishofer, Koschutnig, Delazer, Ebner & Neuper, 2009b; Wu, Chang, Majid, Caspers, Eickhoff & Menon, 2009), and (3) VLPFC and DLPFC regions which support working memory and cognitive control (Bunge, Dudukovic, Thomason, Vaidya & Gabrieli, 2002; Klingberg, Forssberg & Westerberg, 2002; Kwon, Reiss & Menon, 2002; Luna, Garver, Urban, Lazar & Sweeney, 2004). We further hypothesized that MTL activity would be enhanced in children who predominantly use retrieval strategies given the critical role of this region in memory retrieval and re-encoding. Based on previous findings in adults (Delazer et al., 2005; Rivera et al., 2005; Ischebeck, Zamarian, Siedentopf, Koppelstatter, Benke, Felber & Delazer, 2006; Ischebeck et al., 2007), we predicted that children who predominantly use retrieval strategies would show greater reliance on the AG and decreased reliance on the IPS. Lastly, we examined two competing hypotheses about PFC responses in relation to the transition from counting to retrieval strategies in children. On the one hand, children who are mostly dependent on counting may show greater PFC response since counting requires PFC resources for sequencing and execution of procedures, as has been demonstrated in adults (Menon et al., 2000; Ischebeck et al., 2007; Grabner et al., 2009a). On the other hand, PFC response can be greater in children who use memory-based retrieval strategies given that improved cognitive control over memory retrieval and inhibition of irrelevant information also relies on the PFC (Wagner, Maril, Bjork & Schacter, 2001; Bunge et al., 2002; Badre & Wagner, 2007), especially since fact retrieval is not fully automated in children as it is in skilled adults (Zbrodoff & Logan, 1986; Geary et al., 2004).
Materials and methods
Participants
One hundred and three children (age range: 7.0–9.9, 54 females) were recruited from northern California. They participated in three experimental sessions – intelligence and achievement tests were administered in the first, strategy use during addition problem solving in the second, followed by an fMRI scanning session.
Cognitive assessments
Intelligence was assessed using the Wechsler Abbreviated Scale of Intelligence (WASI; (Weschler, 1999). The Wechsler Individual Achievement Test, Second Edition (WIAT-II; (Wechsler, 2001) was used to determine grade-specific achievement.
Addition tasks
A production task whereby children are presented an addition problem without an answer (e.g. 5 + 4 = ?) and are asked to solve it was used outside of the scanner for strategy assessment, and a verification task wherein children are asked to verify whether the answer to a presented addition problem (e.g. 5 + 4 = 9) is correct or not was used inside of the scanner. In a set of experiments, Ashcraft, Fierman, and Bartolotta (1984) demonstrated that the same cognitive processes are engaged during the solving of addition problems in production and verification tasks. The one difference is that verification items take longer to encode, possibly because they include three rather than two numerals. The production task was used outside of the scanner, because it has proven to be a reliable measure of children’s strategy choices (Siegler, 1987). The verification task was used inside of the scanner because is not feasible to ask children to describe how they solved all problems in the scanner and would have resulted in extraneous cognitive processes, and thus a more complex fMRI signal, that are not central to the solution of addition problems.
Strategy assessment
Each child’s strategy use for single-digit addition problems (e.g. 2 + 4 = ?) was first assessed using standardized, well-validated, measures that classify strategies based on reaction time (RT) patterns, experimenter observation, and child report (Geary et al., 2004; Wu et al., 2008). The problems were presented one at a time on a computer monitor. There were 18 problems with random pairs of integers from 2 to 9 (e.g. 2 + 4 = ?) and sums ranging from 6 to 17. Problems with identical addends (e.g. 2 + 2, 5 + 5) or a 0 or 1 were excluded because they evince less strategy variability (Siegler, 1987). No repetition of either addend was allowed across consecutive problems. Children were instructed to speak the answer as soon as they arrived at it. The experimenter then probed the child on which strategy was used during problem solving. Responses were categorized as: retrieval (e.g. ‘just knew it’), count (e.g. ‘counted on my fingers’, ‘counted in my head’), count by numbers (e.g. ‘2, 4, 6’), decomposition (e.g. 9 + 5 = 9 + (1 + 4) = (9 + 1) + 4 = 10 + 4 = 14), fingers (i.e. child looked at his or her fingers but did not count them) and other/multiple strategies. Trials in which the experimenter noted overt signs of counting even when the child reported retrieval were classified as counting. A timer was started at the initial display of each problem, and the experimenter measured RT by pressing a keyboard key as soon as the child spoke the answer; sessions were audio-recorded to check for RT precision. For each child, we computed the proportion of trials in which retrieval or counting strategies were used to correctly solve a problem; counting strategies included both ‘count’ and ‘count by numbers’.
The children were grouped as Retrievers and Counters if they used retrieval or counting, respectively, on more than 60% of correctly solved problems. The child’s self-report and the assessor’s notes agreed on 97% of the trials on average; the experimenter’s judgment was used when the two disagreed. Outlier trials in which the RT was less than 1st percentile or greater than 99th for a given subject across all trials were excluded, if the RT was also less than the 1st percentile or greater than the 99th for the given problem across all participants. Trials in which the child gave multiple verbal responses and the experimenter had stopped the timer after the initial response were also excluded.
fMRI experiment
Behavioral task
The fMRI experiment consisted of alternating blocks of (i) standard addition (hereafter, ‘Addition’ task), (ii) ‘plus 1’ addition (hereafter, ‘Control’ task), (iii) a number identification task and (iv) passive fixation. A block fMRI design was used in order to optimize signal detection (Friston, Zarahn, Josephs, Henson & Dale, 1999). In the Addition task, equations with different addends (e.g. 3 + 4 = 7) were presented and the children indicated via a button box whether the answer was correct or incorrect. One operand ranged from 2 to 9, the other from 2 to 5, and answers were correct on 50% of the trials. Incorrect answers deviated by ± 1 or ± 2 from the correct sum (Ashcraft & Battaglia, 1978). The range of values of the smaller operand (hereafter referred to as the ‘min’ value) was restricted to ≤ 5 to allow children to execute the min counting strategy (i.e. state the value of the larger addend and count the smaller one) within the 5-second window provided for each problem in the scanner. The range was determined based on previous studies of the speed with which children in the assessed age range encode numbers and implicitly count (Ashcraft et al., 1984; Geary & Brown, 1991). In other words, the smaller min values should allow the children to complete the count within the allotted 5 seconds. The Control task was identical except that one addend was ‘1’ (e.g. 5 + 1 = 7). Because the Control task has the same format as the Addition task, it provides a high-level control for sensory and number processing, and response selection. In the number identification task (not analyzed here) the symbols of arithmetic operators were replaced by alternative keyboard characters (e.g. 4 o 5 @ 7) and participants were asked to assess if ‘5’ was among the presented digits. Stimuli were displayed for 5 seconds with an inter-trial interval of 500 milliseconds. Stimuli of the same task condition were presented in four blocks, randomly ordered across participants, with 18 trials per condition. Block length was randomly jittered between 22.5 and 27 seconds.
Stimulus presentation
The task was programmed using E-Prime (Psychology Software Tools, Inc.) on a PC computer. Stimuli were presented visually at the center of a screen using a custom-built magnet compatible projection system.
fMRI data acquisition
Images were acquired on a 3T GE Signa scanner. A total of 29 axial slices (4.0 mm thickness, 0.5 mm skip) parallel to the AC-PC and covering the whole brain were imaged with a temporal resolution of 2 seconds using a T2* weighted gradient echo spiral in-out pulse sequence (Glover & Lai, 1998) with the following parameters: TR = 2 s, TE = 30 ms, flip angle = 80°, 1 interleave. The field of view was 20 cm, and the matrix size was 64 × 64, providing an in-plane spatial resolution of 3.125 mm.
fMRI data analysis
Preprocessing
fMRI data were analyzed using SPM8 (http://www.fil.ion.ucl.ac.uk/spm). The first five volumes were not analyzed to allow for T1 equilibration. ArtRepair software was used to correct for excessive movement (http://spnl.stanford.edu/tools/ArtRepair/ArtRepair.htm). Images were realigned to correct for movement, smoothed with a 4 mm FWHM Gaussian kernel and motion adjusted. Deviant volumes resulting from sharp movement or spikes in the global signal were then interpolated using the two adjacent scans. No more than 20% of the volumes were interpolated. Finally, images were corrected for errors in slice-timing, spatially transformed for registration to standard MNI space, and smoothed again at 4.5 mm FWHM Gaussian kernel. The two step sequence of first smoothing with a 4 mm FWHM Gaussian kernel and later with 4.5 mm FWHM Gaussian kernel approximates a total smoothing of 6 mm.
Univariate analysis
Task-related brain activation was identified using a general linear model. Brain activity related to each task condition was modeled using boxcar functions with a canonical hemodynamic response function and a temporal derivative to account for voxel-wise latency differences in hemodynamic response. Low-frequency drifts at each voxel were removed using a high-pass filter (0.5 cycles/min). Voxel-wise contrast and t-statistics images were generated for each participant by contrasting the Addition versus the Control tasks. Brain responses in Retrievers and Counters were then compared at the group level using t-statistics on contrast images from each participant. Significant clusters of activation were determined using a voxel-wise height threshold of p < .01 and a spatial extent threshold of p < .01 to correct for multiple spatial comparisons. We used a non-parametric approach based on Monte Carlo simulations to determine the minimum cluster size that controls for false positive rate at p < 0.01 for both height and extent. This approach avoids making any assumptions about the underlying distribution of cluster size under the null hypothesis. Monte Carlo simulations were implemented in Matlab using methods similar to the AlphaSim procedure in AFNI (Forman, Cohen, Fitzgerald, Eddy, Mintun & Noll, 1995; Ward, 2000; Slotnick & Schacter, 2004; Rama, Poremba, Sala, Yee, Malloy, Mishkin & Courtney, 2004). Ten thousand iterations of random 3D images, with the same resolution and dimensions as the fMRI data, were generated. The resulting images were smoothed with the same 6 mm FWHM Gaussian kernel used to smooth the fMRI data. The probability distribution of cluster size across all iterations was then estimated. The cluster threshold corresponding to a significance level of p < .01 was determined to be 137 voxels. All stereotaxic coordinates are reported in MNI space.
Multivariate Pattern Analysis (MPA)
A multivariate statistical pattern recognition-based method (Kriegeskorte, Goebel & Bandettini, 2006; Haynes & Rees, 2006) was used to identify brain regions that discriminated spatial activation patterns between Counters and Retrievers. This method utilizes a nonlinear classifier based on support-vector machine algorithms with radial basis function (RBF) kernels (Muller, Mika, Ratsch, Tsuda & Scholkopf, 2001). We used t-scores to examine group differences because defining response patterns in units of standard-error, rather than beta estimates, has been shown to have greater sensitivity for extracting pattern information in fMRI data (Misaki, Kim, Bandettini & Kriegeskorte, 2010). Briefly, at each voxel vi, a 3 × 3 × 3 neighborhood centered at vi was defined. The spatial pattern of voxels in this neighborhood was defined by a 27-dimensional vector. Support vector machine (SVM) classification was performed using LIBSVM (www.csie.ntu.edu.tw/~cjlin/libsvm) software. For the nonlinear SVM classifier, we specified two parameters, C (regularization) and α (parameter for RBF kernel) at each searchlight position. We estimated optimal values of C, α and the generalizability of the classifier at each searchlight position by using a combination of grid search and cross-validation procedures. In earlier approaches (Haynes et al., 2007), linear SVM was used and the free parameter C was arbitrarily set. In the current work, however, we optimized the free parameters (C and α) based on the data, thereby designing an optimal classifier. In the M-fold cross-validation procedure, the data are randomly divided into M-folds. M-1 folds were used for training the classifier and the remaining fold was used for testing. This procedure is repeated M times wherein a different fold was left out for testing each time. We estimated class labels of the test data at each fold and computed the average classification accuracy obtained at each fold, termed here as the cross-validation accuracy (CVA). The optimal parameters were found by grid searching the parameter space and selecting the pair of values (C, α) at which the M-fold cross-validation accuracy is maximum. In order to search for a wide range of values, we varied the values of C and α from 0.125 to 32 in steps of 2 (0.125, 0.25, 0.5, …, 16, 32). Here we used a leave-one-out cross-validation procedure where M = N (where N is the number of data samples in each condition/class). The resulting 3-D map of cross-validation accuracy at every voxel was used to detect brain regions that discriminated between groups. Under the null hypothesis that there is no difference between the two groups, the cross-validation accuracies (CVAs) were assumed to follow the binomial distribution Bi (N, p) with parameters N equal to the total number of participants in two groups and p equal to 0.5, assuming that under the null hypothesis, the probability of each group is equal (Pereira, Mitchell & Botvinick, 2009). The CVAs were then converted to p-values using the binomial distribution (Abrams et al., 2010). The statistical map was thresholded at p < .01 for height and p < .01 for cluster extent using Monte Carlo simulations (Forman et al., 1995; Ward, 2000; Slotnick & Schacter, 2004; Rama et al., 2004).
Results
Strategy assessment
From a group of 103 children, 36 children met criteria for classification as ‘Retrievers’ and ‘Counters’. There were 19 Retrievers (mean % trials retrieved = 85.5%, SE = 2.8%) and 17 Counters (mean % trials counted = 80.3%, SE = 2.6%) (Figure 1A, 1B); as expected, retrieval use was significantly greater in Retrievers than Counters (p < .001). During the strategy assessment session, Retrievers solved 80% (SE = 1.7%) of the problems correctly with a median RT of 2.90 seconds (SE = 187 milliseconds). Counters solved 79% (SE = 2.3%) of the problems correctly with a median RT of 4.06 seconds (SE = 261 milliseconds). The two groups did not differ on accuracy of performance (p > .05) on the strategy assessment but the Retrievers were significantly faster (p < .01) given that the children were allowed unlimited time to solve each problem. Retrievers and Counters did not differ on age, IQ, or reading ability (ps > .05; Table 1). The mathematical competence of both groups was average, with Retrievers scoring somewhat higher than Counters (p < .05; Table 1) as would be expected given that retrieval is a more mature approach to solving arithmetic items on such tests. Additional analyses were conducted to examine performance on trials with a min value ≤ 5, similar to those used during fMRI scanning. In Retrievers, the % of retrieval use was 92% (SE = 2%) and in Counters, the % of counting use was 73% (SE = 4%); as expected, group differences in strategy usage were highly significant (p < .006). In these sets of problems, the median RTs of Retrievers (2.64 seconds, SE = 175 milliseconds) and Counters (3.06 seconds, SE = 250 milliseconds) did not differ (p > .1), nor did they differ for accuracy (% correct = .74% for both Retrievers and Counters).
Figure 1.
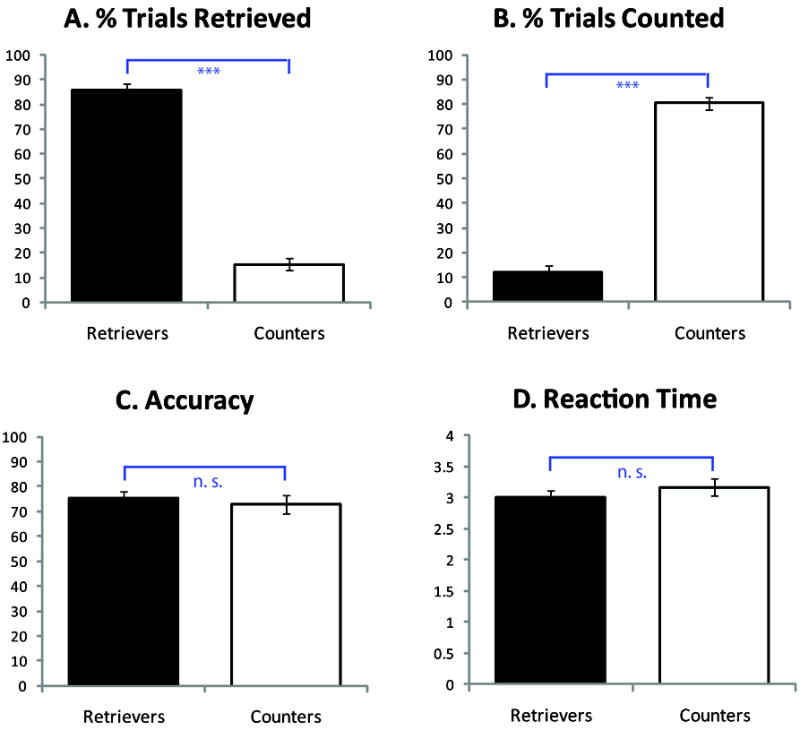
(A, B) Differential strategy use in Retrievers and Counters measured from the strategy assessment session outside the scanner. The two groups differed significantly on percentage of trials in which retrieval or counting were used. (C, D) Performance in Retrievers and Counters on the Addition task performed inside the scanner. The two groups were well matched on performance, with no differences in either accuracy or reaction time (RT). Three asterisks (***) on graph denote p < .001; ns, not significant.
Table 1.
Demographics and neurocognitive assessment scores of Retrievers and Counters
| Measure | Counters’ Mean ± SE |
Retrievers’ Mean ± SE |
t-test |
|---|---|---|---|
| Age | 8.6 ± 0.16 | 8.2 ± 0.15 | t(34) = 1.96, p = .06 |
| WASI Full scale IQ | 107.53 ± 2.38 | 109.32 ± 2.54 | t(34) = -.51, p = .61 |
| WIAT Word Reading | 104.35 ± 2.57 | 111.05 ± 2.98 | t(34) = -1.68, p = .10 |
| WIAT Reading Comprehension | 104.59 ± 2.94 | 107.42 ± 2.29 | t(34) = -.77, p = .45 |
| WIAT Number Operations | 97.00 ± 3.18 | 105.89 ± 2.96 | t(34) = -2.05, p = .05 |
| WIAT Mathematical Reasoning | 101.47 ± 2.75 | 109.16 ± 2.03 | t(34) = -2.28, p = .03 |
SE, Standard Error; WAIS, Wechsler Abbreviated Intelligence Scale; WIAT, Wechsler Individual Aptitude Test.
fMRI task performance
Behavioral performance during the fMRI session was similar for Retrievers and Counters (Figure 1). Retrievers were accurate on 75.4% (SE = 2.3%) of the trials and their correct trial median RT was 3.0 seconds (SE = 105 milliseconds). Counters’ accuracy was 72.9% and their correct trial median RT was 3.17 seconds (SE = 132 milliseconds) (Figure 1C, 1D). Two-way ANOVA with factors Group (Retrievers, Counters) and Task (Addition, Control) revealed no Group by Task interaction (F < 1, p > .6), nor main effect of Group in accuracy or RT (F < 1, p > .3). The main effect of Task was significant, i.e. participants made more errors and took longer to solve Addition problems compared to Control problems (accuracy: F(1, 34) = 28.98, p < .001; RT: F(1, 34) = 86.76, p < .001).
In order to rule out the possibility that the subjects used an approximation strategy to solve addition verification problems in the scanner, we compared the effect of Distance, i.e. the numerical distance between the presented answer and the correct answer for problems in which an incorrect equation was presented (± 1 vs. ± 2) in the two Groups (Retrievers vs. Counters). There was no interaction between Distance and Group, nor were there any main effects of Distance or Group on either accuracy or RT (ps > .1).
To test for differences in problem solving behavior between the strategy assessment session and the in-scanner addition session, we ran a repeated measures ANOVA on the median RTs and accuracy measures with Group (Retriever vs. Counter) as the between-subjects factor and Session (strategy assessment session vs. scanner addition session) as a within-subject factor. The problems in the strategy assessment were chosen to match the difficulty level of the scanner addition task (i.e. min ≤ 5) for this analysis. The Group by Session interaction was not significant for either RT or accuracy (ps > .1), nor were the main effects of session (p > .1) or group (p > .1).
Univariate differences in brain activation between Retrievers and Counters
We first examined brain regions that showed significant differences in activation levels between Retrievers and Counters. Only the left VLPFC showed differences in signal intensity between the two groups and activity was greater for Retrievers compared to Counters (height p < .01, extent p < .01 corrected using Monte Carlo simulation), as shown in Figure 2. There were no brain regions in which activity levels were greater in Counters, compared to Retrievers. Table 2 summarizes the peak location of brain regions that showed significant univariate differences between the two groups.
Figure 2.
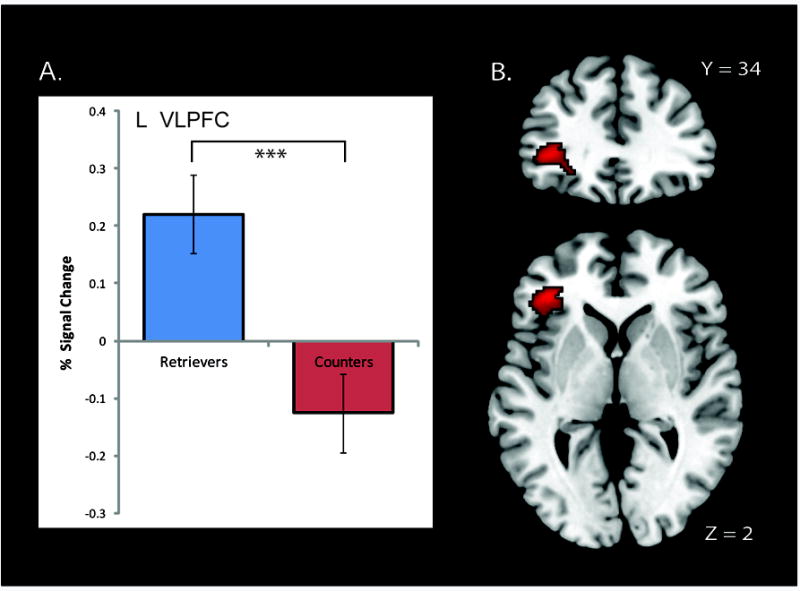
(A) Percentage signal change in the VLPFC across the two groups. (B) Brain areas that showed significant differences in voxel-wise activation levels during the Addition task between Retrievers and Counters. The left ventrolateral prefrontal cortex (VLPFC) showed greater activation in Retrievers compared to Counters. No brain regions showed greater activation in Counters, compared to Retrievers. Three asterisks (***) on graph denote p < .001.
Table 2.
Brain regions that showed significant differences in voxel-wise (univariate) activation levels between Retrievers and Counters
| Region | Cluster Size |
MNI coordinates | Max T | p | BA | ||
|---|---|---|---|---|---|---|---|
| X | Y | Z | |||||
| L VLPFC | 282 | -36 | 36 | 4 | 4.78 | p < .01 | 47 |
MNI, Montreal Neurological Institute; BA, Brodmann’s Area; VLPFC, Ventrolateral Prefrontal Cortex.
Multivariate differences in brain activation between Retrievers and Counters
We then examined brain regions that showed significant differences in multivariate activation patterns between Retrievers and Counters using the searchlight method (Kriegeskorte et al., 2006; Abrams et al., 2010). We performed MPA to examine whether localized patterns of fMRI activity could accurately distinguish between Retrievers and Counters. MPA revealed that Retrievers and Counters had different activation patterns in the left and right MTL, left VLPFC, left premotor cortex and bilateral PPC regions including the bilateral SMG and right IPS and AG (Figure 3). Table 3 summarizes the peak location of the brain regions highlighted in Figure 3 that showed significant multi-voxel differences between the two groups. Classification accuracy in each voxel was greater than 69% (height p < .01, extent p < .01 corrected for multiple spatial comparisons using Monte Carlo simulations). The resulting map of multivariate activity pattern differences showed prominent overlap with left VLPFC voxels identified in the univariate analysis, as illustrated in Figure 4. No other brain regions showed differences in voxel-wise signal level between the two groups (Figure S1).
Figure 3.
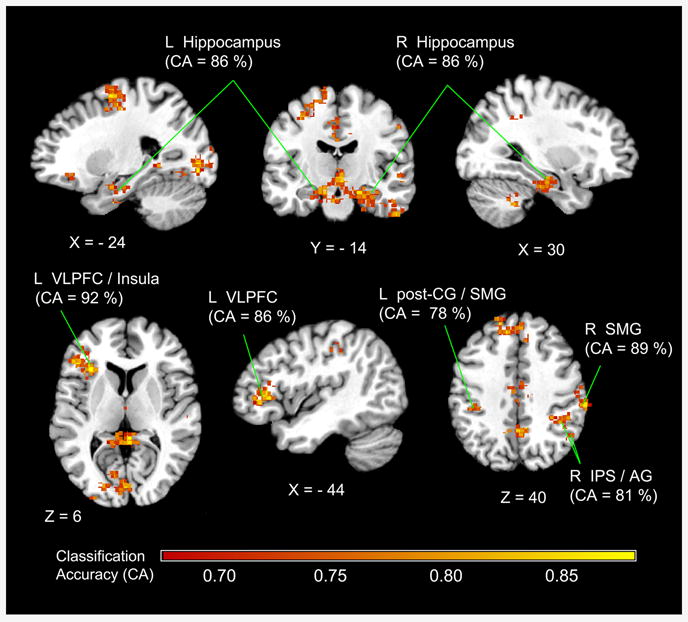
Multivariate pattern analysis (MPA) revealed significant differences in spatial activation patterns between Retrievers and Counters in three brain areas: (1) bilateral medial temporal lobe – hippocampi and parahippocampal gyri; (2) left prefrontal cortex – ventrolateral prefrontal cortex (VLPFC) and adjoining anterior insula; (3) bilateral posterior parietal cortex – left and right supramarginal gyrus (SMG), right intra-parietal sulcus (IPS) and angular gyrus (AG). Peak classification accuracies (CA) in each brain region are shown in parentheses.
Table 3.
Brain regions showing significant differences in multivariate activation patterns between Retrievers and Counters
| Region | MNI coordinates | Max CVA |
BA | ||
|---|---|---|---|---|---|
| X | Y | Z | |||
| L Parahippocampal Gyrus | -24 | -6 | -36 | 0.86 | 36 |
| L Hippocampus | -24 | -16 | -22 | 0.78 | 20 |
| R Hippocampus | 22 | -14 | -18 | 0.86 | 20 |
| L Ventrolateral Prefrontal Cortex | -44 | 38 | 0 | 0.86 | 45 |
| L Anterior Insula | -32 | 26 | 6 | 0.92 | 48 |
| L Supramarginal Gyrus | -62 | -38 | 26 | 0.78 | 40 |
| R Supramarginal Gyrus | 64 | -26 | 38 | 0.89 | 40 |
| R Intraparietal Sulcus | 42 | -42 | 42 | 0.81 | 40 |
Figure 4.
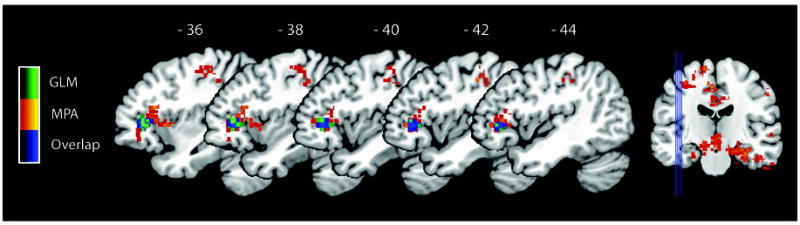
Overlap between multivariate and univariate analyses of group differences between Retrievers and Counters. Voxel-wise univariate analysis (t-test) by General Linear Modeling (GLM) showed that Retrievers had significantly greater brain activity than Counters in the left ventrolateral prefrontal cortex (VLPFC). This activation overlaps with the left VLPFC region that showed group differences using multivariate pattern analysis (MPA). As shown in legend, MPA classification results (same as in Figure 3) are in red, univariate analysis results are in green, and the overlap between the two analyses is in blue. The blue lines on the coronal slice depict sagittal slice loci.
Discussion
The development of efficient problem solving strategies is one of the most important milestones of children’s learning. In this study, we examined the neural correlates of individual differences in the use of retrieval to solve simple arithmetic problems. In contrast to previous studies, we focused on a narrow age range, during which many children show decreased use of counting procedures and increased use of retrieval for arithmetical problem solving. We compared brain responses in these 7–9-year-old children using both univariate and multivariate approaches. Interestingly, at the individual voxel level, the left VLPFC was the only region in which there were signal intensity differences between the two groups (Figure 2). Our analyses further revealed that strategy differences are mainly reflected in multivariate activity patterns across neuronal populations. These latter results are interpreted in a fundamentally different manner from those described for traditional univariate results, which identify voxels with greater magnitude of activation for one group (or experimental condition) relative to another. Multivariate results, in contrast, show which voxels in the brain are able to discriminate between the two groups based on the pattern of fMRI activity measured across sets of multiple voxels. Our multivariate analyses identify the location of voxel groups that together demonstrate a fundamentally different spatial pattern of activity in one group relative to another (Haynes & Rees, 2006; Kriegeskorte et al., 2006; Schwarzlose, Swisher, Dang & Kanwisher, 2008; Pereira et al., 2009; Abrams et al., 2010). Our findings suggest that even when the same brain areas are engaged to a similar degree in the two groups of children, compared to procedural strategies, memory-based arithmetic problem solving evokes distinct fine-scale neural representations. Critically, as described below, such differences were highly prominent in medial temporal lobe regions important for memory formation.
Matching performance in Retrievers and Counters
Although retrieval is a more mature problem solving approach than counting, performance differences between these approaches may not be substantial during the transition from counting to retrieval. This is because when children are first learning to retrieve memorized facts, the process is not fully automated and thus can be effortful and more time consuming compared to adults retrieving the same facts (Geary, Bow-Thomas, Liu & Siegler, 1996). Moreover, counting at this point is a well-practiced skill that can be executed quickly and accurately by many children, especially for the simple problems (min ≤ 5) used in this study. Importantly, for these problems, the two groups did not differ in accuracy or RTs on the strategy assessment or scanner tasks, nor did they differ on age, IQ, or reading ability. Although both groups were in the average range on the mathematics achievement tests, the Retrievers had a small advantage over the Counters. This is a common finding (Geary & Burlingham-Dupree, 1989) and is likely due to the advantages in using retrieval for the solution of test items that are more complex than those used in our scanner task. The critical point for our analyses is that RTs and accuracy of the Retrievers and Counters were well matched on the scanner task. On the basis of this tight performance matching, we highlight three important differences in the brain response associated with children’s differential use of retrieval and counting strategies.
MTL responses related to differential strategy use during early development
Retrieval and counting were associated with different activation patterns in MTL regions important for memory encoding and retrieval. Indeed, some of the highest classification rates between Retrievers and Counters were observed in the MTL. Notably, the hippocampus and the parahippocampal gyrus showed prominent differences between the two groups in both hemispheres. Although these regions are known to be critical for memory formation (Squire et al., 2004; Suzuki, 2007; Wang & Morris, 2010), their potential role in learning arithmetic facts has been largely ignored in previous brain imaging studies. This is because most such studies have focused on adults who are likely to rely more on neocortical than on the hippocampal system for fact retrieval (Suzuki, 2007; Wang & Morris, 2010). Indeed, a previous developmental study found that the hippocampus plays a greater role during arithmetic problem solving in children than adults (Rivera et al., 2005). Our study provides the first definitive evidence for the differential engagement of the MTL – not in terms of the voxel-wise signal intensity but the fine-scale spatial pattern of neural activity across multiple voxels – with respect to children’s strategy shift towards retrieval during early learning. This finding emphasizes that developmental changes cannot be inferred from, or characterized by, a gross comparison between adults and children or by examining the effects of training on novel problems in adults (Karmiloff-Smith, 2010). Combined with results from the study by Rivera and colleagues, these findings suggest that the MTL plays a critical role during the transition from procedural to memory-based problem solving, and that the role of MTL subsequently declines with expertise, i.e. the automation of fact retrieval. Our findings further suggest that the role of MTL memory systems, often ignored in the extant literature on arithmetic learning derived primarily from studies in adults, warrants further consideration in the context of mathematical skill development in children.
Differential engagement of the PPC in Retrievers and Counters
The PPC showed significant differences in spatial patterns of brain activity between Retrievers and Counters. It is noteworthy, however, that the early stages of arithmetic skill acquisition are characterized by changes in the multivariate pattern of neural activity rather than differences in activation level of individual voxels. This is in sharp contrast to findings in adults which have focused on univariate differences in activation levels associated with differential use of retrieval strategies (Delazer et al., 2005; Ischebeck et al., 2007; Grabner et al., 2009a; Wu et al., 2009). In the present study, Retrievers and Counters were found to have distinct patterns of multivoxel activity bilaterally in the SMG and the right IPS and AG. Previous studies of strategy use in adults have not assessed changes in multivariate activation patterns associated with greater retrieval use, so it is not possible to directly compare our findings with those from prior univariate analyses. In adults, greater use of retrieval has been associated with greater left AG response whereas procedural strategies engage more widespread regions in the bilateral IPS and the superior parietal lobule (Grabner et al., 2009a). Parallel studies of learning in which adult participants are trained on particular problem sets also show differential response in the PPC, with reduced activation bilaterally in the IPS and greater responses in both the left and right AG for learned, compared to unlearned, arithmetic facts (Delazer et al., 2005; Ischebeck et al., 2007). Based on these findings in adults, we might predict that greater use of retrieval strategies in children would be associated with greater activation of the AG and reduced activation of the IPS. Contrary to this model, 7–9-year-old Retrievers and Counters showed no differences in IPS or AG activation levels. Rather, the two groups showed dissociable spatial pattern of multivoxel activity in the PPC. One possible reason for these differences is that unlike previous studies in adults in which performance differed across strategy use, the two groups of children in our study were well matched on performance. Critically, our findings show for the first time that retrieval and counting strategies, without performance confounds, are characterized by distinct neural representations in the PPC of young children at an important period for arithmetic skill acquisition.
PFC role in Retrieval versus Counting
The left VLPFC showed prominent differences between Retrievers and Counters, manifesting both greater activation levels in Retrievers compared to Counters in the univariate analysis and significant classification rates in the MPA analysis. It is noteworthy that Counters did not show greater activity in either the VLPFC or any other PFC region. Interestingly, this pattern of VLPFC response is the opposite of findings reported in adult training studies which found that greater use of procedural strategies was associated with slower response times and increased PFC activation in adults (Zago et al., 2001; Delazer et al., 2005; Ischebeck et al., 2007). The left prefrontal cortex, especially the VLPFC is known to play a prominent role in cognitive control over retrieval in both adults (Demb, Desmond, Wagner, Vaidya, Glover & Gabrieli, 1995; Sohn, Goode, Koedinger, Stenger, Fissell, Carter & Anderson, 2004; Badre & Wagner, 2007; Danker, Gunn & Anderson, 2008) and children (Bunge et al., 2002). In children, these control processes are known to be important for retrieval of arithmetic facts (Kaufmann, 2002; DeStefano & LeFevre, 2004; Kaufmann, Lochy, Drexler & Semenza, 2004; Passolunghi & Siegel, 2004), especially in the selection of retrieval strategies and inhibition of procedural strategies (Geary, 2006). These findings together suggest that although counting relies on greater PFC resources for execution of calculation procedures, improved cognitive control over memory retrieval relies on greater left VLPFC specifically in children who predominantly use retrieval strategies (Geary et al., 2004). Furthermore, this finding implies that the shift to memory-based processes may be more effortful than has been assumed. These observations highlight important differences in the nature of PFC mechanisms underlying fact learning and retrieval in children and adults. Further, it should be noted that in our study, performance was equated between the two groups, which was not the case in previous studies. The children in the Counter group were well practiced at counting and could solve arithmetic problems as accurately and as fast as the Retriever group. Thus performance differences between groups were not a confounding factor in the interpretation of results in our study. Further developmental studies with older children are needed to disentangle the changing role of the PFC in relation to learning and differential strategy use, leading to more fully automated fact retrieval in adulthood (Zbrodoff & Logan, 1986).
Multivoxel analysis provided additional insights into left VLPFC differences between Retrievers and Counters, over and above those indicated by the univariate analysis. It is critical to note that, unlike the univariate method, MPA does not provide information about which voxels have greater activation in one group compared to another. Furthermore, MPA is based on demeaned multivoxel data, so that the observed multivariate effects cannot be ascribed to differences in the height of activation observed between the two groups. Rather, high classification rates reflect robust differences in normalized spatial patterns of activation in the two groups. The existence of decodable fine-scale pattern differences in fMRI signals suggests not only that the left VLPFC is differentially engaged in Retrievers, but also that the underlying neural resources are accessed and used differently in each group.
Conclusions
Our findings demonstrate that retrieval and counting strategies elicit distinct patterns of activity in a distributed brain network involved in arithmetic problem solving and controlled retrieval of arithmetic facts during early learning. What appears to be rather distinct behavioral approaches are guided by differential patterns of activity, rather than overall signal intensity in a set of brain regions that are known to support memory formation and long-term memory representation (Tse, Langston, Bethus, Wood, Witter & Morris, 2008; Wang & Morris, 2010) and areas of the PPC important for arithmetic problem solving in children (Menon, 2010). We suggest that functional reorganization and refinement of neural activity within the MTL, PPC and PFC regions identified here may underlie the development of memory-based arithmetical problem solving in young children. Our study highlights several important differences between brain systems related to strategy use in children and adults. In the early stages of arithmetic skill acquisition, children show a different profile of brain responses associated with differential strategy use, compared to those observed during short-term effects in adults. A truly developmental approach requires focusing on a narrow window of schooling in order to understand graduated change over time (Karmiloff-Smith, 2010) and studies comparing children with adults are likely to be insensitive to major developmental changes that occur during early elementary schooling. Future research will determine whether children’s cognitive development in other academic domains relies on similar mechanisms (Siegler, 1996). More generally, our study provides a framework for integrating brain imaging and developmental research in the investigation of cardinal aspects of cognitive development.
Future studies would benefit from better matching of problems in the strategy assessment and the fMRI sessions. It would be a significant advance to be able to assess strategy use on a trial-by-trial basis during fMRI scanning to improve the correspondence between assessed strategy and performance. Finally, the use of arithmetic production during strategy assessment versus verification during fMRI scanning is a limitation of this study, since research has suggested that different memory processes might be involved depending on whether arithmetic production or verification is required (Campbell & Tarling, 1996). A recent study in adults has demonstrated the feasibility of using arithmetic production tasks during fMRI scanning (Andres, Pelgrims, Michaux, Olivier & Presenti, 2011), suggesting the possibility of resolving this limitation in future neurodevelopmental studies.
Supplementary Material
Acknowledgments
We thank Christina B. Young, Tianwen Chen, Miriam Rosenberg-Lee, Arron Metcalfe, Leeza M. Kondos, Sarah S. Wu and Jose M. Anguiano for their assistance with the study. This research was supported by grants from NIH (HD047520, HD059205, HD057610) and NSF (DRL-0750340).
References
- Abrams DA, Bhatara AK, Ryali S, Balaban E, Levitin DJ, Menon V. Decoding temporal structure in music and speech relies on shared brain resources but elicits different fine-scale spatial patterns. Cerebral Cortex. 2010;15:1848–1854. doi: 10.1093/cercor/bhq198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andres M, Pelgrims B, Michaux N, Olivier E, Pesenti M. Role of distinct parietal areas in arithmetic: An fMRI-guided TMS study. NeuroImage. 2011;54:3048–3056. doi: 10.1016/j.neuroimage.2010.11.009. [DOI] [PubMed] [Google Scholar]
- Ashcraft MH. The development of mental arithmetic – a chronometric approach. Developmental Review. 1982;2:213–236. [Google Scholar]
- Ashcraft MH, Battaglia J. Cognitive arithmetic: evidence for retrieval and decision processes in mental addition. Journal of Experimental Psychology: Human Learning and Memory. 1978;4:527–538. [Google Scholar]
- Ashcraft MH, Fierman BA. Mental addition in 3rd, 4th and 6th graders. Journal of Experimental Child Psychology. 1982;33:216–234. [Google Scholar]
- Ashcraft M, Fierman B, Bartolotta R. The production and verification tasks in mental addition: an empirical comparison. Developmental Review. 1984;4:157–170. [Google Scholar]
- Badre D, Wagner AD. Left ventrolateral prefrontal cortex and the cognitive control of memory. Neuropsychologia. 2007;45:2883–2901. doi: 10.1016/j.neuropsychologia.2007.06.015. [DOI] [PubMed] [Google Scholar]
- Bunge SA, Dudukovic NM, Thomason ME, Vaidya CJ, Gabrieli JD. Immature frontal lobe contributions to cognitive control in children: evidence from fMRI. Neuron. 2002;33:301–311. doi: 10.1016/s0896-6273(01)00583-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campbell JI, Tarling DP. Retrieval processes in arithmetic production and verification. Memory & Cognition. 1996;24:156–172. doi: 10.3758/bf03200878. [DOI] [PubMed] [Google Scholar]
- Carpenter TP, Moser JM. The acquisition of addition and subtraction concepts in grades one through three. Journal for Research in Mathematics Education. 1984;15:179–202. [Google Scholar]
- Danker JF, Gunn P, Anderson JR. A rational account of memory predicts left prefrontal activation during controlled retrieval. Cerebral Cortex. 2008;18:2674–2685. doi: 10.1093/cercor/bhn027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dehaene S, Piazza M, Pinel P, Cohen L. Three parietal circuits for number processing. Cognitive Neuropsychology. 2003;20:487–506. doi: 10.1080/02643290244000239. [DOI] [PubMed] [Google Scholar]
- Delazer M, Domahs F, Bartha L, Brenneis C, Lochy A, Trieb T, Benke T. Learning complex arithmetic – an fMRI study. Brain Research Cognitive Brain Research. 2003;18:76–88. doi: 10.1016/j.cogbrainres.2003.09.005. [DOI] [PubMed] [Google Scholar]
- Delazer M, Ischebeck A, Domahs F, Zamarian L, Koppelstaetter F, Siedentopf C, Kaufmann L, Benke T, Felber S. Learning by strategies and learning by drill – evidence from an fMRI study. NeuroImage. 2005;25:838–849. doi: 10.1016/j.neuroimage.2004.12.009. [DOI] [PubMed] [Google Scholar]
- Demb J, Desmond J, Wagner A, Vaidya C, Glover G, Gabrieli J. Semantic encoding and retrieval in the left inferior prefrontal cortex: a functional MRI study of task difficulty and process specificity. Journal of Neuroscience. 1995;15:5870–5878. doi: 10.1523/JNEUROSCI.15-09-05870.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeStefano D, LeFevre JA. The role of working memory in mental arithmetic. European Journal of Cognitive Psychology. 2004;16:353–386. [Google Scholar]
- Friston KJ, Zarahn E, Josephs O, Henson RN, Dale AM. Stochastic designs in event-related fMRI. NeuroImage. 1999;10:607–619. doi: 10.1006/nimg.1999.0498. [DOI] [PubMed] [Google Scholar]
- Forman SD, Cohen JD, Fitzgerald M, Eddy WF, Mintun MA, Noll DC. Improved assessment of significant activation in functional magnetic resonance imaging (fMRI): use of a cluster-size threshold. Magnetic Resonance in Medicine. 1995;33:636–647. doi: 10.1002/mrm.1910330508. [DOI] [PubMed] [Google Scholar]
- Geary D. A componential analysis of an early learning deficit in mathematics. Journal of Experimental Child Psychology. 1990;49:363–383. doi: 10.1016/0022-0965(90)90065-g. [DOI] [PubMed] [Google Scholar]
- Geary DC. Children’s mathematical development: Research and practical applications. Washington, DC: American Psychological Association; 1994. [Google Scholar]
- Geary DC. Development of mathematical understanding. In: Kuhl D, Siegler RS, editors. Cognition, perception, and language. Vol. 2. 2006. pp. 777–810. [Google Scholar]; Damon W, editor. Handbook of child psychology. 6. New York: John Wiley & Sons; [Google Scholar]
- Geary D, Bow-Thomas C, Liu F, Siegler R. Development of arithmetical competencies in Chinese and American children: influence of age, language, and schooling. Child Development. 1996;67:2022–2044. [PubMed] [Google Scholar]
- Geary D, Brown S. Cognitive addition: strategy choice and speed-of-processing differences in gifted, normal, and mathematically disabled-children. Developmental Psychology. 1991;27:398–406. [Google Scholar]
- Geary D, Burlingham-Dupree M. External validation of the strategy choice model for addition. Journal of Experimental Child Psychology. 1989;47:175–192. [Google Scholar]
- Geary DC, Hoard MK, Byrd-Craven J, DeSoto CM. Strategy choices in simple and complex addition: contributions of working memory and counting knowledge for children with mathematical disability. Journal of Experimental Child Psychology. 2004;88:121–151. doi: 10.1016/j.jecp.2004.03.002. [DOI] [PubMed] [Google Scholar]
- Geary DC, Hoard MK, Byrd-Craven J, Nugent L, Numtee C. Cognitive mechanisms underlying achievement deficits in children with mathematical learning disability. Child Development. 2007;78:1343–1359. doi: 10.1111/j.1467-8624.2007.01069.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary D, Widaman K, Little T, Cormier P. Cognitive addition: comparison of learning disabled and academically normal elementary school children. Cognitive Development. 1987;2:249–269. [Google Scholar]
- Glover GH, Lai S. Self-navigated spiral fMRI: interleaved versus single-shot. Magnetic Resonance in Medicine. 1998;39:361–368. doi: 10.1002/mrm.1910390305. [DOI] [PubMed] [Google Scholar]
- Grabner R, Ansari D, Koschutnig K, Reishofer G, Ebner F, Neuper C. To retrieve or to calculate? Left angular gyrus mediates the retrieval of arithmetic facts during problem solving. Neuropsychologia. 2009a;47:604–608. doi: 10.1016/j.neuropsychologia.2008.10.013. [DOI] [PubMed] [Google Scholar]
- Grabner R, Ischebeck A, Reishofer G, Koschutnig K, Delazer M, Ebner F, Neuper C. Fact learning in complex arithmetic and figural-spatial tasks: the role of the angular gyrus and its relation to mathematical competence. Human Brain Mapping. 2009b;30:2936–2952. doi: 10.1002/hbm.20720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Groen G, Parkman J. Chronometric analysis of simple addition. Psychological Review. 1972;79:329–343. [Google Scholar]
- Hamann M, Ashcraft M. Simple and complex mental addition across development. Journal of Experimental Child Psychology. 1985;40:49–72. [Google Scholar]
- Haynes JD, Rees G. Decoding mental states from brain activity in humans. Nature Reviews Neuroscience. 2006;7:523–534. doi: 10.1038/nrn1931. [DOI] [PubMed] [Google Scholar]
- Ischebeck A, Zamarian L, Siedentopf C, Koppelstatter F, Benke T, Felber S, Delazer M. How specifically do we learn? Imaging the learning of multiplication and subtraction. NeuroImage. 2006;30:1365–1375. doi: 10.1016/j.neuroimage.2005.11.016. [DOI] [PubMed] [Google Scholar]
- Ischebeck A, Zamarian L, Egger K, Schocke M, Delazer M. Imaging early practice effects in arithmetic. NeuroImage. 2007;36:993–1003. doi: 10.1016/j.neuroimage.2007.03.051. [DOI] [PubMed] [Google Scholar]
- Karmiloff-Smith A. Getting developmental differences or studying child development? Cognition. 1981;10:151–158. doi: 10.1016/0010-0277(81)90039-1. [DOI] [PubMed] [Google Scholar]
- Karmiloff-Smith A. Neuroimaging of the developing brain: taking ‘developing’ seriously. Human Brain Mapping. 2010;31:934–941. doi: 10.1002/hbm.21074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufmann L. More evidence for the role of the central executive in retrieving arithmetic facts: a case study of severe developmental dyscalculia. Journal of Clinical and Experimental Neuropsychology. 2002;24:302–310. doi: 10.1076/jcen.24.3.302.976. [DOI] [PubMed] [Google Scholar]
- Kaufmann L, Lochy A, Drexler A, Semenza C. Deficient arithmetic fact retrieval: storage or access problem? A case study. Neuropsychologia. 2004;42:482–496. doi: 10.1016/j.neuropsychologia.2003.09.004. [DOI] [PubMed] [Google Scholar]
- Kawashima R, Taira M, Okita K, Inoue K, Tajima N, Yoshida H, Sasaki T, Sugiura M, Watanabe J, Fukuda H. A functional MRI study of simple arithmetic: a comparison between children and adults. Cognitive Brain Research. 2004;18:227–233. doi: 10.1016/j.cogbrainres.2003.10.009. [DOI] [PubMed] [Google Scholar]
- Kaye DB, Post TA, Hall VC, Dineen JT. Emergence of information-retrieval strategies in numerical cognition: a developmental study. Cognition and Instruction. 1986;3:127–150. [Google Scholar]
- Klingberg T, Forssberg H, Westerberg H. Increased brain activity in frontal and parietal cortex underlies the development of visuospatial working memory capacity during childhood. Journal of Cognitive Neuroscience. 2002;14:1–10. doi: 10.1162/089892902317205276. [DOI] [PubMed] [Google Scholar]
- Kriegeskorte N. Relating population-code representations between man, monkey, and computational models. Frontiers in Neuroscience. 2009;3:363–373. doi: 10.3389/neuro.01.035.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kriegeskorte N, Goebel R, Bandettini P. Information-based functional brain mapping. Proceedings of the National Academy of Sciences of the United States of America. 2006;103:3863–3868. doi: 10.1073/pnas.0600244103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kucian K, von Aster M, Loenneker T, Dietrich T, Martin E. Development of neural networks for exact and approximate calculation: a FMRI study. Developmental Neuropsychology. 2008;33:447–473. doi: 10.1080/87565640802101474. [DOI] [PubMed] [Google Scholar]
- Kwon H, Reiss AL, Menon V. Neural basis of protracted developmental changes in visuo-spatial working memory. Proceedings of the National Academy of Sciences of the United States of America. 2002;99:13336–13341. doi: 10.1073/pnas.162486399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luna B, Garver KE, Urban TA, Lazar NA, Sweeney JA. Maturation of cognitive processes from late childhood to adulthood. Child Development. 2004;75:1357–1372. doi: 10.1111/j.1467-8624.2004.00745.x. [DOI] [PubMed] [Google Scholar]
- Menon V. Developmental cognitive neuroscience of arithmetic: implications for learning and education. The International Journal on Mathematics Education. 2010;42:515–525. doi: 10.1007/s11858-010-0242-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menon V, Rivera S, White C, Glover G, Reiss A. Dissociating prefrontal and parietal cortex activation during arithmetic processing. NeuroImage. 2000;12:357–365. doi: 10.1006/nimg.2000.0613. [DOI] [PubMed] [Google Scholar]
- Misaki M, Kim Y, Bandettini P, Kriegeskorte N. Comparison of multivariate classifiers and response normalizations for pattern-information fMRI. NeuroImage. 2010;53:103–118. doi: 10.1016/j.neuroimage.2010.05.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller KR, Mika S, Ratsch G, Tsuda K, Scholkopf B. An introduction to kernel-based learning algorithms. IEEE Transactions on Neural Networks. 2001;12:181–201. doi: 10.1109/72.914517. [DOI] [PubMed] [Google Scholar]
- Mur M, Bandettini PA, Kriegeskorte N. Revealing representational content with pattern-information fMRI: an introductory guide. Social Cognitive and Affective Neuroscience. 2009;4:101–109. doi: 10.1093/scan/nsn044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Passolunghi MC, Siegel LS. Working memory and access to numerical information in children with disability in mathematics. Journal of Experimental Child Psychology. 2004;88:348–367. doi: 10.1016/j.jecp.2004.04.002. [DOI] [PubMed] [Google Scholar]
- Pereira F, Mitchell T, Botvinick M. Machine learning classifiers and fMRI: a tutorial overview. NeuroImage. 2009;45:S199–S209. doi: 10.1016/j.neuroimage.2008.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raizada R, Tsao F, Liu H, Holloway I, Ansari D, Kuhl P. Linking brain-wide multivoxel activation patterns to behaviour: examples from language and math. NeuroImage. 2010;51:462–471. doi: 10.1016/j.neuroimage.2010.01.080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rama P, Poremba A, Sala JB, Yee L, Malloy M, Mishkin M, Courtney SM. Dissociable functional cortical topographies for working memory maintenance of voice identity and location. Cerebral Cortex. 2004;14:768–780. doi: 10.1093/cercor/bhh037. [DOI] [PubMed] [Google Scholar]
- Rivera SM, Reiss AL, Eckert MA, Menon V. Developmental changes in mental arithmetic: evidence for increased functional specialization in the left inferior parietal cortex. Cerebral Cortex. 2005;15:1779–1790. doi: 10.1093/cercor/bhi055. [DOI] [PubMed] [Google Scholar]
- Ryali S, Supekar K, Abrams DA, Menon V. Sparse logistic regression for whole-brain classification of fMRI data. NeuroImage. 2010;51:752–764. doi: 10.1016/j.neuroimage.2010.02.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwarzlose RF, Swisher JD, Dang S, Kanwisher N. The distribution of category and location information across object-selective regions in human visual cortex. Proceedings of the National Academy of Sciences of the United States of America. 2008;105:4447–4452. doi: 10.1073/pnas.0800431105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shrager J, Siegler RS. SCADS: a model of children’s strategy choices and strategy discoveries. Psychological Science. 1998;9:405–410. [Google Scholar]
- Siegler RS. Unities across domains in children’s strategy choices. In: Sloboda J, Rogers D, editors. Cognitive process in mathematics. Oxford: Oxford University Press; 1986. pp. 81–106. [Google Scholar]
- Siegler RS. The perils of averaging data over strategies: an example from children’s addition. Journal of Experimental Psychology: General. 1987;116:250–264. [Google Scholar]
- Siegler RS. Emerging minds: The process of change in children’s thinking. New York: Oxford University Press; 1996. [Google Scholar]
- Siegler RS, Shrager J. Strategy choice in addition and subtraction: how do children know what to do? In: Sophian C, editor. Origins of cognitive skills. Hillsdale, NJ: Erlbaum; 1984. pp. 229–293. [Google Scholar]
- Siegler R, Svetina M. What leads children to adopt new strategies? A microgenetic/cross-sectional study of class inclusion. Child Development. 2006;77:997–1015. doi: 10.1111/j.1467-8624.2006.00915.x. [DOI] [PubMed] [Google Scholar]
- Slotnick SD, Schacter DL. A sensory signature that distinguishes true from false memories. Nature Neuroscience. 2004;7:664–672. doi: 10.1038/nn1252. [DOI] [PubMed] [Google Scholar]
- Sohn M, Goode A, Koedinger K, Stenger V, Fissell K, Carter C, Anderson J. Behavioral equivalence, but not neural equivalence: neural evidence of alternative strategies in mathematical thinking. Nature Neuroscience. 2004;7:1193–1194. doi: 10.1038/nn1337. [DOI] [PubMed] [Google Scholar]
- Squire LR, Stark CE, Clark RE. The medial temporal lobe. Annual Review of Neuroscience. 2004;27:279–306. doi: 10.1146/annurev.neuro.27.070203.144130. [DOI] [PubMed] [Google Scholar]
- Suzuki WA. Making new memories: the role of the hippocampus in new associative learning. Annals of the New York Academy of Sciences. 2007;1097:1–11. doi: 10.1196/annals.1379.007. [DOI] [PubMed] [Google Scholar]
- Tse D, Langston RF, Bethus I, Wood ER, Witter MP, Morris RG. Does assimilation into schemas involve systems or cellular consolidation? It’s not just time. Neurobiology of Learning and Memory. 2008;89:361–365. doi: 10.1016/j.nlm.2007.09.007. [DOI] [PubMed] [Google Scholar]
- Wagner AD, Maril A, Bjork RA, Schacter DL. Prefrontal contributions to executive control: fMRI evidence for functional distinctions within lateral prefrontal cortex. NeuroImage. 2001;14:1337–1347. doi: 10.1006/nimg.2001.0936. [DOI] [PubMed] [Google Scholar]
- Wang S, Morris R. Hippocampal-neocortical interactions in memory formation, consolidation, and reconsolidation. Annual Review of Psychology. 2010;61:49–79. C41–C44. doi: 10.1146/annurev.psych.093008.100523. [DOI] [PubMed] [Google Scholar]
- Ward BD. AFNI 3dDeconvolve Documentation. Medical College of Wisconsin; 2000. Simultaneous inference for FMRI data. [Google Scholar]
- Weschler D. Wechsler Abbreviated Scale of Intelligence: Manual. San Antonio, TX: The Psychological Corporation; 1999. [Google Scholar]
- Wechsler D. The Wechsler Individual Achievement Test-Second Edition (WIAT-II) San Antonio, TX: The Psychological Corporation; 2001. [Google Scholar]
- Wu S, Chang T, Majid A, Caspers S, Eickhoff S, Menon V. Functional heterogeneity of inferior parietal cortex during mathematical cognition assessed with cytoarchitectonic probability maps. Cerebral Cortex. 2009;19:2930–2945. doi: 10.1093/cercor/bhp063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu S, Meyer M, Maeda U, Salimpoor V, Tomiyama S, Geary D, Menon V. Standardized assessment of strategy use and working memory in early mental arithmetic performance. Developmental Neuropsychology. 2008;33:365–393. doi: 10.1080/87565640801982445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zago L, Pesenti M, Mellet E, Crivello F, Mazoyer B, Tzourio-Mazoyer N. Neural correlates of simple and complex mental calculation. NeuroImage. 2001;13:314–327. doi: 10.1006/nimg.2000.0697. [DOI] [PubMed] [Google Scholar]
- Zago L, Petit L, Turbelin M, Andersson F, Vigneau M, Tzourio-Mazoyer N. How verbal and spatial manipulation networks contribute to calculation: an fMRI study. Neuropsychologia. 2008;46:2403–2414. doi: 10.1016/j.neuropsychologia.2008.03.001. [DOI] [PubMed] [Google Scholar]
- Zbrodoff N, Logan G. On the autonomy of mental processes: a case study of arithmetic. Journal of Experimental Psychology: General. 1986;115:118–130. doi: 10.1037//0096-3445.115.2.118. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


