Solvation Properties of N-acetyl-β-glucosamine: A Molecular Dynamics Study Incorporating Electrostatic Polarization

Abstract

N-acetyl-β-glucosamine (NAG) is an important moiety of glycoproteins and is involved in many biological functions. However, conformational and dynamical properties of NAG molecules in aqueous solution, the most common biological environment, remain ambiguous due to limitations of experimental methods. Increasing efforts are made to probe structural properties of NAG and NAG-containing macromolecules, like peptidoglycans and polymeric chitin, at the atomic level using molecular dynamics simulations. In this work, we develop a polarizable carbohydrate force field for NAG and contrast simulation results of various properties using this novel force field and an analogous non-polarizable (fixed charge) model. Aqueous solutions of NAG and its oligomers are investigated; we explore conformational properties (rotatable bond geometry), electrostatic properties (dipole moment distribution), dynamical properties (self-diffusion coefficient), hydrogen bonding (water bridge structure and dynamics), and free energy of hydration. The fixed-charge carbohydrate force field exhibits deviations from the gas-phase relative rotation energy of exocyclic hydroxymethyl side-chain and of chair/boat ring distortion. The polarizable force field predicts conformational properties in agreement with corresponding first-principles results. NAG-water hydrogen bonding pattern is studied through radial distribution functions and correlation functions. Intermolecular hydrogen bonding between solute and solvent is found to stabilize NAG solution structures while intramolecular hydrogen bonds define glycosidic linkage geometry of NAG oligomers. The electrostatic component of hydration free energy is highly dependent on force field atomic partial charges, influencing a more favorable free energy of hydration in the fixed-charge model compared to the polarizable model.

I. INTRODUCTION

N-Acetyl-β -hexosaminides are common in nature. They constitute a broad spectrum of materials such as chitin¹, extracellular matrix glycosaminoglycans^2,3, and are an essential structural component of glycoproteins and glycolipids^4,5. They are also implicated in molecular recognition processes, acting as ligands for a variety of ribonucleases^6–8. On the macromolecular scale, nanofibers of NAG, poly-N-acetyl-glucosamine, applied to cutaneous wounds in diabetic mice, have recently been shown to correlate with increased cellular proliferation and angiogenesis; specifically, poly-N-acetyl-glucosamine fibers induce greater endothelial cell motility via integrin activation⁹. However, functions of poly-N-acetyl-glucosamine and glycosaminoglycans in cell signaling, development and growth are not well understood, due to the lack of detailed information for the polymer solution^3,10. Vibrational spectroscopy^11–13, nuclear magnetic resonance (NMR)^14–18 spectroscopy, and X-ray crystallography^19–21 techniques are applied to investigate the solution structure of related polysaccharides. However, experimental approaches are often limited to certain molecular weight ranges and suffer from difficulties such as crystallization of glycoforms in polysaccharide solution systems.

Complementing experiment, computational methods are a powerful tool to study conformational properties of carbohydrates in solution²². Mobli and Almond²³ performed density functional theory(DFT) calculations to derive Karplus equations (an empirical relationship between the ³J-coupling constant and a bond dihedral angle) suitable for the amino sugar and explored the effects of including solvent implicitly and explicitly. Pogany and Kavacs²⁴ studied the conformational properties of hyaluronan disaccharide units using DFT calculations and found that the favored conformer structures are determined by protonation and salt formation. Besides quantum mechanical methods, which are generally used to examine structures in gas-phase for relatively small systems, Monte Carlo (MC) and Molecular Dynamics (MD) simulations have been successfully applied to studies of more biologically relevant carbohydrate systems, including solutions²³ and protein complexes^25–27. Carbohydrate force fields developed for the CHARMM, AMBER, and GROMOS force fields^28,29 enable MD simulations for polysaccharide solutions. Partly due to the sparsity of experimental data available for parameterization, development of classical force fields for these types of molecules has been relatively slow. Current state-of-the-art force fields for carbohydrate molecular simulations are primarily the work of Woods and co-workers throughout the past several decades²⁸. Ha et al parameterized classical, non-polarizable force fields for the GRO-MOS platform³⁰. Palma and coworkers³¹ later corrected the O-C-C-O term to revise the barrier of hydroxyl rotations (PHLB model). Kuttel, Brady, and Naidoo modified the PHLB parameter set for lower primary alcohol rotational barriers and referred to the force field as the Carbohydrate Solution Force field (CSFF)^32,33. Recently, MacKerell and coworkers have developed atomistic force fields for carbohydrates building upon the CHARMM force field platform²⁹.

In this article, we discuss the development of a polarizable force field for the NAG monomer based on the charge equilibration formalism. We then apply the force field to NAG and NAG oligomers in aqueous solution and analyze conformational properties, dipole moment distributions, self-diffusion coefficients, hydrogen bonding and hydration free energies. Comparisons are made between the PHLB model and polarizable force field developed as well as experimental and first-principles results where available to evaluate force field performance. Another goal of this work is to probe NAG and NAG oligomer solution configurations at the atomic level and to explore specific interactions between NAG and water as described by the different force fields considered. The current aminoglycan force field will be applied in future studies of protein-ligand binding free energetics using statistical mechanical free energy methods in conjunction with polarizable protein and ligand force fields. Polarizable, or non-additive, force fields for modeling of carbohydrate interactions with polar biological components (in particular proteins) may prove influential within the context of quantifying binding free energetics and structures of complexes of carbohydrates and proteins. By analogy to protein-drug binding and structure research, the use of non-additive interactions may allow a broader range of interaction energies so as to provide a larger separation between biologically relevant complexes (based on free energetics and structure) and weakly interacting, less-relevant complexes. Development of polarizable force fields for carbohydrates in general will complement the current efforts in a number of groups working on non-additive models for proteins, nucleic acids, small molecules, and lipid membranes, as well as ions and small-molecule condensed phase systems. Work to date on protein-ligand binding studies suggests that polarization (in the most general sense taken to be the variation of molecular mechanics partial charges or electrostatic multipole moments with relative orientations of ligand and substrate) is important in both polar systems as well as situations where ionic species are involved^34,35. In our continuing future work, we plan to apply polarizable models for the NAG system and compare to nonpolarizable (additive) force fields in the context of free energetics of binding in the hen egg-white lysozyme system.

II. SIMULATION METHODOLOGY AND FORCE FIELDS

A. Charge Equilibration Method and Solvent Force Field

To incorporate polarization effects within a classical molecular force field, we adopt the charge equilibration (CHEQ), or electronegativity equalization, method described in the literature ^36–47. Here we briefly describe the main points. Unlike point dipole polarizable^48,49, Drude oscillator⁵⁰, and higher order multipole based methods for polarization^51–54, the CHEQ method treats polarization as a result of charge transfer. For the present, we consider charge transfer within a single molecular entity or sub-segments of a larger molecular construct. We acknowledge that we do not address quantum mechanical “intermolecular” charge transfer effects. The magnitude of such effects are difficult to quantify unambiguously and in the final analysis may be of little importance in the condensed phase for such non-ionic systems unlike the situation for ions transferring charge between solvent^55–61. Marenich and coworkers demonstrated that charge transfer between neutral solutes can be an order of magnitude smaller than that between ionic solutes and solvent using a supersolute coupled with continuum solvent approach for modeling condensed phase effects⁶². The CHEQ method relies on the equalization of atomic electronegativities^41,42 among the constituent atoms within a molecule,^36,45 redistributing charge as necessary to minimize chemical potential. The charge redistribution in the presence of an external electric field defines the polarization response of the model which implicitly includes many-body effects arising from induced multipole moments beyond simply an induced dipole; in this sense, the model may be accurately described as a polarizable model.

A common approach to the prediction of molecular charge distributions from atomic properties such as ionization potentials, electron affinities and atomic radii derives from the work of Mortier et al.⁶³ and Rappé and Goddard.⁴⁰ Referred to as charge equilibration (CHEQ) or electronegativity equalization (EE) methods, these methods are based on a second order Taylor expansion of the electrostatic energy in terms of the atomic partial charges Q_i as

$$E(\mathbf{Q})={\displaystyle \sum _{i=1}^N{\chi }_i^{○}{Q}_i+\frac{1}{2}{\displaystyle \sum _{i=1}^N{\eta }_i^{○}{Q}_i^2+{\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j>i}^N{J}_{ij}(r_{ij})Q_i{Q}_j.}}}}$$ (1)

The electronegativity and hardness parameters ${\chi }_i^{○}$ and ${\eta }_i^{○}$, respectively, represent derivatives of the electrostatic energy with respect to charge while the off-diagonal interaction elements J_ij(r_ij) describe screened Coulomb interactions between atoms i and j. In the original formulations of the method pertaining to molecular systems^36,40, these were taken to be the molecular Coulomb integral over atomic Slater or Gaussian orbitals located on the respective nuclei^36,40. In the current work, we apply an empirical combining rule to approximate the Coulomb overlap integral. This function depends on the individual atomic hardness parameters and interparticle distance as

$$J_{ij}(r_{ij},{\eta }_i^{○},{\eta }_j^{○})=\frac{\frac{1}{2}\left({\eta }_i^{○}+{\eta }_j^{○}\right)}{\sqrt{1.0+\frac{1}{4}{\left({\eta }_i^{○}+{\eta }_j^{○}\right)}^2{r}_{ij}^2}}$$ (2)

The pair-wise energy term given by equation 1 is accumulated between atom pairs involved in bonds, angles, and dihedral (torsional) interactions within a molecule. For electrostatic interactions between intramolecular sites separated by more than four bonds, a standard Coulomb interaction applies; this is the standard protocol in most non-polarizable force fields. Intermolecular electrostatic interactions are also treated using a Coulomb form.

In the CHEQ formulation, the diagonal atomic hardness terms ${\eta }_i^{○}$ represent the self-Coulomb repulsion or idem-potential J_ii evaluated at zero internuclear separation; however, these terms along with the corresponding atomic electronegativities may also be treated as adjustable model parameters. Together, the various interaction elements J_ij define a square, symmetric matrix J of order N (whose diagonal elements, J_ii are the ${\eta }_i^{○}$), that we will refer to as the atomic hardness matrix. The equilibrium molecular charge distribution is obtained by minimizing the electrostatic energy with respect to the N atomic partial charges; this is readily accomplished with standard linear algebra techniques which make the method fast, easy to implement, and attractive for use in polarizable molecular force fields.

In order to obtain physically reasonable charge distributions, the CHEQ system of equations must be augmented by one or more additional constraints designed to conserve overall charge. For a single molecular charge constraint in which the sum of the atomic partial charges is constrained to be equal to some total charge Q_net, we require the constraint equation^40,63

$${\displaystyle \sum _{i=1}^N{Q}_i=Q_{\text{net}}}$$ (3)

which may be added to the CHEQ energy expression in equation 1 to yield the constrained energy expression

$$E(\mathbf{Q},\lambda ,Q_{\text{net}})=E(\mathbf{Q})+\lambda \left[\left({\displaystyle \sum _{i=1}^N{Q}_i}\right)-Q_{\text{net}}\right].$$ (4)

The charge conservation constraint is enforced via the Lagrange multiplier λ that, when satisfied, does not contribute to the final minimized energy. The resulting energy expression is then valid for both neutral and charged systems depending on the value of Q_net. For larger molecular systems, multiple charge conservation units can be applied with separate Lagrange multipliers accounting for the individual charge constraints; for k charge normalization units, each with a net charge of Q_net,k we write:

$$E(\mathbf{Q},\lambda ,Q_{\text{net}})=E(\mathbf{Q})+{\displaystyle \sum _k{\lambda }_k\left[\left({\displaystyle \sum _{i=1}^{N_k}{Q}_{i,k}}\right)-Q_{\text{net},k}\right].}$$ (5)

During molecular dynamics simulations we propagate all charge degrees of freedom using an extended Lagrangian constrained to preserve molecular charge neutrality. The charge degrees of freedom are propagated via an extended Lagrangian formulation that imposes a molecular charge neutrality constraint, thus strictly enforcing electronegativity equalization at each dynamics step. The system Lagrangian is

$$L={\displaystyle \sum _{1=1}^N\frac{1}{2}{m}_i{\dot{r}}_i^2+{\displaystyle \sum _{i=1}^N\frac{1}{2}{m}_{Q,i}{\dot{Q}}_i^2-E(\mathbf{Q},\lambda ,Q_{\text{net}})}}$$ (6)

where the first two terms represent the nuclear and charge kinetic energies, respectively, while the third term is the total potential energy including charge conservation constraints. The fictitious charge dynamics, analogous to the fictitious wavefunction dynamics in Car-Parrinello (CP) type methods,⁶⁴ are determined with a fictitious charge “mass” (adiabaticity parameter in CP dynamics)^36,39. The units for this mass are $\frac{\mathit{\text{energy}}\cdot {\mathit{\text{time}}}^2}{{\mathit{\text{charge}}}^2}$. The charges are propagated based on forces arising from the difference between the average electronegativity of the molecule and the instantaneous electronegativity at an atomic site. Accounting for charge dynamics using sufficiently small masses for the charge degrees of freedom incurs a cost of 2–4 relative to fixed-charge force fields; this arises solely from the need to use smaller timesteps.

B. Polarizability in Charge Equilibration Models

When the electrostatic energy expression for a single molecule comprised of N atoms is differentiated with respect to charge and set equal to zero,

$$\frac{\partial E}{\partial Q_i}={\chi }_i^{○}+{\eta }_i^{○}{Q}_i+{\displaystyle \sum _{j\ne i}^N{J}_{ij}{Q}_j=0,}$$ (7)

a set of N equations can be solved to determine the set of charges minimizing the energy. In matrix form, this set of equations can be recast as

$$\mathbf{\text{JQ}}=-\mathbf{\chi }$$ (8)

where J is the atomic hardness matrix, Q is the atomic charge vector, and χ is the atomic electronegativity vector. Written explicitly, the matrix representation is:

$$\left[\begin{array}{ccccc}\hfill J_{11}\hfill & \hfill J_{12}\hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill J_{1N}\hfill \\ \hfill J_{21}\hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill \hfill & \hfill ⋮\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill ⋮\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill J_{N1}\hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill J_{NN}\hfill \end{array}\right]\left[\begin{array}{c}\hfill Q_1\hfill \\ \hfill Q_2\hfill \\ \hfill ⋮\hfill \\ \hfill ⋮\hfill \\ \hfill Q_N\hfill \end{array}\right]=-\left[\begin{array}{c}\hfill {\chi }_1\hfill \\ \hfill {\chi }_2\hfill \\ \hfill ⋮\hfill \\ \hfill ⋮\hfill \\ \hfill {\chi }_N\hfill \end{array}\right].$$ (9)

These equations can be augmented to include the charge conservation constraint,

$${\displaystyle \sum _{i=1}^M{Q}_i=Q_{\text{net}},}$$ (10)

to produce a modified set of equations:

$$\mathbf{J}\prime \mathbf{Q}\prime =-\mathbf{\chi }\prime ;$$ (11)

this is written explicitly as:

$$\left[\begin{array}{cccccc}\hfill J_{11}\hfill & \hfill J_{12}\hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill J_{1N}\hfill & \hfill 1\hfill \\ \hfill J_{21}\hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill \hfill & \hfill ⋮\hfill & \hfill 1\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill J_{N1}\hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill J_{NN}\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill 1\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill Q_1\hfill \\ \hfill Q_2\hfill \\ \hfill ⋮\hfill \\ \hfill ⋮\hfill \\ \hfill Q_N\hfill \\ \hfill \lambda \hfill \end{array}\right]=-\left[\begin{array}{c}\hfill {\chi }_1\hfill \\ \hfill {\chi }_2\hfill \\ \hfill ⋮\hfill \\ \hfill ⋮\hfill \\ \hfill {\chi }_N\hfill \\ \hfill Q_{\text{net}}\hfill \end{array}\right]$$ (12)

In Eq. 12 we have enforced the constraint that charge is conserved within the molecule, or equivalently, that the sum of atomic partial charges equals the desired net charge. As alluded to in the previous section, it is appropriate to limit the extent of intramolecular charge transfer by introducing additional charge constraints. For instance, the total charge of the molecule is constrained to Q_net while additionally requiring the sum of charges for a subset of atoms within the molecule to equal a specified quantity, Q_net,k. We refer to this subset of atoms as a charge conservation unit. Since the net charge over the entire molecule must be maintained, the following condition must hold:

$$Q_{\text{net}}={\displaystyle \sum _{k=1}^M{Q}_{\text{net},k},}$$ (13)

in which M denotes the number of charge conservation units. We can expand our previous illustration of the system of equations generated with a single charge constraint (Eq.12) to show the set of equations when a molecule is broken into two charge conservation units (as is done in the current study):

$$\left[\begin{array}{cccccccc}\hfill J_{11}\hfill & \hfill \dots \hfill & \hfill J_{1h}\hfill & \hfill J_{1(h+1)}\hfill & \hfill \dots \hfill & \hfill J_{1N}\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill J_{h1}\hfill & \hfill \hfill & \hfill J_{hh}\hfill & \hfill \hfill & \hfill \hfill & \hfill ⋮\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill J_{(h+1)1}\hfill & \hfill \hfill & \hfill \hfill & \hfill J_{(h+1)(h+1)}\hfill & \hfill \hfill & \hfill ⋮\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill J_{N1}\hfill & \hfill \dots \hfill & \hfill J_{Nh}\hfill & \hfill J_{N(h+1)}\hfill & \hfill \dots \hfill & \hfill J_{NN}\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill \dots \hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill \dots \hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill Q_1\hfill \\ \hfill ⋮\hfill \\ \hfill Q_h\hfill \\ \hfill Q_{h+1}\hfill \\ \hfill ⋮\hfill \\ \hfill Q_N\hfill \\ \hfill {\lambda }_1\hfill \\ \hfill {\lambda }_2\hfill \end{array}\right]=-\left[\begin{array}{c}\hfill {\chi }_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\chi }_h\hfill \\ \hfill {\chi }_{h+1}\hfill \\ \hfill ⋮\hfill \\ \hfill {\chi }_N\hfill \\ \hfill Q_{\text{net},1}\hfill \\ \hfill Q_{\text{net},2}\hfill \end{array}\right].$$ (14)

For this example, atomic sites 1 through h are grouped into one charge conservation unit, while atomic sites h+1 through N are grouped into a second charge normalization unit. In the augmented atomic hardness matrix, values of 1 in element i,N+1 or N + 1,i denote that atom i is assigned to the first charge conservation unit (which has a net charge of Q_net,1). Similarly, values of 1 in elements i, N + 2 or N + 2, i denote that atom i is assigned to the second charge conservation unit (with net charge Q_net,2).

The molecular polarizability can then be calculated as

$${\alpha }_{\gamma \beta }={\mathbf{R}}_{\beta }^T{(\mathbf{J}\prime )}^{-1}{\mathbf{R}}_{\gamma }$$ (15)

where J′ is the atomic hardness matrix augmented with the appropriate rows and columns to treat the charge conservation constraints. R_γ and R_β are the γ and β Cartesian coordinates of the atomic position vectors (which are also augmented to appropriately match the dimensions of the atomic hardness matrix).

C. Water Force Field

To model the solvent, in this case water, we adopt the CHARMM TIP3P water model⁶⁵ for the fixed-charge solution simulations and TIP4P-FQ-like (Transferable Intermolecular Potential Four Point Fluctuating Charge) water for the CHEQ model. The TIP4P-FQ-like model used here, slightly different from the original TIP4P-FQ model³⁶, has Lennard-Jones(LJ) sites on water hydrogens which are only in effect for water-NAG interactions; this is for consistency with the CHARMM protein and small molecule CHEQ force field³⁹. The water-water interactions are identical to the original model of Rick et al³⁶. The polarizable TIP4P-FQ water model employs a rigid geometry having an O-H bond distance of 0.9572 Å, an H-O-H bond angle of 104.52° and a massless, off-atom M site located 0.15 Å along the H-O-H bisector which carries the oxygen partial charge. Water-water repulsion and dispersion interactions are modeled using a single Lennard-Jones (LJ) site located on the oxygen center having parameters σ_O = 3.159 Å and є_O = 0.2862 kcal mol⁻¹. In the next section we discuss the nature of the NAG force field.

D. NAG Force Fields

1. Non-polarizable Model

Since no sugar force field contains complete parameters for the NAG molecule, we employed the PHLB parameter set for the pyranose ring and the CHARMM22 protein force field⁶⁵ for acetamido side group parameters (see Tables I, II, and III for more details). We refer to this non-polarizable force field of NAG as the PHLB model here for simplicity.

TABLE I.

Electrostatic Parameters in the nonpolarizable PHLB and polarizable CHEQ Force Fields (Part I)

Atom	Atom	PHLB	CHEQ
Name	Type	Charge	Chargea	χb	$({\eta }_i^{○})$b/2
C1	CTS	0.125	0.329	310	98
H1	HAS	0.090	0.030	295	251
O1	OHS	−0.660	−0.576	515	154
HO1	HOS	0.430	0.426	88	259
C2	CTS	0.140	0.187	310	98
H2	HAS	0.090	0.082	268	251
C5	CTS	0.250	0.349	290	98
H5	HAS	0.090	0.054	268	251
O5	OES	−0.400	−0.455	500	154
NT	NG1	−0.470	−0.745	557	149
HNT	HG	0.310	0.349	99	297
C7	CG	0.510	0.852	216	123
O7	OG	−0.510	−0.580	626	190
C8	CT3G	−0.200	−0.654	470	120
H81	HA3G	0.090	0.170	271	251
H82	HA3G	0.090	0.170	271	251
H83	HA3G	0.090	0.170	271	251

^aAtomic partial charges in CHEQ model redistribute according to conformational change. Here displayed the average partial charge on each NAG atom based on the solution simulation trajectory.

^bElectronegativity χ and atomic hardness η are in units of $\frac{kcal/mol}{e}$ and $\frac{kcal/mol}{e^2}$, respectively. The values for η correspond identically to J_ii in the text discussion.

TABLE II.

Electrostatic Parameters in the nonpolarizable PHLB and polarizable CHEQ Force Fields (Part II)

Atom	Atom	PHLB	CHEQ
Name	Type	Charge	Chargea	χb	ηb/2
C3	CTS	0.075	0.266	310	98
H3	HAS	0.090	0.070	268	251
O3	OHS	−0.660	−0.680	550	154
HO3	HOS	0.430	0.443	86	259
C4	CTS	0.140	−0.210	380	98
H4	HAS	0.090	0.131	268	251
O4	OHS	−0.660	−0.632	550	154
HO4	HOS	0.430	0.446	86	259
C6	CTS	0.050	0.143	320	104
H61	HAS	0.090	0.036	305	251
H62	HAS	0.090	0.038	305	251
O6	OHS	−0.660	−0.632	540	154
HO6	HOS	0.430	0.423	98	259

^aAtomic partial charges in CHEQ model redistribute according to conformational change. Here displayed the average partial charge on each NAG atom based on the solution simulation trajectory.

^bElectronegativity χ and atomic hardness η are in units of $\frac{kcal/mol}{e}$ and $\frac{kcal/mol}{e^2}$, respectively. The values for η correspond identically to J_ii in the text discussion.

TABLE III.

Nonbond Parameters for CHEQ and PHLB Force Fields

Atom Type Unit	ε (CHEQ) (kcal/mol)	Rmin/2 (CHEQ) (Å)	ε (PHLB) (kcal/mol)	Rmin/2 (PHLB) (Å)
CTS	0.020	2.275	0.020	2.275
HAS	0.082	1.320	0.020	1.320
OHS	0.170	1.630	0.152	1.770
HOS	0.016	0.125	0.046	0.225
OES	0.070	1.803	0.152	1.770
NG1	0.120	1.880	0.200	1.850
HG	0.016	0.125	0.046	0.225
CG	0.160	2.225	0.110	2.000
OG	0.115	1.925	0.120	1.700
CT3G	0.073	2.020	0.080	2.060
HA3G	0.023	1.320	0.022	1.320
ON2	0.070	1.803	0.152	1.770

2. Charge Equilibration Model

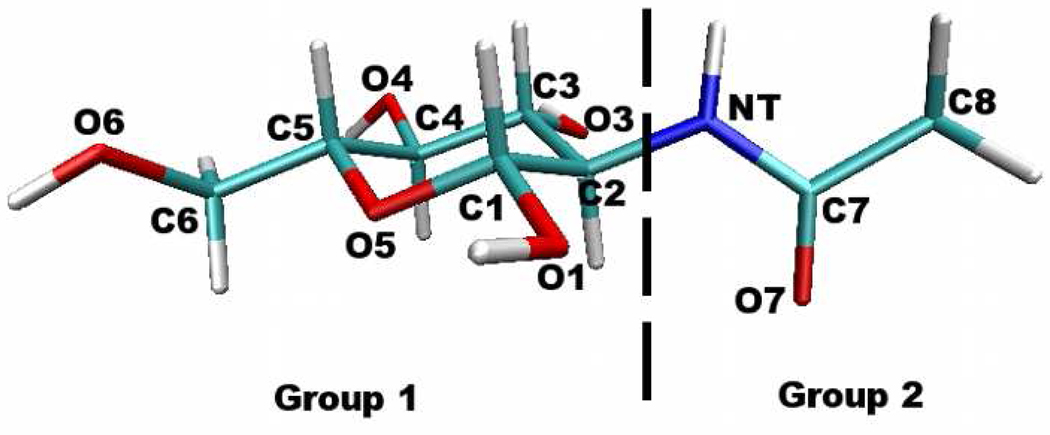
The philosophy we employ for deriving the charge equilibration force field for the monomer NAG is to fit to gas-phase first-principles (ab initio and density functional theory (DFT)) calculation-based properties such as molecular polarizability, dipole moment, and interactions with water in various geometries. As a reference, gas-phase polarizability and dipole moment for NAG are calculated for the geometry optimized using density functional theory (DFT) with the B3LYP/6-311g(d,p) basis. Hardness parameters, ${\eta }_i^{○}$ are determined by fitting to the molecular dipole polarizability (defined above). The augmented hardness matrix, J′, is constructed using two charge normalization groups as shown in Figure 1. Atomic electronegativities are then determined by fitting to DFT gas-phase charges and dipole moment according to the Merz-Singh-Kollman scheme. The force field gas-phase electrostatic properties are shown in Table IV using the optimized electrostatic parameters (atom electronegativities and hardness parameters). Consistent with previous study⁶⁶, DFT method predicts higher polarizabilities than MP2 when using the same basis set. Higher level of theory predicts larger polarizability and DFT method shows similar polarizabilities when using aug-cc-pvDZ and aug-cc-pvTZ basis set. We note that the fitted gas-phase polarizability using the CHEQ model reproduces DFT and MP2 polarizability with the lower level of theory (6-311g(d,p)) and falls below the gas-phase reference values using larger basis set of aug-cc-pvDZ (14% for B3LYP and 15% for MP2). The absolute extent of reduction of molecular polarizabilities in the condensed phase still remains an ongoing avenue of research, with majority of scaling factors determined from empirical tuning of force field quality and associated stability of simulations using the force fields.^39,67

FIG. 1.

Designation of charge conservation groups.

TABLE IV.

Electrostatic Properties for NAG Geometry Optimized with B3LYP/6-311g(d,p) Basis

	Polarizability/Å3	Dipole Moment/ Debye
B3LYP/6-311g(d,p)	17.29	5.1572
B3LYP/aug-cc-pvDZ	19.80	5.1604
B3LYP/aug-cc-pvTZ	19.82	5.1515
MP2/6-311g(d,p)	16.75	5.4377
MP2/aug-cc-pvDZ	19.46	5.4115
CHEQ	16.81	5.1160

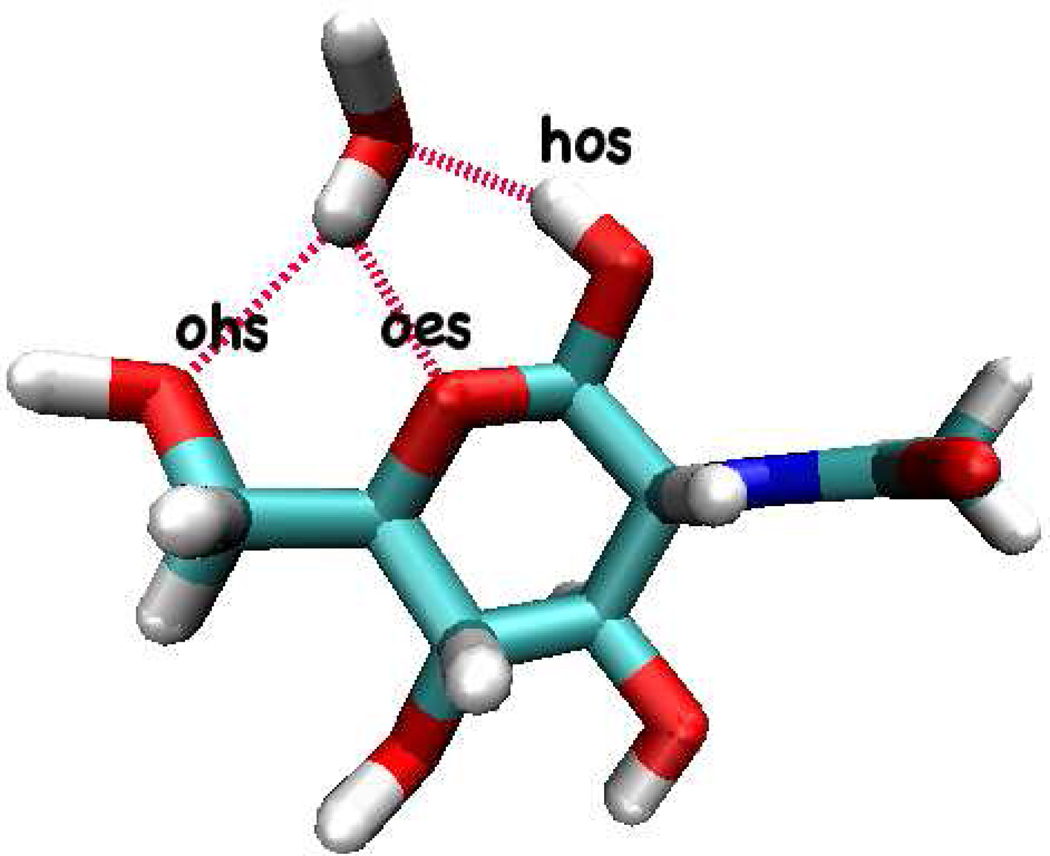
After determining electrostatic parameters, solute-solvent interaction derived non-bond repulsion-dispersion interaction parameters are determined. Solute-solvent nonbond interactions are determined by reproducing vacuum dimer energies and hydrogen binding distances. For reference, the optimized geometry of NAG-water heterodimer(Figure 2) is obtained by DFT calculation using B3LYP/6-311g(d,p) level of theory. Basis-set superposition-error is not applied to the DFT dimer interaction energy in order to be consistent with the existing CHARMM CHEQ force field³⁹ as well as CHARMM additive force field development for carbohydrate²⁹. Table V shows optimized NAG-water interaction energy and geometry for the CHEQ force field, which is found to well-reproduce the reference first-principles results to at least comparable accuracy as the fixed-charge model. With this basic NAG-water interaction model, we address in the next sections methods and results of condensed phase molecular dynamics simulations of the NAG molecule (and its oligomers) in aqueous solution.

FIG. 2.

Interactions between NAG and water in gas-phase.

TABLE V.

NAG-Water Gas phase Interactions and Bond Lengths. Hydrogen bond types are described in Figure 2

	Edimer (kcal/mol)	Rohs (Å)	Roes (Å)	Rhos (Å)
B3LYP/6-311g(d,p)	−14.73	2.44	2.20	1.90
CHEQ	−14.10	2.85	2.18	1.99
PHLB	−9.55	2.82	1.98	2.06
PHLB-PSP	−13.51	2.87	1.60	1.81

E. Solution Dynamics Simulation Details

The CHARMM⁶⁸ program package was used to perform simulations of equilibrated cubic box containing one NAG or one NAG oligomer molecule and water molecules at constant pressure-temperature (NPT). The NAG oligomers studied in this work include up to the tetramer species; this latter is an important model system for studying protein-ligand binding in the well-studied hen egg-white lysozyme system²⁰. Pressure and temperature (298K) are maintained constant by Langevin piston method and Hoover thermostat, respectively. Newton’s equations of motion are integrated for each atom using the Verlet integrator for 20 ns with timestep of 1 fs for fixed-charge simulations and 0.5 fs for CHEQ force field; the first 100 ps of sampling is considered as equilibration and is not used to compute solution properties. Nonbond interactions were switched off via a switching function between 7 and 8 Å. Electrostatic interactions were treated using the Particle Mesh Ewald⁶⁹ method with 50 grid points in each dimension for all systems except the smaller monomer solution (in which 30 grid point were used); a screening parameter of 0.32 was employed. Simulations employing the CHEQ model maintained charge degrees of freedom at 1K using a Nosé-Hoover bath and the mass of charge degrees of freedom was 0.00009 kcal mol⁻¹ .ps².e⁻² for NAG monomer, 0.0001 for NAG oligomers and 0.000069 for water. To obtain the starting configurations of bulk systems, a single solute molecule (NAG monomer, dimer, trimer or tetrameter) was solvated in pre-equilibrated box of water molecules (the number of water molecules varies with the solute ).

F. Free Energy of Hydration Simulation Details

As an evaluation of the nature of solute-solvent interactions, free energies of hydration are computed for NAG and NAG oligomer molecules using the PHLB and CHEQ force fields. Previous studies have revealed the connection between the gas-phase solute-water dimer energy and hydration free energy^50,70,71. To compare the hydration free energies for existing fixed-charge and newly-developed polarizable models, we added explicit, pair-specific Lennard-Jones interaction terms between NAG and water oxygen atom types (SI, Table I) for the PHLB force field (referred to as PHLB-PSP in the remainder of this work) to reproduce the reference gas-phase dimer interaction energies at an accuracy comparable to that of the CHEQ NAG-water gas-phase dimer energy (Table V). This approach has been applied for recent force field development considering hydration free energies for small molecules^50,70,71. We note that NAG-water vacuum interaction energy can also be improved by optimizing LJ parameters and we choose to use pair-specific LJ parameters to keep the PHLB force field consistency. Only NAG-water interactions are modified; other interactions, including intramolecular and NAG-NAG interactions, are the same as in the conventional PHLB model. We emphasize that the modified PHLB force field is only applied in the free energy calculations to compare with the hydration free energy based on CHEQ model and the solution dynamics simulations still use the original PHLB model (no pair-specific LJ parameters). In general, Water-water, water-NAG LJ parameters are constructed from the individual atomic parameters using the Lorentz-Berthelot⁷² mixing rules ${\epsilon }_{ij}=\sqrt{{\epsilon }_i{\epsilon }_j}$ and σ_ij = (σ_i + σ_j)/2, specified in the pair specific parameters (SI, Table I). We finally acknowledge that one can also modify the charge distributions either independently or in combination with the Lennard-Jones interactions between the fixed-charge water and NAG models in order to modulate the dimer interaction energy; indeed they are coupled. However, based on previous work⁷¹ we opt to use the dispersion-repulsion interaction to modulate this component of the energy.

Hydration free energy calculations start from the last snapshot of solution dynamics. We first electrostatically decouple the solute (NAG to (NAG)₄) molecule from the solvent before decoupling the Lennard-Jones (LJ) interactions. The decoupling simulations are performed at constant pressure and temperature (NPT) at 298 K and 1 atm pressure at each coupling parameter (the pressure and temperature control methods are given above). More details about free energy of hydration calculations, including sampling time, lambda value for each window, are shown in SI Table II. The hydration free energy is determined by thermodynamic integration(TI)^73–75 and the Bennett acceptance ratio method(BAR)^76,77. The uncertainties for TI results are estimated by computing the stand deviation of running averages based on every 100 ps block.

III. RESULTS AND DISCUSSION

A. Conformational Properties

Carbohydrates and polysaccharides are known to have high flexibility^78–80, and thus one major challenge of sugar force field parameterization is to produce reasonable conformations and dynamics, preferably consistent with experimental results. In this work, we analyze conformational properties predicted from molecular dynamics simulations using the CHEQ model. Properties include NAG exocyclic dihedral angles and oligomer glycosidic linkages. We compare to the fixed-charge empirical force field PHLB results, as well as first-principles and experimental values where available. We note that CHEQ force field adopts PHLB torsion parameters without further modification.

1. Exocyclic Dihedrals

The populations of six rotatable bond conformations are computed from the fixed-charge and polarizable simulations and compared to a previous explicit solvent MD study²³ (Table VI). The most probable rotamer state (with highest population) for each torsion is consistent for the three force fields. Most exocyclic torsions analyzed, except C2-C3-O3-H and C3-C4-O4-H, have similar populations between PHLB and CHEQ force fields and deviate more from Mobli’s results²³, because PHLB and CHEQ models share the same dihedral parameters. In particular, the 6-hydroxymethyl dihedral O6-C6-C5-O4, which was commonly considered in saccharide computer model development^{28,29,33,81,82}, shows only g+ conformation in PHLB and CHEQ simulations and unlike the other MD study²³, no trans geometry is found.

TABLE VI.

Conformer Population of Rotatable Bonds in NAG

	PHLB			CHEQ			Moblib
Rotamera	g+	g−	t	g+	g−	t	g+	g−	t
O5-C1-O1-H
Population(%)	15	78	7	15	71	14	29	64	7
Average(°)	68	−74	−156	61	−74	−151	36	−45	−159
C2-C3-O3-H
Population(%)	4	64	32	10	45	45	9	52	39
Average(°)	58	−75	−165	61	−78	−169	63	−77	−165
C3-C4-O4-H
Population(%)	85	1	14	64	12	24	76	12	12
Average(°)	67	−45	−212	73	−60	−207	66	−53	−214
O6-C6-C5-C4
Population(%)	100	−	−	100	−	−	53	2	45
Average(°)	56	−	−	58	−	−	60	−76	−174
C5-C6-O6-H
Population(%)	21	8	71	24	11	65	32	23	45
Average(°)	75	−92	−179	74	−88	−178	67	−72	−180
H-NT-C2-H
Population(%)	−	−	100	−	−	100	−	13	87
Average(°)	−	−	−175	−	−	−180	−	3	−180

^aThe g+, g− and trans states are defined as torsion angles of 0° to 120°, −120° to 0° and −240° to −120°,respectively.

^bReference²³.

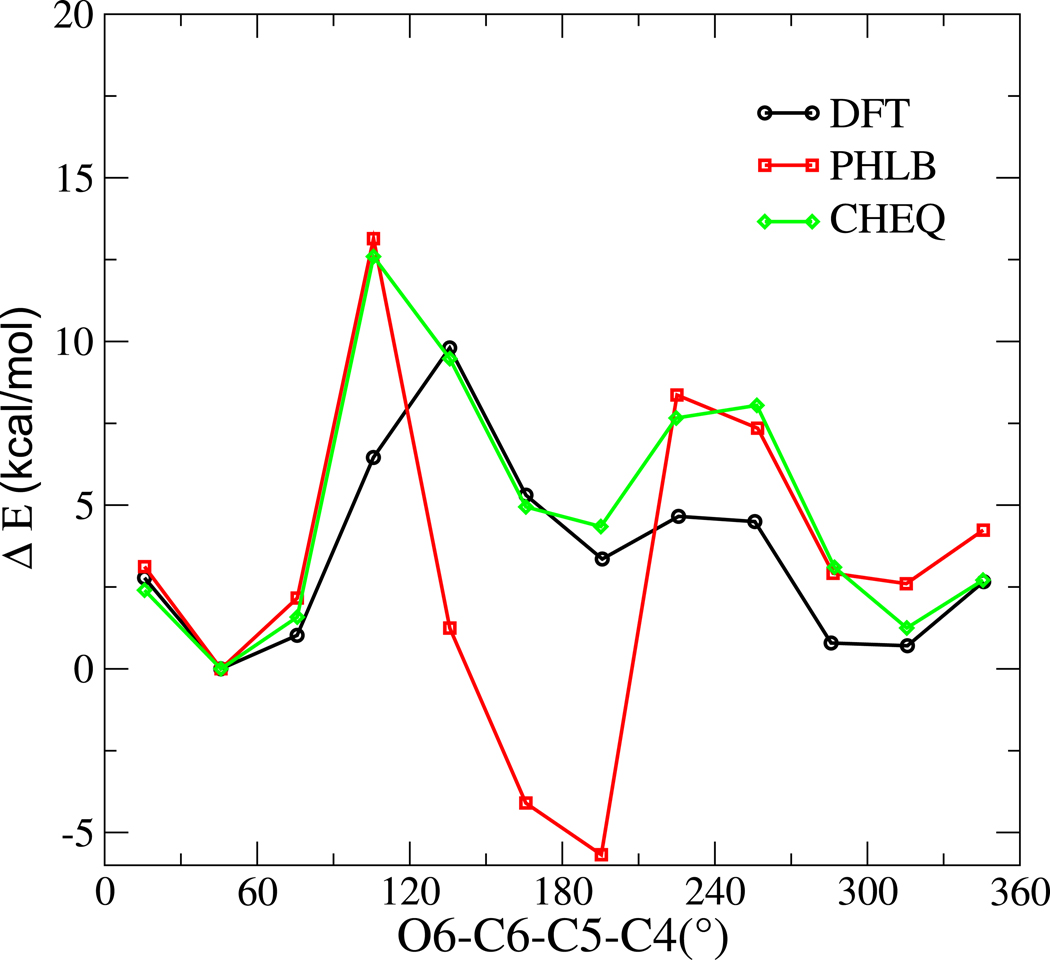
To assess the torsion parameters in the PHLB and CHEQ models, we computed the rotational energy profile of O6-C6-C5-C4 dihedral using the force fields and compared to first-principles results (Figure 3). DFT energies of twelve NAG geometries are optimized at the B3LYP/6-31++g(2d,2p) level of theory with the torsion angle constrained from 0 to 360° in 30° increments. The force field energies are obtained by minimizing the DFT optimized geometry at each torsion angle using the PHLB or CHEQ model and steepest descent minimization; each minimization is performed with the torsion constrained at the corresponding value. PHLB favors the trans geometry and predicts an incorrect relative energy from the first minimum at 45° to the second at 195°, which suggests that the force field revision on the exocyclic primary alcohol from HGFB to PHLB³¹ is not transferable to NAG molecule and torsion parameters may need to be optimized for different type of carbohydrate molecule in the fixed-charge model. Fortuitously, the CHEQ force field predicts the correct relative energy without any modification of the torsion parameters, at most suggesting the importance of electrostatic polarization effects in this system. Both PHLB and CHEQ force fields overestimate the energy barrier between gauche and trans conformations; the peak energies between trans and g+ or g− near 120° and 240° increase by 3 kcal/mol relative to the first-principles reference. This observation implies less transitions between different 6-hydroxymethyl dihedral conformations using force field methods.

FIG. 3.

Rotational energy curve about O6-C6-C5-C4

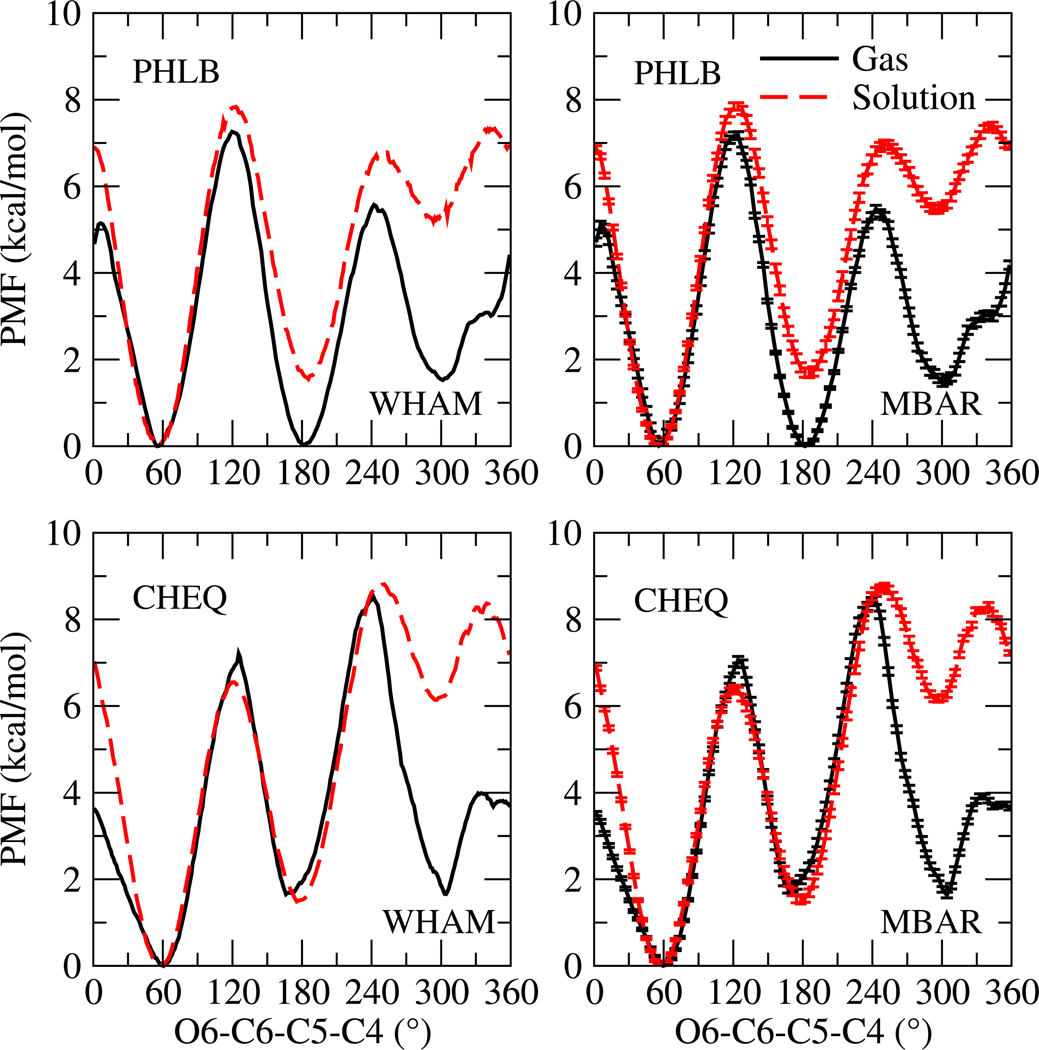
Solvent effects on the O6-C6-C5-C4 torsion are investigated by computing the potential of mean force (PMF)⁸³ around this torsion; the free energy profile is shown in Figure 4. To ensure sufficient sampling along the reaction coordinate, each window restraining 6-hydroxymethyl dihedral at one target value from 0 to 360° with a 10° increment is sampled for 1.5 ns, the first 50 ps of which is considered as equilibration and not used in the PMF calculation. Harmonic force constants applied in different windows, different force fields, and different environments are listed in SI Table III. PMFs⁸³ are calculated using the weighted histogram analysis method (WHAM)⁸⁴ and the multistate Bennett acceptance ratio method(MBAR)^76,77. Uncertainty estimates are based on MBAR and displayed in Figure 4. WHAM and MBAR methods generate PMFs that are essentially the same and the uncertainties of each data point are negligible, suggesting the PMFs are converged within the sampling time.

FIG. 4.

Potential of mean force (PMF) for O6-C6-C5-C4

The PMF curves show a similar shape as the rotational energy profiles (Figure 3) and three energy minima are observed at gauche and trans conformations. The global minimum appears at 60° for both force fields in both environments (gas phase and solution), which is consistent with the first-principles rotational energy profile (Figure 3). Gas phase NAG structures with low energies (not shown) are found to be stabilized by intramolecular hydrogen bonding and some structures exhibit saccharide ring distortion to achieve this. An ab initio metadynamics study reported that the relative energy between the chair (⁴C₁) and boat (B_3,O) conformer is 2.6 kcal/mol for β-D-glucopyranose⁸⁵. We compute the energy difference of MP2 optimized NAG chair and boat geometries using cc-pvdz basis set and find that chair conformation is 4.37 kcal/mol more favorable than boat. Minimizing the MP2-optimized structures with PHLB and CHEQ force fields yields relative energies of the boat-ring distortion of −2.64 and 2.26 kcal/mol, respectively. The CHEQ model captures the relative chair/boat energetics without modification of any torsion parameters from the PHLB model. This again at most suggests that polarization effects on conformational properties are important, though at this time we do not comment on the exact nature of the coupling between the torsional energetics and electronic polarization. When NAG is solvated in water, hydrogen bonds between solute and solvent are found in snapshots near the low-lying regions of the PMF, and contribute to stabilizing the NAG pyranose ring in the chair conformation for both force fields. Also, the solution PMF indicates a 7 kcal/mol energy barrier from g+ to g− and 8 kcal/mol (6.5 for CHEQ) from g+ to trans and explains the 100% population of g+ conformation in dynamics simulations (Table VI).

On the other hand, the acetamido group, as the key substituent, differentiates the NAG molecule from other carbohydrates. Efforts have been made to derive empirical Karplus equations from DFT calculations in order to connect to nuclear magnetic resonance (NMR) observations^23,86. Here, we adopt eight Karplus equations sensitive to the nitrogen-carbon (NT-C2) torsion from previous studies^23,86 (see SI Table V for more details) and compute J-couplings for each snapshot obtained from force field dynamics simulations. The average J-couplings and standard deviations are displayed in Table VII. High J-coupling constant uncertainty suggests broader distribution of a flexible corresponding torsion during the simulation. The acetamido group torsion C2-NT-C7-C8 shows the least dihedral rotation followed by the two torsions in the pyranose ring, H-C1-C2-H and H-C2-C3-H, and the most flexible rotatable bond is C2-NT, the linkage between the ring and the side chain. A general trend of overestimating the J-couplings relative to the experimental values is observed in Table VII, similar to the results in Ref²³. The ring J-couplings, ³J_H1,H2 and ³J_H2,H3, show the largest deviation from experimental observation, the Karplus parameters of which are derived for cyclopentane-1,3-diol⁸⁷. Other than the error introduced by the simplified molecular model of the Karplus equation parameterization, Mobli et al. suggested that further sources of error include exclusion and/or simplification of solvent effects, basis set limitations and intrinsic properties of DFT^23,88 during the parameterization of Karplus relationships. Also, insufficient sampling of the corresponding torsions and incorrect torsion populations arising from force field errors can also contribute to the discrepancy between MD and experimental J-couplings. Future work is needed to diagnose the main error source and improve upon the computed J-couplings.

TABLE VII.

Vicinal Coupling Constants Within N-acetyl Side-chain

	PHLB	CHEQ	Moblia	Expt.
${}^3{{\displaystyle J}}_{H2,NH}^a$	10.75(1.40)	10.58(1.46)	9.27	9.07
${}^3{{\displaystyle J}}_{H2,NH}^c$	10.14(1.22)	9.88(1.36)	−	9.07
${}^3{{\displaystyle J}}_{H1,H2}^b$	12.64(0.47)	12.59(0.48)	11.02	8.46
${}^3{{\displaystyle J}}_{H2,H3}^b$	12.53(0.52)	12.63(0.48)	11.82	10.40
${}^3{{\displaystyle J}}_{H2,C7}^c$	3.61(0.43)	3.44(0.54)	−	3.1
${}^3{{\displaystyle J}}_{C1,C7}^c$	1.65(0.86)	1.47(1.01)	−	1.1
${}^3{{\displaystyle J}}_{C3,C7}^c$	0.99(0.64)	1.18(0.80)	−	1.5
${}^3{{\displaystyle J}}_{C2,C8}^c$	1.53(0.01)	1.53(0.01)	−	1.6

^aSimulation coupling constants calculated according to Karplus equations in ref²³

^bParameters for Karplus equation obtained from ref⁸⁷

^cKarplus equations derived for the N-acetyl fragment based on ref⁸⁶

2. Glycosidic Linkages

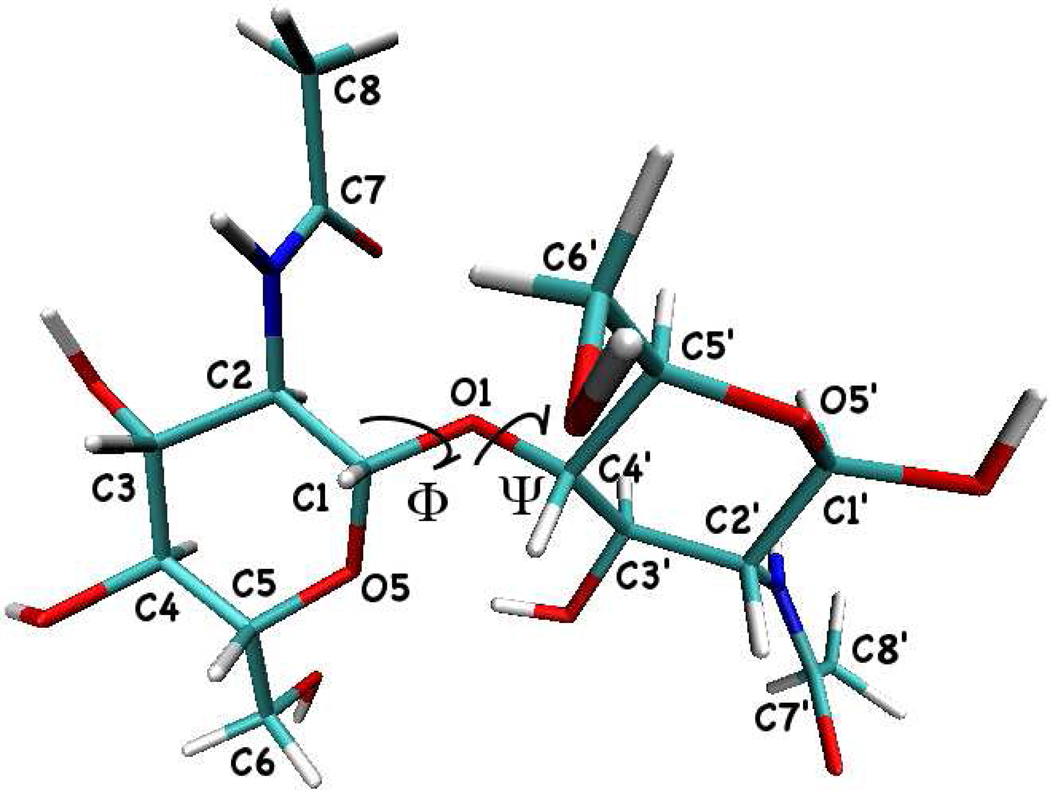
As the original PHLB carbohydrate force field does not parameterize the glycosidic linkage torsions, we adopt the angle and torsion parameters of ribose from the CHARMM27 nucleic acid force field and apply it to both PHLB and CHEQ models in this work. To study the glycosidic linkages of NAG oligosaccharides, we adopted the nomenclature of the two related torsional angles:Φ= O5-C1-O1-C4’ and Ψ= C1-O1-C4’-C5’(Figure 5). Figures 6 and 7 show the population density map of torsional angles for the glycosidic linkage α-(1–4) using the PHLB and CHEQ models, respectively.

FIG. 5.

Molecular structure of α-(1–4) glycosidic linkage of NAG oligosaccharides

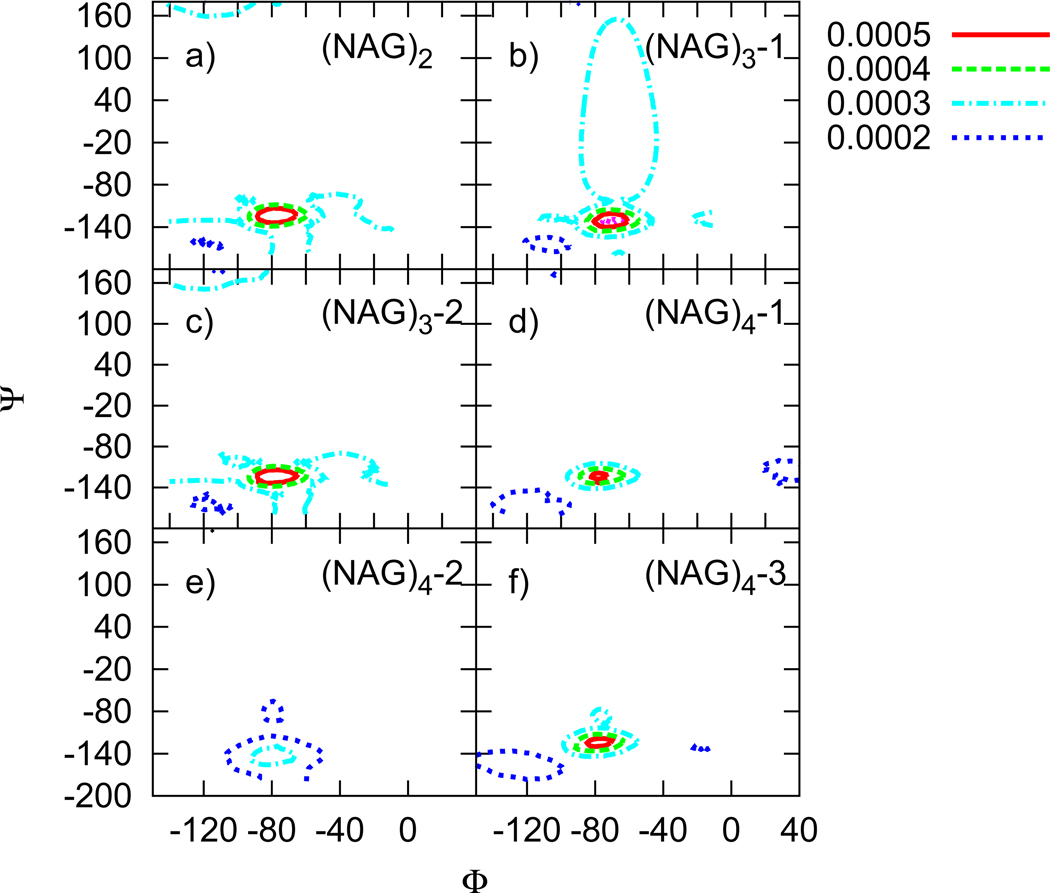
FIG. 6.

Population density maps of glycosidic linkage torsions based on the PHLB model. Mth linkage of an oligomer with n NAG residues are noted as (NAG)_n-M in the figure.

FIG. 7.

Population density maps of the glycosidic linkage torsions based on the CHEQ model. Mth linkage of an oligomer with n NAG residues are noted as (NAG)_n-M in the figure.

The coverage of these contours shrinks from (NAG)₂ to (NAG)₄, reflecting the size effect on glycosidic linkage. CHEQ maps show higher maximum population density at the most favorable conformation, indicating a less flexible glycosidic bond than in the PHLB model. More than one maximum can be observed from the population density maps (Figures 6 and 7); we list the global maximum and values for comparison in (Table VIII). The crystal structure of α-maltose⁸⁹, with Φ= 116° and Ψ = 242°, is favored by hydrogen bonding interactions between O2-O3’. However, such torsions are not observed in NAG oligomers, because the O2 hydroxyl group is replaced by the acetamido group in NAG. Instead, O5 and O3’ are hydrogen bonded to stabilize the glycosidic linkage. Furthermore, similar torsion behavior occurs on both sides of the oligomers (the first and last linkages of NAG chains); while linkages in the middle of the chain (eg. NAG₂-NAG₃ for (NAG)₄) take on slightly different values. The small change of torsions in the middle may imply some secondary structuring for NAG oligomers, though further investigation for longer oligomers is required.

TABLE VIII.

Global Maximum of Population Density Map. Φ and Ψ torsions are displayed in Figure 5

System	Model	NAG1-NAG2		NAG2-NAG3		NAG3-NAG4
		Φ	Ψ	Φ	Ψ	Φ	Ψ
	PHLB	−76	−120	–	–	–	–
(NAG)2	CHEQ	−68	−133	–	–	–	–
	Crystal	−82	−120	–	–	–	–
	PHLB	−76	−124	−77	−121	–	–
(NAG)3	CHEQ	−73	−129	−68	−127	–	–
	Crystal	−79	−122	−74	−125	–	–
	PHLB	−77	−122	−84	−146	−80	−129
(NAG)4	CHEQ	−74	−136	−64	−129	−69	−122
	Crystal	−80	−114	−79	−123	−97	−134

B. Diffusion Coefficient

Solution dynamics is probed by computing self-diffusion coefficients for solute and solvent of NAG and oligosaccharides aqueous solutions based on the Stokes-Einstein relation (Table IX). No experimental data for NAG diffusion coefficient was found. NMR experiments yielded self-diffusion coefficient of 4.2×10⁻⁶cm²/s for methyl-D-isomaltoside⁹⁰. According to the Infrared Thermal Diffusion Forced Rayleigh Scattering (IR-TDFRS) study by Blanco et al. the diffusion coefficient is independent of mono-saccharide structure⁹¹; we assume that NAG’s experimental self-diffusion coefficient should be very close to that of other mono-saccharides. Based on the CHEQ model, the computed solute self-diffusion coefficients are consistently smaller than the values of the fixed-charge model and suggest more consistent solution dynamics when compared to the experimental data for other carbohydrates. The self-diffusion coefficients of solute slightly decrease from NAG to (NAG)₃ due to size effects and converge to a constant value for the trimer and tetramer in both force fields. On the other hand, the self-diffusion coefficient for TIP3P model used in the fixed-charge simulation is almost twice that of the TIP4P-FQ-like model (Table IX) and the experimental value of pure water⁹², which may affect NAG self-diffusion coefficient towards higher value. Meanwhile, solute size appears to have little effect on water self-diffusion coefficients, which may attribute to small solute effect in dilute solutions of this study.

TABLE IX.

Self-diffusion Coefficients of NAG and Water. All values expressed in units of 10⁻⁵cm²/s

	PHLB				CHEQ
	NAG	(NAG)2	(NAG)3	(NAG)4	NAG	(NAG)2	(NAG)3	(NAG)4
NAG	1.58(0.24)	1.12(0.15)	0.89(0.08)	0.90(0.10)	0.52(0.06)	0.41(0.04)	0.34(0.02)	0.36(0.01)
Water	5.43(0.07)	5.55(0.04)	5.47(0.05)	5.63(0.04)	2.12(0.02)	2.15(0.02)	2.13(0.02)	2.20(0.01)

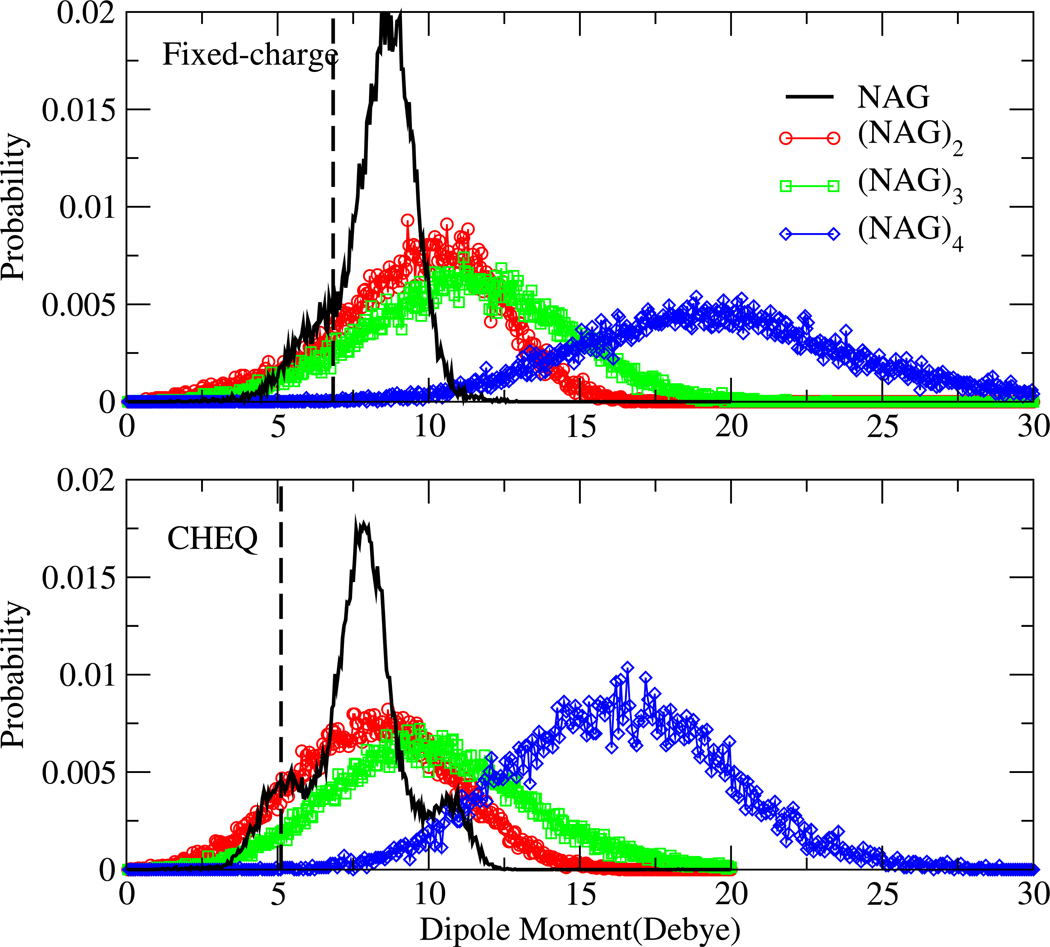
C. Dipole Moment Distributions

Figure 8 displays the dipole moment distribution of NAG in aqueous solution. The dashed vertical lines show the dipole moments of the NAG monomer at the DFT-optimized geometry (see section IID2 for more details) using the PHLB charges (upper panel) and charges obtained from the CHEQ model (lower panel). As indicated in Table IV, the CHEQ vacuum dipole moment reproduces the first-principles value while the PHLB force field overestimates dipole moment for the DFT geometry due to different charges used in that model (we note that in general, classical fixed-charge force fields overestimate static molecular charges in order to emulate condensed phase polarization effects). In solution, the most probable dipole moment of NAG monomer in the fixed charge force field (PHLB) is 2 Debye higher than the corresponding vacuum value, arising from conformational changes in aqueous environment. A global maximum in the CHEQ distribution at 8 Debye (lower panel of Figure 8) suggests an induced dipole moment of 2.8 Debye relative to vacuum. Two broad shoulders are observed on both sides of the global peak (one around 5 Debye, which is the gas-phase dipole moment; the other around 11 Debye); these can be possibly be attributed to conformational and/or charge redistribution effects inherent in the CHEQ formalism. We eliminated the possibility of charge redistribution effects because the partial charge variation on each atom does not correlate with the dipole moment changes (results not shown). Furthermore, the dipole moment distribution computed applying the static PHLB charges to configurations sampled from simulations using the CHEQ force field (SI Figure 1) shows a similar two-shoulder shape. Meanwhile, the plateaus diminish for the PHLB dipole moment distribution, based on PHLB configurations and PHLB charges (Figure 8 top panel). Another observation from SI Figure 1 is that the static PHLB charges produce higher dipole moments than the CHEQ charges do for the same NAG structure. This implies that the shifting of global dipole moment peak to higher value from CHEQ to PHLB model is mainly due to differences in partial charges.

FIG. 8.

Dipole moment distributions of NAG oligosaccharides in aqueous solutions. The dashed vertical lines show the gas-phase dipole moment of the DFT-optimized geometry.

To understand the most important structural component(s) causing the two shoulders in dipole moment distribution of CHEQ model, we consider the correlation of NAG rotatable bond torsion with the dipole moment (SI Figure 2). The torsion probabilities of C3 and C4 hydroxyl groups differ the most from PHLB to CHEQ force field according to Table VI and a dipole moment contour plot of the two torsions (SI Figure 2) confirmed their influenceon dipole moment. The plateau near 5 Debye comes from the conformers with trans hydroxyl bond at C3 and gauche hydroxyl bond at C4 position; such conformation is enhanced in the CHEQ force field compared to the PHLB force field. Similarly, the higher probability for H3-C3-O3-HO3 at −60° and the new peak of H4-C4-O4-HO4 torsion at ±180° introduce the other dipole moment plateau near 11 Debye. We conclude that the shape of dipole moment distribution is highly dependent on the NAG structure (especially the flexible rotatable bonds conformations) in solution; more than one favorable dipole moment may suggest different semi-stable solute geometries.

Dipole moment distributions of NAG oligomers are also displayed in Figure 8. The PHLB model consistently overestimates the dipole moments of NAG oligomers compared to the CHEQ force field. On the other hand, glycosidic linkage at the 1–4 position and hydrogen bond between O5 and HO3 from the neighboring NAG unit (Figure 5) block rotations of C3 and C4 hydroxyl bonds stabilizing oligomer structure and result in a single, dominant dipole moment value for both models. The most probable dipole moment shifts slightly to larger values from NAG to (NAG)₃ and increases by more than 7 Debye for (NAG)₄ in both models. The width of dipole moment distributions increases from monomer to tetramer as there are more structural effects involved in the larger solutes.

D. Hydrogen Bonding

To study intermolecular hydrogen bonding of NAG and its oligomers, radial distribution functions (RDFs), water bridge populations, and hydrogen bond correlation times are analyzed for each oxygen and nitrogen atom in the NAG molecule.

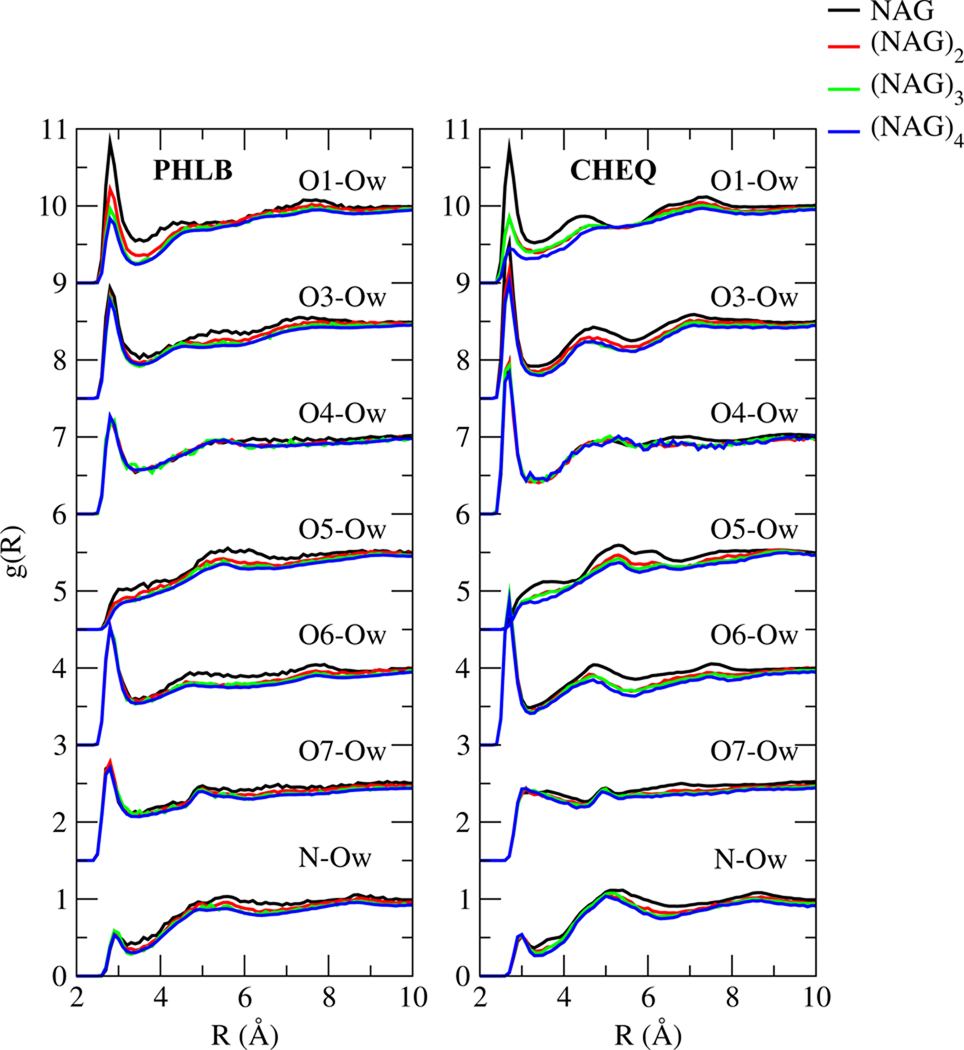
1. Radial Distribution Functions

According to NAG-water RDFs (between water oxygen, O_w and solute oxygen and nitrogen atoms) shown in Figure 9, hydroxyl oxygen atoms around sugar rings (O1, O3, O4, O6) contribute significantly to intermolecular hydrogen bonding, particularly in the CHEQ model. Pyranose oxygen O5 is less likely to form hydrogen bonds with water because of the two neighboring hydroxyl bonds. The carbonyl oxygen O7 shows a well-defined first hydration shell of water in PHLB model, which is diminished in the CHEQ model. The N-Ow RDFs are similar for the two force fields; the small first hydration shell and broad second shell implies that water molecules surrounding the nitrogen are more likely to be affected by other solute atoms than to form directly hydrogen bonding with the nitrogen. The height of the first O1-Ow RDF peak decreases from NAG to (NAG)₄, because for a NAG oligomer with n ( n = 2, 3 or 4 in this study) NAG units, n-1 hydroxyl bonds on O1 atoms change to ether bonds and less water-O1 hydrogen bonds are formed on average for each O1 atom. Compared to RDFs based on the fixed-charge model, the CHEQ models shows a larger reduction of the first solvation shell going from NAG to (NAG)₄. Moreover, the solute size has little effect on hydrogen binding abilities of other oxygen atoms according to the nearly indistinguishable oligosaccharide RDFs.

FIG. 9.

Radial distribution functions of water oxygen and NAG oxygen and nitrogen atoms

To the best of our knowledge, no previous experimental or theoretical study reported radial distribution functions(RDFs) for NAG in water. Naidoo and Kuttel³² calculated the RDF between O3 of β-maltose and water oxygen using the Carbohydrate Solution Force Field (CSFF), a fixed charge model, and found a peak at 2.8 Å with a density of 1.6. Corzana et al.⁹³ compared the RDFs of O3 of methyl-α-D-maltoside to water oxygen using the older fixed-charge HBFG,CSFF and GLYCAM 2000a force fields. The RDF based on HBFG model peaks at 2.8 Å and the peak density is 2.3; the CSFF model RDF displays density at 2.8 Å of 1.6 and the values of GLYCAM 2000a force field is the peak density of 1.0 at 3.0 Å. The RDF based on the PHLB force field has a well-defined first hydration shell peaking at 2.8 Å, consistent with the methyl-α-D-maltoside and β-maltose peak values using the HBFG and CSFF model, but the peak density is 0.9, smaller than the results for the other sugars reflecting the effect from different neighbor side chains. The RDF calculated using CHEQ force field shows a sharper first peak at 2.7Å and density of the first hydration shell is 1.3, indicating more favorable hydrogen bonding. Moreover, the second hydration shell is more well-defined in the CHEQ model than in the PHLB model.

2. Water Bridge Structure

A previous study has suggested that the solute-solvent interaction plays an important role in determining condensed phase sugar ring conformations⁹⁴. Here we investigate possible water hydrogen bonding bridges which may stabilize the torsions (Table X). One water molecule is considered to hydrogen bond to NAG oxygen/nitrogen when Ow-On/Ow-N distance is less than 3.4 and 3.5 Å, respectively, and the O-H…O or N-H…O angle is greater than 120°. Only one-water and two-water bridges are computed here and we found that at least 1/5 snapshots in the trajectories contain water hydrogen bonding bridges. We acknowledge that the water bridge population is sensitive to the hydrogen bond definition. For instance, when using a distance criterion only (3.2 Å for Ow-On and 3.3 Å for Ow-N, based on the first minimum of the Ow-On/Ow-N RDF), 46% of the snapshots have one-water bridge between O3 and O4 and 29% have two-water bridge structure between O3 and O4 for the CHEQ model. Meanwhile, O1-O5, O3-O4, O5-O6 and O3-NT are directly hydrogen bonded based on this distance criterion but such bonds do not fulfill the angular orientation criterion. However, both definitions suggest some important solute-solvent interacting structures in common. In addition to the structure with one water mediating hydrogen bonding between O1-O5 and O5-O6, which we applied as the gas-phase heterodimer structure in parameter development (Figure 2), we found two other water bridge structures are important in solution: 1-water-bridge between O3-O4 (SI Figure 3) and 2-water-bridge between O1-O6 (SI Figure 4).

TABLE X.

Water Bridge Population in NAG Solution

	PHLB		CHEQ		Mobli1
Position	H2O(%)	(H2O)2(%)	H2O(%)	(H2O)2(%)	H2O(%)	(H2O)2(%)
O1-O5	36	21	19	14	18	14
O3-O4	22	24	23	22	22	26
O5-O6	17	14	20	9	15	11
O3-N	1	10	1	7	2	12
O1-O6	1	38	0.4	35	3	40
O4-O6	5	23	5	15	3	12

3. Hydrogen Bond Correlation Function

The dynamics of NAG-water and water-water hydrogen bonding are characterized by the correlation function⁹⁵

$$C_{HB}(t)=\frac{<h(0)h(t)>}{<h>}$$ (16)

where h(t) is an operator, defined as 1 if a tagged pair of molecules are hydrogen bonded, and 0 otherwise. The bracket averages over all possible pairs of molecules and time origins. The function C_HB represents the probability that a hydrogen bond present at time 0 persists until time t.

Figure 10 displays the correlation functions for hydrogen bonds between water and NAG atoms; TIP3P and TIP4P-FQ water hydrogen bond correlation functions are also shown for PHLB and CHEQ force fields, respectively. For quantitative comparison, we fit the correlation functions with the stretched exponential

$$C_{HB}(t)=a_R\cdot exp[-{(t/{\tau }_R)}^{{\gamma }_R}]$$ (17)

The relaxation time τ_R and the exponent γ_R are shown in Table XI. For the fixed charge model, carbohydrate-water hydrogen bonds persist for longer lifetimes than those between water molecules; C_HB of NAG oxygens and nitrogen decay more slowly than the water correlation curve with larger τ_R than that of the water oxygen atom. Using CHEQ model with TIP4P-FQ water, larger relaxation time τ_R and smaller exponent γ_R indicate slower hydrogen bonding dynamics with broader distribution of time scales in the polarizable model. Hydrogen bonds between O5-water and O7-water break and form at a higher frequency compared to water-water hydrogen bonds, Also, based on the correlation functions, O3/O4, O1/O6/N and O5/N have similar hydrogen bonding dynamics, consistent with the similarities of peak heights for corresponding oxygen atoms and nitrogen RDFs (Figure 9).

FIG. 10.

Correlation functions for NAG-water and water-water hydrogen bonds

TABLE XI.

Relaxation time τ_R and exponent γ_R of the correlation function C_HB(t) defined by equation 17

	PHLB		CHEQ
Atom	τR	γR	τR	γR
O1	5.13	0.65	34.54	0.51
O3	4.02	0.62	64.26	0.57
O4	3.24	0.63	63.84	0.58
O5	1.81	0.48	5.98	0.37
O6	3.50	0.62	33.36	0.56
O7	2.50	0.56	5.13	0.44
NT	5.15	0.73	30.13	0.54
Owat	2.02	0.58	11.55	0.64

E. Free Energy of Hydration

Hydration free energy quantifies the effects of both enthalpy and entropy of molecular interactions and serves as a useful property of force field assessment. The balance of solvent-solvent and solvent-solute free energetics has recently been emphasized in the context of describing and quantifying protein-ligand association free energetics. Very few empirical carbohydrate force fields have been characterized with respect to solvation free energetics^29,96. Here, we compute the free energies of hydration for NAG to (NAG)₄ based on PHLB-PSP and CHEQ models; recall that the PHLB-PSP force field includes pair-specific off-diagonal Van der Waals interactions between NAG and water in order to mimic as closely as possible the dimer energies computed using first-principles DFT calculations.

Recently, Shirts and coworkers employed the Bennett acceptance ratio (BAR) method to compute small molecule hydration free energies and found that BAR can be more efficient than ther-modynamic integration(TI) method in such calculations.^97–99 Here we calculate free energy of hydration for NAG to (NAG)₄ via BAR and the conventional thermodynamic integration (TI) method (Table XII). TI results are obtained by averaging free energies based on 100 ps blocks of trajectories, and the standard deviation of these determines the uncertainties. Consistent with studies for other aqueous solutions⁹⁹, the BAR method reproduced the free energy of hydration obtained by TI while efficiently reducing the uncertainty.

TABLE XII.

Free Energies of Hydration for NAG Oligomers

Model	method	ΔG (kcal/mol)	NAG	(NAG) 2	(NAG)3	(NAG) 4
PHLB		ΔGvdw	2.82(0.32)	4.67(0.37)	6.65(0.39)	8.83(0.71)
	TI	ΔGchg	−43.72(0.49)	−69.72(0.63)	−95.57(0.84)	−122.65(1.04)
		ΔGhyd	−40.90(0.58)	−65.05(0.73)	−88.92(0.92)	−113.82(1.26)
		ΔGvdw	2.89(0.08)	4.82(0.13)	6.69(0.05)	8.62(0.15)
	BAR	ΔGchg	−43.40(0.05)	−69.49(0.07)	−95.48(0.03)	−122.11(0.07)
		ΔGhyd	−40.51(0.09)	−64.67(0.14)	−88.79(0.06)	−113.49(0.17)
CHEQ		ΔGvdw	−2.34(0.29)	−4.02(0.78)	−6.02(0.60)	−6.74(0.86)
	TI	ΔGchg	−28.13(0.28)	−47.73(0.57)	−55.50(0.07)	−62.80(2.43)
		ΔGhyd	−30.69(0.38)	−51.93(1.21)	−61.52(0.61)	−69.54(2.58)
		ΔGvdw	−2.35(0.08)	−4.00(0.19)	−5.74(0.09)	−6.66(0.40)
	BAR	ΔGchg	−27.96(0.04)	−47.42(0.06)	−56.24(0.05)	−64.29(0.08)
		ΔGhyd	−29.96(1.18)	−51.42(0.20)	−61.98(0.10)	−70.95(0.41)
ΔGGBSW			−28.59(3.06)	−45.26(3.50)	−59.50(3.48)	−73.61(2.43)

The free energies of hydration are more negative from NAG to (NAG)₄ due to increasing availability of solute-water hydrogen bonding. Moreover, ΔG_hyd decreases the most from NAG to (NAG)₂ and nearly linearly from (NAG)₂ to (NAG)₄. The intramolecular hydrogen bonds in NAG oligomers are largely hampered so more hydroxyl groups are open to interactions with the solvent. From dimer to tetramer such solute-water interactions increase constantly with the number of functional groups and lead to the linear reduction of free energy of hydration. Longer simulations are necessary to estimate free energy of hydration for (NAG)₃ and (NAG)₄ because these larger systems require more time for convergence (see SI Table V for more details).

The PHLB-PSP force field consistently predicts more favorable hydration free energies for NAG oligomers studied compared to the CHEQ values, due to the electrostatic free energy contribution. We attribute the electrostatic free energy difference to the different charge schemes in PHLB-PSP and CHEQ model (SI Tables I and II ) and other studies^100–102 also revealed the strong dependence of small molecule hydration free energies on charge sets. Meanwhile, Van der Waals components of hydration free energies are found to have different signs in the PHLB-PSP and the CHEQ model. To understand the underlying cause, we compute the VDW interaction energy between solute and water molecules within 4 Å of solute for solution structures in the first window of VDW decoupling (full nonbond interactions between solute and solvent molecules) and in the first window of charge decoupling (both nonbond and electrostatic interactions are fully on) (SI Figure 5). The CHEQ VDW interaction energies are more negative than the ones from PHLB-PSP force field, which is consistent with the vacuum NAG-water dimer interaction energy (Table V). The VDW contribution to the hydration free energy can be considered as the free energy change of solvation process with two steps: 1. create an cavity with solute size, ΔG_cav; 2. accommodate solute molecule in the cavity and interact with solvent ΔG_inte. When VDW interactions of solute-solvent are favorable enough, ΔG_inte may compensate the free energy penalty of creating a vacuum space in bulk water ΔG_cav and we might observe an negative VDW component of hydration free energy as in the CHEQ model. Considering the solute size effect, from NAG to (NAG)₄ the VDW interaction energy shifts to lower value, suggesting more negative ΔG_inte. On the other hand, ΔG_cav should increase since a larger cavity is needed to accommodate larger solute. The final VDW hydration free energy is then determined by the sum of the two effects: PHLB-PSP ΔG_vdw increases from NAG to (NAG)₄ dominated by cavity free energy cost; CHEQ predicts more favorable ΔG_vdw for solute with larger size due to the contribution of ΔG_inte. We note that further calculation of ΔG_cav and ΔG_inte are needed for a quantitative conclusion. Another observation is that VDW interaction energies have lower values with broader distribution in the first window of VDW decoupling process than the ones obtained from charge decoupling, because eliminating electrostatic interactions when decoupling VDW interaction enables smaller distance between solute and solvent and reduces the VDW interaction energy. Similar effects of the VDW energy contributions to small organic molecule solvation have recently been analyzed and discussed by Mobley and coworkers¹⁰³.

As stated above, the lack of relative free energies of hydration data, both experimentally and computationally, limits our comparison with other theory. Green⁹⁶ computed the electrostatic solvation energy for NAG monomer using the CSFF model, and yields −32.96(3.10) kcal/mol, which is 17% more favorable than using the CHEQ force field; however, different water models were employed for the two models (TIP3P for the CSFF model and TIP4P-FQ-like water for the CHEQ force field). Similar effects have been observed for methanol and ethanol solvation free energies⁹⁸. Also, Green presented a set of optimized parameters for continuum solvation calculations, which is obtained by fitting to explicit solvent free energy perturbation simulations results for a set of hexapyranose sugars (NAG was not included). We computed implicit solvation energies using the generalized-Born with simple switching (GBSW) model optimized by Green⁹⁶ with the charges taken from the CSFF force field³¹ (Table XII). The GBSW energy for NAG is essentially the same as Green’s result, given that the same parameters including the charges and the VDW radii are employed. We would like to note that the GBSW energies are computed for solute structures generated by solution dynamics simulations under CHEQ model, so the identical GBSW results suggest that CSFF and CHEQ force field provide solute structures with similar solute cavity. Comparing the GBSW free energies to the electrostatic free energies of solvation via TI method, we find larger discrepancy from NAG to (NAG)₄, suggesting that current carbohydrate implicit solvent model may need to be adjusted for future use in oligosaccharides where our TI results of explicit model can be useful as reference.

IV. SUMMARY AND CONCLUSIONS

A polarizable carbohydrate force field is developed for the NAG molecule and longer oligomers that are model systems for carbohydrate substrates to hen egg-white lysozyme, for instance. Based on aqueous solution molecular dynamics simulations, we find that the CHEQ force field captures the relative rotational energetics of the 6-hydroxymethyl side-chain and chair/boat ring conformations without modification of the underlying PHLB force field torsion parameters. The force field simulation predicts glycosidic linkage torsions that are stabilized by the intramolecular hydrogen bonds in oligomers and are in accordance with the crystal structure. Self diffusion coefficients of solute and solvent molecules are smaller in the polarizable model and are in better agreement with related experimental results. The slower solution dynamics in CHEQ model also reflects the longer solute-solvent hydrogen bond lifetimes and larger first hydration shells in NAG-water RDFs. Yielding higher dipole moments, PHLB force field charge consistently overestimates hydration free energy during charge decoupling and results in more favorable total hydration free energy with smaller VDW interaction energy. With the current efforts to include electronic polarization in classical force fields, we believe that this work establishes a platform on which to build more extensive polarizable force fields for an important class of biological macromolecules.