A new estimate of family disease history providing improved prediction of disease risks

SUMMARY

Complex diseases often aggregate within families and using the history of family members’ disease can potentially increase the accuracy of the risk assessment and allow clinicians to better target on high risk individuals. However, available family risk scores do not reflect the age of disease onset, gender and family structures simultaneously. In this paper, we propose an alternative approach for a family risk score, the stratified log-rank family score (SLFS), which incorporates the age of disease onset of family members, gender differences and the relationship among family members. Via simulation, we demonstrate that the new SLFS is more closely associated with the true family risk for the disease and more robust to family sizes than two existing methods. We apply our proposed method and the two existing methods to a study of stroke and heart disease. The results show that assessing family history can improve the prediction of disease risks and the SLFS has strongest positive associations with both myocardial infarction and stroke.

1. INTRODUCTION

Complex diseases including heart diseases, hypertension, and breast cancer, often aggregate within families. Disease history of other family members is highly correlated with the disease outcome of an individual due to common environmental and inherited genetic factors [1–3]. The family history of an individual has been shown to be an important predictor of the individual’s risk of diseases [4–8]. Thus, assessment of family history can potentially increase the accuracy of the risk assessment and allow clinicians to better target on high risk individuals.

A variety of approaches to quantify the family history have been proposed [9–11], with the most common dichotomous score defined by the presence of an ever-affected first degree relative. These approaches have been generalized to capture additional information contained by the gender and specific age at onset of the affected relatives [4, 12–14]. Santo et al. [15] defined a simple risk score that was weighted by the reciprocal of either age at onset for affected individuals or age at censoring for unaffected relatives, and then averaged over all family members. However, these approaches do not reflect the number of family members or family structure, which may also contain information regarding the risk of the individual.

Williams et al. [16] used a family history statistic that measures differences between the observed number of family members with prevalent disease and the number that would be expected given the family structure and the age, sex, race, and birth cohort of the family members. Others have formulated family scores using a similar approach (e.g. [17–21]). Silberberg et al. [22] assessed the relative performance of these formulations in a variety of sample pedigrees and found none of the methods performed uniformly ‘better’ in all sample pedigrees. The distribution of these family risk scores (FRS) is highly skewed and is often categorized into three to five strata for further analysis with outcomes [8, 23, 24]. The family risk scores proposed by Williams et al. [16] and others require the age, race, and birth cohort-specific incidence rates from the general population to calculate the expected cumulative risk.

However, these FRSs were unable to reflect the potentially different influence on an individual’s risk from family members other than first degree relatives [3]. This problem was addressed by a kinship-weighted score proposed by Slattery and Kerber [11] that incorporates information on second to sixth degree relatives. Both Williams et al.’s [16] and Slattery and Kerber’s [11] approaches were shown to improve the precision of family history as a predictor of disease risk [23].

In this paper, we propose an alternative family risk score, a stratified log-rank family score (SLFS) that incorporates the age of onset of family members, gender differences, and the relationship among family members. Via simulation, we demonstrate that the new family history score is more closely associated with the true family risk for the disease. Lastly, we apply this method to a study of stroke and heart disease.

2. METHOD

As others, our goal is to develop a family risk score that captures information from age of disease onset for family members affected with the disease or age at censoring for family members without the disease, the gender and kinship relationship of all the individuals within the family.

Suppose that for each individual and his/her family members, we know whether they had developed a particular disease by their current age, as well as the relationship within families relative to the individual (so-called ‘proband’, through which the family members entered the study). We then define the position of other individuals in the family as the relationship to the proband, e.g. grandfathers, grandmothers, fathers, mothers, brothers, and sisters. Each family member is then assigned a log-rank score indexing their risk of disease development [25] relative to other individuals with a similar family position throughout the study according to the following steps:

1. Let T₁, T₂, …,T_r, be the r distinct time points of observed events in the group and T₀ = −∞.

2. During the kth time period (T_k−1, T_k], $n_0^k$ is the number of observations without observed event during this period (censored) and $n_1^k$ is the number of observed events.

3. For k = 1, 2, …,r, the log-rank scores for censored events and observed observations are calculated as $a_0^k=-{\displaystyle {\sum }_{l=1}^k}$ risk of disease in the $(T_{l-1},T_l]=-{\displaystyle {\sum }_{l=1}^k}{n}_1^l/({\displaystyle {\sum }_{m=l}^r}{n}_0^m+n_1^m),a_1^k=1+a_0^k$, respectively, and $a_0^{r+1}=a_0^r$ [26]. The construction of $a_0^k\text{and}{a}_1^k$ is based on the assumption of random censorship and the fact that the censored times are lower bounds for true event times [26].

Then, within this position group, an individual with an age between T_k−1 and T_k is assigned a risk score $a_0^k$ (if event occurred on him during (T_k−1, T_k]) or $a_1^k$ (otherwise). The SLFS for the ith family is calculated as the mean of the risk scores of all the family members.

We provide a working example to illustrate how the SLFS is calculated. Suppose we have four families, each with four offspring, with event times shown in Table I:

Table I.

The ages of onset for four families in the working example.

Family	Father	Mother	Brothers	Sisters
1	56	65	62, 70*	59, 66*
2	49	70	62	52, 57*, 64
3	60*	55	51, 56, 60*	68*
4	66	85*	76, 79*	71, 75*

^*Indicates censored data.

Then we have four positions: fathers, mothers, brothers, and sisters. For the fathers’ group, $T_1=49,T_2=56,T_3=66,n_0^1=n_0^2=0,n_0^3=1,n_1^1=n_1^2=n_1^3=1$. Thus,

$$\begin{array}{c}{a}_0^1=-\frac{1}{4},a_0^2=-(\frac{1}{3}+\frac{1}{4})=-\frac{7}{12}\hfill \\ a_0^3=-(\frac{1}{3}+\frac{1}{4}+\frac{1}{2})=-\frac{11}{12}\hfill \end{array}$$

and

$$a_1^1=\frac{3}{4},a_1^2=\frac{5}{12},a_1^3=\frac{1}{12}$$

The risk scores (or log-rank scores) for the four fathers in the four families are

$$(a_1^2,a_1^1,a_0^3,a_1^3)=(\frac{5}{12},\frac{3}{4},-\frac{11}{12},\frac{1}{12})\approx (0.42,0.75,-0.92,0.08)$$

Using a similar procedure, the risk scores for the four mothers are 0.42, 0.08, 0.75, and −0.92, respectively; the risk scores for the brothers are 0.33, −1.17, 0.33, 0.88, 0.73, −0.67, −0.17, and −1.17, respectively, in the order they appear in Table I; and the risk scores for the sisters are 0.71, −0.99, 0.88, −0.29, 0.51, −0.99, 0.01, and −0.99, respectively, also in the order they appear in Table I. The SLFS for four families are then (0.42+0.42+0.33−1.17+0.71−0.99)/6=−0.05, (0.75+0.08+0.33+0.88−0.29+0.51)/6=0.38, (−0.92+0.75+0.88+0.73−0.67−0.99)/6=−0.04, (0.08−0.92−0.17−1.17+0.01−0.99)/6=−0.53. Therefore, among these families, family 2 has the largest family history score, family 4 has the smallest family history score, while the other two families have scores intermediate, with family 3’s slightly larger than family 1’s score.

Ideally, we could use data from a large reference population to derive the risk score (a₀ and a₁) for each time interval within each group. However, because such population data are not available, we use all families in the data set to estimate the risk scores, assign individual risks according to their age of onset, sex and family role, and summarize the family risk score for each family using all individuals in the family.

3. SIMULATIONS

We simulated 200 nuclear families with two parents and the number of offspring ranging from 4 to 10. We first generated the father’s age uniformly from 55 to 100 and then mother’s age between 10 years younger and older than the father. The ages of the offspring were randomly generated from Uniform (the maximum parents’ age −40, the minimum parent’s age −18). The sexes of the offspring were randomly chosen with equal probabilities of being either male or female. For the ith family, a true common family risk score, denoted by U_i, was generated from standard normal distribution. Then the individual risk factors for n_i family members within the ith family, R_i, were generated from a multivariate normal distribution MVN(U_i1, V_i), where 1 is a 1 × n_i unit vector and the n_i × n_i variance–covariance matrix V_i is determined by the relationship among family members. Specifically, the element of the jth row and kth column of V_i, υ_ijk, is a number accounting for the background correlation between the jth and kth family members [27]. In particular, ${\upsilon }_{\mathit{\text{ijj}}}=\frac{1}{2}$ for any j; ${\upsilon }_{\mathit{\text{ijk}}}=\frac{1}{4}$ if j and k index parent and offspring or siblings; υ_ijk = 0 if j and k index non-consanguineous individuals. The age of onset for each family member was generated from the exponential distribution, with a hazard rate of λ/100, where λ is a linear combination of age, sex, the risk factor and random error, and is equal to β₀+β₁ Sex+β₂G Age+γR+E, G Age is five-year-interval age groups and E is a standard normally distributed noise. The parameter γ controls the correlation between the event of interest and family common risk U and its magnitude indicates the strength of the association. U and R are underlying variables and cannot be observed in the real data. The goal of our proposed method and others is to quantify the common family risk score U from observed data.

The events are assumed to occur between the ages of 30 and 100. The time to censoring, corresponding to the ‘current’ age for individuals who have not developed the disease, for each family member was then simulated from the exponential distribution with parameter (λ/100)·(1/τ−1), where τ is a parameter that controls the proportion of censoring [28] and is set to 0.6 and 0.8 for the first and second generations, respectively. If the time to censoring, or current age, is less than the time to the event, a right censoring event is recorded (i.e. the person has not developed the disease), while if the age of the event is less than the age of censoring, then that age is the time of disease development.

In addition to calculating our proposed SLFS as described above, we also calculated the family history scores by Williams et al.’s [16] and Reed et al.’s [21] methods.

The FHS by Williams et al. [16] is calculated for the ith family according to

$$\text{FHS}=\{\begin{array}{cc}\frac{(|{\displaystyle {\sum }_j}{O}_{\mathit{\text{ij}}}-{\displaystyle {\sum }_j}{E}_{\mathit{\text{ij}}}|-1/2)}{\sqrt{{\displaystyle {\sum }_j}{E}_{\mathit{\text{ij}}}}}\frac{|{\displaystyle {\sum }_j}{O}_{\mathit{\text{ij}}}-{\displaystyle {\sum }_j}{E}_{\mathit{\text{ij}}}|}{{\displaystyle {\sum }_j}{O}_{\mathit{\text{ij}}}-{\displaystyle {\sum }_j}{E}_{\mathit{\text{ij}}}}\hfill & \text{if}\left|{\displaystyle \sum _j}{O}_{\mathit{\text{ij}}}-{\displaystyle \sum _j}{E}_{\mathit{\text{ij}}}\right|>1/2\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$

where O_ij is 1 if the jth person in the ith family had an event, 0 otherwise and the expected risk E_ij for the jth person in the ith family is the corresponding age, sex-specific incidence rate that is calculated from all available subjects. When the difference between the observed and expected number of affected persons within a family is larger than $\frac{1}{2}$, this score is a standard Z-score statistic to test the difference between observed and expected numbers of affected corrected for continuity and adjusted to a positive number.

Because a single affected person in a small family can result in a high score, Williams et al. [16] reset the score for a family with only one affected individual to 0.99 to stabilize the impact of single affected.

The FHS of Reed et al. used the same observed O_ij and expected E_ij as Williams et al. but is formulated differently for the ith family:

$$\text{FHS}=\frac{({\displaystyle {\sum }_j}{O}_{\mathit{\text{ij}}}-{\displaystyle {\sum }_j}{E}_{\mathit{\text{ij}}})}{\sqrt{{\displaystyle {\sum }_j}{E}_{\mathit{\text{ij}}}}}$$

which is a Z-score statistic and follows a normal distribution asymptotically.

We are interested in comparing the strength of correlations of the three calculated family risk scores (Williams et al.’s method [16], Reed et al.’s method [21], and our SLFS) with the true family risk U; that is, which of the approaches has the strongest correlation (or power to detect a significant correlation) between the estimated family risk score and the true family risk. For each of the three methods, the test statistic is the correlation coefficient ρ between the estimated family risk scores and true family risk U. The null hypothesis is that there is no correlation between each of the estimated family risk scores and true family risk scores, i.e. ρ=0.

Distribution of family risk scores under the null hypothesis

When γ=0, the time to event for each individual does not depend on the risk of the other family members and thus the estimated family history score based on the all family members’ event history is then not associated with the true family risk score, i.e. ρ = 0. Under this null hypothesis, we generated data with a set of parameters: β₀ = 2, β₁ = 0.5, β₂ = 0.1, γ = 0.

We used the Kolmogorov–Smirnov (K–S) test to assess whether there was evidence of non-normality in the distribution of the family risk scores from the three approaches. While there was rarely ever evidence of a non-normal distribution of Reed et al.’s family risk score or of our SLFS, there was frequently evidence of non-normality for Williams et al.’s family score [16], particularly for relatively small family size. See Table II for the frequency with which the K–S test of normality indicated evidence of a non-normal distribution among 10 000 simulations.

Table II.

The proportion of 10 000 simulations where the K–S test of normality indicated evidence of a non-normal distribution of family risk score (α=0.05).

	Family size
Methods	6	8	10	12
SLFS (per cent)	0.3	0.7	0.3	0.3
Williams et al. (per cent)	99.7	70.9	33.6	11.1
Reed et al. (per cent)	1.4	0.1	0.1	0.1

Because of the frequently non-normal distribution for the family risk scores generated under Williams et al.’s approach [16], we assessed the strength of the relationship between each of the measures with the true family risk score U using the non-parametric Spearman correlation coefficient (ρ̂).

Type I Error

Based on 10 000 replications for each family size, the empirical type-I errors of finding significant ρ̂, the means and standard errors of the ρ̂ for each of the three methods are listed in Table III. Under the null hypothesis of no true family risk, the empirical type-I errors for all three approaches closely matched the nominal level of 0.05, and the average Spearman correlation coefficient was very close to 0.0 for all three methods.

Table III.

Type-I error for finding significant correlation and mean with standard error (s.e.) of the Spearman correlation coefficients ρ̂ between the true and estimated family risk scores under null hypothesis.

	Family size
Method	6	8	10	12
Type-I error
SLFS	0.052	0.053	0.047	0.049
Williams et al.	0.054	0.050	0.049	0.048
Reed et al.	0.054	0.051	0.048	0.050
Mean (s.e.) of the ρ̂
SLFS	0.0008 (0.0714)	−0.0001 (0.0720)	−0.0003 (0.0701)	−6 × 10−5 (0.0711)
Williams et al.	0.0004 (0.0714)	0.0004 (0.0714)	−0.0008 (0.0705)	−0.0003 (0.0706)
Reed et al.	−0.0007 (0.0714)	−0.0003 (0.0715)	0.0008 (0.0704)	0.0003 (0.0706)

Correlation between the true and estimated family risks and power under alternative hypothesis

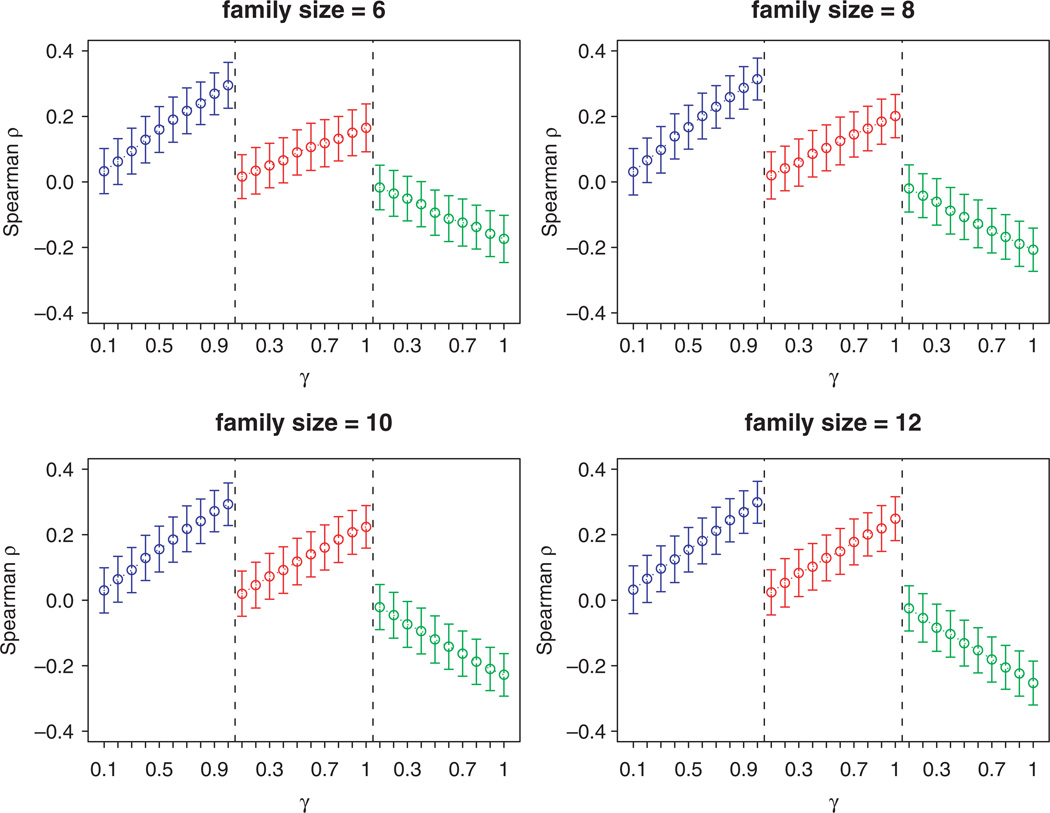
As the absolute value of γ increases, the correlation between an individual’s event and events of other family members increases. The goal of this section is to assess which of the approaches has the greatest power to detect the association between the true family score (U) and the estimated family history score. To test this, we fixed β₀ = 2, β₁ = 0.5, β₂ = 0.1 and let γ vary from 0.1 to 1. For any set of parameters, we replicated 1000 times. The Spearman correlation coefficients (ρ̂) between the estimated family risk scores and U, and their p-values are recorded. Figure 1 shows the mean and standard error bars of the ρ̂ and Figure 2 shows the power of the statistical test at α=0.05, defined as the proportion of simulations that found significant correlations.

Figure 1.

Mean (s.e.) of correlation coefficient between the estimated family risk score and the true family risk. β₀ = 2, β₁ = 0.5, β₂ = 0.1 (SLFS, Williams et al.’s family risk score, and Reed et al.’s are in the left, middle, and right panels, respectively and shown in blue, red, and green in the online figure.).

Figure 2.

Power to find significant correlation coefficients at the significance level of 0.05 and for varying family size (m) and family risk coefficients (γ).

As can be seen, regardless of family size and the magnitude of the true family risk (γ), the correlations with the true family risk was higher for our SLFS than for that of Williams et al. [16] or Reed et al. [21], and the corresponding power to detect associations with the true family risk was substantially higher (frequently as much as 20–30 per cent for moderate values of γ). In addition, while for both the methods of Williams et al. [16] and Reed et al. [21], the power to detect associations with the true family risk declined substantially with smaller family size, SLFS was relatively robust across the range of family sizes.

4. REAL DATA APPLICATION

To compare the performance of our SLFS method to that of Williams et al. [16] and Reed et al. [21] in real data, we used data from the REasons for Geographic and Racial Differences in Stroke (REGARDS) study, a national cohort study of individuals over age 45 years [29]. Recruitment began in January 2003 and was completed in October 2007. The individuals (probands) from commercial lists of residents in the 48 contiguous states were contacted by a combination of mail and telephone. For those agreeing to participate, demographic information, medical history, including prior diagnosis of high blood pressure, family history, and indices of cognitive function and quality of life were collected by computer-assisted telephone interview (CATI). Following the CATI, physical measures were collected at an in-home examination including height, weight, blood pressure, blood and urine samples, electrocardiogram, and an inventory of current medications. Also, a self-administered questionnaire was provided to each participant to collect the information on stroke and heart attack events of their parents and up to four siblings. As of June 2006, 22 927 participants had completed in-home visits, and 18 945 (83 per cent) participants returned the family history questionnaire through the mail. A total of 57 269 first-degree family members of 13 995 REGARDS participants have information available about the age at the onset of stroke or myocardial infarction (MI) events, age at death from other diseases, or age at the time of form completion without event. Informed consent was obtained from all participants, and the study was approved by the University of Alabama’s Institutional Review Board for human use.

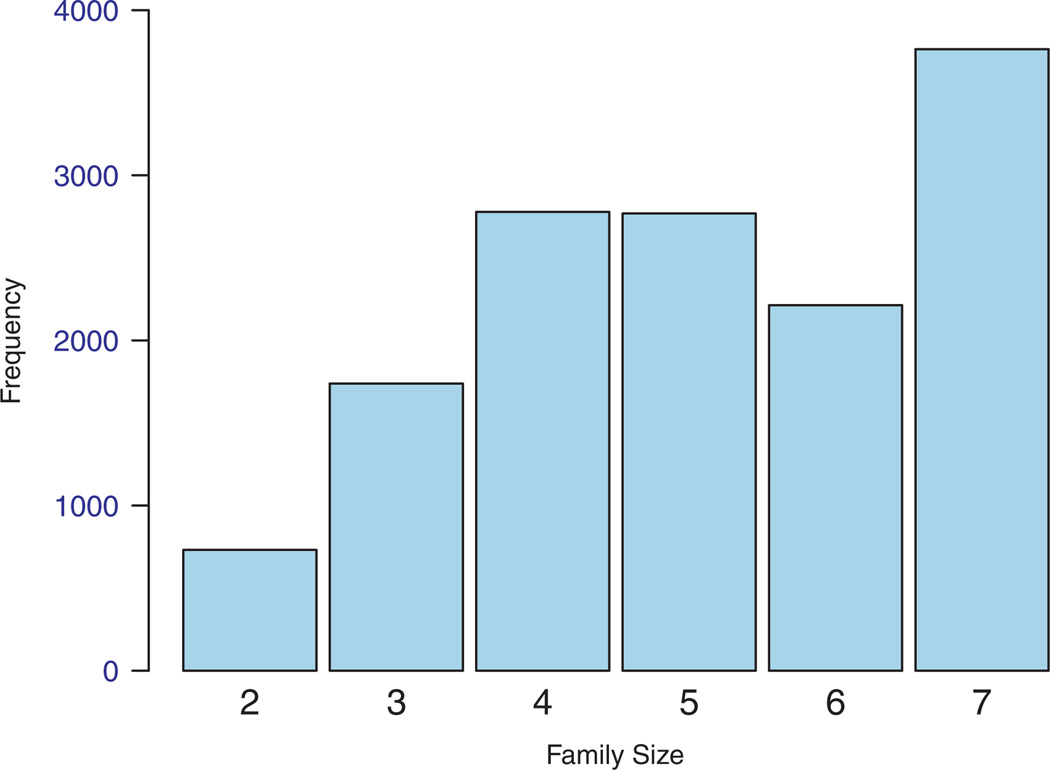
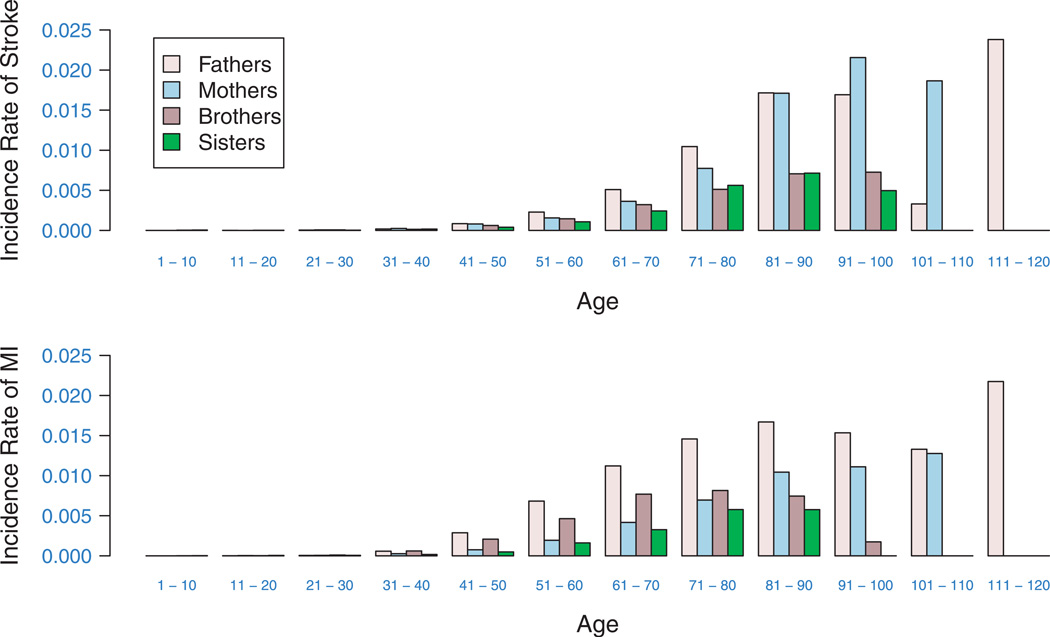
The family size ranged from 2 to 7 with a mean of 5.1. Figure 3 shows the distribution of the family size. Among all probands, 10 747 (46.88 per cent) were males and 12 176 (53.12 per cent) were females, 58.27 per cent were Caucasians and 41.73 per cent were African Americans. The average age of the proband was 66.0 (s.d.=9.12) years. Among other family members, 8148 people had MI with a mean age of onset of 64.5, and 5726 had stroke with a mean age of onset of 69.9 years. The risk of having MI and stroke is age and sex dependent, increasing at younger ages to peaks at older age, and then falling again with advancing age (Figure 4).

Figure 3.

Histogram of family sizes in REGARDS.

Figure 4.

10-year incidence rate (per person per year) of MI and stroke among different groups in REGARDS.

To compare the prediction using the family scores calculated by different methods, we first estimated the family risk scores using the information from available family members of the probands and then predicted the risk of prevalent MI and stroke events for the probands. We estimated family scores using our proposed SLFS, the methods of Williams et al. [16] and Reed et al. [21]. We then used a Cox regression model [30] to predict the risk of an event at the current age for each person in the test set, using family history score, cholesterol level, diastolic blood pressure (DBP), high-density lipoproteins (HDL), C-reactive protein (Crp), age, hypertension and diabetes status as predictors. We repeated the procedure for the two events of interest, MI and stroke, separately.

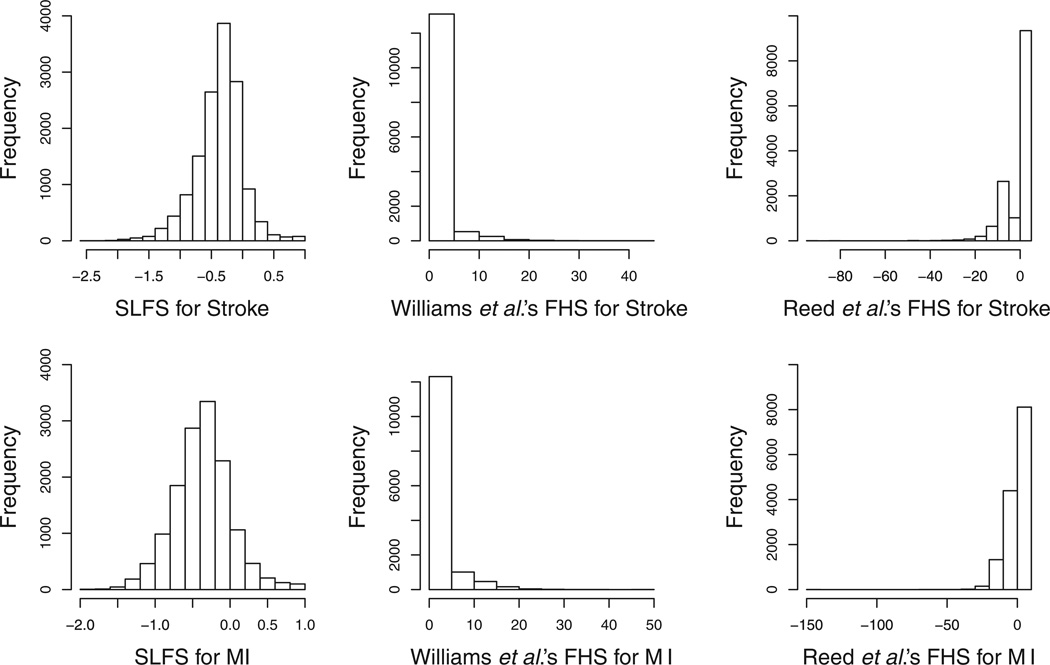
The distributions of predicted risk scores using three methods, SLFS and the methods of Williams et al. [16] and Reed et al. [21], are shown in Figure 5. The SLFS is normally distributed, but the family history scores from other two methods are highly skewed. To make the three methods comparable, we standardized these three family history scores by subtracting means and dividing by standard deviations.

Figure 5.

Histograms of family history scores for MI and stroke.

To have a benchmark for comparison, we also calculated a simple binary index defined as existence of affected first-degree relatives, which is often used as a family history measure in other studies. The results from the models with significant risk factors for two different events are shown in Table IV. The estimated family risk scores from SLFS, Williams et al. and Reed et al. are all significantly related to MI events; however, the direction of the effect of Reed et al.’s score is opposite to the direction of the effects of the other scores and the p-value from SLFS is slightly smaller than from Williams et al.’s. The estimated family risk scores from all three methods are highly significantly related to prevalent stroke events; however, the p-value of estimated SLFS is the smallest among all three. Using the SLFS and the family risk scores by Williams et al. [16] gave positive association between the risk for the event of interest and family history (risk ratio larger than 1), while using Reed et al.’s score [21] leads to negative association between the event risk and family history. The SLFS results in the largest association between the family risk score and the event of interest.

Table IV.

Hazard ratios (p-values) in Cox PH model using estimated family risk scores and other risk factors as covariates.

	Model with a binary family risk score	Model with SLFS	Model with Reed et al.’s family risk score	Model with Williams et al.’s family risk score
Event of interest: stroke
Family risk score	1.141 (1.2 × 10−1)	1.198 (1.2 × 10−5)	0.922 (1.3 × 10−2)	1.102 (8.3 × 10−4)
Cholesterol level	0.997 (2.2 × 10−2)	0.997 (2.0 × 10−2)	0.997 (2.0 × 10−2)	0.997 (2.1 × 10−2)
HDL	0.988 (2.5 × 10−5)	0.988 (3.8 × 10−5)	0.988 (2.8 × 10−5)	0.988 (2.6 × 10−5)
InCrp	1.066 (7.1 × 10−2)	1.061 (8.9 × 10−2)	1.064 (7.7 × 10−2)	1.065 (7.2 × 10−2)
Hypertension	1.972 (2.1 × 10−12)	1.920 (1.6 × 10−11)	1.961 (3.2 × 10−12)	1.960 (3.3 × 10−12)
Diabetes	1.778 (8.9 × 10−11)	1.751 (2.9 × 10−10)	1.769 (1.1 × 10−10)	1.765 (1.6 × 10−10)
Age	0.917 (<1 × 10−16)	0.923 (<1 × 10−16)	0.917 (<1 × 10−16)	0.917 (<1 × 10−16)
Event of interest: myocardial infarction
Family risk score	1.481 (7.8 × 10−10)	1.269 (5.3 × 10−15)	0.835 (<1 × 10−16)	1.188 (3.3 × 10−14)
DBP	0.992 (1.9 × 10−2)	0.992 (2.3 × 10−2)	0.992 (2.0 × 10−2)	0.992 (1.6 × 10−2)
Cholesterol level	0.991 (<1 × 10−16)	0.991 (<1 × 10−16)	0.991 (<1 × 10−16)	0.991 (<1 × 10−16)
HDL	0.978 (<1 × 10−16)	0.978 (<1 × 10−16)	0.978 (<1 × 10−16)	0.978 (<1 × 10−16)
InCrp	1.068 (2.6 × 10−2)	1.061 (3.1 × 10−2)	1.062 (2.8 × 10−2)	1.064 (2.3 × 10−2)
Hypertension	1.409 (2.3 × 10−6)	1.366 (1.0 × 10−5)	1.404 (3.1 × 10−6)	1.392 (5.5 × 10−6)
Diabetes	1.532 (1.8 × 10−9)	1.507 (7.5 × 10−9)	1.529 (2.3 × 10−9)	1.518 (3.9 × 10−9)
Age	0.975 (1.3 × 10−7)	0.982 (2.7 × 10−4)	0.976 (3.4 × 10−7)	0.974 (5.6 × 10−8)

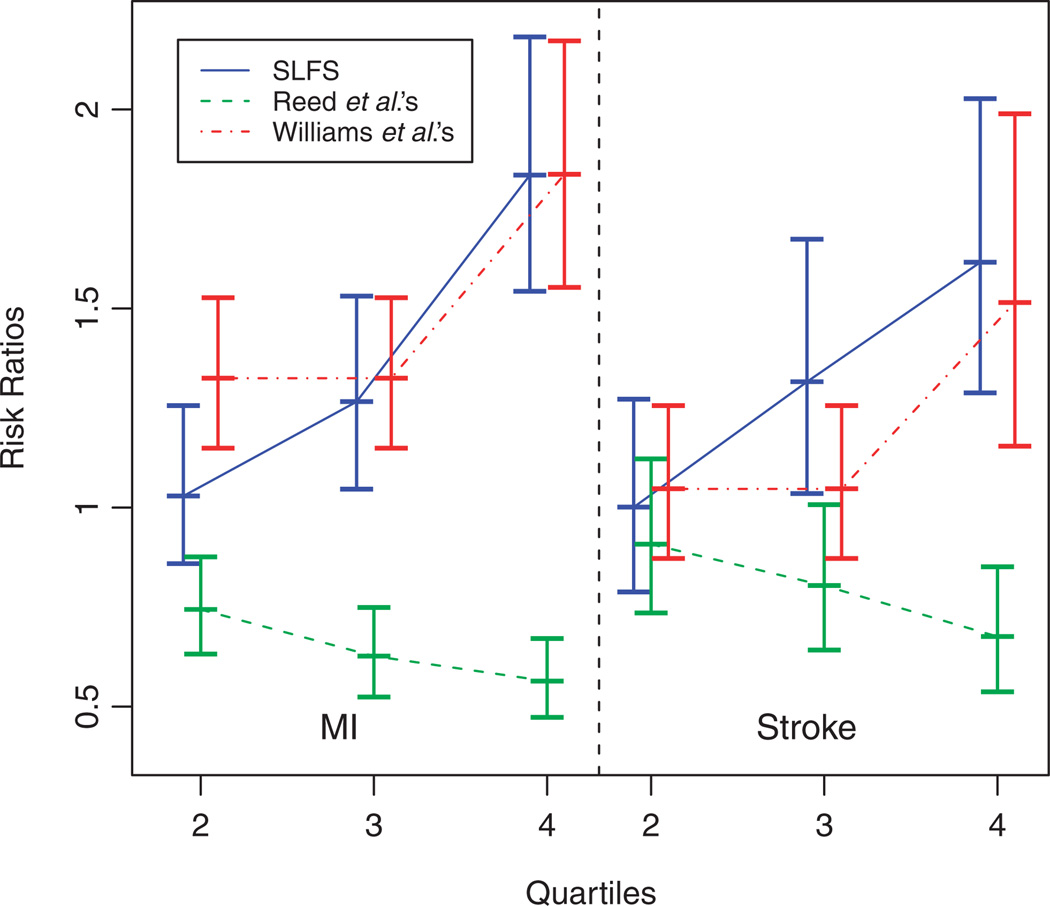
To assess the clinical importance of the choice of scoring methods, we fit additional Cox models using categorized FHSs by quartiles in addition to the significant risk factors listed in Table IV. The risk ratios of having MI or stroke for the other quartiles vs the first quartile of the family history score are shown in Figure 6.

Figure 6.

Effects of quartiles of family history scores on MI and stroke estimated from the Cox models. The effect estimates are connected for each method and vertical bars indicate the 95 per cent confidence intervals of the estimates.

The differences in risk ratios in quartiles are more significant and the linear trend in risk ratios with the increase of quartiles is more apparent using SLFS than the family risk scores by Williams et al. and Reed et al. Despite the significance of continuous family risk scores on MI and stroke, the difference between two adjacent quartiles may lose significance due to discretizing quantitative scores [31]. The lack of differences between lower quartiles for Williams et al.’s score and between higher quartiles for Reed et al.’s score resulted from their highly skewed distributions; thus, the family history scores within two adjacent quartiles cannot be discriminated well. But the overall trends are significantly increasing, which are consistent with other studies. Thus, we confirmed an important finding that family history is important in affecting both MI and stroke using REGARDS data, a study with a much larger sample size than other studies.

5. CONCLUSION AND DISCUSSION

Regardless of family size, the family risk score estimated by our proposed approach is more strongly related to the true family risk implying that our proposed approach has greater power than the other two. All three methods appear to have appropriate Type I error rates. In addition, while the power of both Williams et al. [16] and Reed et al. [21] methods substantially declines in analyses with smaller family sizes, the power of the proposed approach appears to be robust across the spectrum of family sizes considered in the simulations. Hence, the proposed approach appears well-behaved under the null hypothesis and provides greater power to detect associations with true underlying family risk across a broad range of alternative hypotheses.

The results from the real data application suggest that taking family history into account will improve the prediction of disease risk. Family risk scores estimated by all three methods lead to significant associations between the risk for stroke and family history; however, the directions and magnitudes of the association are different. There is a positive association between the heart disease risk and the family risk scores estimated by Williams et al. [16] and our method and the association from the model using SLFS is stronger than others.

Since the family sizes in REGEARD vary, we simulated data using the pedigrees in REGARDS to check Type I errors and power. We kept the family structure, gender and current age untouched and simulated the disease status and age onset based on an exponential model. Our finding is consistent with the results in Section 3.

Both Williams et al. and Reed et al.’s scores are based on observed and expected number of events with families and are close to asymptotic normal distributions when family sizes are large. But they are unavoidably sensitive to small families. In contrast, our SLFS is stratified on observed and censored events across all families [26] and is more sensitive to the number of families. But our SLFS is more robust across different family sizes when the number of families is large enough.

In this paper, we have described the family history score of an individual based on an un-weighted average of his first-degree relatives. Both the simulations and application used only small pedigrees composed of only first-degree relatives. However, our proposed SLFS can be easily extended to large pedigrees using kinship-coefficient-weighted average for pedigrees with more distant relatives and further investigation is warranted.

Our simulation study based on smaller families, with fewer than four offspring (other parameters are the same as above) showed consistent results to those in Section 3. However, for smallest families that include one or no offspring, the correlation between the estimated family history scores and the true family risk score is highly variable due to the high influence of a single individual. Careful scrutinization is needed to apply any family history measure to such small families.

Our method may be helpful for clinicians to screen people with family history of disease. To fully utilize this score, clinicians would need to collect the age of onset for each first degree relative that is affected. Ideally, a clinician can estimate the family history score using the data provided by individuals and a risk ‘calculator’ (i.e. a₁ and a₀ in our notation) for different generation, age and sex groups already calculated from a reference population, such as REGARDS pedigrees, similar to risk calculators already available in other areas. However, this might not be practical without a convenient software or some basic training in statistics.