A critique of statistical hypothesis testing in clinical research

Abstract

Many have documented the difficulty of using the current paradigm of Randomized Controlled Trials (RCTs) to test and validate the effectiveness of alternative medical systems such as Ayurveda. This paper critiques the applicability of RCTs for all clinical knowledge-seeking endeavors, of which Ayurveda research is a part. This is done by examining statistical hypothesis testing, the underlying foundation of RCTs, from a practical and philosophical perspective. In the philosophical critique, the two main worldviews of probability are that of the Bayesian and the frequentist. The frequentist worldview is a special case of the Bayesian worldview requiring the unrealistic assumptions of knowing nothing about the universe and believing that all observations are unrelated to each other. Many have claimed that the first belief is necessary for science, and this claim is debunked by comparing variations in learning with different prior beliefs. Moving beyond the Bayesian and frequentist worldviews, the notion of hypothesis testing itself is challenged on the grounds that a hypothesis is an unclear distinction, and assigning a probability on an unclear distinction is an exercise that does not lead to clarity of action. This critique is of the theory itself and not any particular application of statistical hypothesis testing. A decision-making frame is proposed as a way of both addressing this critique and transcending ideological debates on probability. An example of a Bayesian decision-making approach is shown as an alternative to statistical hypothesis testing, utilizing data from a past clinical trial that studied the effect of Aspirin on heart attacks in a sample population of doctors. As a big reason for the prevalence of RCTs in academia is legislation requiring it, the ethics of legislating the use of statistical methods for clinical research is also examined.

INTRODUCTION

Randomized controlled trials (RCTs) have long been the dominant method of clinical scientific inquiries. With the emergent interest to mine the wisdom of Ayurveda in a modern scientific context, research scholars have started designing RCTs to validate Ayurvedic knowledge and bring it to the mainstream. While the intent of bridging the gap between Ayurveda and modern medicine is laudable, the means of investigation merit more scrutiny, in the light of six decades of severe criticism that has been brought to bear upon the statistics that support RCTs. This scrutiny is particularly important as thought leaders, while making a justifiable call to use Ayurvedic epistemology as the basis for Ayurveda research,[1–3] have so far operated on the assumption that clinical research using statistical hypothesis testing has some value in its own context.

The object of this paper is to give Ayurveda's clinical researchers some pause by challenging the holy cow of statistical hypothesis testing from practical and philosophical perspectives. We will examine two major worldviews of probability – the Bayesian and the frequentist – and present a simple model to show how learning differs given a change in our prior beliefs. We have presented a new perspective in clinical research – that of making decisions, by borrowing distinctions from the field of decision analysis (DA),[4] a philosophy of decision making that helps us get to clarity of action. From this perspective, it will be shown that the distinction of a “hypothesis” is unclear, and hence, placing a probability on such a distinction is devoid of meaning as it is not actionable, regardless of whether one wants to be a frequentist or a Bayesian.

Finally, since clinical research is deeply influenced by public policy, we also present ethical decision-making perspectives that are currently missing in utilitarian public policy discourse.

PRACTICAL PROBLEMS WITH STATISTICAL HYPOTHESIS TESTING

Feynman notes that the first value of science is that it produces results,[5] and we might perhaps restate that value as that of practicality. Using that yardstick, we realize that statistical hypothesis testing is impractical at many levels.

First, the language of statistics is routinely confusing and misleads researchers. For instance, both “significance” and “confidence” do not mean what they normally do in English. Statistical significance has no meaning beyond a probability statement that the chance of seeing results like the one we are seeing is below 5% at the 95% confidence level, provided the null hypothesis holds. Not surprisingly, due to the overloading of a common English word, results that are significant get more attention in journals.

Confidence intervals have nothing to do with confidence and it is easy for people to make the mistake of thinking that a 95% confidence interval implies a 95% chance that the quantity of interest lies in the interval. The classical statistician is quick to correct such misconceptions in class, explaining that if we were to construct the same interval for thousands of tests, then 95% of the time, the true value of the quantity would lie within this interval. Since 95% is not a probability that we are expressing, the second practical problem with this method is that we do not know how to use the results of statistical hypothesis testing to make decisions.

Although confidence intervals do not allow us to use the interval directly, one last resort is in aiding our learning after our experiments are done by updating our confidence interval. This is when the classical statistician would sternly remind us that updating the interval is an illegal operation and amounts to tampering. We need to throw away all of our hard-won data, and construct a new confidence interval for a new study. Therefore, the third practical problem with confidence intervals is that it does not allow the updating of beliefs.

The fourth practical problem is that the conditions that are necessary for us to apply classical statistics require extremely strong assumptions that we would be hard-pressed to justify, namely, we know nothing about our universe and everything is unrelated to everything else.

The fifth practical problem, also alluded to earlier, is a missing focus on individual decision making. How does knowing an average effect at the level of a population help us get to clarity of action on treatment of an individual? The sixth practical problem is that of incentive bias, demonstrated by Cook's slightly exaggerated example.[6] Suppose a hypothesis is untrue, then going by the 95% significance logic, 50 out of 1000 studies will erroneously show statistical significance. Unfortunately, these are the studies that will end up being published while the 950 that did not find significance will tend to get ignored by journals, thus amplifying random noise.

Cohen[7] traced the history of criticism like this surfacing time and time again. He notes:

David Bakan said back in 1966[8] that his claim that “a great deal of mischief has been associated” with the test of significance “is hardly original,” that it is “what ‘everybody knows’,” and that “to say it ‘out loud’ is…to assume the role of the child who pointed out that the emperor was really outfitted in his underwear”. If it was hardly original in 1966, it can hardly be original now. Yet this naked emperor has been shamelessly running around for a long time.

While these problems have been known for decades, the evidence of coming up with bogus theories with such flawed methods is finally presenting itself in medical science. A recent study by Ioannidis[9] reported that 32% of “gold-standard” studies were either contradicted or had reported effects that were stronger than those of subsequent studies. The peculiar phenomena of established results in medical science and psychology becoming harder and harder to replicate, eventually being overturned, has been investigated by some in the popular media like Lehrer,[10] who notes that psychologists have labeled this phenomena the “decline effect.” Both Ioannidis and Lehrer note the incentive bias and the practical problems with statistics as the main causes.

PHILOSOPHICAL PROBLEMS WITH STATISTICAL HYPOTHESIS TESTING

In an unknown time, the Indian god Karthik challenged his reserved brother Ganesh to a contest that involved circumambulating the earth three times, and deputed their parents as judges. No sooner had Ganesh accepted the challenge that Karthik jumped on his vehicle, zoomed off and returned in record time. The pot-bellied Ganesh merely circumambulated his parents three times and declared victory by noting, “I have circled my world three times.” Not surprisingly, the parents judged him the winner.

This mythical story illustrates two distinct worldviews. In Karthik's view, there is a world “out there” that exists objectively. In Ganesh's view, the world is constructed within through perception, and hence exists as a subjective experience. Karthik could be the god of the classical school of statistics, referred to as the “frequentists” for their view of probability as a frequency to be found in past data. Ganesh could be the god of a smaller but older school of statistics, referred to as the “Bayesian” school, after Thomas Bayes (of Bayes’ theorem fame), that does not impose such a restriction and allows beliefs about the future to be used to assign probabilities. Although Ganesh is widely regarded in India as the wiser god and the one whose view ultimately prevails, the story is far more murky in the world of science.

It turns out that the Bayesian view of probability being a measure of belief (and not a frequency derived from past data) was the original view of probability, brought about by Thomas Bayes who showed in a paper read out in 1763 (2 years after his passing) that “probability had epistemological power that transcended its aleatory uses.”[11] In plainspeak, probabilities come from individuals and not from a deck of perfectly shuffled cards or fair coins. In this worldview, I am not limited to believing that the chance of getting a heads on a coin toss is 50-50. In real life, there are no perfectly shuffled decks and fair coins, and therefore, an epistemological or Bayesian view is far more inclusive of practical reality than an aleatory or frequentist view.

The Bayesian worldview allows us to become frequentists if we so choose, for ultimately, the individual is the source of validity of a belief. As a Bayesian looking at frequentism, the question to be asked is, “what do I need to believe to become a frequentist?” I need to believe that “I know nothing about the universe” and “everything I see is unrelated to everything else.” While it is easy to challenge the second assumption, some scientists claim that the first assumption of total ignorance is necessary to pursue science. However, a simple examination of probabilistic inference reveals that our learning (posterior probability) depends on our prior probability and likelihood.

For example, consider a doctor who believes that smoking is relevant to lung cancer given that most of her lung cancer patiens have been smokers. She uses this information to assign a 95% likelihood to a person being a smoker, given that this person has lung cancer. For the likelihood of a person being a smoker, if he or she does not have lung cancer, she declares, “I believe that such a person is equally likely to be a smoker or a non-smoker.” Finally, she refers to her country's census on the number of people with lung cancer and decides to assign a 5% prior probability of someone in the population having lung cancer (Figure 1a shows these assessments). By applying Bayes’ rule, we can now infer that her probability of someone getting lung cancer given that he or she smokes is 9.1%, as compared to a 0.52% chance of getting lung cancer given that the person does not smoke (an over 17-time increase in probability; Figure 1b shows our inference after the application of Bayes’ rule).

Figure 1.

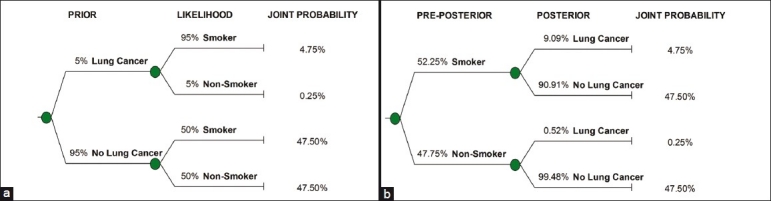
(a) Prior and likelihood shown in the assessed probability tree. (b) Preposterior and posterior shown in the inferred (or flipped) probability tree

We can now examine learning, which we will denote by the posterior probability of someone having lung cancer given that this person is a smoker. Figure 2 demonstrates that we learn differently depending on our priors, and it is clear that if the doctor artificially takes a position of ignorance (or a 50% prior), she will end up with a much larger posterior (66% chance of lung cancer given smoker) than the one implied by her actual position of a 5% prior (9% chance of lung cancer given smoker).

Figure 2.

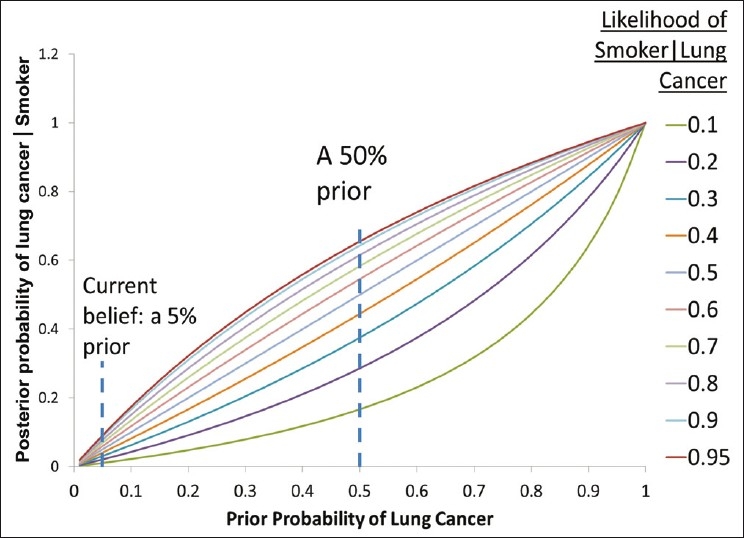
We note that our learning, represented by the posterior probability, varies with our prior beliefs. In this example, P (Individual is a smoker given that individual does not have lung cancer) was set at 50%

Explicitly stating and challenging our starting position of total ignorance can help us avoid distorted results that are not consistent with what we know. A position of total ignorance is just as subjective as a position of some knowledge, and pretending otherwise in the pursuit of objectivity makes us believe in results from the former position more than results from the latter.

By desecrating the holy ground of objectivity with our subjective inclusions, the question arises, “What should be our yardstick for scientific validity?” The decision analyst, standing on a firm Bayesian foundation, would propose “the truth about what you believe,” and not “what's objectively so.”

POPULAR CRITIQUES OF THE FREQUENTIST WORLDVIEW

Cohen[8] takes the Bayesian mindset to point out an embarrassing associative logic error made by the frequentists – they wish to infer about the chance of a hypothesis being true given the data is true, but instead report the opposite – the chance of the data being true given the hypothesis is true. To illustrate this problem with a simple example, consider that virtually all hemophiliacs are male, but very few males are hemophiliacs. We would make a big error of logic if we conflated the two in assigning probabilities.

More damningly, Cohen points out[9] that if there's even a small chance of the null hypothesis being false, with a large enough sample, the results of an experiment will be significant and the null hypothesis will be rejected. If the result of our test is always known for large datasets, then such experiments are useless. And when we do not have lots of data, the methods break down and are not applicable, thus proving useless again.

Ioannidis[12] takes a senstationalist stance with a paper titled “Why Most Published Research Findings are False” and demonstrates with an elegant Bayesian model that it is highly improbable that the method of statistical hypothesis testing will produce results that are more likely to be true than not. He does so by going beyond the so-called Type-1 error (the chance of a false positive) and incorporating “Type-2” errors (the chance of a false negative). In explaining a corollary titled “the hotter a scientific field (with more scientific teams involved), the less likely the research findings are to be true,” he writes:

With many teams working on the same field and with massive experimental data being produced, timing is of the essence in beating competition. Thus, each team may prioritize on pursuing and disseminating its most impressive “positive” results. “Negative” results may become attractive for dissemination only if some other team has found a “positive” association on the same question. In that case, it may be attractive to refute a claim made in some prestigious journal. The term Proteus phenomenon has been coined to describe this phenomenon of rapidly alternating extreme research claims and extremely opposite refutations. Empirical evidence suggests that this sequence of extreme opposites is very common in molecular genetics.

Ironically, Ioannidis has himself gone for an extreme viewpoint, illustrating the Proteus phenomenon. While his conclusions have stirred the hornet's nest, and although his criticisms of frequentist methods, like Cohen's central arguments, are very tempting, they are nonetheless problematic and have not received the scrutiny that should have been forthcoming. We shall next present our own critique using the concepts of DA of the frequentist method and use our approach to also critique Ioannidis and Cohen's critiques.

CAN A HYPOTHESIS BE A CLEAR DISTINCTION?

Before we examine whether a hypothesis can be a clear distinction, we need to first understand the concept “distinction” itself. Howard writes:

A distinction describes a characteristic like a person's sex or the weight of a table. These would be two different kinds of distinction. A distinction can have two or more degrees: The sex of a person has two degrees – male and female on a driver's license, or 32 degrees according to the last conversation I had with a geneticist. Similarly, the weight of a table can have two degrees – like more than or less than 100 pounds – or many degrees corresponding to each pound of weight. The creation of distinctions and the definition of the number of degrees is an inventive act of the author of the characterization.[13]

Howard goes on to discuss distinctions on distinctions, such as clarity, observability, usefulness, possibility trees, probability, relevance, measures and distributions.[13] Of these, we will concern ourselves with the first – clarity. In order to know whether something is clear, decision analysts invoke an imaginary clairvoyant, who can tell us about anything that is physically determinable in the past, present, or future, as long as it does not involve any judgment in it. For instance, whether it will rain tomorrow can only be answered by the clairvoyant if we first define an acceptable standard for “rain” (e.g., at least 5 mm of rainfall) and an acceptable range for “tomorrow” (e.g., between 12:01 AM and 11:59 PM). The process of establishing the standards for what we mean results is what we call a “clarity test.” The clairvoyant cannot answer whether something will be good for us, for “good” would not pass the clarity test. The clairvoyant also cannot tell us what we will do in the future, for that would violate our free will. The clairvoyant can however tell us what others might do, if we can ask the question in a manner that passes the clarity test.

The purpose of the imaginary clairvoyant is to help us establish a clarity test. A clarity test is established when all members of the decision conversation are clear on what the distinctions mean. This helps us avoid placing probabilities on distinctions that are unclear. Distinctions do not have to be observable unless the resolution of a future decision depends on observing them. By limiting the clairvoyant to physical reality, we avoid a fundamental mistake in the form of the question, “What is the chance that this model is valid?” The clairvoyant cannot tell us whether a model is valid, as models do not exist in his/her world.

By implication, probabilities do not exist in the clairvoyant's world; only facts do. This implies that we cannot have distinctions with a notion of probability built into them. Cohen and Ioannidis violate this principle in their critiques, by trying to determine the chance that a hypothesis is true, when the distinction “hypothesis A is true” does not pass the clarity test, and a probability on such an unclear distinction is also unclear. The intent behind the clarity test is to distinguish between the map and the territory, for the map is not the territory. The clairvoyant can only answer questions on the territory, not on the map.

To illustrate, the clairvoyant cannot tell us whether the hypothesis “smoking causes lung cancer” is true, because this is a model of causality, and has no reality in the clairvoyant's fact-driven world. However, we could ask the clairvoyant if someone has lung cancer, provided there is clarity on what “lung cancer” means. The clairvoyant can also tell us if someone is a smoker, after clarifying what we mean by “smoker.” We may now assert relevance between smoking and lung cancer by specifying joint distributions (the chance of both happening together). If we know one of the individual distributions, using the joint, we can find the distribution on the other distinction – this is what we mean by inference (as demonstrated in the smoker-lung cancer example). There is nothing in our inferential process that comes from outside our inputs.

The clairvoyant and the clarity test are potent tools in our examination of any theory that engages with probability. From this perspective, the paradigm of statistical hypothesis testing is a nonstarter as hypotheses are about causal models in our head and can never pass the clarity test.

HOW SHOULD WE FORM BELIEFS?

If we have no decision to make and are only interested in inferences, then we have no need to worry about what we believe. We should be happy to start with a prior belief and our likelihood distributions, and keep updating the prior based on what we see. We can throw away our prior and start again, as we like. There need for rigor arises only if there is a decision to be made.

To make a good decision, in addition to using reliable information, we would also wish to know how sensitive our decision is to the information at hand. For instance, someone facing terminal cancer may find a treatment option with a 50% chance of success acceptable, whereas, a healthy person facing a procedure with a 5% chance of dying may find it too risky. Our decision-making method should be able to handle different preferences and lead to clarity of action.

We should be able to test sensitivity to our preferences as well. The question is not just about how we form our beliefs, but about how we form our beliefs in the context of what we value. In this regard, Howard's work on inference with a decision-analytic approach[14] provides much guidance. We shall illustrate this with an example, borrowed from a Harvard study on aspirin and heart attacks.[15,16] A total of 22,071 subjects (volunteer doctors) were randomly assigned to two groups. One group was given a placebo, while the other was given aspirin. They were observed for 5 years, and the results of that observation are shown in Table 1.

Table 1.

Data from the aspirin study

Using the classical statistical methods, we would typically set up a null hypothesis (H0) as “aspirin has no effect: P1–P2=0” and the alternate hypothesis (H1) as “aspirin does reduce the heart attack rate: P1>P2.” After performing the customary calculations, we end up rejecting the null hypothesis and this result is statistically significant. How do we use this to make decisions? There is no further guidance in the world of classical statistics. We shall next examine how a Bayesian approach (that does not involve placing a probability on a hypothesis) can be used to arrive at a clear decision for experiments where we believe that every observation is irrelevant to every other observation. Our first task is to define clear distinctions. We will need to start by defining the distinctions: “person gets a heart attack within 5 years (yes/no)” and “treatment (aspirin/placebo).” If we were to treat the next subject getting a heart attack within 5 years akin to a coin landing heads, then we can define “φ” as the long-run fraction of heads that would be observed in a very large number of tosses of the coin.”[14] We note that these distinctions have been defined wihtout a trace of uncertainty, and can be clearly posed to a clairvoyant to yield factual answers. We shall initially assume that we know absolutely nothing about φ in both the aspirin and non-aspirin populations, and represent such a position with a uniform prior using the beta (r = 1, n = 2) distribution [Figure 3]. The probability of the next toss in the binomial trial landing heads (or the subject) is given by the mean of the distribution (for beta distributions, mean = r/n), which is 0.5 in our example. Using this setup, we can use Bayes’ theorem to infer the new (or posterior) distribution on φ given the number of heads we have seen. The beta distribution has the neat feature of producing posterior distributions from binomial trialswhich are also beta distributions, and such beta-binomial models may be used for experimentation.[14] The resulting posterior distribution can be obtained through a simple addition operation on the distribution parameters. We can now update the beta distributions as follows:

Figure 3.

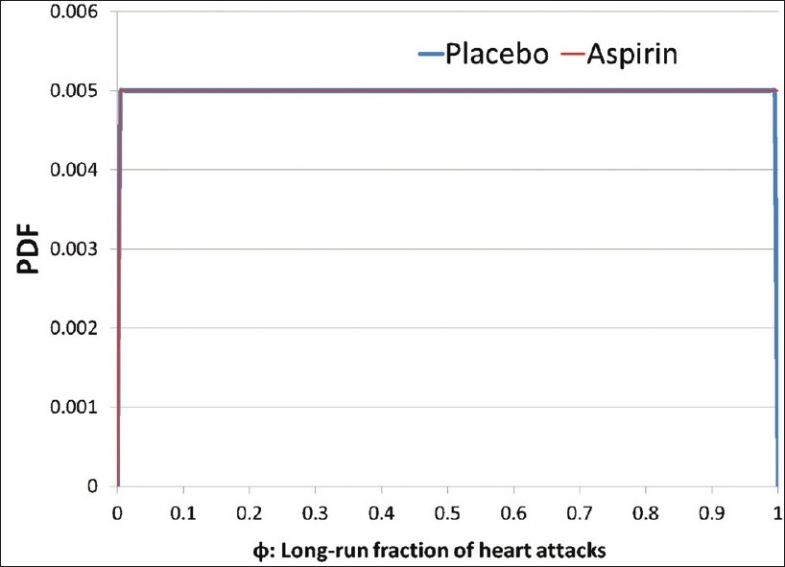
Identical uniform priors placed on the long-run fraction of heart attacks for both the placebo and the aspirin samples

• Placebo: Beta(1+239,2+11034) = Beta(240,11036)

• Aspirin: Beta(1+139,2+11037) = Beta(140,11039).

Examining the resulting posteriors [Figure 4a], we find the two updated distributions to be very close to each other. Since we have renounced the notion of significance, we can now comfortably say that they look quite similar, while keeping in check our tendency to exaggerate the difference by zooming in on the x-axis [Figure 4b].

Figure 4.

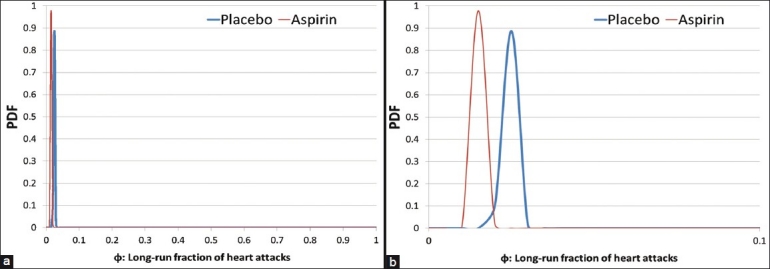
(a)Posterior distributions resulting from the aspirin study. (b) Posterior distributions with exaggerated differences by zooming the x-axis

We can now test how we might learn differently if we selected different priors using different parameters for our starting beta distributions. For large samples like those in this study, it does not matter which priors we pick, for we will get very similar posterior distributions with these observations. We could stop here if our objective was just to learn and not make any decisions. One might object and ask what the point of this exercise was if we could not conclude which effect is stronger. Such an objection can be easily met with the response that we know of no sensible method that can tell us what effect is stronger, as we do not know how to define “stronger.” There is no point using classical statistical methods that pretend to offer such guidance when they don’t.

As decision makers however, we are not content with being unable to do anything with our inference, and this is where decision analysis steps in. To demonstrate, we will model a patient's decision on whether to take an aspirin or a placebo treatment, using the posterior distributions obtained above. To assess the patient's disvalue on getting a heart attack, we may ask, “If you were to get a heart attack right now, and a wizard could cast a spell to protect you from getting one, what is the most you would be willing to pay the wizard to cast their spell?” This is the amount that this person can muster, not just with his or her current resources, but also by borrowing from friends and family, if necessary. Suppose this amount were assessed at $1 million. Next, we would need to assess the patient's preferences on avoiding the side-effects of aspirin, with a question that might look like: “If you had to spend the rest of your life with the effects of heartburn, nausea, or an upset stomach, what would you pay to avoid such a life?” We would add to this the cost of aspirin over the timespan of our decision. Suppose this were assessed at $10,000. By assuming a risk-neutral decision maker, we can calculate the value of each alternative (placebo and aspirin) by multiplying the mean of each posterior with the corresponding dollar valuations, and picking the lower loss amount. In the example where we started with a uniform prior, Value_placebo = –$22,228 and Value_aspirin = –22,844, implying that the patient should prefer the placebo. Moreover, we find that the patient must value the inconvenience caused by aspirin below $9385 in order to prefer aspirin. We can also attempt to check if the decision changes with different priors. For instance, setting the cost of inconvenience caused by aspirin back at $10,000, if r and n were set up to be 5 and 100, respectively, for the placebo case (or a 0.05 chance that the next placebo taker would have a heart attack over the next 5 years), and 1 and 100, respectively, for the aspirin case (or a 0.01 chance that the next aspirin taker would have a heart attack over the next 5 years), we find that the patient should still go with the placebo (with a value of –$22,396) and not aspirin (with a value of –$22,730; Figures 5 and 6).

Figure 5.

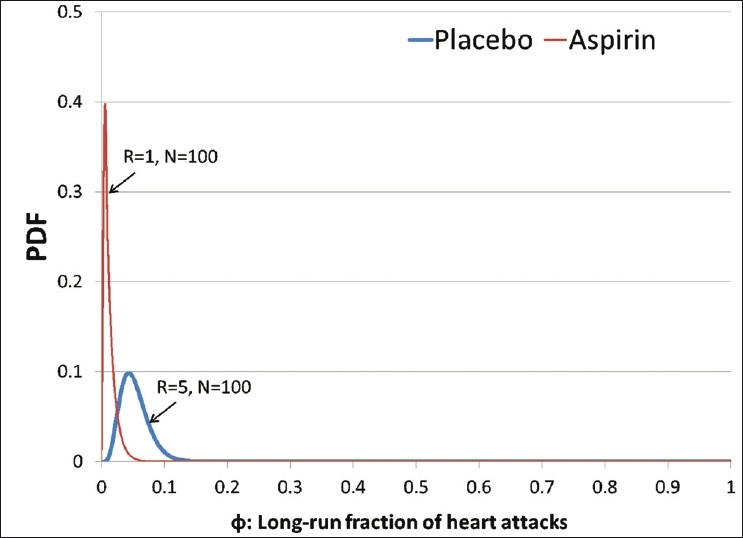
A prior expressing initial beliefs about the distribution of heart attacks for the placebo and aspirin

Figure 6.

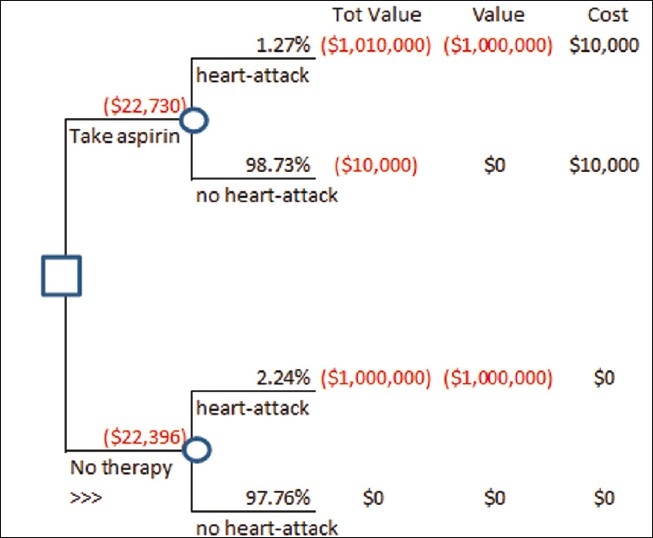
A decision tree modeling the decision to take aspirin with inputs from Figure 5

This example is simplistic, and to improve it, we might consider:

• Assessment biases that have been well reported in the literature[17][18]

• Uncertain side-effects

• Risk-aversion of the decision-maker

• Modeling preferences involving death or disability with micromorts[19][20]

At this point, we would do well to remember that the clairvoyant cannot tell us if this is the right model to use. Upon using this beta-binomial model, as we see more and more data, our confidence will increase, leading to a narrower distribution (as evidenced by our example). A point will come when, to learn anything, we will need a massive amount of experimentation, and this will bring us to acknowledge the practicality of emptying our cup by forgetting some data in order to continue to learn. How much to forget in such models is more in the realm of art than science.

Finally, our tendency to break things into smaller parts without keeping the whole in mind will continue to haunt us even in the Bayesian worldview. There is no substitute for holistic thinking. The tendency of reducing humans to mere mechanistic particles is a product of the industrial revolution, as pointed out by Abraham Maslow.[21] This is unlikely to yield practical insights of a holistic being that is far more than the sum of its parts.

LEGAL AND ETHICAL PROBLEMS WITH STATISTICAL HYPOTHESIS TESTING

As medical decisions may often result in harm to humans, we need to give them due ethical consideration. The gold standard of statistical hypothesis testing involves double-blind studies, wherein, researchers do not inform the caregiver whether the treatment given is for real or a placebo. Such a protocol violates the freedom of individuals under treatment to take their own risks upon full disclosure, and ends up being unethical if our ethical code prohibits deception.

Even if we engage in RCTs without getting into double-blind studies, the calculation of statistical significance involves the computation of the Type I error (the chance that the effect we see is produced randomly) and as long as this error is below 5%, the result is claimed to be statistically significant. Notwithstanding our earlier arguments that the entire setup violates the clarity test, if indeed the chance of being incorrect were 5%, it is still an ethical violation for researchers to decide that this is significant and acceptable for individuals. To bring this home, Professor Ronald Howard would often state in his advanced DA class at Stanford University, “If there were a crazy gunman outside this building, and I was told that there's a 5% chance I could be shot upon venturing out, I would do everything in my power to remain indoors until the situation was resolved.”

Since these critiques are hardly new, why didn’t the scientific community move to more sensible methods of research? If we had to put our finger on why we choose to follow methods of research that we do not agree with either prudentially or ethically, beyond the culture of journals, we may find that it has something to do with the regulatory reach of national health bodies. Clinical testing with statistical significance is still required by the Food and Drug Administration (FDA) in the United States. If most of our research scientists engaging with such methods are unaware of the underlying problems, how can we expect any sensible regulation out of this?

Only in 2010, the FDA has issued guidelines for using Bayesian methods in clinical trials.[22] While these guidelines are nonbinding and maybe considered a step forward (notwithstanding the issue of continuing to violate the clarity test), they only tackle the minor premise of finding the method of clinical research that is most sensible and encouraging it through regulation, while ignoring the major premise, that health regulation on clinical research is sensible in the first place.

The efficacy of regulation has only been discussed in comparison with alternatives that are labeled as “do nothing.” This deliberate mischaracterization of voluntary action has led us away from a healthy dose of skepticism and toward an excessive trust of institutions far beyond what they deserve. As Taleb points out, we can never really be ready for “black swans,”[23] but we can lessen the impact by investing in diversity. Diversity can be easily supported by not doing anything to stop different research methodologies from sprouting.

Moreover, if there is indeed a public outcry due to a tragedy, then one wonders why a voluntary standards body could not do the job by publishing nonbinding guidelines similar to what the FDA has finally done. Such a body would only give its approval under its own guidelines, without obligating all to follow its philosophy. There could be multiple standards bodies trying out different philosophies of research methods, as opposed to the current scenario where we are putting all our eggs in one basket with one school of thought. If that method turns out to be incorrect, as we now have increasing evidence to believe, an entire body of work will be invalidated. In this paradigm, decision-making power would be returned to the people, and they would exercise their choice of standard with their patronage.

The neglect of voluntary social systems in current public policy analyses borders on malpractice owing to the ethical implications of resulting decisions. For instance, in a report that is quite vocal in its advocacy for regulation by 2011 of all herbal medical systems (including Ayurveda), the Herbal Medicines Advisory Committee in the United Kingdom openly admits:

(Question) Given the Government's commitment to reducing the overall burden of unnecessary statutory regulation, can you suggest which areas of healthcare practice present sufficiently low risk so that they could be regulated in a different, less burdensome way or de-regulated, if a decision is made to statutorily regulate acupuncturists, herbalists and traditional Chinese medicine practitioners?

(Response by the committee) We do not have any suggestions in relation to this.[24]

Reports like this suffer from a low-quality decision-making style called "advocacy-driven decision making," that has long been decried in DA, offering instead the six elements of decision quality.[25] Spetzler, et al. point out:[26]

This advocacy/approval process is fundamentally flawed. If you only function in an approval role, you cannot vouch for the quality of a decision. How can you meet your responsibility and be accountable if you lack the background necessary to judge the quality of the decision? To reach a quality decision one must meet six basic requirements: An appropriate frame for the decision; creative, doable alternatives; meaningful, reliable information; clear values and trade-offs; logically correct reasoning; and the commitment to act. The most common violation of these requirements is the absence of alternatives.

Although this was written for corporate boards, the wisdom of the six elements of decision quality in public safety decisions is even higher.

DISCUSSION

While mainstream scrutiny and criticism of RCTs[27] and their underlying mathematical foundations[12] has been increasing, and scholars have attempted to re-examine the frequentist worldview from a Bayesian perspective, the fundamental notion of needing clear distinctions before we can place probabilities on them has been missing in the clinical research discourse. This idea, borrowed from DA, immediately stands to reason, for it prevents circular logic. By implication, we cannot place a probability on our hypothesis being right, for the hypothesis does not exist in the world of fact. Unless this fundamental objection can be addressed, the method of statistical hypothesis testing can no longer be claimed to be a scientific method.

One may question why statistical hypothesis testing continues to be used as a method of scientific research when there are better alternatives. Rawlins examines a variant of this question by tackling why Bayesian methods are not more common in clinical testing.[27] He cites a distaste of subjectivity, perceived difficulty in establishing priors, computational complexity, lack of exposure, unwillingness to learn, and lack of regulatory support. On computational complexity, this paper shows examples that have simple joint probability calculations (smoking–lung cancer example) and beta distribution updating (simple addition operations on the parameter) that are nowhere as complex as calculations needed for statistical hypothesis testing. Rawlins’ other reasons are valid, and perhaps the most insidious reason for the current state of affairs is the lack of exposure and unwillingness to learn.

While an attempt to undertake clinical investigations of Ayurveda in a Western paradigm should be welcome, statistical hypothesis testing is an unfortunate proxy for the Western paradigm of prospective testing. Research methods should be chosen not because they are dominant, but because they give value to the researcher in clarifying thoughts about action. In this regard, Ayurveda researchers might find it more fruitful to engage with the Bayesian paradigm in the context of decision making, utilizing the notion of relevance between distinctions to represent hypotheses. The limitation of Bayesian models should also be recognized in that we can never know which model is right. We would do well to heed Jaynes, who remarked:[28] Let me make what, I fear, will seem to some a radical, shocking suggestion: The merits of any statistical method are not determined by the ideology which led to it. For, many different, violently opposed ideologies may all lead to the same final “working equations” for dealing with real problems. Apparently, this phenomenon is something new in statistics; but it is so commonplace in physics that we have long since learned how to live with it. Today, when a physicist says, “Theory A is better than theory B,” he does not have in mind any ideological considerations; he means simply, “There is at least one specific application where theory A leads to a better result than theory B.” I suggest that we apply the same criterion in statistics: The merits of any statistical method are determined by the results it gives when applied to specific problems. The Court of Last Resort in statistics is simply our commonsense judgment of those results.

Note: The inference model used in the Aspirin example may be downloaded from:

http://www.stanford.edu/~somik/research/papers/BETA.xlsx