Analysis of Ratios in Multivariate Morphometry

Abstract

The analysis of ratios of body measurements is deeply ingrained in the taxonomic literature. Whether for plants or animals, certain ratios are commonly indicated in identification keys, diagnoses, and descriptions. They often provide the only means for separation of cryptic species that mostly lack distinguishing qualitative characters. Additionally, they provide an obvious way to study differences in body proportions, as ratios reflect geometric shape differences. However, when it comes to multivariate analysis of body measurements, for instance, with linear discriminant analysis (LDA) or principal component analysis (PCA), interpretation using body ratios is difficult. Both techniques are commonly applied for separating similar taxa or for exploring the structure of variation, respectively, and require standardized raw or log-transformed variables as input. Here, we develop statistical procedures for the analysis of body ratios in a consistent multivariate statistical framework. In particular, we present algorithms adapted to LDA and PCA that allow the interpretation of numerical results in terms of body proportions. We first introduce a method called the “LDA ratio extractor,” which reveals the best ratios for separation of two or more groups with the help of discriminant analysis. We also provide measures for deciding how much of the total differences between individuals or groups of individuals is due to size and how much is due to shape. The second method, a graphical tool called the “PCA ratio spectrum,” aims at the interpretation of principal components in terms of body ratios. Based on a similar idea, the “allometry ratio spectrum” is developed which can be used for studying the allometric behavior of ratios. Because size can be defined in different ways, we discuss several concepts of size. Central to this discussion is Jolicoeur's multivariate generalization of the allometry equation, a concept that was derived only with a heuristic argument. Here we present a statistical derivation of the allometric size vector using the method of least squares. The application of the above methods is extensively demonstrated using published data sets from parasitic wasps and rock crabs.

The use of ratios of measurements (i.e., of body proportions), has a long tradition and is deeply ingrained in morphometric taxonomy (Reyment et al. 1984, Winston 1999, Lestrel 2000, Schuh and Brower 2009). In many animal groups, the indication of such ratios is a standard of species descriptions, diagnoses, or identification keys (Mayr and Ashlock 1991). This is especially true for many arthropods, where ratios are a convenient means for distinguishing between morphologically similar species which often differ significantly in body proportions but not in qualitative characters. In certain insect groups, such as parasitic wasps, numerous ratios are routinely reported (e.g., Townes and Townes 1981, Kasparyan 1989, Noyes 2004, Horstmann 2009) and sometimes up to 30 ratios form the main body of a species description (see, e.g., Graham 1969, Graham 1991). Often the use of ratios is rather implicit in descriptive terms, for instance, when leaves are described as being “narrow” or “broad,” both attributes that could be translated into ratios without loss of information. In fact, botanists use numerous such terms for various plant parts that could be partly or wholly substituted by ratios (Stuessy 2009). Ratios are also used for phylogenetic analysis where they are treated as continuous characters (Thiele 1993, Wiens 2000, Rae 2002, Goloboff et al. 2006).

Besides tradition and ease of application, the widespread use of ratios is certainly related to a common way of looking at the shape of organisms. A taxonomist who notices similarity or dissimilarity in proportions of two specimens can always adequately translate them into a series of ratios. Any two individuals are then recognized as having the same shape (i.e., the same body proportions), when all measurements differ by a (positive) constant factor, for instance, when all of them are doubled. It does not matter if a head length to width ratio is, say, 2:4 mm or 4:8 mm, as long as the ratio (0.5) is the same, the shape (as captured by the ratio) is the same. The geometric shape expressed by ratios is thus invariant for a particular measure of size (Mosimann 1970).

Often it is useful to go one step further and analyze more than two linear distances in a single analysis with the help of multivariate statistical methods. Over the past decades, a wide array of tools has been developed in the field of multivariate morphometry (Reyment et al. 1984, Marcus 1990, Claude 2008). These methods help to unravel hidden population structure or to arrive at a better differentiation of groups, in other words, they give insights in the multivariate data structure that cannot be achieved solely by ratio analysis. Standard applications are principal component analysis (PCA) and Fisher's linear discriminant analysis (LDA), both with raw data (often transformed into logarithmic scale) as the primary input (see Pimentel 1979 for a readable account for biologists and Sorensen and Foottit 1992 for illustrative applications in insect systematics). Both methods aim to transform the original variables into a new system of coordinate axes, whereby most of the variance is contained in the first two or three axes. Traditionally, the results are then presented as scatter plots. However, the geometric meaning of these plots differs from the one obtained by the analysis of body ratios (Bookstein 1989, Claude 2008).

For this reason, we present versions of the classical LDA and PCA algorithms that are directly adapted to body proportions. In particular, we develop tools that allow us to interpret the numerical results obtained by these multivariate analyses in terms of the body sizes and body proportions of the individuals in question. The first method, adapted to LDA and called the “LDA ratio extractor,” allows the extraction of the ratios that are most informative for distinguishing between two or more groups. In this context, we also introduce a measure for deciding how much of the variation between individuals or groups of individuals is due to shape differences and how much is due to size differences. The second tool, called the “PCA ratio spectrum,” allows the interpretation of principal components in terms of ratios. In a similar manner, the “allometry ratio spectrum” can be used to assess the extent of allometric behavior in ratios. Furthermore, we present several concepts of size and discuss their relation to multivariate allometry (Klingenberg 1996). Central to this discussion is allometric size (Jolicoeur 1963), a concept that was derived only heuristically. In the Appendix, we therefore provide a statistical derivation of Jolicoeur's allometric size vector using the method of least squares. Finally, the above methods are illustrated with a data set from parasitic wasps (Baur 2002) and a classic data set from rock crabs (Campbell and Mahon 1974). The former is ideally suited for our purpose as ratios are commonly used in the taxonomy of these wasps (see above). The latter is often used for testing new statistical methods; it is included here because of the strong allometric behavior of certain variables.

The mathematical framework, especially the definition of shape and size used in this paper, is adopted from the work of Mosimann (1970), Darroch and Mosimann (1985), Sampson and Siegel (1985), and Rao and Suryawanshi (1996) who has a long and acknowledged history in morphometry (see, e.g., Pimentel 1979; Reyment et al. 1984, Marcus 1990, Klingenberg 1996, Dryden and Mardia 1998, Richtsmeier et al. 2002, Claude 2008). The papers of Mosimann (1970) and Darroch and Mosimann (1985) established the theoretical foundation for the use of body ratios in multivariate analysis and thus provided an ideal starting point for our methods. Sampson and Siegel (1985) and Rao and Suryawanshi (1996) were more concerned with particular definitions of size and shape. In contrast to these authors, our focus is on interpretation of body proportions rather than mere size and shape. Of course, other concepts for the analysis of size and shape (e.g., Cadima and Jolliffe 1996, McCoy et al. 2006, Claude 2008, Hotz et al. 2010) or the analysis of ratios (e.g., Aitchison 1986 for compositional data) have been proposed, but these are, in our opinion, less suited in our context (see below).

METHODOLOGY

The methods presented below consist of a number of steps that are briefly itemized here. The data are first standardized and transformed into logarithms, then the shape space is defined and a suitable size vector chosen. Based on these steps, the best ratios for separation of groups are extracted using a new algorithm adapted to LDA, called the LDA ratio extractor. Associated with this method is a particular measure that allows us to compare the discriminatory power of size with that of shape. The second new tool, called the PCA ratio spectrum, allows us to interpret the axes of a PCA in terms of ratios. A related method, the allometry ratio spectrum, is suitable for examination of the allometric behavior of ratios. Computation of all examples was done with the R statistical software, version 2.11.1 (R Development Core Team 2010) (for obtaining data sets and R files for all methods presented here, see Supplementary Material section).

As mentioned in the introduction, the mathematical framework adopted here originates from Mosimann (1970) and followers. A statistical framework frequently used in the Earth Sciences is Aitchison's analysis of compositional data, also called simplicial analysis (Aitchison 1986, Pawlowsky-Glahn and Egozcue 2001). Typically, compositional data vectors have positive components that sum up to one: imagine, for instance, a rock composed of three minerals in proportions 20%, 50%, and 30%. The corresponding data points (0.2,0.5,0.3) lie on a so-called simplex. The unit-sum constraint means a loss of 1 degree of freedom and requires special statistical tools, many of which have been developed by John Aitchison and his followers. We chose not to apply simplicial analysis to morphometric body ratios for two main reasons: First, ratios do not naturally satisfy the unit-sum constraint. Second, ratios have a complicated interrelationship not present in compositional data: the ratios a/b and b/c completely determine the ratio a/c. One could, alternatively, renormalize all body measurements to unit sum and thus obtain scale-free data on a simplex. This would free the path to simplicial analysis. However, it is not obvious to us how to extract statistical information about ratios from these renormalized data in a natural way. Also, our variants of LDA and PCA in Euclidean space would first have to be adapted to simplicial data, and it is not obvious how to do this, either. For these reasons, we preferred Mosimann's framework to that of Aitchison.

Standardizing the Data

For certain multivariate methods, it is important to standardize the data beforehand, otherwise, larger variables will dominate the analysis. As an example, let u = (u₁,…,u_p) represent vectors of body measurements associated with N individuals of some animal population. It may happen that u₁, say, is many times larger than u₂ and u₃, and so the ratio u₂/u₃ will be largely dominated by the ratios u₁/u₂ and u₁/u₃. For this reason the variables u_i should be transformed in a way that they are all in the same order of magnitude. A convenient way to achieve this is to divide each variable by its geometric population mean (Claude 2008). The transformed variables will be called y_i. They and their ratios vary around 1. In this scale, a value of y_i = 1.2, for example, means that the individual's corresponding body trait is 20% larger than the (geometric) average over the population (strictly speaking, this standardization is only crucial in PCA but has no impact on LDA).

Space of log-ratios.—

Our interpretation of results from statistical analysis of shape will mainly take place in the space of ratios (or body proportions)

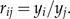For p variables, there are in principle p² ratios; observe, however, that only p(p − 1)/2 of these are informative and that even less, namely p − 1, can vary freely.

The relations between ratios being of multiplicative nature, it is common in multivariate morphometry to pass to log-transformed values (Reyment et al. 1984, Klingenberg 1996, Claude 2008). This transformation allows the application of linear statistical methods and furthermore avoids some problems associated with the statistical analysis of ratios (see Hills 1978, in response to Atchley et al. 1976).

We thus denote x_i = logy_i and

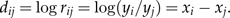(1)

Following Aitchison (1983), we call the numbers d_ijlog-ratios. Note that due to our standardization of the original data, the mean of the variables x_j is zero. Also, if r_ij≈1, we have

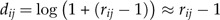and thus the log-ratios roughly correspond to the deviation of the ratios from 100%.

Shape

As mentioned in the introduction, a ratio can be calculated from any two body measurements and be used to describe the form of a specimen. A ratio thus represents one way for defining shape (Claude 2008). Mosimann (1970) generalized this particular concept of shape for many measurements by posing the question, “When do two individuals have the same shape with respect to a finite number of measurements?”. His definitions form the basis for our methods and are in the following formally introduced.

To the (standardized) body measurements y = (y₁,…,y_p)^T of some individual, we would like to assign a set of numbers encapsulating the individual's body shape. We assume that these numbers can be calculated by formulas of the form y₁^b₁y₂^b₂·⋯·y_p^b_p. As shape values should be invariant under scaling λy, the exponents must satisfy the shape restriction

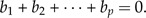(2)

Passing to the log-values x_i, we define

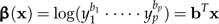(3)

to be the shape function associated to the vector of coefficients b = (b₁,…,b_p) subject to the shape restriction (2). We will also standardize b to length 1 (‖b‖ = 1). Geometrically, these constraints mean that b is a unit vector at right angles to the vector 1 = (1,…,1)^T, that is, it lies in the p − 1 dimensional subspace 1^⊥ (“shape space”) orthogonal to the vector 1. If

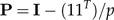(4)

denotes the orthogonal projection onto the shape space 1^⊥, then we calculate the shape values (z₁,…,z_p) according to

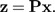(5)

The vector b represents a direction in shape space, and the shape function β(x) is the scalar product of z with the vector b:

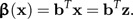Log-ratios d_ij are represented by the log-ratio vectors

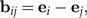(6)

where e_i and e_j are the i-th and j-th standard base vector in ℝ^p. We collect these vectors to a set ℬ = {b_ij}_{1 ≤ i < j ≤ p}. The fact that there are many linearly independent subsets of ℬ spanning 1^T reflects the interdependence of body ratios and poses a major problem for the interpretation of statistical results in terms of body proportions. We will address this problem below.

Size

Analogous to shape functions, a size function can be defined. We stipulate a size function to be of the form y₁^a₁y₂^a₂·…·y_p^a_p, but this time the exponents fulfill the size restriction

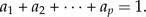(7)

Thus, an individual with all body measurements doubled, say, will be twice as large. In terms of the log-values x, we define

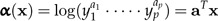(8)

to be the size function corresponding to the size vector a = (a₁,…,a_p). Three size vectors have been commonly proposed in the literature: Isometric size, allometric size, and shape-uncorrelated size, whose definitions are presented in the following. Shape-uncorrelated size is discussed here for the sake of completeness. In developing the methodology below, our focus will be on isometric and allometric size.

Isometric size.—

The “democratic” way is to give equal weight to all body measurements. This is tantamount to the choice a₀ = (1/p)1, and the size α₀(x) = a₀^Tx is simply the arithmetic mean of x. In many cases, the size α₀(x) and the shape values z will show significant correlation over the population. This is a sign of the presence of allometry.

Allometric size.—

Allometry was first observed by Cuvier and intensively studied by Huxley and Teissier for bivariate data (e.g., body weight vs. some body trait); see Gayon (2000) for a short history of allometry. A generalization to multivariate data sets was proposed by Jolicoeur (1963). He arrived at his definition of allometric size in a rather heuristic way, whereas we propose in the Appendix a statistical model that leads to Jolicoeur's generalization in a natural manner. One way to pass from the bivariate to the multivariate case is by putting forth the question: Which is the measure of body size fitting optimally into the set of bivariate allometric power laws

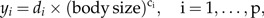for suitable coefficients d_i and exponents c_i? A mathematically more precise formulation is given in the Appendix. The answer to this question is the size function associated to the size vector a_J spanning the first principal component of the log-values x, a fact that is proved in the Appendix by means of the least squares method. More precisely, a_J: = a₁/1^Ta₁ where a₁ is the unit eigenvector of the population covariance matrix Σ = E(xx^T) corresponding to the largest eigenvalue λ₁: Σa₁ = λ₁a₁.

Shape-uncorrelated size.—

A choice of size function that represents the other extreme to allometric size was proposed by Sampson and Siegel (1985) and by Rao and Suryawanshi (1996). Their size vector a_R has the property that size and shape over the population are uncorrelated. The shape-uncorrelated size vector is given by a_R: = Σ ^{− 1}1/1^TΣ ^{− 1}1.

The size vector a_R is harder to interpret geometrically than a_J. An interpretation is offered in Rao and Suryawanshi (1996): A unit increase in shape-uncorrelated size represents the same average increase (or decrease) in all the variables x₁,…,x_p. It is also proved in Rao and Suryawanshi (1996) that a_R^Tx is the only size function that is stochastically independent of shape if x has a multivariate normal distribution. This was already shown by Sampson and Siegel (1985) for linear size functions but it holds even true for nonlinear size functions.

The LDA Ratio Extractor: Selecting the Best Ratios with Discriminant Analysis

As mentioned above, LDA is a standard tool in multivariate morphometry. It often allows to distinguish most similar taxa but the numerical results obtained are then hard to interpret. Our aim is to adapt standard LDA in a way that its results admit a convenient interpretation in terms of the body proportions of the specimens under study. Our algorithm is recursive and the basic idea is as follows. In a first step, the ratio with the largest discriminating power is determined. Then a ratio is chosen that has maximal discriminating power but at the same time is as little correlated as possible to the first ratio. If needed, further ratios can be picked out in the same manner.

Suppose that the values x₁,x₂ stem from two distinct groups with mean m₁,m₂, and a common (nonsingular) within-groups covariance matrix Σ. Then Fisher discriminant vector w is determined by

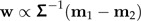(9)

and ‖w‖ = 1. The vector w is a mixture of size and shape.

Often taxonomists prefer to perform LDA purely within shape space 1^⊥, that is to ignore the effects of size. Hence, the method is presented entirely in the shape space. The common within-groups covariance matrix of the shape values z_i = Px_i, i = 1,2, is given by Σ₁ = PΣP, which is symmetric and positive definite on the subspace 1^⊥. Because it is singular in ℝ^p, its pseudo-inverse must be used to perform the LDA. By singular value decomposition, there exists an orthogonal transformation matrix O in such a way that

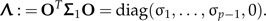Set 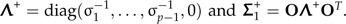. The shape discrimination vector w₁ is now determined by

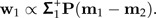(10)

It is hard to interpret w₁ in terms of body proportions because it is a mixture of ratios and, worse, can be written in infinitely many ways as a linear combination of log-ratio vectors (cf., formula 6) from set ℬ. In the next paragraph, we develop an algorithm that extracts the most informative body ratios for between-groups distinction.

Extracting ratios.—

Let x denote the combined data set in which both groups x₁ and x₂ have been centered to 0 individually. Thus, E(x) = 0 and var(x) = Σ. The dominant log-ratio vector from ℬ with respect to discrimination between groups is the one that has the largest correlation with w₁ in the data set x. More precisely, we consider the correlation coefficients

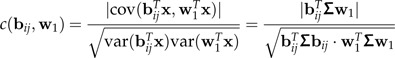and set

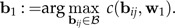(11)

The discriminating power of a vector v∈ℝ^p can be measured by the standard distance D(v), that is, the difference of the means of v^Tx_i, i = 1,2, divided by the common within-groups standard deviation:

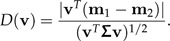(12)

The term “standard distance” was introduced in Flury and Riedwyl (1986) (the square of D is sometimes called Rayleigh coefficient). Note that w₁ is the vector in 1^⊥ that maximizes D(b) among all shape vectors b∈1^⊥. By (10) and because Pw₁ = w₁, we have for any b∈1^⊥:

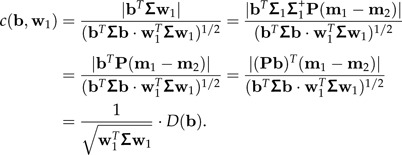Thus, we observe that b₁ defined in (11) has the strongest discriminating power among all log-ratio vectors b_ij∈ℬ. The highest possible standard distance for discrimination within size-and-shape space ℝ^p is D_tot: = D(w), where the discrimination vector w is given by (9). It is necessary to list the values

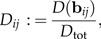(13)

in order to get the magnitude of the discriminating power of each ratio. In this listing, the log-ratio b_ij with the second largest value D_ij is likely to be already largely explained by b₁ due to the strong correlations between ratios. For this reason, we restrict the shape space 1^⊥ to the subspace H₂ such that the values b^Tx for b∈H₂ are uncorrelated to b₁^Tx. It is easy to check that H₂ is orthogonal to the vector Σb₁. Projection onto H₂ is given by the matrix

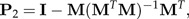where M is the p×2-matrix M = [a₀|Σb₁]. Set Σ₂ = P₂ΣP₂ and calculate the (unit length) discrimination vector w₂ according to

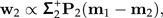where Σ₂⁺ is the pseudo-inverse of Σ₂ (which has rank p − 2). Now, let b₂ be the log-ratio vector b_ij that shows largest correlation to w₂. Iteration of this procedure leads to the following algorithm to compute the sequence of ratios b_i, i = 1,…,p − 1:

1. Let M₁ = a₀ and initialize k = 1.

2. Set P_k = I − M_k(M_k^TM_k) ^{− 1}M_k^T and Σ_k = P_kΣP_k. Determine the pseudo-inverse Σ_k⁺ and set

   

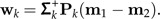
• 3. Let b_k = argmax_bij∈ℬc(b_ij,w_k).

• 4. Add the column Σb_k to the matrix M_k:

  

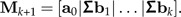
• 5. Increase k by one unit (unless i = p − 1), and continue at Step 2.

In practice, only a few iterations will be performed because the first two or three log-ratios b₁,b₂,… will already explain most of the discrimination between the two groups.

Extracting ratios for multiple groups.—

Suppose we are given K groups (classes) x₁,…,x_K with means m₁,…,m_K and a common within-groups covariance matrix Σ. The between-groups covariance matrix is defined by

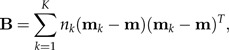where m is the total mean and n_k is the number of individuals in each group. A frequently used criterion for discrimination in the multiple group case is

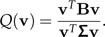The unit vector v₁ maximizing Q(·) is the eigenvector of Σ ^{− 1}B with largest eigenvalue. The generalization of our two-group algorithm explained above to the multiple group case is the following:

1. Let M₁ = a₀ and initialize k = 1.

2. Set P_k = I − M_k(M_k^TM_k) ^{− 1}M_k^T, Σ_k = P_kΣP_k and B_k = P_kBP_k. Determine the pseudo-inverse Σ_k⁺ and let w_k be the eigenvector of Σ_k⁺B with largest eigenvalue.

3. Determine

   

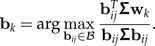
• 4. Add the column Σb_k to the matrix M_k:

  

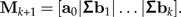
• 5. Increase k by one unit and continue at Step 2.

The philosophy behind this algorithm is exactly the same as in the two-group case: First, we determine the linear discriminant w_k and choose the log-ratio vector b_ij with strongest correlation to w_k. Then we project to a subspace of shape vectors that are uncorrelated to all log-ratio vectors that have already been chosen. Again, two or three iterations will be sufficient in practice.

Judging the influence of size.—

As mentioned above, the LDA ratio extractor was developed in the shape space that is convenient for most circumstances. Sometimes, however, it might be informative to know how well particular groups are separated in relation to size. In order to assess how much of the total separation is due to size, we define D_size: = D(a₀)/D_tot and D_shape = D(w₁)/D_tot. One can then view the number

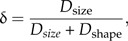(14)

as a measure of how well size discriminates in comparison with shape.

The PCA Ratio Spectrum: Interpreting Principal Components with Ratios

PCA is a very widely used method in multivariate statistics (Jolliffe 2004). In contrast to LDA, specimens are not assigned to different groups for a PCA but are treated as a single group. The resulting scatterplots can then be used to explore the structure of variation in this group. It might be the case that the pattern recovers groupings based on other sets of characters (qualitative morphology, molecular markers, etc.), which would give them additional weight. Usually, individual principal components are interpreted in terms of the original variables (see Jolicoeur and Mosimann 1960 and Manly 2005 for lucid examples). The method developed below allows an interpretation using ratios. The main ingredient of this method is a diagram that we call the PCA ratio spectrum. It allows the user to immediately read off the dominant ratios as well as their interrelationships (recall that ratios are always interdependent in a complex fashion as their number is larger than the degree of freedom in the data).

The technical details of this method and its theoretical justification are presented below. Let the random vector x with E(x) = 0 and cov(x) = Σ (assumed to be nonsingular) represent body measurements of a given population. The first principal components vector u₁ = (u_i)_{i = 1,…,p} of the shape values z = Px is the eigenvector of Σ₁ = PΣP corresponding to the largest eigenvalue λ₁ of Σ₁:

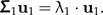For a log-ratio vector b_ij, we have

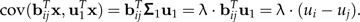(15)

This fact allows a simple graphical interpretation of the first principal component u in terms of body proportions: The numerical values (coefficients) of the components of u₁ are drawn as points on the real line. We call this diagram the PCA ratio spectrum of the vector u₁. To a pair of points u_i, u_j on the spectrum with a large difference corresponds a body proportion log(y_i/y_j) that contributes substantially to the first principal component; on the other hand, close points on the spectrum contribute little. The PCA ratio spectrum represents a mixture of all body proportions and shows how much each of them contributes to the variation in relation to the others. This can be illustrated with the example given in Figure 2b. As can be seen by their comparable separation in the spectrum, the ratios gaster breadth:gaster length and postmarginal vein:tergum 7 length have similar explaining power for the variance. On the other hand, the ratio eye breadth:scape length has no explanatory power because the corresponding points are very close in the spectrum.

FIGURE 2.

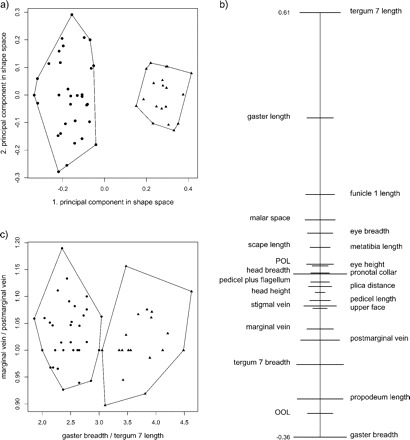
Application of the PCA ratio spectrum using the Pteromalus data, with Pteromalus albipennis (dots) and P. solidaginis (triangles). (a) Scatterplot of a principal component analysis (PCA) in shape space. (b) PCA ratio spectrum of the first principal component. The ratio formed from the extremal points (i.e., gaster breadth:tergum 7 length) explains a large part of the variation of the first component. In contrast, ratios formed from characters lying close to each other in the spectrum (e.g., marginal vein:postmarginal vein) explain very little. This is apparent in the scatterplot (c). Confidence intervals (horizontal bars in (b), see Methodology section) were estimated with a bootstrap.

If desired, the same procedure can be applied to the second and following principal components. Let us emphasize again that the method can only be applied in a statistically consistent manner when a PCA is performed within the shape space.

Statistical stability of the PCA ratio spectrum.—

Sometimes it might be useful to test whether the PCA ratio spectrum is statistically stable. Instability occurs when the largest eigenvalue λ₁ is not sufficiently distinct from the smaller eigenvalues of Σ₁, though this rarely might be the case in practice. In order to obtain confidence intervals for the points u_i on the PCA ratio spectrum we assume that the values x and hence z are normally distributed. More precisely: Let ${\widehat{\mathbf{z}}}_1,\cdots ,{\widehat{\mathbf{z}}}_n$ be a random sample created from a multivariate normal distribution 𝒩(0,Σ₁). Denote by ${\widehat{\mathbf{\Sigma }}}_1$ the sample covariance matrix and by ${\widehat{\mathbf{u}}}_1$ the standardized first principal components vector of ${\widehat{\mathbf{\Sigma }}}_1$, pointing in the same half-space as u₁. The sampling distribution of ${\widehat{\mathbf{u}}}_1$ is complicated but Anderson has established its large-sample distribution (see theorem 13.5.1 in Anderson 2003). It follows from this result that for sufficiently large sample size n, the marginal distribution of the i-th component of the random vector ${\widehat{u}}_i$ is approximatively normally distributed according to ${\widehat{u}}_i\sim 𝒩(u_i,{\sigma }_i^2)$ where

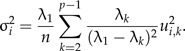(16)

Here, λ₁ > λ₂ ≥ ⋯ ≥ λ_{p − 1} are the positive eigenvalues of the matrix Σ₁ (which has rank p − 1) and u_i,k are the elements of the matrix U = (u₁|⋯|u_{p − 1}) formed by the corresponding standardized eigenvectors u₁,⋯,u_{p − 1}. (The eigenvector u_p corresponding to λ_p = 0 is proportional to the isometric size vector a₀.) Graphically, we represent the 68% confidence intervals [u_i − σ_i,u_i + σ_i] as perpendicular bars of length 2σ_i at the corresponding point u_i on the spectrum (Fig. 2b). If the interval lengths are not too large compared with the separation of the points on the spectrum—as is the case in Figure 2b—then the spectrum can be considered as statistically stable. Even when the normal assumption is violated, the confidence intervals still give some indication of the stability of the spectrum.

Alternatively, one can also sample the original values z directly from the empirical distribution and obtain similar intervals with a bootstrap. The latter was used for estimating the confidence intervals in Figure 2b.

The Allometry Ratio Spectrum: Assessing Allometric Behavior of Ratios

The idea of a ratio spectrum introduced above is also useful for extracting body ratios that show allometric behavior. For a given size vector (like a₀ or a_J), the body ratio that shows the most distinctive allometric growth can be interpreted as the one whose covariance with the body sizes a^Tx is maximal. We obtain

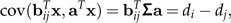where we have set Σa = :d = (d_i)_{i = 1,⋯,p}. Hence, exactly as in the preceding paragraph, the body proportions with strongest allometric growth along the size vector a can be read off the allometry ratio spectrum of d. A reasonable choice of a size vector is Jolicoeur's size vector a_J. In that case, we have d∝a_J and thus the allometric body proportions can be directly determined by the spectrum of a_J. An illustration of such a spectrum is given in Figure 4.

FIGURE 4.

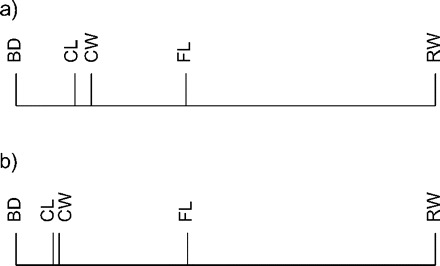
The allometry ratio spectrum for the Leptograpsus variegatus data set for blue type males (a) and for orange type males (b) respectively. The characters shown are carapace length (CL) and width (CW), width of frontal lobe (FL), rear width (RW), and body depth (BD) (see Results section). The bars do not represent confidence intervals here.

RESULTS

Discriminating Species

As an illustration of how to apply the LDA ratio extractor, we revisit a statistical analysis from Baur (2002) where morphometric data from two species of parasitic wasps were examined, namely the species Pteromalus albipennis Walker, 1835 and P. solidaginis Graham and Gijswijt, 1991 from the Pteromalus albipennis group (Insecta: Hymenoptera: Chalcidoidea). The analysis is based on p = 23 characters (called “head breadth,” “OOL,” “eye height,” etc.) measured on n₁ = 32 individuals from P. albipennis (Group 1) and n₂ = 19 individuals from P. solidaginis (Group 2), see Baur (2002) for a complete description. The common within-group variance is estimated by

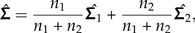where 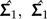are the estimated covariance matrices of the two groups.

Before performing LDA, we would like to add a word of caution rarely mentioned in the textbooks: If the total number of individuals n = n₁ + n₂ is not distinctly larger than the number p of body traits, the results from an LDA can be completely spurious. The reason is that the dimension is large enough that a separating plane is likely to exist between the two groups even if the sample points are completely random. As a rule of thumb, one should always have 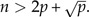A theoretical justification of this rule is given in MacKay (p. 490 2003).

By applying the LDA ratio extractor introduced in the Methodology section, we obtain OOL:gaster length as the most discriminating ratio. We get D_size = 0.064 and D_shape = 0.964, hence δ = 0.063 (cf., formula 14). Thus, discrimination between the groups stems mostly from shape differences. The next discriminating body ratio being as little correlated as possible with OOL:gaster length is eye breadth:marginal vein. Its standard distance D_ij (see formula 13) is 2.1 as compared with the standard distance D_ij = 5.6 for the first ratio. As can also be seen from the scatterplot in Figure 1a, the discriminating power as compared with the first ratio is already much lower. Figure 1b shows the next two ratios extracted from the algorithm, funicle 1 length:propodeum length and scape length:postmarginal vein, with standard distances D_ij = 2.3 and D_ij = 1.7, respectively. By looking at the plots in Figure 1a and b, one could be tempted to simply combine the first (OOL:gaster length) with the third ratio (funicle 1 length:propodeum length) to arrive at an even better separation of groups. However, one should bear in mind that these ratios are highly correlated and therefore stand for more or less the same information.

FIGURE 1.

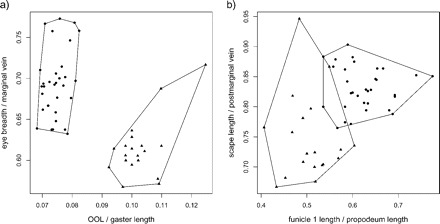
Scatter plots of the four most discriminating ratios for Pteromalus albipennis (dots) and P. solidaginis (triangles). Plot (a) shows first versus second ratio, plot (b) third versus fourth ratio.

Interpreting Principal Components

Figure 2a shows the results of a PCA on the same data set, but this time the two Pteromalus species were entered in the analysis as a single group. A PCA is always useful for examining the structure of variation in a single population, for instance, when it is difficult to assign specimens to different groups beforehand (Pimentel 1979, Reyment et al. 1984, Claude 2008). It can also give additional weight for groupings based on other features. In this case, the specimens in the scatterplot were labeled as either P. albipennis or P. solidaginis according to qualitative character differences, such as coloration or forewing pilosity, and host plant association (see Graham and Gijswijt 1991). As can be seen from Figure 2a, the first principal component is fully congruent with the separation of species. For the interpretation of this component, the PCA ratio spectrum is displayed in Figure 2b. Most of the variation is explained by ratios like gaster breadth:tergum 7 length that correspond to points lying at the opposite end of the spectrum. On the other hand, ratios formed from characters lying adjacent to each other in the spectrum, like marginal vein:postmarginal vein, explain very little. This is visualized in the scatterplot of the two ratios (Fig. 2c). Of course, also the ratio spectra of the second and third principal component could be drawn and sometimes this might be illuminating as well, for instance, for explaining the structure of variation within each species.

The above analysis exemplifies the use of our methodology in the shape space. Sometimes a researcher might be interested to examine differences in the size of the specimens, for instance, for investigating the influence of ecological parameters or different food regimes on populations (McCoy et al. 2006). Here, one could simply plot the isometric size axis (see Size section above) against the first principal component in shape space. From Figure 3 it is evident that the mean size of Pteromalus solidaginis is smaller, but that its range still lies within P. albipennis.

FIGURE 3.

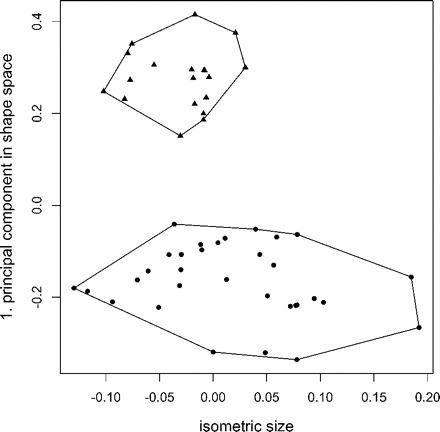
Scatterplot of isometric size versus first principal component in shape space for the Pteromalus data set, with Pteromalus albipennis (dots) and P. solidaginis (triangles). The mean size of P. solidaginis is obviously smaller but it still lies within the range of Pteromalus albipennis.

Assessing Allometry

We will illustrate the use of the allometry ratio spectrum on a classical data set of specimens of the purple rock crab Leptograpsus variegatus (Fabricius, 1793) (Crustacea: Brachyura: Grapsidae) from Western Australia (see Campbell and Mahon 1974). These occur in two color forms, blue and orange. Mahon collected 50 individuals from each color form and from each sex and made five body measurements: carapace length (CL) and width (CW), width of frontal lobe (FL), rear width (RW), and body depth (BD). We calculated the allometric size vectors a_J for the body measurements of the males of both the blue and the orange morph. Figure 4 shows the corresponding allometric ratio spectra for both morphs. As can be seen, the ratio BD:RW shows the largest allometric growth whereas for CL:CW allometry is negligible in both groups. Figure 5 confirms this conclusion: There we display a scatter plot for the orange type males of the isometric sizes versus the log-ratios of BD:RW and CL:CW, respectively. Whereas the first ratio (Fig. 5a) visibly has a strong correlation with isometric size, as is characteristic for allometry as explained in the Methodology section, this is much less the case for the second ratio (Fig. 5b).

FIGURE 5.

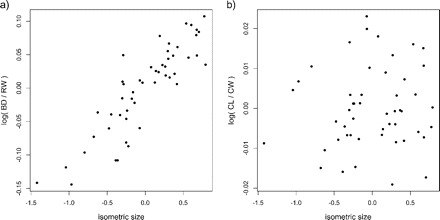
Scatter plots of isometric size versus log-ratios body depth:rear width (a) and carapace length:width (b) for the orange type males in the Leptograpsus variegatus data set.

It is useful to test allometry versus isometry, that is, to test the null hypothesis that a_J = a₀. Such a test, under the hypothesis of normality and relatively large sample size, was developed by Anderson (2003) (see section 11.6.2). Adapted to our situation, the P value of the null hypothesis is given by Prob(χ_{p − 1}² > κ) where the test value κ is determined by

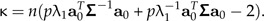Here, Σ is the covariance matrix of the sample x of size n and λ₁ is its largest eigenvalue. For the male Leptograpsus, the P values are virtually zero for both color types, hence the null hypothesis that no allometry is present can safely be rejected.

DISCUSSION

As initially mentioned, a number of body measurements are commonly collected in taxonomic research. This mainly serves two purposes. First, the raw or log-transformed variables are entered in some kind of standard multivariate statistical analysis (MVA) for studying character variation and for discrimination of taxa. PCA and LDA are among the methods of choice in this respect and are the ones we refer to with MVA below. Second, the same measurements are integrated in descriptive works, but this time by calculating ratios (indeed, the numerical output from MVA would be far too awkward for inclusion in descriptions and identification keys). Of course, it would be most useful if, say, a discriminant function could be interpreted in terms of ratios that then could be directly used for a species description. One could, for instance, expect some guidelines for the choice of ratios. So far, this was not possible because the two kinds of analysis were not directly comparable (see below). Thus, ratio analysis usually adheres to certain standards established for a particular group, rather than following the insights gained from MVA. A case in point is the study of the Encarsia meritoria species complex (Insecta: Hymenoptera: Aphelinidae) by Polaszek et al. (2004), where some of the best ratios used for species discrimination were not even included in their elaborate PCA and LDA.

The incompatibility of MVA and ratio analysis results from the way, size and shape functions are defined for each method (see Fig. 6 for further details). However, the methods presented here, namely the newly developed LDA ratio extractor and the PCA ratio spectrum, solve these problems by using the same definitions for size and shape. Therefore, the results from MVA can now be interpreted in terms of ratios that, in turn, can be directly incorporated in a variety of descriptive taxonomic works. In fact, a more sophisticated use of ratios may be achieved, as is demonstrated by our application of the LDA ratio extractor to the data set from parasitic wasp species of the family Pteromalidae. Here, the best ratios found for separating the two Pteromalus species were OOL (distance of lateral ocellus to eye margin):gaster (abdomen) length, funicle 1 (antenna) length:propodeum length, etc. (see Results section and Fig. 1). These ratios relate characters from widely separated body parts and differ from those commonly used in the taxonomy of pteromalid wasps. For instance, in Graham (1969), still the standard reference in the field (Grissell and Schauff 1997), ratios are exclusively formed from characters lying adjacent to each other, like eye height:breadth or thorax length:breadth (see also Graham and Gijswijt 1991). Evidently, the variation of such ratios among specimens can—to a certain extent—be judged by eye. However, as demonstrated here, these ratios are apparently not the best ones for discrimination. It is of course very difficult if not impossible to judge by eye the discriminating power of ratios based on widely separated characters, a task that is best done analytically with the help of an algorithm such as the one presented in this paper.

FIGURE 6.

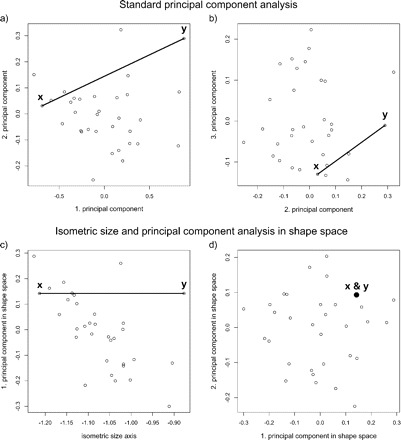
Scatterplots of principal component analyses (PCA) of a single species of Pteromalus (n = 32 specimens of Pteromalus albipennis, p = 23 variables of body measurements; data from Baur 2002), showing the effect of different definitions of size and shape. Specimen labeled y is a clone of specimen x but with all variables scaled by a factor of 1.4. The two specimens have therefore equal values for all their ratios and are only separated along the isometric size axis, as indicated by the line connecting x with y. (a) Scatterplot of first against second and (b) of second against third component respectively of a standard PCA on the covariance matrix of log-transformed data. The first component is considered as a general size measure because its coefficients have the same sign and are of similar magnitude for all variables. However, they are not exactly the same, thus the first component of a standard PCA is usually considered as the allometric size axis (Jolicoeur 1963; Claude 2008). The remaining components define the shape space in this analysis. Note that the line of isometry is not parallel to the first component, and, thus, reflects the different size measures. As a result, specimens x and y are also widely separated points in the shape space, although viewed from their body proportions they are identical. For (c) and (d) the same data were used, but here they were subjected to a PCA after removal of isometric size (for details of computation, see the Methodology section). Now, the line of isometry connecting x with y lies of course parallel to the isometric size axis (c). In the shape space (d) the two specimens form a single point, because only those specimens appear distinct which also differ in body proportions.

The present methodology can thus easily be embedded in a consistent statistical frame work for the multivariate analysis of morphometric data. In particular, it allows us to interpret the results of a PCA and LDA entirely in terms of ratios, which themselves form the core information of most quantitative taxonomic works. The important point of the new methodology is to determine the shape values and to choose a particular size vector beforehand. For the size function, we mainly considered the isometric size vector a₀, except for the allometry ratio spectrum, which relates to Jolicoeur's allometric size vector a_J. Of course, other definitions of shape and size are possible (see Bookstein 1989 for a review). By using the “back-projection” method of Burnaby (1966), some authors (e.g., Klingenberg 1996, McCoy et al. 2006) choose to define their shape values by projecting the log-data x on the space orthogonal to the allometric vector a_J. The reason for this is to transform away shape effects related to allometric growth. According to this view, size is represented by the first, shape by all the following principal components of the log-data. It is, however, unclear how these shape values could be properly interpreted in terms of body proportions; in particular, no ratio-spectrum can be assigned in a mathematically consistent way to “shape” vectors orthogonal to a_J. Moreover, the allometric growth law in its bivariate or multivariate versions is just a convenient statistical model and by no means a “law of nature” (Gould 1966). In our opinion, allometry should rather be treated as a hypothesis to be tested after the size values are determined rather than be incorporated into the framework from the very beginning. We therefore prefer to analyze allometric variation with help of the allometry ratio spectrum, as demonstrated above (see Results section).

Our new methods are obviously rooted in the field of multivariate morphometrics (Reyment et al. 1984). The latter is occasionally dubbed traditional morphometrics (Marcus 1990), as opposed to “modern morphometrics” (Claude 2008) such as the analysis of landmarks (geometric morphometrics, Adams et al. 2004, Zelditch et al. 2004) or outlines (e.g., elliptic Fourier analysis, Lestrel 1989, Lestrel 2000). The main reason why we stay within multivariate morphometrics is simply given by the nature of our data. Landmark and outline data are ideally suited for fixed objects, such as a skull or the body of a fish. For an insect with articulated extremities, those methods are of limited use unless one is willing to study the form of the head, thorax, or wings in separate analyses. This can and should be done. Nevertheless, it is often useful to include measurements from all over the body in a single analysis. For instance, a taxonomist trying to distinguish between two most similar species will be happy about any discriminating character. What if they are best separated by the ratio of, say, the length of the hind leg and the eye height? As we have shown above, it is here where methods of multivariate morphometrics, adapted for the analysis of ratios, could play a major role.

SUPPLEMENTARY MATERIAL

Supplementary material.

APPENDIX

Statistical Derivation of the Allometric Size Vector

We would like to arrive at an estimation of the allometric size vector starting from a statistical model of the allometric growth hypothesis. Let y be the original data and 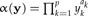a size function. According to Huxley (1932), each trait y_i when graphed against the individual's size α(y) should satisfy the power law

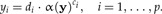(A1)

Here we consider d_i as positive random variables and c_i as constant coefficients. We shall use the approach of least squares to statistically estimate the coefficients a_i and c_i. Taking logarithms on both sides of (A1), we get

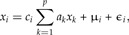where μ_i = E(logd_i) and E(ϵ_i) = 0. In vector notation, this reads

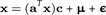with E(ϵ) = 0. Because E(x) = 0, we conclude μ = 0. We estimate a and c in a way that the sum of squares is minimal:

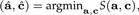where S(a,c) = E‖ϵ‖². We have

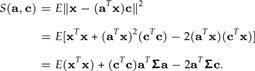Calculating vector derivatives with respect to a and c we get

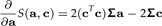and

Setting both equations equal to 0 and dropping the hats over $\widehat{\mathbf{a}}$ and $\widehat{\mathbf{c}}$, we arrive at the system of equations:

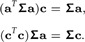Multiplying the second equation from the left by Σ ^{− 1}, solving for c and plugging the result into the first equation, one can see that a is an eigenvector of Σ with eigenvalue

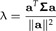and c = a/‖a‖². Replacing these results in S(a,c) one gets:

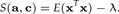Evidently, this expression is minimal if λ is the largest eigenvalue of Σ. Let a₁ denote the unit vector representing the first principal component of the data x. Imposing the size restriction, we arrive at the solution

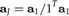and c_J = a_J/‖a_J‖². Historically, Jolicoeur (1963) was the first to introduce a multivariate generalization of Huxley's allometric power law and he proposed our a_J as a measure of size (or rather a₁ to be precise). He did not, however, give a statistical model to motivate his definition.