Learning to Predict Chemical Reactions

Abstract

Being able to predict the course of arbitrary chemical reactions is essential to the theory and applications of organic chemistry. Approaches to the reaction prediction problems can be organized around three poles corresponding to: (1) physical laws; (2) rule-based expert systems; and (3) inductive machine learning. Previous approaches at these poles respectively are not high-throughput, are not generalizable or scalable, or lack sufficient data and structure to be implemented. We propose a new approach to reaction prediction utilizing elements from each pole. Using a physically inspired conceptualization, we describe single mechanistic reactions as interactions between coarse approximations of molecular orbitals (MOs) and use topological and physicochemical attributes as descriptors. Using an existing rule-based system (Reaction Explorer), we derive a restricted chemistry dataset consisting of 1630 full multi-step reactions with 2358 distinct starting materials and intermediates, associated with 2989 productive mechanistic steps and 6.14 million unproductive mechanistic steps. And from machine learning, we pose identifying productive mechanistic steps as a statistical ranking, information retrieval, problem: given a set of reactants and a description of conditions, learn a ranking model over potential filled-to-unfilled MO interactions such that the top ranked mechanistic steps yield the major products. The machine learning implementation follows a two-stage approach, in which we first train atom level reactivity filters to prune 94.00% of non-productive reactions with a 0.01% error rate. Then, we train an ensemble of ranking models on pairs of interacting MOs to learn a relative productivity function over mechanistic steps in a given system. Without the use of explicit transformation patterns, the ensemble perfectly ranks the productive mechanism at the top 89.05% of the time, rising to 99.86% of the time when the top four are considered. Furthermore, the system is generalizable, making reasonable predictions over reactants and conditions which the rule-based expert does not handle. A web interface to the machine learning based mechanistic reaction predictor is accessible through our chemoinformatics portal (http://cdb.ics.uci.edu) under the Toolkits section.

Introduction

Determining the major products of chemical reactions given the input reactants and conditions is a fundamental problem in organic chemistry. Reactions are driven by a complex physical interplay of electronic and structural attributes of the reactants along with reaction conditions, such as temperature, phase, concentration, and solvent attributes. There are a broad range of approaches to reaction prediction falling around at least three main poles: physical simulations of transition states using various quantum mechanical and other approximations,^1-6 rule-based expert systems,^7-14 and inductive machine learning methods.¹⁵

The very concept of a “reaction” can be ambiguous, as it corresponds to a macroscopic abstraction, hence simplification, of a very complex underlying microscopic reality, ultimately driven by the laws of quantum mechanics. At the lowest conceivable level of quantum mechanical (QM) treatment, it remains impossible to find exact solutions to the Schrödinger equation even for relatively small systems. Thus at this level, reactions are modeled as minimum energy paths between stable configurations on a high-dimensional potential energy surface, where saddle points represent transition states.^5,6 This potential energy surface is in practice computed with a number of varyingly accurate approximations, ranging from ab-initio Hartree-Fock approaches or Density Functional Theory to semi-empirical methods or mechanical force fields.⁴ An even higher level of approximation can be made by considering reactions as discrete entities: concerted electron movements through a single transition state, e.g., Ingold’s mechanisms.¹⁶ We denote these single transition state, concerted electron movement, reactions as mechanistic, or elementary, reactions. Mechanistic reactions can be drawn as “arrow-pushing” diagrams¹⁷ explicitly showing the concerted electron movements. An elementary reaction can be associated with a single electron movement (e.g. radical reactions), movement of a single pair of electrons (e.g. simple addition or bond dissociation reactions), or the complex concerted movement of many electrons (e.g. pericyclic or E2 reactions).

In stark contrast to paths on energy surfaces or even mechanistic reactions, rule-based and inductive computational approaches to reaction prediction mostly consider only overall transformations. Overall transformations are general molecular graph rearrangements reflecting only the net change of several successive mechanistic reactions. For example, Figure 1 shows the overall transformation of an alkene interacting with hydrobromic acid to yield the alkyl bromide along with the two elementary reactions which compose the transformation.

Figure 1.

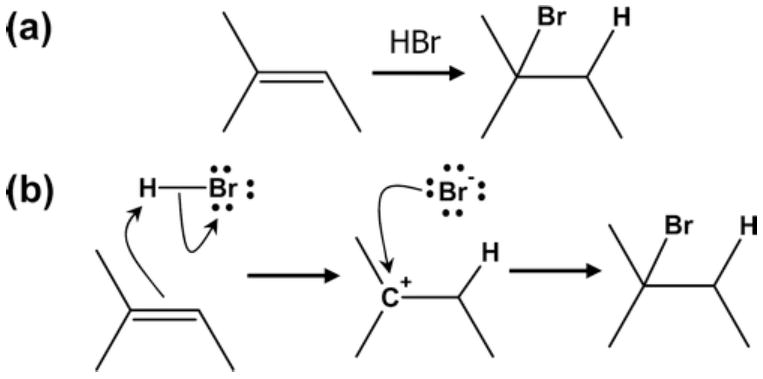
Example overall transformation and corresponding elementary, mechanistic reactions. (a) The overall transformation of an alkene with a hydrobromic acid. This is a single graph rearrangement representation of a multi-step reaction. (b) The details of the two mechanistic reactions which compose the overall transformation. The first involves a proton transfer reaction, and the second involves the addition of the bromide anion. Each detailed mechanism is an example of an “arrow-pushing” diagram¹⁷ involving a single transition state, in which each arrow denotes the movement of a pair of electrons, and multiple arrows on a single diagram denote concerted movement.

Overall transformations obfuscate the underlying physical reality of chemical reactions, while explicitly modeling potential energy surfaces is overly computationally demanding. A useful middle-ground is to consider mechanistic reactions. While mechanistic reaction representations are approximations quite far from the Schrödinger equation, we expect them to be closer to the underlying reality and therefore more useful than overall transformations. Furthermore, we expect them also to be easier to predict than overall transformations due to their more elementary nature. In combination, these arguments suggest that working with mechanistic steps may facilitate the application of statistical machine learning approaches, as well as their capability to generalize. Thus, in this work, reactions are modeled as mechanisms, and for the remainder of the paper, we consider the term “reaction” to denote a single elementary reaction.

Previous Approaches

As discussed above, there is a broad spectrum of physical simulation approaches to reaction prediction, from more or less rigorous QM treatment of paths on energy surfaces to discrete mechanistic steps. At all levels though, reaction prioritization is considered by explicitly modeling transition state energies. As such, these simulations can be highly accurate and generalizable but require careful setup for individual experiments and are computationally expensive. For example, many recent physical simulation studies of reaction mechanisms^18-22 involve in-depth exploration of manually setup variants of single systems. Furthermore, these approaches often provide more detailed information than needed to make decisions regarding common chemical tasks such as validating synthesis design, creating virtual libraries, or elucidating plausible mechanistic pathways. This branch of computational chemistry provides invaluable tools for in-depth understanding of chemistry but is currently not suitable for high-throughput reactivity tasks and is far from being able to recapitulate the knowledge and ability of a human expert.

Around the second pole of the computational spectrum, rule-based approaches are meant to approximate decision making rules of human chemists using libraries of graph rearrangement patterns. In contrast to physics-based approaches modeling atom point geometries and electron distribution over orbital basis sets, rule-based approaches conceptualize overall transformation reactions as the making and breaking of bonds in molecular graph representations, i.e., graph rearrangements. Furthermore, rather than using a scoring function to prioritize all possible graph rearrangements, these systems only propose the rearrangements corresponding to the overall transformation reactions yielding the major products.

An overall transformation can be decomposed into a sequence of “productive” mechanistic reactions. By “productive” mechanistic reactions, we and most previous systems broadly mean the mechanistic steps which eventually lead to the overall major products of a multi-step reaction. In systems which work on a mechanistic level of detail, elementary reactions which are not the most kinetically favorable, but which eventually lead to the overall thermodynamic transformation product may be considered “productive”. For example, a protonation step in a synthesis is usually a kinetically reversible reaction. In the next step of the synthesis, the deprotonation on the protonated product may be kinetically favorable but is neither an interesting nor a “productive” reaction. Therefore, rule-based systems do not predict energies per se. Rather they make predictions about synthetically productive transformations. Fortunately, the the most “productive” mechanistic steps are typically the same as the most kinetically favorable steps.

Seminal work in the area of rule-based reaction prediction is encapsulated in the CAMEO⁷ and EROS⁸ systems. CAMEO is based on a complex set of heuristics divided over different classes of chemistry to predict multi-step reactions. EROS uses a more configurable system composed of multi-step reaction graph based rule libraries with extra modules to add more constraints based on heats of formation, physicochemical properties, or kinetic simulations. Other approaches since CAMEO and EROS have contributed their own ideas to the problem. Beppe¹⁰ and Sophia⁹ focus on first identifying reactive sites before identifying reactions, though both work with multi-step reactions. ToyChem¹¹ and Robia¹² build on the EROS idea of physicochemical constraints by explicitly defining reaction energy functions. The recent Reaction Explorer system¹⁴ uses detailed graph rewrite rules for individual mechanistic steps rather than the common practice of a single transformation for an overall reaction from starting materials to final products. Furthermore, Reaction Explorer describes these rules using an alternative physically motivated “electron-flow” specification allowing the visualization of the “arrow-pushing” diagrams for each mechanistic step.

At their core however, all of the above rule-based systems are knowledge-based, with human encoding of heuristics, graph-rewrite patterns, and constraints. Therefore, although these systems are computationally tractable and return predictions quickly, these expert systems suffer from several drawbacks: (1) They require the curation of large amounts of expert knowledge; rules and exception handling must be explicitly encoded for many different chemistries. (2) They are unmanageable at larger scales, in that adding new rearrangement patterns often involves updating a large proportion of existing patterns with exceptions. It is noted in the Reaction Explorer system that adding new transformations is already a challenging undertaking with 80 reagent modules although several hundreds would be required to cover the breadth of modern chemistry.¹⁴ (3) They lack generality. If a particular reaction pattern has not been explicitly encoded, the system will never be able to return the corresponding reaction.

There have been few previous approaches around the third computational pole of machine learning. Sophia extracts relevant reaction centers from databases of multi-step overall transformations.⁹ Rose and Gasteiger show how to inductively derive multi-step reaction rules for the EROS system using reaction centers mined from reaction databases,¹⁵ though to the best of our knowledge, this was not adopted in EROS moving forward. Given improvements in machine learning techniques over the past 15 years, one can imagine a machine learning system that mines reaction information to learn the grammar of chemistry¹, in which both the conceptualization and scoring of reactions is learned from data. One source of reaction information is the chemical literature. Unfortunately however, chemical publishing is dominated by closed models, and thus literature information is difficult to access. Furthermore, most reaction information within manuscripts is non-standardized and unstructured. Parsing scientific text and extracting relevant chemical information from text and image data is an open problem of research.^24-26 Other potential sources of reaction information are reaction databases. While there are several commercially available reaction databases, such as CAS,²⁷ Reaxys,²⁸ and SPRESI,²⁹ unfortunately the majority of the reactions in these databases are unbalanced, are incompletely atom-mapped, and lack mechanistic definition.³⁰ This is in addition to suffering from an even more acute lack of openness as compared to the chemical literature, in that reaction databases are often priced far beyond academic reach or accessible only through very limited and closed interfaces that prevent any kind of serious statistical data mining. As a result, and to the best of our knowledge, effective machine learning approaches to reaction prediction simply do not exist.

A successful reaction prediction system should emulate, and eventually surpass, the problem solving abilities of human chemists, though this has yet to happen. Human chemists possess a remarkable ability to make reasonable predictions about the outcome of reactions. These predictions are of course based on an underlying physical understanding, but they are certainly not based on in-depth numerical calculations. Furthermore, while memorization of named reactions and their patterns is paramount in chemical education, human predictive decisions are often made without systematic deductive reasoning, but rather using trends and rules of thumb learned from experience.

New Approach

These considerations motivate our new reaction prediction framework which incorporates elements from all the three computational poles considered above. We combine the idea of orbital basis sets with molecular graph representations to describe physically inspired, graph-based idealized molecular orbitals. Using these idealized molecular orbitals, mechanistic reactions are modeled as an interaction between an electron filled (donor) and electron unfilled (acceptor) molecular orbital. This allows the constructive enumeration of all possible elementary reactions over any set of reacting molecules. From the Reaction Explorer rule-based system, we derive a dataset of “productive” reactions to mine. Finally from machine learning, we formulate predicting the productive interacting MOs as a statistical ranking problem.

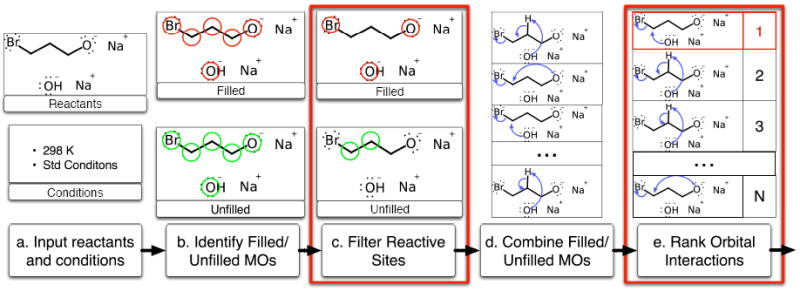
The overall framework leads to the pipeline shown in Algorithm 1, including two machine learning stages outlined in red. Given input reactants and conditions, we first use the idealized molecular orbitals to identify electron sources and sinks within the reactants. Then in the first machine learning stage, highly sensitive predictive models, trained from data derived from Reaction Explorer, are used to filter out electron filled and unfilled unreactive sites, thus pruning the space of reactions to consider. The remaining electron sources and sinks are then paired to construct all reasonable elementary reactions over the reactants. Then in the second machine learning stage, a ranking model, again trained from Reaction Explorer derived data, is used to order the elementary reactions by productivity. Finally, the output top ranked products can be recursively chained as inputs to a new instance of the pipeline, leading to multi-step reaction prediction.

The are multiple benefits resulting from this new approach. By using very general rules to enumerate electron sources and sinks, and thus possible reactions with their pairing, the approach is not restricted to manually curated reaction patterns. By detailing individual reactions at the mechanistic level, the system may be able to statistically learn efficient predictive models based on physicochemical attributes rather than abstract overall transformations. And by ranking possible reactions instead of making binary decisions, the system may provide results amenable to flexible interpretation. However, the new approach also faces three key challenges: (1) the development of appropriate training datasets of elementary reactions; (2) the development of a machine learning approach to control the combinatorial complexity resulting from considering all possible pairs of electron donors and acceptors among the reacting molecules; and (3) the development of machine learning solutions to the problem of predictively ranking the possible productive mechanisms.

The remainder of the manuscript is organized as follows. First, we describe the graph-based idealized molecular orbital reaction model and pose the general machine learning problem. Then we detail the data, specifically constructing a dataset of productive reactions using the Reaction Explorer system to address the first challenge. Next, we describe the implementation and validation of the two machine learning components. The first component is for addressing the combinatorial complexity challenge and the second component is for addressing the ranking challenge. We then describe the overall reaction prediction results and conclude with a summary and discussion of the results.

Molecular Orbital Reaction Model

We propose a fundamental reaction unit model starting from the structure of the reactants to enumerate all conceivable primary idealized molecular orbital interactions³¹ visualizable as “arrow-pushing” diagrams. This approach yields elementary reaction steps that describe the implied transition state. Other formalisms to describe or enumerate possible chemical reactions exist, such as Dugundji-Ugi,³² Temkin et. al.,³³ and Kerber et. al.,³⁴ but these all encapsulate overall transformations, or general graph rearrangements, and none are analogous to such an ubiquitous chemical idea as “arrow-pushing.”

A molecule m is modeled in the standard manner as a labeled connected molecular graph m = G_m(A_m, B_m) where the vertices A_m represent labeled atoms and the edges B_m represent labeled bonds. Then each atom in the graph is augmented with multiple labels to represent approximate electron filled and electron unfilled molecular orbitals (MOs). An electron filled MO is defined as the quadruple

$$f:=(a,t_f,n_f,c_f),$$

where a is the atom being labeled, i.e., the main atom, t_f ∈ {n, π, σ} is the orbital type, n_f is the possibly null neighbor atom for a bond orbital, and c_f is the possibly null, recursively defined adjacent chained filled orbital. Lone pairs are represented with orbital type t_f = n, a null neighbor n_f = 0̸, and without chaining possibility c_f = 0̸. Bonding MOs are represented with n_f referencing the bond partner atom, orbital type t_f = π for double and triple bonds, and orbital type t_f = σ for single bonds. Each bond can have many MO labels if there are chaining possibilities, where chaining possibilities are recursively found by noting π-system filled MOs centered on atoms adjacent to n_f. Enumerating chaining possibilities are necessary to capture resonance rearrangements and certain reactions such as eliminations. Similarly, an electron unfilled MO is defined as the quadruple

$$u:=(a,t_u,n_u,c_u),$$

where a is the main, or current, atom, t_u ∈ {σ*, π*, p} is the orbital type, n_u is the possibly null neighbor atom for a bond orbital, and c_u is the possibly null, recursively defined adjacent chained unfilled orbital. Unfilled MOs are represented in an analogous manner: Empty atomic orbitals are represented with orbital type t_u = p, n_f = 0̸, and c_f = 0̸. Anti-bonding MOs are represented with n_u referencing the bond partner atom, t_f = π* for double and triple bonds, and t_f = σ* for single bonds. Chaining possibilities for a given unfilled anti-bonding MO are constructed by noting π or σ-system unfilled MOs on atoms adjacent to n_u. The basic filled and unfilled orbital types are shown in Figure 3, while an example of all the filled and unfilled orbitals constructed at a single atom of a molecule are shown in Figure 4.

Figure 3.

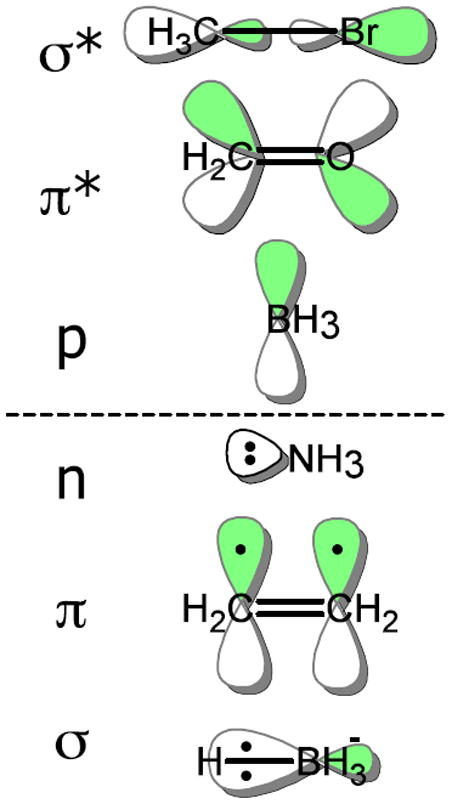
Molecular orbital types in the augmented molecular graph for the core reaction model. Unfilled molecular orbital types are on the top and filled types are on the bottom.

Figure 4.

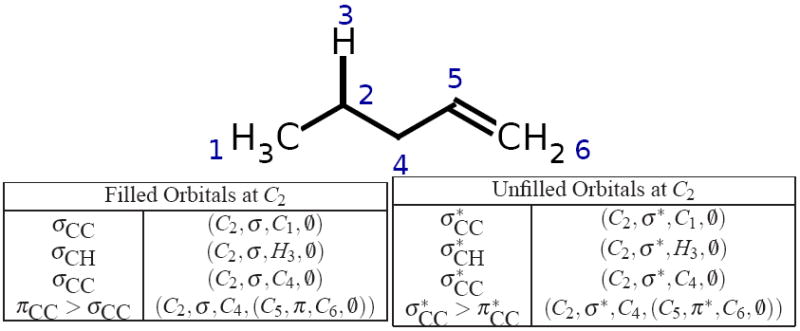
The filled and unfilled orbitals yielded for C₂. Note the π bond adjacent to C₄ acts as either a filled or unfilled chain orbital.

A reaction is then described by the interaction of a single filled and a single unfilled molecular orbital. It is helpful to think of this as an “arrow-pushing” diagram. The filled MO denotes the source of electrons, while the unfilled MO denotes the electron destination, i.e., the interaction is a directed arrow from the filled MO to the unfilled MO. The algorithm in Appendix A shows a simple recursive algorithm used to alter charges and bonds and thus yield the product of an interaction in a molecular graph, in other words, the algorithm to actually “push the arrows”. Examples of the arrow pushing diagrams and corresponding filled and unfilled MO representations are shown in Figure 5. Furthermore, as a reaction is simply a representation of a directed arrows of electrons over a set of molecules, one can easily define “inverse” MO’s for a given reaction. For a given interaction (f, u) on reactants r which yields the products r′, there is a filled orbital (f′) and an unfilled orbital (u′) over r′ such that the interaction (f′, u′) yields the original reactants r. We define f′ and u′ as the inverse filled and unfilled orbitals respectively.

Figure 5.

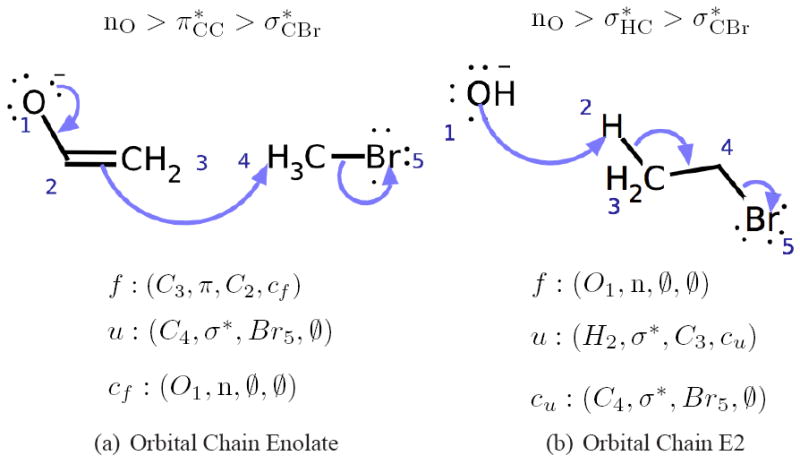
Extended orbital chain interaction examples. (a) Enolate reacting as a lone pair, π-bond chain. Chaining is necessary to capture the implicit pre-reaction resonance rearrangement. (b) E2 elimination where the H-C σ-bond chains into the C-Br σ-bond. The central bond in each chain simultaneously acts as an electron source and sink at different points in the overall flow.

Machine Learning Problems

Let F_m be the set of all electron filled MOs in a molecular graph m, and similarly, let U_m be the set of electron unfilled MOs over m. The set of reactions over a single copy of a pair of reactants r = (m₁, m₂) is equivalent to the set I_r of pairs of interacting filled and unfilled MOs (f, u) over r, i.e. I_r = (F_m1 ∪ F_m2) × (U_m1 ∪ U_m2) The actual number of reactions to consider is more than this, because one must also consider intermolecular reactions between each reactant and a second equivalent of itself. To avoid unnecessarily complicated notation, we will continue to discuss the number of reactions to consider as I_r = (F_m1 ∪ F_m2), though all experiments and presented statistics correctly reflect including second equivalent reactions.

We make the assumption that for each set of reactants and conditions, which we call a “query” denoted with (r, c), there are only a small number of “productive” reactions. For a given query (r, c), denote this set of productive reactions as $I_{(r,c)}^{+}\subset I_r$ and the complementary set of “unproductive” reactions as $I_{(r,c)}^{-}=I_r-I_{(r,c)}^{+}$. The problem of reaction prediction is thus that of identifying the reactions in $I_{(r,c)}^{+}$ given a query (r, c).

For a given query, there are often only one or two productive orbital interactions. On the other hand, with the number of filled orbitals |F_r| approximately equal to 2 times the number of symmetrically distinct bonds plus the number of lone pairs, and the number of unfilled orbitals |U_r| approximately equal to 2 times the number of symmetrically distinct bonds plus the number of empty orbitals, the number of total orbital interactions |F_r × U_r| can be quite large even for moderately sized systems. Consider a system of 20 symmetrically distinct bonds with no lone pairs or empty orbitals, and disregard chained orbitals and second equivalent reactions. Such a system would have (2 × 20)² = 1600 potential elementary steps. Including chained orbitals and second equivalent reactions leads to even larger numbers of total orbital interactions. This highly imbalanced situation motivates identifying productive reactions given a (r, c) query in two stages. In the first stage, we train and use classifiers to filter out filled and unfilled MOs at the level of atoms, similar to the reactive site identification of Beppe¹⁰ and Sophia.⁹ In the second stage, we train and use a ranking model such that given (r, c) all reactions in $I_{(r,c)}^{+}$ are ranked higher than all reactions in $I_{(r,c)}^{-}$.

Reactive site filtering

Both filled and unfilled MOs can be considered labels associated with particular atoms, i.e., the main atom of the MO. For a particular molecular graph m and conditions c, let the set of all filled MOs over m involved in a productive orbital interaction with conditions c be $F_{(m,c)}^{+}=\{f|(f,u)\in I_{(r,c)}^{+}\mathrm{and}m\in r\}$. For each atom a ∈ A_m, we label the tuple (a, c) as “filled reactive” if a is the main atom of any MO in the set of productive filled MOs $F_{(m,c)}^{+}$, and we label the tuple (a, c) as “filled unreactive” otherwise. Similarly, we label each (a, c) tuple as “unfilled reactive” or “unfilled unreactive” using the set of productive unfilled MOs over (m, c). The end result is two reactivity labels for each atom, one each for filled and unfilled.

One can then train separate classifiers for each of the these labels with the goal of filtering as many unreactive labeled atoms as possible while allowing zero filtering errors on the reactive labeled atoms. Any atom predicted as “filled unreactive” by the classifier is then not considered when constructing the set of possible filled MOs, and similarly for unfilled MOs. Let F̂_(m,c) and Û_(m,c) be the set of filtered filled and unfilled MOs, respectively. Then the set of filtered reactions over a query is Î_(r,c) = (F̂_(m1,c) ∪ F̂_(m2,c)) × (Û_(m1,c) ∪ Û_(m2,c)), which can be broken up into productive and unproductive sets, ${\widehat{I}}_{(r,c)}={\widehat{I}}_{(r,c)}^{+}+{\widehat{I}}_{(r,c)}^{-}$. A successful filtering should give ${\widehat{I}}_{(r,c)}^{+}=I_{(r,c)}^{+}$ and $|{\widehat{I}}_{(r,c)}^{-}|\ll |I_{(r,c)}^{-}|$.

Orbital interaction ranking

After filtering, the problem of identifying the subset of productive reactions ${\widehat{I}}_{(r,c)}^{+}$ from Î_(r,c) can be construed as a ranking problem. Learning to rank is a subject of great interest in the machine learning community, in particular for Information Retrieval (IR) and web-page ranking. Some methods pose ranking as ordinal regression,^35,36 where individual instances are regressed to an integer rank. However, many ranking methods use a pairwise formulation which predicts whether a pair of instances are in correct order.^37-40 In this work, we use a pairwise approach using shared weight artificial neural networks training on ordered pairs of productive and unproductive orbital interactions $(i^{+},i^{-})\in {\widehat{I}}_{(r,c)}^{+}\times {\widehat{I}}_{(r,c)}^{-}$.

Data

A mechanistically defined dataset of reactions to use with the proposed framework does not currently exist. In this section, we leverage previous work on a mechanistically defined rule-based system, Reaction Explorer,¹⁴ to construct the first such dataset, consisting of reactant molecules with conditions and their productive orbital interactions.

Details are given in (Chen and Baldi 2009),¹⁴ but briefly Reaction Explorer is a rule-based expert system covering all of the basic undergraduate organic chemistry curriculum. The system is composed of over 1500 elementary rules organized into 80 reagent models encoding conditions and allowable rules. Each rule encapsulates a single mechanistic reaction step via a SMIRKS⁴¹ topological rearrangement pattern and an electron flow specification to capture “arrow-pushing”. An inference engine orders the elementary rules by priority to attempt matching on given reactants. Moreover, in order to validate the rules and to provide examples for a chemistry tutor application,¹³ over 4000 full multi-step “test case” syntheses are encoded including reactants, reagents, products, and all intermediates.

When each individual test case is input to Reaction Explorer, a list of mechanistic steps is output describing the orbital interactions from each previous step; starting at reactants, through intermediates, and to final products. Each one of these mechanistic steps is considered to be a distinct productive elementary reaction. In addition, we assign simple reaction condition descriptions that are shared among all reactions from a particular reagent model. Grouping all the individual favorable orbital interactions over the same reactants and conditions yields the overall set of productive orbital interactions $I_{r,c}^{+}$. With these sets of labeled MO interactions over reactants and conditions (r, c) queries, we then provide each possible atom and conditions (a, c) tuple with filled and unfilled reactivity labels.

Reaction conditions are described with three parameters: temperature, anion solvation potential, and cation solvation potential. Temperature is listed in Kelvin. The solvation potentials are unitless numbers between 0 and 1 meant to represent how easily a cation or anion is solvated and thus provide a quantitative scale at which to map the qualitative ideas of polar protic, polar aprotic, and nonpolar solvents. These parameters have been set for all Reaction Explorer reagent models. Note however, that any mechanistic interaction with solvent is explicitly captured as an elementary reaction. As an example of some of the parameter settings used, the Reaction Explorer “Mix Reactants, Polar Protic” reagent model has a temperature 298 K, a cation solvation potential of 1.0, and an anion solvation potential of 1.0, while the Reaction Explorer reagent model of “2Li, Hexane” for alkyl lithium preparation in a nonpolar solvent has a temperature 298 K, a cation solvation potential of 0.0, and an anion solvation potential of 0.0. In the middle of the solvation spectrum, the “LDA, THF” reagent model has a temperature of 220 K, a cation solvation potential of 0.8, and an anion solvation potential of 0.4. A full listing of the reaction parameters by reagent is presented in Supplementary Table S1.

As an initial validation of the methods and to keep the size of the dataset manageable, we consider general ionic reactions involving C, H, N, O, Li, and the halides, coming from 1630 multi-step test cases over 31 reagent models from Reaction Explorer.¹⁴ Methods to include stereoselectivity and handle pericyclic and radical reactions are discussed in the Conclusion. A complete listing of the 31 reagents and their respective reaction condition parameters is presented in Supplementary Table S1.

Inputting the 1630 test cases to Reaction Explorer yields 2989 productive orbital interactions over 2752 distinct reactants and reaction conditions, i.e., (r, c) queries. These 2752 distinct reactants and conditions consist of 1685 individual molecules and 2342 reactants (possibly pairs of molecules). Using the core reaction unit model to enumerate all remaining possible orbital interactions over the reactants and conditions gives 6.14 million non-productive orbital interactions. Considering all individual molecules, there are 22894 symmetrically distinct atoms. However, including reaction conditions yields 29104 reactive sites, i.e., atom and conditions tuples (a, c). 1262 reactive sites correspond to a productive filled MO, while 1786 correspond to a productive unfilled MO.

The attributes and labels for the reaction ranking and reactive site datasets are available via our chemoinformatics portal (http://cdb.ics.uci.edu) under the Supplementary Materials section and via the UCI Machine Learning Repository at http://archive.ics.uci.edu/ml.

Machine Learning Stage 1: Reactive Site Filtering

Recall that we wish to train two separate classifiers to predict the filled and unfilled reactivity labels of an atom. The feature descriptions and machine learning implementations used are exactly the same for the two separate problems, except for the different labels. As such, a general reactivity labeled dataset will be considered as instances of (a, c, l), i.e. an atom a, a set of conditions c, and a label l ∈ {0, 1}, where l = 1, if (a, c) is labeled “reactive”, and l = 0 otherwise.

Validation

Repeated cross-validation experiments are recommended to obtain reliable accuracy estimates during validation of supervised learning.^42,43 To assess the performance of the reactive site filter training, we perform 10 repeats of 10-fold cross-validation over all distinct tuples of molecules and conditions (m, c). This validation scheme closely mimics the real-life use of such a system, where atoms, conditions (a, c) tuples with unknown label are seen as part of entire molecule in which all atoms are missing labels.

Feature representation

To learn a model predicting the labels l for each (a, c) instance, we must define a feature representation which maps the conceptual atom to a numerical vector. The vector of course includes the reaction conditions, which here are simply temperature, cation solvation potential, and anion solvation potential, as determined by the underlying Reaction Explorer reagent model (Table S1).

Next, the vector includes features to describe the atom and its neighborhood. The following real-valued features are included:

• formal and partial⁴⁴ charges at a;

• minimum and maximum formal and partial charges at topological neighborhoods of distance 1 and 2 bonds from a;

• an exponentially decaying sum of atomic radii in a’s topological neighborhood;

• molecular weight of the entire molecule; and

• the size of the smallest ring of which a is a member.

Molecular fingerprinting techniques for chemical similarity have been proven useful for QSAR/QSPR and database searching applications.^45,46 Motivated by the success of fingerprints, we construct neighborhood fingerprints to provide a topological depiction of the region around the atom a. These neighborhood fingerprints are composed of counts of paths and sub-trees starting or rooted at the atom a. See Figure 6 for an example of paths over the nitrogen of diisopropylamide anion.

Figure 6.

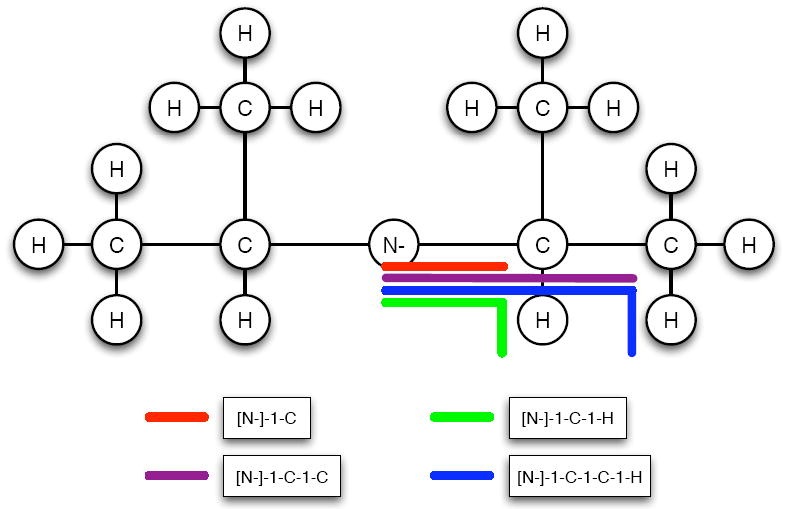
Topological based count features. Diisopropylamide anion is pictured in a cartoon format with all the distinct path types starting at the nitrogen. Sub-trees (not shown) are rooted at the atom with out-degree at most 2.

Separate neighborhood fingerprints are computed for both the standard molecular graph and a pharmacophore point graph.⁴⁷ Pharmacophore point graph features are computed similarly to molecular graph features, except that the molecular graph m = G_m(A_m, B_m) is first mapped to an isomorphic graph p = G_p(A_p, B_p), in which A_p, B_p are atoms and bonds with a small restricted set of labels. The labeling scheme, adapted from Hähnke, et al.,⁴⁷ groups chemical motifs with similar reactivity. For example, all positively charged atoms are labeled the same, all negatively charged atoms are labeled the same, and all halides are labeled the same in the pharmacophore point graph. Details of the mapping and the labels are given in Supplementary Table S2.

These representations schemes generate large but sparse feature vectors. To limit the dimensionality, any feature that is non-zero in less than 25 data points is disregarded. For both the molecular graph and pharmacophore point graph features, standard paths and sub-trees are computed to depth 3 and 2, respectively, while paths and sub-trees through π systems are both computed to depth 6. Furthermore, sub-trees are restricted to have out-degree at most 2. The number of features for each type are listed in Table 1.

Table 1.

Reactive site features

Type	Count
Real-valued	14
Molecular graph	743
Pharmacophore graph	759
Total	1516

Artificial neural network training

Before training, all features are normalized to [0, 1] using the minimum and maximum values of the training set. Then because the (a, c) tuples labeled reactive comprise less than 10% of the data for either filled or unfilled, we oversample sites labeled reactive to ensure approximately balanced classes.

We train artificial neural networks using sigmoidal activation functions in a single hidden layer and a single output node. After some experimentation, an architecture of 10 hidden nodes was chosen. Gradients on the weights of the neural network are calculated with the standard back-propagation algorithm and a L2 regularized cross-entropy error function. The weights are optimized by stochastic gradient descent with per weight adaptive learning rates.⁴⁸ Optimization is stopped after 100 epochs as this is observed to be sufficient for convergence. The end result of training is a neural network model which given an input feature vector outputs a probability of the (a, c) tuple being labeled “reactive”.

Decision threshold fitting

The trained neural networks provide a probabilistic prediction of an (a, c) tuple being labeled “reactive”. However, in order to filter reactions, one must be able to make binary decisions. In our case, we strongly favor sensitivity over specificity, i.e., we will accept a reasonably high number of false positives to ensure a low number of false negatives. Any false negatives translate into misranking entire (r, c) queries. However, because the number of reactions we filter is based on the cross-product of the negative decision rates of our classifiers, modest true negative rates still provide a sizeable amount of negative filtering.

To fit decision thresholds providing high sensitivity, we use internal cross-validation. For each training set, the same cross-validation set creation, normalization, balance, and training procedures described above are used to construct internal three-fold cross-validation predictions. Then on the internal cross-validated predictions, we find the average prediction over all internal folds yielding a false negative rate of 0 for that fold, using this as the decision threshold for the external train and test data.

Results

Important metrics are the number of unreactive labeled sites and unproductive reactions filtered, i.e., the true negative rate (TNR), and the number of reactive labeled sites and productive reactions mis-filtered, i.e., the false negative rate (FNR). The predictive results of these classifiers are shown in Table 2. We can filter 87.7% and 75.6% of filled and unfilled non-reactive sites respectively. This leads to being able to filter 94.0% of the 6.14 million non-productive reactions with 0.012% error on positives, as shown in Table 3.

Table 2.

Reactive Site Prediction Results

Type	Stage	Mean TNR % (SD)	Mean FNR % (SD)
Filled	Test	87.7(2.0)	0.05(0.23)
	Train	87.7(2.0)	8.8 × 10−4(8.8 × 10−3)
Unfilled	Test	75.6(5.8)	0.18(0.38)
	Train	75.5(5.9)	6.2 × 10−4(6.2 × 10−3)

Table 3.

Orbital Interaction Filtering Results

Mean TNR % (SD)	94.0 (1.47)
Mean FNR % (SD)	0.012 (0.027)

In the next section, we describe the implementation and validation of the orbital interaction ranking methods. In order to assess the ranking methods, we construct an overall filtered set of reactions using the best possible filled and unfilled reactive site classifiers. Here, filled and unfilled site predictors are trained using all the available data. Then a decision threshold is fit for each classifier by finding the maximum prediction such that the FNR is 0. The results of the filled and unfilled site predictors as well as overall reaction filtering are shown in Table 4.

Table 4.

Overall Reaction Filtering Results. Here the entire dataset is used to train the best possible filled and unfilled reactive site predictors.

Type	TNR %
Filled	92.1
Unfilled	85.6
Actual Reactions	97.2

Histograms of the predictions from these overall classifiers on the unreactive labeled data are shown in Figure 7 with the predictions on the reactive labeled points jittered in red. One can see that though there are some outlier reactives on which the classifiers exhibit uncertainty, the vast majority of the unreactive prediction density is around 0.

Figure 7.

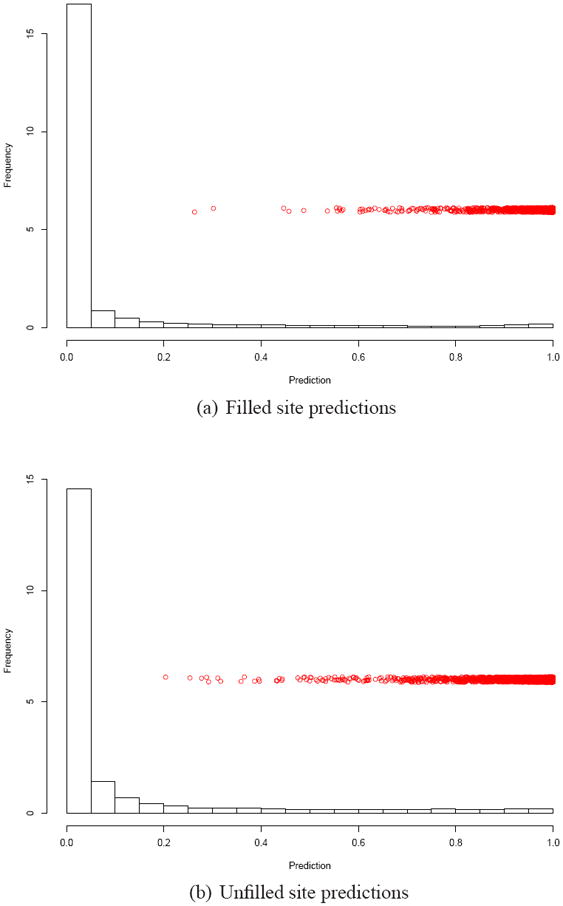
Reactive site predictions using models trained with all the data. The histograms show the distribution of prediction values on the unreactive labeled data. The red points show the prediction values for individual reactive labeled data points jittered for clarity. (a) shows the filled site predictions, while (b) shows the same plot for the unfilled site predictions.

Machine Learning Stage 2: Orbital Interaction Ranking

Validation

As in the reactive site filtering, repeated cross-validation is used to assess the performance of the orbital interaction ranking machine learning component. Using the filtered orbital interaction dataset described above, we perform 10 repeats of 10-fold cross-validation over all reactants, conditions (r, c) tuples. There are 2752 distinct (r, c) queries. With the filtered dataset, there are 1.08 productive reactions and 62.53 non-productive reactions per query on average.

Feature representation

To create feature vectors to represent an orbital interaction, we again include the reaction conditions data. Then, we include features to describe the reactants and the products, constructing a difference vector by subtracting the reactants from the products. These molecular features include counts over:

• bonds;

• anions and cations;

• aromatic bonds and atoms;

• rings of size 3 to 9;

• trans ring π bonds;

• rotatable bonds; and

• multiple, separated formal charges.

The count vector for reactants is subtracted from the count vector for products, and resulting zero elements are discarded. If a difference vector element is positive, it means this feature was “created” during the reaction, while if it is negative, it means this feature was “destroyed” during the reaction. This provides useful information about the reaction, for example broken aromaticity, opening of an epoxide, or charge separation.

Then we add features that represent the filled and unfilled molecular orbitals in the forward reaction. The orbital features include:

• the type of orbital (σ*, π*, p, n, π, σ);

• the type of chained orbital, if it exists;

• actual atoms involved in the orbital;

• formal and partial⁴⁴ charges for each atom involved; and

• an exponentially decaying sum of atomic radii for a neighborhood around the orbital.

To calculate attributes describing the reversibility of a reaction, we also include the same orbital features computed on the inverse filled and unfilled orbitals, i.e., the orbitals of the products whose interaction would yield the reactants.

Finally, we include a subset of the reactive site features for both the filled and unfilled orbitals. Specifically the included reactive site features are non-redundant real-valued features and pharmacophore point graph features with path depth 3, tree depth 2, and π depth 4. Details about the number and types of features are shown in Table 5.

Table 5.

Orbital Interaction Features

Type	Count
Molecular difference	124
Forward Filled and Unfilled	251
Inverse Filled and Unfilled	199
Reactive Site Filled and Unfilled	1103
Total	1677

Artificial neural network training

As in the reactive site prediction, all features are normalized to [0, 1] before training using parameters estimated from each training set. For training speed and memory considerations, 5 sub-splits of each training set are made. Each sub-split includes all productive interactions, but training pairs are constructed with a random partition of the unproductive interactions. Final predictions on test data are made by averaging the predictions from 5 ranking models trained on the individual sub-splits of pairs.

We use a pair of shared weight artificial neural networks each with a single sigmoidal hidden layer and a linear output node. The output of the two networks are tied to a sigmoidal output layer with fixed weights of +1, −1, as shown in Figure 8. The final output of the network will be close to 1 if the shared weight lower network outputs a higher score for the left input than the right input, and close to 0 otherwise. Training is performed by simultaneous forward propagation of both the left and right inputs, and assessment of error at the final output layer with a L2 regularized cross-entropy error function. Then in two separate steps, weight gradients are calculated via back-propagation first in the left network and then the right network. After gradient calculation, the same weight updates are applied to both networks.

Figure 8.

Shared weight artificial neural network architecture. Two shared weight artificial neural networks are connected to a sigmoidal output layer with fixed weights. The output of the final network will approach 1 if the input to the left network is scored greater than the input to the right network, and 0 otherwise. As the lower level networks share weights, they compute the same scoring function.

After some experimentation, an architecture of 20 hidden nodes was chosen. Similar to the reactive site training, weights are optimized using stochastic gradient descent with the same per-weight adaptive learning rate scheme.⁴⁸ Optimization is stopped after 25 epochs as this is observed to be sufficient for convergence.

Results

Next we present results on the orbital interaction ranking. We consider two metrics for evaluating rankings, Normalized Discounted Cumulative Gain (NDCG) and Percent Within-n.

The Normalized Discounted Cumulative Gain (NDCG) is a common IR metric.⁴⁹ For a given result list, the metric sums the usefulness, or gain, of each individual result based on labeled relevance and predicted rank, where the gain for a relevant result is discounted at lower ranks. The NDCG at a level i (NDCG@i) is the metric calculated only considering the top i ranked results. For example, the NDCG@1 will be 1 if the highest ranked reaction is a productive reaction, and 0 otherwise. Therefore, NDCG@1 over all (r, c) queries denotes the percent of the queries in which the highest ranked reaction is a productive reaction.

The Percent Within-n metric is simply how many (r, c) queries have at most n non-productive reactions in the smallest ranked list containing all productive reactions. For example, Percent Within-0 measures the percent of (r, c) queries with perfect rank, and Percent Within-4 measures how often all productive reactions are recovered with at most 4 errors. This metric allows intuitive assessment of close to perfect rankings.

The unproductive orbital interactions vastly outnumber the productive interactions. On average there are 1.08 productive reactions for each reactants, conditions (r, c) query. However, there are 62.53 unproductive reactions on average that pass the reactive site filters for each query. In spite of this imbalance, our results show a remarkable ability to extract the best reactions. The cross-validated ranking results are presented in Table 6. The NDCG metric shows, for example, that for 89.5% of the queries, the top ranked reaction is a productive reaction. Looking at the Within-n data, 89.05% of queries show perfect ranking, while 99.86% of queries recover all productive reactions by considering lists with a small amount of (at most 4) non-productive reactions.

Table 6.

Orbital Interaction Ranking Results. We show Normalized Discounted Cumulative Gain (NDCG) at different levels in addition to the Percent Within-n results. NDCG is a standard information retrieval metric to evaluate rankings, while Percent Within-n is the percent of all queries in which at most n non-productive reactions are in the smallest ranked list containing all productive reactions.

i	Mean NDCG@i (SD)	n	Percent Within-n (SD)
1	0.895(0.016)	0	89.05(1.66)
2	0.939(0.011)	1	96.84(0.98)
3	0.952(0.008)	2	98.94(0.59)
4	0.954(0.007)	3	99.52(0.39)
5	0.956(0.007)	4	99.86(0.25)

Discussion

Multi-step reactions

The strong performance of the ranking system is exhibited by its ability to make accurate multi-step reaction predictions. Figure 9 shows an intramolecular Claisen condensation reaction. To assess whether the ranking system can successfully perform multi-step reaction prediction, we construct a special train/test split of the productive reactions such that the reactions shown in Figure 9 are part of the testing set, while the remaining productive reactions are part of the training set. Using reactive site filters and ranking models trained on this special training set, the ranking method correctly predicts the given reaction as the highest ranked reaction at each of the three steps shown. Note that the predictions are made on data that is unseen during training. Thus, this multi-step reaction prediction is an example of the system’s inductive capability.

Figure 9.

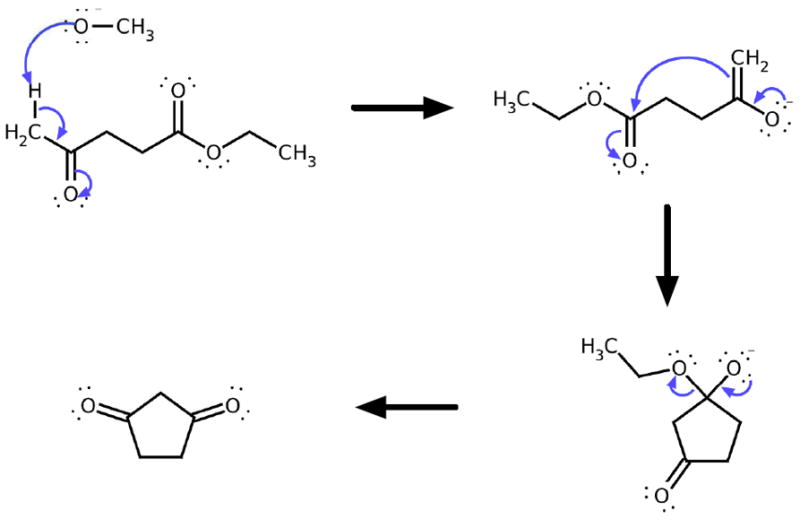
Multi-Step Reaction Prediction. An example of a correctly predicted multi-step reaction from a careful validation experiment. All reactants shown were held out in a special testing set, while all other data in the Reaction Explorer system is used as a training set. Thus, the predictions shown are not seen in training. The products from the top ranked reaction are recursively input to a new instance of the overall pipeline to make a multi-step reaction predictor. The error rate is low enough to make the system usable for prediction of overall transformations.

Ranking provides flexible results

By identifying the productive reactions through ranking, our framework provides flexible and interpretable results. To assess this, we look at the predictions of the ranking system on reactants and conditions in the testing sets of cross-validation splits, i.e., the reactions shown are not seen during training. For example, two ring-forming systems over which productive reactions are correctly ranked are shown in Figure 10. These are the productive reactions for the given reactants under the Reaction Explorer “Mix Reactants, Polar Protic” reagent model. In cross-validation experiments, these are always the top ranked reactions with the reaction conditions corresponding to the reagent model. For the 5-member ring forming reaction in Figure 10(a), the reaction proceeds with the oxygen acting as a nucleophile, and the end product is a heterocycle (2-methylenetetrahydrofuran). However another reasonable, though not as favorable, reaction could occur with an enolate nucleophile and a cyclopentanone product, though this reaction is not labeled as productive by Reaction Explorer. The ranking method correctly returns this particular reaction as the second highest ranked for this set of reactants and conditions.

Figure 10.

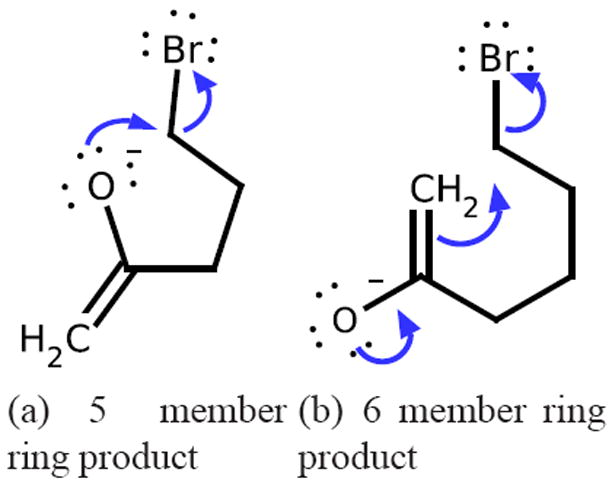
Two correctly ranked ring-forming reactions in cross-validation experiments. These two reactions are labeled productive by Reaction Explorer with the “Mix Reactants, Polar Protic” reagent model. Without seeing these reactions during training, our approach inductively learns to correctly rank these two reactions as the most productive with the corresponding conditions. The system also correctly returns reasonable ring-forming reactions as the second highest ranked for both sets of reactants.

Similarly, for the 6-member ring forming reaction shown in Figure 10(b), the Reaction Explorer productive reaction proceeds via an enolate nucleophile and results in a cyclohexanone product. Another reasonable reaction, via an oxygen nucleophile, leads to the heterocycle product (2-methylenetetrahydropyran), though this reaction is not labeled as productive by Reaction Explorer. Again though, the ranking system correctly returns this as the second highest ranked for this set of reactants and conditions in the test sets of cross-validation experiments. By returning a ranking, the end user has access to much more information about other reasonable mechanisms and pathways.

Generalization

A key goal of the new approach to reaction prediction is to build a system that is generalizable. A generalizable system should be able to make reasonable predictions about reactants and reaction types with which it has only had implicit, rather than explicit, experience. The Reaction Explorer system, as a rules-based expert system without explicit rules about larger-ring forming reactions, does not make any predictions about seven and eight carbon systems similar to those seen in the ring-forming reactions of Figure 10. In reality though, larger ring-forming reactions are possible. Figure 11 shows the top two ranked reactions over both 7-bromohept-1-en-2-olate and 8-bromooct-1-en-2-olate reactant sets. Note, that these reactants are not part of the ranking system’s training set. The ranking model returns the enolate attack as the most favorable, but also returns the lone pair nucleophilic substitution as the second most favorable. Thus the ranking model, in spite of never seeing seven or eight member ring-forming reactions, is able to generalize and make reasonable suggestions, while the rule-based system is limited by the hard-coded transformation patterns. First, the reactive site predictors correctly identify the terminal ene carbon and the oxygen as filled reactive sites and the methylene bromide carbon as the unfilled site. Then the ranking model ranks the enolate substitution reactions as the most productive in both systems, and the lone pair oxygen nucleophile reaction as the second most productive. This is an example of the system inductively learning a reasonable model of productive reactions.

Figure 11.

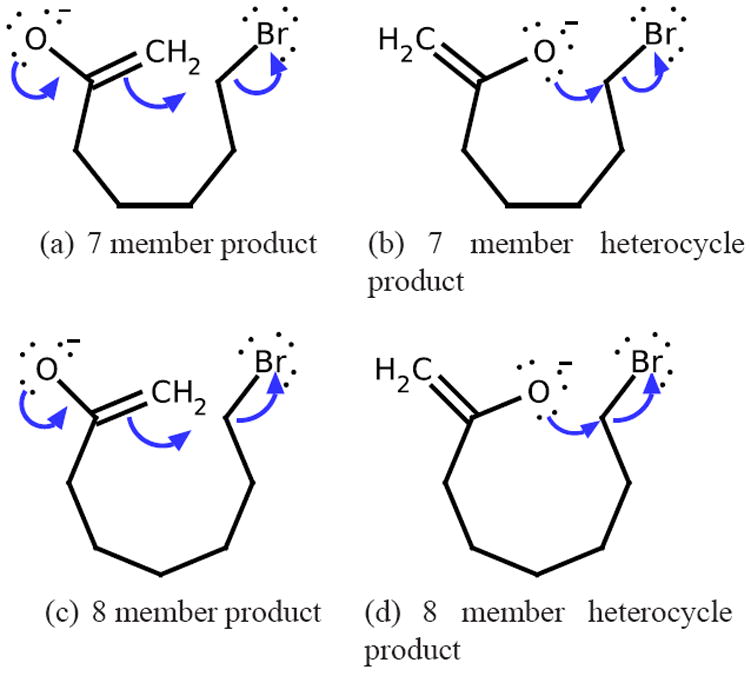
Reasonable reactions not returned by Reaction Explorer, but highly ranked by our system. The reaction conditions for both systems corresponds to the standard conditions from the “Mix Reactants, Polar Protic” Reaction Explorer reagent model. (a) and (c) are the top ranked reactions over the 7-bromohept-1-en-2-olate and 8-bromooct-1-en-2-olate reactants respectively, while (b) and (d) are the second ranked reactions over their respective reactants. Neither set of reactants are included in the training set of productive reactions.

Close rankings are reasonable

While our ranking method is very accurate, it is not perfect. However, the vast majority of errors are close errors, as exhibited by the 99.89% Within-4 recovery rate. Furthermore, upon examination of these close errors in cross-validation experiments, they are largely intelligible and not unreasonable predictions. For example, Figure 12 shows two reactions involving an oxonium compound and a bromide anion. Across all cross-validation experiments where the reactants are part of the testing set, our predictor ranks these two reactions as the highest, with the deprotonation slightly ahead of the substitution. This is considered a within-1 ranking because from the Reaction Explorer system, only the substitution reaction is labeled productive. However, the immediate precursor reaction in the sequence of Reaction Explorer mechanisms leading to these reactions is the reverse of the deprotonation reaction. Hydrogen transfer reactions like this are reversible, and thus the deprotonation is a reasonable mechanism to predict and rank highly. In this case, the deprotonation is likely the kinetically favored mechanism. It is just not productive, in that it does not lead to the final overall product. In a prediction system attempting to predict multi-step syntheses, such reversals of previous steps are easily discarded.

Figure 12.

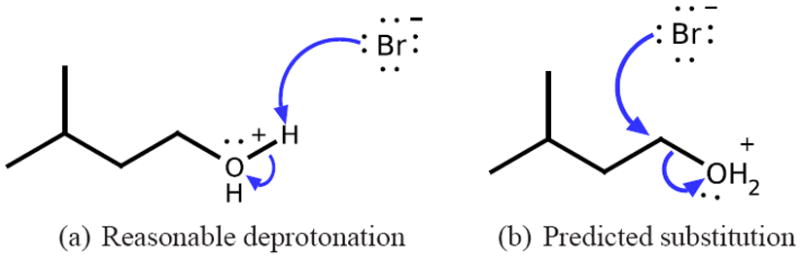
Within-1 ranked system with a reasonable mechanism in cross-validation experiments. The deprotonation is ranked slightly higher than the substitution, although the Reaction Explorer system labels the substitution as productive and does not predict the deprotonation. However, the previous step in this test case was the protonation of the alchohol. As this hydrogen transfer reaction is reversible, the deprotonation is kinetically favorable, just not productive.

There are some interesting ring-forming reactions which we label as mis-ranked in cross-validation experiments. In Figure 13, the Reaction Explorer labeled productive reaction over 2,7-dimethyloct-2-ene under the “Mix Reactants, Polar Protic” reagent model forms a six-member ring product (Figure 13(a)) and results in a 2’ carbocation. This particular reaction is an intermediate step in a multi-step reaction involving a subsequent methyl shift, stabilizing the cyclohexane product. Another plausible mechanism over 2,7-dimethyloct-2-ene exists, leading to a 5-member ring product with a 3’ carbocation as shown in Figure 13(b). In cross-validation experiments when the 2,7-dimethyloct-2-ene is part of the testing set, the ranking system consistently returns the 5-member ring forming reaction as more favorable, while the 6-member ring product is consistently ranked as the second highest. This points to our ranking model has “learned” that increasing alkyl substitution stabilizes carbocations, but has not “learned enough” about the stabilization of potential subsequent carbocation rearrangements. While the stabilized cyclohexane is likely the ultimate thermodynamic product, it is probable that both mechanisms occur, starting from the reactants shown. Thus, although our metrics consider this ranking on the query as an error, it is an intelligible and reasonable error. Again though, by returning a ranking, a multi-step reaction prediction program could easily explore both of these reaction pathways.

Figure 13.

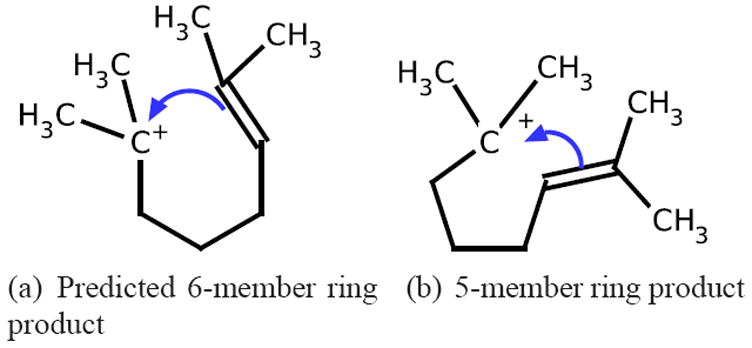
Within-1 ranked system with a reasonable mechanism in cross-validation experiments. The top two ranked reactions with 2,7-dimethyloct-2-ene, an intermediate in a Reaction Explorer multi-step reaction. Reaction Explorer labels only the 6-member ring forming reaction as productive. Although this leaves a 2’ carbocation, it is considered productive because of future methyl shifts in the underlying Reaction Explorer reaction sequence. We consistently rank the reaction yielding a 5-member ring and 3’ carbocation higher in cross-validation experiments where 2,7-dimethyloct-2-ene is in the test set. Although this is considered an error, it is a reasonable one.

Effect of reaction conditions

There are no major differences in performance when considering reactions at different conditions. Figure 14 shows the Within-n results for all the reactions conditions for differenct values of n over all cross-validation experiments. The reaction conditions with the largest number of queries show greater than 90% Within-0 values. However, all conditions show similar performance on the close rankings. When n ≥ 2, then all reaction conditions exhibit > 95% recovery perfomance.

Figure 14.

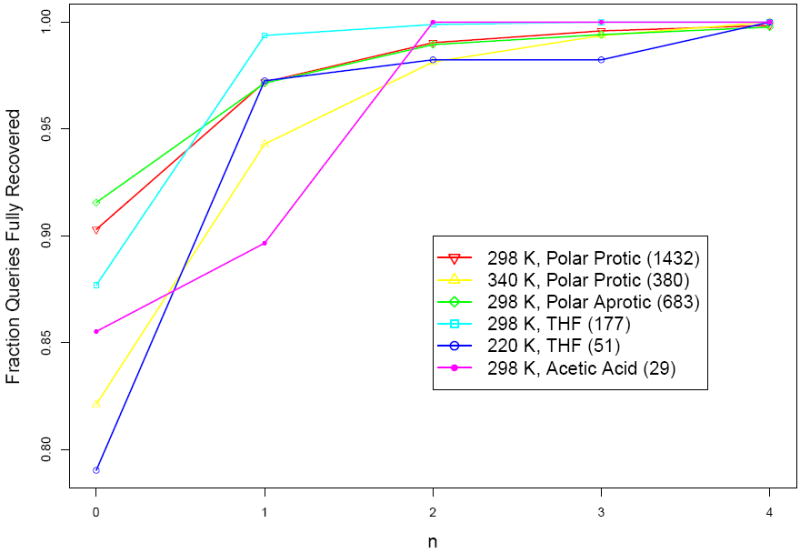
Within-n predicted reaction recovery for different reaction conditions over cross-validation experiments. The fraction of reactant systems in which all productive reactions are recovered is presented on the y-axis, and the n is presented on the x-axis. Color and symbols are used to denoted different reaction conditions. The number of queries with the given reaction conditions are presented in parentheses after the conditions name. Details of the reaction conditions and how they map back to the Reaction Explorer reagent models are presented in Table S1.

Availability

A public web interface to the machine learning based mechanistic reaction prediction system is available under the Toolkits section of our chemoinformatics portal (http://cdb.ics.uci.edu). The interface allows the entry of reactants and conditions, outputting the filtered reactive sites and a ranked list of the filtered reactions. Models trained with all available data are used in the web interface system.

Conclusion

In this work, we describe a novel approach to reaction prediction drawing elements from the three poles of potential approaches. Rather than knowledge engineering a library of transformation patterns commonly used in existing rule-based systems, we define a molecular orbital based reaction unit model to enumerate all possible reactions as flows of electrons from sources to sinks. Then using a two-stage machine learning approach, we return a ranking over all possible reactions for given reactants and conditions, such that the top ranked reactions correspond to the most productive Thus, the ordering is based on a model learned from data rather than explicitly encoded rules.

In terms of scale, our approach is only limited by the amount of data available. If we wish to capture a new set of chemistry, we only need to re-train with sufficient amounts of data covering this chemistry. On the other hand, adding a new set of rules to an expert system often involves having to revisit a large proportion of existing rules to add exception cases. Unfortunately, while there are existing commercial reaction databases, none currently exist with the level of cleanliness or mechanistic detail necessary to validate our proposed approach. However, one could manually curate mechanistically labeled reactions, or use existing expert systems to construct datasets with the required level of detail.

Using an existing mechanistically defined rule-based system, Reaction Explorer, we create an intitial dataset over a restricted set of chemistry. The dataset can be expanded by manual addition of reactions or by expanding the classes of chemistry extracted from Reaction Explorer. We note that this process is significantly easier than the addition of transformation rules to an expert system. Instead of having to manually revisit abstract patterns, our system unleashes powerful statistical techniques to automatically learn the abstraction.

The features and labels for the reactive site and reaction ranking datasets are made available both at our chemoinformatics portal http://cdb.ics.uci.edu under the Supplementary Materials section and as part of the UCI Machine Learning Repository at http://archive.ics.uci.edu/ml/. A web interface to the machine learning based mechanistic reaction prediction system is made available through our chemoinformatics portal (http://cdb.ics.uci.edu) under the Toolkits section.

Based on repeated cross-validation experiments over the Reaction Explorer dataset, our machine learning approach performs well compared to the rule-based system, being able to recover perfect ranking 89.05% of the time. If we allow close rankings, i.e., rankings with up to 4 negatives ranked before the positives, then our method is highly sensitive with respect to the dataset, recovering 99.86% of the productive reactions.

The strong performance of the system is further exhibited by several observations. The high accuracy in the perfect rankings allow multi-step reaction prediction. The highest ranked product from one iteration of the ranking pipeline can be recursively input into a new instance to make the next mechanistic reaction prediction. By allowing the exploration of results further down the ranked list, the ranking system provides flexible and interpretable results, providing plausible reactions of competing favorability.

Furthermore, when the ranking system makes close errors, the mis-ranked non-productive reactions are reasonable and intelligible errors. Reverse reactions of previous steps in a synthesis are often kinetically favorable, though in a reaction simulator application, one could easily ignore reactions which lead to no net change in a reaction mixture. Moreover, as the Reaction Explorer system is constructed to return major products leading to straightforward syntheses, many of the close ranked systems actually represent other reasonable mechanisms that possibly generate side products. Noting these possible side products would be important in a synthesis planning or validation application.

Then, as shown by our prediction of the macrocyclization in Results, our method shows potential to be generalizable. Intramolecular ring-forming reactions are encoded by explicit transformation patterns in the Reaction Explorer. Without explicit patterns for macrocyclizations, the seven and eight membered ring-forming reactions are not predicted. However, the ranking system correctly identifies reactive sites, and the top two reactions ranked in each system are reasonable mechanisms. Even without having specific macrocyclization reactions to train on, the ranking model correctly generalizes from smaller ring systems it has experienced.

Our approach does differ from traditional reaction prediction. Returning a ranking rather than binary decisions is both an advantage and disadvantage of our approach. To use as a direct replacement to an expert system, the number of reactions to consider in the ranking must be fit as an extra hyperparameter or chosen by hand. On the other hand, ranking reactions is an advantage because is allows more flexible use of results. There are usually many different reactions and use of information about the previous and next steps is necessary to be able to make predictions over multi-step syntheses. In addition, one could immediately use our framework with training data with more levels of labeling, i.e., instead of simply labeling reactions as “productive” and “unproductive”, the ranking framework could just as easily use finer labels such as “most productive”, “somewhat productive”, “unproductive”. This could potentially increase the performance of the system.

With this work, we have successfully produced a proof-of-concept on a core subset of chemistry. This lays the framework for a many possible improvements and enhancements to extend the power and generality of the system. Obvious areas for further improvement include radicals, pericyclic reactions, and stereochemistry. For radical reactions, we can allow molecular orbitals to be occupied with 0, 1, or 2 electrons and annotate the orbital interaction with the number of electrons involved. For pericyclic reactions, we can allow the filled and unfilled molecular orbitals to chain such that they are connected, i.e., the final unfilled molecular orbital in a chain of unfilled molecular orbitals is the filled molecular orbital. Stereochemical control mechanics are already handled for simple cases such SN2 reactions, and are easily implemented for reactions involving π systems by augmenting the molecular orbital representations with information to define a face orientation. Features can be extended to account for stereochemistry, for example, by augmenting tree and path features with the proper stereochemical labels. As proposed, these extensions will both increase both the number of reactions to consider and feature dimensionality. However, the promising results on the core proof-of-concept indicate that these difficulties can be overcome.

There are a number of potential uses of our system. The ranking system could be used as a pathway prediction program, in which we wish to discover a plausible mechanistic pathway from a set of reactants to products. Standard depth-first search could be used with the ranking model prioritizing reactions to explore at each stage. One could also use the ranking system to construct virtual libraries; given a database of starting materials and a grid of reasonable reaction conditions to use, rank the orbital interactions over all pairs of molecules, retaining the top ranked one or two products from each ranking. Of course, the system would be very useful validating retro-synthetic proposals. Not only could the system tell whether the proposed pathway is reasonable, the flexible ranking results could be used to flag unintended side reactions and otherwise troublesome reactions in the synthesis.

Reaction prediction is a fundamental problem that has been extensively studied with expert systems. However, a fresh approach is needed. The core reaction model and ranking formulation provides a framework to such a new approach, allowing the utilization of computing power and machine learning to abstract chemical reactivity knowledge from data in an automatic fashion. Furthermore, we present an initial machine learning dataset, an implementation using neural networks, a web interface to the system, and promising results. We hope that this work leads to a resurgence of interest in the problem of reaction prediction and an open environment for the further release of chemical reactivity data.

Figure 2.

Overall reaction prediction framework. (a) A user inputs the reactants and conditions. (b) We identify potential electron donors and acceptors using coarse approximations of electron filled and electron unfilled MOs. (c) Highly sensitive reactive site classifiers are trained and used to filter out the vast majority of unreactive sites, pruning the space of potential reactions. (d) Reactions are enumerated by pairing filled and unfilled MOs. (e) A ranking model is trained and used to order the reactions, where the best ranking one or few represent the major products. The top ranked product can be recursively chained to a new instance of the framework for multi-step reaction prediction.

Appendix A - Orbital Interaction Algorithm

Algorithm 1 Orbital interaction algorithm. Describes a recursive algorithm move electrons from a filled MO f to an unfilled MO u, therefore physically altering the reactants and yielding the product of the reaction. The algorithm consists of updating the FormalCharge on atoms and BondOrder between on bonds denoted by a pair of atoms. A BondOrder of 0 between two atoms denotes no bond.

procedure OrbInter(f = (af, tf, nf, cf), u = (au, tu, nu, cu)) ▷ Move electrons from f to u
 if tf ∈ {σ, π} then
  FormalCharge(nf) ← FormalCharge(nf) + 1
  FormalCharge(af) ← FormalCharge(af) − 1
  BondOrder(af, nf) ← BondOrder(af, nf) − 1
  if cf ≠ 0̸ then
   u′ ← (nf, p, 0̸, 0̸)
   OrbInter(cf, u′)
  end if
 end if
 if u ≠ 0̸ then
  FormalCharge(af) ← FormalCharge(af) + 1
  FormalCharge(au) ← FormalCharge(au) − 1
  BondOrder(af, au) ← BondOrder(af, au) + 1
  if tu ∈ {σ*, π*} then
   FormalCharge(au) ← FormalCharge(au) + 1
   FormalCharge(nu) ← FormalCharge(nu) − 1
   BondOrder(au, nu) ← BondOrder(au, nu) − 1
   if cu ≠ 0̸ then
    f′ ← (nu, n, 0̸, 0̸)
    OrbInter(f′, cu)
   end if
  end if
 end if
end procedure