Mechanical assessment of elastin integrity in fibrillin-1-deficient carotid arteries: implications for Marfan syndrome

Abstract

Aims

Elastin is the primary component of elastic fibres in arteries, which contribute significantly to the structural integrity of the wall. Fibrillin-1 is a microfibrillar glycoprotein that appears to stabilize elastic fibres mechanically and thereby to delay a fatigue-induced loss of function due to long-term repetitive loading. Whereas prior studies have addressed some aspects of ageing-related changes in the overall mechanical properties of arteries in mouse models of Marfan syndrome, we sought to assess for the first time the load-carrying capability of the elastic fibres early in maturity, prior to the development of ageing-related effects, dilatation, or dissection.

Methods and results

We used elastase to degrade elastin in common carotid arteries excised, at 7–9 weeks of age, from a mouse model (mgR/mgR) of Marfan syndrome that expresses fibrillin-1 at 15–25% of normal levels. In vitro biaxial mechanical tests performed before and after exposure to elastase suggested that the elastic fibres exhibited a nearly normal load-bearing capability. Observations from nonlinear optical microscopy suggested further that competent elastic fibres not only contribute to load-bearing, they also increase the undulation of collagen fibres, which endows the normal arterial wall with a more compliant response to pressurization.

Conclusion

These findings support the hypothesis that it is an accelerated fatigue-induced damage to or protease-related degradation of initially competent elastic fibres that render arteries in Marfan syndrome increasingly susceptible to dilatation, dissection, and rupture.

1. Introduction

Elastic fibres play vital mechanical and biological roles in arteries. Loss of integrity of elastic fibres is thus detrimental to arterial function in many conditions, including hypertension, ageing, cerebral and aortic aneurysms, and Marfan syndrome.^1–4 Mouse models wherein specific constituents of elastic fibres are modified promise to increase our understanding of these conditions greatly.^5–9 For example, in contrast to the microfibril fibulin-5, which appears to support effective elastogenesis, fibrillin-1 appears to support the long-term mechanical stability of elastic fibres, which normally have a half-life on the order of the life span of the organism. Mutations to the fibrillin-1 gene (FBN1) are responsible for Marfan syndrome, which manifests clinically via ocular, musculoskeletal, and cardiovascular disorders, the most devastating of which is aortic root dilatation, dissection, and rupture.¹⁰

Prior studies have appropriately contrasted mechanical behaviours of central arteries (aorta and carotids) at different ages from mouse models of Marfan syndrome vs. age-matched wild-type controls.^6,11,12 Among the many findings, ageing-related increases in circumferential wall stiffness are much more rapid and greater in Marfan mice than in controls, and this difference appears to correlate with a progressive increase in a histologically observed fragmentation of elastic fibres. In no case, however, has there been an assessment of mechanical differences in arteries in Marfan syndrome relative to a near total loss of elastin, which is a necessary control. Hence, in this paper, we compare biaxial mechanical responses of carotid arteries from mice heterozygous (mgR/+) and homozygous (mgR/mgR) for the mgR mutation with the same arteries after exposure to pancreatic elastase to remove most of the load-bearing elastic fibres; note that the biomechanical properties of the heterozygous carotid arteries are indistinguishable from those of wild-type mice, hence allowing them to serve as the second necessary control (fully competent elastic fibres). We show that, despite having significantly less fibrillin-1, carotid arteries from mgR/mgR mice at 7–9 weeks of age possess nearly normal load-bearing elastin that presumably becomes increasingly susceptible with ageing to a heightened, fatigue-induced damage or protease-related degradation.

2. Methods

2.1. Specimen preparation

Animal care and use conformed with the Guide for the Care and Use of Laboratory Animals (NIH Publication 85-23) and was approved by the Texas A&M University Institutional Animal Care and Use Committee. Employing methods used previously in our laboratory,^12,13 male mgR/+ and mgR/mgR mice were euthanized at 7–9 weeks of age via an overdose of sodium pentobarbital (250 mg/kg), which has minimal effects on vascular function. Right and left common carotid arteries were then excised, cleaned of excess perivascular tissue, cannulated on custom 300 μm diameter glass pipettes, and secured using 6-O suture. The unloaded length of the cannulated vessels was ∼5 mm.

2.2. Biaxial testing

Specimens were then placed in a custom biaxial testing system¹⁴ within a Hanks phosphate-buffered solution containing 1.26 mM CaCl₂ at 37°C. Briefly, the glass pipettes were connected to stages that are controlled by two stepper motors that move in opposing directions. Hence, the arteries could be held at prescribed axial stretches or stretched cyclically under computer control while maintaining the centre of the specimen at the same location. Similarly, the glass pipettes were connected via rigid tubing to a computer controlled pump, hence the arteries could be maintained at a prescribed pressure or distended cyclically under computer control. Mechanical testing protocols followed those developed previously in our laboratory,^12,13 with luminal pressure P, outer diameter in the central region, axial force f, and axial extension measured on-line. Briefly, all specimens were subjected to two cycles each of pressure–diameter tests (P = 10–140 mmHg) at three different axial extensions (at and ±5% of the estimated in vivo axial stretch ratio 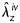) and two cycles of axial force–length tests (f= 0–9.8 mN) at three different pressures (60, 100, and 140 mmHg), all following four cycles of preconditioning. To evaluate smooth muscle cell viability following mechanical testing in the Hanks solution, a sub-set of specimens was returned to near in vivo conditions (i.e. 80 mmHg and 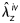) for 15 min and challenged sequentially with 10⁻³ M phenylephrine, 10⁻² M sodium nitroprusside, and 2 × 10⁻³ M EGTA for 15 min each. The rest of the specimens was exposed intraluminally to 3 mL of porcine pancreatic elastase at 7.5 U/mL (Worthington, Lakewood, NJ, USA) for 20 min at the initial in vivo loading conditions. The elastase was washed out, the vessel re-equilibrated for 20 min in normal Hanks solution, and the cyclic pressure–diameter and axial force–length tests repeated.

2.3. Multi-photon and light microscopy

A sub-set of vessels was imaged at both unloaded (0 mmHg and λ_z= 1) and loaded (80 mmHg and 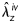) conditions before and after treatment with elastase using a custom nonlinear optical microscopy (NLOM) system to visualize collagen fibre organization in 3-D.¹⁵ Finally, all vessels were fixed in 4% formalin in an unloaded state for 1 h, immersed in a cryoprotectant (30% sucrose) overnight, and placed in optimum cutting temperature medium in 2-methylbutane cooled with liquid nitrogen and stored at −5°C. Frozen samples were serially sectioned at 5 μm and stained with haematoxylin and eosin to identify overall morphology and cell nuclei, Verhoeff van Gieson (VVG) to identify elastin, picrosirius red (PSR) to identify fibrillar collagen, and Masson's trichrome (MTC) to identify non-birifrengent collagen and smooth muscle cells.

2.4. Constitutive modelling

We employed a ‘four fibre family’ hyperelastic constitutive model¹⁶ to quantify the measured passive biaxial mechanical behaviours. This model was motivated by the NLOM images of orientations of intramural collagen and has proven useful in capturing biaxial mechanical responses of diverse mouse carotid arteries.^9,12,17 The specific form of the strain energy function is

(1)

where c and 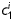are material parameters having units of stress and 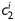are dimensionless, I_c=trC is the first invariant of the right Cauchy-Green tensor, and 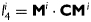is the square of the stretch of the ith collagen fibre family (i.e. 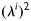). Fibre orientations are defined in the reference configuration by unit vectors that depend on angles 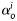defined between fibre and axial directions. Axial and circumferential fibres were thus defined at 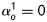and 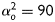degrees, respectively, while symmetrically oriented diagonal fibres were accounted for via a single parameter, 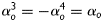. Note that

(2)

where the superscript d denotes ‘diagonal’. These two families of collagen are typically regarded as mechanically equivalent, hence 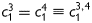, 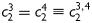. This overall model thus requires eight unknown parameters 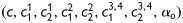to be estimated to describe the passive mechanical behaviour.

Assuming a 2-D state of stress within the central region of the thin-walled biaxially tested arteries, the deformation gradient tensor has the form 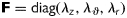. The axial and circumferential stretch ratios were calculated via

(3)

where l (and L) and r_mid (and R_mid) represent loaded (and unloaded) axial length and mid-wall radius, respectively. Assuming incompressibility 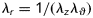during transient loading and a plane state of stress 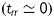, equation (1) yields theoretically calculated Cauchy stresses of the form

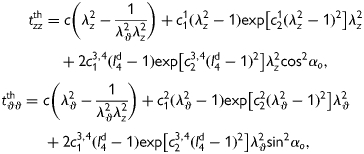(4)

which, in turn, enable a straightforward analysis of biaxial data wherein experimentally inferred stresses in the principal directions are given by

(5)

where a is the inner radius in a loaded state and h is the associated thickness of the wall [note that 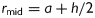in equation (3)₂]. The axial force applied to the artery is given by 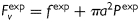, where 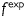is measured by the force transducer and 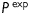is the imposed luminal pressure. Equations (5) are obtained from equilibrium assuming the artery deforms axisymmetrically under distension and axial extension. The thin-walled approximation is well accepted for mouse carotid arteries consisting of but two to three smooth muscle layers.

2.5. Parameter estimation and bootstrapping

Best-fit values of the unknown parameters in equation (1) were determined using a nonlinear least squares minimization of the error e between the theoretically predicted (th) and experimentally inferred (exp) applied loads, namely

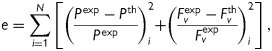(6)

where N is the total number of data points (i.e. equilibrium configurations). Theoretical values of axial force and pressure were calculated from theoretical Cauchy stresses using equations (4) and (5). Hence, 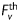and 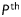represent nonlinear functions depending on measured values of λ_z, 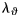, a, and h, as well as the eight unknown parameters. The error e was minimized using the built-in function lsqnonlin in Matlab, subject to physical constraints that 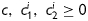and 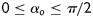due to the symmetry of the diagonal fibres. Finally, the goodness of fit was estimated via the root mean square of the fitting error, defined as follows

(7)

We used the nonparametric bootstrap to approximate probability distributions of the best-fit material and structural parameters, and the BCa (bias-corrected and accelerated) method to calculate associated confidence intervals.¹⁶ Briefly, the bootstrap is a computational method for statistical inference that seeks an objective calculation of confidence intervals for nonparametric distributions. It uses the concept of ‘resampling with replacement’ (or, Monte Carlo resampling) of original data based on an empirical distribution function to estimate a parameter's probability distribution, which then can be used to find confidence intervals.

2.6. Statistical analysis

Data are presented as mean ± standard deviation and were evaluated using two-tailed Student's t-test. Specifically, differences between mgR/+ (n = 7) and mgR/mgR (n = 6) groups were studied using unpaired t-tests assuming unequal variances; differences in unloaded length, unloaded outer diameter, and in vivo stretch within each group before and after elastase treatment were evaluated using paired t-tests. A P-value < 0.05 was considered significant.

3. Results

Age, body weight, and initial unloaded carotid artery dimensions (length and diameter) were statistically similar for mgR/mgR and mgR/+ mice (Table 1). Preliminary vasoactive tests also revealed that both types of arteries retained smooth muscle functionality following biaxial mechanical testing (Figure 1), hence the prescribed ranges of applied pressures and axial loads did not cause mechanical damage. Yet, compared with similar biomechanical tests performed in culture media,^12,13 our data revealed a primarily passive behaviour in the Hanks-buffered solution (Figure 1); this absence of basal smooth muscle tone justified mathematically modelling only passive behaviour during testing.

Table 1.

Age, body weight (mass), and comparisons of unloaded geometry and in vivo axial stretch for mgR/+ and mgR/mgR mice before and after exposure to elastase

	mgR/+	mgR/mgR
n	7	6
Age (weeks)	8.22 ± 0.75	8.04 ± 0.50
Body mass (g)	21.74 ± 2.36	20.13 ± 5.53
Unloaded length (mm)
Untreated	4.79 ± 0.80	4.14 ± 1.06
Elastase	7.80 ± 1.33*	6.39 ± 1.66*
Unloaded diameter (μm)
Untreated	393.86 ± 48.56	398.50 ± 14.60
Elastase	692.86 ± 45.29*	710.83 ± 49.36*
In vivo axial stretch
Untreated	1.69 ± 0.05	1.59 ± 0.06†
Elastase	1.05 ± 0.04*	1.05 ± 0.03*

*P < 0.001 within each group before and after elastase.

^†P < 0.005 between mgR/+ and mgR/mgR.

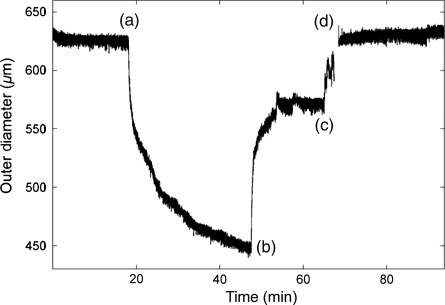
Figure 1.

Measured outer diameter during functional testing of a representative mgR/+ carotid artery following biaxial mechanical testing. Phenylephrine was given at (a) to induce smooth muscle contraction, sodium nitroprusside was given at (b) to induce an endothelial-independent smooth muscle relaxation, and a Ca⁺⁺-free Hanks solution containing EGTA was given at (c) to induce a fully passive behaviour that was reached at (d). Note, therefore, that the original behaviour in the Hanks-buffered solution containing calcium was nearly passive, thus negating any need to model mathematically the smooth muscle tone. Note, too, that all vessels exhibited similar functionality following the initial mechanical testing, thus confirming the lack of significant damage due to biaxial mechanical testing.

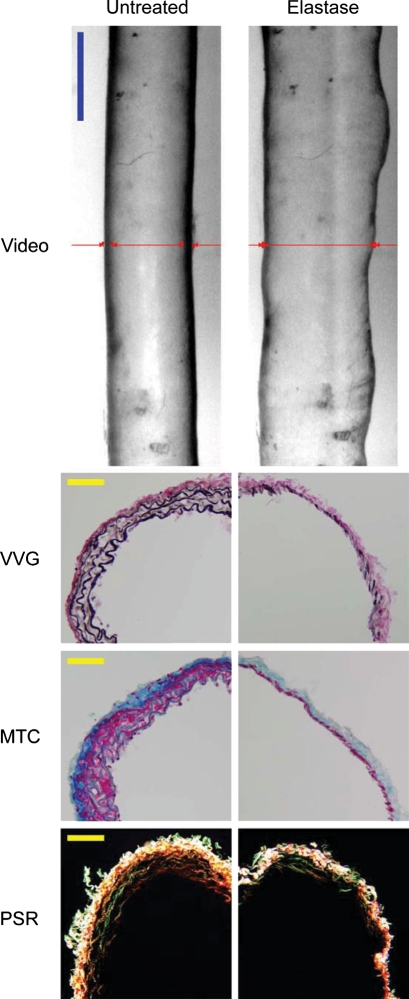
Intraluminal exposure to elastase for 20 min induced marked non-uniform dilatations (Figure 2, top images), with the mgR/mgR and mgR/+ carotids experiencing similar changes in geometry (Table 1) and biaxial mechanical behaviours (Figures 3 and 4). Although not reaching significance, note that the smaller increase in unloaded axial length in mgR/mgR compared with mgR/+ carotids (54.46 ± 9.59 vs. 62.74 ± 5.29%, respectively) contributed to the similar axial behaviours following exposure to elastase (Figure 3). VVG-stained cross-sections confirmed that these changes corresponded to a dramatic loss of elastin in both types of arteries following exposure to elastase, whereas trichrome-stained sections showed that smooth muscle and collagen remained present despite a marked thinning of the medial layer (Figure 2). Polarized light images of PSR-stained sections suggested, however, that thinner collagen fibres may have been lost or compromised following exposure to elastase (Figure 2).

Figure 2.

Video images (top row) of a representative mgR/mgR carotid artery mounted in the testing device (cannulae not shown) and maintained at a pressure of 80 mmHg at its estimated in vivo axial stretch both before (left) and after (right) intraluminal exposure to 7.5 U/mL of pancreatic elastase for 20 min. Note the marked non-uniform increase in diameter after exposure to elastase. Images are to scale with the blue bar representing 700 μm. The red lines show on-line measurement of diameter via a LabView routine. Histological images of VVG-, MTC-, and PSR-stained cross-sections before (left column) and after (right column) treatment with elastase reveal a marked loss of elastin. Note, too, that the smooth muscle layer persisted following elastase despite marked thinning of the media as did the thicker collagen fibres, particularly in the adventitia. Notwithstanding some discontinuities in lamellar organization, mgR/mgR carotid arteries possessed intact elastic fibres that were nearly completely degraded after exposure to elastase. The yellow scale bars represent 50 μm.

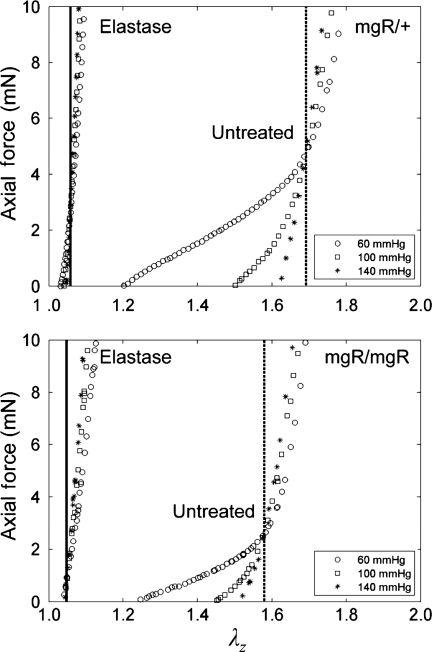
Figure 3.

Data from representative axial force–length responses of mgR/+ (top) and mgR/mgR (bottom) carotids before and after exposure to elastase. Axial force–length tests at multiple fixed pressures estimate the in vivo stretch via a ‘cross-over point’ (cf. Humphrey et al.²⁴), which is denoted by a vertical line. Consistent with Eberth et al.,¹² the vertical dashed lines resulting from tests before elastase exposure revealed a significantly lower in vivo stretch for mgR/mgR (bottom) compared with mgR/+ (top) carotids. Conversely, no difference was found comparing the solid vertical lines between the two groups after elastin degradation; that is, both mgR/mgR and mgR/+ carotids showed a significant reduction in extensibility and much lower value of axial stretch associated with the ‘cross-over point’ in these tests: 1.59 ± 0.06 vs. 1.05 ± 0.03 (P < 0.001) for mgR/mgR and 1.69 ± 0.05 vs. 1.05 ± 0.04 (P < 0.001) for mgR/+ carotids.

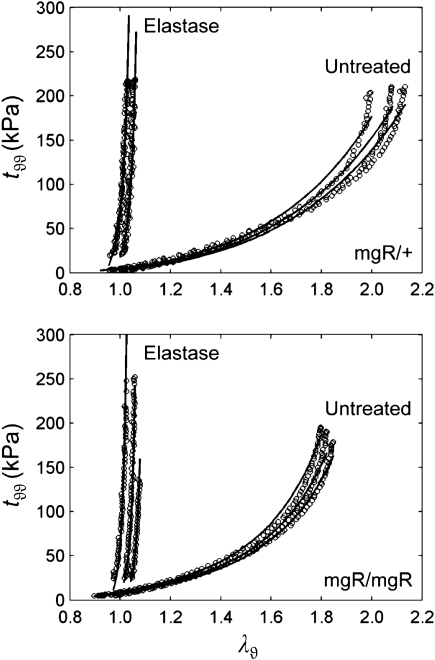
Figure 4.

Passive circumferential mechanical data (symbols) for a representative mgR/+ (top) and mgR/mgR (bottom) carotid before and after exposure to elastase, each subjected to three pressure–diameter test protocols at fixed axial extensions. Note the similarity in behaviours between untreated mgR/+ and mgR/mgR carotids despite the slight stiffening of the latter. Note, too, the dramatic stiffening and the loss of distensibility of both arteries after elastin degradation. Also shown are predictions (solid lines) obtained via equations (4) and (5) and best-fit values of the material parameters (Tables 2 and 3). Predictions tended to overestimate stress after elastase treatment due to the extreme stiffening of the arteries as well as to the higher measurement noise.

The cyclic axial force–length tests prior to exposure to elastase confirmed that mgR/mgR carotids at 8 weeks of age exhibit a significantly lower in vivo axial stretch compared with the mgR/+ carotids (Figure 3); mean values of 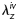were 1.59 ± 0.06 and 1.69 ± 0.05 (P < 0.005), respectively. Albeit not reaching significance, the cyclic pressure–diameter tests and associated Cauchy stress-stretch plots also confirmed that the mgR/mgR carotids are initially slightly stiffer circumferentially when compared with the mgR/+ carotids (Figure 4). Nevertheless, what was most important and striking was the extreme stiffening and loss of extensibility and distensibility by both mgR/mgR and mgR/+ carotids following exposure to elastase (Figures 3 and 4), including loss of the characteristic sigmoidal pressure–diameter behaviour at low pressures (cf. Supplementary material online, Figures S1 and S2).

Equation (1) simultaneously fit well the pressure–diameter and force–length data from all untreated specimens (mean RMSE = 0.079 and 0.082 for mgR/mgR and mgR/+, respectively), which similarly resulted in a good prediction of stress–stretch responses (Figure 4). The fit to mgR/mgR and mgR/+ data following exposure to elastase was less good, but reasonable (mean RMSE = 0.256 and 0.275 for mgR/mgR and mgR/+, respectively)—see Supplementary material online, Figures S1 and S2 for the fit to pressure and axial force data both before and after exposure to elastase. Best-fit values of the model parameters were of the same order of magnitude for all untreated specimens, but markedly different for those exposed to elastase (Tables 2 and 3). In particular, the parameter c (motivated by the elastin-dominated amorphous matrix¹⁸) was comparable on average for mgR/mgR and mgR/+ mice, but orders of magnitude less following exposure to elastase. Conversely, the parameters 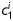and 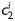(which model locally parallel families of collagen fibres) were generally much larger following exposure to elastase. Note, too, that mean values of 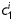tended to be larger than those for 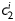in axial and circumferential directions for untreated specimens; in contrast, 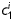tended to be similar to or less than those for 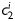following elastase treatment. These values of 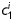and 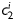reflect the dramatic differences in shape of the stress–stretch curves following exposure to elastase.

Table 2.

Best-fit values of parameters in the four fibre family constitutive model for mgR/+ carotids under biaxial testing before and after exposure to elastase

Specimen	c (kPa)	c11 (kPa)	c21	c12 (kPa)	c22	c13,4 (kPa)	c23,4	α0	RMSE
mgR/+ untreated
1	2.347	5.635	5.14 × 10−13	8.291	2.23 × 10−14	2.490	0.432	30.381	0.095
2	3.487	15.036	0.022	1.622	0.027	0.010	1.263	24.621	0.108
3	3.849	8.996	0.215	3.040	2.99 × 10−3	7.65 × 10−6	2.571	28.962	0.091
4	4.721	15.204	0.058	3.613	5.56 × 10−3	0.010	1.321	23.837	0.079
5	1.393	14.089	0.067	4.387	2.34 × 10−14	8.39 × 10−3	1.039	25.978	0.079
6	11.732	14.058	0.031	8.789	0.016	0.012	1.313	27.055	0.075
7	25.280	1.652	0.213	15.128	0.046	0.385	0.915	37.484	0.051
Mean	7.544	10.667	0.086	6.410	0.014	0.416	1.265	28.331	0.082
SD	8.515	5.358	0.090	4.680	0.017	0.925	0.655	4.646	0.018
mgR/+ elastase
1	3.03 × 10−14	4.07 × 10−6	432.558	3.73 × 10−14	8.51 × 10−8	442.868	141.537	45.843	0.323
2	2.23 × 10−14	9.55 × 10−9	0.020	24.146	66.333	548.010	2.64 × 10−7	27.365	0.352
3	2.28 × 10−7	272.544	11.855	11.151	194.159	358.716	108.033	50.500	0.228
4	7.79 × 10−3	0.547	0.586	93.125	14.467	7.15 × 10-8	1528.040	9.478	0.229
5	8.89 × 10−8	6.93 × 10−5	892.836	6.57 × 10−11	1.15 × 10−5	1399.758	120.148	43.427	0.292
6	5.67 × 10−12	758.625	2.65 × 10−14	53.921	254.450	609.720	92.992	51.796	0.358
7	2.29 × 10−12	472.864	3.12 × 10−12	1.78 × 10−11	5.08 × 10−8	147.309	104.033	52.735	0.145
Mean	1.11 × 10−3	214.940	191.122	26.049	75.630	500.912	299.255	40.163	0.275
SD	2.94 × 10−3	302.765	348.499	35.443	105.682	451.205	543.698	16.065	0.078

Table 3.

Best-fit values of parameters in the four fibre family constitutive model for mgR/mgR carotids under biaxial testing before and after exposure to elastase

Specimen	c (kPa)	c11 (kPa)	c21	c12 (kPa)	c22	c13,4 (kPa)	c23,4	α0	RMSE
mgR/mgR untreated
1a	4.225	3.174	0.166	4.309	2.34 × 10−14	0.416	0.595	36.533	0.081
2	10.196	5.119	0.367	6.745	0.102	1.098	0.833	33.945	0.057
3	6.681	6.033	0.284	5.626	0.043	0.188	1.222	33.235	0.082
4	6.767	3.428	0.309	5.147	0.050	0.035	1.674	30.831	0.086
5	3.318	14.110	0.089	4.434	1.78 × 10−3	0.088	1.209	30.262	0.071
6	3.380	34.107	2.34 × 10−14	1.474	0.044	0.050	1.360	24.296	0.095
Mean	5.761	10.995	0.203	4.623	0.040	0.313	1.149	31.517	0.079
SD	2.665	12.012	0.142	1.780	0.037	0.410	0.383	4.200	0.013
mgR/mgR elastase
1a	3.00 × 10−14	12.951	23.115	8.811	163.557	174.098	90.418	54.341	0.233
2	4.11 × 10−13	68.754	34.621	14.353	43.753	100.488	55.547	50.447	0.275
3	1.67 × 10−7	1.98 × 10−7	1178.276	2.34 × 10−14	0.122	191.301	91.358	51.633	0.208
4	2.21 × 10−3	6.46 × 10−6	403.218	69.153	69.336	137.675	204.194	49.161	0.212
5	1.66 × 10−13	41.147	17.858	0.022	18.406	25.210	15.166	48.351	0.261
6	3.82 × 10−14	309.633	3.82 × 10−14	0.112	65.257	218.882	38.508	42.814	0.350
Mean	3.68 × 10−4	72.081	276.181	15.408	60.072	141.276	82.532	49.458	0.256
SD	9.01 × 10−4	119.404	468.041	26.986	57.303	70.357	66.552	3.873	0.053

^aDenotes that vessel 1 was dissected from a mouse that died from aortic rupture the night before the test and was included in the experimental group because of lack of any difference with the other specimens in terms of macroscopic mechanical behaviour and response to elastase.

Differences in estimated values of the best-fit parameters before and after treatment with elastase were confirmed by the bootstrap analysis. The primary difference was for the neo-Hookean parameter c (Supplementary material online, Figure S3), but another difference was for the fibre angle α_o, suggesting a possible reorientation of collagen fibres relative to the unloaded configuration (data not shown). As for the material parameters related to different families of fibres, they were characterized by greater stochastic variations after treatment with elastase, indicating less precision in the estimation. Interestingly, estimated values and empirical distributions of the parameters after elastase treatment were similar to those obtained from human abdominal aortic aneurysms¹⁶, which possess little intramural elastin.

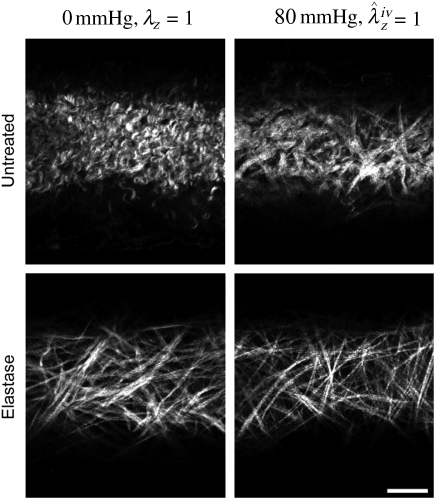
Second harmonic generation images from NLOM (Figure 5) revealed a marked undulation of collagen in all untreated arteries at their unloaded configuration (0 mmHg and λ_z = 1), but recruitment and straightening when loaded at in vivo conditions (80 mmHg and 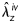). In contrast, all elastase-treated arteries were characterized by little undulation in the unloaded configuration and an apparent complete recruitment in the in vivo configuration, consistent with the measured increase in stiffness and loss of distensibility and extensibility. These microstructural observations are thus consistent with the observed mechanical properties (Figures 3 and 4) and best-fit model parameters (Tables 2 and 3).

Figure 5.

Nonlinear optical microscopy (NLOM) images of fibrillar collagen (from second harmonic generation) in the unloaded (left column) and loaded (right column) states for a vessel both before (top) and after (bottom) treatment with elastase. Note the significant loss of fibre undulation following removal of elastin, consistent with the marked increase in stiffness seen in the mechanical tests. The scale bar represents 50 μm.

4. Discussion

Normal elastin is the most biologically and thermally stable structural protein within the arterial wall; it has a normal half-life on the order of the life-span of the organism (e.g. >40 years in humans²). Nevertheless, elastic fibres appear to suffer a fatigue-induced loss of function in response to long-term cyclic loading (arteries experience over 30 M cardiac cycles per year in humans and 300 M per year in mice). This fatigue can manifest as part of the normal ageing process or be accelerated by increased pulse pressures in hypertension.^2,3,19,20 It appears that fibrillin-1 contributes to the normal long-term structural stability of elastic fibres, essentially providing some protection against fatigue-induced damage.^6,21 Hence, patients having Marfan syndrome, which results from mutations in the gene FBN1, may experience premature dilatation, dissection, and rupture of the aortic root and ascending aorta due to an accelerated loss of structural integrity of elastic fibres due to fatigue.^6,22 In this regard, the aortic root and ascending aorta appear to be unique for they experience large cyclic biaxial (circumferential and axial) strains over the cardiac cycle,²³ which may increase fatigue-induced damage or upregulate the local production of matrix metalloproteinases that increase degradation.¹¹

The mgR/mgR mouse is an accepted model of Marfan syndrome. Although born with an apparently normal vasculature, its elastic fibres can begin to calcify by 6 weeks of age in males and, in some colonies, lethal rupture of the aorta can occur by 9–12 weeks. We previously reported indistinguishable biomechanical behaviour and vasoactive function of common carotid arteries obtained from 10- to 12-week-old male mgR/+ and +/+ mice,¹² consistent with general phenotypic observations;²¹ hence, the mgR/+ mice served as an appropriate control for competent elastic fibres herein. Interestingly, similar findings (indistinguishable mechanical behaviours by heterozygous and wild-type mice) were reported recently for another mouse model (Fbn1+/−) of Marfan syndrome,⁸ whereas this is not the case for the Fbn1^C1039G/+ mouse.¹¹ We are thus reminded to consider each model separately. To carefully assess potential changes in the structural integrity of elastic fibres, however, one also needs a control wherein integrity is completely lost. We introduced the elastase–infusion protocol to serve as such a control for the first time.

Whereas it is important to understand why the aortic root is particularly susceptible to dilatation, leading to aneurysms and dissections in human Marfan patients, few animal models recapitulate this pathology completely. For example, it is the aortic arch that most often becomes aneurysmal and ruptures in the mgR/mgR mouse. Similarly, whereas it is ultimately important to understand how the structural integrity of the elastic fibres evolve in Marfan syndrome during hypertension and ageing,¹¹ particularly in the aortic root, we focused on a much more fundamental question. Does the apparently heightened fatigue of elastic fibres in Marfan syndrome occur because fibres are initially compromised but the rate of fatigue is normal or because the rate of fatigue is increased but the elastic fibres are initially competent? Delineation of such possibilities is fundamental for understanding the progression toward aneurysms. For all of these reasons, we focused on the common carotid artery in mgR/mgR mice at 8 weeks of age, that is, in maturity but prior to the period wherein the first signs of aneurysmal dilatation manifest due to a progressive loss of structural integrity. Because of its simpler geometry, the carotid artery admits rigorous biaxial biomechanical testing and modelling, which provide significantly more information than results from the often used ‘uniaxial ring tests’.

The present data confirmed that, at 8 weeks of age, carotid arteries from mgR/mgR mice exhibit slight circumferential stiffening but a significantly lower in vivo axial stretch. [These mean values of in vivo axial stretch (1.59 and 1.69 for mgR/mgR and mgR/+, respectively) are consistent with those reported by Eberth et al.¹² despite their values being larger (1.63 and 1.72). This difference appears to be due to our use of a Hanks solution rather than the DMEM culture media used by them, noting that culture media induces a basal smooth muscle tone that increases in vivo axial stretch slightly¹³.] We have suggested previously that biomechanical changes in the axial direction may be among the first used by an artery in an attempt to maintain or restore homeostasis.²⁴ Of particular importance herein, however, we found that these differences between the untreated mgR/mgR and mgR/+ arteries were modest compared to the dramatic changes caused by exposure to elastase and the associated loss of integrity of the elastic fibres.

A 20 min exposure time was selected for treatment with elastase based on pilot studies (data not shown) as well as prior reports²⁵ that show a steady-state effect after 15–20 min. Dobrin et al.²⁶ and Fonck et al.²⁷ also found that elastase causes dramatic dilatation, especially at low pressures, and marked circumferential stiffening of carotids from dogs and rabbits, respectively. Fonck et al. reported further that elastase does not alter the amount of fibrillar collagen within the wall, but it causes a slight thinning of the wall, a modest increase in overall length (∼ 10%), and a dramatic decrease in the residual stress-related opening angle. Our results revealed a much greater thinning (Figure 2) and increase in unloaded length (Table 1). One reason for different results for rabbit and mouse carotids is likely the marked difference in the collagen-to-elastin ratio (C:E), which is ∼2.00 in the rabbit but only ∼0.84 in the mouse.²⁴ In other words, elastin constitutes a much greater percentage of the extracellular matrix in the normal mouse carotid than the rabbit carotid, thus loss of elastin should be more dramatic in the mouse.

Fonck et al.²⁷ interpreted their findings using a novel constitutive relation that partitions the strain energy into a part due to elastin and another due to collagen (assumed to be oriented circumferentially). Moreover, they used a log-logistic probability distribution function to model the progressive recruitment of collagen fibres with increasing pressure. Based on this model, they estimated an ∼90% decrease in the load carrying capability of elastin following exposure to elastase; our model suggested a similar decrease (∼98%). Their distribution function for collagen recruitment became much narrower following exposure to elastase, thus ‘suggesting a clear interaction between the two main structural constituents of the arterial wall’. Our findings on elastase-induced changes in the material parameters for collagen (Tables 2 and 3) and in the unloaded collagen microstructure (Figure 5, left column) corroborate this suggestion, but suggest further that the normally highly pre-stretched elastin increases the undulation of collagen at low loads and thereby contributes doubly to the characteristic gradual stiffening of normal arteries over a broad range of stretches. That is, it appears that the pre-stretch of elastin, which results from its perinatal deposition and extreme stability and elasticity combined with its extension due to overall tissue growth during postnatal development, is fundamental to its contribution to wall properties both directly and indirectly.^24,28 Loss of elastin decreases the initial undulation of collagen fibres and consequently changes their stiffening characteristics.

Although we typically think of loss of elastin effectiveness as being particularly important in central arteries, which have the highest normal concentrations of elastin in the vasculature, loss of elastin is also fundamental to the development of aneurysms in cerebral arteries, which consist of only 2–5% elastin.⁴ Moreover, it has been shown that elastin is similarly a fundamental determinant of mechanical properties in small resistance (<250 μm) arteries, which contain a small percentage of elastin.^25,29 These reports are thus consistent with the concept that central arteries are fault-tolerant structures—they can withstand significant losses of elastic fibres prior to extreme dilatation and eventual failure. This concept may suggest that progressive losses of elastin in diseases such as Marfan syndrome or even normal ageing eventually manifest abruptly and only then cause extreme changes in wall geometry or properties. In this regard, note that arterial dilatation appears to result primarily from loss of elastic fibre integrity and smooth muscle contractility, whereas rupture is likely due to the loss of integrity of fibrillar collagen,²⁶ which is consistent with findings on the natural history of aneurysms.⁴ There is still a need for much more attention to the potential roles of elastic vs. collagen fibres in the process of dissection, however.

Fibulin-4 is another elastin-associated microfibrillar glycoprotein. Hanada et al.³⁰ reported pressure–diameter data for aorta from fibulin-4-deficient mice at 14 weeks of age that showed a dramatic dilatation and stiffening reminiscent of our finding associated with elastase treatment. It is interesting to note that the pulse pressure is much higher in the fibulin-4-deficient mice³⁰ (∼77 mmHg) than in the mgR/mgR mice⁶ (∼43 mmHg), again suggesting the importance of the amplitude of cyclic loading in fatigue-related loss of function. Wan et al.⁹ reported biaxial mechanical data and confocal microscopy images for common carotid arteries from fibulin-5 null mice at 13 weeks of age; fibulin-5 is another microfibrillar protein that contributes to functional elastic fibres. They showed that fibulin-5 null mice lacked organized elastic lamellae, that they exhibited a stiffer biaxial behaviour, and that they had a lower in vivo axial stretch ratio despite having a compliance over the physiological range of pressures similar to the control. These results support the hypothesis that the presence of some functional elastic fibres is sufficient to achieve a normal in vivo circumferential mechanical behaviour.

The four fibre family strain energy function fit the data well and the parameter values mirrored microstructural changes that followed elastin degradation. Traditionally, best-fit parameters are determined by minimizing either the errors in stress or errors in pressure and force. The objective functions currently used tend to give more weight either to data at high or low stretches, the latter of which is the case for equation (6) adopted herein. Recently, Wan et al.⁹ suggested a different way to weight data by using mean, rather than point, values of pressure and force as weights. We did not observe major advantages when using their approach, thus we used equation (6) because it is a natural way of determining unknown parameters from distension and extension tests. Nevertheless, there is a need to identify an objective function that more appropriately weights pressure and force data over the entire range of stretches.

In summary, direct comparison of mechanical behaviours of carotid arteries from 7- to 9-week-old mgR/mgR and mgR/+ mice before and after exposure to elastase revealed considerable structural contributions by intact elastic fibres despite the significantly diminished fibrillin-1 (15–25% of normal) in the mgR/mgR mice; that is, the elastic fibres still conferred considerable elasticity to the wall of the mgR/mgR mice. We conclude, therefore, that in addition to its many important biological roles,^2,31 even small amounts of properly organized elastin may confer significant structural as well as potentially biological advantages to the arterial wall both directly and via its impact on other constituents, particularly fibrillar collagens. Although diminished fibrillin-1 appears to render elastic fibres more susceptible to fatigue-induced damage or protease-related degradation under cyclic loading, elastic fibres continue to maintain significant structural integrity early on even in the presence of diminished fibrillin-1. In bioengineering terms, it appears that it is an accelerated fatigue-induced loss of function of initially competent fibres, not a normal fatigue-induced weakening of initially compromised fibres, that leads to eventual dilatation and dissection in Marfan syndrome. Such a finding has important implications for mathematical modelling of evolving changes in mechanical properties, which promises to contribute to our overall ability to understand and treat patients.⁴

Supplementary material

Supplementary material is available at Cardiovascular Research online.

Conflict of interest: none declared.

Funding

This work was supported by National Institutes of Health grants (HL-086418, HL-105297).