Skip to main content
PMC home page
Cognitive Neurodynamics logoLink to Cognitive Neurodynamics
. 2011 Jun 28;5(4):343–359. doi: 10.1007/s11571-011-9161-1

Answering six questions in extracting children’s mismatch negativity through combining wavelet decomposition and independent component analysis

Fengyu Cong 1,✉, Igor Kalyakin 1, Hong Li 2, Tiina Huttunen-Scott 3, Yixiang Huang 4, Heikki Lyytinen 3, Tapani Ristaniemi 1
PMCID: PMC3193978  PMID: 23115592

Abstract

This study combines wavelet decomposition and independent component analysis (ICA) to extract mismatch negativity (MMN) from electroencephalography (EEG) recordings. As MMN is a small event-related potential (ERP), a systematic ICA based approach is designed, exploiting MMN’s temporal, frequency and spatial information. Moreover, this study answers which type of EEG recordings is more appropriate for ICA to extract MMN, what kind of the preprocessing is beneficial for ICA decomposition, which algorithm of ICA can be chosen to decompose EEG recordings under the selected type, how to determine the desired independent component extracted by ICA, how to improve the accuracy of the back projection of the selected independent component in the electrode field, and what can be finally obtained with the application of ICA. Results showed that the proposed method extracted MMN with better properties than those estimated by difference wave only using temporal information or ICA only using spatial information. The better properties mean that the deviant with larger magnitude of deviance to repeated stimuli in the oddball paradigm can elicit MMN with larger peak amplitude and shorter latency. As other ERPs also have the similar information exploited here, the proposed method can be used to study other ERPs.

Keywords: Averaged trace, Event-related potential, Independent component analysis, Mismatch negativity, Projection, Reliability, Support to absence ratio, Wavelet decomposition

Introduction

Independent component analysis (ICA) (Hyvarinen et al. 2001) has been extensively applied to study brain signals (Vigario and Oja 2008). It belongs to the linear transformation model, and assumes that the observation is the mixture of unknown sources. The goal of ICA decomposition is to extract the independent sources from the mixtures through exploiting the spatial independence among different unknown sources (Hyvarinen et al. 2001). ICA does not essentially utilize other prior knowledge of sources, such as, temporal or frequency information which is necessary for the digital or wavelet filter (Kalyakin et al. 2007; Cong et al. 2010a). Using ICA to study electroencephalography (EEG) assumes that EEG collected from any point of the human scalp includes activities generated within a large brain area, and that the spatial smearing of EEG data below 1 kHz by volume conduction does not result in significant time delay (Hämäläinen et al. 1993; Makeig et al. 1997; Makeig et al. 1999; Nunez and Srinivasan 2005). Hence, regarding ICA, the electrical activities of the brain are the sources, and EEG recordings are the mixtures. From the view of mechanisms to generate EEG, components extracted by ICA can be divided into two types, including the spontaneous ongoing EEG (Chen et al. 2008) and the event-related potentials (ERPs) (Vigario and Oja 2008; Pockett et al. 2007). This study is devoted to the latter application.

Although ICA has been extensively used to study ERPs (Vigario and Oja 2008; Delorme and Makeig 2004), in the research of a one of the most interesting ERPs, viz, mismatch negativity (MMN) (Näätänen et al. 1978; Näätänen 1992; Duncan et al. 2009), only few studies have reported the application of ICA to extract MMN (Kalyakin et al. 2009; Kalyakin et al. 2008; Marco-Pallares et al. 2005). MMN studies are usually based on the average over hundreds of single trials of EEG recordings (Näätänen et al. 1978; Näätänen 1992; Duncan et al. 2009). It is one of the small ERPs and its peak amplitude is only up to several micro volts and particularly in children’s MMN, EEG recordings are much noisier. This results in the difficulty to extract MMN through ICA (Huovinen and Ristaniemi 2006). Furthermore, ICA is a novel and complicated signal processing technique, and it might not be well understood and grasped by researchers in the MMN society. MMN was first identified by Näätänen et al. (1978). Since then, many researchers have been devoted to the study of MMN. From 1998 to 2009, the world wide MMN conferences have been held five times already. MMN has been proved to be useful in the research of cognitive studies, clinical neuroscience, and neuropharmacology (Duncan et al. 2009; Garrido et al. 2009).

ICA has been proven to be very promising to study ERPs (Vigario and Oja 2008). This drives us to discuss the application of ICA to extract MMN of children from EEG recordings in details, and to answer the following fundamental questions which have not been well treated before:

  1. Among the averaged EEG recordings over single trials, EEG recordings of a single trial, and EEG recordings of the concatenated trials, which type of the EEG recordings is more appropriate for the ICA decomposition to extract MMN of children?

  2. What kind of preprocessing is beneficial for the ICA decomposition except the conventionally required whitening and sphering (Hyvarinen et al. 2001)?

  3. Which algorithm of ICA can be chosen to decompose EEG recordings under the selected type?

  4. How to determine the extracted independent component as the desired?

  5. How to improve the accuracy of the projection of one desired component in the electrode field?

  6. What can we finally obtain with the application of ICA?

In order to seek solutions for answering these questions, we exploit the temporal, frequency, and spatial information of EEG recordings of MMN and formulate a robust and reliable data processing procedure to extract MMN component. As the core technique to decompose the EEG recordings in this study is to combine the single channel method, namely wavelet decomposition (WLD) (Cong et al. 2010a), and the multichannel method, namely, ICA, together, the proposed method is denoted as wICA hereinafter. It is compared with difference wave (DW) and ICA (Kalyakin et al. 2008) to investigate which method can extract better-defined MMN.

Method

Experiment

Participants

The EEG data were collected at the University of Jyväskylä in Finland, and 114 children participated in the MMN experiment. The children were aged from 8 to 16 years. Data of four subjects were excluded because of strong noise. The subjects for study consisted of 68 control children, 21 children with reading disability, and 21 children with attention deficit, including 76 boys and 34 girls. The mean age of the children was 11 years 8 months (age range: from 8 years 2 months to 16 years 9 months). Huttunen et al. (2007) shown that both clinical groups in our data set produced MMN, and Kalyakin et al. (2008) demonstrated that the control children in our dataset certainly generated MMN. The difference between the groups is not a topic of this study. Please refer to the studies of Huttunen et al. (2007) and Huttunen-Scott et al. (2008) for more information about the group description. This study focuses on data processing methods.

Paradigm to elicit MMN

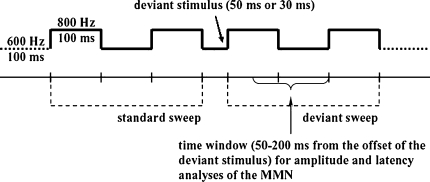
To each subject in the MMN experiment, 700 trials were collected and the experiment lasted for about 11 min. Children were asked to pay attention to a subtitled silent movie while the stimuli were delivered binaurally through earphones with 65 dB intensity. A passive oddball paradigm was adopted to elicit MMN by duration deviants presented in an uninterrupted sound. Figure 1 demonstrates the experimental paradigm. Two alternating 100 ms tones of 600 Hz and 800 Hz composed the repeated continuous tones. The sine wave changed to another frequency without any pause or alternation in the wave amplitude. The deviants were 30 ms and 50 ms tones of 600 Hz (denoted by dev50ms and dev30ms hereinafter) and either of the deviants randomly substituted 7.5% of the 100 ms standard tones of 600 Hz. There were at least three standard pairs between two deviants.

Fig. 1.

Fig. 1

Open in a new tab

A schematic illustration of the stimulus sequence of the 50 ms deviant stimulus. Also the standard and deviant sweeps used for calculating the difference waves are illustrated. The bold solid line of the stimulus sequence indicates the recording period of 650 ms. The time window for the quantitative analyses of the MMN is shown. (Adapted from Kalyakin et al. 2007)

EEG recordings

Three time intervals of responses were available in a recorded trace: (1) the responses elicited by the repeated stimuli; (2) the responses generated by the deviant stimuli; (3) the responses produced by the offset of the deviant stimulus and the responses elicited by the following repeated stimuli. A Brain Atlas-system (Bio-Logic, Chicago, USA) with 50 K gain was used and Tecmar’s Labmaster 12-bit, 16-channel AD-converter and the DSAMP software package (University of Jyväskylä, Finland) were adopted for the EEG data acquisition. The sampling frequency was 200 Hz and an analog band pass filter of 0.1–30 Hz was used. The data was processed offline. Recording started 300 ms before the onset of a deviant stimulus and lasted 350 ms after the onset of a deviant. Thus, each trial contained the recordings of 650 ms, i.e., 130 samples.

EEG at nine locations (frontal F3, Fz, F4; central C3, Cz, C4; parietal (Pz) and mastoids (M1, M2)) were recorded with Electro-Cap International 20-electrode cap using the standard 10–20 system. Silver/silver chloride electrodes were used for the measurement. The potentials were referred to the tip of nose. Eye movements were measured from the upper corner of the left eye (G1) and the lower corner of the right eye (G2). Impedances were less than 10 kOhm and in most cases less than 5 kOhm.

wICA

Averaged trace for wICA

MMN has been extracted by ICA from the recordings of concatenated single trials (Marco-Pallares et al. 2005), and from the averaged recordings over single trials (Kalyakin et al. 2009). The former paradigm supplies more samples for ICA decomposition and benefits the convergence of the ICA algorithm; however, the latter procedure provides ICA with better structured MMN waveform for the decomposition. In reality, both methods implicitly assume that the cognitive processes stay identical from one trial to another. Another application of ICA to extract the brain activity of an ERP out is directly from the EEG recordings of a single trial (Iyer and Zouridakis 2007).

Usually, children’s MMN cannot be significantly visible from EEG recordings of concatenated single trials or EEG recordings of a single trial. This is because MMN is very small, and the signal to noise ratio in the single trial is too low. The goal to apply ICA in this study is to extract the MMN component out, i.e., the desired component at least should possess the well-structured MMN waveform. However, in practice, the ICA algorithm ‘pays attention’ to the relatively large activity in the data (Huovinen and Ristaniemi 2006; Makeig 2002). Therefore, EEG recordings of MMN of children in concatenated single trials or a single trial may be too difficult for ICA to extract the desired MMN component.

ERPs are usually achieved through averaging and filtering over a number of single trials (Picton et al. 2000), so does MMN (Näätänen 1992). Provided that there are enough single trials, MMN activity can at least be roughly observed in the average trace. Then, ICA decomposition on the averaged traces may be easier in contrast to the EEG recordings of a single trial or the concatenated trials. Subsequently, this study performs wICA on the averaged traces of each subject to extract MMN component. We will show the difference between the recordings of single trials and the averaged trace of MMN of children in the section “Diagram of wICA on averaged trace.”

Preprocessing: wavelet decomposition on MMN

Regarding ICA, as stated in the tutorial of EEGLAB, the quality of the data is critical in order to obtain a good ICA decomposition (http://sccn.ucsd.edu/eeglab/quickrej.html). In the previous study, Cong et al. (2010a) has validated that WLD can extract MMN with better properties from the ordinarily averaged trace. Thus, before ICA decomposition, WLD was first used to clean the ordinarily averaged trace with the reversal biothogonal wavelet of order 6.8. Through WLD, the ordinarily averaged trace was decomposed into seven levels, and the coefficients under the fifth and sixth levels were selected to reconstruct the MMN component (Cong et al. 2010a). This was because the frequency responses of such a wavelet filter met the spectral properties of MMN (Cong et al. 2010a). This is desired when using wavelet based analysis to study ERPs (Basar et al. 2001).

Another benefit of WLD is that it probably assists to convert the underdetermined model of data almost to the determined model. In the application of ICA to EEG, the number of sources is usually assumed to be equal to that of electrodes in the low-density array and the determined ICA model is often used (Delorme and Makeig 2004). This study only collected EEG with nine electrodes. Indeed, the averaged EEG recordings may have much more sources than this number (Cong et al. 2011). Hence, in the averaged EEG recordings of our dataset, the ICA model is definitely underdetermined. Our previous study has demonstrated that the number of sources can be severely reduced by the appropriate WLD (Cong et al. 2011). Then, the undetermined model may be probably changed to the determined ICA model, at least quasi-determined model. Indeed, we cannot directly validate that the number of sources in the wavelet-filtered EEG recordings is nine in this study. Implicitly, if we suppose the number of sources is nine here and if the ICA decomposition under the determined model is reliable, we can tell that the assumption of sources’ number is reasonable. This is validated in the next section.

Estimating ERP component with ICASSO

Before ICA was performed, the data was averaged over single trials in this study. The signal to noise ratio can be improved with the proportion to the squared root of the number of trials under the assumption that additive noise is of the Gaussian distribution (Harmony 1984). Thus, it is reasonable to assume that the averaged trace is free to the sensor noise. Then, the averaged EEG recordings can be modeled as

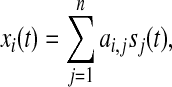graphic file with name M1.gif 1

where, xi(t) denotes EEG recording at the ith electrode, and sj(t) is the source of one electrical brain activity, and ai,j represents the mapping/mixing coefficient from a source in the brain to an electrode along the scalp. Indeed, ai,j also reveals the topography information of the corresponding source (Cong et al. 2010c). The Eq. 1 implies that the EEG recordings are mixtures of the scaled sources. The averaged EEG recordings in the matrix form may be described as

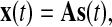graphic file with name M2.gif 2

where, s(t) represents the vector of sources of the electrical brain activities, x(t) is the vector of recordings at electrodes along the scalp, and A symbolizes the mapping/mixing matrix from the sources in the brain to the electrodes along the scalp.

ICA is to seek such an unmixing matrix W to transform x(t) into

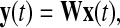graphic file with name M3.gif 3

where, y(t) is the vector of estimated independent components. To the best performance, i.e., the global optimization (Cichocki and Amari 2003), what is pursued is a global matrix C

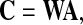graphic file with name M4.gif 4

and in each column and row of C, there is only one nonzero element. Thus, y(t) is the version of permuted and scaled s(t) under the global optimization (Hyvarinen et al. 2001; Cong et al. 2010c; Cichocki and Amari 2003).

ICA is usually realized through an adaptive iteration learning algorithm as below (Hyvarinen et al. 2001),

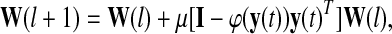graphic file with name M5.gif 5

where, φ(∙) denotes a nonlinear function associated with the probability function of the source, μ represents the learning rate, i.e., the step size between two iterations, and W(l) symbolizes the unmixing matrix at the lth iteration. Usually, the learning converges to some predefined threshold along the gradient decent algorithm through iterations to obtain the unmixing matrix W (Hyvarinen et al. 2001).

However, the threshold may be met when the solution is locally optimized, i.e., there are more than one nonzero elements in some columns and rows of the global matrix. Such a case is called as the local optimization. This happens very often in high dimensional space when using ICA to study ERPs (Himberg et al. 2004). Subsequently, the output is probably uncertain under a single-run ICA through the adaptive learning algorithm. To resolve this problem, Himberg et al. (2004) randomly initialized the learning and ran an ICA algorithm many times. After that, all these extracted components were clustered into the predefined number of common components. As a result, the output from such an ICA procedure can be much more reliable in estimating sources than the single-run ICA. They named the software as ICASSO (Himberg et al. 2004). It has been used to estimate the MMN component by Kalyakin et al. (2008, 2009).

As suggested by Vigario and Oja (2008), the higher order statistical ICA is more appropriate to decompose EEG recordings. As summarized by Daubechies et al. (2009), the extended infomax ICA (Lee et al. 1999) and FastICA (Hyvarinen 1999) are the most used algorithms in the study of brain signals. Indeed, the former usually requires a large number of samples to converge. In this study, we performed ICA on the averaged trace. The number of samples in such a signal is quite limited in any ERP study. Consequently, regarding ICASSO, FastICA (Hyvarinen 1999) was chosen for the ICA decomposition in this study and tanh (∙) was defined for the nonlinear function to FastICA. Please refer to the study of Hyvärinen (1999) for details of FastICA. 100 runs were set for ICASSO, i.e., for the wavelet-filtered traces of each subject, FastICA was run 100 times. At each time, the unmixing matrix was initialized randomly, and nine components were extracted out. Subsequently, 900 components were produced. Finally, those components were categorized into 9 clusters and each cluster corresponded to each component estimated by ICASSO. For the clustering, the agglomerative hierarchical clustering with average-linkage criterion was used (Himberg et al. 2004). This is also the default of the set in ICASSO software. Kalyakin et al. (2008, 2009) discussed this software on the application to the averaged EEG recordings in details. We used the same decomposition algorithm in this study.

Facilitating ICA to estimate MMN sources elicited by two deviants

ICA has a special requirement on the number of samples of the signal to be decomposed. It is usually at least several times larger than the squared number of estimated sources (Makeig et al. 1997, 1999). In this study, we assumed nine sources because of nine electrodes used to collect EEG data. Thus, the number of samples for ICA should be no less than 162. As stated in the “Experiment”, there were 130 samples in the averaged trace. This number in our dataset did not match the necessity of ICA. To facilitate ICA, Kalyakin et al. (2008, 2009) concatenated the averaged traces of different deviants at each channel for each subject. We repeated this procedure here. Then, the connected averaged trace of two deviants had 260 samples. As a result, the constraint of ICA on the number of samples was released.

This paradigm connecting the averaged traces of different deviants is reasonable because the deviant stimui usually substitute the repeated stimuli randomly in an oddball paradigm and the cognitive processes elicited by different deviants are assumed to be identical in the MMN experiment. Due to such a procedure, the sources of MMNs elicited by two deviants were estimated by ICASSO at the same time in this study. However, the following steps of data processing would be implemented separately for each deviant.

Choosing MMN component for wICA

After sources are estimated by ICA, the desired components are usually chosen for further processing. As introduced by Tie et al. (2008), methods used to choose the desired components are usually based on spatial patterns, map polarities, temporal characteristics, spectral criteria, and so on. For example, the MMN peak amplitude is positive in the mastoid and negative at the frontal and central areas with the reference to the tip of nose; MMN elicited by an uninterrupted sound used in this study is time-locked and should appear in the time frame from 50 ms to 200 ms after the deviant offset (Huttunen et al. 2007); the optimal frequency band of MMN is between 2 Hz and 8.5 Hz in our dataset (Kalyakin et al. 2007).

We repeated the approach of Cong et al. (2010b, d) to choose the MMN component in this study. The approach is to determine which component is the best one containing MMN information in the time and frequency domains. Firstly, every extracted component was transformed by the Morlet wavelet to obtain its time–frequency representation (TFR); then, the support to absence ratio (SAR) of the TFR of MMN was calculated for each component; finally, the component with the largest SAR was chosen as the desired MMN component.

Generally speaking, the ‘support’ represents the recordings of the desired responses of the major interest and the ‘absence’ means other recordings. To SAR of MMN in this study, the mean value of energy over the rectangular region of the TFR of a component was the support. The dimensions of this rectangle were time by frequency and the frequency range was set as 2–8.5 Hz (Kalyakin et al. 2007) and the time interval was between 50 ms and 200 ms after the deviant was offset (Huttunen et al. 2007). The mean value of energy of the rest region in the TFR of the component was the absence. Then, a larger SAR corresponded to more evident MMN component. Hence, such an approach to choose the desired component was to seek which component among nine extracted components contained information like MMN as much as possible in the time and frequency domain. Please refer to Cong et al. (2009, 2010b, d) for details of the definition of SAR.

Projecting one component back to electrode field in practice

After EEG recordings are decomposed into independent components, projecting a selected component back to the electrode field often follows to recover the amplitude of the selected component with the unit of the microvolt (Makeig et al. 1997, 1999). This is because the variance and the polarity (positive and negative) of a component extracted by ICA are indeterminate (Hyvarinen et al. 2001) and the determined peak measurements are the basis for ERP research (Luck 2005). Regarding ICA, each column of the inverse of an unmixing matrix W in the Eq. 3 can be interpolated to show the scalp map associated with the corresponding component (Makeig et al. 1997, 1999; Cong et al. 2010c), and the back projection can resolve the ambiguity of the variance and polarity problems in theory (Cong et al. 2010c). Without loss of generality, we assumed n sources and n sensors, and only one component was projected back to electrodes in this study. After the unmixing matrix is produced, its inverse can be obtained as the following

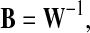graphic file with name M6.gif 6

where, B = [b1, …, bk, …, bn], bk is the column vector of B. For example, the kth estimated component is chosen, and then, the projection of this independent component back onto the electrode field is given by the outer product of the kth column of B with the kth estimated element of y(t) (Makeig et al. 1997, 1999). In the matrix–vector form, the projection can be described as

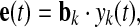graphic file with name M7.gif 7

where, e(t) represent the projected components at all electrodes, 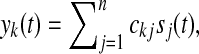Inline graphic and ckj denotes the element of global matrix C at the kth row and jth column.

Correspondingly, if the kth element of y(t) is projected to the electrode i, the scalar form of the Eq. 7 can be expressed as

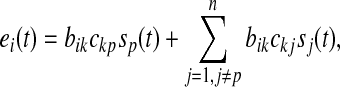graphic file with name M9.gif 8

where, bik is the element of projection matrix. Under the satisfactory ICA decomposition, ckp is assumed to possess the largest absolute value among elements of the kth row of C, and sp(t) is the target source. Supposing only sp(t) exists in the brain, the Eq. 2 can be rewritten as

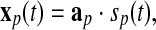graphic file with name M10.gif 9

where, sp(t) is the pth element of the brain sources’ vector s(t) in the Eq. 2, and ap is the pth column of the mapping/mixing matrix A in the Eq. 2, and xp(t) are the recordings at all electrodes, i.e., the mapping of a single source at all electrodes. In contrast to the recordings in the Eqs. 1 and 2, xp(t) only contain the information of one source. Hence, the pursuit of the application of ICA on EEG is to obtain the mapping in the Eq. 9. What follows is that the Eq. 7 is the same to the Eq. 9 in the case that the global matrix C in the Eq. 4 is globally optimized, i.e., in each row and each column, there is only one non-zero element (Cong et al. 2010c). This is an extremely strong condition in the application of ICA on EEG. Specifically, in this condition the second term in the right side of the Eq. 8 disappears and the product of bikckp in the Eq. 8 is the same to the aip, i.e., the ith element of ap in the Eq. 9 (Cong et al. 2010c).

In practice, it is rare to obtain the global optimization (Himberg et al. 2004). Thus, it is necessary to study the projected components in the electrode field as described by the Eq. (7) when the optimization of an ICA algorithm is localized. Cong et al. (2010c) has discussed this issue in details based on simulated EEG recordings. For completeness of this study, it is briefly stated here and the real EEG recordings will be examined in the “Diagram of wICA on averaged trace” and the “Results”. In this presentation, we study the case of practically satisfactory ICA decomposition that only one element in each column and each row of the global matrix has relatively large absolute value, and other elements are not entirely zero under the local optimization. In such conditions, the second term in the right side of the Eq. 8 still exists, but the first term dominates the waveform of the projected component in the electrode field. Under the local optimization, the product of bikckp in the Eq. 8 may be different with the ith element of ap in the Eq. 9, moreover, the sign of bikckp may be indeterminate (Cong et al. 2010c). Subsequently, this results in the fact that the polarity of the projected component in the electrode field is indeterminate. In such a case, polarities of the MMN peak amplitudes of different subjects at a certain electrode might be different. This definitely causes problems in performing further statistical tests on the MMN peak amplitudes. Therefore, such indeterminacy should be corrected. Based on the simulated experiment, Cong et al. (2010c) has demonstrated that the correction of the abnormal polarity assisted to achieve more precise projection through multiplying the projected component in the electrode field by ‘−1’ where the polarity of the projection is reversal. We repeated this procedure in the real experiment here. It should be noted that the correction made in this study is indeed the post processing after ICA, and it can also be regarded as the further processing on certain element of the projection matrix, and the correction does not change the real source of the brain (Cong et al. 2010c).

In this study we assumed that MMN had the same polarity at the same electrode to all subjects. Specifically, the MMN peak referred to the tip of nose was expected to be negative at electrodes F3, Fz, F4, C3, Cz, C4, and Pz, and positive at M1 and M2 (Näätänen 1992). Thus, after the projection, the polarity of the MMN peak was checked in contrast to the expectation. If it was opposite, the polarity of the projection at that electrode would be reversed.

Gain from ICA

As interpreted by the Eq. 1, EEG recordings are mixtures of electrical brain activities. In theory, as shown by the Eq. 3, we can obtain the individual brain activities with indeterminate variances in case the ICA decomposition is globally optimized (Hyvarinen et al. 2001; Cong et al. 2010c; Cichocki and Amari 2003); as illustrated by the Eq. (9), after one of such individual brain activities is projected back to the electrode field, we can gain the determined projection of this brain activity, i.e., the multiplication of the source of this brain activity and its mapping coefficient from its location in the brain to the points along the scalp (Cong et al. 2010c). In practice, we can hardly acquire the global optimization, but the local one (Cong et al. 2010c; Himberg et al. 2004), and in this case, what we can achieve is the approximation of the counterpart in theory. However, it is difficult to measure the error between the unknown theoretical expectation and the practical approximation to judge the performance of ICA. One realistic way is that if the ICA decomposition is not reliable, results should not be acceptable (Himberg et al. 2004).

Diagram of wICA on averaged trace

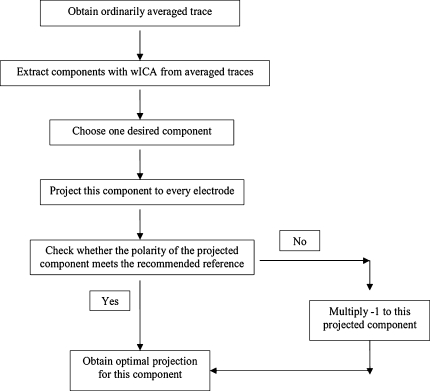
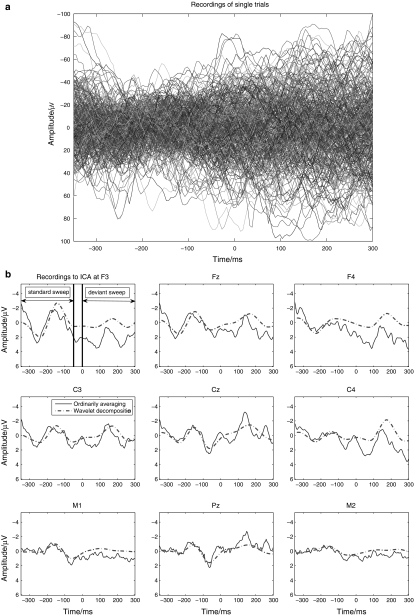
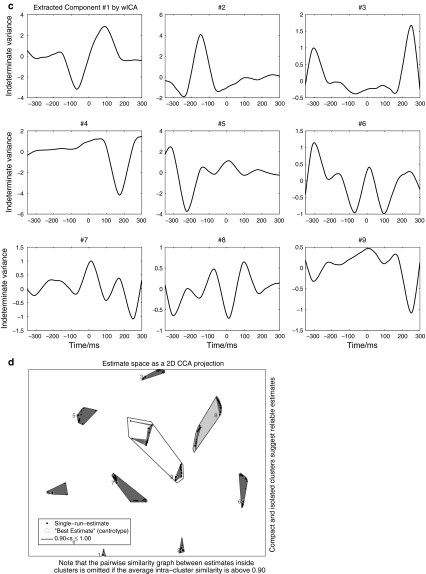
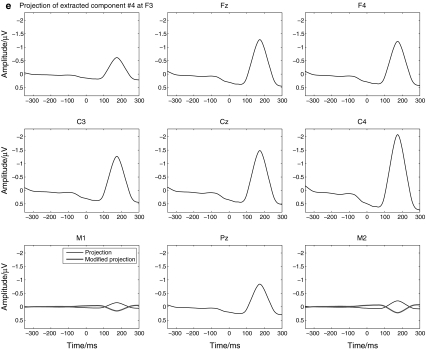
Figure 2 depicts the diagram to summarize all the steps mentioned above for wICA. Particularly, Fig. 3 demonstrates the procedure with the typical and representative data of one subject under dev50ms. Figure 3a exhibits the recordings of 333 single trials at Fz. Figure 3b shows the ordinarily averaged trace and the filtered trace by WLD. In Fig. 3a, the 333 curves represent the EEG recordings of 333 single trials at Fz, respectively, and they are highly variant in contrast to the ordinarily averaged trace at Fz as shown in Fig. 3b. Indeed, this should be very typical in the children’s MMN recordings. Hence, it is not wise to perform ICA on the EEG recordings of concatenated single trials or a single trial in this situation. Figure 3c describes the nine components extracted by wICA from the averaged traces. Figure 3d illustrates that every component estimated by wICA is very reliable since the nine clusters of all components under 100 runs’ decomposition are isolated with each other. Furthermore, the fourth component was chosen as the MMN-like component and was projected back to the electrode field as shown by Fig. 3e. This figure also interprets that the polarities at M1 and M2 were reversal to the theoretical expectations. Thus, they were modified through multiplied by ‘−1’, and then the final wICA trace used to analyze MMN peak amplitude and latency was produced. It should be noted that the abnormal polarity happens with higher probability at the electrode where the peak amplitude is smaller in contrast to those at other electrodes (Cong et al. 2010c).

Fig. 2.

Fig. 2

Open in a new tab

Diagram of data processing in this study

Fig. 3.

Fig. 3

Fig. 3

Fig. 3

Open in a new tab

Demonstration of the data processing for one subject: a recordings of single trials at Fz, b recordings to ICA, c extracted components by wICA, d the similarity graph of every component estimated by wICA under 100 runs, e projection of extracted component #4 in the electrode field

Indeed, Fig. 3 describes how MMN component was extracted from the ordinarily averaged trace by wICA and how it was projected back to the electrode field. To the single trials, MMN activity was not visible, hence, ICA decomposition was not performed on this type of EEG recordings. In the averaged trace, the MMN waveform was visible, but not well structured. After wICA was performed, the MMN component was evidently extracted from the averaged trace. In this example, the mean SAR of the ordinarily averaged trace over nine channels in Fig. 3b was −2.2 dB, and the SAR of the MMN-like component estimated by wICA, i.e., component # 4 in Fig. 3c, was 16.1 dB. Hence, the improvement was very significant, which also validated that the proposed ICA decomposition was effective and its performance was satisfactory in this study.

Data processing

In order to rule out artifacts, two exclusion principles based on visual inspection were used. Firstly, trials including eye movements with EEG recordings exceeding ± 100 μV were removed. Secondly, trials with EEG recordings showing only straight line with null information were rejected. The number of included trials per subject varied from 232 to 350 trials. The mean amount of trials for each subject was 332.

The data processing procedure of wICA included the following six steps:

  1. Averaging EEG recordings over single trials at each channel under each deviant for each subject. The mean of the activity during the first 300 ms of the trace formed the baseline and was removed from the averaged trace.

  2. Appling WLD to filter every ordinarily averaged trace (Cong et al. 2010a) and connecting the filtered traces of two deviants together at each channel for each subject.

  3. Implementing ICASSO (Himberg et al. 2004) on the concatenated wavelet-filtered traces for each subject to estimate the unmixing matrix and to extract nine independent components.

  4. Choosing the estimated MMN-like component.

  5. Computing the inverse of unmixing matrix and projecting the selected component back to the electrode field.

  6. Correcting the reversal polarity of the projected component at any electrode to achieve the final wICA trace.

To compare wICA with other methods, DW and ICA (Kalyakin et al. 2008) were also performed on the averaged trace of the same dataset. These data processing methods were repeated entirely according to the corresponding publications. Subtracting EEG recordings of the standard sweep from the deviant sweep as illustrated in Fig. 1 produced DW; regarding ICA, ICASSO was used to estimate the MMN component from the ordinarily averaged trace directly (Kalyakin et al. 2008, 2009).

Measuring MMN peak amplitude and latency

The peak amplitude and latency are the most frequently used parameters in the analysis of MMN (Näätänen 1992; Duncan et al. 2009). Hence, they were analyzed in this study too. It should be noted that the MMN peak latency here was the duration from the offset of the deviant to the MMN peak. This is often used to study MMN elicited by the duration deviant (Kalyakin et al. 2007; Huttunen-Scott et al. 2008).

For the ordinarily averaged trace, DW was used to produce MMN and to measure the amplitude and latency. The mean of recordings in the first 50 ms of the DW formed the baseline. After the baseline was removed, the peak amplitude and latency were measured.

When a paradigm eliciting practically flat responses to the standard stimulus is available, the responses to the deviant stimulus can be used without subtraction (Sinkkonen and Tervaniemi 2000). Indeed, the data processing methods discussed in this study were supposed to extract MMN component and remove the responses of the standard stimulus simultaneously. Hence, for the ICA or wICA trace, DW was not used, and the peak amplitude and latency were directly measured from the MMN time window in the deviant sweep as shown in Fig. 1. The mean of recordings in the first 50 ms of the deviant sweep formed the baseline. After it was removed, the peak amplitude and latency were measured from the deviant sweep directly.

Statistical analysis

The goal of statistical tests was to investigate the difference of the MMN peaks under two deviants for each data processing method, exploiting the physiological properties of MMN extracted by each method, and the difference of the MMN peaks between wICA and other methods, examining whether different methods extracted different MMNs.

The difference of MMN peaks among different electrodes was not discussed in this study. The peak measurements were averaged over nine channels for each data processing method. It should be noted that the peak amplitudes at M1 and M2 were multiplied by −1 for the consistence of polarities at every electrode before averaging. This was due to their positive values in contrast to the other electrodes where the peak values were negative. After that, the peak measurements were tested by the repeated measure ANOVA in order to examine whether the difference between the MMNs elicited by two deviants was significant under each method; for ANOVA, the deviant to elicit MMN was the factor and two deviants formed two levels. Meanwhile, the difference of MMN peaks between wICA and other methods was also investigated; in this case, MMN was averaged over channels and deviants; anfd for ANOVA, the method to extract the MMN component was the factor and two methods for comparison formed two levels.

Criteria to qualify performance of data processing methods

To evaluate the performance of ICA decomposition usually requires the true sources and the mixing model (Hyvarinen et al. 2001; Cichocki and Amari 2003); however, such information is not available in the real EEG recordings. As suggested by Vigario and Oja (2008), the evaluation of ICA decomposition on EEG recordings should be based on two aspects: (1) the robust estimation of extracted components, (2) the knowledge of ERPs by the expert. Thus, this study validated the proposed systematic data processing methods from the two perspectives.

In this study, ICA was implemented by the software-ICASSO (Himberg et al. 2004). ICASSO provides the stability index to qualify the performance of ICA decomposition. After ICASSO is run, the stability index denoted by Iq is given to each extracted component (Himberg et al. 2004), and Iq may range from 0 to 1. When approaching to 1, it means the corresponding component is extracted out in almost each run of ICA decomposition and the cluster that this component falls into is isolated from other clusters, and consequently, the estimation of this component should be regarded to be reliable and robust. Otherwise, it means the corresponding component does not appear in most of runs of ICA decomposition, and then, the estimation of this component should not be reliable (Himberg et al. 2004). Thus, Iq was used to examine whether the proposed wICA outperformed ICA (Kalyakin et al. 2008, 2009) from the view of reliability of decomposition in this study. As introduced in “wICA”, nine components were extracted and only one MMN-like component was projected back to the electrode field in this study. The projection is the outer product of the selected component and the corresponding column of the inverse of the unmixing matrix (Makeig et al. 1997, 1999; Cong et al. 2010c). Thus, two factors determine the projection. The former corresponds to one Iq, and the latter is associated to all Iqs since any column of the inverse of the unmixing matrix is related to the whole unmixing matrix. Hence, the average over nine Iqs was used to validate the reliability of the ICA decomposition in this study.

In order to reveal the separation ability of the proposed decomposition, the SAR was used. As shown in Fig. 3b, the ordinarily averaged trace included the responses from the deviant stimulus and the repeated stimuli, belonging to the support and absence in the definition of SAR of this study, respectively. It should be noted that MMN originates from the responses of the deviant stimulus (Näätänen et al. 1978; Näätänen 1992). The application of wICA was basically to extract MMN component out from the averaged trace in this study. Hence, as demonstrated by Fig. 3c, the fourth component contained the responses of the deviant stimulus, and for this component, the responses of repeated stimuli became almost flat. In other words, wICA separated the support and absence into different components. As a result, under the definition of SAR according to MMN’s temporal and frequency information, the larger SAR of a MMN component is, the better separation of the responses of the deviant stimulus and the repeated stimuli is. Therefore, SAR of the estimated MMN component also represented the quality of the estimated MMN in our study.

Moreover, we cannot localize the true MMN sources but we still know how MMN functions in practice. Thus, the criteria used to estimate the success of a data processing method should be based on the analysis of neurophysiologic properties of MMN. In this study, the criteria are that the larger magnitude of the deviance to the repeated stimuli elicits a MMN with larger peak amplitude and shorter peak latency. In our experiment, the dev50ms and dev30ms had 50 ms and 70 ms difference from the standard 100 ms tone, respectively. Thus, the dev30ms corresponded to the larger magnitude of deviance to repeated stimuli in this study. Therefore, it was theoretically expected that the MMN peak amplitude was larger and its latency was shorter under dev30ms.

Results

This section focused on analyzing the properties of MMN peak amplitude and latency elicited by two deviants and the extraction of MMN by different data processing procedures. After three methods were independently applied, a four-dimension matrix was obtained for the MMN peak amplitude, as well as latency. The matrix consisted of 3 methods by 2 deviants by 9 channels by 110 subjects. As mentioned above, the topography of the parameters was not analyzed in this study, thus, these parameters were averaged over channels.

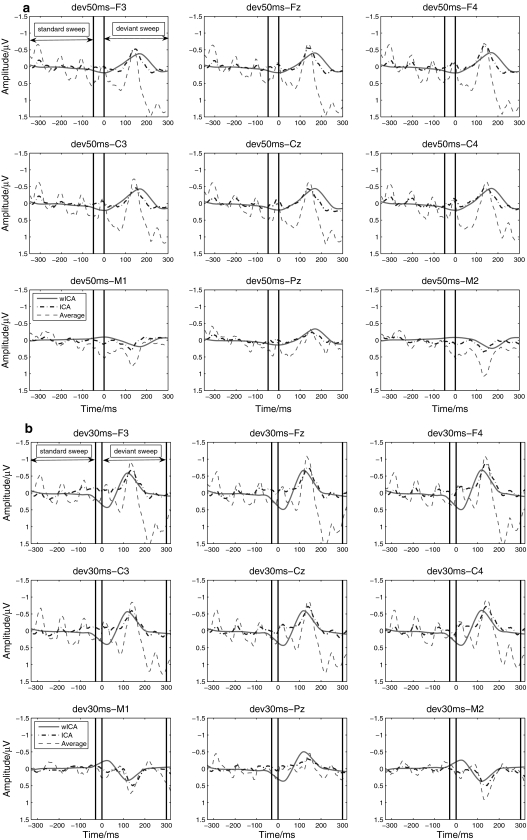
Figure 4 demonstrates the grand averaged waveforms of MMNs elicited by dev50ms and dev30ms with the methods of the ordinarily averaging, ICA and wICA. MMN peaked between 100 and 200 ms. It was apparent that both ICA and wICA extracted cleaner MMN component, i.e., responses in the deviant sweep. In contrast to ICA, wICA removed more interference from the averaged trace.

Fig. 4.

Fig. 4

Open in a new tab

Grand averaged waveform of MMN under the ordinarily averaging, ICA and wICA—a dev50ms; b dev30ms

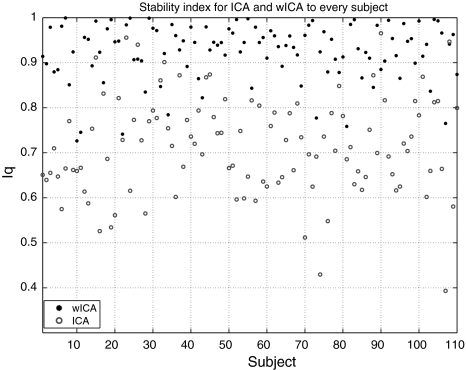
Figure 5 shows the stability index (denoted by Iq) for wICA and ICA for each subject, respectively. The grand averaged Iqs for wICA and ICA were 0.92 and 0.7, and the difference of Iqs between wICA and ICA was significant. Moreover, these results also revealed that the decomposition on the averaged trace under wICA was much reliable than that under ICA for almost every individual subject.

Fig. 5.

Fig. 5

Open in a new tab

Stability index for wICA and ICA, respectively

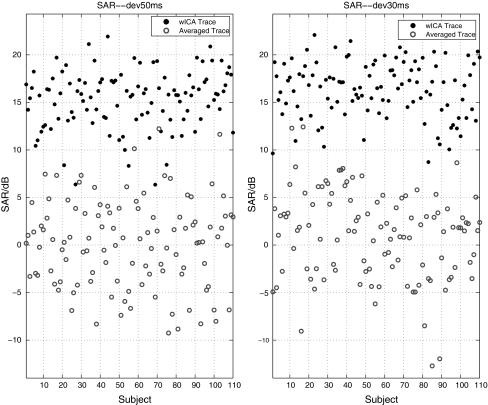
Figure 6 exhibits the mean SAR of the averaged traces over nine channels and the corresponding SAR of the MMN-like component estimated by wICA for each subject. This figure illustrates that the SAR of MMN in wICA trace of each subject was larger than the SAR of the ordinarily averaged trace. Such results indicated that the MMN component estimated by wICA had better temporal and frequency properties than the raw averaged trace had. The results also revealed the high reliability of the selection of MMN component from all extracted components by wICA.

Fig. 6.

Fig. 6

Open in a new tab

SAR of the wICA trace and averaged trace under two deviants

Table 1 depicts statistical tests of the difference of the MMN peak amplitudes between two deviants under each data processing method, as well as the latencies. Only through wICA (with polarity correction in this study), the MMN peak amplitude elicited by the larger magnitude of deviance (dev30 ms) was significantly larger and its peak latency was evidently shorter. With DW or ICA, neither the MMN peak amplitude nor its latency matched the expected properties of MMN in theory. It should be noted that results of wICA without the polarity correction in the electrode field, i.e., without the sixth step as introduced in the “Data processing”, were also analyzed, and as shown in Table 1, the statistical tests of peak amplitudes were not good. This does really reveal the importance to correct the abnormal polarities of the projection in the electrode field when using ICA to study ERP peak amplitudes.

Table 1.

Statistical tests of the difference of MMN peak amplitude and latency elicited by the two deviants under each method

Parameters/methods wICA ICA DW
With polarity correction Without polarity correction
Mean of magnitude (μV) dev50 ms 0.782 0.604 0.991 2.173
dev30 ms 1.074 0.790 1.106 2.063
Statistical tests F(1,109) 15.688 0.22 2.870 0.608
p 0.000 0.642 0.093 0.437
Mean of latency (ms) dev50 ms 150.9 132.0 130.0
dev30 ms 136.5 130.8 131.1
Statistical tests F(1,109) 8.064 1.657 0.199
p 0.005 0.201 0.656
Open in a new tab

Table 2 describes the statistical tests of the difference between wICA and other methods. Before the statistical tests, the peak amplitude and latency were averaged over deviants and channels, respectively. The result was that wICA performed differently with DW or ICA in extracting MMN from the averaged trace.

Table 2.

Statistical tests of the difference between wICA and ICA or DW in the analyses of peak amplitude and latency

Parameters/methods wICA vs. ICA wICA vs. DW
Amplitude F(1,109) 3.322 192.3
p 0.071 0.000
Latency F(1,109) 17.94 23.90
p 0.000 0.000
Open in a new tab

Discussion

Data processing plays a critical role in the MMN research, and its goal is to extract the pure and well-defined potential under study. The proposed method named as wICA exploits the temporal, frequency and spatial information of MMN source, and can extract MMN with much better properties than those estimated by DW only using the temporal characteristic or by ICA only using spatial information (Kalyakin et al. 2008). The better properties in this study are referred to the characteristics of MMN that larger magnitude of the deviance to the repeated stimuli may elicit MMN peak with larger amplitude and shorter latency (Näätänen 1992).

The main difference of the decomposition procedures between ICA and the proposed wICA (Kalyakin et al. 2008, 2009) is that the ordinarily averaged trace is fed to ICASSO under ICA, and the wavelet-filtered trace is fed to ICASSO under the proposed wICA. Indeed, WLD acts as an important preprocessing step in wICA. From the view of the stability analysis of ICA decomposition by ICASSO (Himberg et al. 2004), the decomposition on the ordinarily averaged traces was not satisfactory in this study, but the decomposition on the wavelet-filtered traces became much better. This particularly contributes the difference in estimating the peak latency of MMN between the two methods. As the decomposition under ICA was not sufficient, the MMN peak latency was still dominated by the ordinarily averaged trace, i.e., the mixture. However, the decomposition under wICA was satisfactory, and the MMN component was almost entirely extracted out. As a result, the MMN property was successfully revealed by wICA, i.e., the MMN peak latency was shorter under the larger magnitude of deviance to the repeated stimuli (Näätänen 1992).

Moreover, using ICA implicitly assumes the sources are independent with each other. However, in one ERP experiment, the electrical brain activities elicited by the same stimulus may be related. For example, MMN is basically produced by the deviant stimulus in the oddball paradigm, and during the experiment, the subject is usually instructed not to pay attention to the stimulus (Näätänen 1992; Duncan et al. 2009). Sometimes, the deviant stimulus may inevitably draw some attention of the subject passively, thus, P3a often follows MMN (Näätänen 1992; Huttunen et al. 2007; Huttunen-Scott et al. 2008). From this point of view, P3a and MMN are related. However, this does not prevent the application of ICA to extract MMN component. This is because the pure ERP component looks like the bump (Vigario and Oja 2008), in other words, it is sparse, and Daubechies et al. (2009) have validated that ICA for brain signals does not necessarily select for independence, but the sparsity. Actually, Fig. 3c demonstrates that most of the extracted components by wICA are sparse. It should be noted that this does not mean the sources of the electrical brain activities are all sparse. In this study, the EEG recordings were first averaged over single trials. This produces the evoked brain activities (Görsev and Basar 2010). Furthermore, the wavelet filter in this study was specially designed according to the properties of MMN (Cong et al. 2010a). Hence, a lot of electrical brain activities are removed by the averaging and the wavelet-filter (Cong et al. 2011).

In summary, results associated with the proposed wICA lead to five suggestions: (1) instead of the concatenated-trial based EEG trace as is often used in EEGLAB (Delorme and Makeig 2004), the averaged trace is better fed to ICA in the study of MMN of children; (2) wavelet decomposition can act as the preprocessing method to improve the quality of the recordings and reduce the number of sources in the averaged trace (Cong et al. 2010a, 2011); (3) the FastICA based ICASSO is a very efficient ICA procedure to extract the desired ERP component from the wavelet-filtered averaged traces (Himberg et al. 2004; Hyvarinen 1999); (4) the SAR of the TFR of the extracted component can assist to seek the desired MMN component automatically (Cong et al. 2010b, d); (5) the back-projection of one component extracted by ICA might not entirely overcome its polarity indeterminacy at any electrode, and correcting the wrong polarity of the projected component at any electrode may improve the accuracy of the projection (Cong et al. 2010c). In case one extracted component by ICA is projected back to the electrode field, the ultimate EEG recording at one electrode in theory is the multiplication of the corresponding source and the transfer/mapping coefficient from the source in the brain to the electrode along the scalp, and in practice, it is the approximation to the theoretical expectation.

Furthermore, Fig. 5 interprets the degree of the reliability of ICA decomposition on the ordinarily averaged trace and the wavelet-filtered trace under the determined ICA model, i.e., nine channels of observation and nine sources in the model. The decomposition algorithm was identical, but the results were different. This indicates that the ICA models in the ordinarily averaged traces and the wavelet-filtered traces were different. As the decomposition by wICA is very reliable, it is reasonable to conclude that the real ICA model in the wavelet-filtered traces is at least almost determined, but it is definitely underdetermined in the ordinarily averaged traces in our study (Cong et al. 2011). Seriously speaking, we cannot validate whether the filtered traces can be completely modeled by the determined model. Hence, it is worth investigating the robust underdetermined ICA algorithm to extract MMN components from the filtered traces (Tichavský and Koldovský 2011). Furthermore, this study only used FastICA for the decomposition. Recently, more effective algorithms outperforming FastICA have been reported, including, efficient FastICA (EFICA), weights-adjusted second-order blind identification (WASOBI), combination of them (COBI), and approximate joint diagonalization (AJD), and so on (Koldovský et al. 2006, 2009; Koldovský and Tichavský 2011; Tichavsky et al. 2008; Tichavsky and Yeredor 2009). It is reasonable to predict that if the performance of ICA decomposition is better in single runs under ICASSO, the finally extracted components by ICASSO should be more reliable. Thus, in the future, we plan to examine the ICASSO with those algorithms mentioned above, as well as other robust ICA algorithms.

In this study, the temporal, spectral and spatial information of MMN has been exploited to design the data processing method. The temporal information is derived from the experiment paradigm to elicit ERPs, and the spectral information can be achieved through observing the changes of peak amplitudes of ERPs with a group of low-pass and high-pass digital filters (Kalyakin et al. 2007), and the spatial information naturally exists in the multi-channel EEG recordings. Since almost every ERP possesses the similar properties exploited here, the proposed method in this study can also be used in the research of other ERPs. Moreover, the toolboxes of wavelet decomposition are supplied by MATLAB (The Mathworks, Inc., Natick, MA), and FastICA (Hyvarinen 1999) and ICASSO (Himberg et al. 2004) can be downloaded through internet. It is very convenient for researchers to repeat the same data processing approach proposed in this study. Furthermore, although wICA is a complicated and advanced data processing method, as long as the six steps in “wICA” were implemented carefully, the well-defined ERPs could be extracted reliably.

Acknowledgments

The first and second authors gratefully thank COMAS, a postgraduate school in computing and mathematical sciences offered by the University of Jyväskylä, Finland, for supporting this study. Cong F is also grateful to professor Amir Averbuch for his invaluable suggestions on wavelet analysis.

References

  1. Basar E, Schurmann M, Demiralp T, Basar-Eroglu C, Ademoglu A. Event-related oscillations are ‘real brain responses’—wavelet analysis and new strategies. Int J Psychophysiol. 2001;39:91–127. doi: 10.1016/S0167-8760(00)00135-5. [DOI] [PubMed] [Google Scholar]
  2. Chen Z, Cao J, Cao Y, Zhang Y, Gu F, Zhu G, Hong Z, Wang B, Cichocki A. An empirical EEG analysis in brain death diagnosis for adults. Cogn Neurodyn. 2008;2:257–271. doi: 10.1007/s11571-008-9047-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Cichocki A, Amari S. Adaptive blind signal and image processing: learning algorithms and applications. Chichester: Wiley; 2003. [Google Scholar]
  4. Cong F, Sipola T, Huttunen-Scott T, Xu X, Ristaniemi T, Lyytinen H. Hilbert-Huang versus Morlet wavelet transformation on mismatch negativity of children in uninterrupted sound paradigm. Nonlinear Biomed Phys. 2009;3:1. doi: 10.1186/1753-4631-3-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Cong F, Kalyakin I, Huang Y, Huttunen-Scott T, Li H, Lyytinen H, Ristaniemi T (2010a) Frequency response based wavelet decomposition to extract mismatch negativity of children. No.B8/2010, Series B. Scientific Computing: Reports of Department Mathematical Information Technology, University of Jyväskylä, Finland. http://users.jyu.fi/~fecong/TechnicalReport.html
  6. Cong F, Kalyakin I, Phan AH, Cichocki A, Huttunen-Scott T, Lyytinen H,Ristaniemi T (2010b) Extract mismatch negativity and P3a through two-dimensional nonnegative decomposition on time-frequency represented event-related potentials. In: Zhang L, Kwok J, Lu B-L (eds) ISNN 2010, Part II. Lect Notes Comput Sci 6064:385–391
  7. Cong F, Kalyakin I, Ristaniemi T (2010c) Can back-projection fully resolve polarity indeterminacy of ICA in study of ERP? Biomed Signal Process Control. doi:10.1016/j.bspc.2010.05.006
  8. Cong F, Phan AH, Cichocki A, Lyytinen H, Ristaniemi T (2010d) Identical fits of nonnegative matrix/tensor factorization may correspond to different extracted event-related potentials. In: Proceedings of international joint conference on neural networks 2010 (IEEE world congress on computational intelligence 2010), pp 2260–2264
  9. Cong F, Leppänen PHT, Astikainen P, Hämäläinen J, Hietanen JK,Ristaniemi T (2011) Dimension reduction: additional benefit of an optimal filter for independent component analysis to extract event-related potentials. No. B4/2011, Series B. Scientific Computing: Reports of Department Mathematical Information Technology, University of Jyväskylä, Finland. http://users.jyu.fi/~fecong/TechnicalReport.html [DOI] [PubMed]
  10. Daubechies I, Roussos E, Takerkart S, Benharrosh M, Golden C, D’Ardenne K, Richter W, Cohen JD, Haxby J. Independent component analysis for brain fMRI does not select for independence. Proc Natl Acad Sci USA. 2009;106:10415–10422. doi: 10.1073/pnas.0903525106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Delorme A, Makeig S. EEGLAB: an open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J Neurosci Methods. 2004;134:9–21. doi: 10.1016/j.jneumeth.2003.10.009. [DOI] [PubMed] [Google Scholar]
  12. Duncan CC, Barry RJ, Connolly JF, Fischer C, Michie PT, Näätänen R, Polich J, Reinvang I, Petten C. Event-related potentials in clinical research: guidelines for eliciting, recording, and quantifying mismatch negativity, P300, and N400. Clin Neurophysiol. 2009;120:1883–1908. doi: 10.1016/j.clinph.2009.07.045. [DOI] [PubMed] [Google Scholar]
  13. Garrido MI, Kilner JM, Stephan KE, Friston KJ. The mismatch negativity: a review of underlying mechanisms. Clin Neurophysiol. 2009;120:453–463. doi: 10.1016/j.clinph.2008.11.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Görsev GY, Basar E. Sensory evoked and event related oscillations in Alzheimer’s disease: a short review. Cogn Neurodyn. 2010;4:263–274. doi: 10.1007/s11571-010-9138-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Hämäläinen M, Hari R, Ilmoniemi R, Knuutila J, Lounasmaa O. Magnetoencephalography—theory, instrumentation, and applications to noninvasive studies of the working human brain. Rev Mod Phys. 1993;65:413–497. doi: 10.1103/RevModPhys.65.413. [DOI] [Google Scholar]
  16. Harmony T. Neurometric assessment of brain dysfunction in neurological patients: functional neuroscience. Hillsdale, NJ: Lawrence Erlbaum Associates Publishers; 1984. [Google Scholar]
  17. Himberg J, Hyvarinen A, Esposito F. Validating the independent components of neuroimaging time series via clustering and visualization. Neuroimage. 2004;22:1214–1222. doi: 10.1016/j.neuroimage.2004.03.027. [DOI] [PubMed] [Google Scholar]
  18. Huovinen T, Ristaniemi (2006) Independent component analysis using successive interference cancellation for oversaturated data. Eur Trans Telecomm 17:577–589
  19. Huttunen T, Halonen A, Kaartinen J, Lyytinen H. Does mismatch negativity show differences in reading-disabled children compared to normal children and children with attention deficit? Dev Neuropsychol. 2007;31:453–470. doi: 10.1080/87565640701229656. [DOI] [PubMed] [Google Scholar]
  20. Huttunen-Scott T, Kaartinen J, Tolvanen A, Lyytinen H. Mismatch negativity (MMN) elicited by duration deviations in children with reading disorder, attention deficit or both. Int J Psychophysiol. 2008;69:69–77. doi: 10.1016/j.ijpsycho.2008.03.002. [DOI] [PubMed] [Google Scholar]
  21. Hyvarinen A. Fast and robust fixed-point algorithms for independent component analysis. IEEE Trans Neural Netw. 1999;10:626–634. doi: 10.1109/72.761722. [DOI] [PubMed] [Google Scholar]
  22. Hyvarinen A, Karhunen J, Oja E. Independent component analysis. New York: Wiley; 2001. [Google Scholar]
  23. Iyer D, Zouridakis G. Single-trial evoked potential estimation: comparison between independent component analysis and wavelet denoising. Clin Neurophysiol. 2007;118:495–504. doi: 10.1016/j.clinph.2006.10.024. [DOI] [PubMed] [Google Scholar]
  24. Kalyakin I, Gonzalez N, Joutsensalo J, Huttunen T, Kaartinen J, Lyytinen H. Optimal digital filtering versus difference waves on the mismatch negativity in an uninterrupted sound paradigm. Dev Neuropsychol. 2007;31:429–452. doi: 10.1080/87565640701229607. [DOI] [PubMed] [Google Scholar]
  25. Kalyakin I, Gonzalez N, Karkkainen T, Lyytinen H. Independent component analysis on the mismatch negativity in an uninterrupted sound paradigm. J Neurosci Methods. 2008;174:301–312. doi: 10.1016/j.jneumeth.2008.07.012. [DOI] [PubMed] [Google Scholar]
  26. Kalyakin I, Gonzalez M, Ivannikov I, Lyytinen H. Extraction of the mismatch negativity elicited by sound duration decrements: a comparison of three procedures. Data Knowl Eng. 2009;68:1411–1426. doi: 10.1016/j.datak.2009.07.004. [DOI] [Google Scholar]
  27. Koldovský Z, Tichavský P. Time-domain blind separation of audio sources on the basis of a complete ICA decomposition of an observation space. IEEE Trans Audio Speech Lang Process. 2011;19:406–416. doi: 10.1109/TASL.2010.2049411. [DOI] [Google Scholar]
  28. Koldovsky Z, Tichavsky P, Oja E. Efficient variant of algorithm FastICA for independent component analysis attaining the Cramer-Rao lower bound. IEEE Trans Neural Netw. 2006;17:1265–1277. doi: 10.1109/TNN.2006.875991. [DOI] [PubMed] [Google Scholar]
  29. Koldovský Z, Málek J, Tichavský P, Deville Y, Hosseini S. Blind separation of piecewise stationary non-Gaussian sources. Signal Process. 2009;89:2570–2584. doi: 10.1016/j.sigpro.2009.04.021. [DOI] [Google Scholar]
  30. Lee TW, Girolami M, Sejnowski TJ. Independent component analysis using an extended infomax algorithm for mixed SubGaussian and SuperGaussian sources. Neural Comput. 1999;11:417–441. doi: 10.1162/089976699300016719. [DOI] [PubMed] [Google Scholar]
  31. Makeig S (2002) Frequently asked questions about ICA applied to EEG and MEG data. http://www.sccn.ucsd.edu/~scott/icafaq.html. Swartz Center for Computational Neuroscience, Institute for Neural Computation, University of California, San Diego
  32. Makeig S, Jung TP, Bell AJ, Ghahremani D, Sejnowski TJ. Blind separation of auditory event-related brain responses into independent components. Proc Natl Acad Sci USA. 1997;94:10979–10984. doi: 10.1073/pnas.94.20.10979. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Makeig S, Westerfield M, Jung TP, Covington J, Townsend J, Sejnowski TJ, Courchesne E. Functionally independent components of the late positive event-related potential during visual spatial attention. J Neurosci. 1999;19:2665–2680. doi: 10.1523/JNEUROSCI.19-07-02665.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Marco-Pallares J, Grau C, Ruffini G. Combined ICA-LORETA analysis of mismatch negativity. Neuroimage. 2005;25:471–477. doi: 10.1016/j.neuroimage.2004.11.028. [DOI] [PubMed] [Google Scholar]
  35. Näätänen R. Attention and brain functions. Hillsdale, NJ: Lawrence Erlbaum Associates; 1992. [Google Scholar]
  36. Näätänen R, Gaillard AW, Mantysalo S. Early selective-attention effect on evoked potential reinterpreted. Acta Psychol (Amst) 1978;42:313–329. doi: 10.1016/0001-6918(78)90006-9. [DOI] [PubMed] [Google Scholar]
  37. Nunez P, Srinivasan R. Electric fields of the brain: the neurophysics of EEG. New York: Oxford University Press; 2005. [Google Scholar]
  38. Picton TW, Bentin S, Berg P, Donchin E, Hillyard SA, Johnson R, Jr, Miller GA, Ritter W, Ruchkin DS, Rugg MD, Taylor MJ. Guidelines for using human event-related potentials to study cognition: recording standards and publication criteria. Psychophysiology. 2000;37:127–152. doi: 10.1111/1469-8986.3720127. [DOI] [PubMed] [Google Scholar]
  39. Pockett S, Whalen S, McPhail AV, Freeman WJ. Topography, independent component analysis and dipole source analysis of movement related potentials. Cogn Neurodyn. 2007;1:327–340. doi: 10.1007/s11571-007-9024-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Sinkkonen J, Tervaniemi M. Towards optimal recording and analysis of the mismatch negativity. Audiol Neurootol. 2000;5:235–246. doi: 10.1159/000013885. [DOI] [PubMed] [Google Scholar]
  41. Tichavský P, Koldovský Z. Weight adjusted tensor method for blind separation of underdetermined mixtures of nonstationary sources. IEEE Trans Signal Process. 2011;59:1037–1047. doi: 10.1109/TSP.2010.2096221. [DOI] [Google Scholar]
  42. Tichavsky P, Yeredor A. Fast approximate joint diagonalization incorporating weight matrices. IEEE Trans Signal Process. 2009;57:878–891. doi: 10.1109/TSP.2008.2009271. [DOI] [Google Scholar]
  43. Tichavsky P, Koldovsky Z, Yeredor A, Gomez-Herrero G, Doron E. A hybrid technique for blind separation of non-Gaussian and time-correlated sources using a multicomponent approach. IEEE Trans Neural Netw. 2008;19:421–430. doi: 10.1109/TNN.2007.908648. [DOI] [PubMed] [Google Scholar]
  44. Tie Y, Whalen S, Suarez RO, Golby AJ. Group independent component analysis of language fMRI from word generation tasks. Neuroimage. 2008;42:1214–1225. doi: 10.1016/j.neuroimage.2008.05.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Vigario R, Oja E. BSS and ICA in neuroinformatics: from current practices to open challenges. IEEE Rev Biomed Eng. 2008;1:50–61. doi: 10.1109/RBME.2008.2008244. [DOI] [PubMed] [Google Scholar]

Articles from Cognitive Neurodynamics are provided here courtesy of Springer Science+Business Media B.V.

RESOURCES