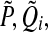Abstract
In this paper, the synchronization problem for delayed continuous time nonlinear complex neural networks is considered. The delay dependent state feed back synchronization gain matrix is obtained by considering more general case of time-varying delay. Using Lyapunov stability theory, the sufficient synchronization criteria are derived in terms of Linear Matrix Inequalities (LMIs). By decomposing the delay interval into multiple equidistant subintervals, Lyapunov-Krasovskii functionals (LKFs) are constructed on these intervals. Employing these LKFs, new delay dependent synchronization criteria are proposed in terms of LMIs for two cases with and without derivative of time-varying delay. Numerical examples are illustrated to show the effectiveness of the proposed method.
Keywords: Synchronization, Neural networks, Time-varying delay, Delay decomposition, Maximum admissible upper bound (MAUB)
Introduction
During the past decade, control and synchronization of chaotic systems have become an important topic, since the pioneering work of Pecora and Carroll in 1990 (Carroll and Pecora 1990, 1991). Chaos synchronization has been widely investigated due to its applications in creating secure communication systems (Yu and Liu 2003; Feki 2003). Both Hopfield Neural Networks (HNNs) and Cellular Neural Networks (CNNs) have attracted considerable attention in recent decades and have been widely applied in number of engineering and scientific fields including image processing, computing technology, solving linear and nonlinear algebraic equations and so on (Lou and Cui 2006; Arik 2003).
Moreover, Haken (2007) has presented a neural net model describing biological activity in visual cortex and coined a problem that synchronization between groups of neurons may be the key to solution of “binding problem”. In addition to that noise-induced complete synchronization and frequency synchronization in coupled spiking and bursting neurons studied in Shi et al. (2008). Also in Jirsa (2008) it has been proved that time delay plays a vital role in synchronized states of spiking-burst neuronal networks.
On the other hand, artificial neural networks models can also exhibit chaotic behavior (Lou and Cui 2007; Gilli 1993; Lu 2002) due to the fact that small perturbation in initial conditions may lead to large deviation in system dynamics and so synchronization of chaotic neural networks has also become an important area of study. Some authors have paid attention to the synchronization of neural networks (Chen et al. 2004; Chao Jung et al. 2006; Cui and Lou 2009; Gao et al. 2009; Wang et al. 2010). In Cui and Lou (2009), some sufficient conditions for exponential synchronization of neural networks with time-varying delays have been given in terms of feasible solution in the form of Linear Matrix Inequalities (LMIs). In Gao et al. (2009), based on the Lyapunov method a delay independent sufficient synchronization conditions in term of LMIs for chaotic recurrent neural networks with time-varying delays using nonlinear feedback control have been obtained. Delay-dependent conditions, which contains information concerning time delay, are usually less conservative than delay-independent ones. In addition, synchronization between neurons both in biological neuronal network and artificial neural network is essential for information processing. The study of synchronization problem of delayed neural networks may proceed to study complex synchronization between spike-burst neurons. In this paper, we propose a novel synchronization criterion based on delay decomposition approach to derive a maximum admissible upper bound (MAUB) of the time delay such that two identical chaotic nonlinear continuous neural networks with time-varying delay is synchronized asymptotically. The larger MAUB of time delay implies less conservatism of delay-dependent synchronization criterion. Moreover the gain matrix of the controller for slave system can be determined based on LMIs, which can be easily solved by various convex optimization algorithms (Boyd et al. 1994). In this paper, in order to obtain some less conservative sufficient conditions, we adapted the method proposed by Zhang and Han (2009). Interior point algorithm implemented in MATLAB LMI toolbox is employed to solve the derived LMIs.
To the best of authors knowledge, the delay decomposition approach to delay-dependent synchronization analysis for continuous time nonlinear complex neural networks with time-varying delay has never been tackled in any of the previous literature. Based on LKF approach, some new synchronization criteria are proposed in the form of LMIs, which are dependent on the size of the time delay. Numerical examples are given to illustrate the feasibility and effectiveness of proposed method.
Notations Throughout this paper,  and
and 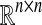 denote n-dimensional Euclidean space and the set of all n × n real matrices respectively. I denotes the identity matrix and P−1 denotes the inverse matrix of P. The notation
denote n-dimensional Euclidean space and the set of all n × n real matrices respectively. I denotes the identity matrix and P−1 denotes the inverse matrix of P. The notation 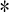 always denotes the symmetric block in one symmetric matrix. The superscript T denotes the transposition and the notation X ≥ Y (respectively, X > Y), where X and Y are symmetric matrices, means that X − Y is positive semi-definite (respectively, positive definite). Matrices, if not explicitly stated, are assumed to have compatible dimensions.
always denotes the symmetric block in one symmetric matrix. The superscript T denotes the transposition and the notation X ≥ Y (respectively, X > Y), where X and Y are symmetric matrices, means that X − Y is positive semi-definite (respectively, positive definite). Matrices, if not explicitly stated, are assumed to have compatible dimensions.
Synchronization problem and preliminaries
Based on the master-slave concept, the unidirectional coupled nonlinear neural networks are described by the following delay differential equation. The master system is
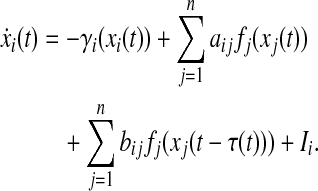 |
1 |
and the slave system is
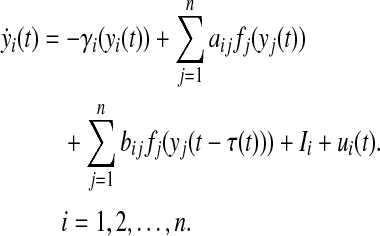 |
2 |
where n ≥ 2 denotes the number of neurons in the networks, xi(t) and yi(t) are the state variables associated with ith neuron of master and slave systems respectively at time t. aij and bij indicate the interconnection strength among the neurons without and with time-varying delay respectively. The neuron activation function fi describes the manner in which the neurons respond to each other. Ii denotes the constant external input and ui(t) be an unidirectional-coupled term, which is considered as control input and will be appropriately designed to obtain certain control objective. Furthermore, τ(t) is the time-varying delay such that 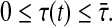 System (1) and (2) possess initial conditions
System (1) and (2) possess initial conditions 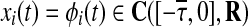 and
and 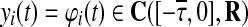 known as delay history functions for master (1) and slave (2) systems respectively, where
known as delay history functions for master (1) and slave (2) systems respectively, where 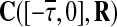 denotes the set of all continuous functions from
denotes the set of all continuous functions from 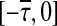 to R.
to R.
We further assume that 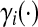 and
and 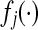 satisfy the following conditions:
satisfy the following conditions:
(A1): Each function
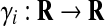 is locally Lipschitz and nondecreasing function, that is, there exists a positive real di such that
is locally Lipschitz and nondecreasing function, that is, there exists a positive real di such that 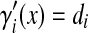 for any
for any 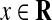 at which γi is differentiable function.
at which γi is differentiable function.- (A2): Each function
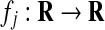 is monotonic nondecreasing and globally Lipschitz, that is, there exists a positive real lj such that
is monotonic nondecreasing and globally Lipschitz, that is, there exists a positive real lj such that
Define the synchronization error ei(t) = xi(t) − yi(t). Thus the error dynamic system can be represented as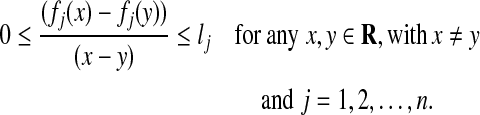
where βi(ei(t)) = γi(xi(t)) − γi(yi(t)) and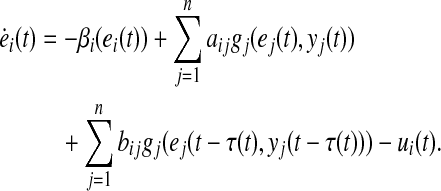
3 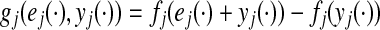 .
.
For notational purpose, we denote 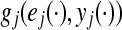 as
as 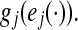 From (A2), one can obtain that
From (A2), one can obtain that 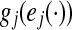 satisfying
satisfying
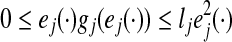 |
4 |
and from (A1) and according to Lebourg theorem (see Theorem 2.3.7 in Clarke 1983), there exists ci ≥ di such that βi(ei(t)) = ciei(t).
In order to ensure synchronization of coupled neural networks, the control input ui(t) is designed as follows
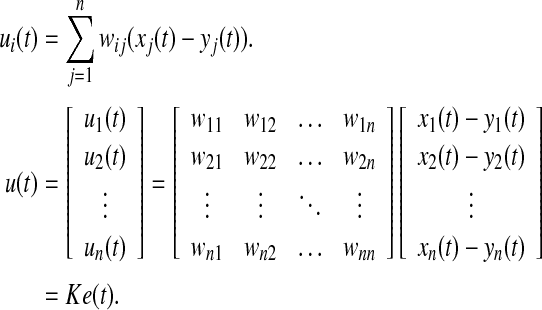 |
5 |
where 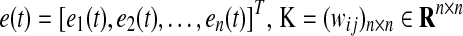 is the state feedback control gain matrix to be determined for synchronizing both master and slave systems. Thus from Eqs. 3 and 5, we rewrite the error dynamic system as
is the state feedback control gain matrix to be determined for synchronizing both master and slave systems. Thus from Eqs. 3 and 5, we rewrite the error dynamic system as
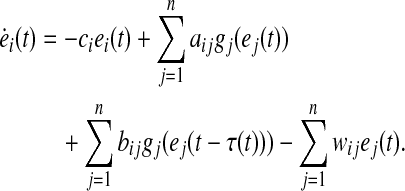 |
6 |
Transforming Eq. 6 into compact form as
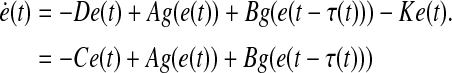 |
7 |
where C = D + K, D = diag{ci}, A = (aij)n×n, B = (bij)n×n, and 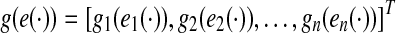 .
.
Now we are stating the following Lemmas, which will be more useful in the sequel.
Lemma 2.1 [Han (Zhang and Han 2009)] For any constant matrix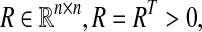 scalar h with
scalar h with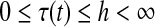 and a vector-valued function
and a vector-valued function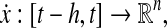 the following integration is well defined, then
the following integration is well defined, then
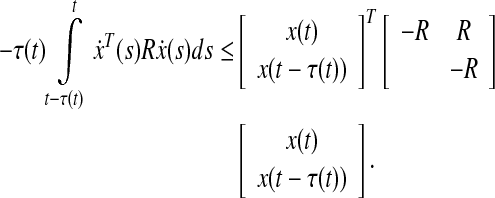 |
Lemma 2.2 (Schur complement) Let P, Q, R be given matrices of appropriate dimensions such thatR > 0. Then
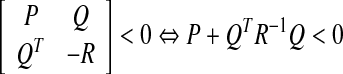 |
Based on the available information on the time-varying delay, we will consider the following two cases.
Case I τ (t) is a continuous function satisfying
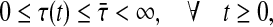 |
8 |
Case II τ (t) is a differentiable function satisfying
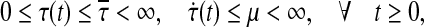 |
9 |
where 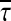 and μ are scalars.
and μ are scalars.
Synchronization criteria
In this section we introduce LKFs to derive some new delay-dependent synchronization criterion for nonlinear continuous neural networks with time-varying delay system described by Eqs. 1 and 2.
Theorem 3.1 Under case I and hypotheses (A1)–(A2), for a given scalar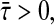 the master-slave neural networks (1) and (2) are completely synchronized with control gain
the master-slave neural networks (1) and (2) are completely synchronized with control gain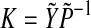 if there exist positive definite symmetric matrices
if there exist positive definite symmetric matrices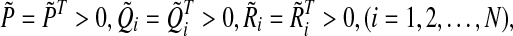 any matrix
any matrix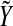 and diagonal matrices
and diagonal matrices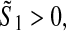
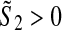 such that the LMI (10) holds for all
such that the LMI (10) holds for all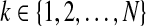 ,
,
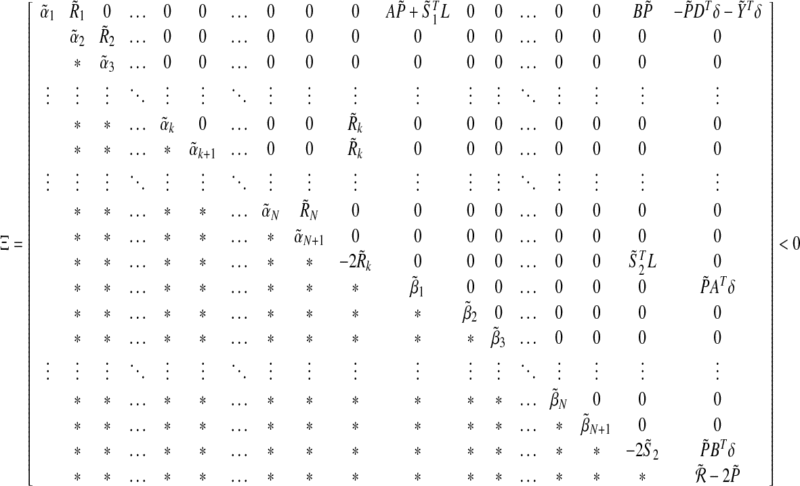 |
10 |
where
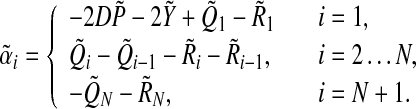 |
11 |
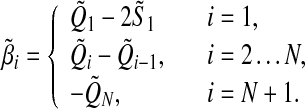 |
12 |
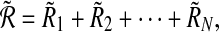 |
13 |
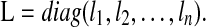 |
14 |
Proof Let N > 0 be an integer. We decompose the delay interval 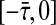 into N equidistant subintervals, that is,
into N equidistant subintervals, that is,
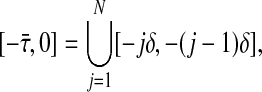 |
where 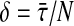 . Then choosing different matrix pairs (Qj, Rj) on
. Then choosing different matrix pairs (Qj, Rj) on 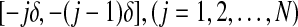 , we construct the following new LKF:
, we construct the following new LKF:
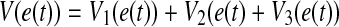 |
15 |
where
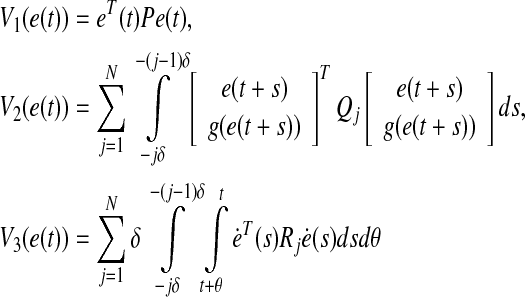 |
with 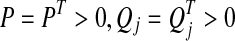 and
and 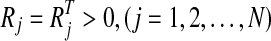 .Taking the derivative of V(e(t)) in Eq. 15 with respect to t along the trajectory of Eq. 7 yields
.Taking the derivative of V(e(t)) in Eq. 15 with respect to t along the trajectory of Eq. 7 yields
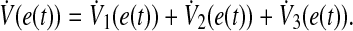 |
16 |
where
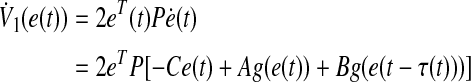 |
17 |
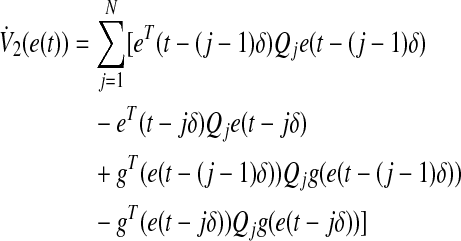 |
18 |
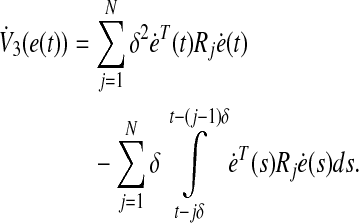 |
19 |
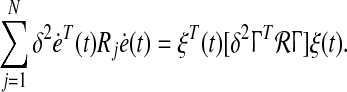 |
20 |
where 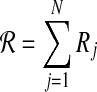 ,
,
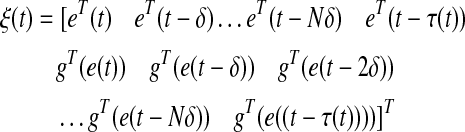 |
21 |
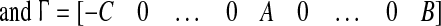 |
22 |
We now disclose the interrelationship between e(t − τ(t)) and 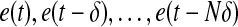 by utilizing the integral terms in Eq. 19. Since τ(t) is a continuous function satisfying Eq. 8 ∀ t ≥ 0, there should exist a positive integer
by utilizing the integral terms in Eq. 19. Since τ(t) is a continuous function satisfying Eq. 8 ∀ t ≥ 0, there should exist a positive integer 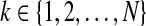 such that
such that 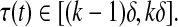 In this situation,
In this situation,
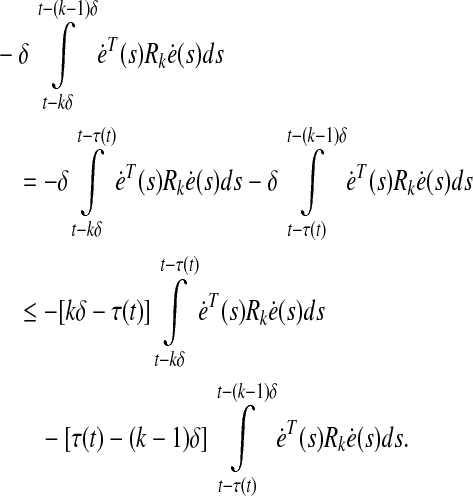 |
23 |
Applying Lemma 2.1 to the last two integral terms in Eq. 23 and after simple manipulations, we have
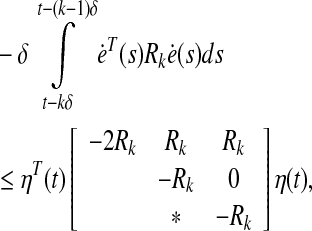 |
24 |
where
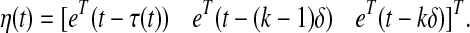 |
For j ≠ k, we also have the following inequality by Lemma 2.1:
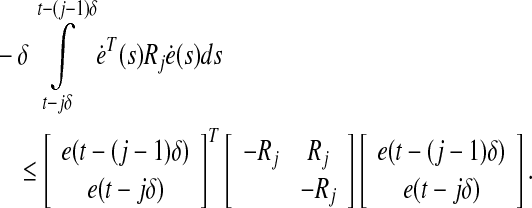 |
25 |
Combining Eqs. 24 and 25, we have
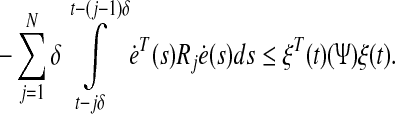 |
26 |
 |
27 |
where 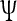 is given in Eq. 27 (see previous page). From the sector condition, the following inequalities hold
is given in Eq. 27 (see previous page). From the sector condition, the following inequalities hold
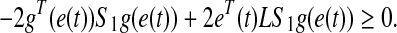 |
28 |
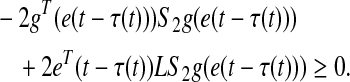 |
29 |
Therefore, using Eqs. 17–26 in Eq. 16 and adding Eqs. 28, 29 to Eq. 16 we have
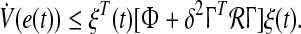 |
30 |
where 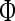 is given in Eq. 31, and
is given in Eq. 31, and
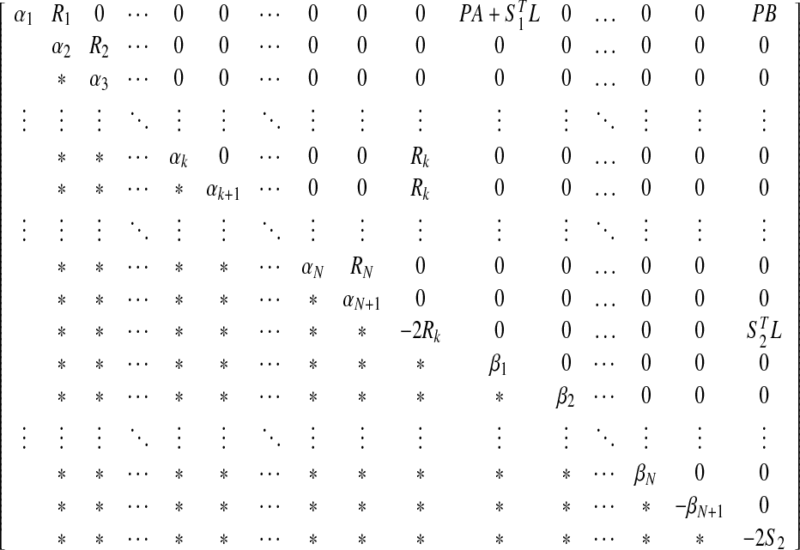 |
31 |
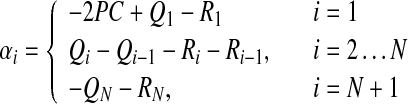 |
32 |
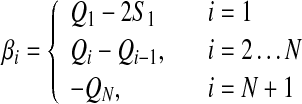 |
33 |
A sufficient condition for synchronization of the master-slave systems described by Eqs. 1 and 2 is that there exist real diagonal matrices S1, S2 and positive semi definite matrices 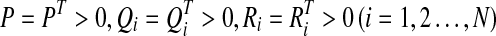 of appropriate dimensions, such that
of appropriate dimensions, such that
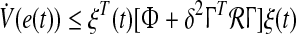 |
34 |
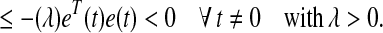 |
35 |
In order to guarantee Eq. 34, we require the following condition
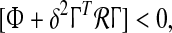 |
36 |
which can be written by Lemma 2.2 as
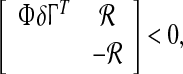 |
37 |
where 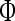 is defined in Eq. 31.Equation 37 contains bilinear matrix inequalities, which may not be solved efficiently if used directly. Thus the novel matrix transformation for LMIs is used. Pre and post multiply Eq. 37 with
is defined in Eq. 31.Equation 37 contains bilinear matrix inequalities, which may not be solved efficiently if used directly. Thus the novel matrix transformation for LMIs is used. Pre and post multiply Eq. 37 with 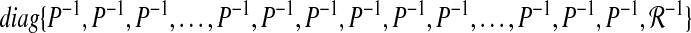 and applying change of variables
and applying change of variables 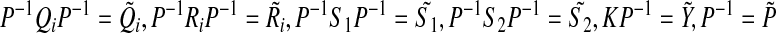 and C = (D + K), we get
and C = (D + K), we get 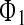 which has represented as an Eq. 38.
which has represented as an Eq. 38.
 |
38 |
It is noted that Eq. 38 is not to be an LMI condition because of the term 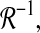 which is equal to
which is equal to 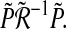 It can be written as
It can be written as 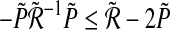 resulting from
resulting from 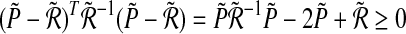 .This leads to LMI (10). Considering all possibilities of k in the set
.This leads to LMI (10). Considering all possibilities of k in the set 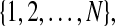 we arrive at the conclusion that Eq. 10 holds for all
we arrive at the conclusion that Eq. 10 holds for all 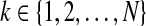 . This completes the proof.
. This completes the proof. 
Remark 3.2 Since 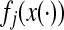 describe the neuron behavior, the results proposed in this paper can be easily applied to Hopefield neural networks
describe the neuron behavior, the results proposed in this paper can be easily applied to Hopefield neural networks 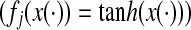 and to Cellular neural networks
and to Cellular neural networks 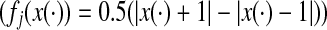 etc., Moreover unlike in Gao et al. (2009) and Hu (2009), we have presented less conservative relaxed sufficient synchronization criterions by removing the constraints
etc., Moreover unlike in Gao et al. (2009) and Hu (2009), we have presented less conservative relaxed sufficient synchronization criterions by removing the constraints 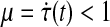 .
.
Case II τ(t) is a differentiable function satisfying Eq. 9. In this case, the derivative of the time-varying delay is available. We will use this additional information to provide a less conservative result. For this goal, we will modify V(e(t)) as
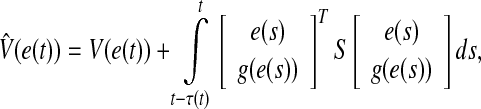 |
39 |
where S = ST > 0 and 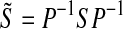 .
.
Remark 3.3 Notice that for constant time delay case, Theorem 1, can be utilized without using the Eq. 23 (without time-varying delay interrelationship). On the other hand using the information on derivative of delay 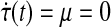 which is based on case II, synchronization criteria for constant time delay neural networks can be obtained from the following theorem.
which is based on case II, synchronization criteria for constant time delay neural networks can be obtained from the following theorem.
Theorem 3.4 Under case II and hypotheses (A1)–(A2), for given scalars τ > 0 and μ > 0, the master-slave neural networks (1) and (2) are completely synchronized with control gain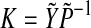 if there exist positive definite symmetric matrices
if there exist positive definite symmetric matrices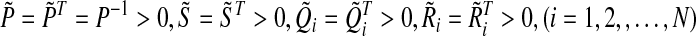 and diagonal matrices
and diagonal matrices 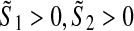 such that the following LMI holds for all
such that the following LMI holds for all 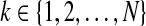 ,
,
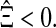 |
40 |
where 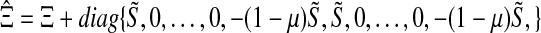 with
with 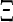 is defined in Eq. 10.
is defined in Eq. 10.
Synchronization algorithm
The main aim of the present study is to design a linear error state feedback controller of the form (5) such that the master (1) and the slave (2) systems synchronized asymptotically. Theorem 3.1 and 3.4 provide new criteria for synchronization which are dependent on the delay. In adequate to the above results, finding the MAUB of 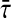 can be formulated as a optimization problem for the symmetric, positive definite decision variables
can be formulated as a optimization problem for the symmetric, positive definite decision variables 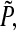
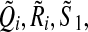 and
and 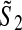 for
for 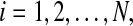 and for all
and for all 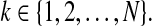 For example, consider the problem of finding MAUB for case I from Theorem 3.1 as
For example, consider the problem of finding MAUB for case I from Theorem 3.1 as
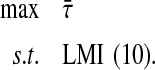 |
41 |
If the problem described in Eq. 41 has a feasible solution set for all i, and k, then there is a delay limit 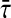 and the corresponding control gain K exists such that the master (1) and the slave (2) systems synchronized asymptotically. The suboptimal problem can be easily solved by interior point algorithm given in Matlab LMI toolbox or cone-complementary algorithm implemented in YALMIP using SeDuMi solver or any other LMI solvers. In order to obtain the control gain K while maximizing the delay
and the corresponding control gain K exists such that the master (1) and the slave (2) systems synchronized asymptotically. The suboptimal problem can be easily solved by interior point algorithm given in Matlab LMI toolbox or cone-complementary algorithm implemented in YALMIP using SeDuMi solver or any other LMI solvers. In order to obtain the control gain K while maximizing the delay 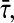 an iterative algorithm is presented as follows.
an iterative algorithm is presented as follows.
- Step 1:
Fix the number of decomposition N′. Set j = 0, N = N′, and δ = 0.
- Step 2:
Solve the LMI feasibility problem given in Eq. 41 for the positive definite matrices
and any matrix
for
and for all
- Step 3:
If a feasible solution exists and positive value for δ exists, then
and the control gain is
- Step 4:
Set j = j + 1. If K and
are desirable end the process. Else Go to Step 2 by taking N = N′ + 1.
Numerical examples
In this section, two examples are provided to show the effectiveness of the proposed methods.
Example 4.1 Consider two dimensional neural network with time varying delay given in Gao et al. (2009).
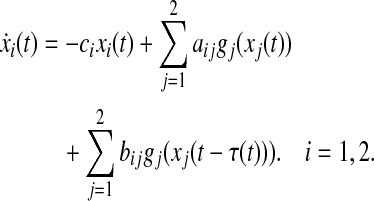 |
42 |
where 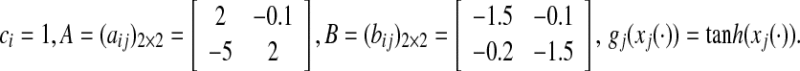 The response system is designed as follows:
The response system is designed as follows:
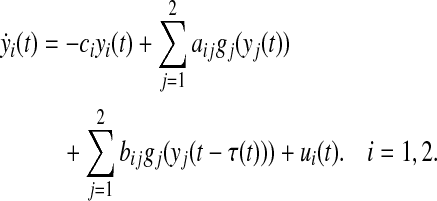 |
43 |
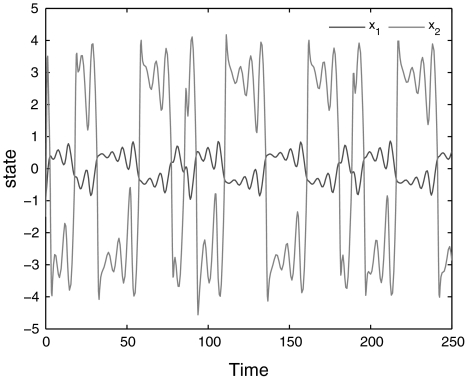
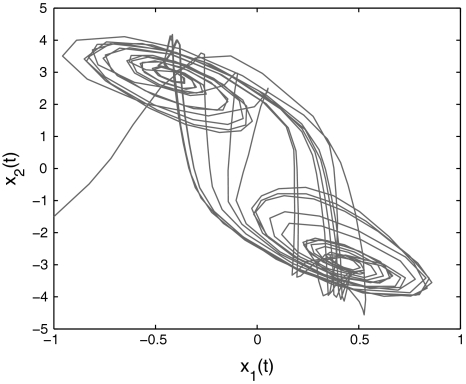
Based on the proposed criteria, the MAUBs of 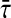 of time-varying delay τ(t) and the corresponding control gain K such that the master (42) and slave (43) systems are synchronized to be determined, which is not dealt in the existing literature. Solving the suboptimal problem given in Eq. 41, the calculated MAUBs and corresponding controller gain matrices for various N are listed in the Table 1 for case 1. When information on derivative of time varying delay is available, using Theorem 3.4 under case 2, calculated MAUBs are given in Table 2 for various values of μ which include μ ≥ 1. The state trajectories and phase-space plot of the master system (42) are given in Figs. 1 and 2, respectively. For simulations, initial condition is taken as ϕ(t) = [ − 1; − 1.5]T and the time-varying delay is considered as
of time-varying delay τ(t) and the corresponding control gain K such that the master (42) and slave (43) systems are synchronized to be determined, which is not dealt in the existing literature. Solving the suboptimal problem given in Eq. 41, the calculated MAUBs and corresponding controller gain matrices for various N are listed in the Table 1 for case 1. When information on derivative of time varying delay is available, using Theorem 3.4 under case 2, calculated MAUBs are given in Table 2 for various values of μ which include μ ≥ 1. The state trajectories and phase-space plot of the master system (42) are given in Figs. 1 and 2, respectively. For simulations, initial condition is taken as ϕ(t) = [ − 1; − 1.5]T and the time-varying delay is considered as 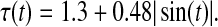
Table 1.
MAUB of τ(t) and controller gains for Example 1
| N | MAUB | CPU time | K |
|---|---|---|---|
| 2 | 0.9750 | 11.42 | 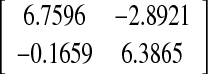 |
| 3 | 1.2936 | 18.89 | 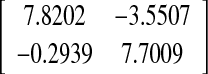 |
| 4 | 1.5544 | 67.01 | 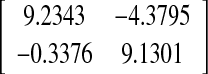 |
| 5 | 1.7750 | 128.36 | 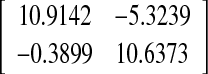 |
| 6 | 1.9686 | 177.37 | 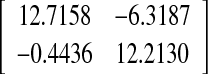 |
Table 2.
MAUB of τ(t) for Example 1 with various values of μ
| N | μ = 0 | μ = 0.5 | μ = 0.7 | μ ≥ 1 |
|---|---|---|---|---|
| 2 | 1.5176 | 1.4420 | 1.3760 | 0.9750 |
| 3 | 2.2764 | 2.1630 | 2.0640 | 1.2936 |
| 5 | 3.7940 | 3.6050 | 3.4400 | 1.7750 |
Fig. 1.
State Trajectories of Master system (42)
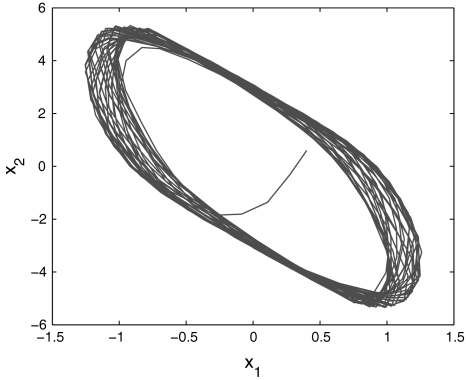
Fig. 2.
Phase space portrait of Master system (42)
In Gao et al. (2009), the authors illustrated the exponential synchronization feasibility of the system (42) and (43) and for a given exponential convergent degree (ECD) α = 0.6, the controller gain matrix has been chosen as 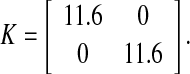
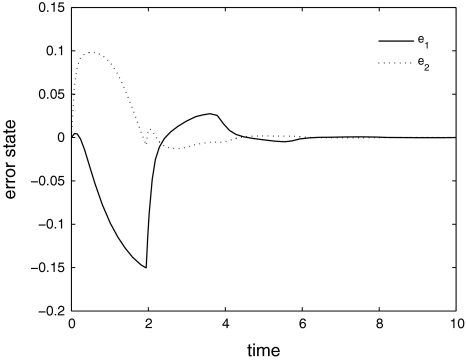
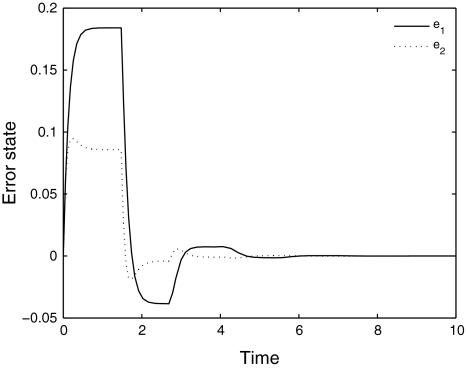
The error dynamics between master (42) and slave (43) is plotted for 10 s in Fig. 3. Applying the computed control gain matrix for 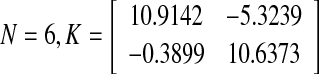 to error system, the master and slave systems are synchronized effectively which is given in Fig. 4. Clearly it shows that the control gains are small and the proposed criteria provides efficient design method for linear error state feedback controller to attain synchronization. Computation of desired MAUB of
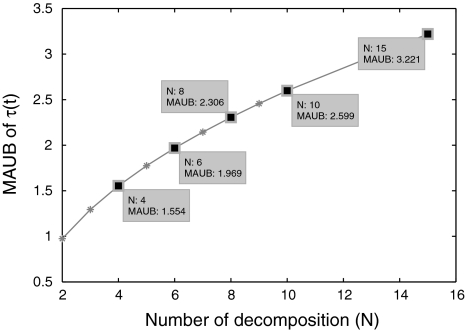
to error system, the master and slave systems are synchronized effectively which is given in Fig. 4. Clearly it shows that the control gains are small and the proposed criteria provides efficient design method for linear error state feedback controller to attain synchronization. Computation of desired MAUB of 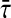 depends on the number of decompositions and CPU time (also known as elapsed time in Matlab) to solve the LMIs. When number of delay decomposition increases (N), MAUB grows larger and attains its analytical delay limit (Zhang and Han 2009). For this example, up to N = 15, the calculated MAUBs are plotted against the decompositions which is given in Fig. 5.
depends on the number of decompositions and CPU time (also known as elapsed time in Matlab) to solve the LMIs. When number of delay decomposition increases (N), MAUB grows larger and attains its analytical delay limit (Zhang and Han 2009). For this example, up to N = 15, the calculated MAUBs are plotted against the decompositions which is given in Fig. 5.
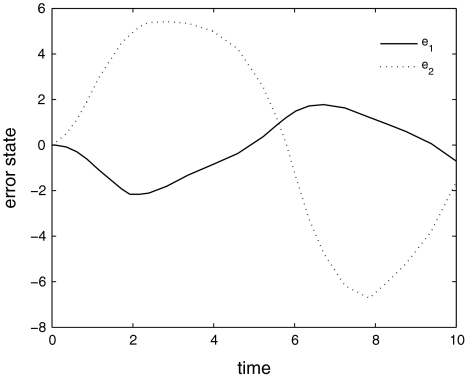
Fig. 3.
Error trajectory between Eqs. 42 and 43 with out any control
Fig. 4.
Error trajectory after applying the controller. Plot shows Eqs. 42 and 43 are synchronized
Fig. 5.
N versus MAUB plot for Example 1
Example 4.2 Consider the example given in Hu (2009). A two dimensional nonlinear neural networks with time varying delays is given by
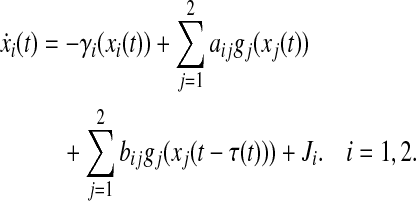 |
44 |
where 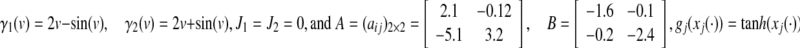 respectively. Clearly it is seen that γ1(v) and γ2(v) satisfy A1 (Hu 2009). Similarly, applying the procedure followed in this paper, Table 3 presents MAUB of time varying delay and controller gain matrices found by solving LMIs. For numerical simulations, consider τ(t) = 1 and ϕ(t) = [ − 1; − 1.5]T. The simulations are presented in Figs. 6, 7 and 8. Figure 8, clearly depicts that the master and slave systems are synchronized with the control applied.
respectively. Clearly it is seen that γ1(v) and γ2(v) satisfy A1 (Hu 2009). Similarly, applying the procedure followed in this paper, Table 3 presents MAUB of time varying delay and controller gain matrices found by solving LMIs. For numerical simulations, consider τ(t) = 1 and ϕ(t) = [ − 1; − 1.5]T. The simulations are presented in Figs. 6, 7 and 8. Figure 8, clearly depicts that the master and slave systems are synchronized with the control applied.
Table 3.
MAUB of τ(t) and controller gains for Example 2
| N | MAUB | CPU time | K |
|---|---|---|---|
| 2 | 0.7056 | 10.08 | 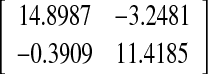 |
| 3 | 0.9051 | 22.12 | 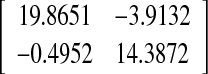 |
| 4 | 1.0724 | 52.83 | 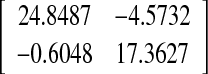 |
| 5 | 1.2185 | 120.55 | 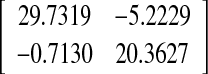 |
| 6 | 1.3494 | 248.75 | 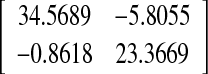 |
Fig. 6.
State trajectory of system (44)
Fig. 7.
Phase-space portrait of Eq. 44
Fig. 8.
Synchronized error trajectory after applying state feedback control for Example 2
Conclusion
In this paper, the problem of synchronization condition for chaotic nonlinear continuous neural networks has been studied. Applying the delay decomposition approach, a new synchronization criterion have been given in terms of LMIs, which is dependent on the size of the time delay. The delay decomposition, delay-dependent synchronization analysis for chaotic nonlinear continuous neural networks are new and novel. In this paper, the determined the MAUBs for 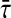 of delay τ(t) and corresponding controller gain matrices, which is not dealt in the existing literature. So we unable to compare the numerical results with other research papers. Finally, two numerical examples have been presented which illustrate the effectiveness and usefulness of the proposed method.
of delay τ(t) and corresponding controller gain matrices, which is not dealt in the existing literature. So we unable to compare the numerical results with other research papers. Finally, two numerical examples have been presented which illustrate the effectiveness and usefulness of the proposed method.
Acknowledgments
The research is supported by University Grant Commission, Government of India, under Faculty Development Programme, XI plan grant. The authors would like to thank the Editor-in-Chief and anonymous reviewers for their valuable comments and suggestions.
Contributor Information
P. Balasubramaniam, Phone: 91-451-2452371, FAX: 91-451-2453071, Email: balugru@gmail.com
R. Chandran, Email: rchandran62@gmail.com
S. Jeeva Sathya Theesar, Email: sjstheesar@gmail.com
References
- Arik S. Global asymptotic stability of a larger class of neural networks with constant time delays. Phys Lett A. 2003;311:504–511. doi: 10.1016/S0375-9601(03)00569-3. [DOI] [Google Scholar]
- Boyd S, et al. Linear matrix inequalities in systems and control theory. Philadelphia: SIAM; 1994. [Google Scholar]
- Carroll T, Pecora L. Synchronizing chaotic circuits. Phys Rev Lett. 1990;64:821–824. doi: 10.1103/PhysRevLett.64.821. [DOI] [PubMed] [Google Scholar]
- Carroll T, Pecora L. Synchronization in chaotic system. IEEE Trans Circuits Syst. 1991;38:453–456. doi: 10.1109/31.75404. [DOI] [Google Scholar]
- Chao Jung Ch, The-Luliao, Jun-JuthYan, Chi-chuan Hwang (2006) Exponential synchronization of a class of neural networks with time-varying delays. Syst Man Cybern Part B 36:209–215 [DOI] [PubMed]
- Chen G, Zhou J, Liu Z. Global synchronization of coupled delayed neural networks with application to chaotic CNN models. Int J Bifurcat Chaos. 2004;14:2229–2240. doi: 10.1142/S0218127404010655. [DOI] [Google Scholar]
- Clarke FH. Optimization and nonsmooth analysis. Newyork: Wiley; 1983. [Google Scholar]
- Cui BT, Lou XY. Synchronization of chaotic recurrent neural networks with time-varying delays using nonlinear feedback control. Chaos Solitons Fractals. 2009;39:288–294. doi: 10.1016/j.chaos.2007.01.100. [DOI] [Google Scholar]
- Feki M. An adaptive chaos synchronizationschemeapplied to secure communication. Chaos Solitons Fractals. 2003;18:141–148. doi: 10.1016/S0960-0779(02)00585-4. [DOI] [Google Scholar]
- Gao X, Zhong S, Gao F. Exponential synchronization of neural networks with time-varying delays. Nonlinear Anal. 2009;71:2003–2011. doi: 10.1016/j.na.2009.01.243. [DOI] [Google Scholar]
- Gilli M. Strange attractors in delayed cellular neural networks. IEEE Trans Circuits Syst. 1993;40:849–853. doi: 10.1109/81.251826. [DOI] [Google Scholar]
- Haken H. Towards a unifying model of neural net activity in the visual cortex. Cogn Neurodyn. 2007;1:15–25. doi: 10.1007/s11571-006-9005-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu J. Synchronization conditions for chaotic nonlinear continuous neural networks. Chaos Solitons Fractals. 2009;41:2495–2501. doi: 10.1016/j.chaos.2008.09.026. [DOI] [Google Scholar]
- Jirsa VK. Dispersion and time delay effects in synchronized spike-burst networks. Cogn Neurodyn. 2008;2:29–38. doi: 10.1007/s11571-007-9030-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lou XY, Cui BT. New LMI conditions for delay-dependent asymptotic stability of Hopfield neural networks. Neurocomputing. 2006;69:2374–2378. doi: 10.1016/j.neucom.2006.02.019. [DOI] [Google Scholar]
- Lou XY, Cui BT. Stochastic exponential stability for Markovian jumping BAM neural networks with time-varying delays. IEEE Trans Syst Man Cybern Part B. 2007;37:713–719. doi: 10.1109/TSMCB.2006.887426. [DOI] [PubMed] [Google Scholar]
- Lu HT. Chaotic attractors in delayed neural networks. Phys Lett A. 2002;298:109–116. doi: 10.1016/S0375-9601(02)00538-8. [DOI] [Google Scholar]
- Shi X, Wang Q, Lu Q. Firing synchronization and temporal order in noisy neural networks. Cogn Neurodyn. 2008;2:195–206. doi: 10.1007/s11571-008-9055-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Ding W, Chen D. Synchronization schemes of a class of fuzzy cellular neural networks based on adaptive control. Phys Lett A. 2010;374:1440–1449. doi: 10.1016/j.physleta.2010.01.029. [DOI] [Google Scholar]
- Yu H, Liu Y. Chaotic synchronization based on stability creterion of linear systems. Phys Lett A. 2003;314:292–298. doi: 10.1016/S0375-9601(03)00908-3. [DOI] [Google Scholar]
- Zhang XM, Han Q-L. A delay decomposition approach to delay dependent stability for linear systems with time varying delays. Int J Robust Nonlinear Control. 2009;19:1922–1930. doi: 10.1002/rnc.1413. [DOI] [Google Scholar]