Semi-supervised joint spatio-temporal feature selection for P300-based BCI speller

Abstract

In this paper, we address the important problem of feature selection for a P300-based brain computer interface (BCI) speller system in several aspects. Firstly, time segment selection and electroencephalogram channel selection are jointly performed for better discriminability of P300 and background signals. Secondly, in view of the situation that training data with labels are insufficient, we propose an iterative semi-supervised support vector machine for joint spatio-temporal feature selection as well as classification, in which both labeled training data and unlabeled test data are utilized. More importantly, the semi-supervised learning enables the adaptivity of the system. The performance of our algorithm has been evaluated through the analysis of a P300 dataset provided by BCI Competition 2005 and another dataset collected from an in-house P300 speller system. The results show that our algorithm for joint feature selection and classification achieves satisfactory performance, meanwhile it can significantly reduce the training effort of the system. Furthermore, this algorithm is implemented online and the corresponding results demonstrate that our algorithm can improve the adaptiveness of the P300-based BCI speller.

Introduction

A brain computer interface (BCI) is a direct pathway between a brain and an external device for the purpose of communication and control, particularly for the paralyzed people who suffer severe neuromuscular disorders, through exploiting the brain signals such as non-invasive electroencephalogram (EEG) or invasive neural spikes (Wolpaw et al. 2002; Dornhege 2007). For EEG-based BCIs, several brain activity patterns, such as event related potentials (ERP) (Farwell and Donchin 1988; Donchin et al. 2000; Serby et al. 2005), spontaneous sensory motor rhythms (Wolpaw and McFarland 2004) and slow cortical potentials (Birbaumer et al. 1999), are often used to produce the control signals. Typically, P300 ERP is an evoked potential of the brain to some specific external stimulus including auditory, visual, or somatosensory stimuli in a stream of frequent stimuli (Röder et al. 1996). P300-based BCI has been implemented to help disabled to communicate with computers through virtual keyboard (Farwell and Donchin 1988; Donchin et al. 2000), and the whole system is called a P300 speller. In P300 spellers as well as most other EEG-based BCI systems, brain signals are collected from the scalp both spatially and temporally via multiple electrodes. Then, feature selection/extraction is performed before task-driven classification.

Prior studies have indicated that the P300 can be recorded via EEG as a positive deflection in voltage at the latency of roughly 300 ms after a target “oddball” stimulus onset. The peak latency of P300 component in the corresponding time window would vary with the subjects and the relevance of eliciting events. Up to present, the time window used in P300-based BCI systems has been manually selected, with large interval containing the specific latency of 250–550 ms (Donchin et al. 2000; Rakotomamonjy and Guigue 2008). In other words, the selected time window is expected to be wide enough to capture all required discriminative information for an effective classification. However, P300 latency is highly subject-specific and event related. Large time window, with only a small segment related to the appearance of P300 potential, may reduce separability of P300 and background signals. Moreover, with such empirical temporal feature selection, dimensional redundancy in feature space is usually unavoidable, which may ultimately impair the performance of classification. In the case of limited training data set, the redundancy can even induce over-fitting behavior. Therefore, it is advantageous to design algorithms that can automatically find out most effective P300 time window and bear adaptiveness to subjects as well as mental tasks.

On the other hand, although P300 can be detected at distributed sites of scalp, it has a dominant parietal topography. Hence, most of the existing P300 based BCI research has focused on the EEG signals from a few standard P300 scalp locations (e.g., Fz, Cz, Pz) (Krusienski et al. 2008). However, as a matter of fact, there exists significant spatial discrepancy of P300 on scalp among individuals. Therefore the fixed sets of standard P300 channels cannot meet the needs of building BCIs with high performance for all the subjects. From the data analysis reports of BCI Competition 2005 (Blankertz et al. 2005), personalized automatic channel selection plays an important role in the overall performance of the P300 BCI speller. As a typical example, in Rakotomamonjy and Guigue (2008), recursive channel elimination based on discriminative score has been used for channel selection. By eliminating four least important channels in each iteration, the classification performance of a large validation data set is adopted as a fitness index to select the significant subset of channels. Channel selection and classification regarding a P300 BCI dataset from BCI Competition 2003 has also been implemented by a genetic algorithm in Citi et al. (2004). When sufficient training data are available, the aforementioned channel selection and classification approaches can achieve outstanding performance.

Although in some cases the effective time window and subset of channels of a P300 BCI can be determined separately, optimal solution is usually achievable through joint selection because the classification accuracy is often a complex function of both parameters. The state-of-art method, stepwise linear discriminant analysis (SWLDA) has been widely used in recent work to identify subject-specific spatio-temporal features for P300 speller (Donchin et al. 2000). SWLDA selects the most statistically relevant spatio-temporal features from the input set, which is essentially equivalent to simultaneous time window and channel selection. However, this method is a supervised method without using the information of the test dataset, which may be not stable over time especially when the training dataset is small. For the purpose of improving the performance of P300 speller, we consider to use a semi-supervised approach in this paper for joint selection of a time window and a subset of channels. Along with the feature selection, classification is also performed. The joint selection is implemented in an alternating way. That is, fixing a subset of features in one domain, we choose a subset of features in the other domain, at the same time realizing a classifier. Then, we search for a subset of features in the former domain and realize a classifier. The iteration continues until the algorithm converges.

Besides the performance, another important concern in the design of a practical BCI system is to reduce the time needed for initial calibration. However, reliable feature selection and classification generally requires a large training data set with labels. Typically, cross-validation as a traditional method for feature selection usually works poorly with a small training data set. Although the collection of sufficient labeled instances for training is either tedious, expensive or even impossible, fortunately in many applications, unlabeled data points are often easy to obtain. These data can be utilized through semi-supervised learning approaches to improve feature selection and classification (Chapelle et al. 2006). For example, in Li and Guan (2008), an iterative semi-supervised support vector machine (SVM) algorithm was proposed for feature re-extraction and classification with small training data set. On the other hand, due to the non-stationary characteristic of brain signals, adaptivity is also crucial to a BCI system for practical applications. Bearing these two concerns in mind, in this paper, we extend the algorithm in Li and Guan (2008) for joint time window and channel selection in P300 speller where labeled data are insufficient. Our proposed algorithms make use of both training data with labels and test data without labels. The statistical distance of two classes is measured by Fisher ratio, the computation of which also involves both labeled and unlabeled data. Our data analysis results from two different P300 spellers validate the effectiveness of the proposed algorithm and the benefit brought by using unlabeled data.

The remaining part of this paper is organized as follows. In section “Self-training algorithms for spatial/temporal feature selection”, we consider the spatial and temporal feature selection in a separate manner. Firstly, an iterative semi-supervised SVM algorithm is proposed for time segment selection with given subset of channels. Then a modified version of this algorithm is presented for channel selection. In section “Joint selection of time segment and channels”, based on the two algorithms in section “Self-training algorithms for spatial/temporal feature selection”, a semi-supervised algorithm is proposed for joint selection of time segment and channel using both labeled and unlabeled data. In section “Data analysis and online implementation”, data analysis results and online experimental results are presented. In the final section “Conclusion”, we review the algorithms of this paper.

Self-training algorithms for spatial/temporal feature selection

In P300-based BCIs, the detection of P300 in a segment of EEG signal can be well described by a two class problem. The signal containing P300 is labeled by 1, and the signal without P300 is labeled by −1. In this section, we first define a Fisher ratio based on SVM score to measure the statistical distance of feature vector ensembles from the two classes. Then we present the details of two self-training semi-supervised SVM algorithms for time segment selection and channel selection respectively.

Fisher ratio based on SVM score

In this paper, we use SVM as a classifier. Given the N_c epochs of training data set 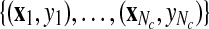where 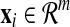is an m-dimensional feature vector and y_i ∈ {−1, 1} is the label indicating the class that x_i belongs to. A standard SVM for two-class problem can be defined as Vapnik (2000)

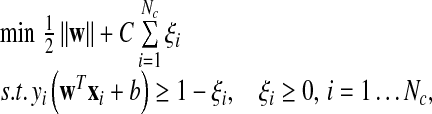1

where w denotes the weight vector of the classifier and ξ_i denotes the ith slack variable; indicates L2-norm operation; and the parameter C > 0 controls the tradeoff between the slack variable penalty and the margin. The training of the SVM classifier finds a suitable weight vector w and new data point x is classified according to the sign of d(x) given by

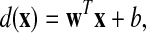2

where d(x) is designated SVM score. SVM score is proportional to the distance between the decision boundary and the data point x. In this paper, we define a Fisher ratio based on SVM score for feature selection as well as classification of P300-based EEG signal.

Generally, Fisher ratio describes the discriminability of data points from two classes. It is defined as the ratio of the interclass difference to the intraclass spread (Bishop 1995) and has been successfully used as an index for feature selection of a motor imagery BCI (Lal et al. 2004). Herein, Fisher ratio based on SVM score is defined as follows to measure the statistical distance of two classes of feature vectors. One class refers to P300, the other one refers to background.

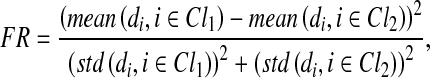3

where d_i denotes SVM score of the ith data point; Cl₁ and Cl₂ denote the two classes of epoches with labels being +1 and −1 respectively; mean(·) and std(·) represent mean and standard deviation operations respectively.

In the case of insufficient training data with labels, however, the SVM model is generally not reliable, and therefore the resultant Fisher ratio calculated from SVM score is subject to bias. We try to solve this problem through semi-supervised learning where unlabeled data points are also utilized together with labeled data.

Self-training algorithm for time segment selection

Assume the availability of an insufficient training data set with labels and a large test data set without labels. Based on these data, we present a self-training SVM algorithm for time segment selection and signal classification for P300-based BCI, where both the Fisher ratio and the SVM classifier are iteratively updated until the algorithm converges.

The two data sets under consideration include a training data set D_c containing N_c epochs of EEG signal matrix 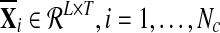with labels y_i ∈ {+1, −1}, (i = 1,…,N_c), and a test data set D_t containing N_t epochs of downsampled EEG signal 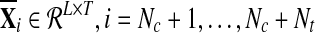without labels, where L denotes the number of EEG channels and T denotes the number of samples in time domain. We divide the T sample points into N_p time segments 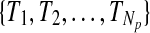that may be overlapped. In the following, we present the procedure of a self-training SVM algorithm for time segment selection as well as classification.

Self-training algorithm for channel selection

In this subsection, we propose Algorithm 3 for channel selection as well as classification. Its major discrepancy to Algorithm 1 lies in the following aspects. Suppose that the total number of channels is L. Firstly, all channels are ranked according to their individual Fisher ratio in descending order. Secondly, the ranked channels are grouped into a number of subsets followed by computing Fisher ratio for each subset. Typically, L subsets can be obtained, with the first subset containing the top ranked channel, the second subset containing the top two ranked channels, and so on. Finally, the subset of channels with the highest Fisher Ratio is supposed to bear the most significant discriminability, and is chosen for classification. The self-trained channel selection and classification algorithm is summarized in “Appendix” for P300-based BCI.

Joint selection of time segment and channels

As mentioned in Section “Introduction”, the selection of time segment and channel affects the performance of P300-based BCI in a significant manner. Although effective time segment and channels can be separately determined, optimal parameters are usually achievable through joint selection in both the time domain and the spatial domain. One possible solution is to define a Fisher ratio for each channel-time segment pair, and search over all the pairs. In order to avoid the exhaustive searching, we consolidate Algorithms 1 and 3 perform the joint selection of time segment and channels in an alternate manner. The ultimate goal is to improve classification performance. Firstly, with the input data and parameters, Algorithm 1 is applied to select a time segment denoted as 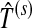, and determine the labels for test data set denoted as 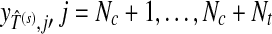. Then we apply Algorithm 3 to select a subset of channels denoted as 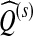regarding the selected time segment 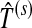and the data set D = D_c ∪ D_t as the new training data set with the labels 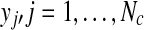and 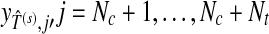. In each of the following iterations, Algorithm 1 is performed with respect to the subset of channels and labels both determined in the previous iteration, followed by Algorithm 3 performed regarding the time segment and labels both determined by the preceding Algorithm 1 in the same iteration. The process goes on until convergence is achieved. The final output includes the selected time segment and subset of channels, as well as the predicted labels for the test set. The outline of the algorithm is given below.

Remarks (1) In Algorithm 2, time segment selection and channel selection are alternately carried out. To avoid initial setting of the iteration stopping thresholds δ₁ and δ₂ for Algorithm 1 (·) and Algorithm 3 (·) respectively, we can fix the number of iterations of these two algorithms, e.g. 3, in this paper. In this way, the performance of Algorithm 2 does not depend on the parameters δ₁ and δ₂. (2) According to our data analysis, Algorithm 2 often converges within a few iterations (e.g., 3 iterations) even if we set δ₀ = 0. (3) In this paper, the adaptivity of the proposed algorithms is realized through iterative updating with newly available data that allows the system to adapt to the change in mental activity of the subject, and therefore leading to better performance.

Data analysis and online implementation

In this section, three examples are presented to demonstrate the effectiveness of the proposed joint time segment and channel selection algorithm. In the first example, we applied Algorithm 2 to the data set of P300 speller from BCI Competition III and compare it to other state-of-the-art algorithms regarding classification performance. In the second example, the performance of Algorithm 2 is tested by the data of 3 subjects collected from a different P300 speller system built by us. Finally in the last example, the adaptability of Algorithm 2 is illustrated through online experiment results from our P300 speller system. The performances of Algorithms 1 and 3 will not be explicitly mentioned as they are wrapped up into Algorithm 2 for joint feature selection. In this paper, the SVM parameter is set as C = 1 for all the SVM-based algorithms.

Example 1: P300 speller data set from BCI Competition III

In this example, we illustrate the application of Algorithm 2 on the data set II of a P300 speller from BCI Competition III (Blankertz et al. 2005). The data is briefly described as follows. Each subject was presented with a 6 × 6 matrix of characters shown in Fig. 1, and was asked to pay attention to one character in each run. His/her 64-channel EEG signal was sampled at 240 Hz. The data set was recorded from two different subjects (A and B). The sequence of 12 row-column intensifications was repeated 15 times (named “repeats” in this paper) for the spelling of each character. For each subject, the data of totally 185 character spellings were provided by the organizer. We adopt similar pre-processing techniques as in (Rakotomamonjy and Guigue 2008) for the convenience of comparison of different algorithms. For each channel, the signals between 0 and 600 ms posterior to the beginning of an intensification have been extracted and processed with a bandpass filter of 0.1–10 Hz. The extracted signal has been decimated by a rate of 10. The data point resulting from a post-stimulus signal is of dimension 14 × 64, representing 14 temporal samples and 64 channels respectively.

Fig. 1.

User intertace of the P300 speller used in BCI Competition III

In the following data analysis with Algorithm 2, we simply use the first 5 consecutive characters provided by the Competition as the initial training set to simulate a small training set scenario. The next 20 characters were used as the test data set without labels for retraining in Algorithm 2. Regarding the independent test set, we use the 100-character test set provided by the Competition so that the results are comparable to the other methods. In each iteration of Algorithm 2, we perform 3 iterations of Algorithms 1 and 3. The threshold δ₀ for stopping the iterations of Algorithm 2 is set as 0. The 14 time points of each data matrix is partitioned into 35 time segments as 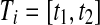, where 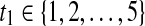and 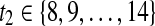. Regarding the number of repeats being 15, results show that the time segment (Farwell and Donchin 1988; Citi et al. 2004) is optimal for subject A, with the number of channels being 35. The selected time segment for subject B is Serby et al. (2005) and Blankertz et al. (2005) and the number of channels is 30. At the same time, we perform prediction of labels for the test data set. Performance has been evaluated according to the percentage of correctly predicted characters in the test datasets and in the independent test sets. For the number of repeats being 3, 4, 5, 10, or 15, the accuracies of the prediction averaged over the two subjects obtained by our Algorithm 2 are shown in Table 1.

Table 1.

Accuracy of character prediction in percentage

	Test set (20)	Ind. test set (100)
Our Algorithm 1 with channels Fz, Cz and Pz (5 training characters)	82.5	83.5
Our Algorithm 3 with time segment 200–500 ms (5 training characters)	90	88.5
Our Algorithm 2 (5 training characters)	92.5	93.5
Semi-supervised SVM without feature selection (5 training characters)	87.5	85.5
Standard SVM (5 training characters)	77.5	80
Rakoto’s method (85 training characters)	Not applicable	96.5
SWLDA (5 training characters)	85	84.5

The results of both our Algorithm 2 and the standard SVM are based on the training set with 5 characters, while Rakoto’s results (Rakotomamonjy and Guigue 2008) were based on 85 characters as training data. “Test set” indicates the 20 unlabelled characters used in retraining in Algorithm 2. “Ind. test set” indicates the independent test set with 100 unlabeled characters, which is the same as the test data set in the Competition

The bold values indicate best performance

For comparison, we applied a standard SVM without self-training to the same data sets as that used in the above evaluation of Algorithm 2. From Table 1, the prediction accuracy of the standard SVM is much lower than the proposed algorithm with respect to both the 20-character test set and the independent test set. In addition, we also use the state-of-art method, stepwise linear discriminant analysis (SWLDA), to identifies subject-specific spatio-temporal features for comparison.

We further compare the results of our Algorithm 2 with the best performance achieved by Rakotomamonjy and Guigue (whose method Rakotomamonjy and Guigue (2008)) will be denoted by Rakoto’s method in the following). Notice that these two methods were applied to different size of the training data set, but the same 100-character independent test set. As mentioned above, the results of our Algorithm 2 are based on the training set with 5 characters. Since the recursive channel elimination approach in Rakoto’s method requires sufficient labelled data, it is not applicable to the case of small training set. Therefore, we cite the results in Rakotomamonjy and Guigue (2008) which were based on 85 characters as training data. From Table 1, it is found that, at the number of repeats from 3 to 15, our proposed algorithm achieves comparable performance to Rakoto’s method although the sizes of their respective training sets are of significant disparity. The outstanding performance of Algorithm 2 can be explained by the iterative update to the model with the test data set and the predicted labels. Meanwhile, the results also confirm the efficiency of the semi-supervised joint time segment and channel selection that utilizes augmented training set instead of the small initial training set for reliable feature selection to improve the classification. As a consequence, this paradigm demonstrates that our algorithm can potentially reduce the training process of BCI speller while not affecting the accuracy.

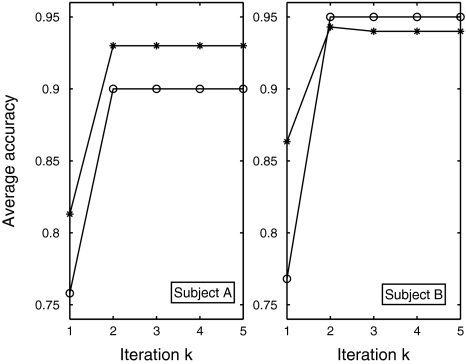
On the other hand, the convergency of Algorithm 2 was also studied. Figure 2 shows the prediction accuracy versus iteration with respect to the two subjects, where we analyzed both the 20-character test set taking part in the semi-supervised training and the 100-character independent test set. In each iteration, time segment selection and channel selection were alternatively carried out through 3 iterations within Algorithms 1 and 3 respectively. From the data analysis results, it is found that Algorithm 2 generally converges very fast, typically within 2 iterations. Meanwhile, compared to the first iteration, the prediction performance after convergency has been significantly improved.

Fig. 2.

Averaged prediction accuracy versus iteration of the two subjects (The curves with “circle” correspond to the 20-character test data set, while the curves with “asterisk” correspond to the 100-character independent test set

Example 2: In-house P300 speller

We have also assembled a data set by collecting EEG signal from three different subjects (aa, bb, and cc) on an in-house P300-based BCI speller. The participants sat upright in front of a computer screen and viewed the display of a 40-character matrix (see Fig. 3). The task was to focus attention on a desired character in the matrix and silently count the repeats of the desired character being intensified. For the spelling of a character, each of the 40 different characters was intensified according to a random sequence. Considering 10 repeats of the intensification sequence, a character epoch comprises totally 400 = 40 × 10 intensifications. The 600 ms EEG data following each intensification were collected from scalp using 30-channel EEG recorder. The signals were digitized at a rate of 250 Hz. Band-pass filtering within 0.1–20 Hz was performed, followed by down-sampling at the rate of 6. Hence the 600 ms time segment corresponds to 25 temporal samples. Then, for each intensification, we constructed feature vector with the length of 750 = 30 × 25 through concatenating the data from all the channels.

Fig. 3.

User interface of our P300 speller

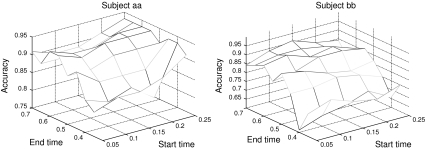
Although it has been widely accepted that the fixed time window of [200 ms 500 ms] is good enough for P300 detection, our first study shows the necessity of time segment selection in the P300 speller. With 20 training characters used in a standard SVM classifier, the spelling accuracies have been obtained at various time segment of the 30-channel signal. The results of Subject aa and bb are illustrated in Fig. 4. With the start time and end time of the segment ranging within [50 ms 250 ms] and [350 ms 700 ms] respectively, we see obvious differences among the spelling accuracies in the range of [0.7 0.95]. Hence, time segment selection can effectively improve the performance of a P300 speller. It is also found that the accuracy becomes relatively flat with the end time of the window larger than 600 ms, which is the reason that we choose the 600 ms initial time window for our P300 BCI system.

Fig. 4.

Illustration of spelling accuracy over different time segment, where the time segment of [Start_time End_time] is given by x-axis and y-axis. The results of Subject aa and bb are shown here

In the following, for each subject, the data set involves 70 characters for training and testing. Our initial training set contains the data of 5 characters. The test set containing the data of 44 characters was used for retraining and testing, while the independent test set containing 21 characters was not involved in retraining. Then we applied Algorithm 2 to the above data set. As an input to Algorithm 2, the initial 25 temporal samples have been organized into 36 time segments, each can be expressed by T_sub = [t₁, t₂], where 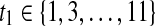and 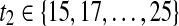. Time segment selection was performed within these 36 segments. The threshold δ₀ for stopping the iterations is set as 0. Table 2 shows the optimal selected time segment and number of channels.

Table 2.

Optimal selected time segment and number of channels

	Time segment (ms)	No. of channels
Subject aa	[192 552]	11
Subject bb	[240 528]	9
Subject cc	[144 480]	14

Number of characters for training dataset is 5

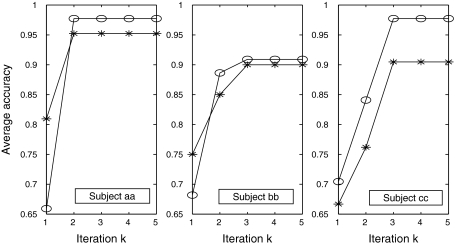
Figure 5 shows the prediction accuracy versus iterations for the three subjects respectively. In each subplot, the curve depicted with “asterisk” corresponds to the independent test set, while the curve depicted with “circle” corresponds to the test data set involved in semi-supervised learning. From Fig. 5, it is observed that Algorithm 2 converges within 3 iterations regarding all the subjects, and the accuracies of classification have been significantly improved when we compare the performance of the first iteration to that after convergency. Therefore, the effectiveness of our proposed algorithms is also verified by this in-house P300 speller in an off-line manner.

Fig. 5.

Curves of averaged prediction accuracies for three subjects. The curves with “circle” correspond to test data sets involved in self-training of Algorithm 2, while the curves with “asterisk” correspond to independent test sets

In order to quantitatively explore the benefit brought by the semi-supervised spatio-temporal feature selection, we have compared the prediction accuracy of our Algorithm 2 to that of the standard SVM algorithm and the iterative semi-supervised SVM algorithm proposed in Li et al. (2008), both of the latter two having no time segment and channel selection. Data analysis results of these algorithms with two different sizes of training set are given in Tables 2 and 3, where the performance is expressed by the prediction accuracy in percentage. Furthermore, we also applied SWLDA to the same data separation as in Algorithm 2 for comparison. As can be seen, our Algorithm 2 consistently outperforms the others. Although the training set used in standard SVM (49 characters) is much larger than ours (5 characters), the result of the standard SVM is still inferior to that of ours. Hence, the training data with labels collection time of the P300 BCI system can be significantly reduced (P = 0, anova1 analysis) without affecting the performance.

Table 3.

Performance comparison of the proposed Algorithm 2 and other SVM-based algorithms

	Test set (44)	Ind. test set (21)
Our Algorithm 1 with channels Fz, Cz and Pz (5 training characters)	85.3	82.6
Our Algorithm 3 with time segment 200–500 ms (5 training characters)	91.1	89.9
Our Algorithm 2 (5 training characters)	95.1	91.9
Semi-supervised SVM without feature selection (5 training characters)	88.9	87.2
Standard SVM (5 training characters)	68.1	75.5
Standard SVM (49 training characters)	Not applicable	89.2
SWLDA (5 training characters)	86.5	84.1

Expressed by accuracy of character prediction in percentage. “Test set” indicates the 44 unlabeled characters used in retraining in Algorithm 2. “Ind. test set” indicates the independent test set with 21 unlabeled characters

The bold values indicate best performance

Example 3: Online experiments of in-house P300 speller

We also implemented Algorithm 2 online to illustrate that this algorithm can be used to improve the adaptivity of the in-house P300 speller in real time. Three able-bodied male subjects participated in this online study. On the P300 speller system, each subject participated two experiments that differed in the size of training set and training data collection time. In experiment 1, a 5-character training set was collected online, while in experiment 2, an 8-character training set was collected 1 year before. In each experiment, the training set was utilized to obtain an SVM model to classify the online data of the subsequent 5 characters. Here, the EEG data of the 5 character input was named as a data ‘batch’. Comparing the online output with experimental input task, we obtained an online accuracy rate regarding these 5 characters. Using the initial training set and the data of these 5 characters with predicted labels, we retrained a new SVM model with Algorithm 2 to classify the next 5 characters and obtained another online accuracy rate regarding these 5 characters. The retraining process was stopped after 4 batches of data collection. Finally, using the resultant SVM model, we classified 60 characters online and obtained an accuracy rate also by comparing the output with the experimental input task given to these subjects.

For each experiment, these online accuracy rates were also averaged across the 3 subjects. Tables 4 and 5 show the spelling accuracy rates using Algorithm 2, where the initial models were obtained online and 1 year before respectively. Although the performance of Batch 1 is similar by using online model and the model obtained 1 year before, it is not satisfactory. (The average accuracy rates are 0.667 and 0.6% for online model and the model 1 year before separately.) Thus we use our semi-supervised learning method to improve the classification performance. It is found that, with our proposed Algorithm 2, the out-of-date initial model can be updated by the unlabelled online data to achieve similar performance as the online model. Generally, with a fixed model, accuracy of a BCI system goes down with time lapse. This can be explained by the non-stationarity nature of EEG signal and model. Here, such effect can be shown by using an SVM model trained by the data of 25 characters collected 1 year before to classify the recent 60-character data set. The resultant accuracy rates of the 3 subjects were 0.8, 0.867, and 0.783 respectively, and averaged as 0.817, which obviously fell behind the results of semi-supervised learning method. These results demonstrate the adaptivity of the proposed Algorithm 2 for the P300 speller in small training set case, since the model initially trained can be adjusted and its performance of classification can be improved using online data.

Table 4.

Spelling accuracy rates with the models obtained online

Subject	Batch 1	Batch 2	Batch 3	Batch 4	60 Char test
S1	0.6	0.8	1.0	1.0	0.967
S2	0.6	0.8	1.0	1.0	0.95
S3	0.8	1.0	1.0	1.0	0.933
Average	0.667	0.867	1.0	1.0	0.95

The initial training set contains the EEG data of 5 character input collected online. For semi-supervised learning, each batch contains the unlabelled data with respect to the input of 5 characters. The final column gives the results on a 60-character independent test set

Table 5.

Spelling accuracy with the models obtained 1 year before

Subject	Batch 1	Batch 2	Batch 3	Batch 4	60 Char test
S1	0.6	0.8	1.0	1.0	0.9
S2	0.6	0.8	0.8	1.0	0.95
S3	0.6	1.0	1.0	1.0	0.933
Average	0.60	0.8667	0.9333	1.0	0.928

The initial training set contains the EEG data of 8 character input collected 1 year before. For semi-supervised learning, each batch contains the unlabelled data with respect to the input of 5 characters. The final column gives the results on a 60-character independent test set

Conclusions

This paper focuses attention on improving the performance of P300 speller when training data is insufficient. In this case, traditional model selection methods, e.g., cross-validation, usually do not work. Herein, we presented two self-trained SVM algorithms, one for time segment selection and the other for EEG channel selection, where Fisher ratio calculated by SVM scores was used as an index for the feature selection. Furthermore, by wrapping up these two algorithms in an alternating manner, a semi-supervised learning algorithm was proposed for joint selection of time segment and channels. In this way, the SVM classifier was retrained with both labeled training data and unlabeled test data to improve its performance of prediction, at the same time to achieve better time segment and channel selection. The data analysis results of two off-line examples demonstrate the effectiveness and fast convergency of our algorithms. Results show that the proposed Algorithm 2 is also applicable to online scenario, where the adaptiveness of the algorithm have been verified through the in-house P300 speller.

Appendix

The self-trained channel selection and classification algorithm is summarized below for P300-based BCI.