Abstract
Microfluidic diagnostic devices promise faster disease identification by purifying and concentrating low-abundance analytes from a flowing sample. The diagnosis of sepsis, a whole body inflammatory response often caused by microbial infections of the blood, is a model system for pursuing the advantages of microfluidic devices over traditional diagnostic protocols. Traditional sepsis diagnoses require large blood samples and several days to culture and identify the low concentration microbial agent. During these long delays while culturing, the physician has little or no actionable information to treat this acute illness. We designed a microfluidic chip using dielectrophoresis to sort and concentrate the target microbe from a flowing blood sample. This design was optimized using the applicable electrokinetic and hydrodynamic theories. We quantify the sorting efficiency of this device using growth-based assays which show 30% of injected microbes are recovered viable, consistent with the electroporation of target cells by the dielectrophoretic cell sorters. Finally, the results illustrate the device is capable of a five-fold larger microbe concentration in the target analyte stream compared to the waste stream at a continuous sample flow rate of 35 μl∕h.
INTRODUCTION
Sepsis is an inflammatory response to, among other causes, microbial infections of the blood. Typically, these infections are introduced during surgery and by intravenous devices to a patient already being treated for another condition. This weakened condition, combined with the severity of the systemic shock, results in the 20–50% mortality in the 750 000 annual cases.1, 2
Complicating the diagnosis and treatment of sepsis is the extremely low microbe concentration in the blood, approximately 100 microbes∕ml in adults.1, 3 Addressing the low abundance of the infecting microbes is the primary challenge to improving sepsis diagnosis. Traditional techniques use culture-based approaches requiring 48 h to 7 days for identification. As septic shock is an acute condition, broad spectrum antibiotics are often administered prior to a definitive diagnosis. The rapid identification of the sepsis-causing microbe would enable microbe-specific therapies and perhaps better patient outcomes.
One solution to the challenge of low abundance microbial targets is to sort and concentrate the microbes from a blood sample, thus providing the required analyte concentration for rapid detection and identification without culturing. A realistic detection assay would require at least 100 microbes and hence a 1 ml blood sample. As the microbe diffusion time to a point detector in a 1 ml sample may be on the order of days, convective or other facilitated transport is required for rapid detection of low concentration analytes. Because the ∼0.7 μl∕min flow rate required to process this 1 ml sample in one day is rather large for most microfluidic sensors, the target microbe may be concentrated away from the other cell types and debris present in the sample to facilitate rapid diagnosis. Unfortunately, membrane filtration is not an option for such high-throughput microfluidic devices as the other cell types and debris would quickly cake against the filter producing high hydrodynamic resistance to the bulk flow.
Typical approaches to sorting include surface-based approaches4 and bulk-based approaches such as dielectrophoretic (DEP) sorting.5, 6, 7, 8 Surface-based approaches including antibody-functionalized microchannels require long contact times and small channel geometries to bind targets flowing in the bulk, a result of the very short range (nm) attraction force requiring the analyte to diffuse to the surface probes across the flow. By acting on the bulk fluid, DEP sorting may offer improved efficiency and smaller devices. Unfortunately, few previous works using DEP sorters are optimized for continuous throughput. Additionally, the majority of these studies present only visual results without demonstrating the ability to deliver a concentrated analyte to a suitable sensor.
In this study, we present a microfluidic device for concentrating a microbe target from blood. Using electrokinetic and hydrodynamic theories, we created a software tool capable of simulating cell trajectories within a microfluidic device. Using this software tool, we optimized the device design for high throughput sorting of the model microbe Escherichia coli from blood. Growth-based viability assays are used to quantify the sorting efficiency, and the implications on using DEP for cell sorting is discussed.
THEORY
The design of our dielectric device was optimized by applying the following electrokinetic and hydrodynamic theories.
Particle geometry and orientation
The red blood cells (RBCs) and E. coli cells, also referred to as particles in this work, will be represented as oblate and prolate spheroids, respectively. The symmetric axis half-length will be denoted as a, and the asymmetric axis half-lengths will be denoted r. Additionally, we will use the eccentricity (e) to describe the aspect ratio for the prolate and oblate spheroids
| (1) |
To capture the geometric difference across the symmetric (‖) and two equal asymmetric (⊥) axes, a depolarization factor (L) may be defined in terms of the eccentricity as9
| (2) |
To capture arbitrary particle orientation, two reference frames are used in the development of electrokinetic and hydrodynamic theories: a fixed device-relative frame (subscript d) and a moving cell-relative (subscript p) frame. The device x-axis is oriented with the narrow channel height with the zero in the channel center, and the y axis is oriented to the channel length in the positive direction of fluid flow. Additionally, the angle between the flow fluid and the electric field is defined in this reference frame. Described as a function of θ in the Results section, this angle is implemented in the electric field vector. The cell-relative x, or “‖,” axis is oriented parallel to the spheroid’s symmetric axis whereas the geometrically equal y and z, or “⊥,” axes are oriented perpendicular. In both systems, the z axis is oriented to give a right-handed coordinate system. Conversion between these frames can be accomplished using a 3 × 3 rotation matrix (R)
| (3) |
| (4) |
where “·” is the dot product, v is a vector, and τ is a tensor.
Dielectrophoresis
Each cell type is represented using a shelled spheroid model, where each layer has an intrinsic complex permittivity, which is a function of the permittivity (ɛ), the conductivity (σ), and the ratio of the imaginary number (j) over the frequency of the applied field (ω).
| (5) |
The complex permittivity (ɛ*) of the core (subscript c) and innermost shell (subscript s) along each particle axis (subscript α) may be combined into an effective complex permittivity10, 11
| (6) |
where is the volume ratio.
Using Eq. 6, each shell may then be iteratively combined with the effective core from the innermost to outermost shell, resulting in an effective complex permittivity () for each cell type. In this study, RBCs are represented as one plasma membrane surrounding the cytoplasm whereas E. coli cells are represented with three shells (inner membrane, periplasmic space, and outer membrane) surrounding the cytoplasm. The parameterization used here was developed by previous works for E. coli12 and RBC (Ref. 13) as summarized in Table TABLE I..
Table 1.
Parameterization of multi-shelled spheroid model.
| E. coli (Ref. 12) | Symmetric axis radius | a | 1 μm | |
| Asymmetric axis radius | r | 0.25 μm | ||
| Cytoplasm | Relative permittivity | ɛcyto | 60 | |
| Conductivity | σcyto | 0.22 S∕m | ||
| Inner membrane | Relative permittivity | ɛim | 5.5 | |
| Conductivity | σim | 10−6 S∕m | ||
| Thickness | dim | 7 nm | ||
| Periplasm | Relative permittivity | ɛpp | 60 | |
| Conductivity | σpp | 3.2 S∕m | ||
| Thickness | dpp | 10 nm | ||
| Outer membrane | Relative permittivity | ɛom | 12 | |
| Conductivity | σom | 10−4 S∕m | ||
| Thickness | dom | 7 nm | ||
| RBC (Ref. 13) | Symmetric axis radius | a | 1 μm | |
| Asymmetric axis radius | r | 3.5 μm | ||
| Cytoplasm | Relative permittivity | ɛcyto | 50 | |
| Conductivity | σcyto | 0.53 S∕m | ||
| Membrane | Relative permittivity | ɛmem | 9.04 | |
| Conductivity | σmem | 10−6 S∕m | ||
| Thickness | dmem | 8 nm | ||
| Buffer medium | Relative permittivity | ɛm | 80 | |
| Conductivity | σm | 0.13 S∕m | ||
| Viscosity | ηmem | 1.002 cP |
Using the effective complex permittivity, the particle-relative Clausius-Mossotti factor (fCM,p) may be defined as the tensor
| (7) |
where i, j, and k are unit vectors in the x, y, and z axes, respectively.
Finally, the DEP force and torque14, 15 exerted on spheroid particles in a medium of permittivity ɛm with an applied nonuniform electric field (E) can be defined as
| (8) |
| (9) |
where “×” denotes a vector cross product. As a result of the cross product in Eq. 9, the non-zero torque for spheroid particles arises from the unequal real part of the Clausius-Mossotti factor along each particle-relative axis.
The electric field for a sorting electrode architecture was found by solving a 2D finite element model of the cross-section perpendicular to the sorting element. The electric field in this model was generated by opposed 50 μm wide top and bottom electrodes in a channel extending 100 μm away from the electrode edge. The solution was found by solving Laplace’s equation using FEMLAB v3.1 (Comsol Inc., Burlington, MA).
Hydrodynamic drag
In addition to the dielectrophoretic forces, the particles encounter hydrodynamic forces resulting from motion relative to the fluid. In the treatment here, the fluid flow is assumed to follow a Hele-Shaw type of profile where only the y component is non-zero
| (10) |
where is the mean fluid velocity and h the half channel height.
The hydrodynamic force and torque on spheroid particles has been developed previously.16, 17, 18, 19 Briefly, the hydrodynamic drag force (Fdrag) resulting from the difference in particle and fluid velocity may be defined as
| (11) |
| (12) |
| (13) |
where μ is the buffer viscosity, K is the translation tensor, and χ0 captures the spheroid asymmetry.
The hydrodynamic torque (Tdrag) is the result of the fluid shear rate and rotation within a stationary fluid, defined below
| (14) |
| (15) |
| (16) |
| (17) |
where Q are the hydrodynamic rotation tensors, □p is the square vector operator as defined by Happel and Brenner,19 ω is the angular velocity, and ΔU is difference between the particle and fluid velocity. The first cross-product term in Eq. 17 represents the torque resulting from the fluid’s shear rate whereas the second dot-product term is the drag resulting from particle rotation.
Particle trajectory integration
With the forces acting on the particles defined, the particle trajectory and orientation can be integrated over time using an appropriate set of kinematic equations.20 In these simulations, the sorting electrode is 50 μm wide and infinitely long at the selected angle from the flow direction. As the hydrodynamic theory presented above does not include a wall lift force, the x position in the narrow channel height is fixed to prevent the artificially close approach of particles towards the device walls. This force has been studied previously,21 but the adaptation and application here is beyond the scope of this work.
E. coli size distribution
As E. coli grows, the cell length elongates before constricting and dividing. Because cell length affects the eccentricity, both the DEP and drag force will vary with the distribution of cell lengths in the E. coli sample. A log normal probability density function is used to represent the previously characterized length distribution of growing E. coli cells22 with a mean length 〈l〉 of 2.5 μm and standard deviation (σ) of 0.238
| (18) |
METHODS
Fabrication
The device was fabricated using standard photolithographic protocols, with an overview of the design23 and fabricated layers presented in Fig. 1. Briefly, 25 × 75 × 1 mm microscope slides (Gold Seal, Thermo Scientific, Waltham, MA) were coated with 30 nm chrome (to promote gold adhesion) and 300 nm gold using a FC 1800 E-beam evaporator (Technical Engineering Services, Inc., Santa Cruz, CA). Slides were then spin coated with Microposit S1813 positive photoresist (Shipley Co., Malborough, MA) at 3000 rpm for 30 s, baked for 60 s at 90 °C, exposed to 120 mJ∕cm2 at 300 nm, and developed in AZ-917 developer (AZ Electronic Materials, Somerville, NJ). The gold and chrome were then etched using AU-5 gold etchant (Sigma Aldrich, St. Louis, MO) and CR-4 (Cyantek Corp., Fremont, CA), respectively. The remaining photoresist was removed using acetone.
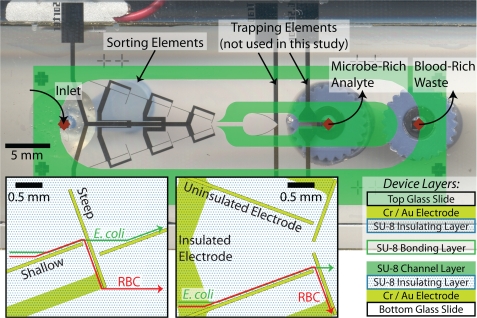
Figure 1.
Microfluidic device design for sorting and concentrating microbes from a sample withdrawn from the left reservoir (left diamond) to the microbe-rich analyte stream (middle diamond) while the remainder of the sample is withdrawn from the waste stream (right diamond). The top and bottom slides have identically patterned electrodes aligned directly opposite each other. The insets show the uninsulated yellow shallow and steep sorting elements along with the SU-8 covered insulated electrode leads as yellow overlaid with a dotted pattern. The designed trajectories of E. coli and blood cells are shown in the insets as green and red lines, respectively. The 15 μm channel is patterned using SU-8 2015 on the bottom slide (overlaid in green for clarity) and the completed device is bonded with a thin layer of SU-8 2015.
The slides with patterned electrodes were prepared for channel fabrication with 15 minutes of oxygen plasma treatment at 1500 W to promoted adhesion of SU-8 (MicroChem Corp., Newton, MA). Following the manufacturer’s instructions, a 0.75 μm layer of SU-8 2000.5 was patterned on both the top and bottom slides to insulate the electrode leads within the channel. Prior to developing the insulating layer, a 15 μm channel layer of SU-8 2015 was patterned on the bottom slides only. The resulting top and bottom slides were then developed in SU-8 developer (MicroChem Corp., Newton, MA), rinsed with isopropanol, and hard baked at 200 °C for 15 minutes to improve the insulating layer to glass adhesion prior to device bonding.
1 mm diameter holes were drilled into the top slides using an Electro Engraver (Wale Apparatus Co, Hellertown, PA). SU-8 2015 was spun at 4000 rpm for 60 s on the bottom slide. The top and bottom slides were then roughly aligned and held using binder clips during a 2 minute bake in a 95 °C oven. After cooling for 1 minute at room temperature to reduce the SU-8 viscosity and prevent the device from separating, the binder clips were removed and the top and bottom slides manually aligned under a microscope. After coming to room temperature, both sides of the device were exposed through a mask to 140 mJ∕cm2 at 300 nm to set the SU-8 bonding layer. The photoresist in the channel was removed using vacuum on an 80 °C hot plate prior to pulling acetone to fully develop the channel.
100 μm ID∕360 μm OD fused silica capillary tubing (Polymicro Technologies, Phoenix, AZ) was connected to the device using Nanoport connector and the syringe using a luer-to-capillary MicroTight adapter (IDEX Health & Science, Oak Harbor, WA). The capillary tubing and fittings allowed greater control over the small volumes introduced into and removed from the device. Finally, copper leads were connected to electrode elements using a two part silver epoxy (MG Chemicals, Surrey, B.C., Canada).
Sample preparation
E. coli DH5α (Invitrogen Corp., Carlsbad, CA) with the pMAL-c2X plasmid (New England Biolabs, Ipswich, MA) were grown overnight in 3 ml LB miniprep tubes with 100 μg∕ml carbenicillin (Teknova, Hollister, CA). 15 μl of bovine blood 1:1 in Alsevers (Quad Five, Ryegate, MT) or human blood collected in heparin vacuum tubes and 250 μl of E. coli culture broth were individually brought to 1 ml and washed three times with buffer (0.3 M sucrose buffer with 10× phosphate-buffered saline (PBS) added to bring the final conductivity to 0.13 S∕m). Unless otherwise noted in the text, the results are for bovine blood. The resulting washed RBC and E. coli suspension concentrations were determined using a standard hemocytometer and a 10 μm deep C-Chip cytometer (INCYTO, Chungchongnam-do, Republic of Korea), respectively. The sample was prepared to a concentration of 106E. coli and 106 blood cells per ml buffer. This ratio of RBC to E. coli allowed shorter run times prior to quantification by growth-based assays.
DEP characterization
The DEP cross-over frequency (COF), the frequency at which the DEP force is zero, was characterized using a quad electrode architecture with oppositely polarized elements. The quad intersection was formed by 34 × 34 μm electrode tips separated by 8 μm gaps. A small volume (10–20 μl) of cells washed 3 times and resuspended in buffer were put at the junction of the quad electrode and the DEP response characterized visually. Because the COF is significantly affected by variability in cell shape, accurately determining the COF is easier for uniformly sized and shaped cells, such as RBC, than for non-uniform or growing cells, such as E. coli.
Device operation
The device surfaces were blocked with a degassed solution of 5 wt. % albumin (Sigma Aldrich, St. Louis, MO) for 30 minutes at 37 °C before rinsing with ultrapure water three times and wetting with degassed buffer. Syringes were filled with buffer and hooked to the waste and analyte ports. With the waste and analyte syringes withdrawing at 31.8 and 3.18 μl∕h, respectively, the 33220A function generator (Agilent Technologies, Santa Clara, CA) was used to drive a 500 kHz sinusoidal wave at 10 volts peak-to-peak across the electrodes. The volume in the inlet reservoir was maintained above 5 μl after this point to prevent the introduction of air into the device.
When the flow profiles stabilized, excess buffer was removed from the inlet reservoir and 20 μl of sample was introduced. After 30 minutes, an additional 20 μl of sample was added and sorted for an additional 30 minutes, after which approximately 5 μl remained in the reservoir. A wash of 100 μl of buffer was introduced into the inlet reservoir to rinse the device for 1 h, with 65 μl of wash buffer remaining in the inlet reservoir at the end of the experiment. The function generator remained on during the wash to sort any additional cells entering the device. The tubing was then removed from the device and sample evacuated from the syringe and tubing with the total sample volume brought to 0.5 ml with buffer.
Growth-based quantification
A portion of the analyte and waste stream samples were passed through a 0.2 μm Microfunnel filter (Pall Life Sciences, Port Washington, NY) and the filters were cultured on LB agar plates with 150 μg∕ml carbenicillin (Teknova, Hollister, CA) overnight prior to colony counting.
RESULTS AND DISCUSSION
Buffer selection
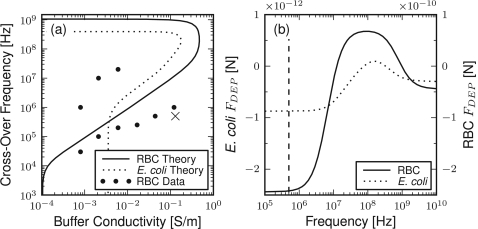
To characterize the effect of buffer conductivity on the DEP force exerted on RBCs and E. coli, the COF is plotted for varying buffers, as shown in Fig. 2a. The theory results show the two COFs at a given buffer conductivity expected of cells with a low permittivity shell. Between these COFs, the DEP force is positive and attractive whereas outside the DEP force is negative and repulsive. The theory results for both cell types display a similar, although slightly shifted, COF profile with the primary difference being the lower frequency limit.
Figure 2.
Dielectrophoretic properties of RBC and E. coli cells. (a) Cross-over frequency as a function of buffer conductivity. The dotted and solid lines are the multi-shelled spheroid theory results using the parameterization from Table TABLE I.. For comparison, observed cross-over frequencies for RBC on a quad-electrode architecture are shown as points. The selected buffer conductivity and operating frequency for sorting is labeled with an “x.” (b) Dielectrophoretic force as a function of frequency for E. coli and RBCs predicted from the multi-shelled spheroid theory in a buffer with a conductivity of 0.13 S/m. The component of the force normal to the electrode is presented at the channel center and electrode edge. The dashed line indicates an operating frequency of 500 kHz.
The COF response of RBCs was measured over varying conductivities of an isotonic sucrose buffer, shown as points in Fig. 2a. The size variability of E. coli made reliable COF estimation difficult and are not presented. The experimentally observed RBC COF results show good agreement in the lower COF but significant disagreement in the upper COF range. This disagreement, near the limit of the waveform generator, is similar to that previously found at high frequencies12 and may be the result of the differing device and conditions used to find the theory parameterization.
Because of the large sepsis sample size, the use of repulsize or negative DEP (nDEP) is desirable to prevent electrode fouling. The buffer conductivity of 0.13 S∕m was thus selected to balance the strength of the DEP force with the viability of the cells in a low conductivity buffer. An isotonic concentration of sucrose was used to reduce the osmotic pressure on the cells in this low conducting buffer. At this buffer conductivity an operating frequency of 500 kHz, denoted with “x” in Fig. 2a, was selected to provide nDEP while not degrading the electrodes (common below 10 kHz at the voltage and buffer combination).
Sorting electrode design optimization
The practical constraints of fabrication were balanced with the theory presented previously to optimize our device design for the highest possible sample throughput. Our device is fabricated on 25 × 75 mm glass slides, on which a 10 mm wide channel was chosen to maximize the sample flow rate. Conversely, a narrow 15 μm height sufficient to allow blood cells to flow freely was selected to maximize the electric field intensity and thus DEP force. Within this geometry, the architecture of the sorting electrodes was optimized to separate the RBC and E. coli into separate streams.
Using the parameterization summarized in Table TABLE I., the DEP force exerted on RBCs and E. coli may be plotted as a function of the applied field frequency, as defined in Eq. 8 and as shown in Fig. 2b. The magnitude of the DEP force is orders of magnitude greater for RBCs than E. coli, 250 times greater at 500 kHz, which is primarily a result of the larger RBC size.
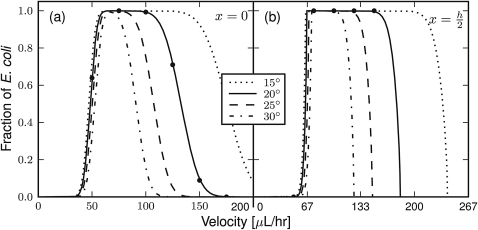
Exploiting the differing magnitudes in the DEP force, a sorting element architecture was selected with sequential pairs of electrodes at shallow and steep angles from parallel to the flow, as shown in Fig. 1. The greater DEP force will be exploited to sort the RBC on both shallow and steep elements, whereas the weaker E. coli DEP force will sort only shallow elements while flowing through the steeper elements. To simplify optimizing the design of the sorting electrodes, only the angle between the shallow element angle and flow, θ, will be optimized with the steep element set at 90°–θ. Given this electrode architecture, the fraction of E. coli cells successfully sorting by the shallow, but not the steep, sorting elements can be found as a function of the shallow element angle and flow rate, as shown as lines in Fig. 3 for stably oriented microbes positioned at the channel center and half-height. The theory results show the shallower angles provide a larger sample flow rate operating range because of the larger difference in DEP forces exerted by the shallow and steep sorting elements at these angles. These larger operating ranges will better accommodate fluid velocity and device fabrication variations in the actual device. Interestingly, the fraction sorted at the channel half-height has similarly sized operating ranges, when accounting for 133% faster bulk flow rate required to achieve the same linear velocity at this channel position. The primary difference is the sharper transitions in the theory results for the same angle at the channel half-height compared to the channel center, which is the result of the differing microbe orientations to the electric field in these two channel positions.
Figure 3.
Theoretical fraction of E. coli sorted as a function of the sample flow rate (for a channel cross-section of 10 mm by 15 μm) at (a) the channel center and (b) the half channel height. Results are shown for several shallow sorting angles (in θ degrees from parallel to flow) with the steep sorting elements set at 90°–θ. Successful sorting is defined by sorting by the shallow but not by the steep element. The lines show the results of static force balances for correctly oriented particles at the electrode edge. The dots show the average of 1000 dynamic simulations of randomly sized and oriented E. coli for θ = 20°.
Taking into consideration the practical channel length available for sorting and the expected range of operating flow rates with near 100% sorting efficiency, a shallow sorting element angle of θ = 20° was selected. The theoretical results show sorting of RBC is successful on both shallow and steep sorting elements at flow rates up to 2 ml∕h for this sorting electrode architecture.
Electro-orientation
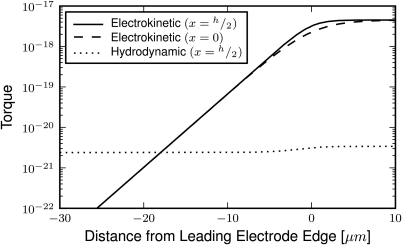
The theory results presented as lines in Fig. 3 are found from static balances of properly oriented particles at the electrode edge. Inherent to this calculation is the assumed proper orientation of E. coli, which is examined through dynamic particle trajectory solutions and static torque calculations. First, the trajectories of 1000 randomly sized and oriented E. coli particles were computationally solved as they encounter the shallow and steep sorting elements. Fig. 4 (enhanced) shows an example trajectory found for two randomly oriented E. coli as they encounter a shallow 20° sorting element. The results of these simulations are presented as points in Fig. 3 and show good agreement to the theoretical results. Second, the electrokinetic and hydrodynamic torques may be compared as a microbe approaches the sorting elements, as shown in Fig. 5. These results show the DEP torque, as defined in Eq. 9, quickly exceeds the shear-induced torque, as defined in Eq. 17, starting 20 μm away from the leading electrode edge and increases to over 1000 times greater in magnitude before reaching the sorting element. These dynamic simulation and torque calculation results support the assumption of proper microbe orientation within the electric field well prior to encountering the sorting element, and thus electro-orientation having a negligible impact on successful cell sorting.
Figure 4.
A movie illustrating the successful sorting of two E. coli particles solved using the presented electrokinetic and hydrodynamic theories. The electrode (in yellow) angle is 20° from parallel to flow and the fluid velocity is 75 μl/h for two microbes restrained to the channel center (blue) and half-height (green). The top three panes present the microbe orientations irrespective of position along with the hydrodynamic (blue) and electrokinetic (red) forces and torques as arrows positioned at the particle center and peripherally, respectively. The center and bottom panes present the position as a function of time from the “top” (Y-Z plane) and “front” (Y-X plane), respectively, as defined in the Theory section with the trajectory path shown as a solid line (enhanced online) .
Figure 5.
Electrokinetic and hydrodynamic torque norms as a function of normal distance from the electrode edge (positive values are between the overlapping sorting electrodes). The electrokinetic torque is provided at the channel center (x = 0) and half-height (x = h/2) for particles 45° out of alignment. Hydrodynamic torque is given for E. coli aligned to the electric field at the channel half-height.
E. coli viability
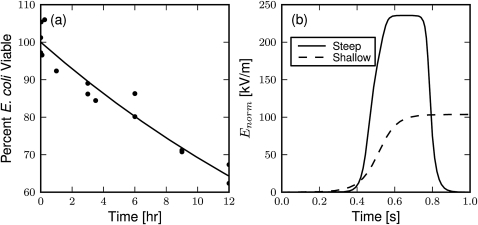
Preserving intact E. coli during sorting significantly simplifies the downstream microbe identification, especially by methods using growth-based or genetic-based metrics, which rely on intact cells to deliver the quantifiable material. Additionally, intact microbes will retain the expected DEP force, which will diminish with membrane integrity as the cytoplasm and medium equilibrate. To assess the effect of prolonged suspension in the relatively low conductivity buffer on microbe viability, growth assays were performed at several time points as shown in Fig. 6a along with a fit exponential decay. With a half-life well over the measured 12 h, approximately 19 h by the exponential fit, these results show E. coli remain viable in the buffer over the typical 3 h required to sort a sample in the experiments presented below. Additionally, the presence of blood cells in the buffer at concentrations used in the sorting experiments did not signficantly reduce E. coli viability over 3 h (data not shown).
Figure 6.
Factors affecting E. coli viability. (a) Observed viability of E. coli in low conducting (σ = 0.13 S/m) sucrose buffer. The points are individual experiment results fit by an exponential decay (line) with a poorly constrained half-life of 19 h. (b) Electric field magnitude along a simulated E. coli trajectory for flowing through a steep element and along a shallow element. The microbe is restricted to the center of the channel at a flow rate of 75 μl/h.
The microbe viability may also be challenged by the magnitude of the applied electric field, which may electroporate and ultimately lyse the cells during the approach to shallow elements and while flowing through the steep elements. To quantify the magnitude of the electric field for E. coli during sucessful sorting at shallow sorting elements and flow-through of steep sorting elements, the norm of the electric field is plotted over the time required to approach the sorting electrode, as shown in Fig. 6b. An E. coli cell is subjected to an average of 80 s (channel center) to more than 110 s (half channel height) on the shallow electrodes at 104 kV∕m during successful sorting. Additionally, the cells must flow through the steep elements an average of 2.4 times, taking approximately 0.6 s at 35 μl∕h for each pass, with an electric field magnitude of 235 kV∕m. The transmembrane potential24 traversing along the shallow and through the steep elements are 0.12 V and 0.26 V, respectively, although the actual potential is expected to be smaller as a result of the high frequency of the applied field preventing full charge accumulation.
Microfluidic device design and operation
The 10 mm channel width coupled with the 15 μm channel height presented a unique challenge as the finite resistance of our electrode material (gold) prevented the use of a single set of sorting elements. The solution employed is a set of three pairs of shallow and steep sorting elements to concentrate the microbes at the center of the channel, as shown in Fig. 1. The portions of the electrodes not required for sorting are insulated with a thin layer of photoresist to yield a high electric field gradient at the sorting elements. Additionally, right angles were avoided to eliminate singularities found in the DEP force at these geometries.25 The removal of blood cells at several points in the sorting device had an additional benefit of reducing the concentration of the RBCs moving on the electrode and the probability of aggregation.
Next the optimum flow rate in the range of 10 to 250 μl∕h was determined visually where the majority of observed E. coli were sorted by the shallow but not the steep sorting elements. This flow rate was found to be 35 μl∕h (linear velocities nearing 65 μm∕s) for the design presented here, which is approximately half the expected maximum presented in Fig. 3. These differences may be the result of additional variability in cell physiology not captured by the theory, assumptions underlying this theory, or an unexpected disruption membrane integrity. While this flow rate is sufficient to sort 0.85 ml∕day, the sample blood cell concentration is an approximately 1000 times dilution of whole blood. Thus, the development of a device with an improved throughput (e.g., with a larger cross-section) would be required to reach commercially viable throughputs for sepsis diagnosis. Increasing the sample concentration or applied field magnitudes would improve sample throughput at the cost of device operation, as discussed in more detail below.
Improving sorting efficiency
Sorting efficiency was improved through blocking cell-surface interaction and reducing cell interaction and aggregation. Aggregated cells, cell debris, and large sample contaminents can slow or stop on sorting electrodes, typically at the junctions between shallow and steep elements as shown in Fig. 7a. Notably, these aggregates behave at meta-particles instead of individual cells. These blockages may alter flow profiles, disrupt sorting, and may attract other RBCs or E. coli. Cell-cell interactions were minimized by using a relatively dilute sample concentration. Additionally, the blocking of the device surfaces with albumin significantly reduces the ability of aggregates and debris to bind to and disrupt the sorting elements. The ability to prevent aggregate formation and binding remains a significant hurdle to commercially viable device, as increasing the sample cell concentration and total sample volume will be required for diagnostically relevant sample sizes.
Figure 7.
Successful sorting challenges overcome by lowering sample cell concentration including (a) aggregating cells and (b) the interaction of blood and E. coli cells pulling the microbes into the waste stream.
The ability of blood cells to interact with and pull E. coli cells to the waste stream also interferes with microbe sorting, shown in Fig. 7b. This interaction occurs more frequency latter in the device where a relatively concentrated microbe stream passes over the RBC at the junction between shallow and steep elements. This challenge was relatively minor at the dilute microbe and RBC concentrations used in this study, but increased sample cell concentrations to reach diagnostically relevant sample throughput would increase this interaction when the recovery of all possible low concentration microbes is paramount. If this challenge is the primary hurdle to successful microbe concentration, RBCs may be specifically lysed prior to processing, for example by low conductivity DI water.26 While this treatment may reduce the microbe viability, the elmination of red blood cells could facilitate higher throughput sample processing.
Cell sorting
Sorting was characterized visually as shown in the composite image shown in Fig. 8. The majority of E. coli cells are sorted by the shallow elements while flowing through the steep elements. Conversely, the RBCs are deflected by both sets of elements and ultimately out of the analysis stream. Two uncaptured E. coli may be seen at the bottom of Fig. 8 where they flow through the steep element and beneath the next shallow element.
Figure 8.
Composite time lapse image of several blood and E. coli cells being sorted from left-to-right flow by the microfluidic device. The E. coli are the smaller and brighter cells which pass through the middle steeper element. A small fraction of uncaptured E. coli flowed through the left and middle electrodes, thus joining blood cells in the waste stream. Blood cells are larger (appearing darker) and are deflected by both the shallow and steep sorting elements through the bottom of this image.
Despite the high sorting efficiency observed visually during the device operation, the growth-based assays show a significantly lower sorting efficiency at 35% of recovered microbes in the analyte stream (n = 3 experiments with 2 technical replicates each) with 30% of all injected E. coli recovered. Our preliminary data show similar results for sorting with human blood (data not shown). This 35% sorted yields an analyte stream with a 5-fold greater microbe concentration than the waste stream, although the low 30% recovery rate results in only a slight increase from the inlet concentration.
The low recovery rate does not appear to be the result of the low conductivity buffer or attack by leukocytes, as previously presented these factors do not significantly reduce viability. Additionally, aggregation or binding to the device electrodes or walls was not significant when the device was visually examined during and after sorting. Finally, lowering the dead volume by changing the device connectors used did not significantly improve the recovery rate.
Instead, the low recovery rate is most consistent with E. coli electroporation, which may also lower the sorting efficiency and sample throughput. During electroporation, E. coli cells are expected to exchange or equilibrate intracellular and extracellular contents. This process is expected to slow as sufficient material has been exchanged to lower the transmembrane potential. In some cells, this process may be irreversible and lead to permanent membrane disruption and thus affect sorting efficiency. Interestingly, this equilibration process would also reduce the DEP force and be consistent with the lower optimal flow rate at 35 μl∕h. As DEP force was not visually observed to weaken during sorting, microbes would likely be electroporated during the initial approach to the sorting electrodes. During this electroporation, the microbe would become unviable if sufficient intracellular material, the chromosome, or the antibody resistant plasmid were lost. In the device presented here, the E. coli are exposed to a transmembrane potential of between 0.12 V and 0.26 V during sorting, which is slightly lower than the typical 1 V lysis threshold,27 but the duration of sorting is significantly longer than the typically millisecond pulses used for electroporation. Thus, the low microbe viability, sample throughput, and sorting efficiency are consistent with electroporation of E. coli on DEP sorters.
If electrolysis is underlying the low E. coli recovery rate, overcoming this challenge would significantly improve the sample throughput by allowing higher applied field voltages and flow rates. One approach is increasing the cell membrane rigidity by polymer cross-linking.28 Unfortunately, this approach would complicate and possibly preclude growth-based quantification and DNA-based identification as it may lyse the cells or otherwise damage the intracellular contents while encapsulating the remaining material in polymer. Instead, antibody-based technologies may be better suited to detecting the whole cells and cell debris resulting from electroporation and provide a better quantification platform. This approach would not solve the effects of electroporation on sorting efficiency, but may provide a more sensitive detection technology for the remaining, and possibly lysed, cell debris.
CONCLUSIONS
Here we present the electrokinetic and hydrodynamic theories relevant to the design of a dielectrophoretic microfluidic device, which have been implemented to solve for the DEP properties of spheroid cells and their trajectories along sorting electrodes. Using this theory, we found an optimal sorting electrode geometry accounting for microbe size variability while balancing fabrication and device operation constraints. A microfluidic device was designed, fabricated, and operated based upon these theoretical results with the performance of sorting experiments quantified with a growth-based metric, a quantification absent from many previous studies. The results of sorting a sample of blood and E. coli show 30% of injected microbes remain viable, consistent with electroporation and a partial loss of microbe membrane integrity. Additionally, a five-fold larger concentration of microbes was recovered in the analyte stream compared to the waste stream. These results suggest possible opportunities to approach a diagnostically relevant sample throughput while supporting the need for future DEP cell sorting studies to appropriately quantify device performance.
ACKNOWLEDGMENTS
We thank Dr. Matthew Marrichi (Allergan, Inc.) and Dr. Ji Youn Lee (University of California, Davis) for assistance quantifying sorting results and Dr. Gulnaz Stybayeva (University of California, Davis) for the E. coli strain. This work was supported in part by UC Davis Point-of-Care Technologies Center (NIBIB U54 EB007959) and an NSF EFRI grant (0937997) awarded to A.R.
References
- Reimer L. G., Wilson M. L., and Weinstein M. P., Clin. Microbiol. Rev. 10, 444 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russell J. A., N. Engl. J. Med. 355, 1699 (2006). 10.1056/NEJMra043632 [DOI] [PubMed] [Google Scholar]
- Wexler H. M., Clin. Microbiol. Rev. 20, 593 (2007). 10.1128/CMR.00008-07 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagrath S., Sequist L. V., Maheswaran S., Bell D. W., Irimia D., Ulkus L., Smith M. R., Kwak E. L., Digumarthy S., Muzikansky A., Ryan P., Balis U. J., Tompkins R. G., Haber D. A., and Toner M., Nature 450, 1235 (2007). 10.1038/nature06385 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng I. F., Chang H. C., Hou D., and Chang H.-C., Biomicrofluidics 1, 021503 (2007). 10.1063/1.2723669 [DOI] [Google Scholar]
- Cheng J., Sheldon E. L., Wu L., Heller M. J., and O’Connell J. P., Anal. Chem. 70, 2321 (1998). 10.1021/ac971274g [DOI] [PubMed] [Google Scholar]
- Choi S. and Park J. K., Lab Chip 5, 1161 (2005). 10.1039/b505088j [DOI] [PubMed] [Google Scholar]
- Wang X. B., Yang J., Huang Y., Vykoukal J., Becker F. F., and Gascoyne P. R., Anal. Chem. 72, 832 (2000). 10.1021/ac990922o [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avelin J. and Sihvola A., J. Electrostat. 56, 19 (2002). 10.1016/S0304-3886(01)00201-7 [DOI] [Google Scholar]
- Asami K., Hanai T., and Koizumi N., Biophys. J. 31, 215 (1980). 10.1016/S0006-3495(80)85052-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carstensen E. L., Biophys. J. 7, 493 (1967). 10.1016/S0006-3495(67)86600-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bai W., Zhao K. S., and Asami K., Biophys. Chem. 122, 136 (2006). 10.1016/j.bpc.2006.03.004 [DOI] [PubMed] [Google Scholar]
- Gimsa J. and Wachner D., Biophys. J. 75, 1107 (1998). 10.1016/S0006-3495(98)77600-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang H.-C. and Yeo L., Electrokinetically Driven Microfluidics and Nanofluidics (Cambridge Univ. Press, Cambridge, England, 2010). [Google Scholar]
- Arnold W. M. and Zimmerman U., Electrostatics 21, 151 (1988). 10.1016/0304-3886(88)90027-7 [DOI] [Google Scholar]
- Chwang A. T. and Wu T. Y., J. Fluid Mech. 75, 677 (1976). 10.1017/S0022112076000451 [DOI] [Google Scholar]
- Datta S. and Srivastava D. K., Proc. Math. Sci. 109, 441 (1999). 10.1007/BF02838005 [DOI] [Google Scholar]
- Weinheimer A. J., J. Atmos. Sci. 44 (18), 2674 (1987). [DOI] [Google Scholar]
- Happel J. and Brenner H., Low Reynolds Number Hydrodynamics with Special Applications to Particulate Media (Kluwer Academic Publishing, Boston, MA, 1983). [Google Scholar]
- The Python scripts used to implement the DEP theory can be found as the DEPpy project on SourceForge (see http://sourceforge.net/projects/deppy/).
- Gavze E. and Shapiro M., J. Fluid Mech. 371, 59 (1998). 10.1017/S0022112098002109 [DOI] [Google Scholar]
- Koppes L. J. and Nanninga N., J. Bacteriol. 143, 89 (1980). [DOI] [PMC free article] [PubMed] [Google Scholar]
- See supplementary material at http://dx.doi.org/10.1063/1.3608135E-BIOMGB-5-004192 for the device design in GDS format with a unit distance of 1 μm.
- Kotnik T. and Miklavčič D., Biophys. J. 79, 670 (2000). 10.1016/S0006-3495(00)76325-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thamida S. K. and Chang H.-C., Phys. Fluids 14, 4315 (2002). 10.1063/1.1519530 [DOI] [Google Scholar]
- Sethu P., Anahtar M., Moldawer L. L., Tompkins R. G., and Toner M., Anal. Chem. 76, 6247 (2004). 10.1021/ac049429p [DOI] [PubMed] [Google Scholar]
- Isambert H., Phys. Rev. Lett. 80, 3404 (1998). 10.1103/PhysRevLett.80.3404 [DOI] [Google Scholar]
- Gordon J. E., Gagnon Z., and Chang H.-C., Biomicrofluidics 1, 044102 (2007). 10.1063/1.2818767 [DOI] [PMC free article] [PubMed] [Google Scholar]