Abstract
The response of an embedded sphere in a viscoelastic medium excited by acoustic radiation force has been studied in both the time- and frequency-domains. This model is important because it can be used to characterize the viscoelastic properties of the medium by fitting the response to the theoretical model. The Kelvin–Voigt model has been used exclusively in these models. An extension to the previously reported models is described so that any viscoelastic rheological model can be used. This theoretical development describes the generalized embedded sphere response both in the time and frequency domains. Comparing the results from derivations in both domains showed very good agreement with a median absolute error (MAE) ranging from 0.0044 to 0.0072. Good agreement is demonstrated with finite element model simulations and the theory with a MAE of 0.006. Lastly, results for characterization of gelatin and rubber materials with the new theory are shown where the MAE values were used to determine which rheological model best describes the measured responses.
INTRODUCTION
The response of a sphere embedded in a viscoelastic medium excited by a force has been addressed in different articles over the past 60 years. Oestreicher made a theoretical investigation of the field and mechanical impedance of an oscillating sphere in a viscoelastic medium.1 This derivation was based in the frequency-domain and used the Kelvin–Voigt rheological model.
Chen et al. utilized the theory proposed by Oestreicher in an application that used the response of the vibrating sphere excited by modulated ultrasound to estimate the viscoelastic material properties of gelatin materials surrounding the sphere.2 The vibration response was characterized at multiple frequencies, and fitting of the response was performed in the frequency-domain. This method has been used in later studies for quantification of the viscoelastic material properties of gelatin materials.3, 4 Norris studied the impedance of a vibrating sphere in an elastic medium when slip was present or absent by adding an interfacial impedance to account for this condition.5
Ilinskii et al. derived relationships for the static and transient displacement responses of a sphere and a bubble embedded in an elastic medium.6 A closed-form, time-domain solution was given for the displacement in both cases. Aglyamov et al.7 extended the work by Ilinskii et al. to find the time response of a sphere in a viscoelastic medium. The solution for this response is given in a closed form and is based on the Kelvin–Voigt rheological model. They performed an extensive parametric study with corresponding experimental results. The agreement between the theoretical and experimental results was excellent. This theory was later used in a study to find the shear modulus of gelatin phantoms.8
To date, solutions for the motion of a sphere have been analyzed in the time- and frequency-domains for elastic and viscoelastic media. However, the Kelvin–Voigt model has been used exclusively to characterize the viscoelastic media. For characterization of viscoelastic materials many other rheological models exist, including the Maxwell, Kelvin–Voigt, generalized Maxwell (GM) model, the Zener model (also known as the standard linear solid), and the Kelvin–Voigt fractional derivative (KVFD) model, but those previously mentioned are commonly used, particularly in characterizing soft tissues.9, 10, 11, 12, 13, 14, 15
These rheological models have been used to characterize different soft tissues with varying degrees of sensitivity. The Kelvin–Voigt model has been used extensively in the viscoelastic characterization of tissue because of its simplicity and intuitive separation of elastic and viscous effects.9, 10, 16, 17 Catheline et al. used the Kelvin–Voigt and the Maxwell models to characterize ex vivo striated muscle.9 The generalized Maxwell model was used by Vappou et al. to model the response from gelatin phantoms.11 Klatt et al. reported results from using the Kelvin–Voigt, Maxwell, and Zener models to fit the dispersive shear wave speed and attenuation results in brain and liver.18 Of those three models, the Zener model provided the best fits for the shear wave speed and attenuation in brain and liver results. In another study examining brains of young and elderly subjects, the Zener model provided better fits of storage and loss moduli compared to the Kelvin–Voigt and Maxwell models.14 Balocco et al. used the Zener model as a basis for the mechanical response of arteries.15 Last, the Kelvin–Voigt fractional derivative model was used to characterize various gelatin phantoms and ex vivo veal livers and ex vivo human prostates.13 These results demonstrate that the viscoelastic behavior of tissue can be fit using different rheological models for characterization.
In this paper, we will extend the theory for the time- and frequency-domain responses for the vibration of a sphere embedded in a viscoelastic medium and generalize these relationships so that any viscoelastic rheological model can be used. We call this theoretical development the generalized embedded sphere response (GESR). We compare the results from both the time- and frequency-domain solutions to ensure their consistency. We demonstrate numerical results from finite element modeling (FEM). Finally, we present results from experiments in gelatin and urethane rubber.
METHODS
Time-domain theory
Aglyamov model
To establish the background of the time-domain response in a viscoelastic medium, the theory presented by Aglyamov et al. will be briefly presented.7 We start with the wave equation for an isotropic, incompressible viscoelastic medium based on a Kelvin–Voigt rheological model,
| (1) |
where p is the internal pressure, u is the displacement vector, μ is the shear elasticity, η is the shear viscosity, ρ is the medium density, and t is time. In soft tissues, the bulk modulus can be 3–6 orders of magnitude larger than the shear modulus, so soft tissue is often considered to be nearly incompressible.19 If incompressibility is assumed, as was done by Aglyamov and his colleagues, then it would be impossible for ultrasound waves to propagate. For the purposes of this theoretical development we will use this assumption of near incompressibility to simplify the mathematics but still allow for the propagation of ultrasound waves. If we take the Fourier transform using the following definition:
| (2) |
Eq. 1 becomes
| (3) |
where P and U are the Fourier transforms of p and u, respectively, and ω is the angular frequency. Note that the minus sign used in μ − iωη arises because of the definition of the Fourier transform in Eq. 2. We now introduce a sphere into the medium and assume that an axisymmetric field is used to produce the radiation force. When inertial forces are accounted for, the relationship that relates U and the external force Fext is given as
| (4) |
where M is the mass of a solid sphere with radius a and k2 = ρω2∕(μ − iωη). The force is assumed to be a step function with amplitude F0 and duration t0 defined as
| (5) |
The Fourier transform of Eq. 5 is
| (6) |
Using Eqs. 4, 6, and the inverse Fourier transform given as
| (7) |
we can write the time-domain displacement as
| (8) |
where β = ρs∕ρ and ρs is the density of the sphere
Generalized time-domain model
In the generalized model, we start by modifying Eq. 1 to
| (9) |
where Gt(t) is the time-domain response of the shear modulus and ⊗t represents a temporal convolution. We follow the same steps set forth earlier by taking the Fourier transform of Eq. 9,
| (10) |
defining Gt(ω) = G1(ω) − iG2(ω), where G1(ω) is the storage modulus and G2(ω) is the loss modulus. The minus sign is retained to conform to the definition of the Fourier transform in Eq. 2. Equation 4 can be written as
| (11) |
where k2 = ρω2∕Gt(ω). The same expression for the force used is given by Eq. 6 and so for the general case Eq. 8 becomes
| (12) |
Frequency-domain theory
Oestreicher model
In the work reported by Chen et al., the authors examined the material properties of a viscoelastic medium with an embedded sphere.2 They used modulated ultrasound to produce harmonic radiation force to vibrate the sphere and then measured the velocity at a frequency ω. This process was repeated over a range of different frequencies to characterize the frequency response of the sphere. This process can be modeled in the frequency domain as2
| (13) |
where V(ω) is the velocity, F(ω) is the force, and Z(ω) is the impedance of the sphere which is the sum of the radiation impedance, Zr(ω), and the mechanical impedance, Zm(ω). The radiation and mechanical impedances are written, respectively, as
| (14) |
| (15) |
where , , λ and μ are the Lamé constants defined as μV = μ + iωη and λ = λ1 + iωλ2, λ1 and λ2 are the bulk elasticity and viscosity, and μ and η are the shear elasticity and viscosity. In this model, the Fourier transform is defined as
| (16) |
which has a sign change in the exponential function compared to Eq. 2. In this case, Eq. 6 changes to
| (17) |
This model does not assume incompressibility as did the time-domain model presented by Aglyamov and his colleagues. However, we are using this model for characterizing materials such as soft tissue, and we can assume near incompressibility which makes h≪k. The relationship in Eq. 14 can be simplified to
| (18) |
and by collecting terms reduced to
| (19) |
Generalized frequency-domain model
In the generalized model, the Lamé constant μV can be changed to a general frequency dependent shear modulus Gf(ω) = G1(ω) + iG2(ω), where G1(ω) is the storage modulus and G2(ω) is the loss modulus. It follows that the above-mentioned wavenumbers change to h2 = ρω2∕(2Gf(ω) + λ(ω)) and k2 = ρω2∕Gf(ω). It is important to note that this formulation provides a model-free approach. Any rheological model could then be fit to the complex function Gf(ω), Therefore, the model can now be different from the Kelvin–Voigt model where G1(ω) = μ and G2(ω) = ωη.
Rheological models
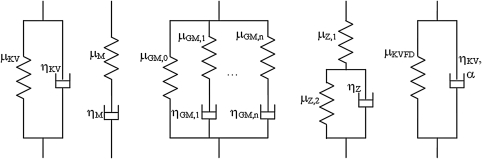
In this paper, we will use five different models, the Kelvin–Voigt, Maxwell, generalized Maxwell, Zener (standard linear solid), and the Kelvin–Voigt fractional derivative models. The models are defined in Fig. 1 with springs (elastic component) and dashpots (viscous component) in different configurations. The equations for G1(ω) and G2(ω) are listed in Table TABLE I.. Each model has a different number of parameters and arrangements of the springs and dashpots. The Kelvin–Voigt model consists of a spring and dashpot in parallel.1 The Maxwell model is a spring and dashpot placed in series.9 The generalized Maxwell model has a single spring in parallel with N Maxwell models.11 The Zener model consists of a spring in parallel with a single Maxwell model.18 A slightly different representation of the Zener model consists of a single spring in series with a parallel combination of a spring and dashpot.12 The Kelvin–Voigt fractional derivative model includes a spring in parallel with a fractional dashpot, that is, the strain rate is calculated with a fractional derivative with power α.13
Figure 1.
Viscoelastic rheological models. (a) Kelvin–Voigt (KV) model, (b) Maxwell (M) model, (c) generalized Maxwell (GM) model, (d) Zener (Z) model, (e) Kelvin–Voigt fractional derivative (KVFD) model.
Table 1.
Expressions for storage and loss moduli for different viscoelastic rheological models.
| Model | G1(ω) | G2(ω) |
|---|---|---|
| Kelvin–Voigt | μKV | ωηKV |
| Maxwell | ||
| Generalized Maxwell | ||
| Zener (standard linear solid) | ||
| Kelvin−Voigt fractional derivative |
Comparison of generalized responses
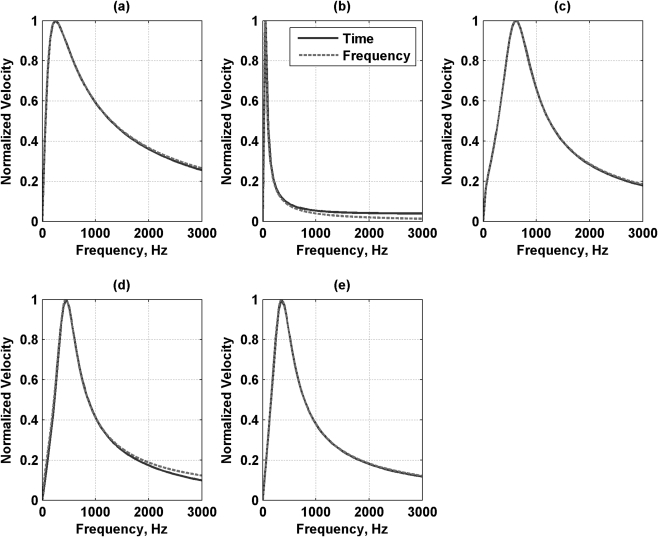
The time- and frequency-domain derivations of the GESR are compared in the frequency domain. For the set of parameters given in Table TABLE II., the responses were simulated for the different models in the time domain [Eq. 12] and frequency domain for the sphere velocity [Eq. 13 with Gf(ω)]. The excitation for the time-domain simulation was a constant force with t0 = 50 μs. The time-domain signal was simulated and then a fast Fourier transform is performed. The displacement signal is multiplied by iω to perform the derivative in the frequency domain so that the spectra of the velocity signals can be compared. This velocity signal is compared with the result from Eq. 13 using Gf(ω). This 50 μs force is, for the purposes of this comparison, equivalent to an impulse being applied in the frequency domain, so F(ω) in Eq. 13 is constant. The results are shown in Fig. 2 and in all cases show very good agreement between the time- and frequency-domain derived responses. The set of responses that shows any significant deviation is that for the Maxwell and Zener models at high frequency.
Table 2.
Model parameters and values for comparison of time- and frequency-domain velocity responses.
| Model parameter | Value |
|---|---|
| Kelvin–Voigt | |
| μKV | 5.0 kPa |
| ηKV | 5.0 Pa s |
| Maxwell | |
| μM | 0.1 kPa |
| ηM | 5.0 Pa s |
| Generalized Maxwell | |
| μGM,0 | 5.0 kPa |
| μGM,1 | 0.1 kPa |
| ηGM,1 | 5.0 Pa s |
| μGM,2 | 10.0 kPa |
| ηGM,2 | 10.0 Pa s |
| Zener | |
| μZ,1 | 5.0 kPa |
| μZ,2 | 3.0 kPa |
| ηZ | 4.0 Pa s |
| Kelvin–Voigt fractional derivative | |
| μKVFD | 5.0 kPa |
| ηKVFD | 5.0 Pa s |
| α | 0.75 |
Figure 2.
(Color online) Comparison of velocity responses from generalized Aglyamov (time-domain) and Oestreicher (frequency-domain) models. (a) Kelvin–Voigt model, (b) Maxwell model, (c) generalized Maxwell model, (d) Zener model, (e) Kelvin–Voigt fractional derivative model. For all panels the solid curve is calculated from the time-domain response and the dashed line is calculated from the frequency-domain response.
EXPERIMENTS
Finite element modeling verification
As an added verification, a model of a sphere embedded in a viscoelastic medium was constructed using the FEM package ABAQUS∕CAE 6.8-3 (SIMULIA, Providence, RI). A cylindrical phantom with radius of 30 mm and height of 80 mm with an interior hollow sphere with radius of 0.75 mm at the center of the cylinder was modeled using axisymmetric elements. This part was meshed with an edge-bias toward the center with a total of 49 440 nodes and 49 921 elements. The hollow portion of the cylinder was filled with a solid sphere with radius of 0.75 mm. The sphere had a total of 163 nodes and 143 elements. A tetrahedral mesh was used for both parts.
The cylinder was assigned material properties similar to that of a typical gelatin phantom (ρ = 1080 kg∕m3, E = 15 kPa, v = 0.499). A Prony series was used to simulate the viscoelastic response of the material using a generalized Maxwell model with one Maxwell element with parameters of g1 = 0.0196, τ1 = 0.05 in ABAQUS where the normalized relaxation function is defined by g(t)=g1(1-e-t∕τ1), where g1 = μGM,1∕(μGM,1 + μGM,0) and τ1 = ηGM,1∕μGM,1.11 For this example, μGM,0 = 5 kPa, μGM,1 = 0.1 kPa, and ηGM,1 = 5 Pa s. The sphere was assigned material properties of steel (ρ = 7840 kg∕m3, E = 200 GPa, v = 0.3). To mimic the acoustic force of the push ultrasound beam, the sphere was accelerated at 250 m∕s2 for a duration of 50 μs. An acceleration was used because the force is directly proportional to the acceleration by Newton’s second law of motion (F = ma). Displacement of the sphere was then recorded in the direction of the push for 10 ms at a sampling frequency of 100 kHz.
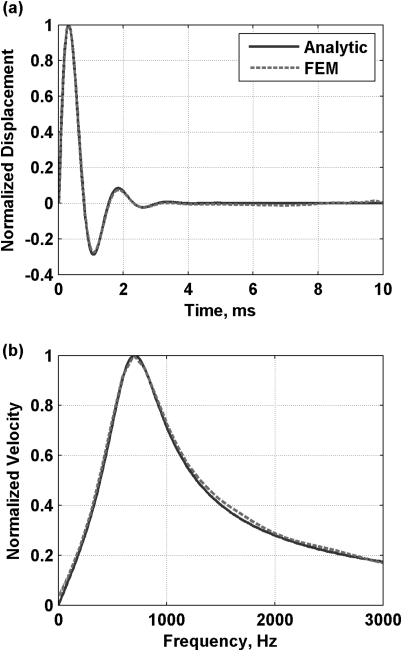
The results from the FEM simulations and analytic solution for the time-domain formulation in Eq. 11 are shown in Fig. 3a. In Fig. 3b, the comparison between the FEM simulation and the frequency-domain analytic solution from Eq. 13 is shown. The agreement between the simulations and analytic solutions is very good. These results are additional verification of the generalized theoretical responses along with the comparisons made in Fig. 2.
Figure 3.
(Color online) Comparison of responses for analytic response and response from FEM model. (a) Time-domain displacement, (b) frequency-domain velocity.
Embedded sphere experiments
Phantoms
Two types of embedding materials were used to construct sphere phantoms for testing, gelatin and urethane rubber. In all experiments a 440-C stainless steel sphere (ρ = 7840 kg∕m3) with radius of 0.75 mm was used, and cylindrical molds with an inner radius of 25 mm were used. Two gelatin phantoms were used in these experiments. The gelatin phantoms were made from 300 Bloom gelatin powder (Sigma-Aldrich, St. Louis, MO) with a concentration of 10% by volume and glycerol (Sigma-Aldrich, St. Louis, MO) with a concentration 10% by volume, respectively. A preservative of potassium sorbate (Sigma-Aldrich, St. Louis, MO) was also added with a concentration of 10 g∕L to the phantom. A layer of the gelatin was poured and allowed to set. A thin layer of the liquid gelatin was then poured and the sphere was placed on the thin layer. This thin layer serves to melt the top portion of the gelatin that has set and the sphere. The rest of the gelatin was then poured over the sphere to complete the phantom. The gelatin phantom was placed in a refrigerator when not being tested. One gelatin phantom had been made fresh the day before testing (gelatin 1) and the other had been made 17 days prior to testing (gelatin 2).
The urethane rubber phantom was made by mixing two components (ReoFlex 20, Smooth-On, Easton, PA) and a softening agent (So-Flex, Smooth-On, Easton, PA). The mixture was made of 25% ReoFlex Part A, 25% ReoFlex Part B, and 50% So-Flex by weight. Graphite powder (Sigma-Aldrich, St. Louis, MO) was added to the rubber mixture as well at 2% concentration by weight. A sphere was attached to a fine thread using superglue and the rubber mixture was poured around it and allowed to cure overnight.
Experiments
A custom-made 3.0 MHz spherically focused transducer with diameter of 45 mm and 70 mm focal length was used to produce repeated tone bursts of ultrasound similar to that used in shear wave dispersion ultrasound vibrometry.10 For the gelatin phantom, five tone bursts of length 100 μs were repeated at a rate of 50 Hz to produce the radiation force push. For the rubber phantom, five tone bursts of length 125 μs were repeated at a rate of 25 Hz to produce the radiation force push. Multiple tone bursts are used to provide an averaging mechanism for increasing the signal-to-noise ratio in frequency components that are harmonics of the tone burst repetition frequency.10, 20
A focused pulse-echo transducer was used for detecting the radiation force induced motion. For the gelatin phantom, a spherically focused 7.5 MHz transducer was used which had a 12.5 mm diameter and 50 mm focal length (IS0704HR, Valpey Fisher, Hopkinton, MA). For the rubber phantom, a spherically focused 5.0 MHz transducer was used which had a 12.5 mm diameter and 50 mm focal length (I3-0508-R, Olympus NDT, Waltham, MA). The pulse repetition frequency used for the gelatin and rubber phantoms was 6.0 kHz. A diagram of the experimental setup is shown in Fig. 4. The pulse-echo detection pulses were interlaced among the repeated tone bursts used for radiation force, similar to the method outlined by Urban and Greenleaf20 and Chen et al.10
Figure 4.
(Color online) Experimental setup for gelatin and rubber sphere phantom experiments. Ultrasound signals were amplified and applied to the push transducer. The detect transducer was driven by a pulser∕receiver and the output signal was digitized for offline analysis.
Analysis
The pulse-echo data were analyzed using a cross-spectral method to obtain the displacement and velocity of the sphere.21 The spectrum of the velocity was used for curve fitting with Eq. 13. With the type of excitation used, the force function is not constant with frequency, so the function F(ω) in Eq. 13 is estimated using theory detailed by Urban and co-workers for repeated tone bursts.4, 20 For curve fitting, a weighted least-squares curve fitting algorithm (lsqcurvefit) was used in matlab (The Mathworks, Natick, MA). The weights used were the normalized values of the velocity spectrum. This weighting was used so that the peak of the spectrum would be preferentially fit as opposed to the lower and upper frequency extremes. Upper and lower bounds were placed on the parameters for each model so that negative or very large values did not result. To assess the quality of the fit, an error metric called the median absolute error (MAE) was used. To evaluate the MAE, the absolute differences, E(f), are computed between the data, X(f), and curve fit, Y(f), and a median of those values is taken. A median is used to give a more general estimate of the error that is less biased from outliers,
| (20) |
| (21) |
RESULTS
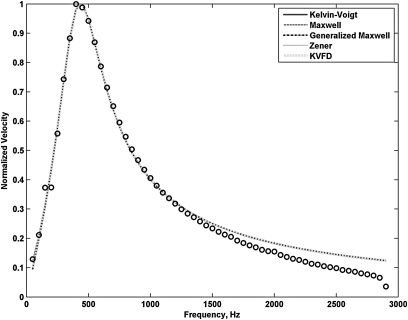
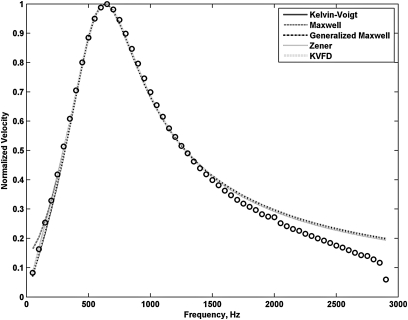
The velocity frequency response and curve fits for the five rheological models are shown in Figs. 56 for the two gelatin phantoms. The location of the peak and the width of the responses are different for gelatin 1 and gelatin 2. The MAE and model parameters for the curve fits are summarized in Table TABLE III..
Figure 5.
(Color online) Experimental data and model fitting for phantom gelatin 1. Open circles are measured data points and the plotted lines are the curve fits to the respective models. The responses lie on top of each other.
Figure 6.
(Color online) Experimental data and model fitting for phantom gelatin 2. Open circles are measured data points and the plotted lines are the curve fits to the respective models. The responses largely lie on top of each other.
Table 3.
Model parameters and values for fitting of experimental data from gelatin and rubber phantoms. MAE is the median absolute error between the acquired data and the curve fit from the model.
| Model parameter | Gelatin 1 | Gelatin 2 | Rubber |
|---|---|---|---|
| Kelvin–Voigt MAE | 0.0207 | 0.0257 | 0.0472 |
| μKV, kPa | 8.06 | 17.52 | 52.95 |
| ηKV, Pa s | 0.27 | 0.75 | 5.92 |
| Maxwell MAE | 0.0192 | 0.0210 | 0.0368 |
| μM, kPa | 7.58 | 15.74 | 45.52 |
| ηM, Pa s | 30.79 | 23.59 | 14.71 |
| Generalized Maxwell MAE | 0.0207 | 0.0256 | 0.0208 |
| μGM,0, kPa | 8.06 | 17.47 | 18.65 |
| μGM,1, kPa | 99.97 | 100.00 | 18.77 |
| ηGM,1, Pa s | 0.14 | 0.37 | 3.73 |
| μGM,2, kPa | 99.97 | 100.00 | 18.74 |
| ηGM,2, Pa s | 0.14 | 0.37 | 3.72 |
| Zener MAE | 0.0207 | 0.0130 | 0.0208 |
| μZ,1, kPa | 8.05 | 13.27 | 18.64 |
| μZ,2, kPa | 49.98 | 4.45 | 37.50 |
| ηZ, Pa s | 0.27 | 1.83 | 7.45 |
| Kelvin–Voigt | 0.0197 | 0.0217 | 0.0366 |
| Fractional derivative MAE | |||
| μKVFD, kPa | 7.51 | 14.14 | 30.72 |
| ηKVFD, Pa s | 7.38 | 100.00 | 100.00 |
| α | 0.58 | 0.43 | 0.66 |
For gelatin 1, most of the models had one of the elastic components with a value of about 7.5–8 kPa. For gelatin 2, the model fits had one of the elastic components with a value of 13.3–17.5 kPa. The reason for the differences in the elastic components is probably due to dehydration that can occur over time which will make the phantom stiffer as gelatin 2 was 16 days older than gelatin 1. This trend has been observed in our laboratory in the past, but not reported. Hall et al. have shown that gelatin materials can increase in stiffness and reach an equilibrium, but that time is on the order of 100 days after being manufactured.22
The velocity frequency response and curve fits for the five rheological models are shown in Fig. 7 for the rubber phantom. The peak of the response is located at a higher frequency compared to the gelatin phantoms and the width is much larger. The MAE and model parameters for the curve fits are summarized in Table TABLE III.. The lowest MAE values for the different models were obtained with the generalized Maxwell model and the Zener model, while the Kelvin–Voigt model had the highest MAE value. Most of the models had one of the elastic components with a value of about 37–56 kPa. The rubber was very stiff compared to the gelatin, and this is reflected in the quantitative results.
Figure 7.
(Color online) Experimental data and model fitting for urethane rubber phantom. Open circles are measured data points and the plotted lines are the curve fits to the respective models.
DISCUSSION
We provided an extension of previously developed theory for the GESR in a viscoelastic medium and excited by ultrasound radiation force. The generalization was applied so that different rheological models could be used. The congruence of the time- and frequency-domain methods for the different models used was demonstrated in the numerical results in Fig. 2.
The time-domain responses for the analytic solution [Eq. 12] and the FEM solutions showed very good agreement. This FEM simulation served as a verification of the GESR in the time domain. It also indirectly serves as a validation for the frequency-domain GESR because we have shown the agreement between the two methods in Fig. 2.
Three laboratory experiments were performed to show the utility of this generalized method in different materials, gelatin and rubber. All of the models fit the responses from the gelatin phantoms relatively well, where the Maxwell model provided the best MAE value for gelatin 1 and the Zener model provided the best MAE for gelatin 2. Qualitatively, the fits look very similar and have trouble capturing the response for frequencies of 2–3 kHz. For the rubber, the Kelvin–Voigt yielded the worst MAE value, and the generalized Maxwell and Zener models performed the best for fitting the data. Qualitatively, the fits look better for the generalized Maxwell and Zener models.
During the fitting process it was found that some parameters had very low sensitivity in fitting the velocity responses. In particular, the parameters μGM,1 and μGM,2 for both gelatin phantoms, μZ,2 for gelatin 1, and ηKVFD for gelatin 2 and the rubber phantom were insensitive and approached the user defined bounds. In the case of the Kelvin–Voigt fractional derivative model, the uniqueness of the results was also questionable because different values for ηKVFD could be used and the exponent α would change such that the value of stayed approximately constant. To evaluate the influence of each model parameter, a sensitivity analysis in which partial differentials of the displacement [Eq. 12] or velocity [Eq. 13] could be computed with respect to a parameter such as μGM,1, i.e., [∂u(t)∕∂μGM,1 or ∂V(ω)∕∂μGM,1], and could be compared. However, this type of analysis has to be done while the other parameters in the model are held constant at a set of values, and sensitivity may change for different settings of the other parameters.
For all three phantoms, the fits deviated from the data at high frequency. The reasons for these deviations are not immediately obvious. The signals were filtered with a bandpass filter with a passband from 10 to 2900 Hz. Part of the discrepancy could be due to the filtering, but these effects should be minimal. One possible explanation could be that there are some aliasing artifacts present as the Nyquist frequency for these experiments was 3 kHz. There may have been some vibration energy above this frequency that could have been aliased down to the frequencies in the 2–3 kHz range. In the FEM simulation a sampling frequency of 100 kHz was used and the simulation results match the analytic results very well, even at the high frequencies, Thus, in the future, we may have to use a higher pulse repetition frequency for the detection transducer operating in pulse-echo mode, such as the 20 kHz pulse repetition frequency used in previously reported studies.7, 8 A weighted algorithm was used for the fitting and the weights were based on the normalized values of the velocity spectrum. This weighting scheme was chosen so that the information that had the most amplitude and energy was used to determine the model parameters rather than data that had lower amplitude and potentially poorer signal-to-noise ratio.
We observed interesting differences between using a generalized Maxwell model with two Maxwell elements and one Maxwell element (Zener model). In the case of gelatin 1 and the urethane rubber, the elastic Maxwell components for the generalized Maxwell model with two Maxwell components were twice that of the elastic Maxwell component in the Zener model. The viscous components had an inverse relationship where the viscous component in the Zener model was two times that of the viscous Maxwell components in the generalized Maxwell model. The MAE values were exactly the same for both models in these two phantoms. These observations indicate that the Zener model is adequate to describe the material behavior for these phantoms.
The generalized method offers the flexibility of adapting to different rheological models based on the material used for embedding the sphere. For each application, one rheological model may work better than another. This was demonstrated in fitting the responses for the gelatin and rubber phantoms. However, within the examination of a certain phantom such as gelatin 1, the MAE values were very similar for several models, and the fits appeared similar. A model with the minimum number of parameters needed to describe the behavior of material adequately may be the most suitable in order to reduce the complexity of the characterization. One could even use a model-free approach and not parameterize the functions G1(ω) and G2(ω). A uniqueness problem could arise in determining these two functions from acquired data. This type of problem would have to be addressed to use the model-free approach.
CONCLUSION
A generalized model for the response of an embedded sphere in a viscoelastic medium subjected to acoustic radiation force was presented. The GESR theory was extended from previous work for responses in the time and frequency domains. The responses predicted by the theory in the time and frequency domains were compared and found to be in good agreement for different viscoelastic rheological models. Three phantoms made of gelatin and urethane rubber were tested and curve fitting was performed using the new generalized response theory. Using data acquired from the different phantoms, it was found that different rheological models fit data best in each case. This generalized method could be used for embedded sphere tests for various types of materials and the best rheological model could be adapted for each application.
ACKNOWLEDGMENTS
This work was supported in part by Grant Nos. EB002167 and DK082408 from the National Institutes of Health. The authors thank Jennifer Milliken for administrative assistance. Some of the authors have patents related to parts of this work.
Portions of this work presented in “Generalized response of a sphere embedded in a viscoelastic medium excited by ultrasound radiation force,” 160th Meeting of the Acoustical Society of America, Cancun, Mexico, November 2010.
References
- Oestreicher H. L., “Field and impedance of an oscillating sphere in a viscoelastic medium with an application to biophysics,” J. Acoust. Soc. Am. 23, 707–714 (1951). 10.1121/1.1906828 [DOI] [Google Scholar]
- Chen S., Fatemi M., and Greenleaf J. F., “Remote measurement of material properties from radiation force induced vibration of an embedded sphere,” J. Acoust. Soc. Am. 112, 884–889 (2002). 10.1121/1.1501276 [DOI] [PubMed] [Google Scholar]
- Urban M. W., Silva G. T., Fatemi M., and Greenleaf J. F., “Multifrequency vibro-acoustography,” IEEE Trans. Med. Imaging 25, 1284–1295 (2006). 10.1109/TMI.2006.882142 [DOI] [PubMed] [Google Scholar]
- Urban M. W., Fatemi M., and Greenleaf J. F., “Modulation of ultrasound to produce multifrequency radiation force,” J. Acoust. Soc. Am. 127, 1228–1238 (2010). 10.1121/1.3294487 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norris A. N., “Impedance of a sphere oscillating in an elastic medium with and without slip,” J. Acoust. Soc. Am. 119, 2062–2066 (2006). 10.1121/1.2171526 [DOI] [PubMed] [Google Scholar]
- Ilinskii Y. A., Meegan G. D., Zabolotskaya E. A., and Emelianov S. Y., “Gas bubble and solid sphere motion in elastic media in response to acoustic radiation force,” J. Acoust. Soc. Am. 117, 2338–2346 (2005). 10.1121/1.1863672 [DOI] [PubMed] [Google Scholar]
- Aglyamov S. R., Karpiouk A. B., Ilinskii Y. A., Zabolotskaya E. A., and Emelianov S. Y., “Motion of a solid sphere in a viscoelastic medium in response to applied acoustic radiation force: Theoretical analysis and experimental verification,” J. Acoust. Soc. Am. 122, 1927–1936 (2007). 10.1121/1.2774754 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karpiouk A. B., Aglyamov S. R., Ilinskii Y. A., Zabolotskaya E. A., and Emelianov S. Y., “Assessment of shear modulus of tissue using ultrasound radiation force acting on a spherical acoustic inhomogeneity,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 56, 2380–2387 (2009). 10.1109/TUFFC.2009.1326 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catheline S., Gennisson J. L., Delon G., Fink M., Sinkus R., Abouelkaram S., and Culioli J., “Measurement of viscoelastic properties of homogeneous soft solid using transient elastography: An inverse problem approach,” J Acoust. Soc. Am. 116, 3734–3741 (2004). 10.1121/1.1815075 [DOI] [PubMed] [Google Scholar]
- Chen S., Urban M. W., Pislaru C., Kinnick R., Zheng Y., Yao A., and Greenleaf J. F., “Shearwave dispersion ultrasound vibrometry (SDUV) for measuring tissue elasticity and viscosity,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 56, 55–62 (2009). 10.1109/TUFFC.2009.1005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vappou J., Maleke C., and Konofagou E. E., “Quantitative viscoelastic parameters measured by harmonic motion imaging,” Phys. Med. Biol. 54, 3579–3594 (2009). 10.1088/0031-9155/54/11/020 [DOI] [PubMed] [Google Scholar]
- Orescanin M., Qayyum M. A., Toohey K. S., and Insana M. F., “Complex shear modulus of thermally-damaged liver,” in Ultrasonics Symposium (IUS), IEEE International (2009), pp. 127–130.
- Zhang M., Castaneda B., Wu Z., Nigwekar P., Joseph J. V., Rubens D. J., and Parker K. J., “Congruence of imaging estimators and mechanical measurements of viscoelastic properties of soft tissues,” Ultrasound Med. Biol. 33, 1617–1631 (2007). 10.1016/j.ultrasmedbio.2007.04.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sack I., Beierbach B., Wuerfel J., Klatt D., Hamhaber U., Papazoglou S., Martus P., and Braun J., “The impact of aging and gender on brain viscoelasticity,” NeuroImage 46, 652–657 (2009). 10.1016/j.neuroimage.2009.02.040 [DOI] [PubMed] [Google Scholar]
- Balocco S., Basset O., Courbebaisse G., Boni E., Frangi A. F., Tortoli P., and Cachard C., “Estimation of the viscoelastic properties of vessel walls using a computational model and Doppler ultrasound,” Phys. Med. Biol. 55, 3557–3575 (2010). 10.1088/0031-9155/55/12/019 [DOI] [PubMed] [Google Scholar]
- Yamakoshi Y., Sato J., and Sato T., “Ultrasonic imaging of internal vibration of soft tissue under forced vibration,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 37, 45–53 (1990). 10.1109/58.46969 [DOI] [PubMed] [Google Scholar]
- Chen S., Fatemi M., and Greenleaf J. F., “Quantifying elasticity and viscosity from measurement of shear wave speed dispersion,” J. Acoust. Soc. Am. 115, 2781–2785 (2004). 10.1121/1.1739480 [DOI] [PubMed] [Google Scholar]
- Klatt D., Hamhaber U., Asbach P., Braun J., and Sack I., “Noninvasive assessment of the rheological behavior of human organs using multifrequency MR elastography: A study of brain and liver viscoelasticity,” Phys. Med. Biol. 52, 7281–7294 (2007). 10.1088/0031-9155/52/24/006 [DOI] [PubMed] [Google Scholar]
- Sarvazyan A. P., Rudenko O. V., Swanson S. D., Fowlkes J. B., and Emelianov S. Y., “Shear wave elasticity imaging: A new ultrasonic technology of medical diagnostics,” Ultrasound Med. Biol. 24, 1419–1435 (1998). 10.1016/S0301-5629(98)00110-0 [DOI] [PubMed] [Google Scholar]
- Urban M. W. and Greenleaf J. F., “Harmonic pulsed excitation and motion detection of a vibrating reflective target,” J. Acoust. Soc. Am. 123, 519–533 (2008). 10.1121/1.2805666 [DOI] [PubMed] [Google Scholar]
- Hasegawa H. and Kanai H., “Improving accuracy in estimation of artery-wall displacement by referring to center frequency of RF echo,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 53, 52–63 (2006). 10.1109/TUFFC.2006.1588391 [DOI] [PubMed] [Google Scholar]
- Hall T. J., Bilgen M., Insana M. F., and Krouskop T. A., “Phantom materials for elastography,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 44, 1355–1365 (1997). 10.1109/58.656639 [DOI] [Google Scholar]