Development and characterization of a dynamic lesion phantom for the quantitative evaluation of dynamic contrast-enhanced MRI

Abstract

Purpose: To develop a dynamic lesion phantom that is capable of producing physiological kinetic curves representative of those seen in human dynamic contrast-enhanced MRI (DCE-MRI) data. The objective of this phantom is to provide a platform for the quantitative comparison of DCE-MRI protocols to aid in the standardization and optimization of breast DCE-MRI.

Methods: The dynamic lesion consists of a hollow, plastic mold with inlet and outlet tubes to allow flow of a contrast agent solution through the lesion over time. Border shape of the lesion can be controlled using the lesion mold production method. The configuration of the inlet and outlet tubes was determined using fluid transfer simulations. The total fluid flow rate was determined using x-ray images of the lesion for four different flow rates (0.25, 0.5, 1.0, and 1.5 ml∕s) to evaluate the resultant kinetic curve shape and homogeneity of the contrast agent distribution in the dynamic lesion. High spatial and temporal resolution x-ray measurements were used to estimate the true kinetic curve behavior in the dynamic lesion for benign and malignant example curves. DCE-MRI example data were acquired of the dynamic phantom using a clinical protocol.

Results: The optimal inlet and outlet tube configuration for the lesion molds was two inlet molds separated by 30° and a single outlet tube directly between the two inlet tubes. X-ray measurements indicated that 1.0 ml∕s was an appropriate total fluid flow rate and provided truth for comparison with MRI data of kinetic curves representative of benign and malignant lesions. DCE-MRI data demonstrated the ability of the phantom to produce realistic kinetic curves.

Conclusions: The authors have constructed a dynamic lesion phantom, demonstrated its ability to produce physiological kinetic curves, and provided estimations of its true kinetic curve behavior. This lesion phantom provides a tool for the quantitative evaluation of DCE-MRI protocols, which may lead to improved discrimination of breast cancer lesions.

INTRODUCTION

Dynamic contrast-enhanced MRI (DCE-MRI) of the breast has developed into an important method for breast cancer diagnosis and screening of high-risk patients. Although the clinical use of this technique has led to improved sensitivity for cancer detection, DCE-MRI has a well-documented low and variable specificity (26%–97%) (Refs. ^{1, 2, 3}), and there is a need for improved standardization of the technique.⁴ Although progress has been made in standardizing terminology for describing lesions^{5, 6} and quantities and symbols for analysis of kinetic data,⁷ the ability of DCE-MRI examinations to reliably measure kinetic curves remains elusive. A recent study by Jansen et al.⁸ highlighted this fact by comparing kinetic curve shapes of lesions imaged on three different clinical imaging systems. They found that the measured initial contrast uptake and kinetic curve shape of lesions imaged on one system differed significantly from those imaged on the other two systems. Additional quantitative methods are needed to ensure that DCE-MRI data accurately reflect the true lesion kinetic curves. The goal of standardization of DCE-MRI for kinetic curve estimation is to have the separation of benign and malignant lesions, and, therefore, the specificity of the technique, be limited by biological variability, not instrumental variations.

Some efforts toward more quantitative approaches to DCE-MRI are currently underway⁹. However, there is a need for additional methods and tools for quantitative evaluation of kinetic curve shape. Well-characterized phantoms, which can reliably reproduce physiological kinetic curve shapes that have been measured independently of DCE-MRI, are a critical step toward this goal.

Dynamic MRI phantoms have been presented in the literature for various applications.^{10, 11, 12} Chai et al.¹⁰ developed a perfusion phantom to test the ability of a new arterial spin tagging protocol to produce tagged images where the signal attenuation was linearly proportional to the tissue flow rates. Their phantom used a layer of plastic beads followed by a compressed sponge to control fluid flow rates, however, this phantom was not developed to produce physiological kinetic curves.

Ivancevic et al.¹¹ developed a flow phantom to investigate how flow rate affects signal intensity in fast gradient-recalled-echo sequences for quantification of arterial input functions (AIFs). To simulate AIFs, Gd-DTPA was injected into a closed-circuit fluid flow system. Although this phantom is able to produce dynamic curves appropriate for its intended use, it was meant to simulate AIFs, not physiological kinetic curves. As a result, the entire wash-in and wash-out behavior is confined to approximately 10 s, and there is no straightforward mechanism to produce longer timescale kinetic curves.

Finally, Ebrahimi et al.¹² have presented a microfabricated dynamic phantom, produced on a silicon wafer, with branching channels of similar diameter to human vasculature. Their objective was to simulate blood perfusion on the microvasculature level. Kinetic curves were produced by introducing a contrast agent into the supply channels of the phantom. While this phantom holds promise, there are several issues that limit its applicability to the evaluation of physiological kinetic curves. Unfortunately, while the authors presented simulation results for flow rate in the phantom, no simulated kinetic curves or other estimations of the true kinetic curve behavior were produced. This means that the true behavior of the phantom was unknown, and it is not possible to compare MRI measurements of the phantom with the true flow behavior. In addition, the kinetic curves occurred on a timescale much faster than physiological curves, about 30 s.

The dynamic phantoms discussed above are important tools for the evaluation of dynamic MRI protocols. However, none of these phantoms produce physiological kinetic curves or have the ability to be easily modified to mimic the variety of kinetic curve shapes seen in the clinic.

We previously presented an MR breast phantom with a static enhancing lesion.¹³ This phantom combined two materials to produce a heterogeneous, anthropomorphic tissue structure similar to that of the human breast. A static, enhancing lesion was included by filling a hollow, plastic mold with gadolinium-doped water. In this paper, we extend that breast phantom with a dynamic lesion capable of producing kinetic curves with shapes and timescales that are similar to those of patient kinetic curves. In addition, the lesion is confined to a physiologically relevant space and can be modified with different border shapes to mimic different lesion types. Independent measurements of the true kinetic curve behavior are performed using high-resolution x-ray imaging. These measurements can be compared with MR measurements in future studies to evaluate MR system performance. An example set of dynamic MR data is also acquired using the phantom. While the simulation of AIFs is not explored in the current study, possible future work in this area is discussed.

Methods

In the following subsections, we describe the design and operation of the phantom, measurements of the fluid flow rate for the phantom, estimation of the true phantom kinetic curve behavior, and example MRI measurements of the dynamic phantom.

Phantom design and operation

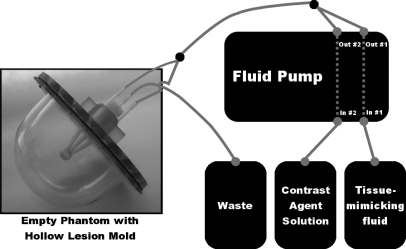
The overall design of the dynamic lesion phantom is diagrammed in Fig. 1. A hollow lesion mold made from plastic is inserted in a static breast phantom. The design of the breast phantom has been previously described in Freed et al.¹³ and consists of a breast-shaped plastic jar filled with a mixture of coagulated egg whites and lard that simulates the adipose-glandular tissue structure in human breasts and has relaxation values that match those of breast tissue. For clarity, in Fig. 1, the phantom is shown without the egg white and lard mixture. The lesion mold has two inlets and one outlet (see Sec. 2A1 for further discussion of the inlet∕outlet configuration). The two inlets are fed via a fluid pump that has two separately controlled internal pumps. One of the internal pumps controls the flow rate of a tissue-mimicking fluid, while the other controls the flow rate of a contrast agent solution. The total fluid flow rate exiting both internal pumps is set to a constant value. After both fluids leave the fluid pump, they are mixed together via a bifurcating tube. This fluid mixture is then separated into two tubes that feed the two inlets of the hollow lesion mold. As fluid flows through the hollow lesion mold, it is expelled through the single outlet and discarded in a waste container. By modifying the relative flow rates of the two internal fluid pumps over time, the shape of the resultant kinetic curve in the hollow lesion mold can be controlled. The following subsections describe the design of the lesion molds, operation of the fluid pump, and example kinetic curves used for evaluation of the phantom.

Figure 1.

Overview of the dynamic lesion phantom setup. On the left is an empty breast phantom jar with a hollow lesion mold inserted. The fluid pump takes in a contrast agent solution and a tissue-mimicking fluid and dispenses them separately with different flow rates as a function of time. The total exit flow rate from the fluid pump is kept constant, but the relative fraction of contrast agent solution is varied over time to produce a physiological kinetic curve. The two fluids are mixed together after exiting the fluid pump via a bifurcating tube and then separated to feed the two inlets in the phantom lesion mold. As the fluid exits the phantom via the single outlet tube, it is discarded in a waste container.

Lesion mold design

The lesion molds are hollow plastic molds designed to mimic mass-like lesions and confine the contrast agent solution to a physiologically relevant area in the breast phantom. The molds were manufactured using stereolithography (Fineline Prototyping, Raleigh, NC) and were produced with the thinnest possible wall for the technology (0.6 mm). A lesion inner diameter of 10 mm was chosen for this study; however, modifying this size for future studies would be trivial.

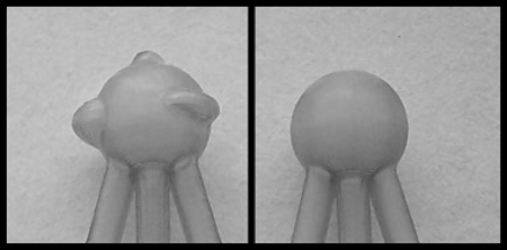
Since lesion border shape is used as a diagnostic feature,^{5, 6} we have selected two different border shapes to demonstrate the ability of the dynamic lesion to mimic variations in this property. Benign lesions tend to have a more smooth and spherical shape, whereas malignant lesions are more irregular. Therefore, a spherical border was selected to represent benign lesions and a spherical border with three additional lobulations was selected to represent malignant lesions (see Fig. 2). Using the technique selected for producing the lesion molds (stereolithography), a variety of border shapes could easily be produced. Although shape changes on a microscopic level cannot be mimicked using this technology, the ability of the phantom to mimic macroscopic border shapes is of value since the ability to visualize spiculations, and irregular borders are aspects of lesion morphology that are incorporated into clinical decisions.

Figure 2.

Example lesion molds with different border shapes mimicking different masslike lesion types: (left) lesion mold with three different irregular border shapes, or lobulations, representing a malignant lesion; (right) lesion mold with smooth, spherical border shape, representing a benign lesion.

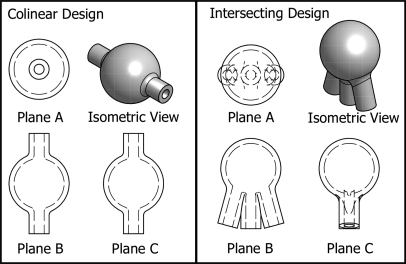
The inlet and outlet configuration of the phantom was selected by examining the influence of this configuration on the distribution of the contrast agent in the lesion mold. The distribution of contrast agent in two different lesion mold designs was investigated using fluid transfer simulations performed with the computational fluid dynamics software package openfoam (openCFD, Ltd., Berkshire, UK). The first design was a 10 mm internal diameter sphere with one 2 mm inner diameter inlet tube and one 2 mm inner diameter outlet tube. The inlet and outlet tubes were colinear and attached to the sphere through its center. This design was chosen as the simplest possible design to manufacture. The second design was also a 10 mm internal diameter sphere, but had two inlets and one outlet, all with 2 mm inner diameters. In this case, all three tubes attached to the sphere on the same side but were separated by 15°. While this design is more complex, it has better mixing properties. Figure 3 shows a diagram of the two different designs.

Figure 3.

Two preliminary lesion mold designs. On the left is a 10 mm inner diameter sphere with a single inlet and a single outlet that are colinear through the center of the lesion mold. On the right is a 10 mm inner diameter sphere with two inlets and one outlet. The two inlets are on opposite sides of the outlet at an angle of 15°. The inner diameter of all inlets and outlets is 2 mm.

The simulations were performed with a total inlet flow rate of 1.0 ml∕s and an element size of approximately 0.04 mm. All boundaries except the inlet assumed a condition of zero-normal derivative in the imposed contrast agent concentration. The input fluid was simulated as a mixture of water and contrast agent, where the concentration of the contrast agent solution started at zero and at a time of 0 s instantaneously jumped to a normalized concentration of 1. Ten seconds of fluid flow were simulated. The density and viscosity of water were assumed to be 1.0 g∕ml and 1.0 cP, respectively. The diffusion coefficient of the contrast agent solution was assumed to be equal to the self-diffusion coefficient of water [2.66 × 10⁻² m²∕s (Ref. ¹⁴)] since the contrast agent will be well mixed in the contrast agent solution in the actual experiments.

Fluid pump operation

The fluid pump was a custom-built, MRI-compatible, programmable, dual-fluid pump (Shelley Medical Imaging Technologies, London, Ontario, Canada). It was manufactured to simultaneously pump two different liquids at different fluid flow rates that could be modified as a function of time. Fluid flow rates of the two liquids were updated on a timescale of 100 ms. One fluid was a tissue-mimicking fluid, and the second was a mixture of tissue-mimicking fluid and contrast agent. These two fluids are described in more detail in the following two subsections. After exiting the fluid pump, the two fluid streams were mixed together via a bifurcated tube. The fluid pump was programmed to output a constant fluid flow rate. The relative fluid flow rates of the two liquids over time were varied by the user to the desired values. In this way, the concentration of the contrast agent in the combined output flow could be modified by the user to reproduce any desired curve as a function of time. For both the x-ray and MRI measurements, the distance between the fluid pump output and the bifurcation where the two fluids joined was 100 cm, the distance between the two bifurcation points was 40 cm, and the distance from the last bifurcation point to the inlets of the lesion mold was 200 cm. The tubing inner diameter was 4 mm.

Example kinetic curves

In a study by Fan et al.,¹⁵ high temporal resolution dynamic contrast-enhanced data at 1.5 T were acquired of 22 patients with a variety of lesion types determined using pathology. In that study, the measured signal intensities were converted to contrast agent concentration and fitted to an empirical mathematical model. Average coefficients of the model were provided for benign and malignant lesions.

In our study, we have selected their average benign and malignant fitted curves to perform initial proof-of-concept measurements with the phantom as described in Sec. 2B2, 2D We have selected these curve types since the primary objective of our phantom is to provide a tool for quantitative evaluation of kinetic curve shape for the purpose of optimally separating benign and malignant lesions. In future studies, a more exhaustive sampling of kinetic curve shapes could be performed. Although these kinetic curve shapes were derived from MRI measurements, we expect them to be reasonably close to the true kinetic curve shapes since an approximate conversion from MRI signal intensity to contrast agent concentration was performed.¹⁵ Inaccuracies in this conversion will not affect our study, since we have the ability to measure the true kinetic curves via x-ray measurements, as described in Sec. 2C

The kinetic curves are directly translated into fluid pump commands to control the flow rates of the contrast agent and tissue-mimicking solutions. The kinetic curve is simply normalized by its maximum value and multiplied by the total fluid flow rate to give the flow rate of contrast agent solution (a mixture of tissue-mimicking fluid and contrast agent). The flow rate of the tissue-mimicking fluid is then simply the total fluid flow rate minus the flow rate of the contrast agent solution.

Fluid flow rate

In order to determine an appropriate fluid flow rate, x-ray data were acquired for the malignant curve shape and four different constant fluid flow rates (0.25, 0.5, 1.0, and 1.5 ml∕s). The spatial distribution of the contrast agent in the lesion as well as the average relative concentration of contrast agent in the lesion was examined over time for each of the investigated fluid flow rates. The lowest possible fluid flow rate that provides a homogeneous distribution of contrast agent and a reasonable match to the desired kinetic curves was chosen for all subsequent experiments. It is preferable to reduce the flow rate as much as possible since rapid flow rates can affect MRI images and an increased flow rate means more fluid waste. The following subsections describe the experimental setup used to acquire the x-ray data and the calculation of the average relative concentration of contrast agent in the lesion mold.

Experimental setup

The x-ray source was a Varian B180 (Varian Corp., Salt Lake City, UT) x-ray tube with a tungsten anode, 0.3 mm focal spot, and 1.0 mm Al internal filtration. The detector, which has been previously described,¹⁶ was a high-resolution CCD camera (Quantix 6303 Photometrics 3072 × 2048 array, 9 × 9 μm pixels, Photometrics, Tucson, AZ) modified with a 4.5 cm length one-to-one fiber optic faceplate with 4.5 μm fibers. This fiber optic faceplate is bonded to the CCD on one side and a Hamamatsu CsI screen (0.15 mm thick CsI, Part No. J8734-01, Hamamatsu Corporation, Bridgewater, NJ) is pressure fitted to the opposite side. The entire camera assembly is covered with a 0.635 mm thick beryllium window cap. The measurements of the detector response to a 30 μm wide beam incident perpendicular to the CsI surface were performed using the same methods described in Freed et al.¹⁶ The full width at half-maximum of the response is 62.2 μm, or 6.9 pixels. Since the incident beam is 30 μm wide, if we assume that the CsI point response function (PRF, the detector response to an infinitely thin beam) and the incident beam can be reasonably well represented by Gaussian functions, we expect that the CsI PRF is about 54.5 μm or 6.1 pixels wide. Therefore, we can expect this amount of blur in the images of the tumor molds.

Images were acquired with the following parameters: 120 kVp, 6.4 mAs, and 80 ms exposure time, temporal resolution that varied between 2.6 and 24.7 s, a single projection view, and the spherical lesion mold. The lesion mold was imaged with no surrounding jar or other phantom structure. Data were acquired with a magnification of 1.2, so the interior of the tumor mold was sampled with 1312 pixels, or approximately 215 (=1312∕6.1) resolution elements. This means that, although data overlap occurs in the direction of the x-ray incidence, good spatial resolution of the lesion mold was achieved in the perpendicular direction. The lesion mold was simultaneously imaged with a vial of constant Gd-DTPA concentration to calibrate the x-ray tube output.

The tissue-mimicking fluid was a mixture of 40% glycerol and 60% deionized water, by volume, as specified by the manufacturer for appropriate lubrication of the fluid pump. The contrast agent solution was 40% glycerol by volume, 60% deionized water by volume, and 150 mM Gd-DTPA. A concentration of 150 mM Gd-DTPA was used to allow for high spatial-resolution measurements with low noise. Lower concentrations in a more physiological range were used for the later MRI experiments. The Gd-DTPA was prepared according to procedures described in Strich et al.¹⁷ using GdCl₃6H₂O (GFS Chemicals, Columbus, OH), DTPA (Agros Organics, NJ), and NaOH (Sigma-Aldrich, St. Louis, MO).

Derivation of average lesion contrast concentration

The spatially resolved, relative lesion contrast agent concentration was derived using the knowledge that the number of primary x rays incident on any given location in the detector is given by

$$I=I_o\exp (-\mu l),$$ (1)

where I_o is the number of x rays incident on the object being imaged, μ is the attenuation coefficient of the object material, and l is the size of the object along the path of the x rays. Note that all variables in this section are a function of the position on the detector. The incoming x rays are assumed to be parallel. In our case, the object being imaged is the lesion mold filled with a mixture of tissue-mimicking and contrast agent solutions. Therefore, we can consider the object to consist of three materials; the plastic making up the lesion mold walls, a, the tissue-mimicking fluid, b, and the contrast agent solution, c. For any given x-ray path through the lesion mold, Eq. 1 can be written using the sum rule as

$$I=I_o\exp [-({\mu }_a{l}_a+{\mu }_b{l}_b+{\mu }_c{l}_c)].$$ (2)

Let us define l_a + l_b + l_c ≡ l_mold, so we can rewrite this equation as

$$I=I_o\exp [-({\mu }_a{f}_a+{\mu }_b{f}_b+{\mu }_c{f}_c)l_{\mathrm{mold}}],$$ (3)

where f_a, f_b, and f_c are fractional distances, and f_a + f_b + f_c is always equal to one. Now, if we have two images, the first of which has no contrast agent solution, 1, and the second which has an unknown amount of contrast agent solution, 2, then f_a1 + f_b1 = 1 and f_a2 + f_b2 + f_c2 = 1. In addition, since the amount of plastic in the lesion mold never changes, f_a1 = f_a2 = f_a. I_o1 and I_o2 can also be assumed to be equal. Although the x-ray tube output does vary over time, the lesion mold was imaged simultaneously with a vial of constant Gd-DTPA concentration, which was used to normalize the signal for changes in the x-ray tube output. Calculating I₂∕I₁ and solving for f_c2, we find

$$f_{c2}=\frac{1}{l_{\mathrm{mold}}({\mu }_b-{\mu }_c)}\mathit{ln}\frac{I_2}{I_1}.$$ (4)

We can now normalize by the maximum fraction of f_c2, so that l_mold, μ_b, and μ_c drop out and we have

$$\frac{f_{c2}}{\max f_{c2}}=\frac{\ln \frac{I_2}{I_1}}{\ln \left(\frac{I_2{|}_{f_{c2}=\text{max})(f_{c2})}}{I_1}\right)}.$$ (5)

The detector efficiency is assumed to be the same for all cases, so I₁, I₂, and I₂|_fc2=max(fc2) are: the image values when there is no contrast agent solution in the lesion mold; an unknown, variable amount of contrast agent solution; and a maximum amount of contrast agent solution, respectively. The error incurred by ignoring beam hardening and assuming that the detector efficiency is the same for any concentration of contrast agent is negligible (see Appendix).

Once the normalized contrast agent fraction, f_c2∕(max f_c2), was calculated for all locations in the lesion mold for each acquired image, an average normalized contrast agent fraction was calculated by averaging the values inside a circular, manually selected region-of-interest that was limited to the area inside of the lesion mold.

Truth estimation

High spatial and temporal resolution x-ray images were used to measure the ability of the fluid pump to produce benign and malignant example curves. To accomplish this the experimental setup described in Sec. 2A1 was used. The lesion was imaged with no surrounding phantom to remove the associated confounding signal and produce a more accurate estimation of the true kinetic curve behavior. Relative contrast agent concentrations at each time point were estimated using Eq. 5. To evaluate repeatability of the fluid pump, x-ray images were acquired for five identical runs for both the benign and malignant curve shapes. Since the x-ray data were acquired at irregularly spaced time points, the resultant average normalized contrast agent concentration values were linearly interpolated to a regular grid before the average and standard deviations were calculated. An overall fluid flow rate of 1.0 ml∕s was used in all cases.

MRI measurements

MRI data were acquired of the dynamic lesion inside of a breast phantom¹³ as a demonstration of the use of the phantom. The orientation of the lesion with respect to gravity was the same as that used for the x-ray measurements. All data were acquired on a 1.5 T Siemens Magnetom scanner with a Siemens CP extremity coil and a fat-suppressed, 3D spoiled gradient-echo imaging protocol. The scan parameters were: repetition time (TR) = 4.4 ms, echo time (TE) = 1.58 ms, flip angle = 10°, matrix size = 320 × 320 × 52, spatial resolution = 0.8 × 0.8 × 1.5 mm³, temporal resolution = 79 s. This imaging sequence was taken from a routine protocol used at a clinical institution with experience in breast imaging. Data were acquired of a spherical lesion with the benign and malignant example kinetic curves. There was no pause between temporal samples in a single dynamic acquisition. Note that the spatial resolution of the MRI data was about 15 times worse than the spatial resolution of the x-ray truth data (0.8 mm for MRI versus 54.5 μm for x-ray). Kinetic curves were calculated as the mean image signal in a hand-selected ROI that contained the entire 3D lesion. The inlet and outlet tubes of the lesion were not included in the ROI.

The tissue-mimicking fluid consisted of 5.0 mM Ni-DTPA in a solution of 40% glycerol and 60% deionized water by volume. Ni-DTPA was used to match the T₁ value of the fluid to that of the glandular-mimicking component of the phantom and was produced following the method described in Tofts et al.¹⁸ The contrast agent solution has the same composition as the tissue-mimicking fluid, but with an additional 4.5 mM Gd-DTPA. A value of 4.5 mM Gd-DTPA was chosen as a representative maximum contrast concentration in breast lesions during DCE-MRI studies.¹⁵

The MR signal of the measured kinetic curves was converted to normalized contrast agent concentration using the theoretical signal equation for a spoiled gradient-echo sequence at steady state¹⁹ and assuming the relaxation rates scale linearly with contrast agent concentration as in the fast exchange limit. The protocol parameters were set equal to those used to acquire the MR data; TR (=4.4 ms), TE (=1.58 ms), and α (=10°). The pre-contrast T₁ value was set equal to that of the glandular-mimicking component of the phantom (=1192 ms) and the pre-contrast $T_2^{*}$ value was arbitrarily set to half of the T₂ value of the glandular-mimicking component of the phantom (=35 ms). The contrast relaxivity values were set to r₁ = 12.0 s⁻¹ mM⁻¹ for Gd-DTPA in a solution of 40% glycerol and 60% water²⁰ and r₂ = 5.49 ± 0.06 s⁻¹ mM⁻¹ as measured on aqueous Gd-DTPA solutions at 1.5 T.¹⁸

RESULTS

Phantom design and operation

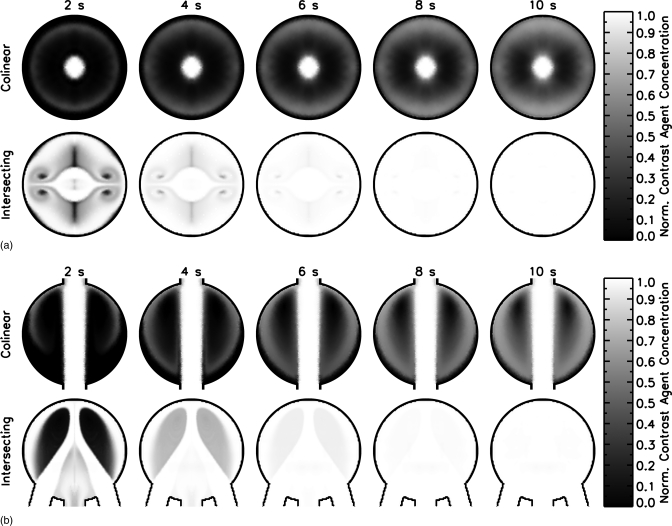
Figure 4 shows the results of the fluid transfer simulations for two different planes in the two preliminary lesion mold designs. The contrast agent distribution is presented between 2 and 10 s for every 2 s of the simulation for planes A and B as defined in Fig. 3. The top row of each panel shows the results for the colinear design and the bottom row for the intersecting design. The contrast agent solution is distributed throughout the lesion mold on a much faster timescale for the intersecting design than for the colinear design. This indicates that the intersecting design will produce a more realistic representation of actual lesions and, as a result, this inlet∕outlet configuration was selected for all further development.

Figure 4.

Comparison of contrast agent distribution in two different mold designs as a function of time a) Plane A view b) Plane B view. The total flow rate for both mold designs was 1.0 ml/s and the mold began filled with water. At a time of 0 s, the inlet concentration of contrast agent solution instantaneously increased to 100%. The contrast solution distributes more evenly in the intersecting design than in the colinear design.

Fluid flow rate

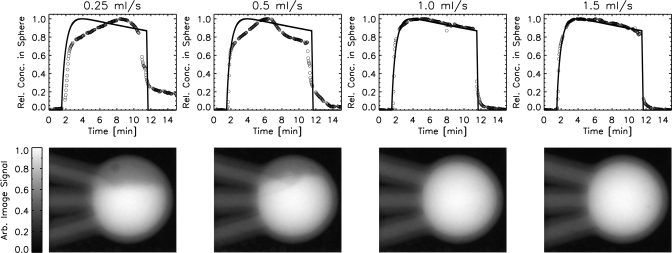
Figure 5 shows the results of a series of experiments to determine the total flow rate for the system. Four different total flow rates were investigated (0.25, 0.5, 1.0, and 1.5 ml∕s). Measured kinetic curves are compared with the desired curve shapes and representative x-ray images of the lesion mold for each of the flow rates are shown. Flow rates of 1.0 and 1.5 ml∕s were both able to reproduce the desired curves and had an even distribution of contrast agent solution throughout the lesion mold. Lower flow rates (0.25 and 0.5 ml∕s) were unable to counteract the effect of gravity and resulted in contrast agent solutions that settled in the bottom of the lesion mold and produced kinetic curves that were significantly different from the desired curves. A total flow rate of 1.0 ml∕s was selected for all further studies, since it was the lowest flow rate that reliably reproduced the desired kinetic curve shapes.

Figure 5.

(top row): Plots of average normalized contrast agent concentration in the lesion versus time for four different total flow rates (0.25, 0.5, 1.0, and 1.5 ml/s). The solid lines indicate what the fluid pump was commanded to output, and the circles are values derived from the acquired data. (bottom row): representative x-ray images of the lesion mold (inner diameter = 10 mm) for each total flow rate (at time = 5 min). A total flow rate of 1.0 ml/s is the lowest flow rate that provides good contrast agent solution mixing and a good reproduction of the desired curve.

Truth estimation

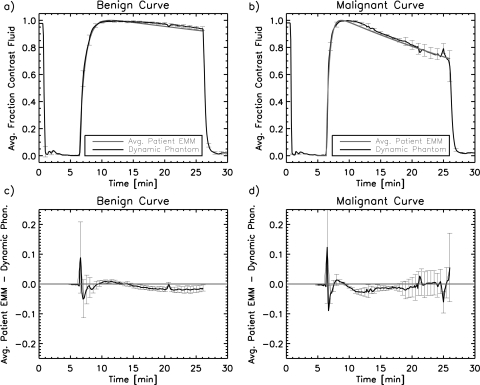
A comparison of the estimations of the true phantom kinetic curve behavior with the benign and malignant example patient curves is shown in Fig. 6. The dynamic phantom produces kinetic curves that match the patient example curves to within approximately two standard deviations of the dynamic phantom kinetic curves. The average deviation of the phantom curves from the patient curves is larger during the wash-in phase than the wash-out phase due to the rapidly varying curve shape in that region. Overall, the x-ray measurements show that the desired curves are well reproduced for both the benign and malignant example cases.

Figure 6.

Averagenormalized contrast agent concentration curves for two curve shapes; (a) benign and (b) malignant. The benign and malignant example curves taken from Ref. 15 are shown as well as the x-ray measured values in the lesion mold averaged over five identical runs. Error bars for the x-ray data were calculated as standard deviations of the five runs for some of the time points. The high values in the first minute are due to the pump homing before the beginning of the curves, which briefly introduced contrast agent solution into the lesion mold. The residuals (patient example curve minus dynamic phantom curve) are shown, with standard error bars for the (c) benign and (d) malignant example curves. The straight line in (c) and (d) indicates a perfect match. The dynamic phantom lesion matches the example patient curves to within at least two standard deviations.

MRI measurements

Figure 7 shows a comparison between the x-ray measurements and the MRI data. MR images and ROIs used to estimate the MR kinetic curves are shown in Fig. 8. The MRI data demonstrate that the dynamic phantom is able to produce dynamic kinetic curves with behavior that is similar to human data; however, there are some differences. A visual comparison indicates that the MRI curves are flatter than the truth measurements and that it is more difficult to distinguish the benign and malignant example curves for the MRI data than the x-ray truth measurements, particularly early in the wash-out phase. Quantitative differences between the normalized contrast agent concentration estimated from MRI and x-ray data are shown in Fig. 7d. Here, it is evident that the MRI data indicate a higher normalized contrast agent concentration both in the wash-in phase (around 5–9 min) and in the wash-out phase (from about 10–25 min). This effect is most likely due to the nonlinear relationship between MRI signal intensity and contrast agent concentration for gradient-echo sequences. The theoretical relationship between contrast agent concentration and MRI signal for spoiled gradient-echo sequences²¹ indicates that this relationship is more nonlinear for lower flip angles such as those used in our MRI protocol. For this reason, multiple contrast agent concentrations will map to very similar MR signal values, making the kinetic curve appear flatter.

Figure 7.

Comparison of x-ray truth measurements and MRI data for benign and malignant example curves. (a) Normalized contrast agent concentration versus time for the x-ray truth measurements, (b) MR image signal versus time for the MRI data, (c) normalized contrast agent concentration versus time for the MRI data, and (d) the difference between the normalized contrast agent concentration for the MRI data and the x-ray truth data versus time.

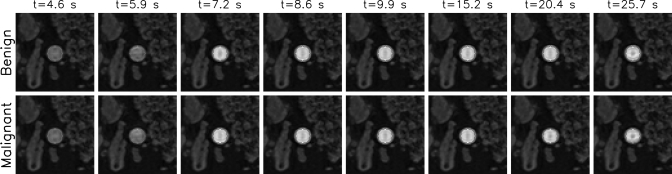
Figure 8.

MR phantom images for benign and malignant example curves corresponding to MRI data shown are in Fig. 7. The ROI used to estimate the kinetic curve is indicated as a solid contour.

DISCUSSION

We have produced a dynamic lesion phantom that mimics physiological kinetic curves. The shape of the kinetic curve can be easily modified by simply adjusting the relative fluid flow rates over time of the tissue-mimicking and contrast agent solutions. In addition, we have estimated the true kinetic curve behavior of the phantom using high spatial and temporal resolution x-ray imaging. Using this validated lesion model, the ability of an MRI system or protocol to measure true kinetic curve shapes as well as differences between curve shapes can be quantitatively examined. Since differences in kinetic curve shape are used in the clinic for lesion diagnosis, the ability to quantitatively evaluate this property gives researchers an important tool for system and protocol optimization.

In an engineering setting, where scanner time is more readily available and detailed optimizations can be performed, this phantom could be used to explore a range of protocol parameters, such as repetition time and flip angle, to determine the optimal settings for separation of benign and malignant lesions (see Ref. 22 for some discussion of this problem in simulation). The results from this type of analysis could provide a basis for recommendations of protocol parameter selection for patient imaging. In a clinical setting, scanner time for system evaluation is very limited and the performance of a specific scanner is of interest. In this case, MR data of the phantom could be acquired for the benign and malignant example curves and compared with the x-ray truth data, as in Fig. 7. Such comparisons could provide a basis for modifications to the scanner or protocol or could simply inform the radiologist of the influence of the scanner on the kinetic curve shapes.

Although in this study, kinetic curves were produced using ROIs covering the entire lesion, ROI placement for clinical exams typically covers only a small portion of the lesion and is generally a subjective practice. Using the high spatial resolution x-ray measurements of the contrast agent distribution in the lesion, studies examining the effect of differences in ROI placement on kinetic curve estimation can also be performed. Although the mechanism for contrast distribution in the phantom lesion is not the same as that for patient lesions, this analysis can explore errors incurred in kinetic curve estimation due to partial volume effects. In addition, while we attempted to produce a homogeneous kinetic curve throughout the lesion in the current study, differences in kinetic curve shape could be imposed by varying the fluid flow rate or modifying the inlet and outlet configurations of the lesion mold. In this case, the kinetic curve shape would vary within the lesion and the effect of ROI placement on quantification of the different kinetic curve shapes could be evaluated.

In the current study, kinetic curves measured by MRI were flatter than the true curves, as measured by x-ray imaging, thus suggesting a more persistent uptake. This effect is likely due to the nonlinear relationship between MRI signal intensity and Gd concentration. Since the true benign curve already exhibits persistent uptake, the signal behavior affects the malignant curve to a greater extent, making the benign and malignant curves appear more similar than they really are. The clinical implication is that a particular choice of MRI sequence may make differentiation of benign and malignant lesions more difficult. These results point to an important application of the phantom, which is investigation of approaches to improve the matching between measured MRI curves and true kinetic curves. Some possible approaches to improve the matching between the measured MRI curves and the true curves include the use of calibration vials with known concentrations of contrast agent,^{23, 24, 25, 26, 27, 28, 29} use of a higher flip angle, or use of a lower dose of contrast agent. Since each of these approaches has advantages and disadvantages, the optimal combination of acquisition parameters must include a careful analysis that takes into account all aspects of the clinical objective.

One area for potential improvement of the current dynamic lesion phantom is modification of the interior structure of the lesion to allow a realistic AIF. In its current implementation, the kinetic curve shape of the dynamic lesion is essentially unchanged from the output of the fluid pump. Although this technique results in a good match to the kinetic curve shape, the underlying mechanisms that produce kinetic curves in patients are not well simulated. In patients, tissue perfusion between vascular and extravascular water compartments as well as intracellular and extracellular subcompartments is responsible for the shape of the kinetic curve. This process essentially converts the AIF to the kinetic curve in the tissue of interest. It is not clear what effect these differences will have on the ability of the phantom to be used for MR system evaluation. This design precludes studies examining the effect of AIF measurement on estimation of pharmacokinetic model parameters, however, the use of non-model techniques can be investigated.^{15, 30} The curve shape could also potentially be modified in the phantom to reproduce AIF-like shapes, thus making studies on estimation of the AIF itself possible, albeit independently from the estimation of the kinetic curve itself. The dynamic lesion is currently a hollow, plastic mold, however, it may be possible to include an internal porous structure to allow for both AIF and kinetic curve production at the same time. Computational fluid dynamics could be employed to investigate how properties of a porous structure impact the kinetic curves. This approach may provide better matching to tissue perfusion processes as well. A related issue is the fact that the walls of the lesion mold do not produce MR signal and, therefore, can produce a small signal void surrounding the phantom lesion. A potential method for minimizing this effect would be to investigate other methods of plastic fabrication that could produce thinner walls. While this approach could minimize the effect, it will never eliminate it. Another method may be to use a gel to form the lesion mold, however, the manufacturing process for constructing such a mold would need to be developed and additional issues might arise from diffusion of the contrast agent solution through the lesion walls and into the surrounding materials.

A point to consider when using the phantom is that proper operation of the fluid pump requires the use of lubricant in the fluids themselves. In the present study, we use 40% glycerol by volume as lubricant, which is recommended by the fluid pump manufacturer. Glycerol is known to affect the relaxivity of Gd-DTPA due to its viscosity. The spin-lattice relaxivity for a Gd-DTPA solution with 40% glycerol is approximately three times faster than that of a purely aqueous solution.²¹ This means that the relationship between MRI signal intensity and contrast concentration will be different for a phantom with Gd-DTPA in a solution of 40% glycerol as compared with a solution of water only. The viscosities of 100% water and a solution of 40% glycerol in water are approximately 1.0 and 5.0 cP at room temperature, respectively.³¹ However, the lesion microenvironment is also known to affect relaxivity³² and has viscosities that are higher than pure water, approximately 1.8–2.9 cP,³³ suggesting that a lower percentage of glycerol may be necessary to appropriately reproduce physiological viscosity. Phantoms produced with purely aqueous solutions of Gd-DTPA would have similar limitations. The reader should be aware of this issue when converting phantom MRI signal into contrast agent concentration.

It is also known that fluid flow rates can affect MRI signal intensity.¹¹ In the current phantom, the total flow rate is 1.0 ml∕s, which corresponds to a linear flow rate of approximately 16 cm∕s in each of the two inlet tubes, 32 cm∕s in the outlet tube, and lower values in the lesion itself. A study, using ultrasound Doppler imaging to measure tumor flow velocities in breast cancer patients, found that peak tumor flow velocities were in the range of 0–49 cm∕s,³⁴ which is consistent with flow rates in our study.

Image quality of patient data (e.g., signal-to-noise ratio and temporal signal stability) will most likely be reduced as compared with that of phantom data. This is due to the use of different transmit∕receive coils for breast MR on patients, differences in geometry for patient experiments, and the absence of respiratory-related artifacts in the phantom data shown here. However, the basic image contrast and response shape should not be significantly affected by these differences.

CONCLUSION

We have developed a dynamic lesion phantom capable of reproducing physiological kinetic curves and border shapes for mass-like benign and malignant lesions. Since the phantom kinetic curves have been independently measured, this phantom is useful for the quantitative evaluation of dynamic contrast-enhanced MRI protocols. Such comparisons may help standardize clinical practice and improve diagnoses and lesion discrimination.

APPENDIX: ESTIMATED ERROR IN CONTRAST AGENT CONCENTRATION DUE TO BEAM HARDENING AND DETECTOR EFFICIENCY APPROXIMATION

To derive the spatially resolved lesion concentration from the x-ray data with the detector efficiency accurately included, we must start from the following equation:

$$I(x,y,E)=I_o(x,y,E)\exp [-\mu (x,y,E)l(x,y)],$$ (A1)

which is equivalent to Eq. 1 but has the full spatial and energy dependence explicitly included. In this equation, x and y are the spatial locations in the detector plane and E is the energy. Now, the number of detected photons can be described as

$$N(x,y)=\sum _E\gamma \hspace{1em}E\hspace{1em}{\eta }_{\mathit{ph}}I(x,y,E)[1-\exp (-{\mu }_{\mathit{csi}}(E)t_{\mathit{csi}})],$$ (A2)

where γ is the number of optical photons generated in the CsI crystal per incoming x-ray energy, η_ph is the efficiency of the optical detector, μ_csi(E) is the x-ray linear attenuation coefficient of the CsI crystal, and t_csi is the thickness of the CsI crystal. If we express I(x,y,E) as

$$I(x,y,E)=I(x,y)S(E),$$ (A3)

where I(x,y) is the total number of x-ray photons incident on the detector at a given spatial location and S(E) is the percentage of x-rays at any given energy, then, we can rewrite Eq. A2 as

$$\begin{array}{c}\multicolumn{1}{c}{N(x,y)=\hspace{1em}\hspace{1em}\gamma \hspace{1em}{\eta }_{\mathit{ph}}\hspace{1em}I(x,y)\sum _E\mathit{ES}(E)[1-\exp (-{\mu }_{\mathit{csi}}(E)t_{\mathit{csi}})]}\end{array}$$ (A4)

$$\begin{array}{c}{\displaystyle \sum _{E}ES(E)[1-\exp (-{\mu }_{csi}(E)t_{csi})]}\\ \equiv \gamma {\eta }_{ph}I(x,y)A.\end{array}$$ (A5)

We can assume that the quantities γ and η_ph are constant with contrast agent concentration in the lesion mold, however, both I(x,y) and A will change with the contrast agent concentration. Now, let us examine these two contributions in more detail to understand their dependence on contrast agent concentration. I(x,y) is equal to

$$I(x,y)=I_o(x,y)\exp [-\mu (x,y)l(x,y)].$$ (A6)

Following from Sec. 2B2, if we consider the object to consist of three materials (a, b, c), we find that

$$\mathit{ln}\frac{I_2(x,y)}{I_1(x,y)}=l_{\mathrm{mold}}(x,y)f_{c2}(x,y)[{\mu }_b(x,y)-{\mu }_c(x,y)].$$ (A7)

Now, we can examine how A of Eq. A5 depends on the concentration of the contrast agent. The quantity S(E) depends on contrast agent concentration since the amount of contrast agent present in the lesion will modify the spectral signature of the x-ray beam. The spectrum of x-rays entering the lesion mold was calculated using a program called SpekCalc³⁵ for the x-ray source used in the experimental setup. This spectrum was modified using the x-ray attenuation coefficients in the NIST x-ray mass attenuation coefficients database³⁶ to calculate spectra of the x-ray beam exiting the lesion mold for different concentrations of contrast agent. The effect of beam hardening due to the contrast agent is included in this step. The quantity A was calculated from those spectra and a linear fit was applied to determine the following relationship:

$$A(f_{c2})=a_0+a_1\hspace{1em}{f}_{c2},$$ (A8)

where a₀ = 23.6139 and a₁ = 0.00276. Now, combining Eqs. A5, A7, A8, we find

$$\mathit{ln}\frac{N_2}{N_1}=[l_{\mathrm{mold}}{f}_{c2}[{\mu }_b-{\mu }_c]]+\mathit{ln}\left(\frac{a_0+a_1{f}_{c2}}{a_0}\right).$$ (A9)

The second term on the right-hand side of this equation has been added by not assuming that the detector efficiency is constant with contrast agent concentration. If we estimate f_c2 from N₂∕N₂N₁N₁ using Eqs. 4 and (A9) we find that the maximum error in the estimated f_c2 is 5 × 10⁻⁵, where values of f_c2 can range from 0 to 1. Therefore, the approximate model as described in Sec. 2B2 was used for all further analyses.