One-dimensional deterministic transport in neurons measured by dispersion-relation phase spectroscopy

Abstract

We studied the active transport of intracellular components along neuron processes with a new method developed in our laboratory, dispersion-relation phase spectroscopy. This method is able to quantitatively map spatially the heterogeneous dynamics of the concentration field of the cargos at submicron resolution without the need for tracking individual components. The results in terms of density correlation function reveal that the decay rate is linear in wavenumber, which is consistent with a narrow Lorentzian distribution of cargo velocity.

2. 1. Introduction

Cells rely on their ability to actively transport macromolecules and even organelles, since the passive diffusive transport of such low mobility objects would simply be too slow. This directed transport of intracellular components is particularly apparent during cell division, but is known to occur during all phases of the cell cycle [1]. The necessity of active transport is especially acute where intracellular cargos need to be carried over long distances, as in the case of the transport of intracellular vesicles and other large objects up and down the axonal and dendritic processes of neurons. In such narrow and elongated structures, the spatial distribution of these cellular transport highways is particularly simple: intracellular traffic is directed along an essentially one-dimensional, tortuous path in a three dimensional space. This bidirectional (i.e. to and from the cell’s soma) transport is known to be mediated by some combination of thermal diffusion and active stochastic transport driven by molecular motors (e.g. kinesin and dynein) [2–4], but these transport phenomena could be better understood through quantitative analysis. The reduction of complex transport networks commonly found in cell bodies to a one-dimension system provides an opportunity for refining experimental techniques for transport measurement and for theoretical modeling.

Using single molecule tracking, precise measurements of individual cargos that are transported by molecular motors have been made previously, see e.g. [5]. In addition, the motion of externally driven particles and the observation of their fluctuating position have been successfully used to monitor the viscoelastic properties of living cells [6, 7] and the “active”, or molecular motor driven, strain fluctuations and cargo transport [8–10] in cytoskeletal networks. The fluctuations of one- and two-dimensional objects (e.g. filaments [1] and membranes [11]) have also been studied to measure the elastic properties and motor activity in living cells. In this article we examine a complementary technique that does not require the tracking of individual particles and that investigates more globally the spatial and temporal nature of cargo transport over tens of microns and thousands of seconds. While we do not resolve the motion of individual cargos, we can quantitatively and spatially map the heterogeneous dynamics of the concentration field of the cargos with submicron resolution. Our method relies on quantifying interferometricaly the path-length map produced by cells [12].

Quantifying cell-induced shifts in the optical path-lengths permits nanometer scale measurements of structures and motions in a non-contact, non-invasive manner [13]. Thus, quantitative phase imaging (QPI) has recently become an active field of study and various experimental approaches have been proposed [14–23]. We have shown that the knowledge of the amplitude and phase associated with the image plane is equivalent to extremely sensitive elastic and quasi-elastic light scattering measurements [24–26]. This new approach, represents the spatial equivalent of Fourier transform spectroscopy and is, thus, referred to as Fourier transform light scattering (FTLS). Recently, FTLS proved sensitive enough to quantify actin dynamics in unlabeled live cells [27].

Despite all these advances, the range of QPI applications in cellular biophysics has been largely limited to red blood cell imaging [11, 28–30] or assessment of global cell parameters such as dry mass [15, 31], average refractive index [32], and statistical parameters of tissue slices [25, 33]. This limitation is mainly due to the speckle generated by the high temporal coherence of the light used (typically lasers), which averages out the morphological details. Thus the contrast in QPI images has never matched that exhibited in white light techniques such as phase contrast and Nomarski.

Recently we developed SLIM (Spatial Light Interference Microscopy), a novel, highly sensitive QPI method, which promises to enable unprecedented structure and dynamics studies in biology and beyond [34]. SLIM reveals the intrinsic contrast of transparent samples like phase contrast microscopy [35], while rendering quantitative phase information, like holography [36]. Taken together, SLIM’s features advance the field of quantitative phase imaging by several accounts: i) provides speckle-free images, which allows for spatially sensitive optical path-length measurement (0.3 nm); ii) uses common path interferometry, which enables temporally sensitive optical path-length measurement (0.03nm); iii) renders 3D tomographic images of transparent structures; iv) due to the broad band illumination, SLIM grants immediate potential for spectroscopic (i.e. phase dispersion) imaging; v) is likely to make a broad impact by implementation with existing phase contrast microscopes; vi) and inherently multiplexes with fluorescence imaging for multimodal, in-depth biological studies.

The remainder of this article is organized as follows: In section 2 we describe SLIM in more detail, focusing on its application to one-dimensional transport in neurites in section 3. In section 4 we discuss our analysis of the data in terms of simple advection diffusion models. We present the results of that analysis in section 5. Finally, we conclude with a discussion of the results and our interpretation thereof in section 6.

3. Spatial Light Interference Microscopy

SLIM is described in more detail elsewhere [34]. In short, it is implemented as an extension to an existing phase contrast microscope that makes the instrument capable of quantifying phase shifts across the field of view. Both SLIM and phase contrast microscopy exploits the concept of imaging as an interference phenomenon, which has been recognized more than a century ago by Abbe in the context of microscopy: “The microscope image is the interference effect of a diffraction phenomenon” [37]. Describing an image as a (complicated) interferogram later set the basis for Gabor’s development of holography [36].

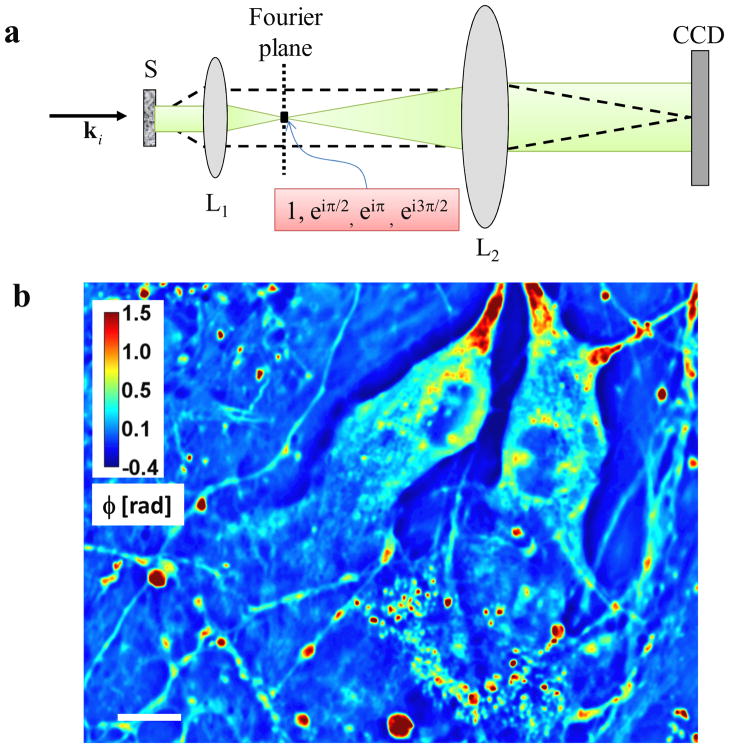
Unlike the traditional phase contrast microscope, where a phase ring with a fixed phase shift of π/2 is introduced at the back focal plane of the phase contrast objective [37], in SLIM we map the back focal plane onto a phase-only spatial light modulator that introduces additional phase delays of 0, π/2, π, 3π/2, as shown in Fig. 1a. The Fourier lenses L2 and L1 form a 4f system, such that the spatially modulated image of the sample is recorded by the CCD. The phase shift distribution associated with the object, φ(r), can thus be retrieved from a combination of 4 phase shifted intensity images,

Figure 1.

a) Microscope as a scattering instrument: dash line, scattered field; green, unscattered field; L₁, L₂ lenses; CCD, charged coupled device; k_i wave vector associated with the incident plane wave. c) Quantitative phase images of live hippocampal neurons in culture. The objective was 40×, 0.65NA for b. Color bar indicates phase in radians. Scale bar: 10 μm.

$$\phi (\mathbf{r})=arg\left[\frac{\beta (\mathbf{r})sin[\mathrm{\Delta }\phi (\mathbf{r})]}{1+\beta (\mathbf{r})cos[\mathrm{\Delta }\phi (\mathbf{r})]}\right].$$ (1)

In Eq. 1, β(r) = |U₁(r)|/|U₀| is ration between the amplitudes of the scattered (U₁) and unscattered (U₂) field; Δφ is the phase difference between the scattered and unscattered light, defined as

$$\mathrm{\Delta }\phi (\mathbf{r})=arg\left[\frac{I(\mathbf{r};3\pi /2)-I(\mathbf{r};\pi /2)}{I(\mathbf{r};0)-I(\mathbf{r};\pi )}\right],$$ (2)

where I (r;δ) is the intensity image associated with each of phase shift δ. Equations 1–2 show how the quantitative phase image is retrieved via 4 successive intensity images measured for each phase shift.

Compared to existing methods for quantitative phase imaging, SLIM benefits from a number of features, such as spatial sensitivity (0.3 nm) and temporal sensitivity (0.03 nm) in measuring optical path-lengths [34]. Since a minimal modification is brought to the existing phase contrast microscope, SLIM can also overlay with fluorescence imaging at the same time and render the high quality phase images as one channel for the multimodal imaging.

The ability of SLIM to render quantitative phase images of live, unlabeled cells is shown in Fig. 1b. Due to the white light illumination, which alleviates the detrimental effects of speckle, SLIM reveals the structure of the cell in great detail. The measured pathlength fluctuations report on the dry mass transport within the cell [31]. Since most neuronal processes exhibit microtubule-mediate transport along their elongated structures, we can assume 1D dry mass density fluctuations, i.e., mass transport along the neurite, ρ (s) ∝ Δn(s), with $s=\sqrt{x^2+y^2}$. From the time-lapse data, the microtubule-mediated transport along these neurites can be observed very clearly. However, the quantitative analysis of mass transport in these 1D structures is difficult due to their nonlinear shape. Therefore, first we numerically processed the images to “straighten” the dendrites, as described in the following section.

4. Image processing for studying 1D transport

For image processing, we used ImageJ, a Java-based program developed at the National Institutes of Health [38]. This platform allows the implementation of a plugin, referred to as NeuronJ, which was originally developed by Meijering et al. to numerically trace neurites in fluorescence images [39]. We used this algorithm for SLIM images to delineate and segment neurites of arbitrary trajectories. Further, we used a cubic-spline interpolation method to straighten the neurites from a 2D path, $s=\sqrt{x^2+y^2}$, to a 1D trajectory. This computational tool was developed by Kocsis et al. in the context of electron microscopy (for more details, see Ref. [39]). Figures 2–3 illustrate how the pathlength information along individual neurites is extracted and represented along single lines. This numerical procedure was repeated for all the frames in the time-resolved data. The resulting x-t phase images were analyzed in terms of the dispersion relation, as detailed below.

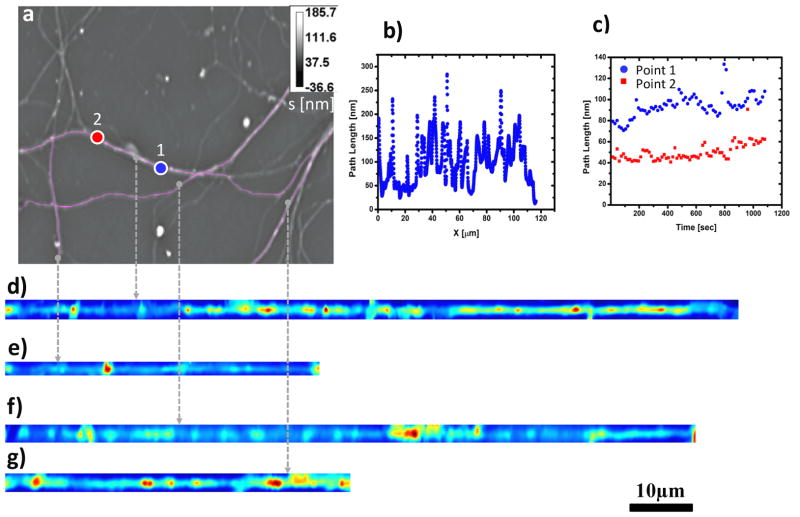
Figure 2.

a) Phase image of neuron at 40X with frame rate of about 15sec/frame to determine mass transport in neurites labeled with a pink line. b) Path length static distribution along an individual neurite(d). c) Path length dynamic fluctuations over time at two locations (labeled blue (point1) and red (point2)) of a neurite (d); d–g) Neurites of image (a) were traced and straightened with Image J plugins - Neuron J and Straighten.

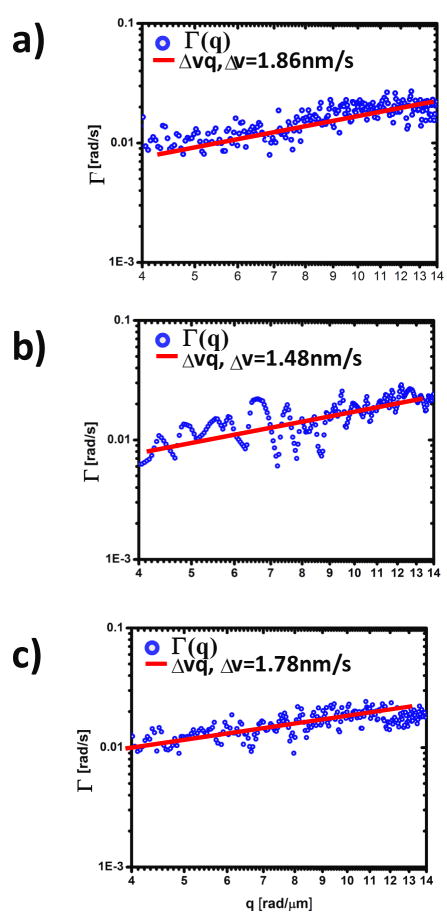
Figure 3.

a–c) Dispersion relation curves(blue) for straightened neurites d–f) of figure 2. Solid lines indicate linear fit. The fit parameter, Δv, represents the bandwidth of directed motion speed distribution.

5. Dispersion-relation Phase Spectroscopy (DPS)

The data from the phase images of many neurities are combined to compute the two-point correlation function of the mass density fluctuations ρ(x,t) (assumed to be proportional to the fluctuations in the local index of refraction) in them:

$$g(x,\tau )={\langle \rho (x^{\prime }+x,t+\tau )\rho (x^{\prime },t)\rangle }_{x^{\prime },t},$$ [3]

where the angled brackets here denote a spatial and temporal average. The observed temporal decay of this correlation function allows us to interpret the experimental data in terms of the stochastic dynamics of mass transport in the system. Fourier transforming the data

$$\stackrel{\sim }{g}(q,\tau )=\int dxg(x,\tau )e^{-\mathit{iqx}},$$ [4]

we find that the decay of g˜(q,τ) is well fit by a single exponential so that we can determine the q-dependence of that rate constant λ(q), characterizing stochastic dynamics on length scales of ℓ = 2π/q. Representative examples of these extracted decay rates are shown in Fig. 3 as a function of wavenumber q.

The decay of correlations reflects the net effect of the motion of material having various indices of refraction and velocities. We cannot distinguish a priori the independent contributions to the signal coming from various equilibrium (e.g. diffusion) and nonequilibrium processes such as the molecular-motor-driven motion of vesicles or the dynamics of polymerization and depolymerization of e.g. microtubules. Examining the data – see Fig. 2(d–g) – one notes that the observable dynamic heterogeneities appear to be localized or point-like objects, consistent with vesicles or groups of vesicles moving within the neurites. For brevity we refer to mass transport dynamics generating the decay of correlations as “vesicle motion” hereafter, although this cannot be concluded from the phase images alone. Independent of the ultimate identification of these mobile structures, we propose to characterize their dynamics in terms of an advection diffusion model in one dimension

$$D{\nabla }^2\rho (x,t)-\text{v}\nabla \rho (x,t)-\frac{\partial }{\partial t}\rho (x,t)=0$$ [5]

describing the dynamics of the mass density field in terms of the combination of diffusion with collective diffusion constant D and advection or active transport with speed v. We note that the effective diffusion constant is not expected to be coincide with the equilibrium one as active stochastic active transport processes contribute to the effective diffusion of mass density in the system. We then assume that the observed decay of correlations results from the incoherent motion of many compact bodies having a distribution of advection speeds P(v). We discuss the suitability of these assumptions below.

There is a long history of studying transport in one-dimensional (1d) or nearly (to be defined below) 1d structures, which has implications for any analysis of mass transport in neurites. The long length scale properties of 1d transport is strongly influenced by two features. First the effect of steric interactions between the moving elements can be significant, an effect commonly encountered in traffic jams [40]. Alexander and Pincus showed that the non-driven or equilibrium dynamics particles on a 1d track is actually subdiffusive, due to such steric effects [41]. The dynamics of the transport system of current interest is, however, expected to be dominated by the non-equilibrium advective effects of molecular motors at long length scales. Two classes of models have been studied that generate such steady-state currents, i.e. net mass transport that are distinguished by how they break the break the left/right symmetry of the problem in order to generated such currents. In the first class the symmetry breaking term is introduced via boundary conditions by attaching the 1d track to a particle source and sink on opposite sides, as done in, e.g., Ref [52]. In the second class one postulates a nonzero mean force acting on the particles. We expect this latter class of models to be appropriate for system of current interest since it is known that molecular motors actively transport cargos in fixed directions relative to polarized tracks within neurites [40, 42]. More generally, both inherently symmetric models driven by boundary conditions, known as symmetric exclusion processes (SEP), and symmetry breaking systems or asymmetric exclusion processes (ASEP) have been explored in a variety of contexts including models of proton transfer in water channels [43], mRNA translation [44], in addition to the problem under consideration, the motion of cargos driven by molecular motors along microtubules [40, 42, 45]. The more idealized system of perfectly unidirectional stochastic motion (i.e. no backwards steps allowed) motion, known as totally asymmetric exclusion processes (TASEP) has also generated intense interest in part from its role as a tractable model system with which to explore nontrivial non-equilibrium steady-states [46].

Our approach to the dynamics is in the spirit of various hydrodynamic approximations to the ASEP models used to treat the long wavelength and low frequency dynamics of such systems. These models, often including binding/unbinding or Langmuir kinetics in addition to the 1d motion, result in complex dynamics for the particle density field [47–49]. These dynamics can be described by a Burgers equation for the density field, which is well-known to exhibit moving shock fronts [47] or rapid jumps in particle density. Of course, transport in the neurite takes place along a bundle of 1d tracks with driven transport in both directions. Such generalizations having multiple tracks [50, 51] have been explored for both ASEP [52–54] and SEP systems.

Our analysis of the dynamics as the sum of a variety of independent advection/diffusion processes neglects large correlated motions resulting from the excluded volume interaction. We believe that this linearized model is a reasonable starting point for data analysis for two reasons. There is evidence that multiple tracks or allowing for slippage of cargos past each other (i.e. “nearly 1d models”) minimizes the role of large correlated motions [Chou 1999]. In the presence of such strong interactions, however, we expect the collective excitations of the particle density (e.g. Burgers shocks) to move roughly independently so that even in the case of strong correlations in the density of moving particles, the index of refraction changes, to which we are sensitive, should reflect the dynamics of weakly interacting collective phenomena when viewed at long length scales.

Returning to our advection diffusion model, we determine from Eq. 5 the temporal decay of the autocorrelation function of the mass density g˜ (defined by Eqs. [3,4]). It is straightforward to show that at wavenumber q, this function takes the form

$$\stackrel{\sim }{g}(q,\tau )=g_0{e}^{[\mathit{iqv}-{Dq}^2]\tau }.$$ [6]

Equation 6 relates the measured temporal autocorrelation function to the diffusion coefficient, D, and advection velocity, v, of the matter in the system. The experimental data, however, reflects the net effect of the motion of many vesicles, each having its own local transport velocity depending on e.g. the size of the vesicle and number of molecular motors attached to it. The observed autocorrelation function then should be the sum or average over a broad distribution of advection velocities P(v). The advection-velocity-averaged autocorrelation function is proportional to the Fourier transform of the advection velocity distribution

$${[\stackrel{\sim }{g}(q,\tau )]}_P=g_0{e}^{-{Dq}^2\tau }\int \mathit{dvP}(v)e^{\mathit{ivq}\tau },$$ [7]

where the square brackets [•]_P denote an average over the distribution of advection velocities P(v). This distribution remains to be determined. The integral in Eq. 7 is the moment generating function of P(v) with iqτ as the independent variable. Thus the natural logarithm of Eq. 7,

$$ln({[\stackrel{\sim }{g}(q,\tau )]}_P)=ln{g}_0-\tau \left\{{Dq}^2-\frac{1}{\tau }K(iq\tau )\right\},$$ [8]

can be written in terms of the cumulant generating function K(x) = ln ∫dvP(v)e^ixv. For any distribution having a finite second moment we find from Eq.8 that

$$ln({[\stackrel{\sim }{g}(q,\tau )]}_P)=ln{g}_0-\tau {Dq}^2-iq\tau \langle v\rangle -\frac{1}{2}{q}^2{\tau }^2\left[\langle v^2\rangle -{\langle v\rangle }^2\right]+\cdots ,$$ [9]

where the higher order terms are proportional to the product of the n^th cumulant of the advection velocity distribution and (qτ)ⁿ. Examining Eq. 9 we note that the dominant terms controlling the time evolution of the correlation function at small wavenumber consist of an oscillatory term linear in q and proportional to the mean advection velocity plus a term quadratic in q that depends on a combination the diffusion constant D and the variance of the advection velocity distribution. Comparing this result to our data, we observe two things. First this result is not consistent with the observed decay rate that is linear in wavenumber q and does not exhibit oscillations. Second we do not observe a term proportional to τ². We conclude the mean velocity must be sufficiently small that the oscillatory contribution to the correlation function is a frequencies so low as to be not observable over the time of observation. This is not surprising in that we expect to observe the net effect of mass transport along both directions in each neurite. Such bi-directional transport is in itself not surprising. Since there is little or no net transport of mass down these structures over the period of observation, the observed mean velocity should vanish. Moreover, we note that advection velocity distribution must be sufficiently broad as to have a divergent second moment.

Based on this analysis we attempt to fit the data by choosing a Lorentzian distribution with width Δv and small but nonzero mean 〈v〉_v ≠ 0. This leads, by direct integration of Eq.7, to a linear dependence of the decay rate on wavenumber

$${[\stackrel{\sim }{g}(q,\tau )]}_P=e^{-{Dq}^2\tau }{e}^{i\langle v\rangle q\tau -\mathrm{\Delta }v\mid q\tau \mid }.$$ [7]

Of course is not possible for the distribution of motor velocities to be truly Lorentzian since the motors’ maximal speed is finite. For kinesin motors, this maximum is know to be approximately v_max=0.8 μm/s [55]. Accordingly, we take a P(v) to be Lorentzian with a both a mean v_m and width Δv much smaller than the cutoff velocity, v_m,Δv ≪v_max:

$$P(v)=\frac{P_0}{{(v-v_m)}^2+\mathrm{\Delta }{v}^2}\mathrm{\Theta }(v_{max}-\mid v\mid )$$ [8]

where Θ(x) is the Heaviside step function and the normalization constant $P_0\approx \mathrm{\Delta }v/2arctan\left(V_{max}/\mathrm{\Delta }v\right)$ for a small mean velocity. The normalization is exact in the limit that v_m = 0. Since we expect to observe transport in both directions with essentially equal probability, we expect the mean advection speed to be significantly lower than the maximum motor speed. Of course the assumption that both the width and mean of the advection velocity distribution are small compared to the maximum velocity can be checked a posteriori.

Applying this cutoff Lorentzian model to the integral in Eq. 7 one can show that

$$\stackrel{\sim }{g}(q,\tau )\approx g_0{e}^{iq\tau v_m-{Dq}^2\tau }{e}^{-q\tau \mathrm{\Delta }v}\left[1+\frac{2\mathrm{\Delta }v{e}^{q\tau \mathrm{\Delta }v}cos(v_{max}q\tau )}{\pi v_{max}}+\frac{2q\tau \mathrm{\Delta }v{e}^{q\tau \mathrm{\Delta }v}}{\pi }\left(\text{Si}(v_{max}q\tau )-\frac{\pi }{2}\right)\right]$$ [9]

where Si(x) is the sine integral. The final term in the product may be neglected in the limit that $\mathrm{\Delta }v/v_{max}\ll 1$ and v_max qτ ≫1, both of which are valid for the data in question. Thus, the effect of the large velocity cutoff is subdominant and the wavenumber dependent decay rate of the autocorrelation function is a sum of linear and quadratic terms in q, representing the effect of motor-generated advection and diffusion, respectively. We may write this decay rate as

$$\mathrm{\Gamma }(q)=\mathrm{\Delta }vq+{Dq}^2.$$ [10]

This relationship between the decay rate λ and its wavenumber q represents the dispersion relationship associated with intracellular transport and provides insight into the diffusion coefficient and velocity distribution. We refer to this method as dispersion-relation phase spectroscopy (DPS).

6. Results

We applied DPS to various neuronal structures in different cultures and over a broad range of temporal and spatial scales. Figure 2 summarizes the results obtained by imaging a field of neurites for 18 minutes at a rate of 1 frame per 15 seconds. A quantitative phase map measured by SLIM is shown in Fig. 2a, where the grayscale bar indicates path-length in nm and the neuritic structures of interest are highlighted. Figure 2b exemplifies the pathlength fluctuation around a single neurite and indicates the highly inhomogeneous nature of the neurites structure. Further, this signal, which is, up to a constant, the mass density, ρ(x), is characterized by high signal to noise, which translates into high spatial sensitivity to density fluctuations. Temporally, the density fluctuations associated with two arbitrary points are shown in Fig. 2c. These signals show that SLIM can detect nanometer scale path-length changes, which translate into minute changes in local mass density.

We applied the algorithm described in Section 3 to numerically “straighten” the dendrites (Fig. 2d–g) such that the 1D diffusion-advection equation can be employed in a straight forward manner. For each neurite, the x-t data was Fourier transformed both spatially and temporally and the decay rate, λ(q), was retrieved. Remarkably, as shown in Fig. 3, all the λ(q) plots exhibit linear behavior, which is consistent with a signal resulting from a broad distribution of advection velocities. It is not consistent with an advection velocity distribution that has a finite second moment. We do not observe a signal consistent with diffusive transport. This is reasonable since it is known that diffusion is not an efficient mechanism for this type of long-range transport associated with neurites [56] compared to active, or motor-driven mass transport. Interestingly, we found that the bandwidth of the speed distribution for the three neurites, Δv = 1.86 nm/s, 1.48 nm/s, 1.78 nm/s are very close in value, which may indicate a universal mechanism for this directed stochastic motion.

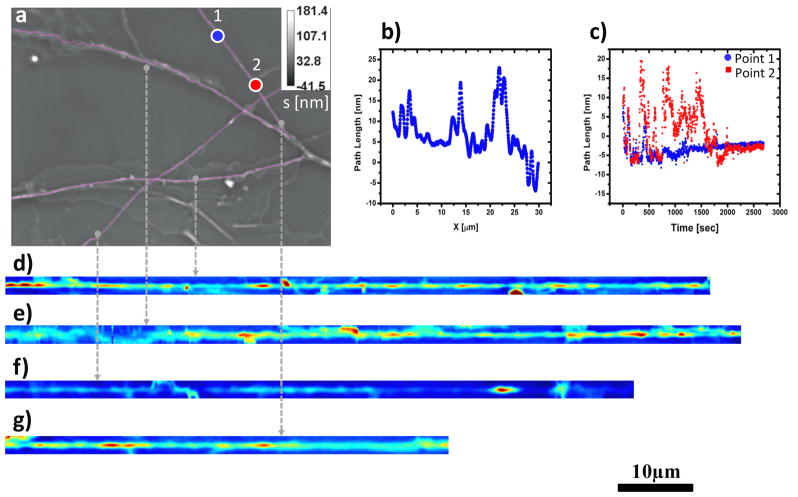
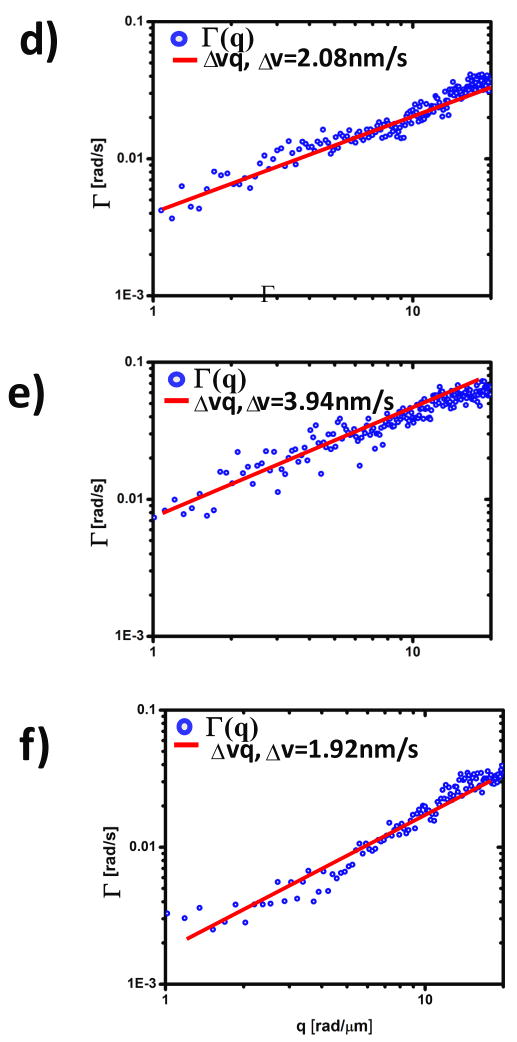
In order to confirm these findings on a different cell culture, with different imaging resolution and acquisition rates, we applied DPS to a neurite system where the acquisition rate was 7.5 times faster and the spatial resolution higher by a factor of 2 (Figure 4). The analysis procedure is analogous to that shown in Figs. 2–3. Notably, the results of these measurements at different spatio-temporal resolutions match closely those obtained before. Thus, for all dendrites the results indicate deterministic transport, as shown in Fig. 5. The speed bandwidth values, Δv =2.08 nm/s, 3.94 nm/s, 1.92 nm/s, are somewhat higher that in the previous case, but still in the same range. This similarity in the measured values suggests a commonality of transport mechanisms in the dendritic arbor of neurons.

Figure 4.

a) Phase image of mass transport in neurites of hippocampal neurons. The image was acquired at 63X with a frame rate of 2 sec/frame, the pink lines represent the data subsets analyzed in b–g. b) Path length static distribution along an individual neurite(g). c) Path length dynamic fluctuations over time at two locations (labeled blue (point1) and red (point2)) of a neurite (d); d–g) Neurite of image (a) were traced and straightened with Image J plugins - Neuron J and Straighten.

Figure 5.

a–c) Dispersion relation curves (circles) for straightened dendrites d–f) of figure 4. Note the broad q-coverage due to the high NA objective. Solid lines indicate linear fit. The fit parameter, Δv, represents the bandwidth of directed motion speed distribution.

The mean advection velocity extracted from the data is consistent with zero. From the resolution limit (≈1μm) and observation time ( ≈1000s), we may set an upper limit on the net drift velocity of 1 nm/s. We do not observe net mass transport down the neurites. Finally, we note that the assumptions made in the use of the cutoff Lorentzian appear to be justified.

7. Summary and discussion

We have found that the autocorrelation function in the neurites is inconsistent with purely passive diffusive motion of cargos, but can be interpreted using a simple model of advective transport in which individual cargos are moved in both directions and with a Lorentzian range of speeds having nearly zero mean (due to equal rates of mass transport towards and away from the cell’s soma) and a fairly narrow distribution about that vanishing mean, at least compared to the maximum velocity associated with active motors. This result is puzzling in that given the extracted distribution of advection velocities, one cannot expect to observe cargos transported at speeds comparable to the reported maximum motor velocities. We may speculate as the cause of the absence of fast movers. Assuming that the observed mass transport reflects the motion of individual motors, there are two possible interpretations of this result. First, the motors may, in fact, be operating near the stall force, where mean velocities are low and velocity fluctuations become significant. This proposed scenario seems to be physiologically inefficient and therefore unlikely. Alternatively, the motors are operating at forces where cargo detachment becomes frequent. If the cargos detach from the motors sufficiently frequently in the crowded viscoelastic environment of the neurites, then although the motors are still moving rapidly, the fraction of the time in which the cargos are being actively transported is small and consequently their observed advection speeds may be much smaller than that of the motors. Finally, it is possible that the mass transport to which we are sensitive reflect slow collective motions of many cargos, e.g. shock fronts in the density field, that may not move with the same velocity as the underlying motor-driven cargos. This appears to be the most reasonable explanation since it is known that the shock fronts can be significantly slower than the transport speeds of the individual cargos [57]. Clearly, simultaneous tracking of the cargos, motors, and mass density is necessary resolve this issue. Similarly, theoretical advances are necessary to better understand the collective behavior of the mass density field in multi-track driven systems with steric interactions. We note that our results, i.e. the linear in wavenumber decay rate of the autocorrelation function is not consistent with a velocity distribution that decays sufficiently rapidly at large velocities to have a finite second moment. The proposed Lorentzian, albeit with a narrow width compared to the maximum motor velocity, reflects a broad probability distribution.