Abstract
Although the principles of optimization of HPLC have a long history starting with the work of Giddings in the 1960s, and continuing with work by Knox and Guiochon extending into the 1990s we continue to see statements that flatly contradict theory. A prominent example is the notion that optimum ‘performance’, as measured by plate count, is always obtained by operating conventional length columns (e.g., 5 to 15 cm) at eluent velocities corresponding to the minimum plate height in the van Deemter curve. In the last decade the introduction of ‘Poppe plots’ by Poppe and ‘kinetic plots’ by Desmet and others has simplified the selection of ‘optimum’ conditions, but it is evident that many workers are not entirely comfortable with this framework. Here we derive a set of simple, yet accurate equations that allow rapid calculation of the column length and eluent velocity that will give either the maximum plate count in a given time, or a given plate count in the shortest time. Equations are developed for the optimum column length, eluent velocity and thus plate count for both the case when particle size is pre-selected, and when particle size is optimized along with eluent velocity and column length. Although both of these situations have been previously considered the implications of the resulting equations have not been previously made explicit. Lack of full understanding of the consequences of the differences between these two cases is very important and responsible for many erroneous conclusions. The simple closed-form equations that result from this work complement the graphical, iterative approaches of Poppe and Desmet; the resulting compact framework allows practitioners to rapidly and effectively find the operating parameters needed to achieve a specific separation goal in the shortest time, and to compare emerging technologies (e.g., high pressure, high temperature, and different particle types) in terms of their impact on achievable plate counts and speeds in HPLC. A web-based calculator based on the equations presented here is now available (http://homepages.gac.edu/~dstoll/calculators/optimize.html).
“The fastest possible analysis with any column design will be achieved with a column operated at the maximum possible pressure drop and having a length as to give the plate number necessary to perform the desired separation.”1
Georges Guiochon, 1980
Introduction
Clearly, over the past few years there has been a robust renaissance of interest in improving the speed and plate count of HPLC. Various approaches have been examined including the use of very small totally non-porous particles2, higher pressures3, higher temperatures4, monolithic columns5, and very small superficially porous particles6. There is now becoming evident a number of discrepancies between theory and practice of chromatography, especially concerning the process of optimizing performance7–9. A prominent example is the practice of basing the optimization of the system, that is the instrument and the column, on equations founded on the conditions which optimize only the HETP of a specific column10. It is absolutely true as stated by Plumb et al. that “The highest performance of an HPLC column is reached at the minimum of the plate-height versus velocity curve.” The specific language “an HPLC column” is particularly important here; clearly the authors are talking of a specific column. Below we will refer to the conditions that optimize the HETP of a given column as the “van Deemter optimum” conditions. The statement above referring to the performance of an HPLC column is limited in several ways. It should be clear that this language implies that a column of specific length packed with particles of a specific diameter is being optimized, rather than the system as a whole, which requires simultaneous optimization of column length, eluent velocity, particle size, and maximum system pressure. It is also tacitly assumed that the pressure needed to achieve the performance (plate count) corresponding to the van Deemter optimum conditions can be delivered by the instrument. Further we must emphasize that it is erroneous to draw any truly general conclusions concerning column design and use such as the relative effect of operating pressure, temperature, particle size etc. on equations derived on the basis of the van Deemter optimum conditions.
In their authoritative contributions to the theory of optimization in HPLC Knox11, and Guiochon12 using the well known method of LaGrangian multipliers, showed that the fastest production of any desired plate count occurs at the velocity corresponding to the van Deemter optimum provided that the particle diameter and column length are also simultaneously optimized so as to work at a pressure corresponding to the maximum possible delivered by the instrument. As shown below we reach the same conclusion by a simpler procedure.
Although implicit in Guiochon’s review, and clearly at the heart of Poppe’s seminal analysis13 of speed in HPLC, we emphasize that neither the fastest separations nor the highest plate counts for the system are obtained by working at the van Deemter optimum when the particle size is pre-selected. Henceforth we will refer to the velocity and column length that produce the highest plate count at a given analysis time and system pressure as the “Poppe optimum conditions”. The Poppe optimum velocity and the van Deemter optimum velocity are equal only if one uses a column packed with the particles of the optimum size and having the optimum length as described in Guiochon’s analysis (see below). One of the major thrusts of this work is to make explicit the important distinction between these two ways to optimize performance. They certainly are not equivalent, and the lack of a clear distinction between them is in our opinion a source of considerable confusion in the literature on optimization of performance and speed in HPLC.
Another belief which is widely held, but also is not generally correct, is the belief that better separations (more plates in a given time or less time for a given number of plates) are always obtained with the smallest available particles. The basic issue is: under practically useful conditions, how does one optimize plate count and speed to solve real problems. We believe that most real problems fall into two classes:
Given a desired resolution (and therefore a particular plate count for the resolution of a critical pair of target analytes), how does one generate the minimum requisite plate count in the shortest possible time?
Given a specified amount of time for a separation (e.g., high-throughput applications, or separations of very complex samples) how can one maximize the number of plates generated in that time, and therefore maximize the productivity of the separation (plates/time)?
The pioneering work of Giddings14, Knox11, 15, and Guiochon12 developed and refined a framework that worked well in answering these questions. In the early days of HPLC the decisions to be made during optimization were relatively simpler than they are now; typical instrument pressure limits were around 400 bar, most columns could only be operated near ambient temperature, most packing materials were fully porous (although superficially porous or pellicular phases have a long history as well16), and only few particle sizes were available. Today we are faced with many more options, with expanded instrument capabilities in terms of pressure and temperature ranges, numerous particle sizes and porosity options ranging from 1.5 to 5.0 micron and non-porous to superficially and fully porous respectively, and the rather recent introduction of commercially available monolithic columns.
Ultimately all questions about optimization are related to the compromise between efficiency (as measured by plate count) and time. More than a decade ago Poppe13 introduced the concept of plotting the ‘plate-time’ (to/N, where to is the column dead time) against the plate count (N), which elegantly captures the speed/efficiency compromise in a way that is easy to visualize. Since then, many groups17–19 have made good use of this type of plot and several derivatives of it, changing the metrics plotted on the two axes to emphasize different practical considerations with respect to optimization20. However, the approach as described by Poppe involves an iterative calculation of each point on the ‘Poppe curve’ (see Figure 3 of ref 5) for the original ‘Poppe curves’), and thus is somewhat tedious and not very accessible to practitioners who may not be as comfortable with the theory and the required calculation scheme. A recent paper by Desmet gives a brief overview of the development of the theory of optimization which spans over four decades, starting with the work of Giddings, Knox, and Guiochon20. The practical value of such plots (both the ‘Poppe’ and ‘kinetic’ types) has been demonstrated by Desmet and coworkers21, as well as several other groups18, 19, 22, 23, by showing agreement between curves predicted from theory (e.g., from a set of kinetic parameters) and curves consisting of data measured in experiments involving real columns. Desmet and coworkers have improved on the original approach of Poppe by developing a framework in which experimental plate height (H) vs. eluent velocity (u) data are transformed via simple equations and scaling factors to produce a suite of ‘kinetic plots’. Most recently, Desmet and coworkers have also included estimates of extra-column broadening in the calculation of kinetic curves, which become more and more important as particle and column technology improve, producing peaks with lower and lower volume24.
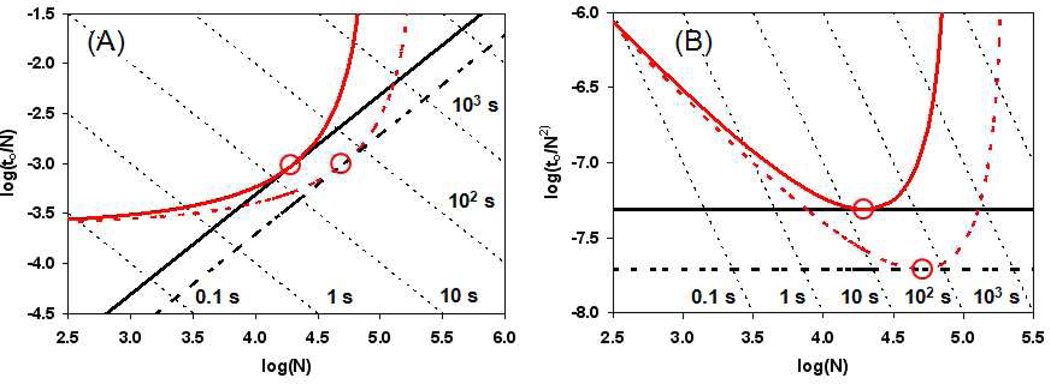
Figure 3.
Isocratic ‘Poppe curves’ for 1.8 µm particles at 400 (solid) and 1000 (dashed) bar, and the ‘Knox-Saleem lines’ for the same set of conditions. The circles indicate the points were , in which case each ‘Poppe curve’ is exactly tangent its respective ‘Knox-Saleem line’. The results are plotted in two different sets of coordinates to emphasize the advantages of each coordinate system: A) log(to/N) vs. log(N), B) log(to/N2) vs. log(N). Conditions: T = 40 °C, Φ = 500, 40% ACN (v/v), A = 1.0, B = 5, C = 0.05, Dm = 1 × 10−5 cm2/sec at 40 °C, εe = 0.38, εi = 0.30.
A major objective of the present paper is to provide an introduction to a set of simple, yet accurate equations that can be used to better understand the interplay between particle size, column length, eluent velocity, and pressure, in HPLC. Three optimization schemes are considered in the order of increasing complexity: 1) only the velocity is varied at fixed particle size and column length; 2) both the velocity and column length are varied while particle size is fixed; (3) the velocity, column length and particle size are varied concurrently to achieve the best performance, which we define as the time required to achieve a specified plate count. For each case, closed-form equations (subject to the practical constraints of time and pressure in cases 2 and 3) are derived which allow one to rapidly find the optimal conditions. These equations complement the work of Desmet et al. in that they allow rapid, yet accurate prediction of the effects of important operational parameters such as the maximum operating pressure, eluent viscosity, column permeability, and dynamic characteristics of the column (e.g., van Deemter A, B, and C terms) on performance. Surely these same effects can be predicted using the approaches of Poppe, Desmet, and others albeit after much more labor and requiring more expertise because entire curves (often many of them) and plots have to be constructed to see the effects. To the best of our knowledge, this report is the first time that the closed-form equations for the optimal conditions as well as the relationship between plate count, analysis time and pressure have been developed for the three-parameter optimization case (i.e., Case 3).
The equations resulting from the two-parameter optimization case (i.e. Case 2) allow rapid calculation of ‘Poppe curves’, and the values of the column length and eluent velocity that correspond to each point on the curve. Although we do not show them here, further manipulation of these equations should also yield other types of ‘kinetic curves’. The equations resulting from the three-parameter optimization case (i.e., Case 3) provide the values of the particle size, column length, and eluent velocity at any given analysis time which correspond to performance at the so-called ‘Knox and Saleem limit’11. Although this limit is occasionally referred to, we are unaware of any previous reports describing the complete set of equations that allows rapid calculation of the parameters that correspond to this limit. We briefly show how the equations can be manipulated to assess new technologies currently being introduced to the HPLC community; in this paper we specifically emphasize the role of the maximum operating pressure, Pmax. We do not provide an exhaustive treatment of all issues related to optimization that can be addressed, but rather the fundamental equations and a brief discussion of their derivation and interpretation. As an example of their value, we use both the two-parameter and three-parameter equations to address some of the discrepancies between the theory and practice of optimization alluded to above. Specifically, we will show that, ceteris paribus, the best one can hope for by increasing the maximum operating pressure is a first-order decrease in the analysis time with increased pressure. We also show that once the particle size is chosen, the maximum available pressure does not improve the limiting speed of analysis. Finally, we use the three-parameter equations to quickly assess the effect of increased operating pressure on the optimum particle size for very fast (1 s < to < 10 s) separations, where to is the column dead time.
Theory
Case 1) Unconstrained optimization (Only vary velocity at fixed particle size and column length)
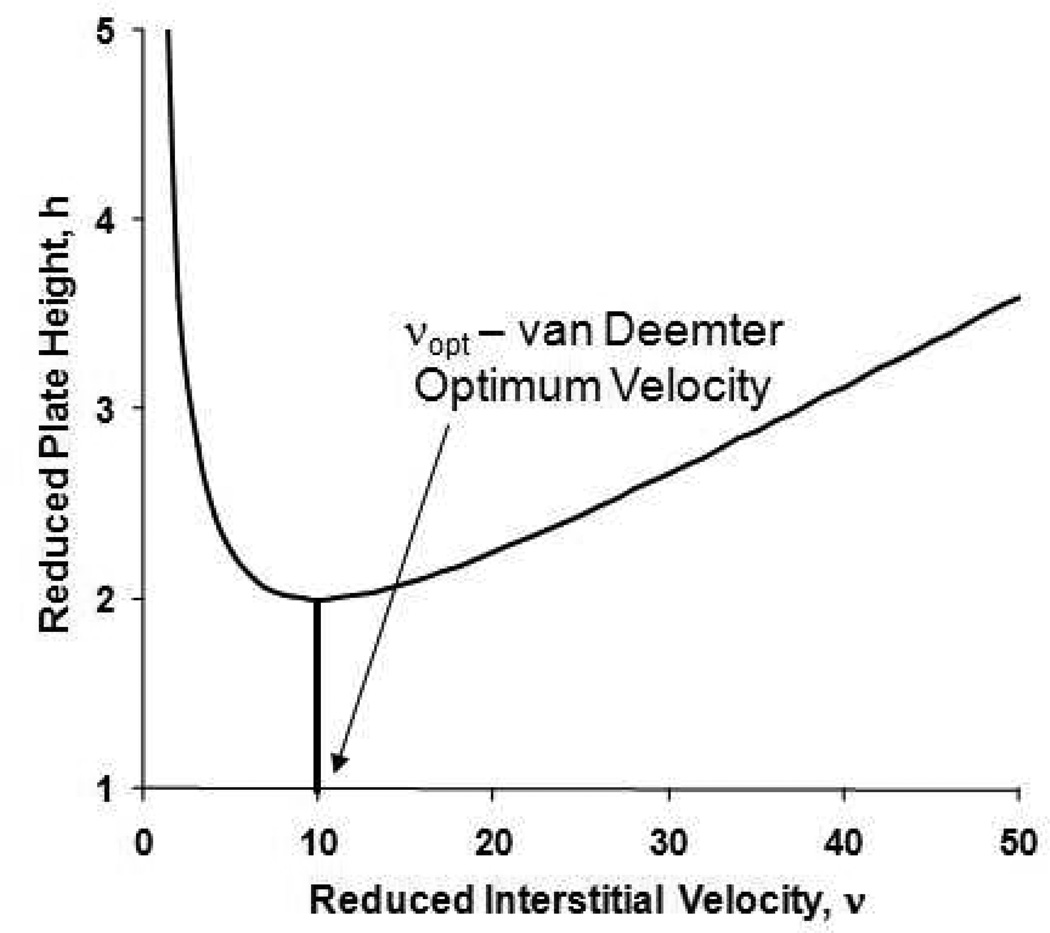
Many times, it is stated that one can optimize the performance of an HPLC column by working at the velocity that produces the minimum in the plate height10. We refer to this velocity as ue,opt (νopt in reduced coordinates); Figure 1 shows a typical van Deemter curve in reduced coordinates with νopt clearly indicated. In the immediate vicinity of such a minimum the shape of the curve is adequately approximated25 by an equation of the form:
| (1.) |
In fact, near the minimum the value of α can scarcely matter so we may as well use an equation of the van Deemter form26 and take α equal to zero for mathematical simplicity. Some trivial calculus then leads to:
| (2.) |
And
| (3.) |
The reduced velocity (ν) and reduced plate height are defined as:
| (4.) |
| (5.) |
If one were to operate a column at νopt and the corresponding value of the interstitial linear velocity (ue,opt) the velocity, plate height and plate counts would be:
| (6.) |
| (7.) |
| (8a.) |
| (8b.) |
In the above equations dp, and L represent the particle size and column length respectively while Dm is the analyte’s diffusion coefficient in the mobile phase and ue is the eluent velocity in the interstitial space27, 28. Note that following Horvath27 and Knox28 we use the interstitial velocity as the basis for the reduced velocity, rather than the chromatographic velocity (i.e. the velocity at which eluent percolates through the column).
Figure 1.
A representative flow curve in reduced coordinates; van Deemter parameters: A = 1.0, B = 5, C = 0.05.
Some believe while others merely base their conclusions on the implicit belief that the maximum possible plate count for a given particle size is always obtained at the velocity corresponding to the minimum in the plot of plate height vs. velocity (νopt, see Figure 1). It has been known for a long time that this is not so12, 13, 29. It is obvious that, in terms of practice, it might not be possible to actually operate any arbitrary column under these “optimum” conditions. For example, the chosen column length and particle size might, at the van Deemter optimum, demand a pressure above that which can be provided by the pumping system. A more important point which will be developed in more detail below is that by operating a column at ue,opt one may not be using the system at its maximum pressure capability thereby neither minimizing analysis time nor maximizing plate count.
Once one has chosen the column length and particle size it is true that the dependence of HETP on velocity, as in the van Deemter curve, controls the maximum number of plates. Under a fixed pressure constraint when maximizing N, both the column length and velocity should be treated as variables. One then sees that the dependence of N on ue is less important than the dependence of N on L. Under the condition of variable L we find that the maximum value of N is achieved by working - not at ue,opt - but by working with a very long column at a very low velocity compared to ue,opt13. It is the mistaken idea that somehow there is something special about working at ue,opt that is the source of much confusion in the optimization of plate count and speed, especially in liquid systems.
Erni30 following in the footsteps of Giddings14, Knox11 and Guiochon1, 12 cogently and succinctly summarizes two seemingly contradictory but nonetheless true ideas: “To obtain optimum N with a given pressure, a very long column with large particles and a mobile phase with a low diffusion coefficient is required. In order to obtain the optimal performance, P, (defined as dN/dto insert by us) the inverse is required: small particles and a mobile phase with a high diffusion coefficient”. These ideas have subsequently been re-iterated13, 31 using modern representations of the speed/efficiency compromise. Based on the work of Knox’s work11 it is evident that optimum performance (the maximum plate count for the column) is obtained at the minimum in Figure 1 only when the particle size, length and velocity are all simultaneously optimized; this was re-iterated by Guiochon12, and then by Poppe as well13. Consequently for an arbitrary column, that is, one which is not of the optimum length or is not packed with the optimum size particles neither the best plate count nor the highest speed will be obtained by working at the velocity corresponding to the minimum in Figure 1.
Case 2) Practically Constrained Optimization with Fixed Particle Size – ‘Two-Parameter Optimization’
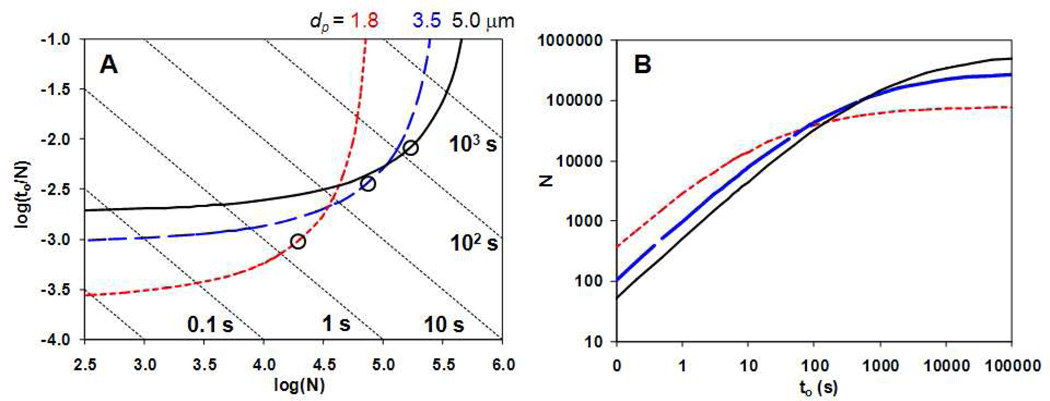
The pragmatically correct question is: for a given set of column parameters (particle diameter, temperature, solvent composition) what velocity and column length maximize the operational (achievable) plate count. This is quite a different question than the above. Guiochon12 has reviewed in great detail the various conditions under which one might want to optimize various kinds of column “performance” including optimization of analytical sensitivity or amount of solvent used. For our present purposes, let us restrict the consideration to choosing the optimum column length and velocity for a column packed with a predetermined (fixed) particle size. We set as our goal the highest plate count that can be achieved at a desired column dead time (to) and pre-determined (fixed) pressure at this particle size. This is precisely the problem solved by Poppe in his elegant paper mentioned above13. He described an iterative approach to choose the column length and velocity that maximizes the plate count for a given maximum pressure drop, and analysis time for a column filled with a pre-set particle size. Figure 2 is a series of ‘Poppe curves’ computed by us using a simple Excel program with the Solver “add-in” that reproduces Figure 3 of ref 5. Note that on each of these curves we have marked the velocity which corresponds to the van Deemter optimum velocity. For any given size particles we can improve the plate count from Nopt (obtained by working at ue,opt, see eq. 6) to Nmax (obtained at , see eq 11 below) by simultaneously lowering the velocity below ue,opt and increasing the column length to maintain the pressure drop at Pmax; this constitutes a ‘move’ up and to the right on the ‘Poppe curve’. It should be evident (see eq 10) that the product of ue with L is constant along any ‘Poppe curve’ as the pressure drop is fixed along that curve.
Figure 2.
A) Isocratic ‘Poppe plot’ for three different particle sizes. The marked points represent the conditions where the velocity is equal to that at the minimum of the van Deemter curve. It is evident that by working to the right of the van Deemter optimum one gains plates at some cost in time. Conversely by working to the left one gains speed at some cost in plates. B) Plot of N vs. to for the same three particle sizes as in (A). Conditions: T = 40 °C, Pmax = 400 bar, Φ = 500, 40% ACN (v/v), A = 1.0, B = 5.0, C = 0.05, Dm = 1 × 10−5 cm2/sec at 40 °C, εe = 0.38, εi = 0.30.
The relationship between dead time, column length and eluent percolation velocity (u) is:
| (9.) |
Here εtot and εe represents the total and interstitial porosity of the column respectively and the parameter λ = (=εe/εtot) is defined for subsequent mathematical convenience. Clearly if one requires that the “performance” meet some desired time constraint then this establishes a relationship between column length and velocity that did not exist in developing equations 6–7. This is a very important restriction that must be imposed beforehand not afterwards in defining the “optimum” plate count.
If we further require that some pressure not be exceeded we need to consider the relationship between pressure and the column variables:
| (10.) |
This equation is known as Darcy’s Law and is semi-empirical in nature. It works for incompressible, Newtonian fluids operated under laminar conditions32. Furthermore the dimensionless flow resistance parameter (Φ) is a function of the interstitial porosity. It is found that Φ is about 500 for reasonably well packed random beds33. The term η is the eluent’s viscosity. Eq 10 like eq 9 also establishes a relationship between velocity and length that was not considered when eqs 6–8 were developed. Evidently, if one pre-determines the value of dp (particle size) one is then no longer free to vary it when one chooses the velocity and column length so as to simultaneously satisfy eqs 9 and 10 as well as then choose the velocity and length to optimize the number of plates. Indeed, as soon as we decide to satisfy eqs 9 and 10 with some desired time and pressure, the column length and velocity are fully determined as we have but two eqs (i.e. eqs 9 and 10) and two unknowns (L and ue). This lack of freedom means that the plate count is also established as soon as these two conditions are imposed.
Because the equations relating velocity and length to pressure and time are linear the required values of column length and velocity are easily obtained by simple algebra:
| (11.) |
| (12.) |
And finally
| (13.) |
Note that we use and N* rather than the symbols used in eqs 6 and 8 to denote that these values are not hypothetical optima. They are real and achievable; that is, they are conditioned on the actual operational parameters including, particle size, operating pressure, analysis time and implicitly on the eluent composition and temperature through their dependence on the viscosity and diffusion coefficient. In contrast to the van Deemter optimum velocity which gives Nopt the velocity that maximizes N* at the desired time and pressure does not depend on the column’s dynamic parameters (A, B and C) as is the case in eq 6 and in fact has nothing whatever to do with equation 1. However, note the resulting plate count does depend on the column’s dynamic parameters. As stated above this problem is precisely that addressed by Poppe13.
We point out that eqs 11–13 allow the exact generation of the Poppe curves in Figure 2 without recourse to any iterative scheme. This should not have been surprising as all the equations involved are linear. That is, once one decides on dp, to and Pmax there are no degrees of freedom left and thus both L* and are fixed. Clearly once the velocity and length are fixed then so is N* and one gets exactly the same value of N* by using eqs 11–13 as by use of Poppe’s iterative method
It is evident that as t0 approaches infinity, eq 13 reduces to:
| (14.) |
This is the maximum possible plate count that can be generated at Pmax regardless of the amount of time invested17, 30, 34. Clearly depends only on the van Deemter B parameter which tells us that in the limit of maximum plate count the only important broadening process is longitudinal diffusion. As discussed by Giddings14 and Guiochon12, the larger are the particles and the smaller is the analyte diffusion coefficient the larger the number of plates that can be generated. There is clearly a first power dependence on Pmax. Thus in this limit doubling the pressure will double the plate count but that is all it will do. Eq 13 can also be rearranged to:
| (15.) |
The short analysis time limit for the plate count (denoted ) can easily be derived from equation 15. As to becomes very small it is obvious that the last term in the denominator becomes dominant resulting in the following limiting value:
| (16.) |
Eq 16 tells us that in the limit of high speed small particles and fast diffusion give better plate counts. This is in stark contrast to eq 14 for the limiting plate count at long time where just the opposite conditions apply. However, in the context of recent developments and claims for ultra high pressure chromatography we see that the high speed limiting plate count is completely independent of the maximum pressure available although the plate count definitely depends inversely on the square of the particle size. We also note that in the high speed limit the plate count is directly proportional to the dead time. Thus the more time one allows for the analysis the better is the plate count.
The limiting speed (taken here as to/N) is easily found by rearranging eq 1613:
| (17.) |
Eqs 16 and 17 make it quite clear that neither the plate count nor the speed depend on system pressure in the limit of very fast analysis which is in exact accord with the two red ‘Poppe curves’ shown in Figure 3A and the two kinetic curves shown in Figure 3B. At the very least the implication is that elevating the available system pressure does not universally provide a meaningful improvement in the speed or plate count. Given that at very long time the plate count is proportional to Pmax and at very short time the plate count is independent of Pmax we conclude that at intermediate times the plate count will depend on less than the first power of Pmax.
Case 3) Constrained Optimization with Variable Particle Size – ‘Three-Parameter Optimization’
These clearly different conclusions, that is, those based on using the van Deemter optimum velocity from eq 6 (case 1) and that based on a real velocity satisfying a time and pressure constraint (i.e., the ‘Poppe optimum’, eqs 9 and 10, case 2) can be fully rationalized. One needs to understand that in the second case both the velocity and column length were allowed to vary whereas in the first case the column length was fixed and only the velocity was optimized. In both cases the particle size was assumed to be fixed. If we impose the same conditions of time and pressure but now allow the particle size to become a variable, eqs 9 and 10 no longer suffice to define all three adjustable parameters . That is, we only have two equations to determine three variables . This is the case considered by Poppe13 and also by Antia and Horvath35 both of whom concluded that the plate count is optimized at a velocity not generally equal to the van Deemter optimum (see Fig 1). We can now impose a third constraint which is required if we want to maximize the plate count by working at a velocity at the minimum in the plate height vs. velocity curve11. Thus the fact that we can now vary the particle size allows us to use eq 2 to drive the optimization process. These three equations can be solved simultaneously to determine the best values of the particle size, column length and eluent velocity to be used at the desired maximum pressure and analysis time.
When we optimize by allowing all three variables to meet the three constraints we find the following three predictive equations:
| (18.) |
| (19.) |
| (20.) |
We note in passing that if one were to construct a Poppe plot using his approach to the maximization of N by varying all three parameters, the resulting values of velocity, length and particle size agree exactly with eqs 18–20. If these equations are used the corresponding values of hmin and νopt are given exactly by eqs 2 and 3 as in case 1 above. But this means that and ue,opt only agree if we use a column packed with the optimum size particles and one that also is of the optimum length11, 13. We note that because dp is now a variable the optimum values of velocity and column length are given by different equations from case 2 above. If one were to carry out the optimization as in case 2 but do so with dp equal to that required by equation 19 then one gets exact agreement of the two methods of optimization. While Guiochon12 developed equations for the optimum velocity and particle size for the case of 3-parameter optimization because he used the Knox and Giddings coupling equations for the plate height he did not obtain an explicit dependence of these parameters on the analysis time. Eqs 18–19 make it quite clear that the best velocity, particle size and column length all vary with the desired analysis time. It follows that the best particle size is not always the smallest but varies with the desired analysis time. We point out that the importance and novelty of eqs 18–20 is the explicit dependence on time scale. Others 11, 12, 14, 29, 30 have developed closely related eqs but did not make the temporal dependence explicit.
It is most important to note that in actual practice we never optimize column performance by simultaneously varying particle size, velocity and length. Indeed, we do not even allow column length to be continuously varied rather we chose particle sizes and column lengths that are approximately compatible with the desired plate count and analysis time and then optimize the velocity. Clearly, with a fixed particle size we must not choose a length so long that an excessive column backpressure prevents us from increasing the velocity to achieve the best value.
Based on eqs 18–20 we can compute Nmax as a function of the desired analysis time and allowable pressure.
| (21.) |
In eq 21, hmin is given exactly by eq 3, and the result is in exact accord with the previous work of Knox15, Guiochon12, 29, and Desmet17. It must be understood that in order to achieve this result all three conditions (equations 18–20) must be exactly met. That is we must be working exactly at the optimum velocity with the optimum length column and with the optimum size particles; if this is not done then we should not use these design equations.
The speed (to/N) is easily derived as well:
| (22.) |
In contrast to the two-parameter case it is clear that the plate count and speed are always improved by increasing the available system pressure. However, this result is only obtained if we can continue to decrease the particle size as required by eq 19 when to is decreased.
The black lines (with positive slope) shown in Figure 3A were generated from eq 21; we refer to these lines as ‘Knox-Saleem lines’ because each point on the line represents the ‘Knox-Saleem limit’ at that time. We also proved that the results calculated from eq 21 are numerically the same as solving the three-parameter (dp, L, ue) optimization of N at to and Pmax using an iterative approach. Note that the straight line formed is exactly tangent to each of the two parameter Poppe curves (red curves) at the optimum velocities indicated by the circled points.
Eq 21 is particularly valuable and provides very significant insights into the best possible performance. Holding N, Pmax, or to constant yields a triad of simple yet instructive relationships (eqs 23–25). First, if we hold everything else constant including plate count (N) we have:
| (23.) |
Thus it is evident that if nothing but the system pressure is changed the best one can hope for is a proportional improvement in analysis time. On the other hand if we assume a fixed pressure maximum (Pmax) and other conditions we find that:
| (24.) |
which shows that under fixed conditions (temperature, composition, pressure) plate count drops with the square root of the analysis time In isocratic chromatography resolution varies with the square root of the plate count thus it is evident that huge increases in analysis time are needed to have any significant effect on resolution.
Finally, at constant analysis time (to) we find:
| (25.) |
Thus eq 21 makes it clear that under fully optimized conditions (Case 3), the maximum plate count achievable in a given analysis time depends on the square-root of the maximum available pressure, Pmax.
This dependence is evident in Figures 3A and 3B where the two ‘Knox-Saleem lines’ at two different values of Pmax are parallel and the spacing is independent of time. However, once a particular particle size is chosen (case 2), the dependence of N* on Pmax depends on the analysis time; for the practitioner, this is an inconvenient truth. We see that at very long times the relationship between N* and Pmax tends to a first-order dependence, which is consistent with eq 14. It is critical to recognize that although this dependence is stronger than the square-root dependence that results from case 3 (eq 21 and 25), this is only because a particular particle size has been chosen, and that if the particle size is allowed to vary (increase at long times) the dependence relaxes back towards the square-root relationship.
The second area of interest is the region of analysis times where the ‘Poppe curves’ are almost tangent to the ‘Knox-Saleem lines’ at a given pressure. In this region the pre-selected 1.8 µm particle size used to calculate the ‘Poppe curves’ is close to the values that result from eq 19 for the same value of Pmax and thus the relationship between N* and Pmax is very close to the square-root dependence discussed in the preceeding paragraph. This means that when one is using the most appropriate particle size and the available pressure is doubled the plate count will only increase by 40–50%.
A third area of interesting the Poppe plot is that of very fast analyses (to < 5 s). In this region we see that both ‘Poppe curves’ in Figure 3A approach the same asymptotic limiting speed, despite the significant difference in Pmax (400 vs. 1000 bar). This behavior is in exact accord with eq 17, and emphasizes the point that once one decides to use a particular particles size, increasing Pmax has very little effect on performance for ultra-fast analyses.
Figures 3A and 3B are plots of the same data plotted in different coordinates; each plot has advantages for understanding optimization. The coordinates of to/N vs. N used in Figure 3A are the same as those used by Poppe11, 13, whereas the coordinates of to/N2 vs. N are the same as those used by Desmet36. An advantage of the Poppe-style plot in Figure 3A is that the vertical and horizontal asymptotes for the ‘Poppe curves’ are clearly evident, and these correspond to the limiting plate count and speed, respectively, that can be achieved with a given particle size. An advantage of the Desmet-style plot in Figure 3B is that the curves plotted in these coordinates are similar in shape to van Deemter H vs. u curves (albeit with high velocity on the left in this case), and thus each curve clearly has a minimum and two branches that correspond to either B-term (right) or C-term (left) limited performance. The circled points in Figure 3B, as in Figure 3A, correspond to those very special points where the ‘Knox-Saleem lines’ are tangent to the ‘Poppe curves’. Because there is a minimum in each ‘Poppe curve’ in Figure 3B, one does not have to calculate the ‘Knox-Saleem line’ to know where it intersects with the ‘Poppe curve’. On the other hand, in Figure 3A it is not evident where the Knox-Saleem limit is reached on each ‘Poppe curve’ unless the ‘Knox-Saleem line’ is actually calculated and plotted to see where they intersect.
Discussion
In the following discussion we give examples of how these equations can be used to rapidly address questions related to optimization, from both theoretical and practical perspectives. These examples do not constitute an exhaustive treatment, but rather address some of what we believe are of current interest.
In contrast to the mobile phase velocity and column length which can be nearly continuous variables in practice (nearly any length above 2 cm can be achieved by coupling columns), the optimum particle diameter predicted by eq 19 for a given value of to may not be commercially available (especially if a particular stationary phase chemistry is needed). For this reason one can argue that eqs 18–20 that result from optimization in case 3 where the particle size is treated as a freely adjustable parameter are not practical per se. However, manipulation of these equations yields some very insightful relationships that help guide optimization, and provides a clear path to optimum values of dp, L and ue which we should always attempt to approach, even if we cannot realize them exactly in practice. We will use the relationships developed below to address two important questions with respect to the impact of changes in the maximum operating pressure:
How does changing the maximum operating pressure impact the minimum analysis time needed to achieve a specific separation goal under practical conditions (e.g., to ~ 100 s)? In other words, for a specific resolution of a critical pair of peaks (and thus the corresponding minimum plate count that is required), what degree of improvement in analysis time should we expect when we move from an instrument operating at 400 bar maximum pressure to one operating at 1000 bar, and how do we choose the particle size, column length, and eluent velocity to actually realize this improvement?
What are the particle sizes and column lengths needed to achieve optimum performance (as measured by N/to) in very fast separations (1 s < to < 10 s) such as those used in the second dimension of comprehensive 2D-HPLC separations, and how does changing the maximum operating pressure affect these parameters?
Effect of Available Pressure on Analysis Time at Constant Plate Count (Resolution)
Eqs 18–20 give, for a given value of to, the values of dp, L, and ue that will maximize the plate count at that analysis time. This combination of parameters will give the absolute maximum performance at that time, for a given operating temperature and maximum pressure (and other ‘constants’, including Φ, van Deemter coefficients, etc.). Since it is assumed in Case 3 that we are always working at the minimum in the van Deemter curve, the plate count is easily calculated by dividing the optimum column length (L*, eq 20) by the plate height which is the product of the minimum reduced plate height (hmin, eq 3) and the optimum particle diameter (, eq 19). This results in eq 21 which gives the maximum number of plates (Nmax) achievable at a given time (to). Eq 21 shows the best improvement that can be achieved by changing the maximum pressure at a given time, and we see because of the square-root dependence on Pmax, the best improvement in the plate count that can be expected by increasing Pmax from 400 to 1000 bar (2.5-fold) is an increase of 60 % (1.6-fold). Of greater interest to this discussion is the dependence of to on Pmax. Rearranging eq 21 we find:
| (26.) |
This is exactly the result given by Knox15, Poppe13, Guiochon12, 29, and Desmet36 (with the exception of the λ term which accounts for differences in the type of velocity that is used in relating the plate height to the eluent velocity). The practical consequence of eq 26 is that the analysis time required to achieve a given Nmax value is inversely proportional to the first power of the maximum pressure. This is the best we can hope for given that the equations in Case 3 are developed assuming we can always work at ue,opt by choosing exactly the optimum values of and L*. So, for an increase in Pmax from 400 to 1000 bar, the biggest decrease in the analysis time we should expect while maintaining the plate count is 2.5-fold.
This result stands in stark contrast to many claims made regarding the benefits of increased pressure limits, both by accomplished practitioners and expert chromatographers. Claims of 5-fold and greater improvements in analysis times upon moving from an instrument with a 400 bar pressure limit to one with a 1000 bar limit are common7–9, 37–39. As an example, the results presented in a recently published paper8 in support of this type of claim (9-fold in this case) are summarized in Table 1. It is clear that the implication in comparisons of this kind is that dramatic reductions in analysis time on the order of 5- to 10-fold are due to an increase in the instrument pressure limit. A closer examination of the data and comparison to trends based on theory show that this is not so.
Table 1.
Summarized results of a comparison of HPLC (400 bar limit) and UPLC (1000 bar limit) at constant resolution (Estimates from Figure 1 of Ref. 8)
| Case | dp (µm) | Dimensions (L × i.d., mm) |
F (mL/min) | ΔP (bar)a | % Useage of Pmaxb |
tr (min) | Fold Improvement in trc |
|---|---|---|---|---|---|---|---|
| 1 | 5.0 | 150 × 2.1 | 0.2 | 42 | 11 | 8.5 | |
| 2 | 3.5 | 100 × 2.1 | 0.3 | 86 | 22 | 3.5 | 2.4 |
| 3 | 2.5 | 75 × 2.1 | 0.5 | 211 | 53 | 1.7 | 2.1 |
| 4 | 1.7 | 50 × 2.1 | 0.6 | 366 | 37 | 0.97 | 1.8 |
Estimated assuming 38 °C, εe = 0.38, 5/95 (v/v) acetonitrile/water
Estimated assuming 400 bar limit for cases 1–3, and 1000 bar limit for case 4
At constant resolution
We believe there are two major problems with this type of comparison of theory and experiment. First, a critical metric shown in Table 1 is the fraction of the available pressure used for the analysis with a given particle size. In Case 4 37% of the available 1000 bar pressure is used in the analysis involving 1.7 µm particles, while only about 11% of the available 400 bar pressure is used in the analysis involving 5.0 µm particles (Case 1). The implication in Ref. 8 is that in comparing Cases 1 and 4 is that the 2.5-fold increase in the available pressure and the concomitant use of sub-2 micron particles leads to 9-fold decrease in analysis time. This is misleading because the change in the actual pressure drops across the columns is about 8.5-fold. Second, the first power dependence of to on Pmax in eq 23 is arrived at assuming that the particle size is freely adjustable, and that the optimum particle diameter is used at each condition (to and Pmax) that is considered. Clearly the comparisons summarized in Table 1 do not involve freely variable particle sizes and in fact the particle sizes used in some cases are nowhere near optimum for some of the conditions used (as is also indicated by the small fraction of the available pressure that was used). Both of these issues are resolved by considering the scenario discussed below and summarized in Table 2.
Table 2.
Systematic approach to comparison of effects of optimization steps on apparent improvements in analysis speed at constant plate count a
Using typical values of important particle and column characteristics (see Table 2 for details) and eqs 11 and 12, we find that with a 25 cm column packed with 5 µm particles we should be able to generate 23,600 plates at a column dead time of 120 s using a pressure drop of 100 bar across the column. The parameters related to this result are summarized in Table 2 in the row labeled ‘Condition A’. These conditions obviously violate the first rule of optimization quoted at the beginning of this paper, that “The fastest analysis is obtained by operating the column at the maximum available pressure…”. In condition B we simply increase the operating pressure to 400 bar, and we see that the analysis time needed to achieve 23,600 plates decreases nearly 2-fold, with concomitant significant increases in L* (to 37 cm!) and . Thus, it is already clear that significant improvements (ca. 200%) in the productivity of separations involving 5 µm particles at typical analysis times (20–30 min for k’ = 10) can be realized by simply operating columns packed with these particles under optimum conditions – not the van Deemter optimum velocity, but the velocity and column length which maximizes the ratio N/to for a given plate count.
Consider next conditions C and D which give the analysis time needed to generate 23,600 plates using either 3.5 or 1.7 µm particles, but keeping the maximum pressure constant at 400 bar. Here we see additional decreases in to of 38 and 57%, respectively, relative to condition B involving 5 µm particles at 400 bar. At this point we realize that once the decision is made to take full advantage of the available pressure, significant gains in productivity can again be made by changing the particle size. But we must be mindful that the optimum particle size (from the standpoint of productivity) is dependent on the plate count that is needed (or the time one can commit to the analysis). This was pointed out graphically by Poppe13, but is underappreciated. The recent work of Desmet and coworkers40 and Sandra and coworkers19 is shedding more light on this issue.
In the next step of the comparison in Table 2 the pressure limit is increased to 1000 bar, while maintaining the particle size at 1.7 µm. Here there is an additional 58% decrease in analysis time compared to condition D (1.7 µm, 400 bar). In comparing conditions A and E, the total decrease in to is 90%, but much of this improvement (i.e. 76% decrease from A to D) is realized without increasing the pressure limit of the instrument itself, rather it is gained by more effectively using the available pressure and choosing a more appropriate particle size for the separation at hand. Each of the calculations for the step-wise improvements in Table 2 were made using the two-parameter equations developed in Case 2. It is most important here to realize that the three-parameter equations of Case 3 provide the values of dp, L, and ue that maximize the plate count at a column dead time of 12.5 s and Pmax of 1000 bar (T = 40 °C, εe = 0.38, A = 1.0, B = 5.0, C = 0.05). Using eqs 18–20 (Case 3 - three-parameter equations) we see that (corresponding to 0.62 mL/min with a 2.1 mm i.d. column), yield a plate count of 25,300. Most likely a 1.3 µm particle would not be commercially available at this time and thus the closest available size must be chosen. In this case a new value of dp (we choose 1.7 µm) is plugged into eqs 11–13 (Case 2 – two-parameter equations) to give new values of L* = 8.6 cm, and , which yields a plate count of 23,400. This example shows that for a given column dead time, maximum operating pressure, and temperature, the three-parameter equations developed in Case 3 can be used to very efficiently and effectively find the combination of the particle size, column length, and eluent velocity that maximize the plate count at that time. Note the actual velocity which optimizes N is 72% higher than the van Deemter optimum in this case.
We note in passing that this type of conditioned calculation is not limited to setting our hypothetical pressure limit at 400 bar. If for practical purposes it seems more reasonable to operate the system at, say, 80% of the pressure limit, the same calculations could be done for pressure limits of 320 and 800 bar, with more or less the same conclusions. The critical point is not that practical work should be done at some constant fraction of the available pressure, but that in fundamental studies of the effect of pressure on performance that the actual pressure drop across the column is used as the metric, and not the available pressure drop if it is not fully utilized.
Optimal Particle Diameters and Column Lengths for Ultra-Fast Separations (1 s < to < 10 s)
Experienced chromatographers are well able to make changes to re-optimize methods in the space of conventional conditions. However, for extreme separations (short time, high pressure, high temperature, etc.) looking at trends predicted by theory is often very instructive to avoid wasting time exploring experimental conditions that are not optimal. Our particular interest is in ultra-fast separations for use in the second dimension of two-dimensional (2D) HPLC systems where very rapid sampling of the first dimension separation is vital for high performance 2D separations41–43. In particular we are interested in the dependence of performance under these conditions on such operational variables as the pressure and temperature limits, and characteristics of columns and packing materials such as optimum particles size and column length and van Deemter A, B, and C coefficients.
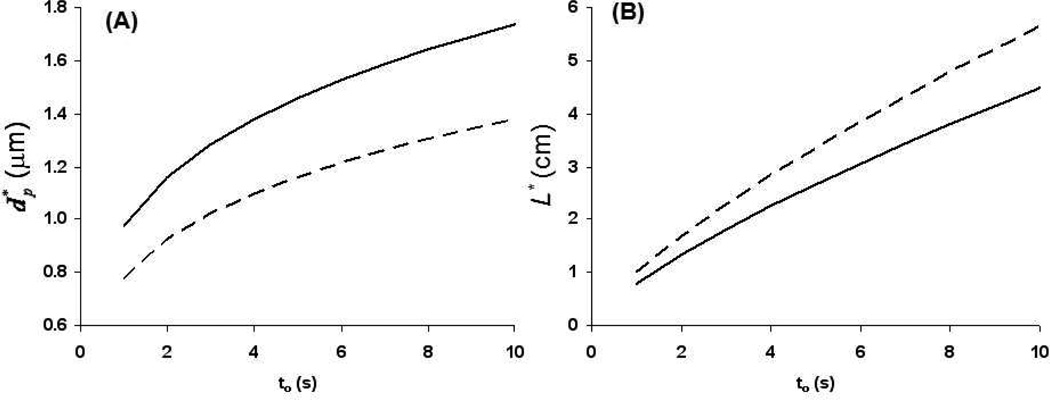
The framework developed in this paper for optimization provides the tools to efficiently explore these dependencies. As examples, in Figure 4 we show the dependence of the optimum column length and particle size, and L*, on the column dead time at relatively short times. We use the three-parameter eqs 19 and 20 which give the values of the particle size and column length which maximize the plate count (N) at a given value of to. The solid line in Figure 4A (400 bar pressure limit) shows that increases with increasing to. Note this increase in the best particle size is also echoed by the fact that the Poppe curves in Figures 2 and 3 cross-over one another and show that as to increases the best particle size must be increased to obtain the better plate count and plate-time. At a to of 1 s, is about 1 µm which is prohibitively small considering that very few materials of this size are commercially available, and difficulties with column packing increase as the particle size is decreased44. The dashed line in Figure 4A shows the same type of curve, but for a pressure limit of 1000 bar. We see that the effect of increasing the pressure limit is actually to decrease the optimum particle size, and move further away from commercially available materials. Although extra-column effects are not a focus of this paper, previously expressed concerns about the consequences of peak broadening due to extra-column effects when using sub-two micron particles will be very serious in the application of ultra-fast separations where such small optimum particle diameters are predicted40, 45.
Figure 4.
Optimum particle size (A) and column length (B) as a function of analysis time (to) at pressure limits of 400 (solid lines) and 1000 (dashed lines) bar. Other parameters: T = 40 °C, εe = 0.38, εi = 0.30, Φ = 500, van Deemter terms A, B, and C of 1.0, 5, and 0.05, respectively.
Figure 4B shows the same two curves (solid – 400 bar, dashed – 1000 bar) for the optimum column length as a function of dead time. Here increasing the pressure limit has the opposite effect, pushing L* to longer lengths. Interestingly, even at a to of 5 s, the optimum column length is still on the order of 2.5 cm. It is only at extremely short times on the order of 1 to 2 s that very short columns become optimal.
Conclusions
We have developed a compact theoretical framework that allows rapid calculation of the optimum conditions (ue, L, and dp (case 3 only)), for separations constrained by time and pressure, and situations involving columns packed with either pre-constrained or freely variable particle sizes. These equations allow much more facile evaluation of the impact of a variety of factors affecting performance (e.g., pressure, temperature, column permeability, and van Deemter coefficients) than does the iterative approach developed by Poppe13.
When particle size is pre-set and fixed, the best performance (measured by the number of plates that can be generated in a given time) is not always obtained by working at the van Deemter optimum velocity; in fact, this is very rarely the case. Working at the van Deemter optimum merely minimizes HETP for a column of a specific length packed with particles of a particular size, but does not maximize plate count or minimize analysis time for an optimally designed column. Whenever one uses a non-optimum value of the particle diameter one can either improve the plate count or the analysis time, but not both, by deliberately working at a velocity other than the van Deemter optimum value.
Optimum particle size, velocity and column length are functions of the desired analysis time and available maximum pressure.
When particle size is optimized as a continuous variable along with velocity and column length, theory predicts that at constant plate count (N), analysis time is inversely proportional to maximum operating pressure (Pmax, first power); the maximum benefit to be expected upon raising the Pmax from 400 to 1000 bar is therefore a 2.5-fold decrease in analysis time. On the other hand, at constant analysis time, again assuming simultaneous optimization of particle size, column length and eluent velocity theory predicts a square-root dependence of N on Pmax; the maximum expected benefit of increasing Pmax from 400 to 1000 bar is just a 41% increase in N.
When particle size is pre-set, the dependence of N on Pmax is a function of analysis time. At very short times there is very little effect of pressure (approaching no effect whatsoever in the limit of very fast separations), at intermediate times there is a square-root dependence of N on Pmax, and at very long times there is a first-power dependence of N on Pmax. Thus, when considering the effect of increased instrument pressure limits on performance, it is very important to consider the range of analysis times that is of greatest interest.
To make a fair comparison of performance (as measured by to at fixed N) on two HPLC systems with different pressure limits, it is imperative that the columns and systems be operated at the same fraction of the available maximum pressure on each system. Failure to do this can and has lead to serious over-estimations of the role of pressure in performance and apparent discrepancies between experiment and well-established theory.
We believe the simple, yet accurate equations presented here for the calculation of the parameters (ue, L, and dp) required to achieve optimum performance complement the primarily graphical approaches of other groups including Poppe and Desmet et al., and will allow a rapid, fair and sensible evaluation of emerging technologies for modern HPLC.
Acknowledgements
This work was supported by a grant from the National Institutes of Health (Grant GM54585), and a Faculty Start-Up Award from the Camille and Henry Dreyfus Foundation to D.R.S. The authors thank Steven Weber for many helpful discussions.
Glossary
- to
the column dead time; the time required for a pulse of unretained analyte to travel through the column
- N
column plate count
- Nopt
the value of the plate count obtained by operating a given column at ue,opt
- H
height equivalent to a theoretical plate
- h
reduced plate height
- hmin
the value of h at the minimum in the van Deemter curve (reduced coordinates)
- ue
interstitial eluent velocity
- ue,opt
the value of ue that corresponds to the minimum in the van Deemter curve (H vs. ue)
- ν
reduced interstitial eluent velocity
- νopt
the value of ν that corresponds to the minimum in the van Deemter curve (reduced coordinates)
- A, B, and C
coefficients obtained from a fit of h vs. ν using the van Deemter formalism (see eq 1 with α = 0)
- dp
particle size
- Dm
diffusion coefficient of the analyte in the eluent
- L
column length
- εe
interstitial porosity
- εi
intraparticle porosity
- εtot
total porosity of a particle packed bed, including intraparticle porosity
- λ
the ratio εe/εtot
- P
pressure drop across the length of the column
- Pmax
maximum operating pressure of the instrument
- η
eluent viscosity
- Φ
dimensionless flow resistance (typically 500)
the value of the interstitial eluent velocity that maximizes the plate count at a given value of to
the value of particle size that maximizes the plate count at a given value of to
- L*
the value of the column length that maximizes the plate count at a given value of to
- N*
the value of the plate count obtained by operating a column of length L*, operated at an eluent velocity , and particles of a pre-selected size, not necessarily equal to ; this is the value of the plate count that results from optimization in Case 2
- Nmax
the value of the plate count obtained by operating a column of length L*, operated at an eluent velocity , and particles of size equal to ; this is the value of the plate count that results from optimization in Case 3
Contributor Information
Peter W. Carr, Department of Chemistry, University of Minnesota, 207 Pleasant St., S.E., Minneapolis, MN 55455
Xiaoli Wang, Department of Chemistry, University of Minnesota, 207 Pleasant St., S.E., Minneapolis, MN 55455.
Dwight R. Stoll, Department of Chemistry, Gustavus Adolphus College, 800 West College Avenue, Saint Peter, MN 56082
References
- 1.Guiochon G. Anal. Chem. 1980;52:2002–2008. [Google Scholar]
- 2.Macnair JE, Lewis KC, Jorgenson JW. Anal. Chem. 1997;69:983–989. doi: 10.1021/ac961094r. [DOI] [PubMed] [Google Scholar]
- 3.Thompson JW, Mellors JS, Eschelbach JW, Jorgenson JW. LC-GC North Am. 2006;24(16):18–20. [Google Scholar]
- 4.Yan B, Zhao J, Brown JS, Blackwell J, Carr PW. Anal. Chem. 2000;72:1253–1262. doi: 10.1021/ac991008y. [DOI] [PubMed] [Google Scholar]
- 5.Wu NJ, Thompson R. J. Liq. Chromatogr. Relat. Technol. 2006;29:949–988. [Google Scholar]
- 6.DeStefano JJ, Langlois TJ, Kirkland JJ. J. Chrom. Sci. 2008;46:254–260. doi: 10.1093/chromsci/46.3.254. [DOI] [PubMed] [Google Scholar]
- 7.Kofman J, Zhao Y, Maloney T, Baumgartner T, Bujalski R. American Pharmaceutical Review. 2008:88–93. [Google Scholar]
- 8.Neue UD. In: Encyclopedia of Separation Science, online update. Poole CF, Wilson ID, editors. Oxford: Elsevier Science Ltd.; 2007. pp. 1–6. [Google Scholar]
- 9.Wu NJ, Clausen AM. J. Sep. Sci. 2007;30:1167–1182. doi: 10.1002/jssc.200700026. [DOI] [PubMed] [Google Scholar]
- 10.Plumb R, Mazzeo JR, Grumbach ES, Rainville P, Jones M, Wheat T, Neue UD, Smith B, Johnson KA. J. Sep. Sci. 2007;30:1158–1166. doi: 10.1002/jssc.200600492. [DOI] [PubMed] [Google Scholar]
- 11.Knox JH, Saleem M. J. Chromatogr. Sci. 1969;7:614–622. [Google Scholar]
- 12.Guiochon G. In: High-Performance Liquid Chromatography: Advances and Perspectives. Horvath C, editor. Vol. 2. New York: Academic Press; 1980. pp. 1–56. [Google Scholar]
- 13.Poppe H. J. Chromatogr. A. 1997;778:3–21. [Google Scholar]
- 14.Giddings JC. Anal. Chem. 1965;37:60–63. [Google Scholar]
- 15.Knox J. Annu. Rev. Phys. Chem. 1973;24:29–49. [Google Scholar]
- 16.Horvath CG, Lipsky SR. J. Chromatogr. Sci. 1969;7:109–116. [Google Scholar]
- 17.Desmet G, Clicq D, Gzil P. Anal. Chem. 2005;77:4058–4070. doi: 10.1021/ac050160z. [DOI] [PubMed] [Google Scholar]
- 18.Eeltink S, Desmet G, Vivo-Truyols G, Rozing GP, Schoenmakers PJ, Kok WT. J. Chromatogr. A. 2006;1104:256–262. doi: 10.1016/j.chroma.2005.11.112. [DOI] [PubMed] [Google Scholar]
- 19.Lestremau F, de Villiers A, Lynen F, Cooper A, Szucs R, Sandra P. J. Chromatogr. A. 2007;1138:120–131. doi: 10.1016/j.chroma.2006.10.042. [DOI] [PubMed] [Google Scholar]
- 20.Desmet G. LCGC Eur. 2008;21:310–317. [Google Scholar]
- 21.Desmet G, Clicq D, Nguyen DTT, Guillarme D, Rudaz S, Veuthey J-L, Vervoort N, Torok G, Cabooter D, Gzil P. Anal. Chem. 2006;78:2150–2162. doi: 10.1021/ac051280+. [DOI] [PubMed] [Google Scholar]
- 22.Tanaka N, Kobayashi H, Ishizuka N, Minakuchi H, Nakanishi K, Hosoya K, Ikegami T. J. Chromatogr. A. 2002;965:35–49. doi: 10.1016/s0021-9673(01)01582-5. [DOI] [PubMed] [Google Scholar]
- 23.Zhang Y, Wang X, Mukherjee P, Petersson P. J. Chromatogr. A. 2009 doi: 10.1016/j.chroma.2009.03.071. In Press. [DOI] [PubMed] [Google Scholar]
- 24.Heinisch S, Desmet G, Clicq D, Rocca J. J. Chromatogr. A. 2008;1203:124–136. doi: 10.1016/j.chroma.2008.07.039. [DOI] [PubMed] [Google Scholar]
- 25.Bristow PA, Knox JH. Chromatographia. 1977;10:279–289. [Google Scholar]
- 26.van Deemter JJ, Zuiderweg FJ, Klinkenberg A. Chem. Eng. Sci. 1956;5:271–289. [Google Scholar]
- 27.Horvath C, Lin H. J. Chromatogr. 1978;149:43–70. [Google Scholar]
- 28.Knox JH, Scott H. J. Chromatogr. 1983;282:297–313. [Google Scholar]
- 29.Guiochon G. J. Chromatogr. A. 2006;1126:6–49. doi: 10.1016/j.chroma.2006.07.032. [DOI] [PubMed] [Google Scholar]
- 30.Erni F. J. Chromatogr. 1983;282:371–383. [Google Scholar]
- 31.Cabooter D, de Villiers A, Clicq D, Szucs R, Sandra P, Desmet G. J. Chromatogr. A. 2007;1147:183–191. doi: 10.1016/j.chroma.2007.02.055. [DOI] [PubMed] [Google Scholar]
- 32.Karger BL, Snyder LR, Horvath C. An Introduction to Separation Science. New York: Wiley & Sons; 1973. [Google Scholar]
- 33.Bird RB, Stewart WE, Lightfoot EN. Transport Phenomena. New York: Wiley & Sons; 1960. [Google Scholar]
- 34.Giddings JC. Dynamics of Chromatography. New York: Marcel Dekker; 1965. [Google Scholar]
- 35.Antia FD, Horvath C. J. Chromatogr. 1988;435:1–15. [Google Scholar]
- 36.Desmet G, Cabooter D, Gzil P, Verelst H, Mangelings D, Vander Heyden Y, Clicq D. J. Chromatogr. A. 2006;1130:158–166. doi: 10.1016/j.chroma.2006.05.082. [DOI] [PubMed] [Google Scholar]
- 37.Swartz ME. J. Chromatogr. Rel. Technol. 2005;28:1253–1263. [Google Scholar]
- 38.Novakova L, Matysova L, Solich P. Talanta. 2006;68:908–918. doi: 10.1016/j.talanta.2005.06.035. [DOI] [PubMed] [Google Scholar]
- 39.Jacoby M. Chem. Eng. News. 2008;86:17–23. [Google Scholar]
- 40.Desmet G, Cabooter D, Billen J, Broeckhoven K, Lynen F, Sandra P. Baltimore, MD, USA: 2008. [Google Scholar]
- 41.Murphy RE, Schure MR, Foley JP. Anal. Chem. 1998;70:1585–1594. [Google Scholar]
- 42.Davis JM, Stoll DR, Carr PW. Anal. Chem. 2007;80:461–473. doi: 10.1021/ac071504j. [DOI] [PubMed] [Google Scholar]
- 43.Stoll DR, Wang X, Carr PW. Anal. Chem. 2007;80:268–278. doi: 10.1021/ac701676b. [DOI] [PubMed] [Google Scholar]
- 44.Jorgenson J, Lieberman R, Thompson J, Eschelbach J. Chicago, IL, USA: 2007. [Google Scholar]
- 45.Thompson JD, Carr PW. Anal. Chem. 2002;74:4150–4159. doi: 10.1021/ac0112622. [DOI] [PubMed] [Google Scholar]