Remembering forward: Neural correlates of memory and prediction in human motor adaptation

Abstract

We used functional MR imaging (FMRI), a robotic manipulandum and systems identification techniques to examine neural correlates of predictive compensation for spring-like loads during goal-directed wrist movements in neurologically-intact humans. Although load changed unpredictably from one trial to the next, subjects nevertheless used sensorimotor memories from recent movements to predict and compensate upcoming loads. Prediction enabled subjects to adapt performance so that the task was accomplished with minimum effort. Population analyses of functional images revealed a distributed, bilateral network of cortical and subcortical activity supporting predictive load compensation during visual target capture. Cortical regions - including prefrontal, parietal and hippocampal cortices - exhibited trial-by-trial fluctuations in BOLD signal consistent with the storage and recall of sensorimotor memories or “states” important for spatial working memory. Bilateral activations in associative regions of the striatum demonstrated temporal correlation with the magnitude of kinematic performance error (a signal that could drive reward-optimizing reinforcement learning and the prospective scaling of previously learned motor programs). BOLD signal correlations with load prediction were observed in the cerebellar cortex and red nuclei (consistent with the idea that these structures generate adaptive fusimotor signals facilitating cancellation of expected proprioceptive feedback, as required for conditional feedback adjustments to ongoing motor commands and feedback error learning). Analysis of single subject images revealed that predictive activity was at least as likely to be observed in more than one of these neural systems as in just one. We conclude therefore that motor adaptation is mediated by predictive compensations supported by multiple, distributed, cortical and subcortical structures.

1. Introduction

In Lewis Carroll’s Through the Looking Glass (Carroll, 1871), the white queen remarks, “It is a poor sort of memory that only works backwards.” Indeed, if memory is to improve fitness for survival it must shape future actions to satisfy changing environmental demands. Take for example the capture and retrieval of an early-morning cup of coffee. Lifting the cup over a laptop computer requires accurate estimation of the cup’s weight. Misestimating the load can have costly consequences. As the coffee level decreases, the nervous system compensates by adjusting muscular activities through a form of motor learning known as motor adaptation (Lackner and Dizio 1994; Shadmehr and Mussa-Ivaldi 1994; Thoroughman and Shadmehr, 1999). Motor adaptation relies on limited memory of prior sensorimotor experiences to adjust muscle activity in anticipation of future loads (Scheidt et al. 2001) so as to minimize kinematic performance errors (Shadmehr and Mussa-Ivaldi, 1994; Flanagan and Rao, 1995) while also minimizing “effort” (Nelson 1983; Hasan 1986) or other costs of control (for a review see Shadmehr and Krakauer 2008). Experimental data show that minimization of kinematic errors progresses faster than does minimization of kinetic effort in goal-directed arm movements such that overall performance is dominated by kinematic optimization (Scheidt et al. 2000). The present study exploits these observations to ask “Which brain structures contribute to the processing of recent sensorimotor memories for the prediction and compensation of future environmental loads during goal-directed movement?”

Psychophysical studies have provided compelling evidence that motor adaptation involves compensatory responses that occur on (at least) two time scales (Lee and Schweighofer, 2009; Smith et al 2006), and that the different adaptive processes may have distinct neural bases (Keisler and Shadmehr, 2010). In fact, three computationally distinct forms of neural plasticity have been implicated in motor learning (Houk and Wise, 1995; see Doya 1999, 2000 and Hikosaka et al 2002 and Hikosaka et al 2008 for reviews) and the extent to which each contributes to predictive load compensation is unknown. First, supervised learning within microzones of the cerebellum is thought to facilitate the estimation or modeling of the state of the limb and its environment (Kawato and Gomi 1992; Miall et al. 1993; Wolpert et al. 1995, 1998; Imamizu 2000; Ito 2000, 2005; Bursztyn et al. 2006), information that can be used to predict the sensory consequences of action (Angel 1976; Blakemore et al. 2001; Bell et al. 2008). By comparing predicted and realized sensations, deviations from expectation provide a signed error signal (i.e. one that has magnitude and direction) that can drive both corrective actions via model reference feedback control (Houk and Rymer, 1981; see also Seidler et al. 2004) and internal model updating via feedback error learning (Kawato et al 1987; Kawato and Gomi 1992; see also Fagg et al. 1997). Second, reinforcement learning within the basal ganglia is thought to improve selection of motor commands based on information of the current sensorimotor state, thereby maximizing rewards or minimizing costs associated with action (cf. O Doherty et al., 2003; Haruno and Kawato 2006; Houk et al 2007; Jueptner et al. 1997; Schultz et al. 1997, 2000; see also Mink 1996; Graybiel 2005). Commonly, rewards (costs) for reinforcement learning are modeled as scalar-valued signals that are maximized (minimized) when the desired task is performed successfully (Gurney et al 2001a, 2001b). Third, unsupervised learning within cerebral cortex is thought to construct arbitrary mappings (associative memories) that maximize information transmission between input/output pathways via Hebbian potentiation and activity-dependent synaptic decay (cf. Lucke and Malsburg, 2004; Sanger 1989; see also Linsker 1988). Unsupervised learning enables the cortex to encode the current and recent state of the limb and its environment (Andersen and Buneo 2002; Buneo and Andersen 2006; Gandolfo et al 2000; Gribble and Scott 2002; Li et al. 2001) as well as the subject’s own internal state in working memory (Fuster and Alexander 1971; Jonides et al 1993; D’Esposito et al. 1995). This may provide a common representational basis for sensorimotor information processing within the cerebellum and basal ganglia (Houk 2011). Are motor adaptation and the prediction of future environmental loads largely the responsibility of just one of the neural systems described above (i.e. the cerebellum, its associated pathways and their targets; Doyon et al 2003; Kawato and Gomi 1992; Imamizu et al. 2000, 2004; Spoelstra et al. 2000; Wolpert et al. 1998), or are these important computational functions subserved by multiple distributed modules as predicted by recent models of sensorimotor learning (Grosse-Wentrup and Contreras-Vidal 2007; Houk and Wise, 1995; Houk 2010; see also Doyon et al. 2003, 2009; Hikosaka et al. 2002)?

Here we examined trial-by-trial adaptation to changing mechanical loads during goal-directed wrist flexion movements. We conducted a novel neuroimaging experiment that combined human motor psychophysics, functional magnetic resonance imaging (FMRI), and engineering systems analysis techniques to identify neural responses (blood oxygenation level dependent BOLD signal fluctuations) that correlate with behavioral variables relating to signed performance errors (for supervised learning), unsigned errors (for reinforcement learning) and representations of current and past states (for unsupervised learning). Importantly, our approach allows us to form a priori estimates of each subject s prediction of impending environmental loads (i.e. the output of an internal model of the environment) and to identify neural correlates of these predictions. Population analysis of functional MR images and follow-on analyses of individual subject BOLD data test the hypothesis that activities in select regions of cerebral cortex, basal ganglia, and lateral cerebellum predict changes in the limb’s mechanical environment. Implications for the adaptive real-time control of limb movement are then discussed. Portions of this work have been presented previously in abstract form (Zimbelman et al. 2007, 2008; Salowitz et al. 2010).

2. Methods

2.1. Subjects

Twenty healthy volunteers participated in this study (6 female, 14 male; mean age = 29 years, range: 19 to 46 years). All subjects scored greater than 68 on the Edinburgh Handedness Inventory (strongly right-handed; Oldfield 1971). Potential subjects were excluded from the study if they had significant neurological, psychiatric or other medical history, or were taking psychoactive medications. Additional exclusion criteria were specific to MR scanning: pregnancy, ferrous objects within the body, low visual acuity, and a history of claustrophobia. Written informed consent was obtained from each subject in accord with the Declaration of Helsinki and institutional guidelines approved by Marquette University and the Medical College of Wisconsin.

2.2. Experimental Setup

Subjects rested supine within a GE Signa 3T EXCITE MR scanner equipped with a standard quadrature head coil. We minimized head motion within the coil using foam padding. Visual stimuli were computer-generated and projected onto an opaque screen that subjects viewed using prism glasses attached to the head coil. With arms at their sides, subjects grasped the handle of an MR-compatible, single degree-of-freedom, robotic manipulandum with their right hand (Fig 1A). For each subject, the handle s axis of rotation was aligned with that of the wrist, and the frame of the device was secured to the forearm for support. The manipulandum was mounted on an adjustable support structure fixed to the subject s waist, positioning the manipulandum comfortably while reducing motion of the subject s proximal arm segments. The manipulandum includes a pneumatic actuator that exerts computer-controlled torques about the wrist. Wrist position and wrist torque were monitored within 0.05° and 0.001 Nm, respectively. Analog measurements of pressure within the actuator were amplified and low-pass filtered with a cutoff frequency of 20 Hz. Joint angle measurements were also filtered at 20 Hz. Wrist angle and actuator pressure data were acquired at the control loop rate of 1000 Hz. Robot control was achieved using custom hardware and software designed to use the XPC target, real-time operating system (The Mathworks Inc., Natick, MA). Additional details of the device design, performance and MR-compatibility are described elsewhere (Suminski et al. 2007b).

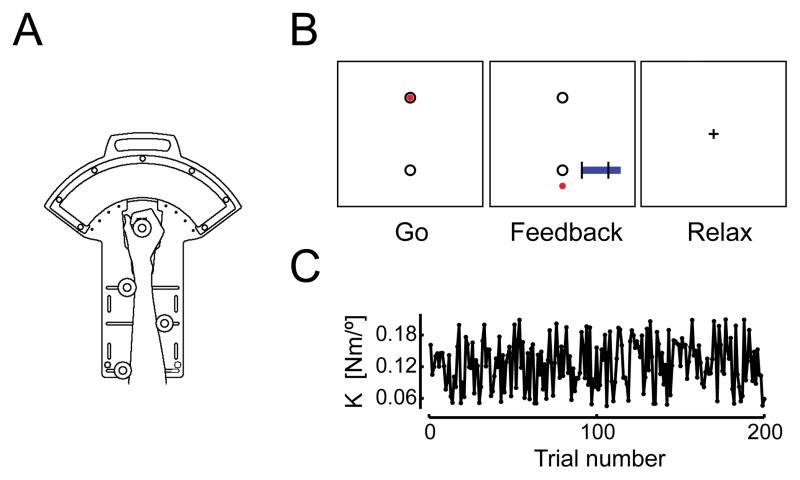
Figure 1.

(A) Schematic representation of the one-degree of freedom pneumatic manipulandum. (B) Illustration of the visual cues, summary feedback and instructions provided to subjects. Trials began with a “Go” cue wherein a black target appeared near the bottom of the screen. There was a one-to-one correspondence between the subject’s actual wrist angle and the location of a red cursor on the screen. No visual feedback was provided during the movement. Instead, feedback of peak wrist angle and movement duration was presented after movement completion (“Feedback”; see METHODS for details). Subjects then relaxed and visually fixated between trials (“Relax”). (C) The environmental load applied to the hand varied from trial-to-trial. For the purpose of this study, the sampling interval of behavioral data sets is 1 trial.

2.2.1. Behavioral Task

Subjects made 250 goal directed wrist flexion/extension movements in five blocks of 50 trials (1 movement per trial). Prior to the start of a trial, subjects were instructed to relax and visually fixate on a central crosshair stimulus while the robot held the hand at the home position of 30° wrist extension. Trials began with the appearance of a “Go” cue that consisted of a pair of black circles (1 cm dia.) representing the home position (top) and goal target (bottom) at 10° wrist extension (Fig 1B; “Go”). A circular red cursor (0.5 cm dia.) representing the current wrist angle appeared within the home target along with the GO cue. Subjects were instructed to “Wait for the GO cue, then move out-and-back to the target in one fluid motion, reversing direction as accurately as possible within the target goal without pausing.” The cursor disappeared at movement onset such that no visual feedback of ongoing motion was provided during movement. This was done to minimize the occurrence of corrective movements in the neighborhood of the target. We provided knowledge of results (KR) of kinematic performance for 1.0 s immediately upon movement reversal to promote movement accuracy (Fig 1B, “Feedback”). KR consisted of a static display of the red cursor at the location corresponding to the end of the flexion movement (i.e. at the angle where wrist flexion velocity fell below 10 °/s) on the linear scale established by the home and goal targets. A secondary graphical element provided feedback of movement duration on a linear scale that also indicated the desired movement time (400±25 ms). This information was intended to encourage consistency of movement duration across both trials and subjects. Subjects were instructed to relax after the movement. Once performance feedback had disappeared, they were to visually fixate the central cross hair while the robot maintained the hand at the start location in preparation for the next trial (Fig 1B, “Relax”). The interval between GO cues varied randomly from 8 to 18 sec, with a mean of 10 sec. This variable inter-trial interval maximized the ability of the FMRI deconvolution analysis (described below) to extract hemodynamic response functions (see Toni et al. 1999).

During the trials, the robot applied resistance that increased in proportion to wrist rotation in the flexion direction (i.e. a position-dependent, “spring-like” load). The first 50 trials (the practice block) were conducted prior to functional MR imaging and were performed against a load stiffness (K) of 0.13 Nm/°. This was done to familiarize subjects with the temporal and spatial accuracy requirements of the task. These initial practice trials were excluded from subsequent analyses. The next four blocks (the test blocks) were performed while undergoing concurrent functional MR imaging (one block per functional imaging ‘run’). Here, the load was sampled from a uniform distribution between 0.05 and 0.21 Nm/° such that K varied pseudorandomly from trial to trial about a mean value of 0.13 Nm/°. This mean value corresponded to information about the perturbation sequence that the subject might learn. All subjects experienced the same sequence of loads (Fig 1C). The sequence was designed to ensure insignificant correlation between loads on consecutive trials (required by the systems identification analysis described below). The total time to complete all 250 trials was about 45 minutes. Subjects rested 2 to 5 minutes between test blocks.

2.2.2. MR Imaging

After the initial block of practice trials and prior to functional imaging, we acquired 146 high-resolution spoiled GRASS (gradient-recalled at steady-state) axial anatomic images on each subject (TE = 3.9 ms, TR = 9.5 ms, flip angle = 12°, NEX = 1, slice thickness = 1.0 mm, FOV = 240 mm, 256 × 224 matrix). These images allowed localization of functional activity and spatial co-registration between subjects. Functional echo planar (EP) images were collected using a single-shot, blipped, gradient echo EP pulse sequence (TE = 25 ms, TR = 2 s, FOV = 240 mm, 64 × 64 matrix). Thirty-five contiguous axial 4 mm thick slices were selected in order to provide coverage of the entire brain (3.75 × 3.75 × 4.00 mm voxel size). An additional 4 images were collected at the beginning of each run to allow the FMRI signal to equilibrate and 7 more were added to the end of each run to accommodate the rise and fall of the hemodynamic response.

2.3. Behavioral Data Analysis

We computed four kinematic measures of task performance from the flexion phase of each movement. Movement onset occurred when wrist flexion velocity first exceeded 10°/s. Flexion movement offset occurred when wrist flexion velocity subsequently dropped below 10°/s. Movement error, ε, was defined as the angular deviation from the target at flexion movement offset. Absolute error, |ε|, was defined as the absolute magnitude of the quantity (ε_i- ε̄) where ε̄ was the across-trials average movement error in the last 100 trials (i.e. at steady-state). We next computed secondary performance measures including reaction time RT (the time delay between GO cue presentation and movement onset) and flexion movement duration (the time between flexion movement s onset and offset). Movements were considered unsuccessful if they were less than half the desired extent, if movement occurred in anticipation of the GO cue (RT < 100 ms) or if subjects were inattentive (RT > 800 ms). Unsuccessful movements were excluded from further analysis.

2.3.1. Adaptation Modeling

We constructed three behavioral time series from the four test blocks performed by each subject. These included the environmental load K_i as a function of trial number i (1 ≤ i ≤ 200), a directional or signed kinematic error ε_i, and the absolute error |ε_i|, which is uncorrelated with ε_i as a result of nonlinear rectification. As we will show below, K_i and ε_i both provide information relevant to the current state of the limb and its environment. Because |ε_i| is zero when performance is successful and increasingly positive otherwise, it is inversely proportional to task success regardless of whether subjects over- or under-shot the target. For the purpose of our analysis, we consider |ε_i| a suitable proxy for a graded reward signal that might drive reinforcement learning. Note that |ε_i| may be correlated with other signals of importance for reinforcement learning such as the magnitude of a prediction error (assuming subjects expect to hit the target on each trial), salience (more noticeable error, more “fast” learning; cf. Keisler and Shadmehr, 2010) and, possibly, mechanisms supporting procedural learning and/or error correction processes that are themselves dependent on the magnitude but not sign of kinematic errors.

The sequence of environmental loads was uncorrelated from one trial to the next. Therefore, history-dependent changes in performance errors could not have originated from the perturbation sequence itself but rather must have originated from the processing of sensorimotor memories within the neuromotor controller (i.e. learning). Studies of motor adaptations during goal-directed movements of the arms (Scheidt et al 2001; Takahashi et al., 2001; Scheidt and Stoeckmann 2007), legs (Emken and Reinkensmeyer 2005) and fingers (Liu et al 2010) have shown that this learning is well-described by a family of limited-memory, autoregressive models with external inputs:

$${\widehat{\epsilon }}_i=\sum _{m=1}^N{a}_m{\epsilon }_{i-m}+\sum _{p=0}^Q{b}_p{K}_{i-p},$$ [1]

where the a’s and b’s are constant coefficient factors scaling the influence of prior performance errors ε_i-m as well as current (K_i) and previous (K_i-p) perturbations, respectively. Constants N and Q correspond to the minimum number of memory elements needed to describe the evolution of trial-by-trial errors. The family of model structures described by Eqn 1 can represent processes having very limited memory requirements (e.g. when both N and Q are small), as well as processes having more complex dynamics.

We sought to determine the most parsimonious model structure characterizing adaptive performance changes in our wrist flexion task. We first averaged movement error across subjects on a trial-by-trial basis, thus reducing the effect of inter-subject execution variability on the structure estimation procedure. We then used the systems identification toolbox (ident) within the Matlab computing environment to fit all model structures of moderate complexity (N and Q ≤ 10) to one half of the data (the estimation dataset), and evaluate the models’ abilities to predict the sequence of errors in the other half (the cross-validation dataset). We used the minimum descriptor length (MDL) criterion (Ljung 1999) to identify the structure most consistent with the information filtering manifest in the sequence of errors observed during adaptation. Of all models considered, the MDL model is the one that minimizes a modified mean-square-error (MSE) function:

$${\mathit{MSE}}_{\mathit{MDL}}=\mathit{MSE}(1+n\mathit{log}(k)/k)$$ [2]

where n is the total number of parameters in the model being considered (N+Q) and k is the number of data points in the estimation data set. The MDL criterion offers an efficient compromise between model complexity and the quality of fit to the data. We then re-fit the resulting model to each individual subject’s time series to obtain individualized estimates of model coefficients a_m and b_p.

An important observation from prior studies of adaptation to stochastic loads is that the relationship between current performance error and magnitude of current load is often linear about the adapted load magnitude K̂:

$${\widehat{\epsilon }}_i=b_0\left(K_i-\widehat{K}\right).$$ [3]

As shown in (Scheidt et al. 2001), it is possible to obtain a trial-by-trial estimate of each subject s prediction of upcoming perturbation amplitudes, K̂_i, based on the model coefficients derived from Eqns [1] and [3] above. For example, if the adaptation model includes a single memory term for both kinematic error and environmental load (as in horizontal planar reaching; Scheidt et al., 2001; Scheidt and Stoeckmann, 2007), we obtain:

$${\widehat{K}}_i=-\frac{a_1}{b_0}{\epsilon }_{i-1}-\frac{b_1}{b_0}{K}_{i-1}.$$

Likewise, if the adaptation model were to include two memory terms for load, but no memory of prior errors:

$${\widehat{K}}_i=-\frac{b_1}{b_0}{K}_{i-1}-\frac{b_2}{b_0}{K}_{i-2}.$$ [4]

Of course, subjects cannot actually predict future loads because the sequence K_i is unpredictable by design, but this in no way precludes subjects from attempting to use recent sensorimotor memories to minimize errors. K̂_i is ideally suited for neuroimaging analyses of motor adaptation because it provides a trial-by-trial signature of the subject s prediction of future load based solely on memories of observable behavioral variables.

2.4 Image Analysis

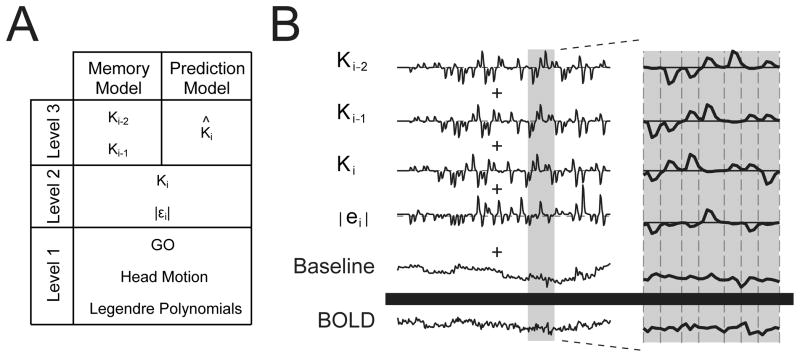
Functional imaging datasets were generated and analyzed using the Analysis of Functional NeuroImages (AFNI) software package (Cox 1996). Slice values were time shifted to the midpoint of the corresponding volume using Fourier interpolation. The first 4 volumes were removed from each imaging run (test block) and the 4 imaging runs were concatenated together for each subject to yield the functional imaging datasets analyzed using sequential multilinear regression (Draper and Smith, 1998). The rationale for this analysis is based on the fundamental geometry of least squares, which permits the partitioning of a multilinear regression into separate (sequential) regressions when the input regressors are mutually independent (orthogonal). We modeled BOLD signal fluctuations within each voxel as a combination of four independent sources of variability: a) nuisance variables (cofactors) typical of FMRI data collection; b) factors related generally to the performance of the visuomotor task (i.e. factors that do not change from one trial to the next, including the processing of visual stimuli and production of wrist flexion movements); c) factors related to how current-trial performance variables change from one trial to the next (eg. |ε_i|, K_i); and d) factors identified by adaptation modeling to be related to memories of prior events (eg. K_i-1, K_i-2), including memory-based predictions of upcoming environmental loads (eg. K̂_i ). We therefore performed a sequential multilinear regression analysis wherein the unmodeled (residual) signal variations that remained after an initial Level-1 analysis became the dependent variables to be predicted by a subsequent Level-2 analysis. Similarly, the unmodeled signal variations that remained after the Level-2 analysis became the dependent variables to be predicted by two subsequent Level-3 analyses (Fig 2A). Thus, four regression analyses were performed in total. By separating analysis of current-trial regressors from memory-related regressors, differences in the degrees of freedom inherent to the two Level-3 models could not influence the distribution of data variance attributed to the Level-1 and Level-2 regressors. That is, by splitting our regression into stages or Levels, we can fairly compare the relative merits of the two Level-3 models (see Section 2.5 below) without potential confound due to re-partitioning of variance for the earlier Level regressors, as would occur if we had instead performed separate nonsequential multilinear regressions for the memory- and prediction-model analyses (see Supplemental Information online).

Figure 2.

Description of functional imaging analyses. (A) Two models were investigated using a sequential regression analysis comprised of three levels. Image preprocessing removed from the raw BOLD signal those signal components correlated with nuisance variables of no interest. Level-1 analysis identified and removed from the baseline-corrected BOLD signal the general task-related activity. Level-2 analysis identified and removed from the Level-1 residual those signal components related to current-trial performance variables of interest. Separate Level-3 analyses identified BOLD signal components related to memory processing and load prediction. (B) Schematic representation of the statistical model comprising our “Memory Model” analysis. Individual behavioral regressors (mean removed) were convolved with a gamma-variate function approximating the canonical hemodynamic response. These time series were scaled and summed to best fit the raw BOLD signal using multi-linear regression. The gray band (left) illustrates the expanded region (right) with “GO” cue timings shown by vertical dashed lines.

2.4.1 Baseline Noise Model and the Level 1 Analysis: Main Effect of Task

We sought to eliminate from the functional image dataset those BOLD signal modulations correlated with covariate factors expected to mask signal changes of interest and to identify the task-related BOLD signal components that did not vary from one trial to the next. We considered as noise all baseline drift (modeled as the linearly-weighted set of orthogonal Legendre polynomials inclusive to order 4) as well as head motion parameters identified using an interactive, linear, least squares method for spatial registration of the image time series (AFNI program 3dvolreg; Cox 1996). Registration yielded six scalar head motion indices per functional imaging interval (period: 1 TR): rotation about the superior-inferior S/I, anterior-posterior A/P, and left-right L/R axes along with translation along each of those axes. The across-subjects average magnitude of head rotation was 0.12° ± 0.07° (mean ± 1 SD, here and elsewhere), 0.17° ± 0.12° and 0.35° ± 0.28° about the S/I, A/P, and L/R axes, respectively. Average translations were 0.34 ± 0.35, 0.91 ± 0.28 and 0.08 ± 0.05 mm in the superior, posterior, and left directions (range: 0.03 mm and 1.51 mm); no subject was excluded from analysis due to head motion.

We considered as a main effect of the subject’s task those BOLD signal fluctuations related only generally with task performance. We therefore created a trial onset time reference function using a comb function (a series of 1 s and 0 s) with 1 s assigned to TR times of trial onset (the GO cue) and 0 s assigned to the remaining imaging intervals. This time series was then convolved with a gamma variate function resembling the canonical hemodynamic response (Cohen 1997). Note that the Legendre polynomials modeling baseline drift were fit only to functional data from TRs wherein the estimated hemodynamic response to the GO reference function fell below 1% of its maximum value, thereby removing the approximate mean of the raw BOLD signal while preserving those signal components having potential correlation with trial-by-trial fluctuations in the behavioral regressors in this and subsequent analyses.

Because the visuomotor task was persistently challenging, we expected to find robust GO-related activity in brain regions known to engage in visuomotor tasks, including primary and non-primary sensorimotor cortices, visual and parietal association cortices as well as regions of the cerebellum (CER), thalamus (TH) and basal ganglia (BG).

2.4.2 Level 2 Analysis: Current-Trial Dependencies

The purpose of this analysis was to identify BOLD signal fluctuations that correlated significantly in time with small, trial-by-trial fluctuations in specific behavioral variables of interest (ε_i, |ε_i|, and K_i). Because the signed kinematic error ε_i generally demonstrates strong correlation with K_i, K_i can be interpreted as representing both environmental load and performance error, equivocally. Thus, the BOLD signal residuals resulting from the Level-1 analysis were modeled as a linearly weighted combination of input reference functions corresponding to the state variable K_i and the absolute value of kinematic error |ε_i| (representing a reinforcement reward signal). The choice to use K_i as a current-trial regressor as opposed to ε_i was further motivated by the appearance of K_i (and not ε_i) in the time series model of error we obtained from the systems identification analysis of behavioral data described below (see Eqn 6 below). As with the GO cue events, each behavioral reference function was constructed using a comb function with (typically) non-zero values assigned to TR times of trial onset and 0 s assigned to the remaining imaging intervals. Unlike the GO reference function, the non-zero values were drawn sequentially from the trial-by-trial behavioral time series resulting from the kinematic analysis performed for each subject. These subject-specific reference functions were convolved with a gamma-variate function prior to multilinear regression (Fig 2B, zoomed panel). Note that correlations between |ε_i| and K_i are negligible because of the nonlinearity introduced by rectification.

2.4.3 Level 3 Analyses: Memory and Prediction Models

We performed two separate Level-3 analyses to assess the strength of neuroimaging evidence supporting the participation of the cerebellum, basal ganglia and cerebral cortices in memory-based motor adaptation. The first Level-3 analysis (the Memory Model Analysis) was motivated by the results of our systems identification efforts (see Fig 4C and section 3.1 of RESULTS): BOLD signal residuals resulting from the Level-2 analysis were modeled as a linear combination of reference functions corresponding to memories of prior trial performance variables (K_i-1 and K_i-2). The second event-related analysis (the Prediction Model Analysis) was motivated by Eqn [4], which was also based on the results of system identification and describes how these memories may be combined to predict upcoming environmental loads. For this analysis, we evaluated the extent to which the Level-2 residuals correlated with K̂_i. Because K̂_i is a particular, subject-specific, weighted combination of K_i-1 and K_i-2, the two analyses differed in the degrees of freedom available for partitioning the variability within the Level-2 residual and therefore addressed different questions. Whereas the first assessed whether and how BOLD signal fluctuations correlated generally with trial-by-trial variations in sensorimotor memories of behavioral significance, the second analysis asked whether and how BOLD signal changes correlated with the one particular combination of sensorimotor memories that emulates trial-by-trial changes in the subject’s prediction of upcoming load. In both analyses, model reference functions were convolved with a gamma-variate function prior to regression analysis. The means of all Level-2 and Level-3 regressors were removed prior to entering into the regression analyses to minimize the potential for spurious correlation between them and any steady-state bias missed by the noise model and Level-1 analysis.

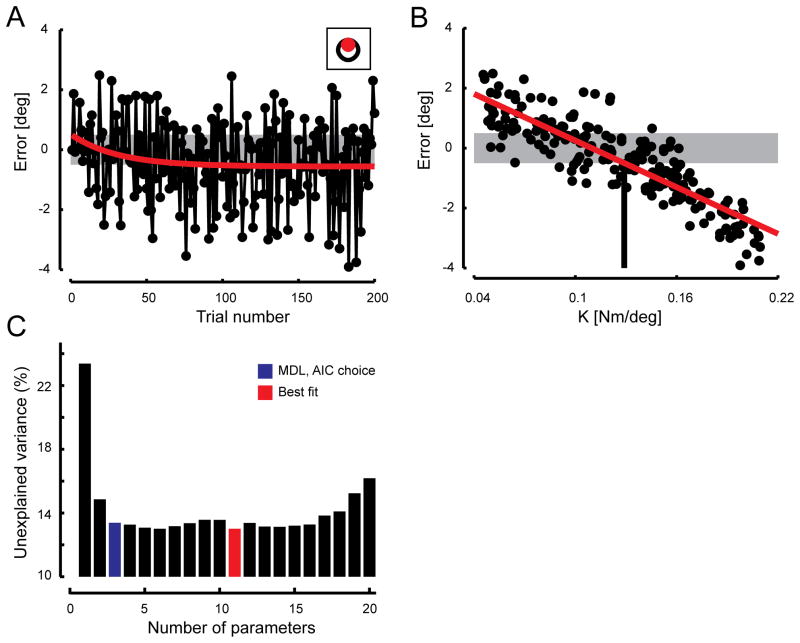
Figure 4.

Group behavioral results. (A) Time series of average movement error (black) and the line of best fit (red). Gray band indicates target tolerance. Inset shows target (black) and cursor (red) corresponding to the average subject performance at steady-state (i.e. within the last 100 trials of the experiment). (B) Average movement error plotted as a function of load stiffness on a trial-by-trial basis. The best fit linear regression is shown in red. The intersection of the regression line with the lower bound of the target tolerance indicates the mean perturbation strength that subjects had adapted to, K̂_i. (C) Comparison of performance (data variance not accounted for) for models of increasing structural complexity (number of model terms, or parameters). Unexplained variance decreases dramatically with the inclusion of additional model terms up until the MDL choice model (blue) after which improvement is incremental, if at all.

2.5 Statistical Inference

Prior to performing multilinear regression (AFNI program 3dDeconvolve), we verified the independence of all input regressors for each subject to ensure that the analyses would be free from confound due to multicollinearity.

Subject-specific anatomical and functional images were cubically interpolated to 1 mm³ voxels, co-registered and converted to stereotaxic coordinate space following the method of Talairach and Tournoux (Talairach and Tournoux 1988). Functional images were blurred using a 4 mm full-width half-maximum Gaussian filter to compensate for subject-to-subject anatomical variations. For each analysis, voxel-wise t-tests were performed to compare the deconvolution fit coefficients to zero. These across-subject comparisons identified voxels with statistically significant correlation between the hemodynamic response and the input regressors. A cluster-size and thresholding technique was used to correct for multiple comparisons in the group analysis. Appropriate cluster size and individual voxel p-value thresholds were estimated by performing 10,000 iterations in a Monte-Carlo simulation using the 3dClustSim tool included within the AFNI toolkit (Cox 1996). For the Level-1 analysis, we used a minimum cluster size of 113 μl and an individual voxel probability of t = 7.407 (p= 1×10⁻⁶) to yield a whole brain family-wise error threshold of α = 0.0001. For the Level-2 and Level-3 analyses, where the regressors of interest were small trial-by-trial fluctuations in performance, this approach was unduly conservative. For these analyses, we used a lower individual voxel probability of t = 3.950 (p = 0.001) to identify regions of ‘significant’ activation (minimum cluster size of 20 μl). To further ascertain the level of confidence in our behavioral correlates, we performed a jackknife analysis (df = 16) repeating the population t-test analysis 18 times, each time removing a different subject from the pool. We compared the resulting clusters to the original 18-subject analysis and report the number of times each cluster dropped from significance in the jackknife analysis. We consider as high-confidence those activation regions that dropped from significance rarely (≤ 1 time) whereas low-confidence activations dropped from significance frequently (≥ 10 times).

We visualized the relationship between each regressor and the residual BOLD signals within selected, masked, brain regions of interest (ROI). We identified the centroids of the selected ROIs and warped these locations back onto each individual subject s dataset. We then extracted a trial sequence of scalars (α_i, β_i) from each centroid voxel. The trial sequences consisted of regressor magnitude α on trial i and the raw BOLD signal β at the approximate peak of the hemodynamic response on that same trial. We then plotted the relationship between the regressor of interest and the residual BOLD signal values computed by subtracting the contributions of all other regressor variables, excepting the variable of interest, from the raw BOLD signal. To do so, we sorted the data pairs into five bins of equal width and ascending values of α before averaging within subjects for each bin. We then computed the across-subjects correlation coefficients between regressor magnitude and the residual BOLD signal.

Finally, for regions of overlap between the two Level-3 models (memory and prediction), we compared the ability of each model to account for variance in the individual-subject BOLD signal using a maximum power test (Bohlin, 1978; cf. Ljung, 1999 p. 508). The null hypothesis stated that the data were generated by the model with fewest free parameters (i.e. the prediction model). The test compared the MSE computed from the residuals of each model while correcting for the difference (d = 1) in degrees-of-freedom between the two models. The correction factor was k_d(α)/N with α = 0.95 for a χ² distribution k_d(α) with d degrees-of-freedom and N data points. Here, N was the number of trials with a full set of valid data [i.e. no unsuccessful movements for trials i, i -1 and i-2; across subjects, N averaged 177 ± 15; range: 144 to 195]. Data were taken from the local voxel having greatest within-subject correlation so as to maximize the BOLD signal:noise ratio for this comparison (one datum per trial). The null hypothesis is rejected if the following holds true:

$${\mathit{MSE}}_{\mathit{pred}}-{\mathit{MSE}}_{\mathit{mem}}\ge {\mathit{MSE}}_{\mathit{mem}}\ast \frac{1}{N}{k}_d(\alpha )$$ [5]

Error bars in figures represent ± 1 SEM.

3. Results

3.1. Behavioral results

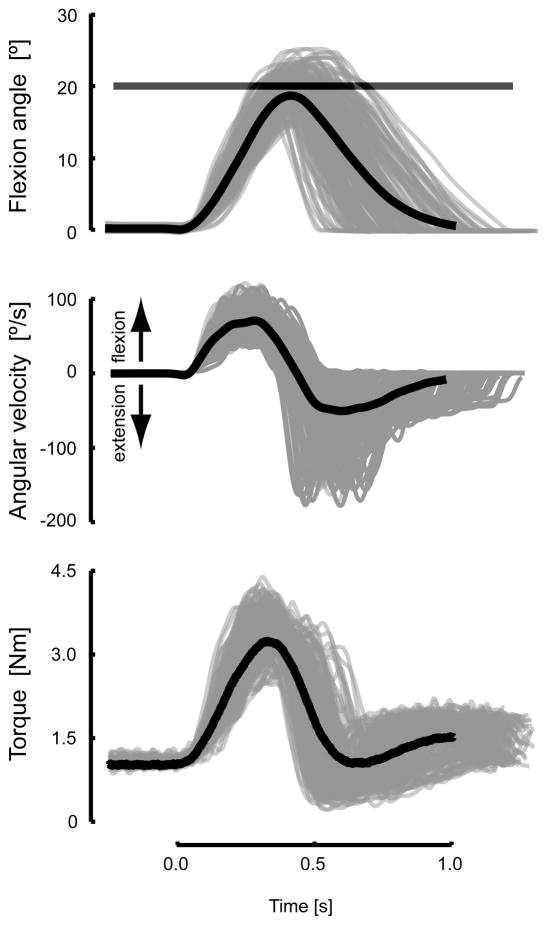
As shown for a representative subject (Fig 3), wrist angle trajectories out and back to the target were performed smoothly with an across-subject average reaction time of 490±62 ms and an average flexion duration of 400±18 ms. Both average values were well within their respective desired ranges. Few trials were unsuccessful (see section 2.3 in Methods), averaging only 8±5 trials across subjects. Unpredictable changes in spring-like load produced considerable trial-to-trial variability in the peak extent of movement (Fig 3 top, grey traces). However, performance was reasonably accurate on average (Fig 3 top, black trace); this was true for all subjects. Angular velocities peaked at about 80°/s during flexion (Fig 3, middle). The extensor torque applied by the manipulandum varied smoothly in time (Fig 3, bottom), in approximate proportion to wrist angle displacement. As desired, peak torque scaled linearly with commanded load (across-subject average r² = 0.82).

Figure 3.

Time profiles of wrist displacements (top), velocities (middle) and torques (bottom) obtained during testing of a representative subject. Individual trial profiles are presented in gray whereas the average profiles over the entire testing session are presented in black. Wrist displacement target tolerance is shown by the horizontal bar.

On average, subjects overshot the target at the beginning of the testing session, giving rise to initial movement errors that were positively biased in the first test block (Fig 4A, first eleven trials). This is consistent with a modest fatigue-dependent reduction in force production at the end of the baseline block, and subsequent recovery during anatomical scanning (cf. Bigland-Ritchie and Woods 1984). If the same descending commands were applied initially after the rest as were applied before, slight overshoot would be expected at the beginning of the test blocks. We fit a falling exponential to the movement error time series, which decreased with a time constant of 31 trials (Fig 4A, red). Asymptotic performance was approached within 100 trials; final error within the last 100 trials averaged -0.47±2.46° across subjects. This value closely matched the minimum movement extent (−0.50°) for which the cursor fully penetrated the target (Fig 4A, inset). Movement errors were clearly load-dependent, varying in approximate proportion to load stiffness (Fig 4B). When the perturbation strength was strong, the hand undershot its target whereas when the load was weak, the hand overshot its goal. This relationship was approximately linear (r² = 0.75). The intersection of the regression line with the asymptotic error value represents the perturbation to which subjects had adapted on average ( K̂ = 0.129 Nm/°).

We considered whether trial-by-trial changes in kinematic error might reflect the influence of prior performance on subsequent movement attempts (cf. Scheidt et al. 2001; Scheidt and Stoeckmann 2007; Takahashi et al., 2001). We therefore analyzed a family of linear adaptation models of moderate complexity (see Eqn 1 in section 2.3.1 in Methods) and found the model of Eqn 6 to be the minimum descriptor length structure (Ljung 1999):

$${\widehat{\epsilon }}_i=b_0{K}_i+b_1{K}_{i-1}+b_2{K}_{i-2}$$ [6]

with 86.6% of cross-validation data variance accounted for (VAF) in the average response (Fig 4C). While other structure selection techniques were also evaluated (including the Akaike s Information Criterion choice, AIC) (Ljung 1999), the best improvement in data VAF over the MDL choice was 0.37% at a cost of considerable model complexity (i.e. 8 additional memory terms: 3 for perturbations and 5 for errors). Thus, Eqn [6] parsimoniously describes the average trial-by-trial changes in wrist flexion movements, demonstrating that only recent sensorimotor memories influence the updating of motor commands on subsequent trials in this task. Table 1 details the model coefficients obtained by refitting Eqn [6] to each individual subject’s time series. We used these coefficients and the subject-specific behavioral time series to estimate the trial-by-trial fluctuations in each subject’s prediction of the upcoming environmental load (Eqn [4]). The time series |ε_i|, K_i, K_i-1, K_i-2, and K̂_i obtained from these analyses were used as input regressors in the sequential analysis of functional images.

Table 1.

Model coefficients of behavioral time series

Subject	b0	b1	b2	r2
1	−42.7	24.1	3.5	35.2%
2	−28.4	3.9	−0.1	31.4
3	−33.0	27.1	4.4	23.0
4	−43.0	7.8	−1.6	30.5
5	−43.4	14.3	1.7	34.2
6	−32.8	4.0	9.5	28.9
7	−25.7	8.9	−1.8	16.6
8	−27.0	17.0	6.8	28.4
9	−47.5	21.2	2.4	54.6
10	−46.7	15.3	8.6	41.2
11	−28.0	5.1	10.3	14.4
12	−40.2	10.3	6.7	44.6
13*	−69.0	−0.4	−4.2	47.3
14	−45.7	25.5	12.2	44.6
15	−38.8	8.1	14.6	34.6
16	−39.9	1.4	9.9	35.9
17	−26.0	5.5	8.5	14.2
18	−38.2	14.6	13.1	20.7
19*	−33.7	17.7	14.7	38.2
20	−44.1	−5.8	−4.4	29.0
mean±SE	−39±2.3	11±2.0	5.7±1.4	32±2.5

^*Subjects excluded from image analysis due to spurious correlation between |ε_i| and K_i

3.2. Functional imaging results

To obtain reliable model coefficients, sequential regression analysis requires statistical independence of its input regressors. We assessed pair-wise correlations between the behavioral regressor time series (GO, |ε_i|, K_i, K_i-1, K_i-2) for each subject and found spurious, but statistically significant, correlations between |ε_i| and K_i in two subjects, who were excluded from further analysis (see Table 1). Because K̂_i is by definition a linear combination of K_i-1 and K_i-2, it also was uncorrelated with the GO, |ε_i|, K_i regressors.

3.2.1. Level-1 Analysis - Main Effect of Task

We sought to identify those BOLD signal components related generally to task performance (recall that the GO signal waveform was identical on each trial). Target capture elicited widespread and distributed BOLD activation changes correlated in time with the production of goal-directed wrist movements (Fig 5; Table 2). As expected for a right-handed visuomotor task (cf. Kawashima et al. 1995; Toni et al 1999) requiring substantial muscle force production (Dai et al. 2001), large activation volumes spanned the central sulcus in the left hemisphere, encompassing primary sensorimotor (S1 and M1), dorsal and ventral premotor (PMd and PMv), and posterior parietal cortices (PPC). Because the subjects’ target was presented visually, we expected and found widespread and distributed cortical activities in areas that contribute to visual perception, processing of visuospatial instruction cues and the encoding of visual targets relative to the initial position of the hand: middle occipital gyrus (MOG), middle temporal gyrus (MTG), fusiform gyrus (FG), lingual gyrus (LG) and anterior intraparietal sulcus/supramarginal gyrus (BA 40). Smaller cortical activation volumes were located bilaterally in cingulate, inferior parietal and insular cortices, areas thought to be involved in motor response selection in the presence of uncertainty and errors (Paus 2001; Seidler et al. 2006; Kayser et al. 2010; Picard and Strick 1996; Grinband 2006; see also Singer et al. 2009). By construction, our task minimized the importance of online feedback stabilization of wrist posture because the ballistic motions emphasized spatial accuracy at mid-movement. Nevertheless, transcortical feedback mechanisms probably were active during the initial “ballistic” phase of the reach (Prablanc and Martin 1992; Seidler et al. 2004; Grafton 2008; see also Desmurget et al. 1999, 2001). Consistent with so-called long-loop reflex actions (Evarts and Fromm 1981; Evarts and Tanji 1976; Miall et al. 1993; Strick 1978), we observed general task-dependent activations (Fig 5) in cortical and subcortical areas previously implicated in the closed-loop feedback compensation for limb positional errors during wrist postural stabilization (Suminski et al. 2007a, their Fig. 6) and movement (Diedrichsen et al, 2005; Grafton et al, 2008; Seidler et al, 2004). These included subcortical activations spanning anterior (lobule V) and posterior (lobule VI) regions of right lateral cerebellar cortex, deep cerebellar nuclei (interposed and/or dentate), bilateral red nucleus and bilateral activations in the cingulate motor areas that extended into the superior frontal gyri: left supra-adjacent supplementary motor area (SMA), and right pre-SMA.

Figure 5.

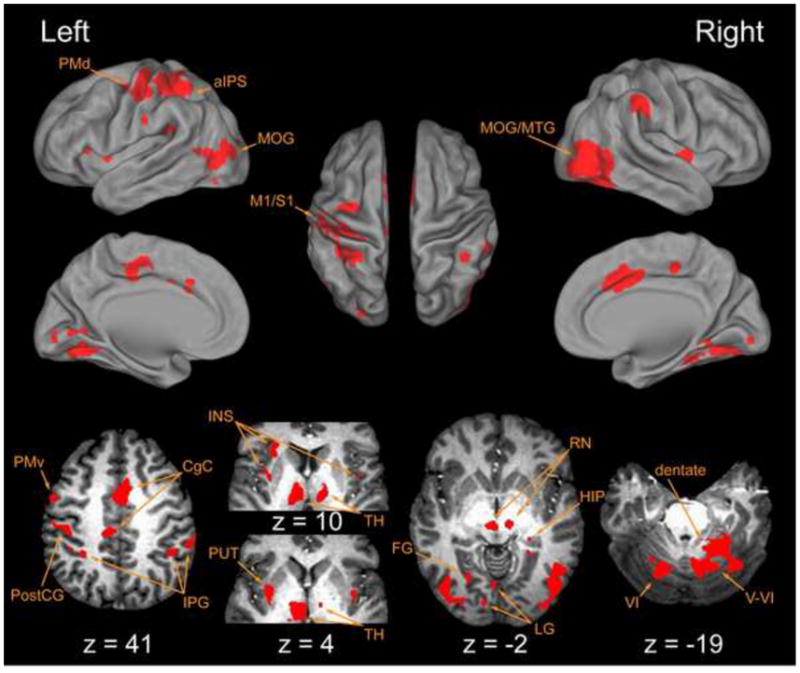
Voxel-wise t-tests compared fit coefficient values versus 0.0, identifying regions that showed a statistically significant correlation between the hemodynamic response and the “GO” cue regressor. Lateral, medial and dorsal surface plots (top) and axial views (bottom) indicate cortical regions with BOLD signal components generally correlated with task execution. Here and elsewhere, left hemispheric activities are shown to the left of each panel. Abbreviations: aIPS anterior intraparietal sulcus; CgC cingulate cortex; FG fusiform gyrus; HIP hippocampus; INS insula; IPG inferior parietal gyrus; LG lingual gyrus; M1 primary motor cortex; MOG middle occipital gyrus; MTG middle temporal gyrus; PMd dorsal premotor cortex; PMv ventral premotor cortex; PostCG post central gyrus; PUT putamen; RN red nucleus; S1 primary sensory cortex; TH thalamus; V cerebellar lobule V; V1 cerebellar lobule V1.

Table 2.

Location (center of mass) and volume of activations related to Level-1 Go cue

	H	Vol	Coord			T
Anatomy Label		μl	x	y	z
Cortical
PreCG (BA 6) (PMd)	L	209	−32	−10	51	11.8
(PMv)	L	324	−52	1	38	10.8
PostCG (BA 3); SPL (BA 5,7); PreCG (BA 4)	L	4349	−40	−26	52	15.1
SPL (BA 5,7) (IPS)	L	2405	−31	−46	50	11.6
IPL (BA 39, 40)	R	1309	54	−37	40	12.7
	L	227	−52	−19	27	9.8
	L	832	−45	−33	23	13.5
CgC (BA 32, 24); SFG (BA 6)	R/L	2421	3	6	40	13.2
pCgC (BA 31, 23); SFG (BA 6)	L/R	1255	−5	−25	45	12.0
aINS	L	587	−27	18	12	11.8
pINS	L‡	1163	−34	−3	10	16.9
	R	241	39	−5	4	11.5
HIP	R	165	23	−34	3	9.2
MTG (BA 37)	L	120	−45	−57	7	9.1
MOG (BA 19); LG (BA 18); FG (BA 20)	L*	8084	−30	−69	−5	14.2
MOG (BA 19); MTG (BA 37); FG (BA 20)	R†	15328	31	−61	−11	13.7
LG (BA 18)	L	181	−2	−68	0	9.8
	L/R	144	−4	−83	−4	8.9
Subcortical
pPUT; claustrum	L	see‡
TH(VL, DM, LP), RN	L	2654	−8	−20	6	11.0
	R	323	10	−20	−1	8.9
TH(VL, DM, LP)	R	624	14	−17	12	9.8
CER(lob VI)	L	see *
CER(lob V, VI); dentate; vermis(IV, V, VI, VIII)	R	see†

^{*,†, ‡}indicates activities that extend between cortical and subcortical regions

Abbreviations: H Hemisphere; L left; R right; Vol Volume; Coord Coordinates; T peak T; BA Brodmann’s area; a anterior; p posterior; lob lobule

CER cerebellum; CgC cingulate cortex; DM dorsomedial nucleus; FG fusiform gyrus; HIP hippocampus; IPL inferior parietal lobule; IPS intraparietal sulcus; INS insula; LG lingual gyrus; LP lateral posterior nucleus; MOG middle occipital gyrus; MTG middle temporal gyrus; PMd dorsal premotor cortex; PMv ventral premotor cortex; PostCG post-central gyrus; PreCG pre-central gyrus; PUT putamen; RN red nucleus; SFG superior frontal gyrus; SPL superior parietal lobule; TH thalamus; VL ventrolateral nucleus

Figure 6.

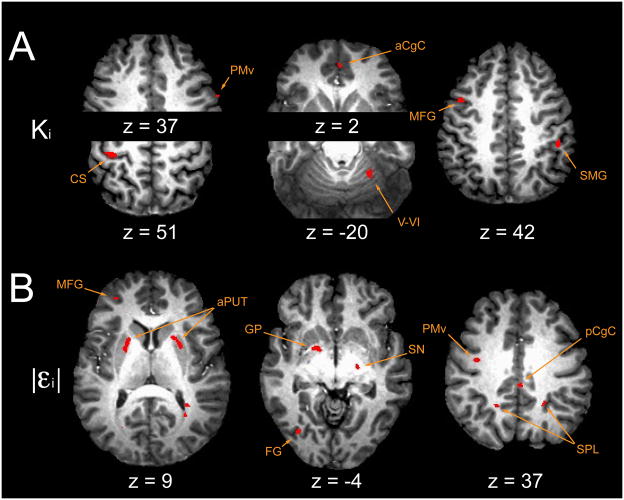
FMRI results: current state regressors. (A) K_i, current trial perturbation amplitude and (B) |ε_i| current absolute value of trial error. See Table 2. Abbreviations: aCgC anterior cingulate cortex; aPUT anterior putamen; CS central sulcus, pre/post central gyrus; FG fusiform gyrus; GP globus pallidus; MFG middle frontal gyrus; pCgC posterior cingulate cortex; PMv ventral premotor cortex; SMG supramarginal gyrus; SN substantia nigra; SPL superior parietal lobule; V–VI cerebellar lobule V, VI.

Although the task was persistently novel, subjects did optimize performance by adapting to the approximate mean of the load distribution (Fig 4B) and thus, we expected BOLD activation in areas previously implicated in the feedforward compensation for altered kinematic or kinetic behavior of a hand-held tool (Grafton et al. 2008; Imamizu et al. 2000, 2004; Jueptner et al. 1997; Krakauer et al. 2004; Seidler et al. 2004, 2006; Shadmehr and Holcomb, 1997; see also Desmurget et al. 2004). Indeed, the primary-, pre-, supplementary- and cingulate-motor area activities highlighted above could reflect these areas’ contributions to motor learning (cf. Sanes, 2003). The observed activity in lobule VI of the left posterior cerebellum was in an area frequently implicated in visuospatial motor learning (Imamizu et al. 2003, their Fig 4; Krakauer et al. 2004; Diedrichsen et al. 2005; see also Boyd and Winstein, 2004; Gilbert and Thach 1977). Additional subcortical activations were observed in motor regions of the left striatum (posterior putamen) and bilateral thalamic nuclei: ventrolateral (VL), dorsomedial (DM) and lateralposterior (LP), structures thought to be part of cortico-thalamo-striatal-cortical loops important for procedural and motor skill learning (Doyon et al., 2003; Graybiel 1995; Houk 2011; Houk and Wise 1995; see also Seidler et al. 2006). Smaller cortical activation volumes were located in the right hippocampal/parahippocampal region, areas thought to be important for the formation and maintenance of sensorimotor and spatial memory (Burguess et al. 2002; Rolls 1991, 1999; Fuster 2009; Nadel, 1991) as well as other functions supporting sensorimotor integration and learning (see Bland and Oddie, 2001; Cohen and Eichenbaum 1991; Dypvik and Bland, 2004).

3.2.2 Level-2 and Level-3 Analyses

The sequential Level-2 and Level-3 analyses were intended to identify small signal modulations superimposed on the average task-related activity removed by the Level-1 analysis. Based on Eqn [6], we hypothesized that the Level-1 residual BOLD time series would reflect trial-by-trial fluctuations in environmental load and kinematic performance (Level-2) as well as fluctuations related to memories of prior loads and performances (Level-3).

Altogether, the Level-2 and Level-3 analyses revealed robust activity in multiple areas previously implicated in processing motor performance errors and the acquisition of compensatory responses reducing such errors (Table 3) (Desmurget et al. 1999; Doyon et al. 2009; Graybiel 2005; Hikosaka et al. 1999, 2000; Imamizu et al. 2003; Jueptner and Weiller, 1998; Miall et al. 2001; Seidler et al. 2006; Tunik et al. 2005). Confidence in the activity within each region was further assessed by a post-hoc jackknife analysis (Table 3), which counted the number of times a region dropped from significance when each subject, in turn, was excluded from analysis. Note that many regions with “small” activation volumes (< 50 μl) were robust against dropout in the jackknife analysis.

Table 3.

Location (center of mass) and volume of activations related to Level-2 and Level-3 terms

Anatomy Label	|εi|						Ki						Ki - 1						Ki - 2						K̂
	H	Vol	Coord			T	H	Vol	Coord			T	H	Vol	Coord			T	H	Vol	Coord			T	H	Vol	Coord			T
		μl	x	y	z			μl	x	y	z			μl	x	y	z			μl	x	y	z			μl	x	y	z
Cortical
SFG (BA 6) {pre-SMA}																			R	51	6	9	62	4.3	R↓	21	7	−1	68	4.6
MFG (BA 6) {pre-PMd}	R↓	21	31	8	52	4.3	L↑	69	−41	5	42	4.9	R↑	121	46	2	49	5.6	R↑	67	51	1	47	5.1	R↑	126	44	1	49	5.5
MFG (BA 9,46,10) {prefrontal Ctx}	L↑	44	−32	37	19	4.9													L↑	65	−26	32	21	4.9
	L	55	−32	45	10	4.4
IFG (BA 44)																			R↑	49	36	16	16	4.7
PreCG (BA 6) {PMd}							R↑	78	35	−16	65	4.8
PreCG (BA 6) {PMv}	L↑	52	−37	−9	37	5.7
	L↓	24	−27	−7	35	4.3	R↓	26	59	−1	37	4.2
	R↑	40	54	−9	32	5.4
PreCG, CS, PostCG, (BA3,4)							L↑	372	−37	−28	50	5.2
Precuneus (BA 7)	R	67	5	−50	34	4.6
SPL	L↑	80	−18	−50	40	5.0													L↓	34	−17	−71	41	4.6
	R↑	49	19	−59	40	5.3
	R↑	126	23	−47	37	4.8
IPS (BA7)																									R	71	29	−65	46	4.4
																									R	52	28	−72	36	4.6
AG (BA 39)	L	44	−49	−63	30	4.5
	L↓	23	−51	−62	26	4.5
SMG (BA 40)							R↑	57	46	−34	42	4.5
STG (BA 21)	R↓	22	64	−30	5	4.5
MTG (BA 21)													R↑	41	69	−20	−3	5.7	R↓	24	53	−22	−7	4.3	R	24	69	−20	−2	5.6
MTG (BA 37)																			L↑	43	−37	−58	1	6.1
FG (BA 20,37)	R	22	36	−58	−9	4.5							R	38	38	−42	−18	4.8	R↑	76	35	−34	−14	5.6	L ↑	see* below
																									L↑	72	−44	−58	−13	5.1
FG (BA 19)	L↑	58	−32	−72	−4	6.7
aCgC (BA 32)	R↓	22	2	34	29	4.4	R	31	3	47	1	4.7	R↑	87	16	42	6	5.4
	R↑	335	16	23	29	6.7
	R↓	27	7	46	6	4.4
pCgC (BA 23)	R	37	2	−31	38	4.8													L↑	60	−23	−36	32	5.5
	L	26	−13	−24	29	4.6													L↑	53	−17	−41	28	5.0
	R	53	5	−25	23	4.4
	R↓	23	8	−34	21	5.1
	L	36	−24	−67	11	5.1
IST																									R↑	52	11	−33	−10	5.3
SP													-↓	26	1	12	12	4.5
PHIP (BA 36)													R	24	27	−33	−9	4.3	R	61	35	−34	−14	5.5
HIP																									R↓	21	35	−16	−7	4.6
																									R↑	122	32	−25	−11	5.5
Subcortical
aPUT	L↑	332	−20	5	10	4.7
	R↑	229	24	8	8	4.5
GP	L↑	179	−16	5	−2	5.1																			R↑	64	15	0	1	5.3
SN	R↑	39	20	−15	−4	5.9																			R	37	10	−20	−10	4.6
TH (CM)																									R	38	9	−25	7	4.6
RN																									L↑	63	−3	−26	−3	4.7
																									R↑	178	11	−25	−3	5.1
CER (lob V, VI)							R↑	182	25	−47	−19	4.5													*L	273	−34	−52	−16	5.2
CER (lob VIIIB, IX)																									L↑	65	−15	−47	−43	4.6
CER vermis (lob VI–VII)																			R↓	32	5	−64	−20	4.5
PMJd	R↑	136	4	−40	−36	4.8

^*indicates activities that extend between cortical and subcortical regions.

Bootstrap results:^↑: high confidence (dropped 0–1 times);^↓: lower confidence (dropped 10–14 times). No region dropped 15 or more times from significance.

Abbreviations: H Hemisphere; L left; R right; Vol Volume; Coord Talairach coordinates; T peak T; BA Brodmann’s Area; a anterior; p posterior; lob lobule; Ctx cortex AG angular gyrus; CER cerebellum; CgC cingulate cortex; CM centromedian nucleus; CS central sulcus; FG fusiform gyrus; GP globus pallidus; HIP hippocampus; IFG inferior frontal gyrus; IST isthmus; IPS intraparietal sulcus; MFG middle frontal gyrus; MTG middle temporal gyrus; PHIP parahippocampal gyrus; PMd dorsal premotor cortex; PMv ventral premotor cortex; PMJ ponto-medullary juntion; PostCG post-central gyrus; PreCG pre-central gyrus; PUT putamen; RN red nucleus; SFG superior frontal gyrus; SMA supplementary motor area; SMG supramarginal gyrus; SN substantia nigra; SP septum; SPL superior parietal lobule; STG superior temporal gyrus; TH thalamus

Level-2 analysis identified two large clusters of activation correlated with trial-by-trial fluctuations in K_i (Fig 6A): left sensorimotor cortex and right cerebellar hemisphere lobule V/VI. Smaller clusters were identified in areas previously implicated in the spatial planning and execution of visually-directed movements (Boussaoud 2001; Dieber et al. 1998; Taira et al. 1990; see also Paus 2001): left pre-PMd, right PMd and PMv, anterior cingulate and inferior parietal cortices. BOLD signal changes in the basal ganglia correlated with trial-to-trial fluctuations in unsigned errors |ε_i| (Fig 6B): bilateral anterior dorsal putamen (rostral to the anterior commissure), left globus pallidus and right substantia nigra. These areas are thought to support reinforcement learning and the conditional selection of spatially-directed motor actions and sequences of actions (Graybiel 1998; Graybiel and Kimura 1995; Gurney et al. 2001). We also found |ε_i|-correlated activities distributed throughout neocortical areas with reciprocal connections to the basal ganglia (Middleton and Strick, 2001b; Alexander et al. 1986; see also Selemon and Goldman-Rakic 1985, 1988): left hemispheric pre-frontal (BA 10) and inferior parietal (BA 39) cortices; right hemispheric pre-PMd (per the convention of Picard and Strick, 2001), anterior cingulate, superior parietal and superior temporal cortices; bilateral activity in PMv, posterior cingulate, fusiform and precuneate cortices. We also found |ε_i|-correlated activity within the pontomedullary tegmentum, an area that includes the inferior olive, serotonergic raphe nuclei and reticulospinal projections.

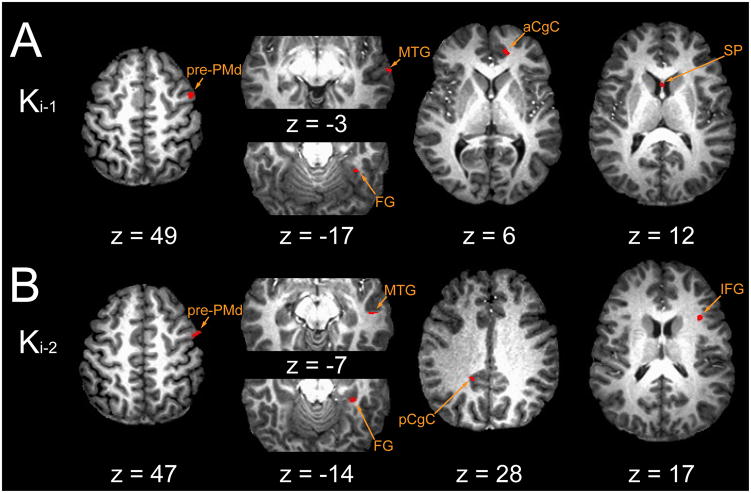
Both of the Level-3 analyses modeled the Level-2 residuals as a weighted combination of prior trial perturbation K_i-1 and K_i-2 reference waveforms. In the memory model analysis (Fig 7), the regression treated the memories independently and so they competed to capture variability within the residual BOLD data. Signal components that correlated with K_i-1 (Fig 7A) were located cortically, broadly distributed throughout right hemispheric regions associated with the formation and maintenance of sensorimotor memories (Lenartowicz and McIntosh 2005; Gazzaley et al. 2004): in dorsal prefrontal cortex (pre-PMd) and in anterior cingulate, middle temporal, and fusiform cortices, areas thought to interconnect with the basal ganglia and/or cerebellum (eg. Bostan et al. 2010; Goldman–Rakic, 1988; Hoshi et al. 2005; Hoover and Strick, 1993, 1999; Kelly and Strick 2003; Middleton and Strick 1998, 2001; Selemon and Goldman-Rakic 1988). Moreover, memory-related activity in the septal area is consistent with engagement of a septo-hippocampal system important for maintenance of spatial memories (Olton, 1977). BOLD signal components correlating with K_i-2 also spanned neocortex (Fig 7B): right superior- (i.e. pre-SMA, BA 6) and inferior- (BA 44) frontal gyri, pre-PMd (BA 6), middle temporal (BA 21) and fusiform cortices; left prefrontal (BA 46), superior parietal, middle temporal (BA 37) and posterior cingulate cortices (BA 23). Areas with activities correlated with K_i-2 did not overlap with those correlated with K_i-1. We also observed memory-model correlations with both K_i-1 and K_i-2 in the right parahippocampal cortex (BA 36); parahippocampal cortex is part of an interconnected network of prefrontal and hippocampal formation regions (Goldman-Rakic et al 1984) thought to play a critical role in the encoding/retrieval (Burgess et al. 2002) and maintenance of novel, short-term sensorimotor memories (Ranganath and D’Esposito 2001; Hasselmo and Stern 2006; for a review see Eichenbaum 2000), particularly those of spatial locations within a visual scene (but see also Eichenbaum et al. 1999).

Figure 7.

FMRI results: regions with BOLD signal changes correlated with memory model terms: (A) K_i-1 and (B) K_i-2. Abbreviations: aCgC anterior cingulate cortex; FG fusiform gyrus; IFG inferior frontal gyrus; MTG middle temporal gyrus; pCgC posterior cingulate cortex; PMd dorsal premotor cortex; SP septal area.

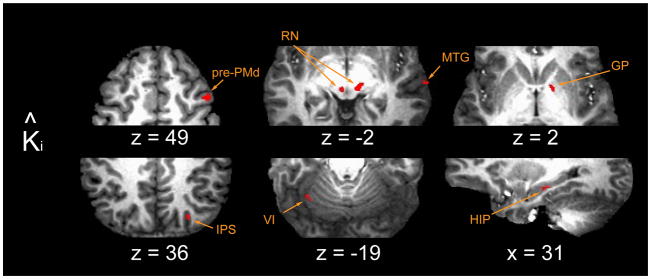
In the prediction model (Fig 8), K_i-1 and K_i-2 entered the regression in a subject-specific proportion corresponding to our best estimate of his or her prediction of the upcoming load (Eqn. [4]) and so the two memory terms did not compete for data variance in the analysis. We found high-confidence correlation with K̂_i in the left cerebellar hemisphere (lobules VI and VIII/IX), regions thought to contribute to internal representation of novel hand-held tool behaviors (Imamizu et al. 2000, 2003; Diedrichsen et al. 2005; for a review see Wolpert et al. 1998), reward-based behavioral learning (Haruno et al. 2004) and, potentially, the prediction of neural events (Dugas and Smith 1992; see also Coenen and Sejnowski 1996; for a review see Courchesne and Allen 1997). High confidence clusters were also located bilaterally in the region of the red nuclei, which receive cerebellar output through the deep cerebellar nuclei (Courville 1966; cf. Glickstein et al. 2011; for review and discussion see Kennedy 1990) and which influence spinal gamma motor neurons via the rubrospinal and rubrobulbospinal tracts (Appelberg 1962a, 1962b; Appelberg et al. 1975; Johansson 1988). The red nuclei also send projections back to the cerebellum via the principal olive (Appelberg 1967; Jeneskog 1974; Nathan and Smith 1982), a pathway that appears to play an important role in the control of limb posture (Kennedy et al. 1982) and movement (Jeneskog 1974). Several smaller clusters were observed in the right substantia nigra, globus pallidus and centromedian nucleus of the thalamus. These nuclei contribute to cortico-striatal and thalamo-striatal “loops” (Ilinsky et al. 1985; Matsumoto et al. 2001; Glimcher and Lau 2005) thought to be involved in reward-optimizing behaviors (Schultz et al. 1993; Middleton and Strick 2001b; see also Schultz et al. 1995) and the selection of actions in response to unexpected stimuli (Matsumoto et al. 2001; Minamimoto et al. 2005, 2009; see also Tunik et al. 2009). Additional BOLD signal correlations with K̂_i were found in the region of the hippocampus, an area thought to be important for the formation of spatial memories (Mahut 1971), maps of the body in space (Nadel and MacDonald 1982; Nadel 1991) and “memory spaces” (Eichenbaum et al. 1999), as well as in the anterior and posterior intraparietal sulcus, areas involved in the estimation of dynamic limb state and prediction of the sensorimotor consequences of motor commands (Desmurget et al. 1999; Tunik et al. 2005), the on-line feedback control of goal-directed actions (Tunik et al. 2005) and the multimodal sensory integration (Beuchamp et al., 2010) required for a mixed body- and gaze-centered spatial encoding of motor goals (Bernier and Grafton, 2010).

Figure 8.

FMRI results: regions with BOLD signal changes correlated with prediction model term K̂ _i. Abbreviations: GP globus pallidus; HIP hippocampus; IPS intraparietal sulcus; MTG middle temporal gyrus; PMd dorsal premotor cortex; RN red nucleus; VI cerebellar lobule VI.

BOLD signal components correlating with K̂_i overlapped with two regions identified in the memory model analysis [right pre-PMd and middle temporal gyrus (BA 21)] but were distinct in other cortical areas including the right hippocampus, right superior parietal lobule (anterior and posterior intraparietal sulcus, IPS; BA 7) and left fusiform gyrus (BA 37). In pre-PMd, a comparison of MSE values from the two models revealed a slight explanatory advantage for the memory model over the prediction model (memory model: median MSE = 343 %², range: 81 to 1235 %²; prediction model: median MSE = 345 %², range: 82 to 1242 %²; 1-sample sign test on the intrasubject difference between MSE values: p<0.0005). However, when we account for the memory model’s additional degree of freedom (Bohlin, 1978; cf. Ljung, 1999 p. 508), we find no compelling evidence to reject the prediction model as the most parsimonious explanation of the data variance. Based on this equivocal outcome, we cannot conclude whether activity in pre-PMd corresponds to the storage/recall of sensorimotor memories needed to compose a prediction of upcoming loads or the composition of that prediction itself. We also found equivocal results for the MTG overlap region.

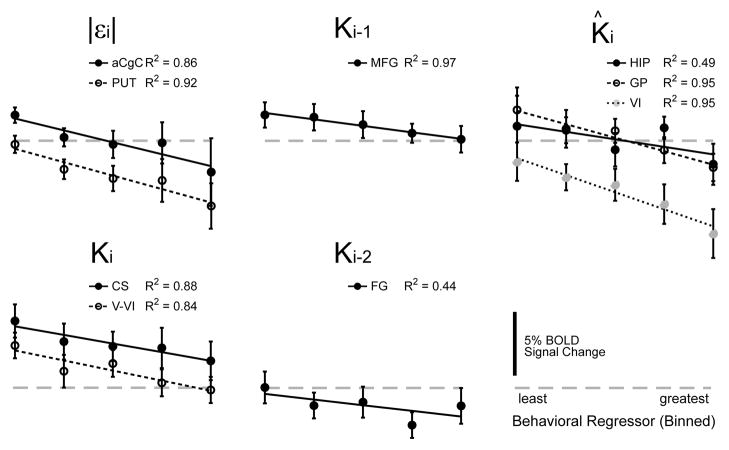
In regions of interest throughout the brain, the relationship between the regressor magnitude and BOLD signal change was approximately linear (Fig 9). The linearization of kinematic performance about the operating point defined by the currently predicted load (Fig 4B) was matched by a corresponding linear relationship between BOLD signal change and the behavioral variables contributing to that prediction. For example, the BOLD signal varied by 3.5%±6.2% across the range of K_i values in the cerebellar cortex (across-subjects mean ± SD, n=18), by 1.9%±4.9% across the range of K_i-1 values in MFG, by 1.4%±7.7% with variation in K_i-2 in FG, by 4.8%±8.7% with variation in |ε_i| in the PUT and by 4.5%±6.7% with variation in K̂ in the GP. We then evaluated the extent to which the population trends of Figures 8 and 9 reflected predictive neural activity within individual subjects (Table 4). We performed within-subject fits of a linear equation to the binned (regressor α_i, response β_i) data within GP, HIP and CER. We considered as significant those fits with linear trends with p ≤0.1. Out of 18 subject datasets analyzed, three demonstrated predictive activity in all three regions of interest (GP, HIP and CER), four subjects had predictive activity in two out of the three regions whereas seven subjects had predictive activity in just one of them. We found no compelling evidence of predictive BOLD signals in four subjects. Thus, subjects were just as likely to exhibit predictive activity in multiple neuroadaptive systems as they were to have it in just one. Subjects were unlikely to exhibit no predictive activity in any of these regions. There was no clear grouping of subjects according to which regions displayed predictive signals: For subjects exhibiting multiple predictive responses at p ≤0.1, four displayed the combination GP and HIP, four had the combination GP and CER, whereas five had the combination HIP and CER. Although the absolute counts differ somewhat if we instead use a significance threshold that is more strict (p ≤ 0.05) or more liberal (p ≤ 0.15), the relative frequency of single vs. multiple predictive responses would not change meaningfully.

Figure 9.

BOLD activity versus binned parameter magnitude, averaged across subjects. Vertical error bars: ±1 SEM.

Table 4.

Single-subject analysis of predictive BOLD activity. Significance of linear term (slope)

Subject	GP	HIP	CER
1	***	***	***
2	*
3	**
4
5			**
6
7	*	***	***
8	**	**	**
9		***
10	*	***	*
11	*	***	**
12		**
14	**	***	***
15
16	***		***
17		*	***
18	***	***	*
20	**

^***p ≤ 0.05;

^**p ≤ 0.10;

^*p ≤ 0.15

4. Discussion

Subjects performed goal-directed wrist movements against spring-like loads that varied randomly from one trial to the next. Although the loads were in fact unpredictable, subjects tried to use sensorimotor memories from recent movements to predict and compensate for upcoming loads (Fig 4C). These predictions enabled subjects to adapt performance so that the task was accomplished, on average, with a minimum of effort (Fig 4A, inset). Using an approach proposed by Scheidt and colleagues (Scheidt et al. 2001), we estimated each subject’s prediction of upcoming load based solely on performance variables observed during the most recent trials. We used these estimates to identify neural correlates of memory-based sensorimotor prediction - a subject-specific ‘signature’ of prediction within the neuromotor system (Eqn 4). We used this time series, along with others reflecting trial-by-trial modulations in perturbation strength and performance errors, as inputs to a set of event-related analyses of the functional MR images obtained as subjects practiced the visual target capture task. The input time series were crafted (and verified) to be statistically independent, thereby enabling us to decompose, sequentially, the overall BOLD signal into components related only generally to performance of the task (Fig 5), components correlating with current-trial variations in performance (Fig 6), and components related to the storage/recall (Fig 7) and integration (Fig 8) of sensorimotor memories. The analyses revealed a distributed, bilateral network of cortical and subcortical activity supporting predictive compensation for changing environmental loads during visual target capture. Cortical regions exhibited trial-by-trial fluctuations in BOLD signal consistent with the associative storage and recall of task-relevant sensorimotor memories or “states” (Figs 6A and 7); bilateral activations in associative regions of the striatum were consistent with reward-optimizing reinforcement learning (Fig 6B); activity in the cerebellar cortex implicated this structure in both the online (Figs 5 and 6A) and predictive (Fig 8) compensation for environmental disturbances. These results suggest active engagement of each of the three primary neuroadaptive mechanisms thought to contribute to motor learning and adaptation (Houk and Wise, 1995; Doya, 1999, 2000). Importantly, BOLD signatures of memory-based prediction of upcoming load were not limited to the cerebellum, but were also observed in an output pathway of the basal ganglia and in several cortical areas, including the hippocampus and posterior parietal cortex. Analysis of individual subject images in these regions found that subjects were just as likely to exhibit predictive activity in multiple regions, as they were to display it in one. Although the multiplicity of predictive activity might have been due, in part, to the highly-constrained nature of our task (discussed in section 4.2.1 below), the results demonstrate that compensation for environmental load relies on contributions from multiple neuroadaptive mechanisms.

4.1. BOLD signal correlates of current sensorimotor state

By design, the applied load K_i correlated strongly with peak torque applied to the subject’s hand during wrist flexion. Because neuromuscular control of the wrist is compliant, K_i also correlated with “signed” kinematic error: subjects undershot the goal (a negative error) when the load was stiffer than average and overshot the goal (positive error) when the load was more compliant than average (Fig 4B). A limitation of the regression analyses we used is that they cannot determine whether BOLD signals that correlate with K_i actually depend on load, error, or some combination of factors that co-vary with load. The Level-2 analysis identified K_i-related activities in areas previously implicated in the representation and online (moment-by-moment) compensation for kinematic performance errors, including left primary sensorimotor and right inferior parietal and anterior cingulate cortices as well as right cerebellar lobules V–VI (cf. Diedrichsen et al. 2005; Suminski et al. 2007a; see also Jueptner et al. 1997). The same analysis also identified activities in areas implicated in the production of graded force at the hand: primary sensorimotor, premotor, and anterior cingulate cortices (cf. Cramer et al., 2002; Dai et al., 2001; Vaillancourt et al. 2003, Ward et al. 2008). Although the question of whether cortical neurons encode information related to movement kinematics or kinetics has received great interest (Georgopoulos et al. 1989; Georgopoulos et al. 1992; Kalaska et al. 1989; Moran and Schwartz 1999; but see also Hatsopoulos et al. 2007), recent theoretical and experimental evidence suggests that the brain adjusts its neural tunings (feedback sensitivities) according to prevailing task demands (i.e. optimal feedback control: cf. Loeb et al. 1990; Loeb and Marks 1985; Todorov and Jordan 2002; Scott 2004). Consistent with this idea, a recent FMRI study found that separate brain regions contribute to the moment-by-moment feedback regulation of wrist angle during a stabilization task and the adjustment of feedback set-point and/or sensitivity on a longer time scale when the moment-by-moment control fails to achieve subjective performance criteria (Suminski et al. 2007a). The fact that the regressor K_i (commanded load) correlates with signed kinematic error (ε_i) is not a limitation in our analysis, but rather makes K_i an ideal proxy for whatever kinematic or kinetic sensorimotor states contribute to feedback control in our task.

4.2. Mechanisms supporting predictive compensation during visually-directed movement

Predictive compensations must be guided by past experience if they are to be effective in improving performance. Even trial-and-error exploration requires storage of recent performance information so that actions with greater reward are repeated. Behavioral analysis (Fig 4) identified K_i-1 and K_i-2 as a minimal set of memories/states contributing to trial-by-trial evolution of performance observed in our task. Image analysis found K_i-1 and K_i-2 represented in multiple, widely-separated, and non-overlapping regions in the right hemisphere, including prefrontal (pre-PMd) and temporal (MTG) association areas, cingulate cortex, septum and parahippocampal areas. These results are consistent with the idea that a fundamental role of cortex is to encode states of behavioral significance (Houk and Wise 1995; Doya 1999, 2000). More specifically, they are consistent with studies exploring the neural basis of working memory (for reviews see Eichenbaum 2000; Fuster 2009; see also Ullman 2004), which implicate reentrant cortical-cortical and cortico-subcortical loops in the storage and maintenance of memoranda. Unit recording evidence in animals and functional imaging and lesion studies in humans demonstrate that memory networks are “largely interregional, linking neuron assemblies and smaller networks in separate and noncontiguous areas of the cortex” (Fuster 2009). Procedural memory, which facilitates the learning and adaptation of sensorimotor skills, is mediated by prefrontal and middle temporal cortices, in connection with anterior putamen and caudate (Knowlton et al. 1996; Miyachi et al. 2002). In contrast, prefrontal, parietal, septal, parahippocampal and thalamic areas contribute to the formation and maintenance of episodic memories (of personal experience) and spatial memories, (of object location; for reviews see Aggleton and Brown 1999; Burgess et al. 2002; Fuster 2009) and to the consolidation of new declarative memories (memories that can be held in consciousness; cf. Tulving 1987). Because these forms of memory may be important during the initial stages of adapting to a novel visuomotor perturbation (cf. Anguera et al. 2009; Keisler and Shadmehr, 2010; see also Redding and Wallace 2002), both may have contributed importantly to subject performance in our persistently novel task.

Although activation sites for K_i-1 were adjacent to those for K_i-2 in executive and sensory association cortices (pre-PMd and MTG), they were non-overlapping in other areas (cingulate, fusiform and inferior frontal cortices, septum). This result implies a distributed network encoding of serial order in goal-directed reaching. That is, as information cascades through working memory, it shifts from circuits associated with the most recent movement attempt to circuits representing events further in the past.

Predictive BOLD signals based on these memories were located in cerebral cortex [including right hippocampus, right posterior parietal (anterior IPS) and right PMd cortices], in the right globus pallidus and centromedian nucleus of the thalamus (an output pathway of the basal ganglia) and in the left cerebellar cortex (lobule VI) and bilaterally in the red nucleus. These regions are thought to play very different roles in the planning and control of sensory-guided movements. In addition to it’s role in declarative memory formation in general, the right hippocampal system is also believed important for forming spatial memories and/or “maps of the body in space” (Piekema et al. 2006; but see also Eichenbaum et al. 1999), information that is conveyed to neocortical association areas via cingulate cortex (Sutherland et al. 1988) for possible use in determining which joints to move, in which direction. In contrast, anterior intraparietal cortex plays a critical role in the estimation of dynamic limb state for use in the prediction of the sensorimotor consequences of motor commands (Desmurget et al. 1999; Tunik et al. 2005) and the on-line feedback control of goal-directed actions (Tunik et al. 2005; see also Suminski et al. 2007). The basal ganglia play a critical role in selecting movements (Graybiel 1998; Gurney et al 2001a, 2001b; Houk 2010; Tunik et al. 2009) and in the scaling of movement amplitudes (Desmurget et al. 2004; Krakauer et al. 2004; see Jueptner and Weiller 1998). The cerebellum is implicated in the ongoing feedback regulation of limb position (Eccles 1967; Mackay and Murphy 1979), in the predictive cancelation of sensory afference (Blakemore et al. 1998, 2001; see also Serrien and Wiesendanger 1999) and in the adaptation to novel visuomotor (Imamizu et al. 2000, 2003, 2004, 2007; Seidler et al. 2004; Tseng et al. 2007) and dynamic environments (Diedrichsen et al. 2005; Shadmehr and Holcomb 1997) that require complex adjustments in the coordination of phasic activations in muscles driving limb motion (see Krakauer et al. 2004; see also Liu et al. 2011). How might these predictive signals have contributed to adaptive control in the present experiments?

4.2.1. Strategies…

At least three different adaptive strategies could have been used to solve the visual target capture task. First, subjects could have implemented a spatial remapping strategy to capture the target. Here, the appropriate response to overshoot (undershoot) would be to move the internal representation of the target closer to (farther from) the starting point of the hand. As the right hippocampus is thought to be involved in storing and maintaining the topographic memory (spatial map) needed to move to a remembered goal (Maguire et al. 1996, 1998; Nadel and MacDonald 1980; Vargha-Khadem et al. 1997; for a review see Burgess et al. 2002), our data suggest that subjects may have recruited the hippocampus to remap the visuospatial relationship between visually-perceived target distance and desired movement extent. Cingulate cortex conveys hippocampal information to neocortical association areas (Sutherland et al. 1988), thus providing a means by which the hippocampus could influence the spatial planning of subsequent movements (cf. Anderson and Buneo 2002). We also found two clusters of predictive activity in the right SPL around the IPS, one located near the parieto-occipital junction and the other located more anteriorly - areas previously shown to display reach-related activity (Filimon et al. 2009; Bernier and Grafton 2010). Our observations are consistent with the idea that posterior parietal cortex plays a critical role in multimodal sensory integration for spatially directed action (Avillac et al. 2005; Prevosto et al. 2009; Bisley and Goldberg 2003, 2010). Spatial remapping could be part of a ‘fast’ compensatory response to kinematic error that shares critical resources with the declarative memory system (Keisler and Shadmehr, 2010)

Second, because the manipulandum constrained the wrist in all dimensions except the task-relevant degree-of-freedom, subjects could have compensated for target overshoot (undershoot) by decreasing (increasing) the amplitude of any preexisting pattern of feed-forward motor commands inducing wrist flexion. A large body of evidence suggests that the basal ganglia play a vital role in selecting which movement to make in a given circumstance and in planning/controlling the selected movement’s amplitude (Desmurget et al. 2003, 2004; Krakauer 2004; see also Houk 2010). In our experiments, anterior putamen, globus pallidus and substantia nigra all demonstrated strong activity related to reward, prediction error and/or other error correction processes that are dependent on the magnitude but not sign of kinematic errors. Moreover, the observation of predictive activity in right CM thalamus is suggestive because this structure receives projections from the globus pallidus and sends reciprocal projections back to striatum (Glimcher and Lau 2005; Matsumoto et al. 2001; McLardy 1948), thus providing a way for load predictions in the basal ganglia to influence movement selection and/or amplitude planning on the subsequent movement attempt (see Schultz et al. 1995; see also Minamimoto 2005).

Third, subjects could have adapted to the novel spring-like dynamics of the manipulandum by adjusting coordination among the multiple muscles spanning the wrist. Numerous experimental, lesion, and theoretical/modeling studies implicate the cerebellum in the sensorimotor adaptation and learning of coordinated movement (for example: Martin et al. 1996; Thach 1996; Imamizu et al. 2000, 2003, 2004; Bastian 1996; see also Miller and Sinkjaer 1997; Tseng et al. 2007). In one model of cerebellar function (Kawato and Gomi 1992; Wolpert et al. 1998; Imamizu et al. 2003), a feedback controller, in conjunction with an inverse model of the controlled object, transforms a desired trajectory of the arm into an appropriate set of motor commands. Learning an accurate inverse model is facilitated by action of the feedback controller, which transforms trajectory error into a feedback motor command that can both augment the ongoing movement and train the inverse model used to generate the commands in the first place. The controller also includes a forward model that takes as input the current state of the arm and an efferent copy of motor commands (von Holst and Mittelstadt 1950, as cited in von Holst 1996) and produces an estimate of the new state of the arm. One possible use for the predictions provided by a forward model is to serve as an estimate of sensory signals during the delay associated with sensory transduction and transport (Wolpert et al. 1995; Miall et al. 1993; Bell et al. 2008; Ebner and Pasalar 2008).

The observation of bilateral predictive activity in the mesodiencephalic area of the red nucleus in the current study suggests another use for predictive signals. Recall that the red nuclei are an important output channel of the cerebellum that receives projections from the deep cerebellar nuclei (Courville 1966; cf. Glickstein et al. 2011) and send projections back to the cerebellar nuclei and cortex via the principal olive (Appelberg 1967; Nathan and Smith 1982; Onodera 1984; DeZeeuw et al. 1998). The red nuclei also send descending projections to the spinal cord, where they act primarily on gamma motor neurons γMNs (Appelberg et al. 1975; Johansson 1988) to encode the dynamics of limb muscle activity (Miller and Sinkjaer 1998). Whereas the reciprocal connections may provide a way for current load predictions to influence cerebellar feedback control of ongoing movement, the descending projections provide a means for the cerebellum to assert conditional feedback control over the movement (see Houk and Rymer 1981). Accordingly, the cerebellum need not produce the primary motor commands that drive limb motion via extrafusal muscle fiber activation (although it may play a primary role in the learning of these commands). Instead, we take the traditional view that the cerebellum serves as an “accessory adjustor” to primary motor commands generated elsewhere, for example primary motor cortex (MacKay and Murphy 1979). Based on our observations, we speculate that predictive mechanisms in lateral cerebellar cortex compute motor commands sent to γMNs, which innervate intrafusal muscle fibers that give rise to muscle spindle afferents. As noted by Houk and Rymer (1981), the intrinsic parallel configuration of intrafusal and extrafusal muscle fibers make muscle spindles ideal model reference error detectors - elements designed to “cancel” expected sensory feedback signals under conditions in which the controlled system (the extrafusal muscle fibers) responds precisely as does the model (the intrafusal fibers).

In conditional feedback control, movement control is exclusively feed-forward except when disturbances interfere with ideal performance, thus producing a model reference error signal (see Houk and Rymer, 1981). For this to work, however, γ-drive to the intrafusal fibers must predict the response of the limb as coupled to its (variable) external load - which can only occur if the γ command is itself adaptive. The cerebellar and red nucleus activity we observed (Fig 8) could be the origins of this adaptive command. Since spindle feedback projects back to the cerebellum via the spinocuneocerebellar tract, it is possible that conditional error signals originating from muscle spindles could be used to drive online feedback corrections (the conditional feedback control of Houk and Rymer 1981) and/or to update the forward and inverse models that may have been used to learn the commands in the first place (Fagg et al. 1997; Kawato and Gomi 1992).

4.2.2. …speculations…

All three of these compensatory strategies are viable solutions to our visual target capture task. To the extent that predictive BOLD activity in the hippocampal and posterior parietal cortices, basal ganglia and cerebellum reflect the different adaptive approaches, the pattern of activations displayed in Table 4 suggests that all three may have been recruited to compensate for the imposed loads. For example, movement planning in frontal parietal networks may have been conducted within a spatial reference frame established by the hippocampus and associated structures. The basal ganglia may then have selected one particular sequence and scaling of muscle activations (a feedforward motor program) likely to realize that plan. Finally, the cerebellum may have monitored the ongoing movement by predicting the sensory consequences of the evolving action and by initiating feedback corrections and internal model updates when the realized sensations deviated from expectation. Future studies should examine how the brain might integrate multiple predictive compensations to achieve a final overall motor response and whether the multiple predictive mechanisms identified here compete or cooperate to compensate for imposed environmental loads.

We observed two regions of overlap in the two Level-3 analyses (right pre-PMd and right middle temporal gyrus). When we accounted for differences in model degrees of freedom, we found no compelling evidence to accept one model over the other in these areas and so, this activity equivocally corresponds to the representation of sensorimotor memories needed to compose a prediction of upcoming loads and/or the composition of that prediction itself. A previous PET study of motor adaptation and consolidation (Shadmehr and Holcomb, 1997) found activity “specific to the recall of a recently acquired internal model of the field” at nearly the same pre-PMd location as observed in our level-3 analyses, except in the left, not right, hemisphere (their Figure 3B). In the experiments of Shadmehr and Holcomb, subjects were required to adapt to the novel dynamics of a viscous curl force field while moving a planar, 2-joint manipulandum in 8 different directions and so, they could not have adapted using either a simple rescaling of existing coordination patterns or a spatial remapping of the target relative to the hand’s starting location. In contrast, a PET study by Krakauer and colleagues (Krakauer et al. 2004) and an FMRI study by Imamizu and colleagues (Imamizu et al. 2007) both found right-hemispheric premotor activity associated with visuomotor adaptation of right-handed movements in the presence of cursor rotation. Given the hemispheric difference between dynamic and visuomotor adaptations revealed by these previous studies and others (Sainburg 2002; Sainburg and Kalakanis 2000), the fronto-parietal activity observed in our Level-3 analysis may well indicate that subjects in our study adopted a visuospatial solution to the movement task rather than a dynamic adaptation. Indeed, subjects may have been predisposed to this kind of solution because they were already forced to solve a novel visuospatial transformation: they were required to lay recumbent in a scanner while making flexion/extension movements of the wrist, movements that were translated into vertical motions of a visual cursor.

4.2.3. … and implications

This study provided direct experimental evidence that prediction of hand-held load is a distributed computation supported by a bilateral network of cortical and subcortical activity, thus reflecting active engagement of three neuroadaptive mechanisms previously implicated in motor learning and adaptation (cf. Houk and Wise, 1995; Doya, 1999, 2000): cortical regions for the storage and recall of task-relevant sensorimotor and visuospatial memories, basal-ganglionic networks for selecting and scaling movements to optimize reward or a related signal, and cerebellar pathways for both the online and predictive compensation for environmental disturbances. Based on neurophysiological considerations and evidence from the literature, we concluded that these predictions likely represent distinct computations within cerebellar, basal ganglionic and hippocampal loops that engage cortical working memory. Although multiplicity of representations of predictive activity may have been facilitated by the highly constrained nature of our task, the results nevertheless demonstrate that compensations for environmental load can recruit multiple neuroadaptive mechanisms. By disambiguating load prediction from the processing, storage/recall, and weighted integration of recent sensorimotor memories, the present study demonstrates a new experimental approach that can be exploited to advance understanding of how the neural systems supporting motor adaptation are altered by experience, neurologic disease and pharmacological intervention.

Highlights.

• We used FMRI, a robot and time series analysis to study motor adaptation

• People use limited memory from recent movements to predict and cancel imposed loads

• Image analysis used state variables and predictions estimated from behavioral data

• BOLD correlates of prediction in: cerebellum, basal ganglia,several cortical areas

• Prediction is a distributed computation served by cortical/subcortical memory systems