Abstract
With the use of an endoscopic, high-speed camera, vocal fold dynamics may be observed clinically during phonation. However, observation and subjective judgment alone may be insufficient for clinical diagnosis and documentation of improved vocal function, especially when the laryngeal disease lacks any clear morphological presentation. In this study, biomechanical parameters of the vocal folds are computed by adjusting the corresponding parameters of a three-dimensional model until the dynamics of both systems are similar. First, a mathematical optimization method is presented. Next, model parameters (such as pressure, tension and masses) are adjusted to reproduce vocal fold dynamics, and the deduced parameters are physiologically interpreted. Various combinations of global and local optimization techniques are attempted. Evaluation of the optimization procedure is performed using 50 synthetically generated data sets. The results show sufficient reliability, including 0.07 normalized error, 96% correlation, and 91% accuracy. The technique is also demonstrated on data from human hemilarynx experiments, in which a low normalized error (0.16) and high correlation (84%) values were achieved. In the future, this technique may be applied to clinical high-speed images, yielding objective measures with which to document improved vocal function of patients with voice disorders.
INTRODUCTION
In recent years, voice scientists have utilized high-speed and multiple-camera imaging techniques to intensify their study of vocal fold dynamics. One important part of normal vocal fold vibration is the traveling wave which propagates along the vocal fold mucosa, commonly referred to as “mucosal wave propagation” presented by Hirano1 and Baer,2 and further developed by recent studies (e.g., Refs. 3, 4). The wave propagates not only in the transverse plane (lateral-longitudinal) but also in the sagittal plane (longitudinal-vertical) and coronal plane (lateral-vertical). The medial edge of the vocal fold exhibits wider and faster movements than more ventral and dorsal regions. Also, larger amplitudes of vibration are observed superiorly along the medial surface of the folds, as compared to more inferior regions.3, 5
Healthy vocal folds vibrate more symmetrically and periodically than vocal folds with pathologies.6 In clinical diagnosis, morphological pathologies of the larynx such as unilateral vocal fold polyps can be visually observed using a standard endoscope. However, some pathologies may not exhibit static, morphologic alterations, but only manifest themselves dynamically during phonation, e.g., functional dysphonias.7 Clinically, such voice disorders may exhibit left-right asymmetries or non-periodic oscillations, and usually result in a hoarse voice.8 These asymmetric and irregular vocal fold vibrations may be induced by pathological changes in biomechanical properties of vocal fold tissues.6, 7, 8, 9, 10, 11, 12
To determine whether an acoustic voice signal is abnormal, it is evaluated with respect to its perceived vocal quality, variability, pitch, and loudness.13 Such parameters may be dependent on subglottal pressure, vocal fold posture, tension,11, 14 and morphology.15 Common and widespread methods for diagnosing laryngeal diseases are generally classified into subjective and objective categories. Trained listeners use running speech for auditory assessment of voice quality, which is a subjective method capturing only the symptomatic information of a laryngeal disease.16 Indeed, discrepancies between auditory and laryngoscopic findings may occur.17 Moreover, the diagnosis and differentiation of voice disorders is often marked by ambiguity.9 Conventional visual methods like stroboscopy (high spatial resolution) and videokymography [high temporal resolution: approx. 8000 frames per second (fps)] may assist with clinical diagnosis. However, stroboscopy is limited by low temporal resolution,18 and videokymopraphy is limited by low spatial resolution (i.e., a single line of the sensor data).19 Not surprisingly, the increased temporal and spatial resolution offered by high-speed (HS) imaging of the vocal folds during phonation may further enhance clinical diagnosis.7, 20 Clinically, this is performed by using an endoscopic HS digital imaging technique (2000–4000 fps).21, 22, 23
Currently, analysis of HS recordings serves as basis for objective and quantitative measures of normal and pathological vocal fold vibrations.21, 23 However, so far endoscopic in vivo HS recordings only permit analysis of horizontal vocal fold dynamics along the vocal fold edge.21 While a recent attempt has been made to analyze vertical dynamics,21 most of the biomechanical characteristics of three dimensional (3D) mucosal wave propagation during phonation (i.e., medio-lateral, inferior-superior, and anterior-posterior)4, 5 are not captured by endoscopic imaging.3 Such 3D characteristics were first detected and investigated in in vitro laryngeal experiments.4, 24, 25 For deeper analysis of such vibration patterns, a biomechanical numerical 3D-multi-mass-model (3DM)26 was proposed. It was designed to simulate not only lateral and longitudinal vocal fold vibrations, but also vibrations in the vertical direction. The 3DM was a vertical extension of the previous two dimensional multi-mass-model (2DM),20 and was introduced in detail in Ref. 26. Numerical modeling of vocal fold dynamics and physiological interpretation of the biomechanical parameter values may help to increase our understanding of both normal and pathological voice production.27 For example, all the measured aspects of vocal fold dynamics (including amplitudes of vibration, phase delays, velocities and accelerations across a large region of tissue locations) were evaluated to reveal viscoelastic properties of vocal fold tissues.26 Significantly, even biomechanical parameters of pathological vocal folds may be deduced using the 3DM. Thus, the derived parameters may serve as an objective measure to quantify the physiological states of vocal fold vibration. For example, observed left-right asymmetries can be detected and further analyzed by comparing the resultant bilateral, biomechanical parameters of the model. Therefore, the 3DM provides a convenient way to describe the biomechanical properties of measured 3D vocal fold dynamics.
In recent attempts using the two-mass-models (2MM)7, 28, 29 and the 2DM20, 30 only 1D trajectories at one or more specific locations on the vocal fold edges along the longitudinal direction were fitted. Classification schemes between healthy and pathological vocal fold vibrations were presented. However, such models considered the vocal fold oscillations only in the lateral dimension. The corresponding dynamic behaviors in the remaining dimensions were negligible, due to undue restriction of the models. In this work, the 3D modeling approach is proposed to be able to reproduce the 3D vibrations of the entire medial surface of the vocal fold. This can be regarded as an important step for linking with the classification of the various 3D vocal fold vibratory modes as well as the production of the acoustic voice signal in future studies.
In order to refine the quantification of the biomechanical properties of human vocal folds and to support clinical diagnosis, the goal is to adapt the 3DM for both in vitro4, 31, 32, 33 and in vivo 3D HS recordings. To this end, an optimization procedure with a corresponding objective function for the 3DM adaption is presented. Modifications of the 3DM can be imposed by expressing the model parameters in terms of their initial values by introducing optimization factors, which influence the constants of spring, mass, subglottal pressure and rest position, respectively. As objective functions, minimizing the normalized error between the model adapted 3D trajectories and the trajectories to be fitted are chosen. The non-convex objective function contains a large number of local minima which make the optimization procedure complicated.7 Hence, a combination of global and local optimization techniques is applied, e.g., Particle Swarm Optimization,34 simulated annealing35 and Powell’s direction set method.36 In order to yield appropriate results progressive optimization sub-procedures are implemented along each side, each coronal cross section and each transverse plane within the 3DM. The optimization strategy is focused on a refinement, wherein gradually increasing numbers of individual mass elements are taken into account. Due to characteristics of the 3D vocal fold motions, special weighting coefficients for different dimensions, cross-sections and planes are considered. Overall the methodology of optimization gets more important, since the complexity of the 3D modeling increases. The optimization procedure is verified on 50 synthetically generated vocal fold vibrations encompassing five well-known glottal closure types.37, 38, 39 Finally, as an essential basis of the application of the 3D modeling to different laryngeal data (excised or in vivo) in future, the optimization procedure is demonstrated on data from an in vitro experiment. Once the biomechanical parameters have been derived using this method, an interpretable physiological representation of the vocal fold dynamics will be presented and discussed.
METHODS
3D biomechanical model
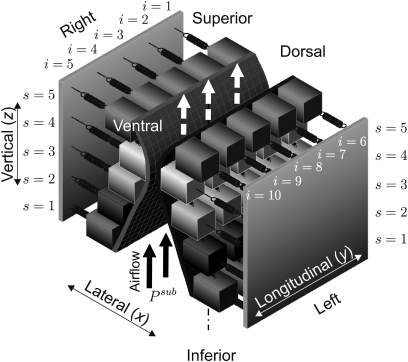
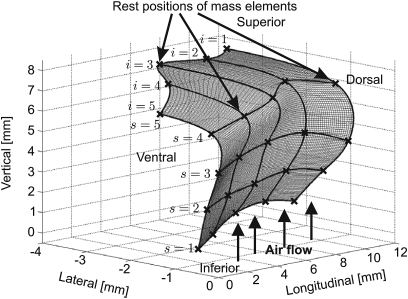
For modeling realistic 3D vocal fold dynamics a 3D-multi-mass-model was previously proposed.26 It consists of five transverse planes (from inferior to superior) with five coronal cross-sections (from dorsal to ventral). The subglottal pressure Psub acts as a driving force for air flowing in the inferior to superior direction, causing vocal fold oscillations. Figure 1 shows a 3D view of the 3DM.
Figure 1.
Schematic representation of the 3DM for biomechanical modeling of human vocal fold dynamics. Every mass element is elastically connected to a rigid body with an anchor spring. Moreover, at each side every mass is connected to its adjacent masses with springs in vertical and longitudinal directions. The indices denote the different planes s and columns i for the mass elements.
The model parameters serve as an approximation of tissue properties of the vocal folds, i.e., distributions of masses mi,s, dampings ri,s and different spring stiffness coefficients (anchor spring), (vertical spring), (longitudinal spring). Index s = 1,…, 5 numbers the transverse planes from inferior to superior. Index i = 1,…, 5 is for labels of mass elements on the right side from dorsal to ventral, and i = 6,…, 10 is on the left side, see Fig. 1.
The biomechanical model can be described by a system of 50 Ordinary Differential Equations (ODE). For each mass element mi,s the following differential equation holds:
| (1) |
The 3D position of each mass element is denoted as xi,s=[xi,s,yi,s,zi,s]T. Its first and second derivatives with respect to time are the velocity and acceleration , respectively. The applied forces acting on each mass element are defined as follows.
-
(1)
The anchor force is due to the anchor spring and the damping
-
(2)
The vertical coupling force arises from the vertical spring stiffness and the damping coefficient
-
(3)
The longitudinal coupling force is caused by the longitudinal spring stiffness and the corresponding damping coefficient
-
(4)
The collision impact force is derived from the collision restoring spring
-
(5)
The driving force is generated by the glottal flow. It is derived from the subglottal pressure Psub and the corresponding effective area using Bernoulli’s Law.
The different damping coefficients are dependent on mi,s and of the adjacent mass elements. The collision impact force plays a vital role in phonation, especially for higher resonant frequency components.40 With the aid of the 3DM, not only the small amplitude oscillation but also the large amplitude oscillation are modeled. Nonlinearities of the deflection of muscles and ligaments cannot be ignored at large amplitudes of vibration and at high subglottal pressure.41, 42 As underlined by Titze43 human tissue does not exhibit linear stiffness characteristics. Also, Titze and Durham44 demonstrated that the fundamental frequency is significantly affected by nonlinearity in the stiffness. Therefore, to incorporate variation of fundamental frequency of large∕small oscillations with subglottal pressure into the 3DM, the nonlinear coefficient η for spring stiffness is set to 100 cm−2.41, 45
The detailed mathematical definition of the model and the forces were described in Ref. 26. The ODE-system is solved by using the Runge-Kutta algorithm with a step-size of 0.25 ms.7
Automatic parameter optimization
In order to match the model dynamics with the dynamics of human vocal folds, the model parameters must be optimized. Compared to previous studies applying 2MM41 and 2DM,20 the 3DM has a high dimensionality captured by the spring stiffnesses masses (50mi,s), damping coefficients rest positions , subglottal pressure Psub, and boundary conditions (including the vertical anchors and fixed positions at the ventral∕dorsal ends of vocal folds). Overall, the 3DM yields 531 degrees of freedom.
Initialization of model and optimization parameters
First, a default model configuration is set. That is, standard model parameters (e.g., stiffness, mass, thickness, rest position, etc.) are chosen to serve as an initial approximation of biomechanical properties of the vocal fold.26, 46 The initial values for the model parameters are chosen not only on the basis of previous 2MM41 and 2DM20, 30 configurations, but also on the basis of propagation properties of the mucosal wave, as observed in human laryngeal experiments.4, 25 A detailed description of the applied standard model parameters was presented previously.26 Thus, the configuration of the 3DM is imposed by expressing the model parameters in terms of the previously introduced standard model parameters In order to reduce the dimensionality of the parameter space and to decrease computational costs, certain model parameters were coupled together by introducing an optimization parameter set:30Q:=(Qp,Qi,s,Qr), with index i,s for each mass element mi,s within the 3DM. The parameters influence the stiffness of anchor spring the stiffness of longitudinal spring kli,s and vertical spring , respectively. Using the optimization parameters Qai,s, modifications of mass and anchor spring parameters (i.e., lateral stiffness) can be performed simultaneously, due to the mass-spring systems as well as the highest vibratory displacements in the lateral direction.4, 26 In addition, Qp affects the subglottal pressure Psub, and modifies the rest position of each mass element. Overall, the various model parameters can be derived completely from the initial standard model parameters:7, 20
| (2) |
| (3) |
| (4) |
| (5) |
Moreover, it is also considered that the damping coefficients ri,s are modified as Corresponding scaling factor is initialized to 1, since the damping coefficients were initialized with the relationship among the standard values of stiffness and mass as well as damping ratio.26 However, they are negligible in validation of the optimization, because their effects on model-generated dynamics are small enough, compared to the stiffness and mass.26 After reducing the dimensionality, it results in 491 Q scaling factors to be optimized.
Since the model contains 50 simple mass-spring-oscillators with mass mi,s and reciprocal coupling spring constant ki,s, the fundamental frequency fi,s for each mass can be approximated as follows:7
| (6) |
To get initial parameters Eq. 6 can be rewritten:7
| (7) |
which shows that the optimization parameter Qi,s primarily affects the fundamental frequency of oscillation.28
The optimization parameter Qp mainly influences the oscillation amplitude.30 An appropriate value of the initial optimization parameter yields smaller amplitude differences between the curves ci,s[n] to be fitted and the model generated curves where n = 1,…, N denotes the frame number. Namely, by comparing the amplitude differences under different values (2–35 cm H2O) of subglottal pressure p, the initial value of is determined:
| (8) |
| (9) |
| (10) |
where Ai,s denotes the amplitude of the experimental 3D data. is the amplitude of the 3D curves generated by 3DM with a specified subglottal pressure value.
Additionally, the optimization parameter is initialized to 1, since the rest positions were initialized with the standard values.
Objective function
In general, the optimization of the 3DM compares the dynamic properties between the adapted model-generated 3D trajectories and the experimental 3D trajectories, such as amplitudes and corresponding correlations.
In this work, unlike the definition of the objective function in 2DM20 which also used a glottis area consistency measure, a trajectory consistency measure in 3D is applied. Additionally, according to the previous studies of laboratory larynx experiments,4, 24, 47 it is revealed that the displacements along three orthogonal directions are highest in the superior region of the vocal folds. Moreover, the vocal fold displacements in the lateral direction are significantly higher than those in the other directions, while the longitudinal displacements are the smallest. In consideration of such characteristics, different weighting coefficients for each mass element in each dimension, each coronal cross section and each transverse layer are taken into account within the computation of the objective function, so that the main components of vocal fold dynamics can be determined. For the purpose of minimizing the error between the experimental 3D trajectories ci,s[n] and the theoretical trajectories of the 3DM, the following objective function r which measures the error is suggested:
| (11) |
with
| (12) |
where μ denotes x- (lateral), y- (longitudinal), and z-dimension (vertical), respectively. i = 1,…, 10 denotes the number of the mass elements at each plane. s = 1,…, 5 denotes the number of the planes. Equation 11 corresponds to the energy of the error normalized to the energy of the experimental trajectories.30 Hence, the objective function Г can be regarded as a measure for the normalized relative error.
The weighting coefficients for 3D trajectories are introduced as They refer to different dimensions (superscript d) and different mass elements (superscript m) as well as different planes (superscript p), respectively. All of the weighting coefficients are located in the range between 0 and 1. By observing the mucosal wave dynamics of the vocal folds in hemilarynx experiments3, 4, 24 and excised canine larynx experiments,47, 48 the lateral displacement (x-component) is in general highest. The corresponding local vertical displacement maxima (z-component) predominantly range between longitudinal (y-component) and lateral values.4, 25 Based on these reasons, the weighting is derived as
| (13) |
where n = 1,…, N.
In addition, the 3D displacements differ along the length of the vocal folds. Usually the highest amplitude of displacement is found midway between anterior and posterior ends of the fold.4, 49 The 3D displacements at the anterior and posterior ends of the vocal folds are lower, being almost fixed during oscillation.24, 50 Larger and faster movements occur in the central section of the vocal fold than near the glottal extremities.5 According to these properties, we assume the weighting gm corresponding to each mass element as follows:
| (14) |
where n′ = n + 1 denotes the frame number. Here, n = 1,…, N – 1.
From earlier studies of hemilarynx experiments, it was concluded that the superior part of the vocal fold exhibits greater amplitudes of vibration.47 Therefore, for optimization, 3D movements in the upper planes receive relatively more attention than movements in the lower planes. The weighting for each plane from inferior to superior is defined as follows:
| (15) |
where n = 1,…, N – 1.
The weighting coefficients are computed based on 3D trajectories from in vitro hemilarynx experiments:4
| (16) |
| (17) |
These values are used in the following validation and application of the optimization procedure.
A second criterion for judging the quality of fit is the correlation coefficient κ. It measures how closely the shapes of the optimized 3D trajectories match the experimental 3D trajectories. Thus, the similarity and phases of the trajectories are taken into account:
| (18) |
with
| (19) |
Now, the condition for the quality of the optimization procedure is defined as
| (20) |
If this is fulfilled, the optimization quality can be regarded as sufficiently successful. The lower bound 75% for κ is on the basis of results of Wurzbacher et al.28 The upper bound 0.2 for Г is defined in accordance with the relative endoscopic HS image processing error.28
Optimization algorithm
Since the resulting optimization problem is nonconvex,7 applying only local (gradient) optimization techniques will not yield sufficiently accurate results. Therefore, various combinations of global and local optimization algorithms are applied. During the optimization procedure, the global optimization algorithm is used to determine preliminary parameter values. Then, on the basis of the preliminary minimum, a local optimization algorithm is applied to find parameter values that are even closer to the global minimum of the objective function Г. However, reaching the global minimum cannot be guaranteed in nonconvex optimization problems. For controlling the switch of the global optimizations, the following heuristic condition is defined as κ < 80%. If this condition is fulfilled, both the global and local optimization algorithms are sequentially applied. Otherwise, only the local optimization algorithm is carried out. This switch condition is implemented once at the beginning of each phase within each optimization sub-procedure, which is introduced in the next section.
For the selection of the optimization algorithm, conjugate gradient algorithms (e.g., Fletcher-Reeves) and variable metric algorithms (e.g., Broyden-Fletcher-Goldfarb-Shanno)36 have proven to be inadequate and relatively time-consuming because of the complex partial derivatives of the objective function. Thus, in this work, the more suitable global methods for minimizing the objective function are the Particle Swarm Optimization (PSO) and the Simulated Annealing (SA). Briefly, the PSO is a population-based stochastic optimization technique.34, 51 It was first used to model the social behavior of bird flocking, bee swarming or fish schooling.52 Similar to Genetic Algorithms (GA),53 PSO also uses many evolutionary computation techniques,54 including random searches, fitness values, iteration time, and so on. The system is initialized with a population of potential solutions and searches for optima by updating generations. Each individual (particle) traverses the problem space with its own vector, which determines its next trajectory following the optimum particle. However, no evolution operators such as crossover and mutation are applied in PSO. Therefore, PSO has the advantage of simply controlling and robustly adjusting parameters. The SA is known to work as a generic probabilistic metaheuristic for optimization problems of large scale, especially the ones in which a desired global extremum is hidden among many local extrema. A detailed description of Simulated Annealing can be found in Ingber.35 Accordingly, we choose a combination between PSO and SA to globally seek the minimum of the objective function, since in a study of metaheuristic methods54 Ercan confirmed that PSO-SA combinations outperform the basic PSO algorithm. A heuristic condition (Γ≥0.1)∨(κ≤90%) is defined as a switch to the PSO-SA combination. Namely, if it is fulfilled, the PSO will be implemented first, followed by the SA (with the results of the PSO used as initial solutions for the SA). Otherwise, only the SA will be executed. Moreover, for the local optimization algorithm, the Powell’s Direction Set Method (PDSM)30 [which belongs to the class of conjugate direction algorithms] is adapted, which in this instance has been proven to be faster and more stable than other optimization algorithms such as the Nelder-Mead algorithm.7
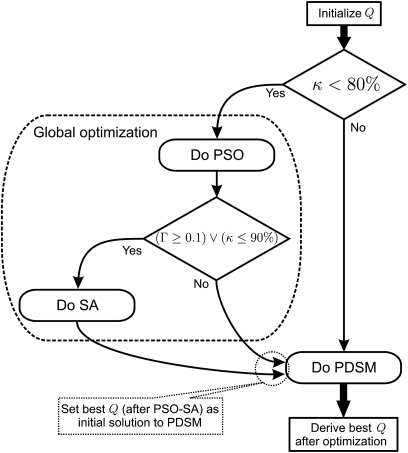
Compared to the use of any single algorithm (PSO, SA, or PDSM), the consecutive use of different optimization algorithms improves the consistency and stability in approximating the global minimum. However, it may also pose a computational burden. To better clarify the proposed optimization algorithm, a flow chart is sketched in Fig. 2. It is implemented in each phase of the optimization procedure, which is introduced in the following section.
Figure 2.
Flow chart of the combined optimization algorithms. PSO, SA, and PDSM are applied to optimize the parameters Q to fit the model-generated dynamics to the vocal fold vibrations ci,s[n]. This is performed in each optimization phase, Fig. 3.
Progressive optimization procedure
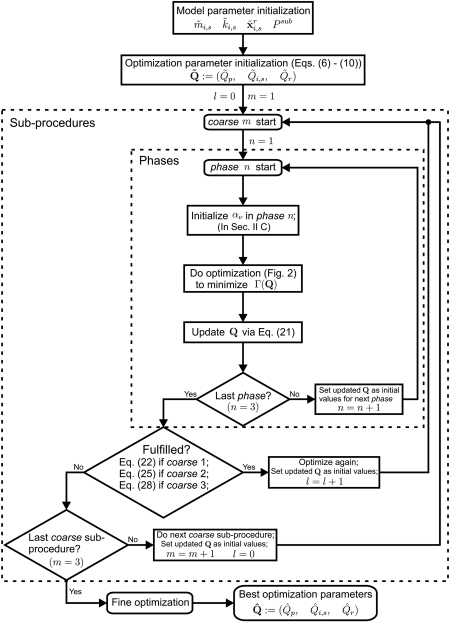
In optimizing the 3DM, a progressive concept is introduced, wherein the search space consists of the following optimization parameters: (Qp,Qi,s,Qr). Due to the location of each mass element in 3D, three aspects (plane, side, cross section) are taken into account, which affect the optimization of the 3DM. In accordance with various combinations among the three aspects, the so-called progressive optimization procedure consists of three main coarse optimization sub-procedures (Fig. 3). The basic idea of the optimization procedure is to gradually adapt the model parameters from a rough state to a more refined state, to overcome the difficulties of multidimensional optimization. In this work, the simple global optimization approach has proven to be inconsistent in fitting model-generated dynamics to experimental data. However, using a hierarchical coarse optimization, the global minimum can be consistently and stably approached.
Figure 3.
General flow chart of the hybrid optimization procedure. represent the initial optimization parameters. represent the best optimization parameters. There are three coarse sub-procedures and a fine optimization process. Each coarse sub-procedure has three phases. In this flow chart, m, n, l temporarily denote the index of the coarse sub-procedure, the phase, and the loop, respectively.
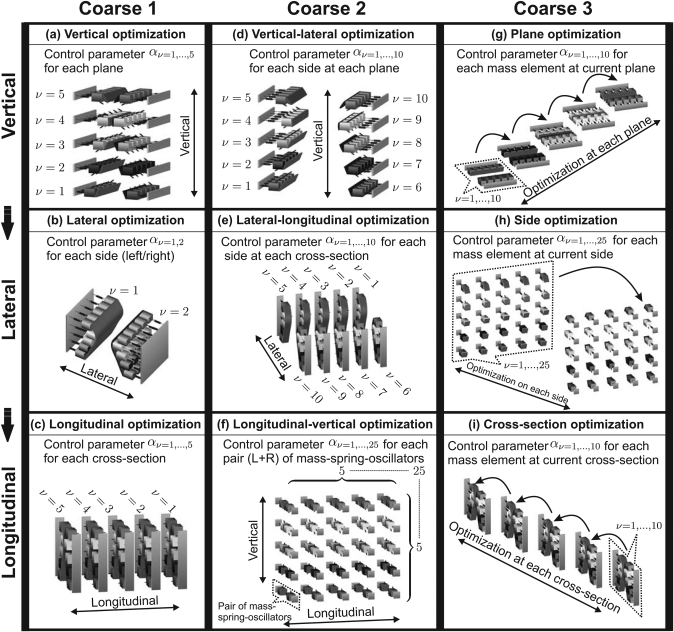
Within each sub-procedure, three phases are implemented one after another (see Fig. 4) Moreover, within each phase, the combination (Sec. 2B3) between global optimization algorithm (PSO-SA) and local optimization algorithm (PDSM) is implemented. Switching from the current phase to the next phase occurs when the objective function r falls below a predefined threshold or when the maximum iteration value is reached. The configuration of each individual optimization procedure is detailed below:
-
(1)
PSO. The number of particles is set to 100. The maximum number of iterations is 1000. An inertia weight of the particle is 0.73. Two acceleration constants of the particle, which represent the cognitive and social learning of the particle, are set to 1.49.
-
(2)
SA. The number of steps is set to 2. The maximum iteration number at each step is 300. The temperature is initialized to 10. The density of the randomly chosen points of the initial simplex is 0.1. For determining a local extremum, a so-called fractional tolerance is set to 0.001, which measures the difference between the objective function values in two consecutive steps. The non-linear constant is set to 2. The more nonlinear the objective function is, the lower the non-linear constant should be set.
-
(3)
PDSM. The maximum iteration number is set to 600. A parabolic extrapolation algorithm “Parabolic-Bracketing” is used as the bracketing algorithm. To determine where an extremum value lies, a minimum distance between the end points of any bracketing interval is set to 0.5. The localization algorithm in PDSM is Brent’s algorithm.36 Similarly, a fractional tolerance is set to 0.001. In addition, a tolerance value which is used to check the exit condition for PDSM is set to 0.5. As a rule, the smaller the tolerance value, the more accurate the result of PDSM algorithm. However, the algorithm also becomes more computationally demanding.
Figure 4.
Block charts for the three course optimization sub-procedures. Each sub-procedure is divided into three phases: Along each row, the intercommunities are vertical, lateral, and longitudinal, respectively.
The value assignments are based on heuristic analysis and experience. More detailed descriptions of the applied algorithms can be found in Refs. 34, 36.
Additionally, in each phase, control parameters serve as scale factors to control the modification of the optimization parameters Q:
| (21) |
where Qold and Qnew are the optimization parameters before and after each phase, respectively. Thus, the optimization parameters can be continuously updated in each phase.
The concept of three sub-procedures and their individual conditions for switching to the next sub-procedure are introduced in the following sections. Each sub-procedure (coarse 1–3) is terminated if its cycle index reaches a recommended limit value of l = 10.
In addition, at the end of the optimization procedure a fine optimization process (Fig. 3) is implemented. In this process, all of the model parameters are one-to-one optimized, in order to further improve the optimization results.
Overall, in each phase of the optimization procedure, the objective function r either decreases or remains momentarily unchanged. Г is bounded by greatest lower bound 0, which indicates no error.
Sub-procedure coarse 1
The purpose of this sub-procedure is to roughly adapt the model dynamics to the experimental data. It is continuously performed until the following condition is no longer fulfilled:
| (22) |
where the subscript l denotes the index of the loop. l – 1 and l represent two consecutive loops. The threshold value of κ is defined as 92%, based on experience gained in former work.28 In general, it is separated into three phases [Figs. 4a, 4b, 4c]:
-
(1)
Vertical optimization. Parameters for each plane are modified with the same factor αν=1,…,5.
-
(2)Lateral optimization. Parameters for each side are modified with the same factor αν with
(23) -
(3)Longitudinal optimization. Parameters for each cross section are modified with the factor αν with
(24)
Sub-procedure coarse 2
The parameters resulting from coarse 1 are set as initial values for this sub-procedure. The exit-condition for coarse 2 is defined as follows:
| (25) |
where 0.04 is a heuristic threshold value for the normalized error, in accordance with results presented in Wurzbacher et al.28 Three phases are employed as follows [see Figs. 4d, 4e, 4f]:
-
(1)Vertical-lateral optimization Parameters for each side of each plane are modified with the same factor αν, with:
(26) -
(2)
Lateral-longitudinal optimization Parameters for each side of each cross section are modified with the same factor αν, with ν = i.
-
(3)Longitudinal-vertical optimization Parameters for each pair of mass-spring-oscillators are modified with the same factor aν with:
(27)
Sub-procedure coarse 3
The aim of this sub-procedure is to adapt the optimization parameters even more thoroughly, on the basis of the preceding coarse 2. The exit-condition for coarse 3 is defined as follows:
| (28) |
where 95% is defined as the threshold value of κ in this sub-procedure, based on former work28 as well as the preceding sub-procedures. Three phases are implemented as follows [see Figs. 4g, 4h, 4i]:
-
(1)
Plane optimization. Parameters for the 10 mass elements (m1,s,…, m10,s) at the current plane s are allowed to be modified with different control parameters aν=1,…,10, while the parameters for mass elements at the other four planes are not adjusted.
-
(2)
Side optimization. Parameters for 25 mass elements on the current side are modified with different control parameters aν with ν = 1,…, 25.
-
(3)
Cross section optimization. Parameters for 10 mass elements at the current cross-section are modified with different control parameters aν=1,…,10, while the parameters for the mass elements at the other cross-sections are not modified.
Validation and application
Synthetic data
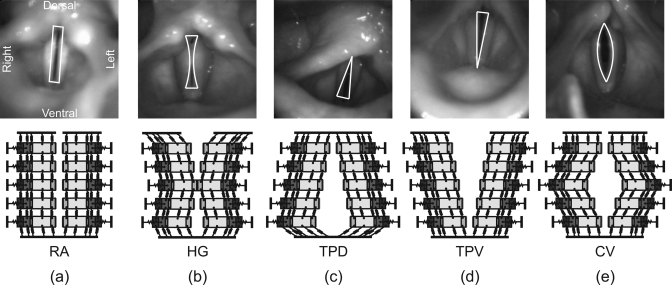
In order to evaluate the reliability and capability of the optimization procedure, synthetically generated data are analyzed. Fifty sets of synthetic, laterally-symmetric 3D trajectories are produced by the 3DM with known optimization parameter values (see TableTABLE I.). To simulate a wide variety of vocal fold vibrations (i.e., frequencies for males and females, amplitudes between 0.3 and 1.2 mm),55 the scale factors of the predefined model parameters are randomly set in the follow ing range: , By using these values, masses, elastic modulus of the model, the subglottal pressure, and the rest positions are correspondingly modified.
Table 1.
Fifty synthetic data sets with predefined parameters to be optimized. The data are separated by glottal closure types (Fig. 5) and gender.
| GCT | Gender | No. | Frequency (Hz) | |||
|---|---|---|---|---|---|---|
| RA | male | 5 | 0.8 ± 0.2 | 0.9 ± 0.2 | 0.9 ± 0.2 | 110 ± 10 |
| female | 5 | 2.2 ± 0.3 | 1.5 ± 0.6 | 0.8 ± 0.2 | 216 ± 22 | |
| HG | male | 5 | 0.7 ± 0.1 | 0.9 ± 0.2 | 0.9 ± 0.1 | 110 ± 11 |
| female | 5 | 2.1 ± 0.4 | 1.4 ± 0.5 | 0.8 ± 0.1 | 206 ± 19 | |
| TPD | male | 5 | 0.7 ± 0.1 | 0.9 ± 0.1 | 0.9 ± 0.2 | 114 ± 6 |
| female | 5 | 1.9 ± 0.3 | 1.5 ± 0.6 | 1.0 ± 0.2 | 209 ± 15 | |
| TPV | male | 5 | 0.9 ± 0.1 | 0.9 ± 0.2 | 0.9 ± 0.2 | 113 ± 10 |
| female | 5 | 1.8 ± 0.1 | 1.4 ± 0.5 | 0.9 ± 0.1 | 204 ± 17 | |
| CV | male | 5 | 0.9 ± 0.3 | 0.9 ± 0.2 | 21.0 ± 0.1 | 114 ± 5 |
| female | 5 | 2.0 ± 0.6 | 1.5 ± 0.6 | 0.8 ± 0.2 | 226 ± 33 |
From a physiological and clinical point of view, the glottal closure type (GCT) is described as an important aspect of laryngeal behavior.38, 56 Hence, in generating synthetic data, five well-known glottal closure types are considered: rectangle (RA), hourglass (HG), triangular-pointed dorsal (TPD), triangular-pointed ventral (TPV) and convex (CV) (see Fig. 5 and Table TABLE I.). Since the mean fundamental frequency for males is considerably lower than for females,57 the frequency range of the 50 synthetic dynamics is roughly divided into two groups: ≤120 Hz for male, ≥180 Hz for female. Results from Sulter et al.58, 59 indicate that GCT and glottal chink locations are different for males and females. Thus, in this work, GCT and gender are regarded as two factors that influence optimization accuracy. A variety of vocal fold behaviors was produced for different GCT and gender types, in order to validate optimization of the 3DM as thoroughly as possible.
Figure 5.
Schematic representation of occurring glottal closure-types and corresponding modeling: (a) rectangle (RA), (b) hourglass (HG), (c) triangular-pointed dorsal (TPD), (d) triangular-pointed ventral (TPV), (e) convex (CV).
An accuracy value is defined to measure how closely the optimized parameters () approximate the predefined values :
| (29) |
Overall, the assessments of similarity between the adapted dynamics and the synthetic dynamics are implemented by using the following: the accuracy λ of optimization parameters, the correlation coefficient κ verifying the similarity between both 3D trajectories, and the objective function (i.e., normalized error) Г. In this way, the performance of the optimization procedure and the corresponding reproducibility of the optimization results could be evaluated.
Hemilarynx experimental data
As a prelude to the future optimization of both in vivo and in vitro with physiological relevance,4 the optimization procedure is also applied to an in vitro hemilarynx experimental data set, which includes recorded 3D trajectories of 25 marker-points attached along the medial vocal fold surface. Vertical distance between marker-points was approximately 1.7 ± 0.2 mm, and horizontal distance was approximately 2.0 ± 0.2 mm. A detailed description of the hemilarynx experiments can be found in Refs. 4, 25, and 31. For comparison with the dynamics of the 3DM (which includes both left and right vocal folds), bilateral symmetry was assumed for the in vitro hemilarynx data set, since the dynamics of only one vocal fold could be observed in hemilarynx experiments. The fundamental frequency was 120 Hz, and the subglottal pressure was 22.6 cm H2O.
With the proposed parameter optimization procedure, a set of optimization parameters is derived from the adapted 3DM. To adapt the 3D rest positions of the 50 mass elements (i.e., for each mass element in each dimension) 150 are computed, since the adaptations of the complex marker-point locations would not be accurate if only one scale factor were used to modify all of the 3D rest positions.
RESULTS
Validation of optimization
Global measures
TableTABLE II. shows the accuracy λ, the correlation coefficient κ and the normalized error Г for the fifty synthetic data sets. The best value of r occurred in the glottal closure type RA with 0.05 ± 0.03, while the worst occurred in HG and TPV with 0.09 ± 0.03. For κ, the best value (97% ± 2%) occurred in TPD and CV, while the worst (94% ± 2%) was in HG. The value of λ was the highest in RA with 92% ± 5%, while the lowest (89% ± 3%) was in HG. The measures by different genders were essentially equal, except for Г (better value for males). Overall, the measures (Г, κ, λ) were 0.07 ± 0.03, 96% ± 2% and 91% ± 4%, averaged over all 50 synthetic data sets. The corresponding ranges for these values were 0.007–0.153, 90%–100%, and 83%–99%, respectively. Additionally, the given symmetry ratio (perfect symmetry= 1) right to left was reproduced as 1.01 ± 0.08 in an acceptable range (0.8 to 1.2).
Table 2.
Optimization results for the synthetic data: The global accuracy λ, correlation coefficient κ and objective function Γ exhibit sufficient good performance. Each glottal closure type covers 10 subjects (5 male, 5 female).
| GCT | Γ | κ | λ |
|---|---|---|---|
| RA | 0.05 ± 0.03 | 96% ± 2% | 92% ± 5% |
| HG | 0.09 ± 0.03 | 94% ± 3% | 89% ± 3% |
| TPD | 0.07 ± 0.03 | 97% ± 2% | 90% ± 5% |
| TPV | 0.09 ± 0.03 | 95% ± 3% | 92% ± 2% |
| CV | 0.05 ± 0.02 | 97% ± 2% | 91% ± 3% |
| total | 0.07 ± 0.03 | 96% ± 2% | 91% ± 4% |
| Gender | Γ | κ | λ |
|---|---|---|---|
| male | 0.05 ± 0.03 | 96% ± 2% | 91% ± 5% |
| female | 0.09 ± 0.03 | 96% ± 3% | 91% ± 3% |
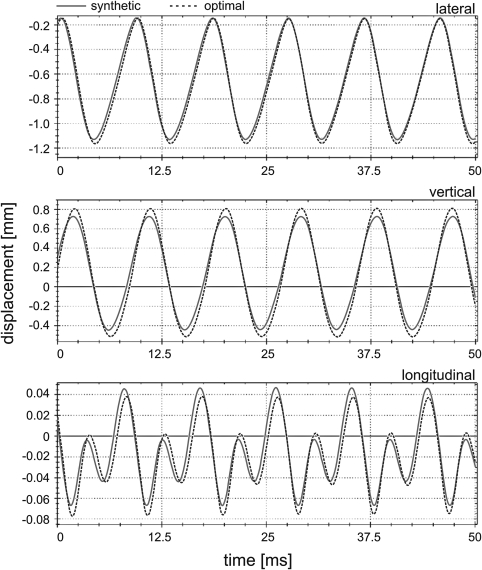
To illustrate the optimization results, Fig. 6 compares the adapted 3D trajectories and the synthetic 3D trajectories corresponding to the mass element m4,4 of a subject with a rectangular glottal closure pattern and a fundamental frequency of 120 Hz.
Figure 6.
(Color online) Exemplary results of the 3D dynamics of the mass element m4,4 are given. Synthetic trajectories (solid lines) and optimized trajectories (dotted lines) are presented for all three displacement directions. The corresponding accuracy values are: (Γ, κ, λ) = (0.05, 97%, 96%).
Reproducibility of parameters
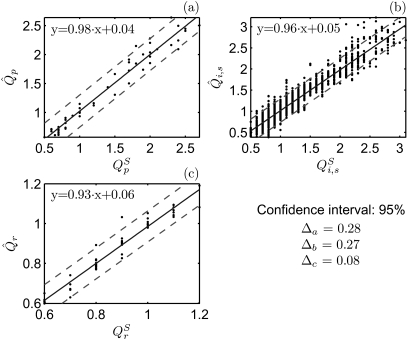
To determine the reproducibility of the parameters, the individual accuracies (λp,λi,s,λr) for the predefined optimization parameters were derived as: 92 ± 5%, 91% ± 9%, and 97% ± 3%, averaged over all of the synthetic subjects. The lowest value of the individual accuracy was for whereas the highest was for To facilitate an intuitive feel for the reproducibility of the parameters, the relationship between the adapted optimization parameters and the predefined optimization parameters is illustrated in Fig. 7. In each chart, the regression lines with their respective regression functions are sketched. The corresponding regression fits were high percentage (i.e., close to one), and their disturbance terms were low. Additionally, the 95% confidence interval is very narrow: the distances between the regression lines and the boundaries of the regions were 0.28, 0.27, and 0.08.
Figure 7.
Comparison between the adapted optimization parameters and pre-defined values . The solid lines indicate the regression lines for the optimization parameters. The corresponding regression functions are shown including the 95% confidence interval. The distances between the regression lines and the confidence interval boundaries are indicated (Δa, Δb, Δc exhibiting the reliability of the algorithm).
Influence from weighting coefficients
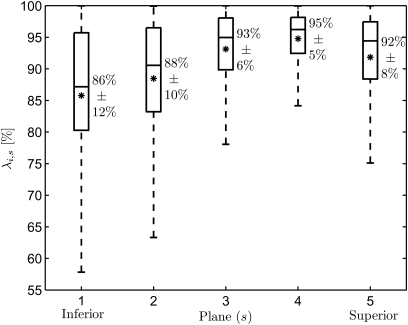
In order to examine whether the measures of the optimization results influenced the weighting coefficients, the variations of the individual accuracies λi,s at different planes are shown in Fig. 8. Higher accuracies were achieved at the superior planes s = 3, 4 with λi,3 = 93% ± 6% and λi,4 = 95% ± 5% averaged over all mass elements, while the lowest was at the inferior plane s = 1. Additionally, statistical analysis (analysis of variance) showed that optimization accuracy was statistically significantly dependent on plane (p < 0.01).
Figure 8.
Boxplots of the accuracies λi,s averaged over all 10 mass elements (i = 1,…, 10) at each plane (s = 1,…, 5) for the 50 synthetic data sets. The mean values are marked with *. Higher performances occur at the superior planes, while lower values occur at the inferior planes.
Influence from GCT and gender
As shown in Table TABLE II., the optimization results may be affected by different GCT and gender. To further investigate how a response is affected by the two factors, two-way analysis of variance (analysis of variance) was applied. It shows that GCT and gender both exhibit statistically significant effects for Г at the 99% confidence interval (significance level a = 0.01, probability of a Type I error), since ratios of F-test (6.61 for GCT, 26.68 for gender) are larger than the corresponding critical values and 7.31, respectively. The larger the F ratios, the more GCT and gender differ. Also, the corresponding lower p-values (3.5E-04 < 0.01 for GCT, 7.0E-06 < 0.01 for gender) provided sufficient evidence for such a conclusion. Additionally, for the analysis of κ and λ, no statistically significant differences based on GCT or gender, or the interaction between the two, were found, due to smaller F ratios () and larger p-values (> 0.05). Overall, analysis of variance for (Г, κ, λ) confirmed the assumption (displayed in Table TABLE II.) that GCT and gender partly influence (normalized error Г) the optimization results.
Application to an in vitro hemilarynx experiment
In order to adapt the model dynamics to a hemilarynx data set, the initial rest positions of the mass elements were first estimated in accordance with the mean values of the 3D movements of the mounted marker points. Figure 9 shows the initial rest positions at one side of the 3DM. The average values of the computed optimization parameters were 0.79, 0.75 ± 0.36, 0.94 ± 0.26. The corresponding global measures (Г, κ) were 0.16 and 84%, respectively. Accuracy of the optimization parameters could not be reported, since no predefined optimization parameters existed for the experimental data. However, the optimized subglottal pressure (19.0 cm H2O) and fundamental frequency (120 Hz) were sufficiently accurately reproduced.
Figure 9.
The rest positions of the 25 mass elements for one side are estimated in accordance to the mean values of the marker points placed on the hemilarynx. The marks × denote the rest position of the 25 mass elements.
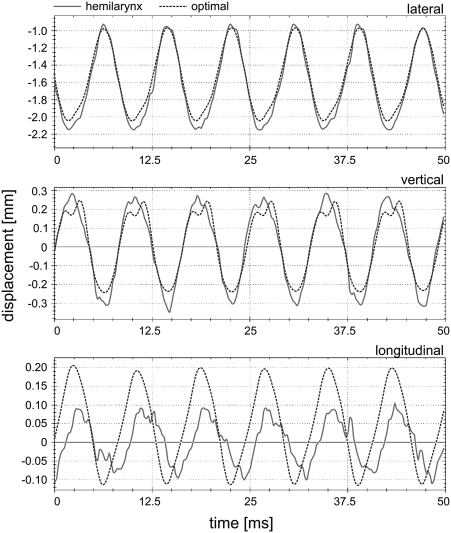
Figure 10 shows the high similarity between the hemilarynx experimental 3D trajectories c3,3[n] and adapted theoretical 3D trajectories of the mass element m3,3, which responds to the marker-point located in the third vertical column and fourth sagittal line in the hemilarynx. The corresponding fundamental frequency was 120 Hz. The normalized errors Γ for trajectories in lateral, longitudinal, and vertical directions were 0.04, 1.5, and 0.26, respectively. Their correlations κ were 99%, 68%, and 97%, respectively. The smallest error with highest correlation occurred in the lateral direction, while the highest error with lowest correlation occurred in the longitudinal direction.
Figure 10.
(Color online) Results of the adapted 3DM (dotted lines) of the mass element m3,3 located in the median cross section at the plane s = 3 on the right side of the model, compared to the hemilarynx trajectories (solid lines) at the corresponding suture-point. The fundamental frequency is 120 Hz.
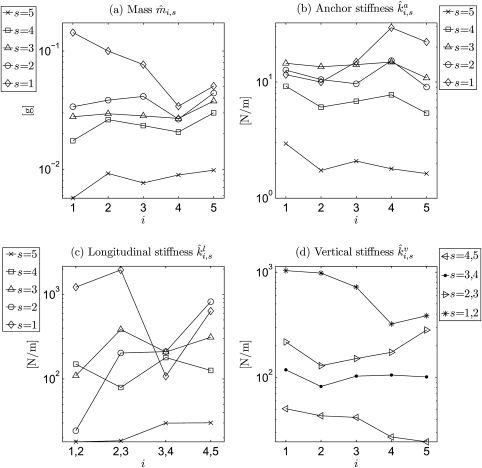
Figure 11 shows the optimized model parameters applied to the hemilarynx experimental data set. The derived masses decreased from inferior to superior (s = 1 to s = 5) for all five coronal cross-sections [see Fig. 11a]. They ranged between 5.7 × 10−3 and 0.14 g. Additionally, from dorsal to ventral, the highest value occurred at the most ventral cross section i = 5 for four planes (s = 2 to s = 5), except the most inferior plane s = 1 (which had the highest value at i = 1 near the vocal fold dorsal extreme). The lowest values at the superior planes (s = 4, s = 5) were at the most dorsal cross section i = 1, while the inferior three planes (s = 1, 2, 3) had the lowest values in cross section i = 4. A large difference occurred at the transition from the most superior plane s = 5 to the second plane s = 4 [see Fig. 11a].
Figure 11.
Logarithmic charts for the optimized model parameters after application to a hemilarynx experimental data set. (a)–(d) describe the mass , anchor stiffness , longitudinal stiffness , and the vertical stiffness at∕between different transverse planes s and coronal cross-sections i. occurs between the current plane and the next upper plane. occurs between the current cross section and the next one. The achieved subglottal pressure was equal to 19.0 cm H2O, and the estimated glottis length was 13.0 mm. i = 1,…, 5 denotes the coronal cross-sections from dorsal to ventral. s = 1,…, 5 denotes the transverse planes from inferior to superior. In general, the values of the model parameters at inferior plane (s = 1) are higher than those at superior plane (s = 5).
In Fig. 11b, at the superior planes (s = 3 to s = 5), the anchor spring decreased from inferior to superior for all five coronal cross-sections (i = 1 to i = 5). Moreover, the highest value occurred at the most inferior plane s = 1, i = 4. The lowest value was found at the most superior plane s = 5 near the ventral extreme (i = 5). Values of at the two inferior planes (s = 1, 2) were nearly equal at the dorsal cross-sections i = 1, 2. Also, planes s = 2, 3 had nearly equal values at i = 4. The values ranged between 1.63 and 29.37 N∕m.
Figure 11c shows that the longitudinal spring had comparatively lower values at the most superior plane s = 5. For planes (s = 2, 5), there was an increase from dorsal (i = 1, 2) to ventral (i = 4, 5). In general, the lowest value of occurred at the most superior plane s = 5 between the two dorsal cross-sections (i = 1, 2), while the highest was found at the most inferior plane s = 1 between cross-sections i = 2 and i = 3, shown in Fig. 11c. The stiffnesses ranged between 17.98 and 1954.36 N∕m.
In Fig. 11d, the vertical spring obviously decreased from inferior to superior for all five coronal cross-sections. A decrease occurred from dorsal to ventral for the superior spring (s = 4, 5), and the inferior spring (s = 1, 2). Values for the spring (s = 3, 4) were nearly equal in all five coronal cross-sections. The highest value was found in the spring (s = 1, 2) near the dorsal extreme (i = 1), while the lowest was in s = 4, 5 near the ventral extreme (i = 5). The stiffnesses ranged between 24.53 and 1035.50 N∕m.
DISCUSSION
In this work, a mathematical optimization approach for approximating 3D vocal fold dynamics by a biomechanical model was suggested and verified. Validation of the optimization with fifty synthetic data sets and application to an in vitro human hemilarynx experiment reflect its suitability and applicability. Among other things, the proposed method may be used to objectively quantify vocal fold asymmetries. A long-term goal of this method is to support clinical diagnosis and treatment of voice disorders through a better knowledge of the biomechanical parameters underlying the disorders.
Validation of optimization
Validation of feasibility via global measures
Using the proposed optimization procedure, the synthetic 3D trajectories were effectively approximated, as evidenced by the small normalized error (Γ = 0.07 ± 0.03), the large correlation coefficient (κ = 96 ± 2%) and the high accuracy (λ = 91 ± 4%) over all cases, as shown in Table TABLE II.. Since the optimization procedure is based on stochastic search-algorithms in which the calculated parameter values may not be unique, an ideal accuracy of 100% cannot be guaranteed for synthetic data. However, the derived measures (Γ, κ, λ) reflect the high reliability and robustness of the optimization procedure. Sufficiently high symmetry between right side and left side was reproduced. Also, it was shown that the performance of the optimization procedure was improved by using combinations of the PSO, SA, and PDSM algorithms. However, it was achieved at an expense of increased complexity of the optimization procedure.54 Compared to the verification procedure in Wurzbacher et al.,28 the ranges of the measures (Sec. 3A1) in this work were reduced by more than 15%. Overall, the results confirm that the proposed optimization algorithms appropriately utilize dynamical information (e.g., from highspeed imaging) to estimate biomechanical parameters of vocal folds.
Reproducibility of parameters
To further evaluate the inversion capability of the optimization, individual accuracies (λp, λi,s,λr) for different predefined optimization parameters after optimization were investigated (see Sec. 3A). The differences among the individual accuracies (λp, λi,s, λr) may be explained by the fact that vocal fold dynamics may be more sensitive to changes in mass and stiffness than to changes in pressure and rest position. Additionally, relationships between the predefined parameters QS and the derived parameters are described in Fig. 7. High strengths of such relationships are demonstrated by the regression functions for (Qp, Qi,s, Qr), in Fig. 7, due to the high-percentage regression fits and the low disturbance terms. Also, these derived regression functions confirmed the high individual accuracies of (Qp, Qi,s, Qr) as shown in Sec. 3A. Furthermore, compared to the whole value ranges of (Qp, Qi,s, Qr), the widths± Δ (seeFig. 7) of the 95% confidence intervals were relatively small. This shows that most of the variability in the relationships between and QS occurs very close to the regression lines. Overall, these results reflect a high reproducibility of model parameters using the proposed optimization algorithms.
Influence from weighting coefficients
Since the observed vocal fold 3D dynamics along the glottal surface are anisotropic, a concept of the weighting coefficients ( see Sec. 2B2) was utilized in the optimization procedure. The estimated weighting coefficients [Eqs. 16, 17] reflect the relative amplitudes of vibration on different parts of the vocal fold. In Fig. 8 it was shown that the individual accuracies λi,s were different between planes. In particular, the variation in the accuracies corresponded to the variations in weighting coefficient for the different planes [see Eq. 15]. That is, higher values of weighting coefficients yielded comparatively better individual accuracies for the corresponding planes. A reason might be that the parameter optimization procedure was influenced by the weighting coefficients . In other words, it can be inferred that the weighting coefficients may be used to help guide the optimization results. Or put another way, by means of the weighting coefficients, the optimization procedure can be designed to selectively focus on portions of the vocal folds deemed most significant for a particular application, such as where the greatest amplitudes of vibration occur, or where diseased or scarred portions of vocal fold tissue may occur.
GCT and gender
In determining the effects of GCT and gender on the optimization results, one significant issue is how the interaction of these two variables may influence the results. Analysis of variance revealed that both factors significantly affected the objective function Γ, while there was not sufficient evidence to suggest that the correlation coefficient κ or the accuracy λ was significantly influenced by these factors (see Sec. 3A4). This conclusion might be explained by the fact that the initial setup of GCT may implicitly influence the normalized error between adapted and synthetic dynamics, since mass distributions of the model differ for GCTs. Moreover, synthetic female data sets, which exhibit higher fundamental frequencies and larger sub-glottal pressures,45 yield larger Γs (see Table TABLE II.). This may be attributed to the fact that larger subglottal pressures may result in short-term irregularities in the 3D dynamics of the model, since higher subglottal pressures are more likely to induce irregular and asymmetric vibrations.60, 61 Therefore, for larger subglottal pressures, the distance between synthetic and adapted 3D trajectories may be increased. However, the results of the analysis of variance for (Γ, κ, λ) show that neither factor significantly affected either dynamic correlation or optimization accuracies.
Application to an in vitro hemilarynx experiment
Since human vocal fold 3D dynamics are governed by biomechanical tissue properties which can be expressed in terms of quantitative parameters, it is important to examine whether the physiologically relevant properties can be accurately extracted using the 3DM with the proposed optimization procedure. For this purpose, the optimization procedure was also applied to an experimental hemilarynx data set. Compared to optimization results for synthetic data sets, the correlation coefficient (κ = 84%) was lower, while the corresponding normalized error (Γ = 0.16) was higher. This might be attributed to two causes. One reason is that the boundary conditions, such as the 3D positions of the ventral∕dorsal vocal fold extremes are not known exactly, and the corresponding estimates of such fixed positions might not be sufficiently close to the actual values. Another reason is that the recorded experimental curves might not be sufficiently smooth as shown in Fig. 10, due to the image processing errors (up to 20%). However, the optimization results reasonably fulfilled the combined condition Eq. 20. It exhibits a successful optimization, and reveals a sufficient similarity between the adapted model dynamics and the hemilarynx dynamics.
As an example of an optimization result, the adapted 3D trajectories of the mass element m3,3 and corresponding hemilarynx experimental 3D trajectories were compared in Fig. 10. This supported the evidence that values of normalized errors Γ and correlations κ were steered by the weighting coefficients for different displacement directions. Relatively lower normalized errors with higher correlations were derived in the lateral and vertical directions, since the corresponding weighting coefficients were explicitly higher [ = 0.5, = 0 4 in Eq. 16]. The values of Γ and κ in the longitudinal direction were less accurate, due to the lower value of the weighting coefficient for the longitudinal direction . However, longitudinal displacements are usually considered a relatively minor aspect of 3D vocal fold dynamics. In other words, at the dimension where a higher value of the weighting coefficient appears, a lower Γ with higher κ can be achieved.
Overall, the derived stiffness increased from superior to inferior [see Figs. 11b, 11c, 11d]. These results support the suggestion proposed by Story et al.62 that vocal fold vibration can best be modeled if the stiffness of the superior parts of the vocal fold is smaller than that of the inferior parts. In addition, from an anatomic point of view, the decrease [Fig. 11a] of the mass from inferior to superior could be explained by the fact that the inferior parts of the vocal fold are closer to the stiff tissue of the trachea as well as the cricoid cartilage. The relatively high differences in the stiffness and from inferior to superior implicitly reflect that relatively significant variations in tissue environments occur along the vertical direction. Also, either the ventral or dorsal cross-sections had slightly higher stiffness∕mass values. This could be due to the locations of the ventral∕dorsal cross-sections which are close to the vocal fold fixed endings. Similar to the conclusions in Berry et al.63 and Alipour et al.,64 a finding was that the longitudinal stiffness was stronger than the stiffness in the other two directions (i.e., lateral and vertical). This nonisotropic nature of the stiffness might be regarded as an important consideration for phonosurgeons who wish to avoid subluxation of the cricoarytenoid joint in patients, as suggested in Ref. 63.
Performance of optimization procedure and outlook
Extending the optimization procedure of the 2DM,30 the 3DM and resulting optimization parameters are computed in a 3D space to more realistically investigate the physiological properties of the vocal folds.24 Based on the hemilarynx experimental data and laryngeal physiological structure,4 50 mass-spring oscillator units are coupled within the 3DM. With this greater complexity, computational costs of the optimization procedure are significantly increased. However, it is significantly more useful for analyzing the 3D dynamics of vocal folds. For parameter optimization of a 175 millisecond segment of sustained synthetic 3D dynamics, the required optimization time is currently approximately 3–5 days on a standard PC [Intel(R) Core(TM)2 Duo E8500, 3.16 GHz, 3.50 GB RAM, C#]. The optimization procedure was also successfully applied to a hemilarynx experimental data set. These results provide an important first step in fitting 3D vocal fold dynamics, in preparation for larger systematic studies of both in vitro and in vivo experiments. In the future, the proposed 3DM optimization approach may be further adapted to investigate specific voice disorders, studying specific pathological regions of the vocal folds, perhaps with especially designed weighting coefficients to focus on the region of interest.
On the whole, this study shows that the 3DM with its optimization procedure enables modeling of human vocal fold 3D dynamics. The model parameters capture the biomechanical properties of vocal fold vibrations. Thus, the adapted model parameters may be used to further disclose essential characteristics of vocal fold dynamics, not only in planar forms, but also in spatial forms. The future goal is the clinical application: to adapt the model toward vocal fold 3D dynamics, which are extracted from in vivo human laryngeal recordings using endoscopic HS imaging in combination with a laser-spot projection system (necessary for computation of 3D tissue coordinates). The left-right asymmetry quantification for local vocal fold parts (five positions along the vocal fold length) may play a vital role in objective judgments of surgical interventions or conventional laryngeal therapy. Additionally, from a clinical perspective, the consequences of surgical treatment (i.e., scarring) resulting in different spring and damping components can be interpreted and analyzed by future parameter studies of the 3DM.
SUMMARY
The aim of the proposed 3DM parameter optimization procedure was to provide an opportunity to objectively quantify biomechanical properties of 3D human vocal fold vibrations. Investigating the relationships between model parameters and vocal fold dynamics may be beneficial to voice therapy and surgical treatments of voice disorders. Due to non-convexity of the optimization problem, different global and local optimization algorithms were applied to yield appropriate results. To validate the reliability and feasibility of the optimization procedure, different synthetic data sets were adapted with five different glottal closure types and genders. The results of the optimization procedure were further investigated using data from an in vitro hemilarynx experiment. In future studies, both in vitro and in vivo hemilarynx data will be systematically adapted to conduct an in-depth investigation regarding the correspondence between biomechanical tissue parameters and the resulting vocal fold vibrations.
Finally, the proposed optimization strategy need not be confined to the study of vocal fold vibration, but is sufficiently general that it may also be applied to other fields of interest.
ACKNOWLEDGMENTS
This work was supported by DFG (Deutsche Forschungsgemeinschaft, German Research Foundation) Grant No. FOR 894∕1 “Strömungsphysikalische Grundlagen der Menschlichen Stimmgebung” (i.e., fluid dynamical basics of human voice production). Support for D.A.B. on this project was funded by NIH∕NIDCD Grant No. R01 DC03072.
References
- Hirano M., “Phonosurgery: Basic and clinical investigations,” Otologia (Fukuoka) 21(Suppl. 1), 239–262 (1975). [Google Scholar]
- Baer T., “Investigation of phonation using excised larynxes,” in Ph.D. disseration (Massachusetts Institute of Technology, Cambridge, MA, 1975). [Google Scholar]
- Döllinger M., Berry D. A., and Berke G. S., “A quantitative study of the medial surface dynamics of an in vivo canine vocal fold during phonation,” Laryngoscope 115(9), 1646–1654 (2005). 10.1097/01.mlg.0000175068.25914.61 [DOI] [PubMed] [Google Scholar]
- Boessenecker A., Berry D. A., Lohscheller J., Eysholdt U., and Döllinger M., “Mucosal wave properties of a human vocal fold,” Acta Acust. Acust. 93(9), 815–823 (2007). [Google Scholar]
- Sonninen A. and Laukkanen A.-M., “Hypothesis of whiplike motion as a possible traumatizing mechanism in vocal fold vibration,” Folia Phoniatr. Logop. 55, 189–198 (2003). 10.1159/000071018 [DOI] [PubMed] [Google Scholar]
- Baken R., “Irregularity of vocal period and amplitude: A first approach to the fractal analysis of voice,” J. Voice 4, 185–197 (1990). 10.1016/S0892-1997(05)80013-X [DOI] [Google Scholar]
- Döllinger M., Hoppe U., Hettlich F., Lohscheller J., Schubert S., and Eysholdt U., “Vibration parameter extraction from endoscopic image series of the vocal folds,” IEEE Trans. Biomed. Eng. 49(8), 773–781 (2002). 10.1109/TBME.2002.800755 [DOI] [PubMed] [Google Scholar]
- Isshiki N., Tanabe M., Ishizaka K., and Broad D., “Clinical significance of asymmetrical vocal cord tension,” Ann. Otol. Rhinol. Laryngol. 86(1), 58–66 (1977). [DOI] [PubMed] [Google Scholar]
- Niimi S. and Miyaji M., “Vocal fold vibration and voice quality,” Folia Phoniatr. Logop. 52(1–3), 32–38 (2000). 10.1159/000021510 [DOI] [PubMed] [Google Scholar]
- Neubauer J., Mergell P., Eysholdt U., and Herzel H., “Spatio-temporal analysis of irregular vocal fold oscillations: Biphonation due to desynchronization of spatial modes,” J. Acoust. Soc. Am. 110(6), 3179–3192 (2001). 10.1121/1.1406498 [DOI] [PubMed] [Google Scholar]
- Titze I. R., Principles of Voice Production (Prentice Hall, Englewood Cliffs, NJ, 1994), pp. 23–52, 307–322. [Google Scholar]
- Titze I., Baken R., and Herzel H., in Vocal Fold Physiology: Frontiers in Basic Science, edited by Titze I. (Singular Publishing Group, San Diego, CA, 1993), pp. 143–188. [Google Scholar]
- Aronson A. E. and Bless D. M., in Clinical Voice Disorders, edited by Hiscock T. Y. (Thieme Medical Publisher, New York, 2009), pp. 2–9. [Google Scholar]
- Fujimura Q., in Vocal Fold Physiology, edited by Stevens K. N. and Hirano M. (University of Tokyo Press, Tokyo, 1981), pp. 271–288. [Google Scholar]
- Titze I. R., in The Myoelastic Aerodynamic Theory of Phonation, edited by Klemuk S. (National Center for Voice and Speech, Iowa City, IA, 2006), pp. 1–62. [Google Scholar]
- Hadjitodorov S. and Mitav P., “A computer system for acoustic analysis of pathological voices and laryngeal diseases screening,” Med. Eng. Phys. 24(6), 419–429 (2002). 10.1016/S1350-4533(02)00031-0 [DOI] [PubMed] [Google Scholar]
- Fleischer S. and Hess M., “The significance of videos in laryngological practice,” HNO 54, 628–634 (2006). 10.1007/s00106-006-1437-0 [DOI] [PubMed] [Google Scholar]
- Wendler J., “Stroboscopy,” J. Voice 6(2), 149–154 (1992). 10.1016/S0892-1997(05)80129-8 [DOI] [Google Scholar]
- Švec J. G. and Schutte H. K., “Videokymography: High-speed line scanning of vocal fold vibration,” J. Voice 10(2), 201–205 (1996). 10.1016/S0892-1997(96)80047-6 [DOI] [PubMed] [Google Scholar]
- Schwarz R., Döllinger M., Wurzbacher T., Eysholdt U., and Lohscheller J., “Spatio-temporal quantification of vocal fold vibrations using high-speed videoendoscopy and a biomechanical model,” J. Acoust. Soc. Am. 123, 2717–2732 (2008). 10.1121/1.2902167 [DOI] [PubMed] [Google Scholar]
- Döllinger M., “The next step in voice assessment: High-speed digital endoscopy and objective evaluation,” Curr. Bioinf. 4(2), 101–111 (2009). 10.2174/157489309788184774 [DOI] [Google Scholar]
- Braunschweig T., Schelhorn-Neise P., and Döllinger M., “Diagnosis of functional voice disorders by using the high speed recording technics,” Laryngorhinootologie 87(5), 323–330 (2008). 10.1055/s-2007-967068 [DOI] [PubMed] [Google Scholar]
- Deliyski D. D., Petrushev P. P., Bonilha H. S., Gerlach T. T., Martin-Harris B., and Hillman R. E., “Clinical implementation of laryngeal high speed videoendoscopy: Challenges and evolution,” Folia Phoniatr. Logop. 60(1), 33–44 (2008). 10.1159/000111802 [DOI] [PubMed] [Google Scholar]
- Döllinger M., Berry D. A., and Montequin D. W., “The influence of epilarynx area on vocal fold dynamics,” Otolaryngol. Head. Neck. Surg. 135(5), 724–729 (2006). 10.1016/j.otohns.2006.04.007 [DOI] [PubMed] [Google Scholar]
- Döllinger M. and Berry D. A., “Visualization and quantification of the medial surface dynamics of an excised human vocal fold during phonation,” J. Voice 20(3), 401–413 (2006). 10.1016/j.jvoice.2005.08.003 [DOI] [PubMed] [Google Scholar]
- Yang A., Berry D. A., Lohscheller J., Voigt D., Eysholdt U., and Döllinger M., “Biomechanical modeling of the three-dimensional aspects of human vocal fold dynamics,” J. Acoust. Soc. Am. 127(2), 1014–1031 (2010). 10.1121/1.3277165 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng X., Bielamowicz S., Luo H., and Mittal R., “A computational study of the effect of false vocal folds on glottal flow and vocal fold vibration during phonation,” Ann. Biomed. Eng. 37(3), 625–641 (2009). 10.1007/s10439-008-9630-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wurzbacher T., Schwarz R., Döllinger M., Hoppe U., Eysholdt U., and Lohscheller J., “Model-based classification of nonstationary vocal fold vibrations,” J. Acoust. Soc. Am. 120(2), 1012–1027 (2006). 10.1121/1.2211550 [DOI] [PubMed] [Google Scholar]
- Schwarz R., Hoppe U., Schuster M., Wurzbacher T., Eysholdt U., and Lohscheller J., “Classification of unilateral vocal fold paralysis by endoscopic digital high-speed recordings and inversion of a biomechanical model,” IEEE Trans. Biomed. Eng. 53(6), 1099–1108 (2006). 10.1109/TBME.2006.873396 [DOI] [PubMed] [Google Scholar]
- Wurzbacher T., Döllinger M., Schwarz R., Hoppe U., Eysholdt U., and Lohscheller J., “Spatio-temporal classification of vocal fold dynamics by a multi-mass model comprising time-dependent parameters,” J. Acoust. Soc. Am. 123, 2324–2334 (2008). 10.1121/1.2835435 [DOI] [PubMed] [Google Scholar]
- Döllinger M. and Berry D. A., “Computation of the three-dimensional medial surface dynamics of the vocal folds,” J. Biomech. 39(2), 369–374 (2006). 10.1016/j.jbiomech.2004.11.026 [DOI] [PubMed] [Google Scholar]
- Döllinger M., Tayama N., and Berry D. A., “Empirical eigenfunctions and medial surface dynamics of a human vocal fold,” Methods Inf. Med. 44(3), 384–391 (2005). [PubMed] [Google Scholar]
- Luegmair G., Kniesburges S., Zimmermann M., Alexander, Sutor, Eysholdt U., and Döllinger M., “Optical reconstruction of high-speed surface dynamics in an uncontrollable environment,” IEEE Trans. Med. Imaging 29(12), 1979–1991 (2010). 10.1109/TMI.2010.2055578 [DOI] [PubMed] [Google Scholar]
- Kennedy J. and Eberhart R., “Particle swarm optimization,” in Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia (IEEE Service Center, Piscataway, NJ, 1995), Vol. 4, pp. 1942–1948.
- Ingber L., “Adaptive simulated annealing,” J. Control Cybernetics 25(1), 33–54 (1996). [Google Scholar]
- Press W. H., Teukolsky S. A., Vetterling W. T., and Flannery B. P., Numerical Recipes in C: The Art of Scientific Computing, 2nd ed. (Cambridge University Press, New York, 1994), pp. 348–455. [Google Scholar]
- Lohscheller J., Eysholdt U., Toy H., and Döllinger M., “Phonovibrography: Mapping high-speed movies of vocal fold vibrations into 2-d diagrams for visualizing and analyzing the underlying laryngeal dynamics,” IEEE Trans. Med. Imaging 27, 300–309 (2008). 10.1109/TMI.2007.903690 [DOI] [PubMed] [Google Scholar]
- Rasp O., Lohscheller J., Döllinger M., Eysholdt U., and Hoppe U., “The pitch rise paradigm: A new task for real-time endoscopy of non-stationary phonation,” Folia Phoniatr. Logop. 58, 175–185 (2006). 10.1159/000091731 [DOI] [PubMed] [Google Scholar]
- Dejonckere P., Bradley P., Clemente P., Cornut G., Crevier-Buchman L., Friedrich G., Heyning P. V. D., Remacle M., Woisard V., and Committee on Phoniatrics of the European Laryngological Society (ELS), “A basic protocol for functional assessment of voice pathology, especially for investigating the efficacy of (phonosurgical) treatments and evaluating new assessment techniques. guideline elaborated by ELS.,” Eur. Arch. Otorhinolaryngol. 258(2), 77–82 (2001). 10.1007/s004050000299 [DOI] [PubMed] [Google Scholar]
- Ikeda T., Matsuzaki Y., and Aomatsu T., “A numerical analysis of phonation using a two-dimensional flexible channel model of the vocal folds,” J. Biomech. Eng. 123(6), 571–579 (2001). 10.1115/1.1408939 [DOI] [PubMed] [Google Scholar]
- Ishizaka K. and Flanagan J. L., “Synthesis of voiced sounds from a two-mass model of the vocal cords,” Bell Syst. Techn. J. 51(6), 1233–1268 (1972). [Google Scholar]
- Chan R. W., “Vocal fold tissue failure: Preliminary data and constitutive modeling,” J. Biomech. Eng. 126(4), 466–474 (2004). 10.1115/1.1785804 [DOI] [PubMed] [Google Scholar]
- Titze I. R., “The physics of small-amplitude oscillation of the vocal folds,” J. Acoust. Soc. Am. 83(4), 1536–1552 (1988). 10.1121/1.395910 [DOI] [PubMed] [Google Scholar]
- Titze I. and Durham P., in Laryngeal Function in Phonation and Respiration, edited by Baer T., Sasaki C., and Harris K. (College Hill, San Diego, CA, 1986). [Google Scholar]
- Fulcher L. P., Scherer R. C., Melnykov A., Gateva V., and Limes M. E., “Negative coulomb damping, limit cycles, and self-oscillation of the vocal folds,” Am. J. Phys. 74(5), 386–393 (2006). 10.1119/1.2173272 [DOI] [Google Scholar]
- Cataldo E., Soize C., Sampaio R., and Desceliers C., “Probabilistic modeling of a nonlinear dynamical system used for producing voice,” Comput. Mech. 43, 265–275 (2009). 10.1007/s00466-008-0304-0 [DOI] [Google Scholar]
- Berry D. A., Montequin D. W., and Tayama N., “High-speed digital imaging of the medial surface of the vocal folds,” J. Acoust. Soc. Am. 110(5), 2539–2547 (2001). 10.1121/1.1408947 [DOI] [PubMed] [Google Scholar]
- Kobayashi J., Yumoto E., Hyodo M., and Gyo K., “Two-dimensional analysis of vocal fold vibration in unilaterally atrophied larynges,” Laryngoscope 110, 440–446 (2000). 10.1097/00005537-200003000-00022 [DOI] [PubMed] [Google Scholar]
- Döllinger M., Berry D. A., and Berke G. S., “Medial surface dynamics of an in vivo canine vocal fold during phonation,” J. Acoust. Soc. Am. 117(5), 3174–3183 (2005). 10.1121/1.1871772 [DOI] [PubMed] [Google Scholar]
- Spencer M., Siegmund T., and Mongeau L., “Determination of superior surface strains and stresses, and vocal fold contact pressure in a synthetic larynx model using digital image correlation,” J. Acoust. Soc. Am. 123(2), 1089–1103 (2008). 10.1121/1.2821412 [DOI] [PubMed] [Google Scholar]
- Schutte J. F., Koh B.-I., Reinbolt J. A., Haftka R. T., George A. D., and Fregly B. J., “Evaluation of a particle swarm algorithm for biomechanical optimization,” J. Biomech. Eng. 127(3), 465–474 (2005). 10.1115/1.1894388 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khanesar M., Teshnehlab M., and Shoorehdeli M., “A novel binary particle swarm optimization,” in Proceedings of the 15th Mediterranean Conference on Control and Automation [Mediterranean Control Association (MED), Athens, Greece, 2007], Vol. T33–001, pp. 1–6. [Google Scholar]
- Ingber L. and Rosen B., “Genetic algorithms and very fast simulated reannealing: A comparison,” Mathl. Comput. Modelling 16(11), 87–100 (1992). 10.1016/0895-7177(92)90108-W [DOI] [Google Scholar]
- Particle Swarm Optimization, edited by Lazinica A. (In-Tech Education and Publishing, Vienna, Austria, 2009), pp. 155–168. [Google Scholar]
- Schuster M., Lohscheller J., Kummer P., Eysholdt U., and Hoppe U., “Laser projection in high-speed glottography for high-precision measurements of laryngeal dimensions and dynamics,” Eur. Arch. Otorhinolaryngol. 262(6), 477–481 (2005). 10.1007/s00405-004-0862-5 [DOI] [PubMed] [Google Scholar]
- Gelfer M. P. and Bultemeyer D. K., “Evaluation of vocal fold vibratory patterns in normal voices,” J. Voice 4, 335–345 (1990). 10.1016/S0892-1997(05)80051-7 [DOI] [Google Scholar]
- Titze I. R., “Physiologic and acoustic differences between male and female voices,” J. Acoust. Soc. Am. 85(4), 1699–1707 (1989). 10.1121/1.397959 [DOI] [PubMed] [Google Scholar]
- Sulter A. M. and Albers F. W. J., “The effects of frequency and intensity level on glottal closure in normal subjects,” Clin. Otolaryngol. Allied Sci. 21, 324–327 (1996). 10.1111/j.1365-2273.1996.tb01079.x [DOI] [PubMed] [Google Scholar]
- Sulter A. M., Schutte H. K., and Miller D. G., “Standardized laryngeal videostroboscopic rating: Differences between untrained and trained male and female subjects, and effects of varying sound intensity, fundamental frequency and age,” J. Voice 10(2), 175–189 (1996). 10.1016/S0892-1997(96)80045-2 [DOI] [PubMed] [Google Scholar]
- Jiang J. J., Zhang Y., and Stern J., “Modeling of chaotic vibrations in symmetric vocal folds,” J. Acoust. Soc. Am. 110(4), 2120–2128 (2001). 10.1121/1.1395596 [DOI] [PubMed] [Google Scholar]
- Zhang Y. and Jiang J. J., “Asymmetric spatiotemporal chaos induced by a polypoid mass in the excised larynx,” Chaos 18(4), 043102 (2008). 10.1063/1.2988251 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Story B. H. and Titze I. R., “Voice simulation with a body-cover model of the vocal folds,” J. Acoust. Soc. Am. 97(2), 1249–1260 (1995). 10.1121/1.412234 [DOI] [PubMed] [Google Scholar]
- Berry D. A., Montequin D. W., Chan R. W., Titze I. R., and Hoffman H. T., “An investigation of cricoarytenoid joint mechanics using simulated muscle forces,” J. Voice 17, 47–62 (2003). 10.1016/S0892-1997(03)00026-2 [DOI] [PubMed] [Google Scholar]
- Alipour-Haghighi F., Berry D. A., and Titze I. R., “A finite-element model of vocal fold vibration,” J. Acoust. Soc. Am. 108(6), 3003–3012 (2000). 10.1121/1.1324678 [DOI] [PubMed] [Google Scholar]