Quantitative pharmacological analysis of antagonist binding kinetics at CRF₁ receptors in vitro and in vivo

Abstract

BACKGROUND AND PURPOSE

A series of novel non-peptide corticotropin releasing factor type-1 receptor (CRF₁) antagonists were found to display varying degrees of insurmountable and non-competitive behaviour in functional in vitro assays. We describe how we attempted to relate this behaviour to ligand receptor-binding kinetics in a quantitative manner and how this resulted in the development and implementation of an efficient pharmacological screening method based on principles described by Motulsky and Mahan.

EXPERIMENTAL APPROACH

A non-equilibrium binding kinetic assay was developed to determine the receptor binding kinetics of non-peptide CRF₁ antagonists. Nonlinear, mixed-effects modelling was used to obtain estimates of the compounds association and dissociation rates. We present an integrated pharmacokinetic–pharmacodynamic (PKPD) approach, whereby the time course of in vivo CRF₁ receptor binding of novel compounds can be predicted on the basis of in vitro assays.

KEY RESULTS

The non-competitive antagonist behaviour appeared to be correlated to the CRF₁ receptor off-rate kinetics. The integrated PKPD model suggested that, at least in a qualitative manner, the in vitro assay can be used to triage and select compounds for further in vivo investigations.

CONCLUSIONS AND IMPLICATIONS

This study provides evidence for a link between ligand offset kinetics and insurmountable/non-competitive antagonism at the CRF₁ receptor. The exact molecular pharmacological nature of this association remains to be determined. In addition, we have developed a quantitative framework to study and integrate in vitro and in vivo receptor binding kinetic behaviour of CRF₁ receptor antagonists in an efficient manner in a drug discovery setting.

Introduction

Corticotropin releasing factor (CRF) is a 41-amino-acid peptide hormone first isolated from ovine hypothalamus by Vale et al. (1981). It exerts its effects through activation of two GPCRs belonging to the class B GPCR family of neuropeptide receptors, CRF₁ and CRF₂ (Chalmers et al., 1996; Dautzenberg and Hauger, 2002; Hoare, 2005; Alexander et al., 2008). CRF receptors are primarily coupled to Gs-proteins, resulting in activation of adenylate cyclase and increased cAMP levels after receptor stimulation (Dautzenberg and Hauger, 2002; Wietfeld et al., 2004).

CRF plays a key role in the regulation of the hypothalamic–pituitary–adrenal axis and central signalling in the physiological response to stress (Vale et al., 1981; Rivier and Vale, 1983) and is also involved in other brain functions such as memory and learning, locomotion, food intake and anxiety (Coskun et al., 1997; Heinrichs et al., 1997; Eckart et al., 2002; Kehne and De Lombaert, 2002). CRF receptors have therefore become a potential target for pharmacological modulation. Efforts have been specifically directed towards discovering non-peptidic, small molecule antagonists for the CRF₁ receptor for the treatment of depression, anxiety and stress disorders (Schulz et al., 1996; Grigoriadis, 2005).

Several examples have been reported of CRF₁ receptor antagonists demonstrating non-competitive or insurmountable antagonism (Li et al., 2005; Berger et al., 2006), and during the course of an in-house medicinal chemistry programme, we discovered a series of non-peptide CRF₁ antagonists that displayed varying degrees of insurmountable and non-competitive behaviour in functional in vitro assays.

In this paper, we describe how we attempted to relate this behaviour to ligand receptor-binding kinetics in a quantitative manner and how this resulted in the development and implementation of an efficient pharmacological screening method based on principles described by Motulsky and Mahan (1984), Karlsson and Neil (1989), Ernest II et al. (2010) and Benson et al. (2010). We also discuss how the translatability of the in vitro findings was confirmed by studying ex vivo receptor occupancy in rat brain. We present an integrated pharmacokinetic–pharmacodynamic (PKPD) approach, whereby the time course of in vivo CRF₁ receptor binding of novel compounds can be predicted on the basis of in vitro assays. Although the present paper focuses on the CRF₁ receptor, we believe these methods have general applicability in the field of GPCR research and drug discovery and could contribute to more efficient in vitro and in vivo pharmacological approaches for studying receptor binding kinetics.

Methods

Materials

SN003 (Zhang et al., 2003), DMP904 (Li et al., 2005), R121919 (Chen et al., 2004), PF-4659901 (dicyclopropylmethyl-[9-(4-methoxphenyl)-2,8-dimethyl-9H-purin-6-yl]-amine), PF-4325743 [(2-methoxy-ethyl)-[1-(4-methoxy-2-methyl-phenyl)-3,6-dimethyl-1H-pyrazolo[3,4-d]pyrimidin-4-yl]-propyl-amine], PF-4734666 (dicyclopropylmethyl-[9-(4-difluoromethoxyphenyl)-2,8-dimethyl-9H-purin-6-yl]-amine) and PF-4850890 (N-(dicyclopropylmethyl)-9-(4-(difluoromethoxy)-2-methoxyphenyl)-2,8-dimethyl-9H-purine) were all synthesized at Pfizer Research and Development (Sandwich, Kent, UK). SN003 was radiolabelled to [³H]-SN003 by GE Healthcare (Buckinghamshire, UK). Ovine CRF (oCRF) was obtained from Bachem (St. Helens, UK). Minimum essential medium (MEMα), geneticin and Dulbecco's PBS (DPBS) without CaCl₂ and MgCl₂ were all obtained from Invitrogen Ltd (Paisley, UK). Fetal bovine serum (FBS, EU approved) was obtained from PAA (Yeovil, UK). DiscoveRx Hithunter™ cAMP II kit (90–0034) was obtained from GE Healthcare. All other chemicals were obtained from Sigma Aldrich (Poole, UK). For all the in vivo experiments, male Sprague–Dawley rats (∼8–10 weeks and 200–400 g) were purchased from Charles River (Margate, Kent, UK).

In vitro methodologies

Cell culture

CHO-pro5 cells expressing the rat CRF₁ (rCRF₁) receptor were cultured as monolayers in roller bottle flasks in MEMα containing 10% heat inactivated FBS and 200 µg·mL⁻¹ geneticin at 37°C with 5% CO₂. Cells were grown to 70–80% confluency before harvesting. Cells were removed from the roller bottle surface via mechanical action using a Cellmate and centrifuged into pellets and stored at −80°C.

Preparation of membranes

Cell pellets were thawed on ice and re-suspended in 3 mL of membrane preparation buffer (20 mM HEPES, pH 7.4 NaOH) per mL of packed cell volume. Cell solutions were then Dounce homogenized with 20 strokes using the tight-fitting pestle. The homogenate was then spun at 500×g for 10 min to spin down nuclei and unbroken cells; the supernatant was decanted and stored on ice. Remaining cell pellets were re-suspended in membrane buffer, and homogenization and centrifugation steps were repeated. The combined supernatant was centrifuged at 35 000×g for 60 min. Pellets were combined and re-suspended in 1 mL of freezing buffer (20 mM HEPES, pH 7.4, 120 mM NaCl, 20% glycerol) per mL of original cell pellet. Protein concentration was determined using a method previously described by Bradford (1976).

Competition binding studies

CHO-pro5 membranes (20 µg per well) were incubated with the test compound (solubilized in 100% dimethyl sulphoxide (DMSO)) and 5 nM final assay concentration [³H]-SN003 in assay buffer (50 mM HEPES, pH 7.4, 10 mM MgCl₂, 2 mM EGTA and 0.05% pluronic acid) in a total assay volume of 250 µL for 120 min at room temperature. A final assay concentration of 1% DMSO was used to define total [³H]-SN003 binding. 10 µM DMP904 at 1% DMSO was used to define non-specific binding. Assays were terminated via vacuum filtration using a Brandel Harvester (Brandel Inc., Gaithersburg, MD, USA) over GF/B filters pre-soaked in 0.5% polyethyleneimine (PEI). Filters were washed three times with 1 mL wash buffer (50 mM HEPES, pH 7.4 at 4°C) and dried at 40°C for 1 h prior to the addition of scintillation cocktail solution. Plates were counted on a TopCount NXT scintillation counter (PerkinElmer, Waltham, MA, USA).

For saturation studies, specific binding of [³H]-SN003 was determined over a range of concentrations (0.02–100 nM), using a 120 min incubation time at room temperature.

Non-equilibrium method of association kinetics (initial experiments)

Non-equilibrium association kinetic studies were performed to determine the ‘on’ and ‘off’ rates of unlabelled antagonists at the rCRF₁ receptor. Two concentrations of each test compound, unlabelled SN003, DMP904, R121919, PF-4325743, PF-4659901, PF-4734666 and PF-4850890, at 1 and 10 times the compound K_i (predetermined from competition binding studies as described above) were incubated in quadruplicate in assay buffer with 5 nM of [³H]-SN003 and 20 µg of CHO-pro5 membranes. Twenty-two replicates of this plate layout were made, one for each of the 22 time points used (1, 2, 3, 5, 10, 15, 20, 25, 30, 40, 50, 60, 90, 120, 150, 180, 240, 300, 360, 420, 480 min). On each assay plate, eight wells were used to define total [³H]-SN003 binding, and eight wells were used to define the non-specific [³H]-SN003 binding as described above. For each experimental time point, the assay reaction within a plate was terminated via rapid filtration using the method described above.

Dissociation of [³H]-SN003 pre-equilibrated with rCRF₁ receptors was also measured by adding 10 µM DMP904 at time points 1, 2, 5, 10, 15, 20, 30, 45, 60, 75, 90 and 120 min. Saturation of rCRF₁ receptors with [³H]-SN003 was also performed as described above.

Modification of non-equilibrium method of association kinetics

Three concentrations of each test compound (1, 10 and 100 nM final assay concentration) were incubated in duplicate with 5 nM [³H]-SN003 and 20 µg CHO-pro5 membranes. Assay plates also included two sets of total and non-specific binding controls. One set to define specific binding of 5 nM [³H]-SN003 in the absence of test compound and the other set to determine specific binding of 2.5 nM [³H]-SN003. Measuring the association of two concentrations of [³H]-SN003 to the CRF₁ receptor allowed for the quantification of [³H]-SN003 binding kinetics without the need for separate association and dissociation experiments. Eleven replicate plates were made, one for each assay time point (1, 5, 15, 30, 60, 120, 180, 240, 300, 360, 420 min). A saturation binding assay was also performed on the day of the kinetic experiment.

Functional cell-based experiments

CHO-pro5 cells expressing the rCRF₁ receptor were re-suspended in DPBS containing 500 µM IBMX and incubated with a concentration range of oCRF in either the presence or absence of antagonist (0.02, 0.06, 0.2, 0.6, 2, 6 and 20 µM) made up in PBS with final assay concentrations of 10 000 cells, 0.03% pluronic acid, 1% DMSO and 166 µM IBMX. The assay was incubated for 90 min at room temperature before being stopped with reagents 1 and 2 from the Hithunter™ cAMP II kit. The assay plate was left for a further 4 h prior to reading on a LJL Biosystems Analyst™ using a luminescence protocol (LJL Biosystems Ltd., Wokingham, Berkshire, UK). This assay was also run in a reduced format, performing a concentration-response curve to oCRF in the absence or presence of a single concentration, 20 µM, of each antagonist. Suppression of the maximal control response by the antagonist at 90 min was calculated.

Combined concentration-ratio analysis

In order to test whether DMP904 and SN003 acted at the same site (syntopically), a combined concentration-ratio analysis (Shankley et al., 1988) was performed according to the procedure described by Stam et al. (1999). Briefly, when two antagonists act syntopically, then their combined concentration-ratio (r_B+C) is given by:

(1)

where r_B and r_C are the concentration ratios obtained independently in the presence of the antagonists B and C, respectively. This relationship can be re-written in terms of logEC₅₀ values of the agonist E/[A] curves in the presence and absence of antagonists B and C using the following equation:

(2)

where S_A is the test statistic for the additive model. Thus, if the experimental data comply with the additive model, S_A should have a value of zero. In contrast, when two antagonists act at different sites, that is allotopically, their combined concentration ratios multiply:

(3)

and expressed in terms of log EC₅₀ values:

(4)

where S_M is the test statistic for the multiplicative model. If the antagonists behave allotopically, S_M should have a value of zero.

As the distributions of S_A and its standard estimator are unknown, there is no formal statistical method available to decide in which cases the additive model should be accepted or rejected. In the present study, the null hypotheses (H₀) was formulated as ‘B + C act syntopically’, and it was assumed that S_A and S_M and their associated standard error estimators are approximately normally distributed. Deviations of S_A and S_M from zero were tested for significance using two- and one-sided t-tests, respectively, and H₀ was accepted in cases when S_A = 0 and S_M < 0. In all other cases, H₀ was rejected (Stam et al., 1999).

Estimates of EC₅₀, Hill slope (n_H) and maximum response (E_max) were obtained by fitting the standard Hill equation (Equation 11) to individual E/[A] curves using Prism 5 (GraphPad Software, Inc, La Jolla, CA, USA).

In vitro data analysis

All IC₅₀ values were calculated by fitting the data through standard competition and simulation equations, respectively, in the non-linear regression curve fitting program Prism 5 (GraphPad Software, Inc). K_i values for the antagonists in competition binding experiments were determined using the Cheng–Prusoff equation. Unless otherwise indicated, data are reported as geometric means ± SEM.

In vivo methods

Animal experimentation

Male Sprague-Dawley rats (200–250 g, Charles River) were housed in groups of 4 (unless stated otherwise) in a well ventilated room with a temperature of 20 ± 2°C under a 12 h light/dark cycle with access to food and water ad libitum. All in vivo work was performed in accordance with the Animals (Scientific Procedures) Act 1986, in compliance with UK national legislation and was subject to local ethical review. At all stages, consideration was given to experiment refinement, reduction in animal numbers and replacement with in vitro techniques.

Receptor occupancy DMP904 dose–response study

Male Sprague–Dawley rats were housed five per cage with free access to food and water in a room maintained on a 12 h light/dark cycle and temperature (22 ± 1°C) and humidity (55 ± 5%) controlled, at least 7 days before experimentation. On the day of the experiment, animals were administered, p.o., DMP904 (0.04, 0.4, 4 or 40 mg·kg⁻¹) or vehicle (0.1% sodium lauryl sulphate, 0.1% Tween 80 and 1% hydroxypropyl beta-cyclodextran). Four animals were included for each concentration of drug. After 75 min, blood samples were taken by venepuncture, and animals were killed by a schedule 1 method. The brain of each animal was removed, and the frontal cortex was dissected out. Each hemisphere was snap-frozen individually and stored at −80°C.

Receptor occupancy time course studies

Male rats were dosed p.o. (5 mL·kg⁻¹) with R121919 (10 mg·kg⁻¹), PF-4734666 (10 mg·kg⁻¹), PF-4850890 (8 mg·kg⁻¹) (0.5 % methylcellulose/0.1% Tween 80) or DMP904 (10 mg·kg⁻¹) (wet milled suspension in 0.1% sodium lauryl sulphate, 0.1% Tween 80, 1% hydroxypropyl cellulose in water), or vehicle, n = 4 per group. Rats were killed at time intervals between 0.5 and 24 h by non-schedule 1 decapitation, and trunk blood was collected (spun at 1000×g, 4°C for 10 min and plasma frozen on dry ice until analysis). The brain was removed, and the left and right frontal cortices were dissected out and frozen on dry ice.

Ex vivo receptor occupancy

On the day of the ex vivo binding assay, cortex samples were thawed and homogenized using a Polytron® homogenizer (Kinematica, Lucerne, Switzerland) (top speed for 10 s) in a 1:25 weight/volume ratio of assay buffer (50 mM HEPES, 10 mM MgCl₂, 2 mM EGTA, 0.05% pluronic acid, pH 7.4, room temperature) plus Complete protease inhibitor tablet (Roche, Basel, Swtizerland); 200 µL of each homogenate sample was incubated in quadruplicate with final assay concentrations of 5 nM [³H]-SN003 and either 1% DMSO (total binding) or 10 µM DMP904 at 1% DMSO (non-specific binding) in a total volume of 250 µL for 1 h at room temperature. Bound radioactivity was separated from free by rapid filtration with three times 1 mL washes of ice-cold wash buffer (1× DPBS, pH 7.4) over GF/B filters pre-soaked in 0.5% PEI. Filters were placed in vials, scintillation cocktail was added and after 1 h the vials were counted using a Tricarb scintillation counter (PerkinElmer). Specific [³H]-SN003 binding was calculated for each animal by subtracting non-specific binding from total binding counts. Receptor occupancy was calculated as 100 − (specific counts of samples / average vehicle specific count) × 100.

Satellite oral pharmacokinetics in rat

DMP904 or PF-4734666 was administered p.o. via gavage (1 mg·kg⁻¹, n = 2). Blood samples (200 µL) were collected into heparin-treated tubes before dosing and at time points over a 24 h period from the jugular vein cannula.

Analytical methods

Plasma protein binding determination

Protein binding of the compounds was determined in vitro by the standard equilibrium dialysis technique, with samples of rat or human plasma (150 µL, n = 4) containing compound at 1 µg·mL⁻¹, dialysed for 4 h at 37°C in a Teflon 96-well equilibrium dialysis block.

Plasma analysis

PF-4850890: 50 µL plasma was added to 50 µL 1 M MCA (10:90, water : acetonitrile), and 30 µL was injected directly onto a micro-Turboflow system on a Psiex API4000. PF-4734666, DMP904 and R121919: 50 µL plasma was analysed by a liquid–liquid extraction method using borate buffer (pH 10) and TBME to selectively extract the compound and internal standard from the plasma. Detection was by multiple-reaction monitoring for specific transitions using either an API3000 or API4000 mass spectrometer.

Data analysis

Determination of pharmacokinetic parameters

Pharmacokinetic parameters were determined by a standard one-compartment oral PK model (Gabrielsson and Weiner, 2000). All parameters were calculated using NONMEM (version VI, release 6.2; Icon Development Solutions, Ellicott City, MD).

Motulsky and Mahan parameter estimation method

A population modelling approach was used with a simple competitive binding model assumed for estimating the association and dissociation rate constants as described by Benson et al. (2010). The following sets of differential equations were used (Equations 5–7):

(5)

(6)

(7)

(8)

where [R] = receptor concentration, [T] = radioactive labelled tracer concentration, [D] = drug concentration, [RT] = concentration of the receptor–tracer complex, [RD] = concentration of the receptor–drug complex, k_onT = association rate constant of the tracer, k_offT = dissociation rate constant of the tracer, k_ond = association rate constant of the drug, k_offd = dissociation rate constant of the drug. The initial conditions for the [RT] complex = 0, [R] = B_max and [RD] = 0.

For the saturation binding experiment of the radiolabelled tracer compound, the data were described as follows:

(9)

where B_max = total receptor concentration (Equation 8), T = free tracer concentration and K_dT is the equilibrium binding constant for [³H]-SN003 binding to CRF₁.

The equilibrium binding constant for the test drugs were calculated according to:

(10)

where K_d is the equilibrium binding constant for unlabelled drug.

Modelling the receptor occupancy data using NONMEM

The in vivo receptor occupancy data were fitted in NONMEM VI using a standard sigmoid E_max model. The equation used in this model is given below:

(11)

where E_max = maximum receptor occupancy (fixed to 100% in model), CP = plasma concentration, EC₅₀ = in vivo measure of potency and n_H = Hill coefficient.

Simulating the receptor occupancy data using Berkeley Madonna

The in vivo rat receptor occupancy data were simulated in Berkeley Madonna using a standard K_d binding model, and the kinetic parameters were determined from the in vitro Motulsky and Mahan experiments. The differential equation used to calculate the receptor occupancy is given below (Yassen et al., 2006):

(12)

where [D] = concentration of drug in the plasma, [RD] = concentration of bound receptor, B_max = total receptor concentration, k_on = association rate constant of the drug and k_off = dissociation rate constant of the drug.

Computation

Data were analysed using the nonlinear mixed-effects modelling approach implemented in NONMEM software (version VI, release 6.2; Icon Development Solutions). The models were compiled using Digital Fortran (version 6.6, Compaq Computer Corporation, Houston, TX) and executed on a PC equipped with an Intel Core2 Duo dual processor under Windows XP. The results were analysed using the statistical software package S-Plus for Windows (version 8.0, Insightful Corp., Seattle, WA). Parameters were estimated using the first-order conditional estimation method with interaction between the two levels of stochastic effects (FOCE interaction). Residual variability was explored with both proportional and additive error models. Goodness-of-fit was determined using the minimum value of the objective function defined as minus twice the log-likelihood and by visual inspection of the plots of predictions and the diagnostic plots of weighted residuals.

Results

rCRF₁ radioligand binding competition under (pseudo) equilibrium conditions

All antagonists inhibited specific [³H]-SN003 binding at the rCRF₁ receptor in an apparently simple competitive manner (Figure 1, Table 1) with the following rank order of affinity (pK_i): DMP904 > R121919 > SN003 > PF-4734666 > PF-04850890 > PF-4659901 > PF-4325743.

Figure 1.

Inhibition of specific [³H]-SN003 binding to rCRF₁ receptor by CRF₁ non-peptide antagonists. Data points represent mean of n = 4 ± SEM.

Table 1.

Affinity estimates of antagonists at the rCRF₁ receptor determined by competition binding experiments using [³H]-SN003

Compound	Ki (nM) (pKi)
SN003	3.8 ± 0.32 (8.42)
PF-4325743	8.1 ± 0.43 (8.09)
PF-4659901	7.1 ± 0.53 (8.15)
PF-4734666	3.9 ± 0.39 (8.41)
DMP904	1.2 ± 0.05 (8.91)
R121919	3.0 ± 0.16 (8.52)
PF-4850890	4.9 ± 0.25 (8.30)

K_i data represent mean of n = 4 ± SEM.

Functional antagonism of the rCRF₁ receptor expressed in CHO-pro5 cells

Subsequently, the antagonistic effects of a single concentration (20 µM) of all seven ligands were investigated in the functional assay of oCRF-induced cAMP accumulation (Figure 2A). All compounds produced not only a rightward shift but, with the exception of SN003, also suppression of the maximum response of the oCRF concentration response curve, inconsistent with expectations of simple competitive, surmountable behaviour. A plot of the degree of suppression of the maximum oCRF response versus the antagonist concentration (20 µM) normalized by the apparent affinity (K_i as measured in the radioligand-binding experiment; Table 1) suggested that the degree of suppression of the maximum oCRF response was compound-specific and not simply a function of affinity-normalized antagonist concentration. DMP904 and R121919 showed the most pronounced depression, whereas SN003 did not cause any significant reduction (Figure 2B).

Figure 2.

(A) Effect of a single concentration of antagonist on oCRF-induced cAMP accumulation in CHO-pro5 cells expressing rCRF₁ receptor. (B) Percentage suppression of 20 µM oCRF response caused by 20 µM of each of the CRF₁ antagonists expressed as a ratio of its K_i derived from competition binding studies. Data points represent mean of n = 4 ± SEM.

A more detailed study of six antagonists (PF-4325743, PF-4734666, DMP904, R121919, SN003 and PF-4659901) in the functional assay of oCRF-mediated cAMP accumulation showed that for a given compound, the degree of insurmountability was concentration-dependent (Figure 3).

Figure 3.

Effects of multiple concentrations of CRF₁ antagonists (A, PF-4325743; B, DMP904; C, R121919; D, PF-4734666; E, PF-4659901; and F, SN003) on oCRF-induced cAMP accumulation in CHO-pro5 cells expressing recombinant rCRF₁ receptor. Assays were incubated for 90 min. Representative data from one experiment.

Combination antagonism of DMP904 and SN003

A combined concentration-ratio analysis experiment using the functional assay of oCRF-induced cAMP accumulation was designed to test whether DMP904 (which displayed the most pronounced non-competitive behaviour) and SN003 (which behaved in a simple competitive manner) act syntopically at the CRF₁ receptor.

As shown in Figure 4A, following 5 h pre-incubation, DMP904 (60 nM) and SN003 (2 µM) alone produced rightward shifts of the oCRF E/[A] curve with associated pA₂ values of 8.31 ± 0.04 and 7.25 ± 0.03, respectively (n = 4). Combined concentration-ratio analysis of the shift of the CRF E/[A] curve in the presence of both antagonists suggested that DMP904 and SN003 competed for binding to the same site, since the test statistic for the additive model (S_A = −0.13 ± 0.06) was not significantly different from 0 (P > 0.05), whereas the test statistic for the multiplicative model was significantly smaller than 0 (S_M = −1.12 ± 0.11; P < 0.05). Similar results were obtained when the incubation time was increased from 5 to 20 h (S_A = 0.00 ± 0.13; P > 0.05 and S_M = −0.97 ± 0.32, P < 0.05; Figure 4B). However, although these data did not provide evidence for different antagonist binding sites, it should be noted that the slope of the oCRF E/[A] curve in the presence of DMP904 alone was significantly flatter compared to the oCRF E/[A] curves obtained in the presence of SN003 or in the absence or presence of both antagonists following both 5 and 20 h pre-incubation (P < 0.001, anova followed by t-test), inconsistent with expectations for simple competitive antagonism.

Figure 4.

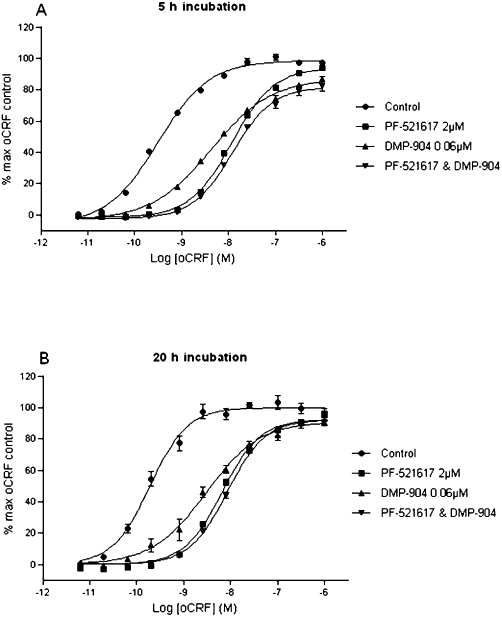
Effect of single and combined concentrations of DMP904 (0.06 µM) and SN003 (2 µM) on oCRF-induced cAMP accumulation in CHO-pro5 cells expressing recombinant rCRF₁ receptor. Assays were incubated for either (A) 5 h or (B) 20 h. Data points represent n = 4 ± SEM.

Effect of incubation time on the insurmountability of DMP904

The effect of incubation time on both the stability of the oCRF response and the surmountability of DMP904 was investigated using the functional cell based experiment. Figure 5A shows the control experiment in which it was confirmed that increasing the incubation time with vehicle from 30 to 2400 min did not alter the response to oCRF. The same increase in incubation time had no significant effect on the degree of depression of the oCRF E/[A] curves in the presence of 6 and 20 µM DMP904 (Figure 5B and C respectively)

Figure 5.

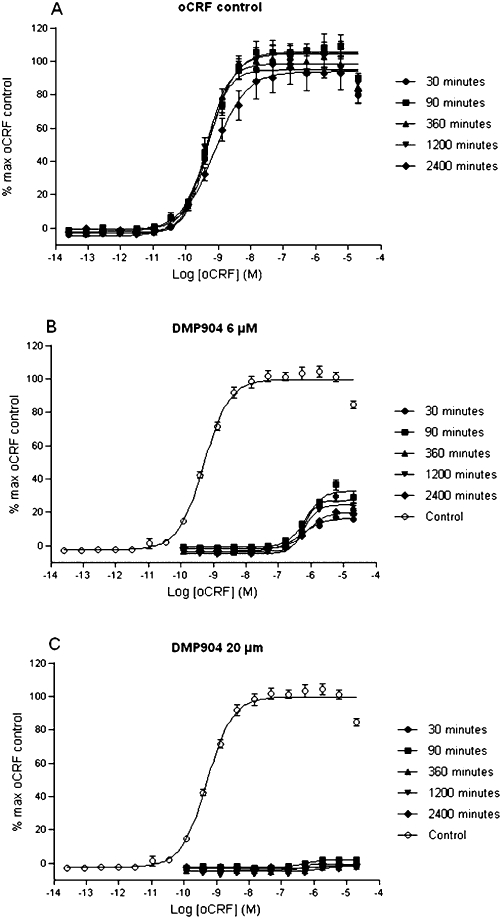
Effect of incubation time on (A) stability of oCRF response and the surmountability of either (B) 6 µM or (C) 20 µM DMP904 by oCRF-induced cAMP accumulation in CHO-pro5 cells expressing recombinant rCRF₁ receptor.

rCRF₁ radioligand binding competition under non-equilibrium conditions

Since insurmountable antagonism has often been associated with (pseudo) irreversible binding, we decided to quantify the CRF₁ receptor binding kinetics of the seven compounds in a non-equilibrium binding assay using three concentrations (1, 10 and 100 nM) as described in the Methods section. All compounds produced concentration-dependent suppression of the [³H]-SN003 kinetic binding isotherm at 1 and 10 nM and completely inhibited [³H]-SN003 binding at 100 nM. It appeared that based on the kinetic binding profiles shown in Figure 6, the compounds could be separated into two classes. Unlabelled SN003, PF-4659901, PF-4325743 and PF-4734666 produced a concentration-dependent inhibition of [³H]-SN003 binding to the rCRF₁ receptor with no further reduction in tracer ligand binding in the plateau phase of the kinetic binding isotherm. DMP904, R121919 and PF-4850890 also produced a concentration-dependent inhibition of [³H]-SN003 binding but caused a decrease in tracer ligand binding during the plateau phase of the kinetic binding isotherm.

Figure 6.

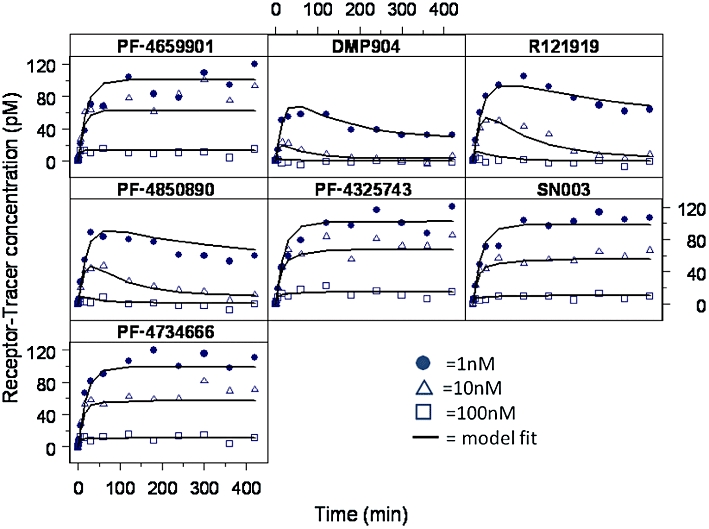
Effects of the seven CRF₁ antagonists on the receptor–tracer concentration in the in vitro non-equilibrium binding kinetic assay. Representative data from one experiment; n = 3–5 experiments performed in duplicate. Data fitted to Equations 5–7.

All data were analysed simultaneously using the model comprising the set of differential Equations 5–8 implemented in NONMEM to obtain estimates of the receptor association and dissociation rate for each compound (Figure 6), from which equilibrium dissociation constants (K_d = k_off/k_on) and half-life of dissociation (t_1/2,off = ln2/k_off) could be calculated. From the results summarized in Table 2, it can be seen that whereas all compounds displayed very similar onset binding kinetics (k_on rates within 5-fold), there were marked differences in the dissociation rates with an almost 20-fold range in estimated half-lives of dissociation.

Table 2.

Kinetically derived parameters from the in vitro non-equilibrium binding kinetic data and the in vivo derived EC₅₀

	In vitro kinetic parameters			Dissociation half-life (h)	In vivo
Compound	Kd (nM)	kon (M−1·min−1)	koff (min−1)		EC50 (nM)
SN003 (tracer)	3.64 ± 0.59	7.72e6± 1.6e6	0.026 ± 0.004	0.44	ND
SN003	5.62 ± 0.53	6.2e6± 8.9e5	0.033 ± 0.004	0.35	ND
PF-4325743	8.22 ± 1.48	4.06e6± 4.6e5	0.0316 ± 0.004	0.37	ND
PF-4659901	4.24 ± 1.2	7.88e6± 1.8e6	0.028 ± 0.008	0.41	ND
PF-4734666	3.06 ± 0.39	4.6e6± 5.1e5	0.0146 ± 0.003	0.79	13.4 ± 0.002
DMP904	0.275 ± 0.07	1.47e7± 1.4e6	0.0038 ± 0.001	3.04	ND
R121919	0.549 ± 0.15	3.69e6± 6.1e5	0.0019 ± 0.0005	6.08	0.290 ± 0.0003
PF-4850890	0.734 ± 0.17	2.79e6± 6.4e5	0.0017 ± 0.0002	6.79	1.48 ± 0.002

Mean values ± SEM; n = 5–7 per compound.

K_d = equilibrium dissociation constant, k_on = association rate constant, k_off = dissociation rate constant, Dissociation half life = time for half the compound to dissociate from the receptor (calculated by ln2/k_off), EC₅₀ = concentration that causes 50% occupancy in vivo, ND = not determined.

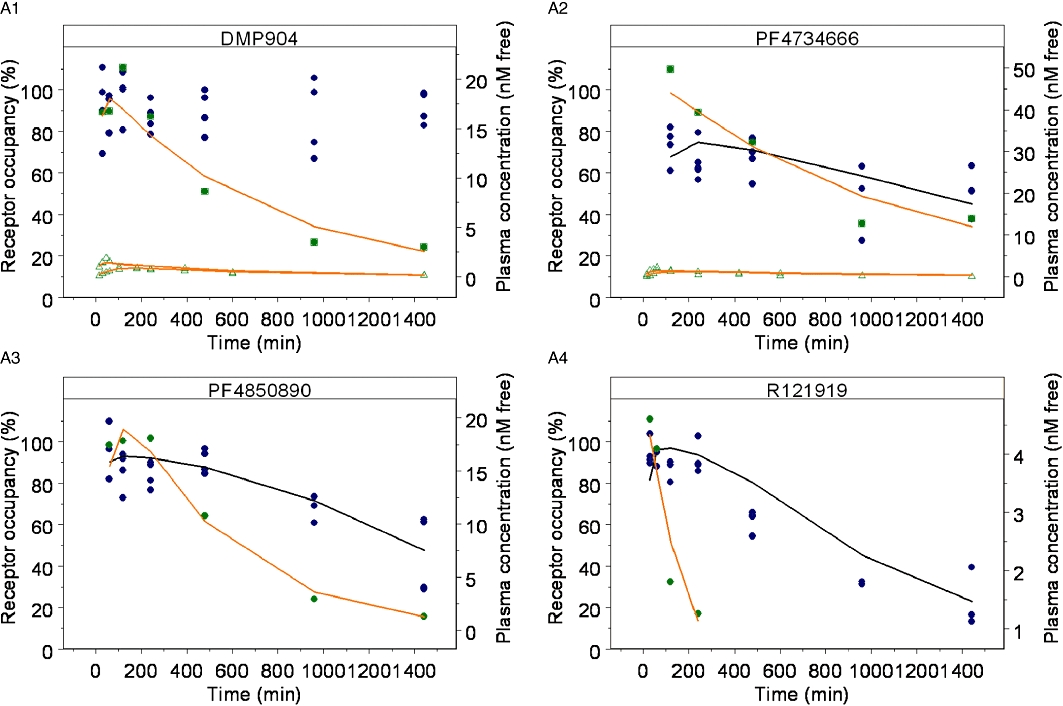
In vivo PKPD receptor occupancy studies

DMP904 (0.04–40 mg·kg⁻¹ p.o.) produced a dose-dependent increase in CRF₁ receptor occupancy in rat cortex 75 min after oral dosing, as determined by the ex vivo[³H]-SN003 binding assay. A standard Hill equation could be fitted to the data describing the relationship between unbound plasma concentration of DMP904 at the time of brain removal and CRF₁ receptor occupancy (Figure 7) to yield estimates (mean ± SEM) of in vivo potency (pEC₅₀ = 9.6 ± 0.15) and upper asymptote (E_max = 97.6%).

Figure 7.

Relationship between unbound plasma concentration of DMP904 at the time of brain removal and ex vivo CRF₁ receptor occupancy. Data points represent mean of n = 4 ± SEM.

In vivo receptor occupancy time course profiles of a single oral dose of four CRF₁ antagonists were also determined using the ex vivo[³H]-SN003 binding competition assay (Figure 8A). PF-4734666, PF-4850890 and R121919 displayed a time-dependent decline in receptor occupancy. In contrast, DMP904 produced maximal CRF₁ receptor occupancy during the entire time course of the experiment.

Figure 8.

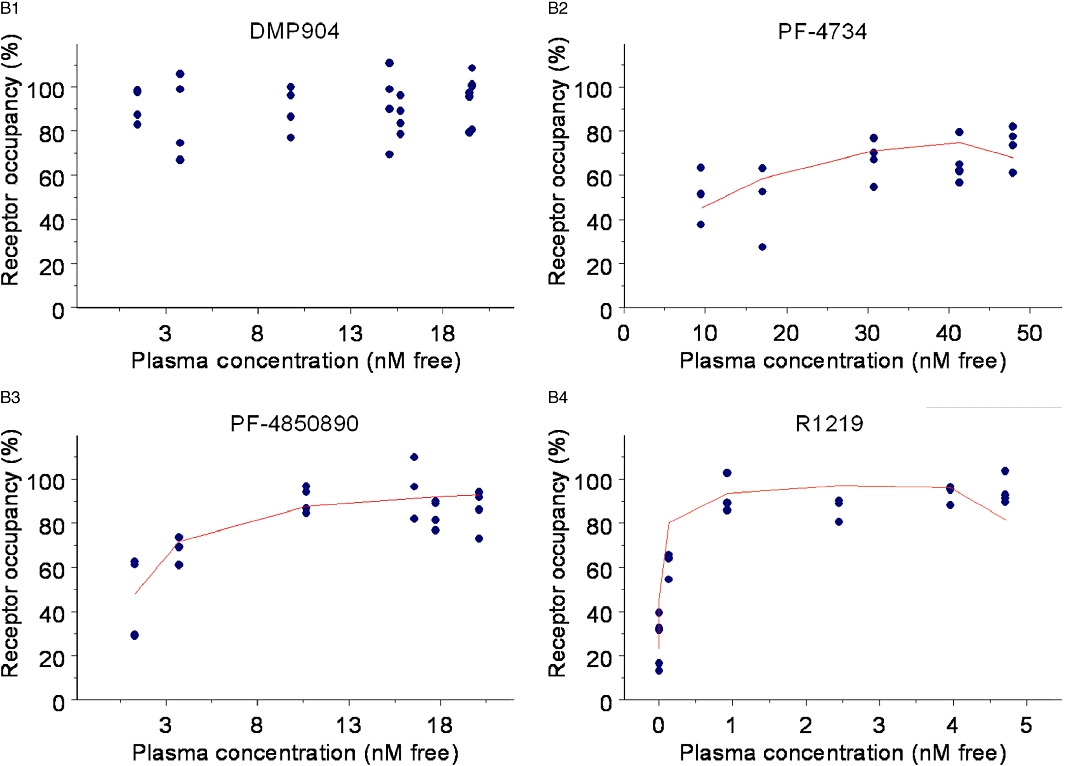
In vivo receptor occupancy time-course profiles of a single oral dose of four CRF₁ antagonists determined using the ex vivo[³H]-SN003 binding competition assay. (A) Observed receptor occupancy () and model fit (solid black line), and plasma concentration from receptor occupancy study (), or satellite oral pharmacokinetic study () and model fit (solid orange line) versus time relationships. Since DMP904 did not display a significant decay in receptor occupancy during the time course of the experiment, no attempt was made to fit a PKPD model to the data for this ligand. (B) In vivo concentration versus receptor occupancy relationship: () = observed data, solid red line = model fit. Since DMP904 did not display a significant decay in receptor occupancy during the time course of the experiment, no attempt was made to fit a PKPD model to the data for this ligand.

For all four compounds, the time course of the plasma concentration during the in vivo receptor occupancy and additional satellite pharmacokinetic (DMP904 and PF-4734666) experiments could be described adequately by a standard one-compartment pharmacokinetic model (Table 3 and Figure 8A). Plasma protein binding was also determined (Table 3) to calculate unbound plasma concentrations. The pharmacokinetic models were then used to generate in vivo concentration–effect relationships for each compound (Figure 8B), which suggested a direct relationship between unbound plasma concentration and receptor occupancy.

Table 3.

Pharmacokinetic parameters obtained in the rat following oral administration in receptor occupancy studies and satellite oral pharmacokinetic studies

Compound	ka (1 min−1)	kel (1 min−1)	Vd/F (L·kg−1)	Rat PPB % (Fu)
PF-4850890	0.0175	0.00219	5.09	99.3 (0.007)
PF-4734666	0.0381	0.00099	7.70	98.5 (0.015)
R121919	0.125	0.00646	25.6	99.8 (0.005)
DMP904	0.0628	0.00143	8.63	99.4 (0.006)

K_a = absorption rate constant, k_el = elimination rate constant, V_d/F = oral volume of distribution, PPB = plasma protein binding, Fu = fraction unbound in the plasma.

Accordingly, a simple, direct PKPD model (Equation 11) was fitted to the data to obtain estimates of in vivo EC₅₀ for PF-4734666 (13.4 ± 0.002 nM), PF-4850890 (1.5 ± 0.0002 nM) and R121919 (0.290 ± 0.0003 nM). Since DMP904 did not display a significant decay in receptor occupancy during the time course of the experiment, no attempt was made to fit a PKPD model to the data for this ligand. An attempt was also made to fit the more complex receptor binding kinetics PKPD model (Equation 12) to the data, but, the goodness-of-fit did not improve compared to the simpler model (not shown). However, although a formal model fit of the data was not obtained, we did use the complex receptor binding kinetics model to simulate the expected time course of in vivo occupancy constraining the k_on and k_off parameters in Equation 12 to the values estimated in the in vitro experiments (Table 2). The results of these simulations superimposed on the actual experimental data (Figure 9) show that reasonable predictions were obtained in the case of PF-4850890 and DMP904; however, the model over- and under-predicted the occupancy levels for PF-4734666 and R121919, respectively. In the case of R121919, this apparent mismatch could be reconciled by increasing the value of k_on by approximately fivefold, whereas changing k_off alone did not result in an improved description of the data (as judged by eye). In the case of PF-4734666, the discrepancy between model simulations and experimental data could be resolved to the same extent by either decreasing the k_on or increasing the k_off value by approximately fivefold.

Figure 9.

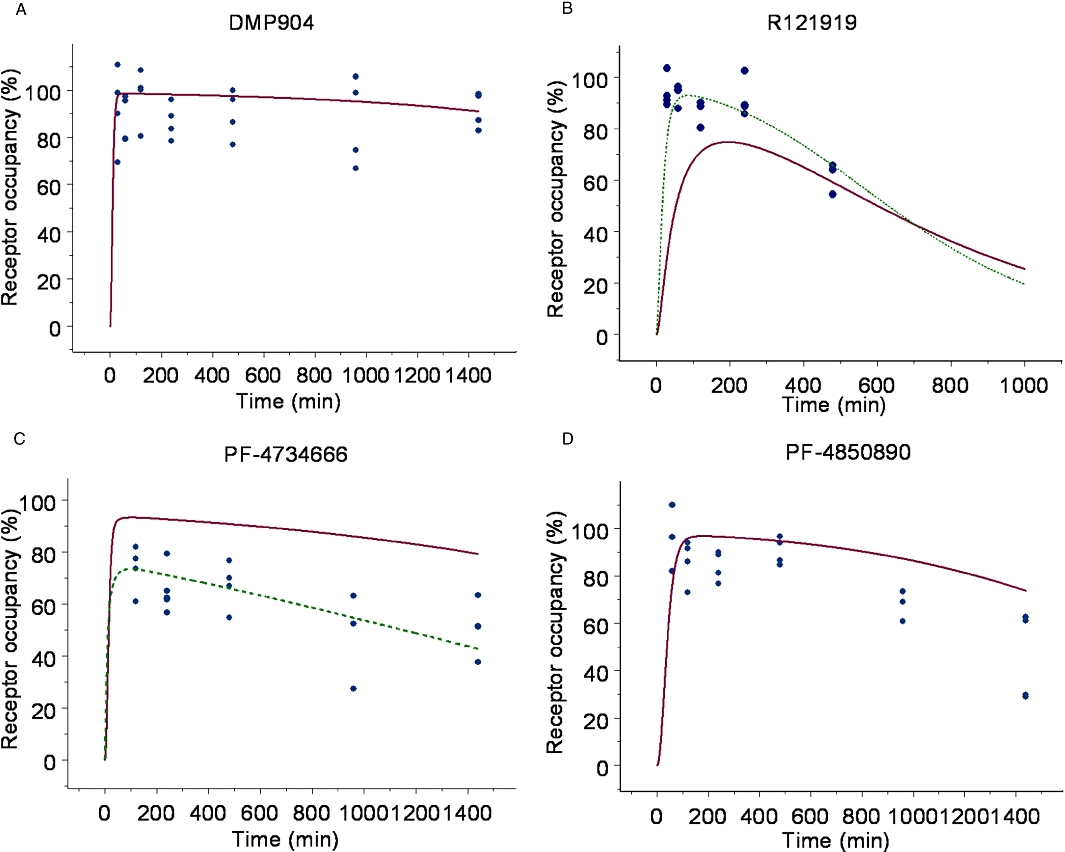
Simulations of receptor occupancy versus time profiles using the in vitro non-equilibrium binding kinetic k_on and k_off values (solid line), or k_on optimized fit (dashed line), superimposed on observed receptor occupancy data (). (A) DMP904, (B) R121919, (C) PF-4734666, (D) PF-4850890.

Discussion

Non-competitive antagonism at the CRF₁ receptor by non-peptide antagonists has been widely reported in the literature. Li et al. (2005) observed that both DMP904 and DMP696 antagonized CRF stimulated adenylate cyclase activity in rat cortical membranes in a non-competitive manner. Although the assay incubation time was only 10 min, it was believed that the insurmountable antagonism observed was not due to non-equilibrium conditions as affinity estimates for both antagonists at 10 min were similar to those determined within ACTH release experiments incubated for 4 h. Similarly Gully et al. (2002) demonstrated that the CRF₁ non-peptide antagonist, SSR125543A, inhibited ACTH secretion induced by CRF in mouse pituitary AtT-20 cells when co-incubated for 120 min. Again, the observed rightward shift in the CRF concentration–effect curve was associated with a concentration-dependent reduction in ACTH secretion, suggesting non-competitive inhibition.

Berger et al. (2006) investigated the possible differences in the antagonism of Gs- and Gi-protein coupling of the rat CRF₁ receptor by a peptide [α-helical CRF (9–41)] and a non-peptide antagonist (antalarmin) to determine the conformational requirements of the activated CRF₁ states for Gs- and Gi-coupling. They demonstrated that in contrast to the peptide antagonist α-helical CRF, the non-peptide antagonist antalarmin exhibited competitive antagonism only towards the activation of Gs-protein but strongly antagonized Gi-protein activation non-competitively in HEK293 rCRF₁ cell membranes. Their results suggest that Gs- and Gi-protein activation by CRF₁ is accomplished through different conformations of the receptor. Similarly, Hoare et al. (2008) demonstrated that the CRF₁ non-peptide ligands NBI 35965 and NBI 77173 reduced the E_max of CRF-induced cAMP accumulation in AtT-20 cells in a concentration-dependent manner. They concluded that this finding suggested that these non-peptide ligands reduced G-protein coupling efficacy of a CRF-bound receptor state.

In the present study, we attempted to shed new light on the complex pharmacological behaviour of CRF₁ antagonists and characterized the receptor binding kinetics of several reference and novel ligands in vitro and in vivo. Our main finding was that the non-competitive behaviour appeared to be correlated to the CRF₁ receptor off-rate kinetics, that is ligands with the slowest dissociation rate constant produced the most pronounced suppression of the maximal response to CRF. This is further illustrated in Figure 10, which shows the correlation (r² = 0.87) between the k_off as measured in the radioligand binding assay and the % suppression of the maximum response to 20 µM CRF in the cAMP functional assay. The exact mechanistic interpretation of this finding remains unclear at present. If the insurmountable behaviour was entirely due to a lack of agonist–antagonist equilibrium, we would expect to see a reversal to simple competitive behaviour with increased incubation times (Kenakin, 2004). However, we were not able to demonstrate such an effect when we increased the co-incubation time of oCRF and DMP904 in the functional assay of CRF₁ receptor-induced cAMP accumulation by 80-fold (Figure 5), which leaves open the possibility that other molecular mechanisms also play a role in the non-competitive behaviour. A similar hypothesis of slow-offset kinetics working in concert with an additional pharmacological property has been proposed to explain insurmountable antagonism at, for example, angiotensin II AT₁ (Liu et al., 1992; Vanderheyden et al., 1999) and cholecystokinin CCK_B receptors (Corsi et al., 1993).

Figure 10.

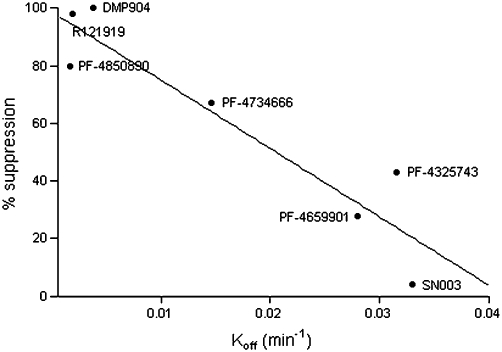
Correlation between the off rate (min⁻¹) of each antagonist from the rat CRF₁ receptor and percentage suppression of a 20 µM oCRF response by 20 µM of each of the CRF₁ antagonists in the cAMP functional assay.

Another hypothesis we explored was whether insurmountable CRF₁ antagonists (as exemplified by DMP904) act at different sites than ligands that behave in an apparently simple competitive manner (as exemplified by SN003), but the combined concentration-ratio experiment summarized in Figure 4 did not provide evidence for such a mechanism. It should be noted that this finding does, of course, not exclude the possibility that in other assays, and under different experimental conditions the ligands could act in a non-competitive manner and further work is required to explore this.

Our findings cast doubt on the accuracy of previously reported potency estimates reported for some CRF₁ receptor ligands. For example, we showed that for the three compounds that displayed the longest receptor dissociation half-life (DMP904, R121919 and PF-4850890), there was at least a fourfold increase in affinity when determined from kinetic experiments compared with competition binding studies using a 2 h incubation time.

To validate the non-equilibrium binding methodology, the binding kinetics of SN003 were determined directly using [³H]-SN003 and indirectly using the cold SN003. The kinetic data obtained between the two methodologies were highly comparable (Table 2). The kinetic and affinity data obtained for SN003 were also similar to those presented by Zhang et al. (2003) at the human CRF₁ receptor. It was also observed that the free plasma concentration of DMP904 that produced 50% receptor occupancy of the rat CRF₁ receptor in a single time point study better equates to its kinetically-derived affinity estimate than its competition binding measure of affinity (Figure 7).

Typically, analyses of receptor binding kinetic data, such as those reported in this manuscript, are carried out in a stepwise, sequential manner and by making assumptions about the inter-experiment and tracer parameter variability, for example fixing the latter at given values. In this paper, we used an alternative, population-based mixed-effect modelling, method as described recently by Benson et al. (2010), which allows for a simultaneous analysis of all individual data from multiple experiments. The superiority of this simultaneous analysis approach compared with the sequential one has recently been demonstrated by Benson et al. (2010) and Ernest II et al. (2010). We also used the simultaneous modelling approach to optimize the efficiency of the non-equilibrium competition binding assay. The original experimental protocol used 22 time points, two concentrations of each antagonist in quadruplicate which were used at 1 and 10 times the antagonist's K_i, previously determined from competition binding studies. Within the original protocol, tracer–ligand association and dissociation and saturation experiments were also performed. Through simulations with the mathematical model, the protocol was optimized to halve the number of assay time points. Also, it allowed us to simplify the protocol and use universal concentrations (1, 10 and 100 nM) for all compounds that were tested in duplicate, which again halved the number of assay points. Finally, protocol optimization also removed the need to perform a separate tracer–ligand dissociation experiment by determining the binding kinetics of the tracer–ligand in an association time course binding experiment at two concentrations of tracer–ligand. Overall, the simultaneous modelling approach provided the basis for improving the efficiency of the assay by fourfold, which allowed us to implement it as a standard screen in our drug discovery project.

The association rates of all compounds tested did not differ by more than fivefold and were within the typical range (10⁵–10⁸ M⁻¹·s⁻¹) reported for GPCR interactions of small molecules (e.g. Copeland et al., 2006; Dowling and Charlton, 2006; Tummino and Copeland, 2008; Malany et al., 2009). A wider range (almost 20-fold) was observed for the dissociation rates, consistent with the idea that k_off is often a greater determinant of affinity differences between ligands from a similar series than k_on (Copeland et al., 2006; Tummino and Copeland, 2008). It should be stressed that the validity of the kinetic binding parameters depends on the assumption that the various ligands do bind competitively at the CRF₁ receptor. Although the combined concentration-ratio experiment in the functional assay did not provide evidence for non-competitive behaviour, further work is required to fully establish the nature of ligand interaction in the radioligand binding assay.

A main objective of this study was to explore how in vitro data could be used to design, interpret and predict in vivo receptor occupancy studies. The rank order of in vivo potency (R121919 > PF-4850890 > PF-4734666) based on the EC₅₀ estimates obtained from the PKPD model (EC₅₀ = 0.290, 1.5 and 13.4 nM, respectively) matched the in vitro results (Table 2), suggesting that at least in a qualitative manner the in vitro assay can be used to triage and select compounds for further in vivo investigations. It should be noted that such good accordance was not obtained in pilot in vivo experiments (data not shown) where we used single time point occupancy measurements at multiple dose levels, instead of the full time course design reported in this paper. The reasons why single-time-point designs can lead to erroneous conclusions and should be avoided are discussed in a recent review by Gabrielsson et al. (2010). The simulations reported in Figure 9 suggest that the in vitro measurements of k_on and k_off were within fivefold of the in vivo values; however, more data would be required to obtain reliable in vivo estimates and to draw any further conclusions as regards the concordance between in vitro and in vivo data and compounds. One potential reason for this fivefold error could be due to the temperature the non-equilibrium kinetic binding studies were performed at, as these experiments were completed at room temperature, and in vivo the binding events will occur at 37°C. It is believed that reaction rates double for every 10°C increase in temperature (Benson et al., 2010). Therefore, going from room temperature to 37°C, we may expect an approximate fourfold increase in kinetic rates of binding. However, as the fivefold error was not consistent across the four compounds, temperature alone cannot fully explain the observed in vitro–in vivo mismatch.

Initially, we were somewhat surprised that there was no clear evidence of ‘hysteresis’ (a delay between the time course of concentration of drug in plasma and receptor occupancy) (Gabrielsson et al., 2010; 2011;) in the in vivo experiments, given the relatively slow offset binding kinetics of the ligands. However, a simulation using the PKPD receptor binding model (Equation 12) showed that the ‘counter-clockwise’ concentration–effect relationship characteristic of hysteresis would only have been apparent if more occupancy measures had been obtained at earlier time points and/or more (lower) doses had been studied (Figure 11). This illustrates the utility of a PKPD modelling and simulation approach to guide optimal design and interpretation of in vivo studies in a drug discovery setting.

Figure 11.

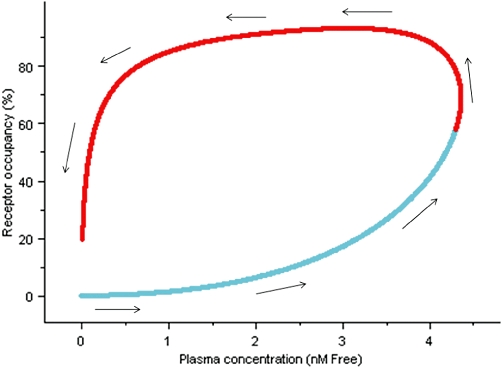
Simulation of R121919 receptor occupancy versus concentration profile using rat pharmacokinetic parameters and k_on and k_off rates determined from in vitro non-equilibrium binding kinetic experiments. Arrows indicate the time order of concentration data, the light blue line represent concentration data not captured by in vivo receptor occupancy study and the red line represent concentration range covered with the in vivo study.

Another application of the proposed integrated in vitro–in vivo PKPD approach is to guide translational research and design clinical experiments based on preclinical data. For example, Kunzel et al. (2003) tested R121919 in an open-label study in 24 patients with major depressive episodes at doses ranging from 5 to 80 mg. They reported that even at the highest dose (80 mg) tested, there were no adverse effects or impairment of the hypothalamic–pituitary–gonadal system, the hypothalamic–pituitary–thyroid axis, renin–angiotensin system and prolactin or vasopressin secretion. Furthermore, no changes were seen in serum corticotropin and cortisol levels, and there were no effects on routine clinical laboratory parameters including liver enzymes, EEG and ECG. We employed our PKPD model to simulate the predicted CRF₁ receptor occupancy achieved in this study. Figure 12 shows that if the in vitro estimates of k_on and k_off are used, the model predicts that maximum receptor occupancy level achieved in the study is predicted to be ∼10%, which is typically not believed to be sufficient for a GPCR antagonist to exert a meaningful pharmacological effect (Grimwood and Hartig, 2009). Two additional simulations were performed, which incorporated the uncertainty factor of approximately fivefold on the k_on and k_off estimates derived from the simulations (see Results). These simulations represent the extreme scenarios where k_on and k_off would be modified by a factor of 5 simultaneously in opposite directions (Figure 12). The main conclusion that can be drawn from this exercise is that the expected occupancy is highly sensitive to the receptor binding kinetic parameters, and that at present, it is not possible to conclude whether hardly any or a significant (>50%) degree of CRF₁ receptor occupancy was achieved in the clinical study reported by Kunzel et al. (2003).

Figure 12.

Simulations of an 80 mg clinical dose of the CRF₁ antagonist, R121919 (see text for details). Solid line represents a simulation using the in vitro derived parameters, whereas the dotted and dashed lines represent a fivefold increase and decrease of k_on respectively.

In conclusion, this study provides evidence for a link between ligand offset kinetics and insurmountable/non-competitive antagonism at the CRF₁ receptor. The exact molecular pharmacological nature of this association remains to be determined.

In addition, we have developed a quantitative framework to study and integrate in vitro and in vivo receptor binding kinetic behaviour of CRF₁ receptor antagonists in an efficient manner in a drug discovery setting. The PKPD approach provides the basis to refine, reduce and replace (three Rs) animal experiments (Russell and Burch, 1959), which has obvious ethical and economical benefits and can be used in translational research to guide the design and interpretation of clinical experiments. This approach can be applied to other drug discovery targets, for example other GPCRs or ion channels, and illustrates how PKPD can bridge the gap between in vivo pharmacology and medicinal chemistry (Van Der Graaf and Gabrielsson, 2009; Gabrielsson et al., 2010; 2011;).

Glossary

Abbreviations

B_max

maximum receptor concentration

CRF

corticotropin releasing factor

K_dD

equilibrium dissociation constant of the drug

K_dT

equilibrium dissociation constant of the tracer

k_offD

dissociation rate constant of the drug

k_offT

dissociation rate constant of the tracer

k_onD

association rate constant of the drug

k_onT

association rate constant of the tracer

R

receptor

RD

receptor–drug complex

RT

receptor–tracer complex

T

tracer

Conflicts of interest

SR, NA, RF and PvdG are all full-time employees of Pfizer. Otherwise, there are no other conflicts of interest.