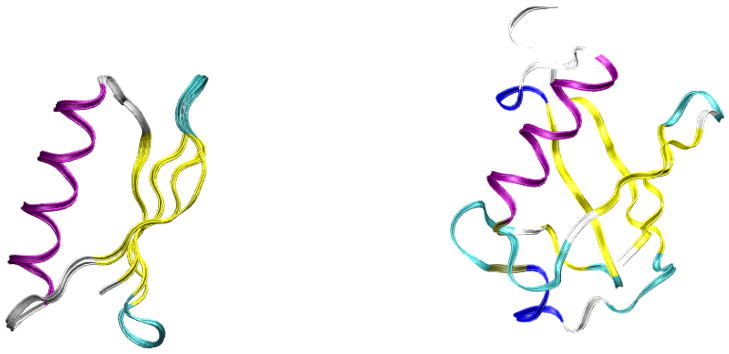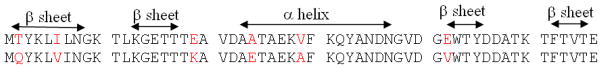Calculation of Chemical Shift Anisotropy in Proteins

Abstract

Individual peptide groups in proteins must exhibit some variation in the chemical shift anisotropy (CSA) of their constituent atoms, but not much is known about the extent or origins of this dispersion. Direct spectroscopic measurement of CSA remains technically challenging, and theoretical methods can help to overcome these limitations by estimating shielding tensors for arbitrary structures. Here we use an automated fragmentation quantum mechanics/molecular mechanics (AF-QM/MM) approach to compute ¹⁵N, ¹³C′ and ¹H chemical shift tensors for human ubiquitin and the GB1 and GB3 fragments of staphylococcal protein G. The average and range of variation of the anisotropies is in good agreement with experimental estimates from solid-state NMR, and the variation among residues is somewhat smaller than that estimated from solution-state measurements. Hydrogen-bond effects account for much of the variation, both between helix and sheet regions, and within elements of secondary structure, but other effects (including variations in torsion angles) may play a role as well.

1 Introduction

Nuclear magnetic resonance (NMR) spectroscopy provides valuable information about the three dimensional structures of macromolecules. Chemical shifts can be easily measured and used as restraints in protein structure determination and refinement (Wishart and Case, 2001; Shen et al, 2008). Chemical shift anisotropy (CSA) can also be an excellent indicator of the local electronic and molecular environment (Sitkoff and Case, 1998; Gu and McDermott, 1993; Lipsitz and Tjandra, 2003), but much less is known about its connection to structure, especially for N, C′ and H atoms in the peptide group itself. (Scheurer et al, 1999; Tjandra and Bax, 1997; Sitkoff and Case, 1998). The interpretation of chemical shift tensors in proteins is expected to be complicated by their dependence to a large number of environmental factors, such as the conformation of neighboring residues, hydrogen bonding and long-range electrostatics (Sitkoff and Case, 1998; Brender et al, 2001). A better understanding of these issues could help in characterizing protein and structure and dynamics, and in aiding the interpretation of the CSA components of spin-relaxation.

In solution NMR, the direction and magnitude of chemical shift tensors cannot be directly measured due to isotropic tumbling. Instead, anisotropies can be estimated from relaxation and CSA-dipolar cross-correlation experiments at multiple spectrometer fields (Kroenke et al, 1999; Fushman et al, 1998), or from shifts in peaks upon partial alignment (Burton and Tjandra, 2007). Solid state NMR experiments provide more direct information, but often require site-specific labeling and multiple independent CSA measurements, which can be technically challenging. As a result, most direct CSA measurements and interpretations have been performed on small peptides (Yao et al, 2002; Wei et al, 2001; Hartzell et al, 1987; Wei et al, 1999; Poon et al, 2004; Wu et al, 1995). Nevertheless, recent advances in solution and solid state NMR techniques have allowed CSA to be systematically measured for a few small, globular proteins, including the GB1 and GB3 fragments of staphylococcal protein G, binase and ubiquitin (Cisnetti et al, 2004; Hall and Fushman, 2006; Wylie et al, 2007; Loth et al, 2005; Pang and Zuiderweg, 2000; Yao et al, 2010a,b). These revealed a significant but inconsistent dependence of the CSAs on the protein backbone conformation.

Theoretical predictions can compensate for the limited dataset from experimental studies and help elucidate the structural information implicated in experimental measurements (Case, 2000). Over the past decade, quantum mechanical calculations have facilitated NMR structure refinement by establishing empirical relationships between structural features and isotropic chemical shifts (Oldfield, 1995; Casabianca and De Dios, 2008). Density functional theory (DFT) based methods have been used extensively to characterize chemical shielding tensors for di- and tri-peptide species (Poon et al, 2004; Heller et al, 1997; Havlin et al, 2001; Sitkoff and Case, 1998; Bim et al, 2004). More recently, Czinki and coworkers mapped the ¹⁵N and ¹³C CSA surface using L-Ala-NH₂ as a model for peptides and proteins (Czinki et al, 2007). Cai et al. (2009; 2011) also calculated the ¹⁵N chemical shift tensors of the selected residues in GB3 protein using a variety of peptide models. While these recent studies provide some understanding to the influence of protein geometry on chemical shift tensors, the effects of the complete protein environment remains to be assessed quantitatively.

In the present study, we adapted and extended the automated fragment-quantum mechanics/molecular mechanics (AF-QM/MM) model developed by He and coworkers (He et al, 2009). In this model, the central protein fragment is treated with quantum mechanics and the rest of the protein and solvent environment are represented by point charges. It was originally applied to Trp Cage mini-protein to predict proton isotropic shieldings and achieved considerable agreement with experimental measurements (He et al, 2009). We report here the CSA tensors of ¹⁵N, ¹³C and ¹H nuclei for GB1, GB3 and ubiquitin using a number of different experimental structures, where the quality of the CSA predictions are evaluated and the environmental effects are assessed.

2 Methods

2.1 Structure regularization

Table 1 lists the protein structures used here, which were determined by NMR spectroscopy or X-ray crystallography. Some “regularization” of the experimental structures via 10 steps of molecular mechanics based energy minimization appears to improve the results. During energy minimization, the aqueous environment was approximated by the Hawkins, Cramer and Truhlar (HCT) form of pairwise generalized Born (GB) model approach implemented in the Nucleic Acid Builder (NAB) program (Hawkins et al, 1995; Macke and Case, 1998). Each of the structures were relaxed for 10 steps using the Polak-Ribiere conjugate gradient algorithm. This mainly serves to bring bond lengths and bond angles close to the “ideal” values specified in the force field, while changing little else in the structure. As shown in Table 1, the backbone change is 0.1 to 0.2 Å. This procedure also removes side-chain steric clashes, while preserving the backbone geometry (including φ, ψ and ω angles) of the experimental structure. This stage proved to be crucial in achieving relatively consistency, given different starting PDB structures acquired under different experimental conditions. For example, prior to minimization, the ¹³C CSA values calculated from 1P7E and 1IGD structures deviate by as much as 9.34 ppm for individual nuclei, but this difference is reduced to 3.32 ppm after minimization. Furthermore, partial minimization leads to better trends with regards to secondary structure. For example, in the 1IGD structure, the helix-sheet difference (discussed below) for the¹⁵N CSA increased from 3.9 ppm to 9.8 ppm after the refinement, which is much closer to the experimental difference of 9.9 ppm.

Table 1.

RMSD change upon 10 steps of minimization, relative to the original crystal structure. The fitted atoms include all backbone atoms for residues 3–54 for GB1/GB3, and residues 3–74 for ubiquitin. For the 1D3Z entry, coordinates from model 1 were used.

Protein	PDB ID	Backbone RMS
GB3	1P7E	0.15
“	1IGD	0.21
“	2OED	0.14
GB1	1PGA	0.20
“	2QMT	0.11
ubiquitin	1UBQ	0.07
“	1D3Z	0.18

2.2 Chemical Shift Tensor Calculations

The AF-QM/MM model takes the entire protein and solvent effects into consideration in the following fashion. The protein is partitioned into the core and buffer region to be treated with quantum mechanics, whereas the rest of the protein and solvent effects are represented by point charges. The core region includes the CA-N-CA segment of the backbone of the n^th amino acid, together with directly attached side-chains.

The buffer region is defined to include residues described by the following criteria:

• i) The (n•2)^th, (n−1)^th, (n+1)^th and (n+2)^th residues in the protein.

• ii) The residues within 4 Å of the core region, where at least one of the contacting atoms is nonhydrogen.

• iii) The residues within 3 Å of the core region, where both contacting atoms are hydrogens.

• iv) The residues within 5 Å of the core region, where the contacting atoms include a heavy atom from an aromatic ring from the buffer region, and any atom from the core region.

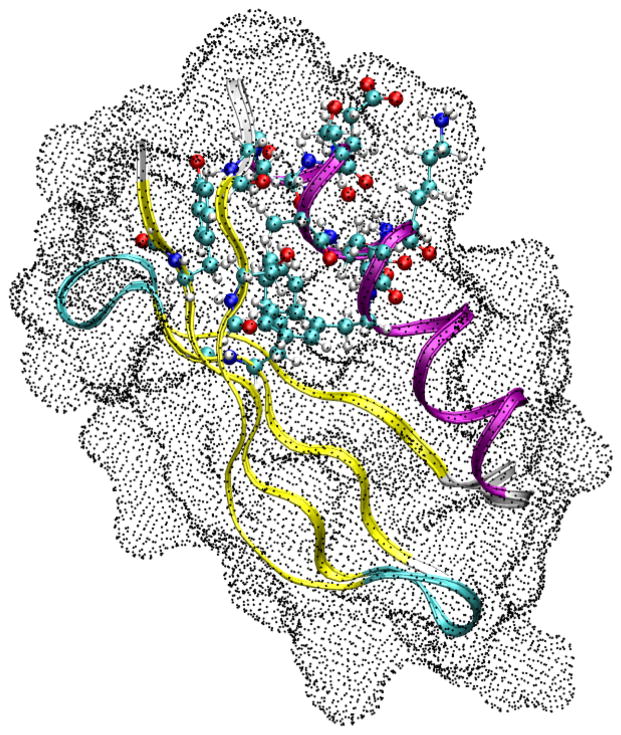
The rest of the protein environment is represented by partial atom charges defined in the AMBER94 forcefield (Cornell et al, 1996). In addition, the solvent effect is approximated by Poisson Boltzmann based grid charges, as shown in Fig. 1. In order to generate these surface charges, the self consistent reaction field was calculated by solving the Poisson Boltzmann (PB) equation iteratively using the Amber pbsa program:

$$\nabla ·[\epsilon (r)\nabla \phi (r)]-{\kappa }^2(r)\phi (r)=-4\pi \rho (r)$$

where κ is the modified Debye-Huckel parameter reflecting the salt concentration (here taken to be 0.1 M of a 1-1 electrolyte) and temperature. ε(r) is the dielectric constant distribution in space, which were set to 1.0 and 80.0 for solute and solvent, respectively. φ(r) is the electrostatic potential to be calculated. ρ(r) is the solute charge distribution, described by the Amber force field atomic charges. According to PB theory, the solute produces an electrostatic field in the solute region and solvent region, including the solvent reaction field and the Coulomb field. The reaction field is generated by the polarization in the solvent, and can be represented by a set of point charges on the molecular surface; we employed a spacing of 0.75 Å for these surface charges, yielding between 5,000 and 12,000 charges, depending on the size of the fragment.

Figure 1.

AF-QM/MM model for CSA Calculation. The central QM region, represented by ball-and-stick model, is calculated on B3LYP/6-31G* level. The rest of the protein, represented in ribbons, are treated as AMBER charges. The entire protein is embedded in surface charges rendered as dots.

With these fragments, two quantum chemistry methods (somewhat arbitrarily chosen) were used to compute shielding tensors. In the first (method 1), Gauge Independent Atomic Orbital (GIAO) calculations of the chemical shielding tensors (Ditchfield, 1974) were performed using the B3LYP functional (Becke, 1993) with the Gaussian 03 program (Frisch et al, ????). The second method (method 2) used the DeMon 2k program (Koster et al, 2006) to compute shieldings, using OLYP functional (Tozer and Handy, 1998; Wilson et al, 1999) and the independent gauge for localized orbitals (IGLO) model. Within the core region, the central fragment CA-C(O)-N(H)-CA was treated with a locally dense basis set, whereas the rest of the core region and buffer region were treated with a smaller basis set (Tang and Case, 2007). In the Gaussian and deMon calculations, the locally dense basis set scheme is cc-pvTZ/6-31G** and iglo-iii/dzvp, respectively.

The differences in results between the two methods we have chosen here have little to do with the program used for the calculation, and are mainly from the difference in functionals. As we have discussed earlier (Moon and Case, 2006), relative values of isotropic shieldings and their anisotropies are rather insensitive to either the density functional used or the basis set (beyond a certain level); absolute anisotropies are generally larger with hybrid functionals than with non-hybrids, and the results found here confirm this, with the hybrid results being closer to experiment than the non-hybrids. But in general, the less-expensive non-hybrid calculations give trends that are nearly as useful those from hybrid calculations. Further discussions of this point, covering isotropic shifts for a much larger range of proteins, will be published elsewhere.

The calculated chemical shift tensors were symmetrized and diagonalized to obtain the three principal components. The magnitude of these principal components was ranked according to their deviation from the isotropic shift, δ_iso.

$$\mid {\delta }_{zz}-{\delta }_{\mathit{iso}}\mid \ge \mid {\delta }_{xx}-{\delta }_{\mathit{iso}}\mid \ge \mid {\delta }_{yy}-{\delta }_{\mathit{iso}}\mid$$ (1)

The reduced anisotropy (Δδ_red) is defined as the difference between the largest tensor and the isotropic chemical shift according to the Haeberlen conventions (Haeberlen, 1976):

$$\mathrm{\Delta }{\delta }_{\mathit{red}}={\delta }_{zz}-{\delta }_{\mathit{iso}}$$ (2)

Solution NMR analyses often use a shielding anisotropy (Δσ), which is the difference between the largest tensor and the average of the other two tensors:

$$\mathrm{\Delta }\sigma ={\sigma }_{zz}-\frac{({\sigma }_{xx}+{\sigma }_{yy})}{2}=-\frac{3}{2}\mathrm{\Delta }{\delta }_{\mathit{red}}$$ (3)

For consistency, we will use the “reduced” anisotropy of Eq. 2 here. The asymmetry parameter describes the deviation from axial symmetry:

$$\eta =\frac{{\delta }_{xx}-{\delta }_{yy}}{\mathrm{\Delta }{\delta }_{\mathit{red}}}$$ (4)

3 Results and Discussion

GB1 and GB3 proteins are the B1 and B3 domains of immunoglobulin G, respectively. They have exactly the same fold, including one α-helix and four antiparallel β-strands (Figure 2). Their sequences are comprised of 17 types of amino acids and differ by only 7 residues from each other (Figure 3). Human ubiquitin has a mixed topology, with a smaller fraction of amino acids in regions of regular secondary structure. Both systems have had experimental structures determined by X-ray crystallography and by NMR, as shown in Table 1.

Figure 2.

(Left:) overlapped GB1 and GB3 structures. The α-helix is rendered in purple and the β-sheets are rendered in yellow. (Right:) same for ubiquitin.

Figure 3.

Sequence alignment of GB1 and GB3 proteins

3.1 ¹³C and ¹⁵N tensors in GB1

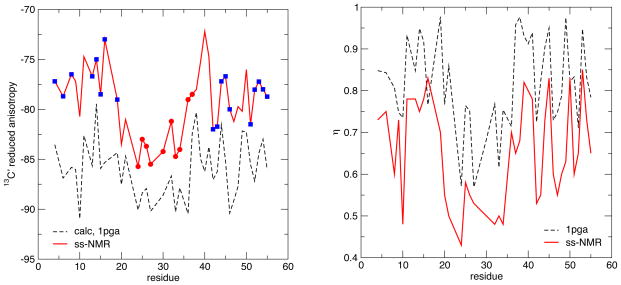
Solid-state NMR measurements offer the most direct method to obtain information about chemical shielding tensors, and we begin with a comparison to such results for GB1 (Wylie et al, 2007), given in Table 2 and Figs. 4 and 5. For the ¹³C′ shieldings, the experimental anisotropies are systematically larger in absolute magnitude than the method 2 (OLYP) results by around 5 ppm, but systematically smaller than results from method 1 (B3LYP) predictions by about the same amount (Table 2). Both calculated and observed results show a clear trend where Δδ_red is more negative in the helical regions (near the center of the sequence) than in the sheet regions (nearer the termini); the asymmetry η is also lower in helical than in sheet regions. [For tensors with asymmetries near unity, small changes can flip the sign of Δδ_red; this happened for two residues in the calculations; for simplicity, we have plotted all values in Fig. 4 as negative.] Some, but not all, of the variations within regions of secondary structure are also captured in the calculations, and the range of anisotropies is nearly the same in the calculations (12 ppm) as in the experiment (13 ppm). The fact that the calculated results are larger in absolute magnitude than the observed values (at least for method 1), is qualitatively consistent with the fact that the observed results are motionally averaged whereas the calculated results are not. Multiplying the calculated results by an order parameter of 0.95 would markedly improve agreement with experiment, and this amount of motional averaging is roughly consistent with (although somewhat larger than) estimates we derived earlier from studies on model peptides (Tang and Case, 2007). However, given the reasonably strong dependence of the calculated CSA on basis set and functional (Moon and Case, 2006), it is not possible from these data to draw more than very qualitative conclusions about the extent of motional averaging that might be present in the observed data.

Table 2.

Reduced ¹³C and ¹⁵N CSA (Δδ_red) averages for α-helical and β-sheet regions of GB1; also reported are the uncertainties in the mean values.

PDB	method	Nuclei	Helix	Sheet	Difference
2qmt	1	13C	−86.3±0:8	−84.5±0:5	−1.8
	2	13C	−76.2±0:8	−74.9±0:5	−1.4
1pga	1	13C	−87.6±0:5	−84.1±0:5	−3.5
	2	13C	−76.8±0:8	−74.3±0:5	−2.5
experimental		13C	−83.0±0:8	−78.2±0:5	−4.8
2qmt	1	15N	108.2±1:5	102.1±0:8	6.1
	2	15N	101.8±1:4	95.6±0:8	6.2
1pga	1	15N	107.9±0:9	103.6±0:9	4.3
	2	15N	101.6±1:3	96.6±0:8	5.0
experimental		15N	114.0±1:3	106.7±0:7	7.3

Figure 4.

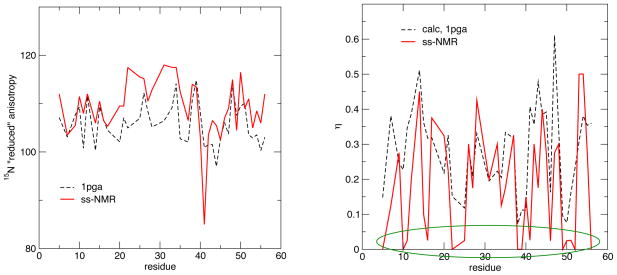
Comparison of reduced ¹³C anisotropy (left) and asymmetry (right) for GB1, based on the 1PGA structure and computational model 1. Circles and squares denote regions of helical or sheet secondary structure, respectively. Experimental data is from (Wylie et al, 2007).

Figure 5.

¹⁵N anisotropies (left) and asymmetries (right) for GB1. See the caption to Fig. 4.

For the ¹⁵N nuclei, the calculated CSAs are systematically lower than that of the experimental observables (Table 2). This systematic difference amounts to about 11 ppm for the OLYP functional and about 5 ppm for B3LYP. The helix and sheet dependence of Δδ_red mirrors that seen for ¹³C′, with the helical regions being larger in absolute magnitude than the sheets. As is shown in Fig. 5, however, the trend is rather clearer in the experimental data than in the calculations. The extent of variation in Δδ_red is about 12 ppm in both the calculated and observed results, with the exception of one unusual value at residue 41, whose experimental estimate is far outside the range of all other values. This is a glycine residue in a loop region, which also shows unusual values for ¹⁵N–¹H and ¹³C–¹H dipolar couplings (Franks et al, 2005; Wylie et al, 2007), which may reflect unusual dynamics that would not show up in the current static calculations. As with the ¹³C′ results, a wide range of asymmetries η are seen, with much of the variation being reproduced in the calculations. There were a number of residues for which the ¹⁵N asymmetry parameter extracted from the data was very small, and these points are circled in green in the right side of Fig. 5. The calculations often show relatively small values for these asymmetries, but all of the calculated values are above 0.1, whereas there are more than a dozen experimental estimates below this.

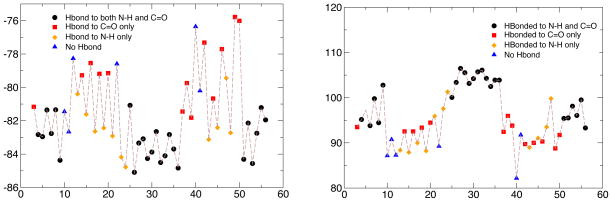
One good aspect of the AF-QM/MM model used here is that it, at least in principle, includes many contributions to the shielding tensor, including local geometries, hydrogen bonding, side chain identity and conformation, and solvation effects. At the same time, this can lead to difficulties in identifying individual contributions to the results. Fig. 6 shows one attempt to isolate hydrogen bonding effects from other contributions. The calculations shown there employ the “method 1” quantum model, but with a quantum region that just includes an N-methylacetamide (NMA) molecule at the position of the residue in question, and zero, one or two additional NMA molecules at the position of peptide groups that are hydrogen bonded to either the NH or C=O moiety of the central peptide; no point charges arising from the rest of the protein, or from the solvent response, are included. The calculations thus primarily illustrate the effects of backbone hydrogen bonding on the shift anisotropies.

Figure 6.

Effects of hydrogen bonds on Δδ_red values for ¹³C′ (left) and ¹⁵N (right). Results are from a simplified (NMA)₃ model described in the text.

The results are color-coded according to the nature of the hydrogen bonding pattern, and show some clear trends. Peptide groups with two hydrogen bonds to other peptide groups (black circles) generally have anisotropies that are higher in absolute magnitude than other peptide groups, for both ¹³C′ and ¹⁵N tensors. Among peptide groups with one backbone H-bond partner (these are primarily in sheet regions) the ¹³C′ anisotropy is clearly more negative (higher in absolute magnitude) for H-bonds to the NH side of the central peptide than for groups where the single H-bond is to the C=O side; this trend is somewhat reversed (although less clear) for the ¹⁵N tensors, where hydrogen bonding to C=O side tends to increase the absolute magnitude of the anisotropy. The main trends seen in Fig. 6, with large alternating asymmetries in the sheet regions and a helical central region (residues 22–37) that is systematically higher in absolute magnitude, are visible in the experimental and calculated profiles in Fig. 4 and 5, suggesting that a significant component of the differences seen between helical and sheet reasons arises from number of hydrogen bonds; this does not rule out other systematic effects (such as from dihedral angles), and further computational studies are ongoing to explore these issues.

3.2 ¹⁵N tensors in GB3

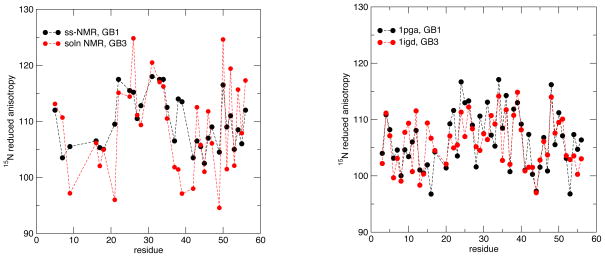
Liquid-state estimates of the ¹⁵N shielding tensor for GB3 have been made by two groups (Hall and Fushman, 2006; Yao et al, 2010a). We used three PDB structures (PDB codes: 1IGD, 1P7E and 2OED) to calculate the chemical shift tensors of GB3 protein; results are shown in Table 3 and Fig. 7. The calculated CSA values are systematically smaller in absolute magnitude than the experimental values by about 5 ppm for method 1 and 12 ppm for method 2. The difference between the averages of ¹⁵N CSA for the α-helical versus the β-sheet region is between 6 and 7 ppm, depending on the PDB structure and method used, in good agreement with the experimental estimate. Given the close similarity of GB1 and GB3, it is of interest to compare results for the two proteins, as shown in Fig. 8. The range of values from the solid state measurements is 16 ppm (from 102 ppm to 118 ppm, leaving out residue 41, for reasons discussed above), whereas the range in the solution estimates is 30 ppm (from 95 ppm to 125 ppm). For the calculations, the range is 20 ppm for GB1 and 18 ppm for GB3. Hence the computed variability in anisotropies is is nearly the same in the calculations (for either protein) as in the solid-state measurements, and rather lower than that extracted from solution data. [Recall that the Δσ parameter commonly used for relaxation analysis in solution is 50% larger and opposite in sign to the Δδ_red values used here, so that the calculated range of Δσ would be 27–30 ppm.] One possible explanation (consistent with our DFT results) is that the very low and very high anisotropies seen in the left-hand side of Fig. 8 may be reflecting some other property of those peptide groups in addition to variations in shielding anisotropies. Similar problems may have affected earlier solution estimates for GB3 (Hall and Fushman, 2006), which suggested a range of Δδ_red values of 86 ppm (from 74 ppm to 160 ppm) that is much larger than the values shown in Fig. 8.

Table 3.

Reduced ¹⁵N CSA for α-helical and β-sheet regions of GB3. Experimental values are from Yao et al. (2010).

PDB	method	Helix	Sheet	Difference
1igd	1	109.42±1.33	102.93±0.77	6.50
	2	102.94±1.22	96.32±0.74	6.63
1p7e	1	109.21±1.26	102.86±0.72	6. 36
	2	102.53±1.18	96.23±0.72	6.30
2oed	1	111.54±1.23	105.34±0.71	6.19
	2	102.56±1.17	95.74±0.74	6.82
exp		114.88±1.30	108.26±0.89	6.62

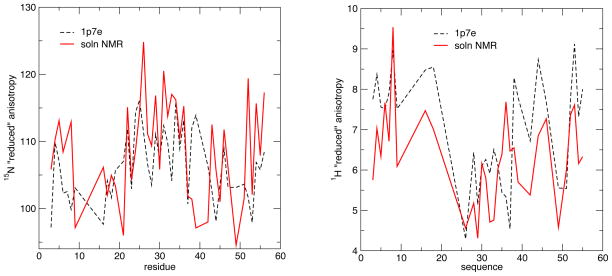
Figure 7.

Reduced anisotropies for GB3 for ¹⁵N (left) and ¹H (right). Calculations used method 1 and the 1p7e structure; experimental data is from Yao et al. (2010, 2010a).

Figure 8.

Comparison of reduced ¹⁵N anisotropies for GB1 and GB3. Left: experimental data from Wylie et al (2007) and Yao et al (2010a); right: calculated values (method 1) using the 1igd and 1pga structures from the PDB.

3.3 ¹H tensors in GB3

Yao and co-workers also measured the ¹H chemical shift anisotropy with cross-correlation relaxation experiments in liquid crystalline state (Yao et al, 2010b). Two models were used to produce fitted CSA values: The three-parameter model uses three cross-correlated relaxation parameters to determine the CSAs, while assuming tensor symmetry relative to the peptide plane. In contrast, the five parameter model takes advantage of the precise RCSA measurements and does not require the assumption of symmetry, but has more fitting parameters. Results are shown in the right-hand side of Fig. 7 and in Table 3. (For both experimental and calculated tensors, a few tensors with large asymmetries have “flipped” signs for Δδ_red; we have treated all values as positive for this analysis.) As expected, anisotropies are much smaller for protons than for heavier nuclei. The average and range of the calculated values is nearly the same as that extracted from experiment, but details of the pattern of variation are not captured. On average, the ¹H CSA of the α-helical region is lower in absolute magnitude than that of the β-sheet region, by about 1.2 ppm. The difference in the AF-QM/MM results is slightly larger, from 1.3 to 2.0 ppm, but in the same direction.

3.4 ¹³C′ and ¹⁵N tensors in ubiquitin

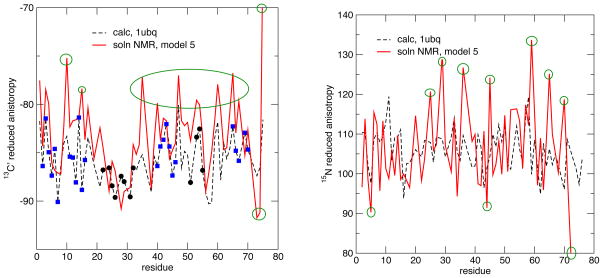
The Bodenhausen group has reported extensive liquid state relaxation measurements for human ubiquitin, extracting site-specific tensors for backbone ¹³C and¹⁵N nuclei (Loth et al, 2003, 2005). Results are collected in Table 5 and Fig. 9. Several assumptions and approximations must be made to extract tensors from the experimental data, and Models 1 to 5 are presented by Loth et al. (2005); the end results do not differ by a lot, with Model 5 being closest to both calculated results and the average anisotropies extracted from solid state measurements on GB1 (Wylie et al, 2007). As shown in Table 5, helical regions show reduced anisotropies that are larger in absolute magnitude than those for sheets, in agreement with calculated results and with the trends seen for GB1 and GB3. The helix–sheet differences are smaller here than for GB1 for both the experimental and calculated data sets.

Table 5.

Estimates of Δδ_red for ubiquitin. Details and assumptions of Model1 to Model5 are given in (Loth et al, 2005). Calculations used the 1ubq crystal structure.

Method	Src	Helix	Sheet	Difference	Src	Helix	Sheet	Difference
Model1	13C	−95.63	−91.86	−3.77	15N	113.57	109.85	3.72
Model2	13C	−94.17	−90.48	−3.69	15N	107.48	103.86	3.62
Model3	13C	−98.41	−95.17	−3.24	15N	102.19	97.30	4.89
Model4	13C	−85.10	−81.67	−3.43	15N	100.66	96.18	4.48
Model5	13C	−85.19	−81.69	−3.50	15N	109.98	105.19	4.79
method1	13C	−87.60	−85.20	−2.40	15N	107.48	105.50	2.00

Figure 9.

¹³C (left) and ¹⁵N (right) anisotropies for ubiquitin. Green circles mark experimental estimates that are well outside the range of calculated results.

Fig. 9 compares calculated and experimental anisotropies. The general trend is similar to that seen for GB3 above: the average anisotropy and many site-specific variations are common to experiment and calculation, but many of the experimental estimates (marked in green) are well outside the range of calculated results. For example, the range of experimental estimates for nitrogen anisotropies is 53 ppm (from 80 ppm to 133 ppm), whereas the range of computed results is only about half as great (25 ppm, from 94 ppm to 119 ppm). Similar comments apply to the carbonyl tensors.

4 Conclusions

The AF-QM/MM approach described here allows systematic explorations to be made of chemical shift tensors in biomolecules. At least in principle, it incorporates contributions from the entire protein and its solvent environment, and requires about 2–4 hours of computer time per residue, depending on the options chosen. Results for isotropic shifts will be discussed in a separate paper; in brief, results approach (but do not match) the quality of current empirical predictions, e.g. from sparta+ (Shen and Bax, 2010) or shiftx+ (Han et al, 2011). Here we examine predictions for shift tensor anisotropies and asymmetries, for which there is only a few previous studies on full proteins.

The overall results shown here offer encouraging evidence that the basic features of site-to-site variation in backbone tensors are reasonably well understood, and are reproduced in the calculations. The predicted range and variation of anisotropies, and systematic differences between helix and sheet regions of regular secondary structure, are in good agreement with values extracted from solid-state NMR measurements. The somewhat more indirect determination of shielding tensors from existing liquid state studies yields similar trends, but with a magnitude of variation that is larger than that seen in the solid-state results or in calculations. To be sure, the calculations reported here are based on crystal structures, and do not attempt to include effects of motional averaging; such effects are expected to be rather small for the fairly rigid proteins considered here (Tang and Case, 2007), but further study of this point is certainly warranted. A fair part of the variation in backbone anisotropies appears to arise from variations in hydrogen bonding patterns, (see Fig. 6), but an understanding of the effects of torsion angles and other geometric variables also warrants further study. The methods described here could be an important complement to experiment as the field moves forward.

Table 4.

Helix-sheet difference of ¹H values for Δδ_red for GB3.

PDB	Method	Helix	Sheet	Difference
1IGD	1	5.60±0.77	7.14±1.29	−1.54
	2	5.70±0.74	7.03±1.49	−1.33
1P7E	1	5.52±0.72	7.40±1.23	−1.88
	2	5.63±0.73	7.33±1.40	−1.70
2OED	1	5.37±0.71	7.36±1.46	−1.99
	2	5.58±0.74	7.46±1.51	−1.88
exp, parm3	N/A	5.38±0.96	6.51±0.96	−1.13
exp parm5	N/A	5.59±0.92	6.79±0.93	−1.20