MetSign: A Computational Platform for High-Resolution Mass Spectrometry-Based Metabolomics

Abstract

Data analysis in metabolomics is currently a major challenge, particularly when large sample sets are analyzed. Herein, we present a novel computational platform entitled MetSign for high-resolution mass spectrometry-based metabolomics. By converting the instrument raw data into mzXML format as its input data, MetSign provides a suite of bioinformatics tools to perform raw data deconvolution, metabolite putative assignment, peak list alignment, normalization, statistical significance tests, unsupervised pattern recognition, and time course analysis. MetSign uses a modular design and an interactive visual data mining approach to enable efficient extraction of useful patterns from data sets. Analysis steps, designed as containers, are presented with a wizard for the user to follow analyses. Each analysis step might contain multiple analysis procedures and/or methods, and serves as a pausing point where users can interact with the system to review the results, to shape the next steps, and to return to previous steps to repeat them with different methods or parameter settings. Analysis of metabolite extract of mouse liver with spiked-in acid standards shows that MetSign outperforms the existing publically available software packages. MetSign has also been successfully applied to investigate the regulation and time course trajectory of metabolites in hepatic liver.

INTRODUCTION

Metabolomics is the systematic analysis of metabolites in an organism that participate in a large network of metabolic reactions.^1–6 With the advantages of high sensitivity and accuracy, wide dynamic range, and the ability to identify metabolites from complex samples, high-resolution mass spectrometry has become the workhorse of metabolomics research. The analytical methods of high-resolution mass spectrometry-based metabolomics can be categorized as liquid chromatography – mass spectrometry (LC-MS) and direct infusion – mass spectrometry (DI-MS). Even though the LC-MS method is beneficial to comprehensive analysis, the chromatographic step limits its throughput. The DI-MS approach, by avoiding any prior chromatographic steps, has the greatest potential for high-throughput required for analysis of large numbers of samples.⁷ However, matrix effects are inevitable because the samples are infused together without separation, which results in a high rate of false-positive metabolite identifications and limited peak capacity of the analytical system. Therefore, DI-MS has been recommended to fast diagnostic analysis and LC-MS for comprehensive screening of biomarkers.⁸

A high-resolution mass spectrometry-based metabolomics study generates a large volume of information-rich data. Bioinformatics tools are needed to extract the chemical and biological information from these extremely complex data. XCMS², an open source software package designed for metabolite profiling, enables peak picking, alignment, statistical analysis, metabolite identification, and structural characterization.⁹ Tautenhahn et al. provided a feature detection algorithm, centWave, to determine the boundaries, centers and intensities of the two-dimensional high-resolution LC-MS data.¹⁰ MZmine2 is also capable of peak detection, peak list alignment, normalization, statistical analysis, visualization, and peak identification for LC-MS data. ¹¹ MZedDB uses adducts and neutral loss fragments as predicted ionization behavior rules to annotate LC-MS data; in addition, the correlation analysis and the isotope enumerator were presented to confirm the m/z versus signal relationships and to verify the exact isotopic distribution, respectively.¹² Finally, Sturm et al. developed a framework called OpenMS for LC-MS data analysis, including visualization, data reduction, alignment, and retention time prediction by using a support vector machine (SVM) method.¹³

The existing bioinformatics tools for LC-MS analysis are often not flexible enough to be adapted by users. Moreover, there are no efficient implementations of some known algorithms and analysis methods with mature data mining theory. In the present study, we developed a computational platform entitled MetSign for the processing of high-resolution mass spectrometry data for metabolomics studies. MetSign is able to process both the LC-MS and DI-MS data by providing solutions for peak detection, visualization, metabolite putative assignment, peak list alignment, normalization, and clustering. Compared to existing bioinformatics tools, MetSign provides additional unique features for the metabolomics community with temporal analysis and the ability to analyze the stable isotope labeled data. The performance of MetSign was first compared to existing publically available software packages and further demonstrated by analyzing liver samples from mice fed with drinking water consisting of ²H₂O (or D₂O), followed by two different diets.

EXPERIMENTAL SECTION

Mouse Plasma Samples

Male C57BL/6 mice were obtained from Harlan (Indianapolis, IN). All mice were treated according to the experimental procedures approved by the Institutional Animal Care and Use Committee. To label lipids in adipose tissues, an approach using ²H₂O as the metabolic tracer was followed.¹⁴ Mice at 2 months old were given an initial priming dose of 99.8% ²H₂O via intraperitoneal injection to achieve 2.5% of body water enrichment, followed by administration of 5% ²H₂O in drinking water for 5 weeks. Mice were then fed an alcohol-containing liquid diet or pair-fed an isocaloric maltose dextrin control liquid diet for 2, 4 or 8 weeks. The amount of food given to the pair-fed mice was that of alcohol-fed mice measured the previous day. At the end of each feeding time point, mice were anesthetized, and liver tissues were collected for measuring lipid components labeled by deuterium. Hepatic lipids were extracted by methanol-chloroform (v:v = 2:1), which resulted of two metabolite sample groups, the sample group D and the sample group DE. The sample group D refers to mice fed with deuterated water followed by normal drinking water, while the sample group DE represents mice fed with deuterated water followed by drinking water plus ethanol. There were {5, 5, 3, 2}, and {5, 7, 4, 3} mice at time point {0, 2, 4, 8} weeks for the sample group D and the sample group DE, respectively.

Each sample of liver tissue was weighed and then homogenized for 2 min and stored at -80 °C until use. To extract metabolites from the homogenized liver tissue, a 100 μL of homogenized liver tissue, 20 μL of butylated hydroxytoluene (BHT) mixture (50 mg BHT into 1 mL methanol), and 1.5 mL chloroform:methanol (v:v = 1:2) were mixed and vortex for 1 min followed by adding 0.5 mL chloroform, vortexing 1 min, adding 0.5 mL water and vortexing for 1 min. The mixture was then centrifugated at room temperature at 15000 rpm for 8 min. 400 μL of the organic phase (bottom) were aspirated into another glass tube and dried under nitrogen evaporator. The dried sample was dissolved into 100 μL chloroform:methanol (v:v = 1:1) and further diluted 25 times before analysis on mass spectrometer.

Spiked-in Samples

About 180 mg of liver tissue of three mice was mixed with deionized water at a ratio of 100 mg/mL. The mixture was then homogenized for 2 min and stored at −80 °C till use. To extract metabolites from liver, a 200 μL of homogenized liver sample was mixed with 1.6 mL methanol and vortex for 1 min, followed by centrifugation at 4 °C for 10 min at 15000 rpm. 1.4 mL of the top solution was aspirated into a plastic tube and dried by N₂ flow. After dissolving the dried sample with 200 μL methanol, a stock solution was prepared by diluting the sample 10 times. Thirty aliquots of the stock solution were then prepared with a volume of 50 μL per aliquot.

A mixture of 15 acid standards was prepared at a concentration of 10 μg/mL per acid. The acids included L-Proline, L-Cystine, L-Histidine, L-Phenylalanine, L-Tyrosine, L-Lysine, L-Glutamic acid, L-Aspartic acid, L-Leucine, nonadecanoic acid, hepadecanoic acid, heptanoic acid, nonanoic acid, pentadecanoic acid, and undecanoic acid. 20 μL of the acid mixture was added to each of the first 10 aliquots of the stock solution, while 24 μL and 100 μL of the acid mixture were added to each of the second 10 aliquots and the third 10 aliquots, respectively. Methanol was then added to each of the 30 aliquots to make the total volume of each aliquot to 200 μL. This resulted in three sample groups with spiked-in acid standards. The acid concentration in each of the spiked-in sample groups is 1.0 μg/mL, 1.2 μg/mL and 5.0 μg/mL, respectively.

FT-MS Analysis

The direct infusion experiments were performed on an FT-MS instrument (LTQ-FT; Thermo Electron Corporation, Bremen, Germany) equipped with a chip-based nano-electrospray ionization (nESI) ion source (Triversa NanoMate) (Advion Biosciences, Ithaca, NY, USA). Each sample was measured for 10 minutes and covered the m/z = 100–1,600 range. The mass spectra were recorded using Fourier transform ion cyclotron resonance (FT-ICR) in the profile mode and the resolving power (RP) was set at 400,000 @ m/z = 400. The maximum ion accumulation time was set at 1,000 ms. The ion optics was tuned for the sodium adduct of tricaprylin ([C₂₇H₅₀O₆+Na⁺]) at m/z = 493.25 using the linear ion trap (LIT). The two most important nESI parameters were as follows: the spray voltage = +1.8 kV and the nitrogen gas pressure = 0.5 psi.

THEORETICAL BASIS

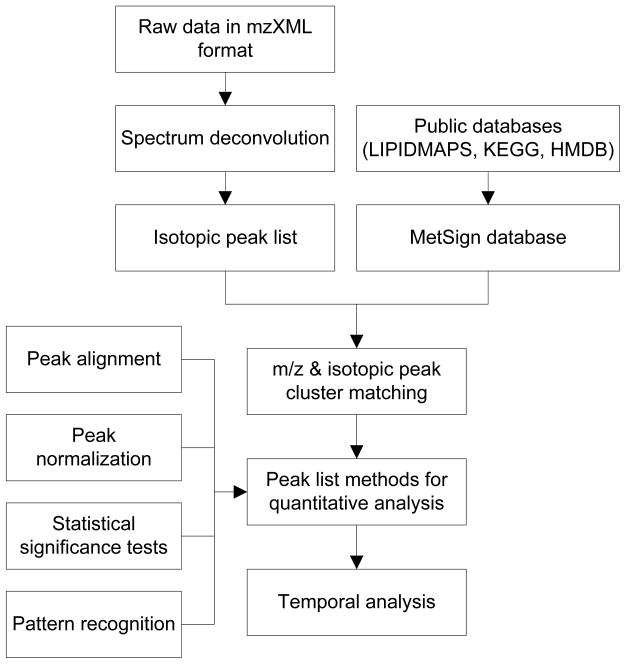
Figure 1 shows the workflow of the MetSign software that has two major components: project management and data analysis. The project management part takes care of samples and data meta-information. For data analysis, MetSign first reduces the raw instrument data into a peak list via spectrum deconvolution. It then performs initial metabolite assignment. The peak alignment recognizes peaks of the same type of metabolite in different samples. Four normalization algorithms were implemented for the user to choose from. MetSign also enables both presence/absence tests and abundance tests for statistical significance analysis. K-means, agglomerative hierarchical clustering, and fuzzy C-means clustering algorithms are available for clustering all sample features. Temporal analysis can automatically generate the metabolite time course plot and cluster the metabolites based on their time course trajectories.

Figure 1.

The workflow of the MetSign software.

Spectrum Deconvolution

MetSign supports importing the mzXML raw data format for spectrum deconvolution. Let {pl₁ , pl₂ ,..., pl_n} be the profile list of all scans in each mzXML raw data, where pl_i is the profile data of scan i, and n is the number of total scans. In case of direct infusion experiment, MetSign summarizes pl₁ , pl₁ ,..., pl_n to get a summed profile P. A wavelet transformation (WT) is then employed for noise removal. After removing the noise, many isolated peak profiles {p₁ , p₁ ,..., p_n} are left in P, where p_i ={(x_{1(i,1) ,} , y_(i,1 ), (x_{(i,2 )} , y_{(i,2 )} ),..., (x_{(i, p )} , y_{(i, p)})}, p_i is the i^th peak profile, x_(i,j) and y_(i,j) represent the m/z value and the peak area of the j^th isotopic peak ion in the peak profile p , respectively. A second-order polynomial fitting (SPF) function is then introduced to centralize each peak profile {p₁ , p₂ ,..., p_n} in P to get the peak area and m/z value of each peak profile, respectively. In case of multiple peaks overlapping each other, a Gaussian mixture model (GMM) is employed to deconvolute the overlapping peaks. The overlapping peaks are detected if at least one side of a peak is higher than two times of the baseline, deduced from the removed noise signals detected by WT.

Metabolite Putative Assignment

MetSign performs metabolite putative assignment by matching the experimentally measured metabolite ion m/z value and the profile of the isotopic peaks with the theoretical data of metabolites recorded in the MetSign database, which is composed of all metabolites recorded in the Kyoto Encyclopedia of Genes and Genomes (KEGG),¹⁵ LIPID MAPS,¹⁶ and the Human Metabolome Database (HMDB).¹⁷ After incorporating all user-defined possible stable isotopes and adduct ions, MetSign first matches all the molecular ion m/z values of the MetSign database metabolites to each experimental m/z value of the centralized peaks. An experimental peak may be assigned to multiple isotopic peaks of different elemental compositions of database metabolites due to limited mass accuracy. In other words, the isotopic peaks of these putatively assigned metabolites are overlapped. Therefore, an iterative mean square error (MSE) algorithm is used to deconvolute the overlapped isotopic peaks.

Let P₀ ={P₁ , P₂ ,..., P_n} be a group of experimental peak clusters that were assigned to the overlapped isotopic peaks of multiple metabolite elemental compositions, where n is the number of metabolite elemental compositions, P_i ={(x _{(i ,1 )}, y_{(i ,1 )} ), (x _{(i ,2 )} , y_{(i ,2 )}),..., (x_{(i, mi)} , y_{(i, mi)})} is a collection of isotopic peaks of the i^th overlapped metabolite elemental composition, and m_i is the index of the isotopic peaks of P_i. The intensity MSE aims to find a_i, that satisfies

$$arg{min}_{\left\{a_i\right\}}\sum _{i=1}^n\sum _{j=1}^{m_i}{\left(y_{(i,j)}-a_i{Y}_{(i,j)}\right)}^2,y_{(i,j)}\ge a_i{Y}_{(i,j)}$$ (1)

where Y_{(i , j)} is the theoretical abundance corresponding to y_{(i , j)} . Through MSE deconvolution, the isotopic distribution of each overlapped metabolite elemental compositions is approximated to its theoretical distribution by minimizing the overall fitting error.

After initial isotopic peak deconvolution, Pearson s correlation coefficient is used to measure the similarity between the deconvoluted isotopic peaks and the theoretical isotopic peaks of each putatively assigned metabolite. A large similarity value, i.e., close to 1, indicates a high probability that this metabolite is present in the experimental data. Recognizing a metabolite via its elemental composition is clearly not reliable and increases the chance of identifying false-positive metabolites and therefore, decreasing the peak intensity of true metabolites during MSE fitting. For this reason, MetSign employs an iterative MSE fitting procedure by setting an empirical threshold of the Pearson s correlation coefficient such as 0.7. Any metabolite elemental composition with a less than the user defined correlation coefficient threshold is discarded during the iterative MSE fitting. For example, assuming there are 10 metabolite elemental compositions and each of their mono-isotopic peak matches to one of the experimental peaks in a peak cluster. The metabolites with these 10 elemental compositions are considered as potential overlapping metabolites. MetSign first performs the MSE fitting using these 10 metabolite elemental compositions. After fitting, the Pearson s correlation coefficient between the fitted isotopic peak envelope and the corresponding theoretical isotopic peak envelope is calculated for each elemental composition. Any metabolites with a correlation coefficient less than the predefined threshold 0.7 are removed. MetSign repeats this process until all of the metabolite elemental compositions have a larger than 0.7 correlation coefficient. Finally, MetSign outputs all fitted metabolites ranking from high to low according to Pearson s correlation coefficients.

The iterative MSE optimization is for putative metabolite assignment only. The fitted isotopic peak envelope of each metabolite is only used for the calculation of Pearson s correlation coefficient to estimate the reliability of the metabolite putative assignment. For each peak that matched to a mono-isotopic peak of one or more metabolite elemental compositions, the original peak area of the matched peak is carried forward for quantification analysis. Therefore, the potential false-positive putative assignment of metabolites via the iterative MSE optimization will not affect the metabolite quantification in the downstream statistical analysis.

Peak List Alignment

The purpose of peak alignment is to recognize the metabolite peaks generated by the same type of metabolite in different samples. Alignment uses the results generated from the metabolite putative assignment as its input. MetSign performs peak alignment based on peak m/z values and the peak intensity profile of isotopic peaks from the direct infusion experiments. An additional feature, a user-defined retention time window, is further employed to restrict the alignment searching space for LC-MS data. In case multiple matches are detected in a target sample during the alignment of a peak in the reference sample, discrete convolution is used to find the peak in the target sample that correlates best with the peak in reference sample.¹⁸

Normalization

Three literature-reported normalization algorithms were implemented into MetSign for the user to select from including quantile normalization, cyclic loss normalization, and contrast-based normalization.^{19, 20} The well-known quantile normalization is a technique for making two distributions identical in statistical properties, which may not be true for the comparison of samples acquired from different biological conditions. Therefore, MetSign also implemented a novel normalization method, entitled sample group-based quantile (SGQ) normalization. The hypothesis of SGQ is that the distributions of metabolites within the same sample group are identical. SGQ first performs quantile normalization for the samples that belong to the same sample group. After the quantile normalization, it then employs a trimmed constant mean method to normalize all samples across the sample groups.

Statistical Significance Tests

The purpose of statistical analysis is to find metabolites that have significantly different expression levels in different sample groups. Due to the limitation of the analytical platform, some low-level metabolites may not be detected and such metabolites are represented as missing values in the normalization table. MetSign first employs the Fisher s exact test to study the presence and absence of each metabolite between sample groups. It then employs the Grubbs test ²¹ for outlier detection to find the responses of a metabolite that are not consistent with the responses of the same metabolite in the remaining samples of the same sample group. After removing the outliers, an abundance test such as the pairwise two-tail t-test is performed to detect the abundance changes of each metabolite between two sample groups, and the false discovery rate (FDR) is used to correct for multiple comparisons.²²

Unsupervised Clustering

Pattern recognition aims to study the differences of the metabolite expression profiles acquired under different physiological conditions. The samples that have similar features are grouped into the same cluster. MetSign first filters data based on a user-defined frequency threshold f_t, defined as the number of samples in which a metabolite was detected divided by the number of all samples. The k-nearest neighbor (KNN) imputation algorithm is then used to estimate the missing data.²³ Due to the nature of the data, i.e., the large number of metabolites and the small number of samples, the data dimensionality reduction method can be used before clustering to eliminate redundancy information in the original data and to enhance the computing efficiency. MetSign provides two data dimensionality reduction methods, principal component analysis (PCA)²⁴ and partial least squares (PLS)²⁵ as options for the user to select from, if the user decided to employ data dimensionality reduction before clustering. Three clustering methods were implemented in MetSign, including k-means clustering, agglomerative hierarchical clustering, and fuzzy C means clustering.²⁶ The clustering accuracy (CA) is further calculated as the number of correctly clustered samples divided by the number of all samples.

Temporal Analysis

Temporal analysis can generate the time course plots of all metabolites and cluster the metabolites based on their time course trajectories (response vs. time). MetSign automatically displays the time course trajectories of a metabolite generated from different sample groups in the same plot, and then employs the correlation and distance to characterize the relation between the time course trajectories. The correlation between the time course trajectories of the same metabolite is calculated using Spearman s rank-order correlation coefficient. For the calculation of the distance between the time course trajectories, MetSign first calculates the difference of the metabolite response (i.e., peak area) between sample groups at each time point, which is represented as the probability of one-way analysis of variance (ANOVA).²⁷ The Fisher value p_F is then computed to show the degree of difference (i.e., the distance) between the time course trajectories. p_F is defined as follows:

$$p_F=-2\sum _{i=1}^{n}ln(p_i)$$ (2)

where p_i is the probability of the ANOVA results of a metabolite at the i^th time point, and n is the number of time points. A higher Fisher value p_F indicates a large distance between the time course trajectories of the metabolite of interest in the comparing sample groups.

RESULTS AND DISCUSSION

MetSign software was developed in MATLAB 2010a using a modular design. The analysis steps are designed as containers for different analysis routines. The containers are connected through a standardized input and output (I/O) protocols, and are tied through a transaction manager. Analysis steps are presented with a wizard for the user to follow the analyses. Each analysis step serves as a pause point where user can interact with the system to review the results, to shape the next steps, and to return to previous steps to repeat them with different methods or parameter settings. The I/O protocol enables tracking by indexing results from each step. MetSign was implemented on a Dell Precision T5500 workstation with an Intel CPU E5603 1.6GHz, 4G Memory.

Spectrum Deconvolution

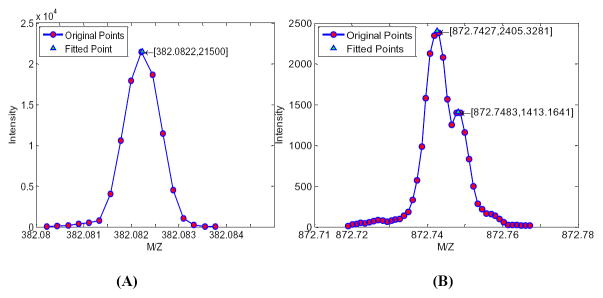
MetSign employs SPF and GMM approaches to centralize the profile data. The SPF approach is fast, but not able to quantatively deconvolute the overlapping peaks. The GMM approach can accurately deconvolute the overlapping peaks, but is computationally expensive. After wavelet filtering, MetSign first detects the local maximums to locate the peaks. It then checks the peak intensity difference between the left and the right side of each peak to decide the presence of overlapping peaks. If a peak is not overlapped with other peaks, SPF is employed for centralization. Otherwise, GMM is used. Figure 2 shows a sample deconvolution case of SPF and GMM after summarizing all spectra in a direct infusion experiment.

Figure 2.

An example of spectrum deconvolution for direct infusion experiment by second-order polynomial fitting (A) and Gaussian mixture model fitting (B). The points with the red circle are the original experimental data while the points with green triangle are the fitted data.

Metabolite Putative Assignment

The metabolite putative assignment includes MetSign’s database generation and isotopic peak matching. MetSign provides options for the user to decide the scope of the metabolites to be investigated by incorporating the metabolites recorded in the HMDB, KEGG and/or LIPID MAPS databases into the MetSign database. The MetSign database can have up to 43,245 records, if all database records in the current version of the three databases were selected for matching. Any user-defined adduct ions can be further included into MetSign for analysis. By default, MetSign provides H⁺, Na⁺, K⁺, and NH₄⁺ as possible positive-mode adduct ions, and H⁻ and Cl⁻ as possible negative-mode adduct ions.

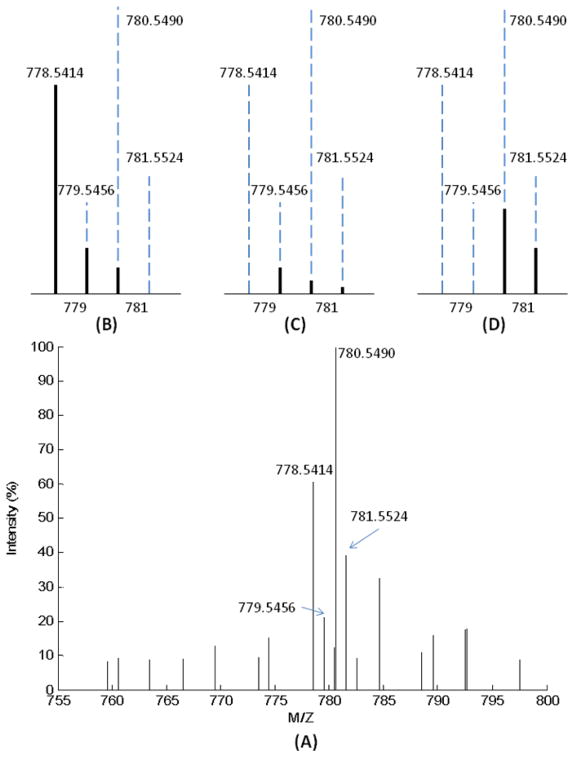
The stable isotope labeled metabolites are recognized in the same manner as the non-labeled metabolites based on their isotopic peak profiles and accurate m/z values (Figure S-1 in Supporting Information). During the isotopic peak matching process, the iterative intensity MSE method is employed to deconvolute the overlapping metabolite peaks. Figure 3 is an example of deconvoluting a cluster of overlapping isotopic peaks. The metabolite isotopic peaks were split into three groups by m/z value matching with a variation window of ≤5 ppm that was defined by the performance of the FT-MS. The first group (m/z = 778.5414, 779.5456, and 780.5490) had a putative metabolite assignment with an identity of C₄₄H₇₆N₁O₈P₁-[M+H⁺], while the identities of the second group (m/z = 779.5456, 780.5490, and 781.5524) and the third group (m/z = 780.5490, and 781.5524) are C₄₃H₇₀O₁₀-[M+Na⁺]-²H-10 and C₄₂H₈₀N₁O₈P₁-[M+Na⁺], respectively. The Pearson s correlation coefficients between the deconvoluted isotopic peaks and the theoretical isotopic peaks of the three overlapped metabolites are 0.95621, 0.99971 and 0.99946, respectively. These high values of similarity indicate a high probability that these three metabolites are present in the biological sample.

Figure 3.

Results of deconvoluting the isotopic peaks by intensity MSE method for the tentative metabolite assignment. (A) is a segment of the centralized MS spectrum. Based on the match of the m/z values of all metabolites recorded in the MetSign database, the m/z values of the isotopic peaks of three metabolites were matched. (B), (C) and (D) are three deconvoluted isotopic peak profiles of the three metabolites, respectively. In (B), the metabolite is C₄₄H₇₆N₁O₈P₁-[M+H⁺], by fitting {m+1} and {m+2} isotopic peaks with the theoretical intensity, the fitted experimental intensity is given as solid lines. Pearson s correlation coefficient between the deconvoluted isotopic peaks and the theoretical isotopic peaks is 0.95621, indicating a high confidence of tentative metabolite assignment. In (C) and (D), the metabolites are C₄₃H₇₀O₁₀-[M+Na⁺]-²H-10 and C₄₂H₈₀N₁O₈P₁-[M+Na⁺], and the similarities of isotopic peak profiles are 0.99971 and 0.99946, respectively.

Peak List Alignment and Normalization

Both alignment and normalization algorithms are implemented in MetSign using an interactive visual data mining approach. In order to monitor the quality of the alignment and normalization, MetSign provides a suite of quality control and quality assessment (QA/QC) methods. The results of all QA/QC methods are displayed as plots, which enable the user to quickly view the quality of the data analysis. The details of all QA/QC methods for peak list alignment and normalization are provided in the Supporting Information as Figure S-2.

Statistical Significance Tests

MetSign employs the Fisher s exact test for the presence and absence analysis of each metabolite in different sample groups, while it provides options of multiple statistical tests for quantitative analysis. FDR is used to correct for multiple comparisons. After the statistical significance tests, the metabolites are automatically sorted in descending order of significance based on the probability of the Fisher s exact test and the quantitative test. The plot of the peak intensity of any metabolites in different samples can be sequentially generated on-the-fly based on the user s interactive selection of the metabolite of interest (Figure S-3 in Supporting Information). Figure 4 shows two sample cases of such peak intensity distribution. The probabilities of the Fisher s exact test and the pairwise two-tail t-test of these two metabolites are 0.0008 and 0.0116, respectively, indicating that the regulation levels of these two metabolites are significantly different between sample group D and sample group DE.

Figure 4.

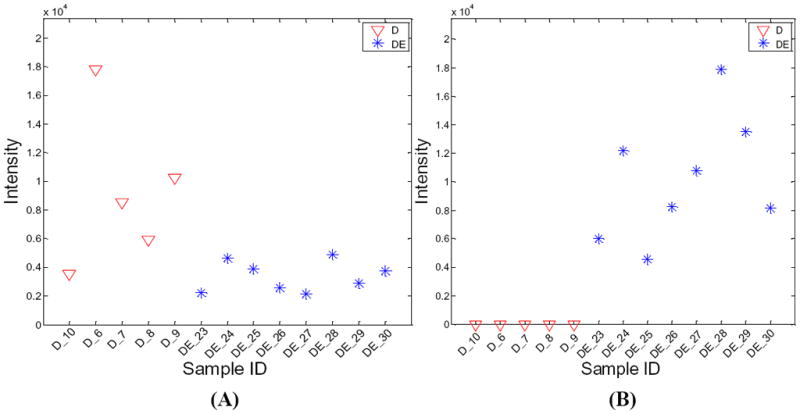
Regulation changes of two metabolites in two different physiological conditions. (A) shows the regulation change of a metabolite with a MetSign identity of C₃₇H₅₈O₁₀-[M+Na⁺]-²H-1. The abundance test (pair-wise t-test) shows that the regulation of this metabolite in the sample group DE is up-regulated with a fold change of 2.7 and a p-value of 0.0116. (B) shows the regulation change of a metabolite with a MetSign identity of C₄₅H₈₈N₁O₁₃-[M+K⁺]-²H-12. This metabolite was not detected in the sample group D and the abundance test could not be applied. The Fisher s exact test shows that this metabolite has different regulation between the sample group D and the sample group DE with p-value of 0.0008.

Unsupervised Clustering

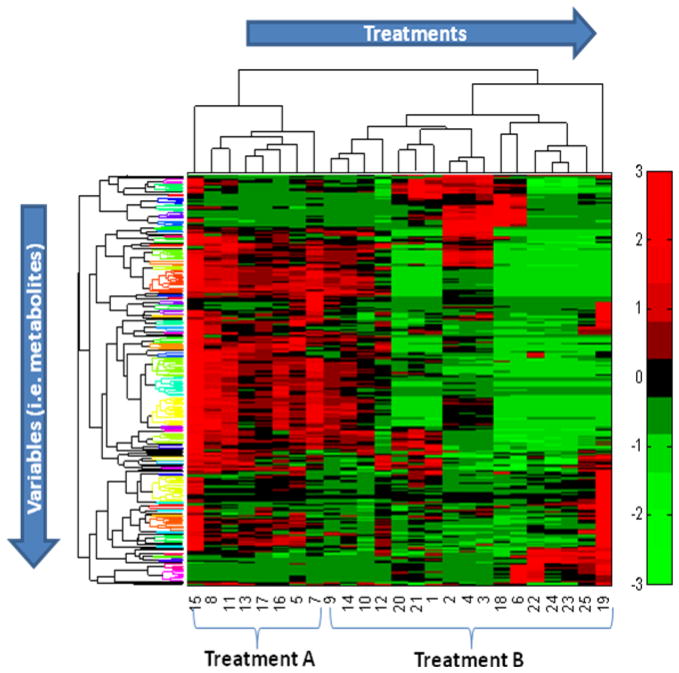
MetSign requires the user to setup a threshold f_t for the appearance frequency of each metabolite detected in all samples. It then employs the KNN imputation method to create a complete data set. MetSign also provides PCA and PLS as an option of data dimensionality reduction for unsupervised clustering. The user can perform clustering using either k-means clustering, agglomerative hierarchical clustering, or fuzzy C means clustering (Figure S-4 in Supporting Information). Figure 5 displays the clustering results of 10 samples from the sample group D and 15 samples from the sample group DE, collected from 0-8 weeks. Combining with two-dimensional hierarchical agglomerative clustering (HAC),²⁸ the heat map reveals trends within the treatments while the HAC provides different similarity levels for both the treatments and the metabolites. Of the 10 samples in the sample group D, 8 samples were correctly clustered, while 12 out of 15 samples were correctly clustered in the sample group DE. The overall clustering accuracy of the sample treatments is 0.8.

Figure 5.

A sample of an unsupervised clustering result for the analysis of metabolite profiles of 10 samples from the sample group D and 15 samples from the sample group DE. The threshold of the appearance frequency of each metabolite detected in all samples was set as f_t = 75% and the PCA method was employed to reduce the data dimensionality. Fluctuations in the heat map are illustrated in the concentration of metabolites between treatments by color-scale. Two-dimensional hierarchical clustering analysis combined with heat map indicates the trends both in treatments and variables. The metabolite regulation grouped with same color in variables clusters reveals the similar attributes among them.

Temporal Analysis

MetSign uses the correlation and distance to characterize the relation of time course trajectories of each metabolite between different sample groups. The correlation is measured by Spearman s rank-order correlation coefficient, while the distance between the trajectories is measured by a Fisher value. Due to the high complexity of the data, MetSign enables user to focus on a group of metabolites with a certain range of correlation coefficient values and then to view the time course plot of these selected metabolites in an interactive manner (Figure S-5 in Supporting Information). Figure 6 displays the time course trajectories of a metabolite in two sample groups, group D and group DE. The Spearman s rank-order coefficient and the Fisher value of these two time course trajectories are 1.0 and 29.3, respectively. A large correlation coefficient means that the shapes of the comparing time course trajectories are similar to each other, while a large Fisher values indicates that the comparing trajectories are far away from each other. Compared to the time course trajectory of the sample group D, the large peak area of the time course trajectory of this metabolite in the sample group DE indicates that ethanol induced the accumulation of this metabolite in mouse liver. Further MS/MS data analysis indicates that this metabolite is 1-(8Z,11Z,14Z-eicosatrienoyl)-2,3-di-(5Z,8Z,11Z,14Z-eicosatetraenoyl)-sn-glycerol labeled with three ²H, even though the exact locations of ²H could not be determined (data are not shown). Detailed biological discovery of this experiment will be summarized in an upcoming separate report.

Figure 6.

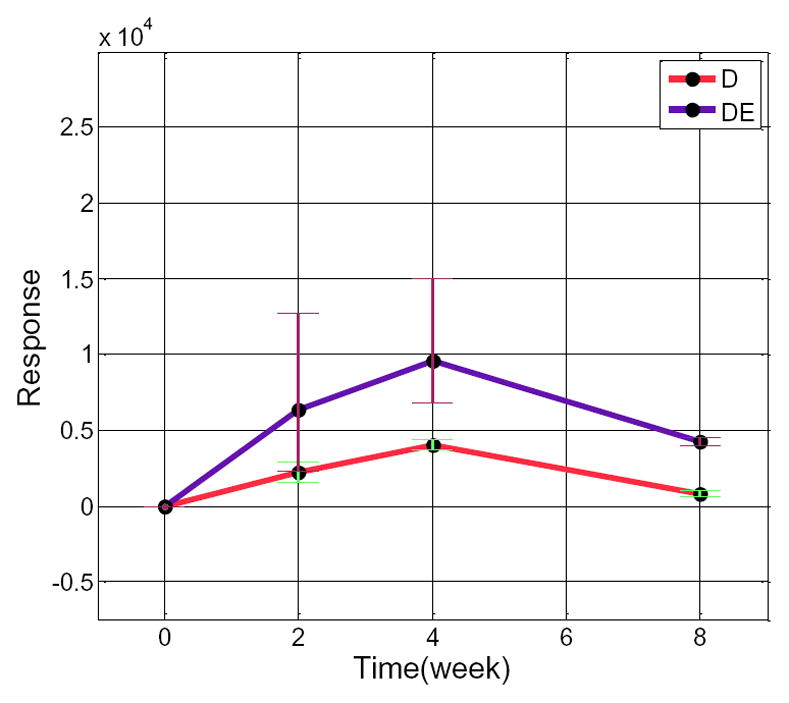
The time course trajectories of a metabolite (MetSign identity: C₆₃H₁₀₀O₆-[M+H⁺]-²H-3) in the sample group D and the sample group DE. This metabolite was labeled with three ²H and had an adduct ion of H⁺ in all samples. The black points, the upper bound and the lower bound of each bar represent the mean, the maximum, and the minimum of the response of this metabolite in all samples at a certain time, respectively.

Performance Comparison

To compare the performance of MetSign to existing publically available software packages like XCMS² and MZmine2, a spiked-in experiment was performed, where 15 acid standards were spiked into a metabolite extract of mouse liver with different concentrations to form three sample groups. The raw FT-MS instrument data were first converted into mzXML format and the mzXML files were submitted to MetSign and XCMS² for data analysis. MZMine2 applies Xcalibur (the instrument control software package of the LTQ-FT) to process the direct infusion data. For this reason, the raw instrument data were first reduced to peak lists by Xcalibur and the resulting peak lists were subjected to MZmine2 for further analysis. Out of the 15 spiked-in acids, the metabolite peaks of 10 acids (L-Proline, L-Cystine, L-Histidine, L-Phenylalanine, L-Tyrosine, L-Lysine, L-Glutamic acid, L-Aspartic acid, L-Leucine, and nonadecanoic acid) were recognized by all three software packages based on the match of m/z values with a variation window of ≤5 ppm. Out of the 10 detected acids, L-Histidine, L-Lysine and nonadecanoic acid were already present in the liver metabolite extract before the addition of the acid standards. The raw instrument data of the spiked-in experiment and the peak lists reduced by Xcalibur can be downloaded at http://stage.louisville.edu/faculty/x0zhan17/software/softwaredevelopment.

Compared to XCMS² and MZmine2, Metsign has similar functions such as spectrum deconvolution, alignment, and statistical analysis. However, MetSign software provides additional unique functions for the analysis of stable isotope labeled data and temporal data. For a comparison purpose, we focused on the accuracy of the statistical significance test to analyze metabolite concentration differences between sample groups, which is the key function of the three comparing software packages and can be viewed as the product of spectrum deconvolution, peak alignment, normalization, and the statistical significance test. A pairwise two-tail t-test was performed to recognize the metabolite peaks with significant peak area changes between two sample groups constructed from the three sample groups of the spiked-in experiment. Based on the design of the spiked-in experiment, all of the 10 detected spiked-in acids are the true-positive metabolites that have different concentration between the two sample groups, while any other metabolites are false-positives if they are detected by a software package as the metabolites with significant concentration change between two sample groups.

To measure the performance of each software package, the true-positive rate (TPR), positive predictive value (PPV) and their harmonic mean F1 score were calculated as follows:

$$\mathit{TPR}=\frac{TP}{TP+FN}$$ (3)

$$\mathit{PPV}=\frac{TP}{TP+FP}$$ (4)

$$F1=\frac{2\times \mathit{TPR}\times \mathit{PPV}}{\mathit{TPR}+\mathit{PPV}}$$ (5)

where TP (true-positive) is the number of spiked-in acids that were detected as molecules with significant peak area changes by the statistical analysis, FP (false-positive) is the number of molecules that were not spiked-in acids but detected as molecules with significant peak area changes, and FN (false-negative) is the number of spiked-in acids that were not detected as molecules with significant peak area changes. TPR is called recall and PPV precision and their harmonic mean F1 score can be used as an accuracy of the statistical significant test.

The three sample groups of the spiked-in experiment were used to construct three datasets for comparison (Table 1). The first column in Table 1 lists the information of the two comparing sample groups. For example, “1.0 μg/mL vs. 1.2 μg/mL” represents that the comparison was performed between the two sample groups, in which the concentration of the spiked-in acids were 1.0 μg/mL and 1.2 μg/mL, respectively. It can be seen that MetSign outperforms both XCMS² and MZmine2 in the analysis of 1.0 μg/mL vs. 1.2 μg/mL data in all three measures (precision, recall, and accuracy) regardless the value of the p-value threshold, while MZmine2 has a better performance than XCMS² in both recall and accuracy even though XCMS² performed better then MZmine2 in precision except at the p-value threshold of 0.001. There is no significant difference in the precision between the three software packages in the analysis of the three datasets, even though MetSign performed slightly better than XCMS² and MZmin2. However, the recall of MetSign and MZmine2 is more than two times better than XCMS², resulting that the accuracy (F1 score) of the three software packages in the analysis of the spiked-in data is in a descending order as follows: MetSign > MZmine2 > XCMS². This analysis shows that MetSign outperforms the existing software packages MZmine2 and XCMS².

Table 1.

Performance comparison of XCMS², MZmine2 and MetSign for analysis of the spiked-in data.

Dataset	p-value cut off		XCMS2	MZmine2	MetSign
1μg/mL vs. 1.2 μg/mL	0.05	Precision	0.50	0.32	0.62
		Recall	0.30	0.70	0.80
		F1	0.38	0.44	0.70
	0.01	Precision	0.50	0.35	0.58
		Recall	0.20	0.60	0.70
		F1	0.29	0.44	0.63
	0.001	Precision	0.33	0.50	0.60
		Recall	0.10	0.50	0.60
		F1	0.15	0.50	0.60
1.2 μg/mL vs. 5 μg/mL	0.05	Precision	0.40	0.18	0.31
		Recall	0.40	0.70	0.70
		F1	0.40	0.29	0.43
	0.01	Precision	0.40	0.23	0.34
		Recall	0.40	0.70	0.70
		F1	0.40	0.35	0.46
	0.001	Precision	0.20	0.20	0.29
		Recall	0.10	0.50	0.50
		F1	0.13	0.29	0.37
1 μg/mL vs. 5 μg/mL	0.05	Precision	0.25	0.21	0.32
		Recall	0.20	0.80	0.80
		F1	0.22	0.33	0.46
	0.01	Precision	0.29	0.20	0.31
		Recall	0.20	0.70	0.70
		F1	0.24	0.31	0.43
	0.001	Precision	0.33	0.26	0.38
		Recall	0.20	0.70	0.60
		F1	0.25	0.38	0.47

CONCLUSIONS

MetSign was developed to fill the need for a flexible and modular software platform to process the high volumes of experimental data generated from high-resolution mass spectrometry-based metabolomics. By converting the instrument raw data into the mzXML format as its input data, MetSign provides a suite of bioinformatics tools for raw data deconvolution, metabolite putative assignment, peak list alignment, normalization, statistical significance tests, unsupervised pattern recognition, and time course analysis. MetSign uses the modular design and interactive visual data mining approach to enable efficient extraction of useful and potentially unsuspected patterns from data sets. Analysis steps, designed as containers, are presented with a wizard for the user to follow the analyses. Each analysis step might contain multiple analysis procedures and/or methods, and serves as a pause point where users can interact with the system to review the results, to shape the next steps, and to return to previous steps to repeat them with different methods and/or parameter settings. Analysis of metabolite extract of mouse liver with spiked-in acid standards shows that MetSign outperforms the existing software packages MZmine2 and XCMS².