Musicians demonstrate experience-dependent brainstem enhancement of musical scale features within continuously gliding pitch

Abstract

In contrast to language, where pitch patterns consist of continuous and curvilinear contours, musical pitch consists of relatively discrete, stair-stepped sequences of notes. Behavioral and neurophysiological studies suggest that both tone-language and music experience enhance the representation of pitch cues associated with a listener’s domain of expertise, e.g., curvilinear pitch in language, discrete scale steps in music. We compared brainstem frequency-following responses (FFRs) of English-speaking musicians (musical pitch experience) and native speakers of Mandarin Chinese (linguistic pitch experience) elicited by rising and falling tonal sweeps that are exemplary of Mandarin tonal contours but uncharacteristic of the pitch patterns typically found in music. In spite of musicians’ unfamiliarity with such glides, we find that their brainstem FFRs show enhancement of the stimulus where the curvilinear sweep traverses discrete notes along the diatonic musical scale. This enhancement was note specific in that it was not observed immediately preceding or following the scale tone of interest (passing note). No such enhancements were observed in Chinese listeners. These findings suggest that the musician’s brainstem may be differentially tuned by long-term exposure to the pitch patterns inherent to music, extracting pitch in relation to a fixed, hierarchical scale.

1. INTRODUCTION

Musical pitch patterns differ substantially from those used in other domains, including language. Linguistic pitch patterns, for instance, are continuous and curvilinear [9] whereas in Western music, notes unfold in a discrete, stair-stepped manner [3]. The discrete nature of musical pitch stems directly from the fact that in Western tonal music, the octave is divided into 12 equally spaced pitch classes (i.e., semitones). Subsets of these pitches are then used to construct the intervals, chords, and hierarchical scales that define tonality and musical key [11].

Although curvilinear pitch contours can occur in specific musical instruments (e.g., trombone), these tend to be exceptions rather than the norm. Slides/sweeps and other such continuous changes are isolated events used primarily for ornamentation to embellish the otherwise discrete notes of a musical line [3]. It is universally accepted that pitch patterns in music are built upon a foundation of discrete, stair-stepped contours and that local “curvilinear” deviations from that model are simply decorations [3, 7]. Indeed, the discrete nature of musical pitch—and the intervals it creates—is a necessary ingredient for both the perception and memorization of musical melodies [6, 7].

Musicians spend countless hours listening to and manipulating tones of the musical scale. As such, they develop an internalized, cognitive representation (i.e., categories) for these discrete notes in otherwise continuously changing pitch [4, 21]. This mental “grid” is quite robust to manipulation in that even distorted pitches are heard (i.e., mapped) in relation to an internalized musical scale [16]. Neurophysiological evidence supports this notion of an “internalized scale”. As indexed by the mismatch negativity (MMN), musicians show heightened sensitivity to intervallic (cf. discrete) alterations in pitch compared to untrained listeners [19].

Indeed, recent evidence suggests that musicians may extract discrete features of the musical scale even at the level of the brainstem. In a cross-domain experiment, Bidelman et al. [1] examined frequency-following responses (FFRs) in both musicians and tone language speakers (Mandarin Chinese) in order to compare the effects of long-term pitch experience from music (musicians) and language (Chinese) pitch experience on subcortical encoding of pitch-relevant information. In one condition, FFRs were evoked by presenting listeners with a continuous linguistic (nonmusical) pitch sweep spanning the interval of a major third (DO→MI). Importantly, the passing tone of this sequence (i.e., DO-RE-MI¹) was in no way demarcated as it would be had it occurred in a typical (discrete) musical sequence, i.e., the stimulus swept through this note without pause. Yet, despite the fact that such a glide is uncharacteristic of pitch patterns found in music, musicians’ FFRs showed selective enhancement for the intermediate passing tone (RE) of the sweep. No such music-specific enhancements were observed in Chinese listeners, despite their enhanced representation for curvilinear pitch patterns [10, 18]. These findings suggest that musicians may extract perceptually relevant features of the musical scale even at a subcortical level of processing.

However, such inferences were based on only a single, sweeping stimulus. In the present study, we hypothesize that if in fact musicians do have selective brainstem enhancement to intermediate, discrete scale tones within a sweeping pitch contour, then this effect must satisfy three criteria: (1) it must persist with changes in the absolute pitch height of the sweep (i.e., invariance with transposition); (2) it must persist regardless of sweep direction (ascending vs. descending); (3) it should be localized such that it is specific to musical pitches, i.e., the enhancement should not occur directly before or after the scale tone in question. Three pitch sweeps are used to test these manipulations and the selective scale tone enhancement effect. We compare brainstem FFRs between musicians and native speakers of Mandarin Chinese because both groups have exhibited subcortical enhancements in the encoding of complex pitch relative to English-speaking nonmusicians [1]. Here, Chinese nonmusicians serve as a control group to rule out that the observed scale tone enhancements are not simply related to pitch experience per se, but rather, are specific to musicians.

2. MATERIALS & METHODS

2.1 Participants

Fourteen English-speaking musicians (8 male, 6 female) and 14 native speakers of Mandarin Chinese (6 male, 8 female) participated in the experiment. The two groups were closely matched in age, years of education, handedness, and had normal hearing. Musicians were practicing amateur instrumentalists having ≥ 9 years of continuous instruction on their principal instrument (12.4 ± 2.4 yrs), beginning at or before the age of 11 (8.3 ± 2.2 yrs) (Table S1). None had any prior experience with a tone language. Chinese participants were born and raised in mainland China. None had received formal instruction in English before the age of 9 (12.1 ± 2.5 yrs) nor had > 3 years of musical training on any combination of instruments. Participants gave informed consent in compliance with a protocol approved by the Institutional Review Board of Purdue University.

2.2 Stimuli

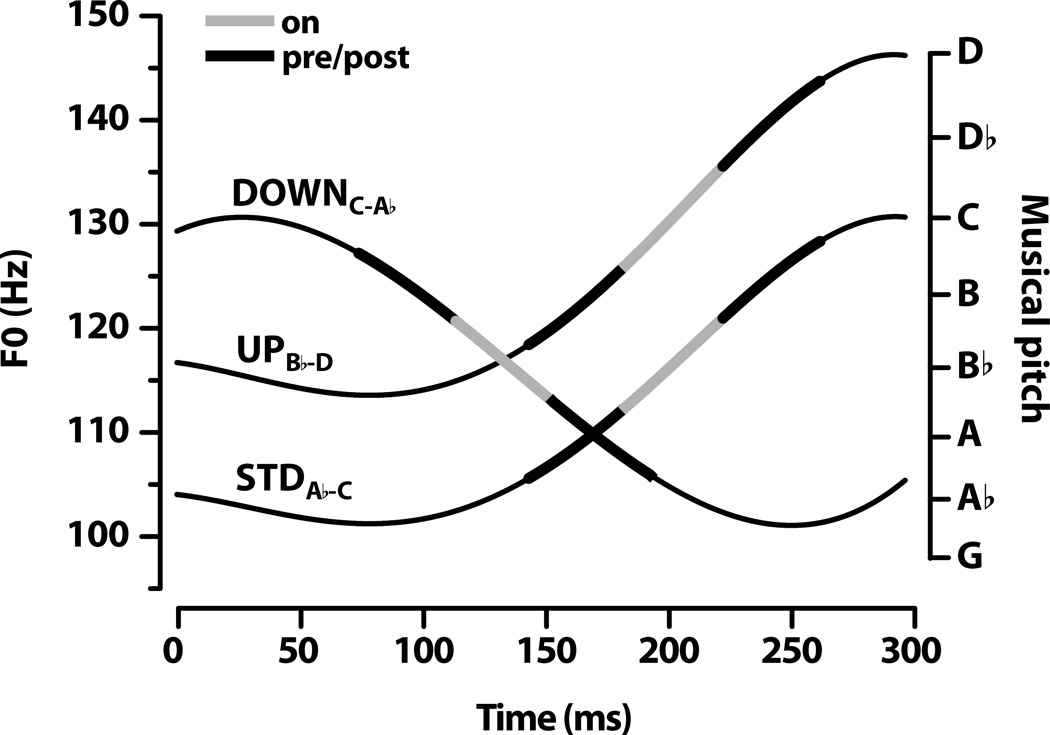
Three time-varying fundamental frequency (F0) sweeps which are exemplary of Mandarin tonal contours, but uncharacteristic of the pitch patterns typically found in music, were created using an iterated rippled noise (IRN) algorithm [17] (Fig. 1). The first, standard (STD), was a replicate of the rising tonal sweep employed in our previous study [1]. Its F0 spanned a major third from A♭2 to C3 on the piano, 104 to 131 Hz, respectively. The second (UP), was identical to the STD sweep except that it was transposed upward by two semitones, i.e., a musical whole step. Its F0 spanned a major third from B♭2 to D3, 116 to 146 Hz, respectively. The third (DOWN), represented a mirrored version of the STD sweep, i.e., a falling tonal sweep, whose F0 spanned a major third from C3 to A♭2, 131 to 104 Hz, respectively. Thus, all three F0 contours traverse a major third in either the ascending (DO-RE-MI) or descending (MI-RE-DO) direction. However, the exact location of where the pitch contour intersects the passing note (RE) differs across stimuli. Compared to STD, UP moves this passing tone upward in absolute frequency whereas DOWN shifts it earlier in time (Fig. 1).

Figure 1.

Fundamental frequency (F0) contours of the stimuli. Each condition represents a continuous pitch sweep uncharacteristic of prototypical musical pitch patterns, which are typically discrete and stair-stepped. Compared to the standard (STD) condition, UP is transposed upward by two semitones, whereas DOWN represents a mirrored version which descends in pitch. All three F0 contours span a major third in either the ascending (DO-RE-MI) or descending (MI-RE-DO) direction. Analysis segments of interest (Pre, On, Post) are demarcated along the trajectory of each contour.

For all three stimuli, a high number of iterations (n = 32) was used in the IRN algorithm with the gain set to 1. At 32 iterations, IRN stimuli exhibit clear bands of spectral energy at the fundamental and its harmonics thus producing a salient sensation of pitch [20]. Yet, unlike speech or music, these stimuli are devoid of formant structure or a recognizable instrumental timbre [1]. The duration of all three waveforms was fixed at 300 ms (10 ms cos² ramps). All waveforms were matched in overall RMS amplitude, bandwidth (30–3000 Hz), and were presented at a sample rate of 40 kHz.

2.3 Data acquisition and analysis

2.3.1 Frequency-following response (FFR) recording protocol

Participants reclined comfortably in an electro-acoustically shielded booth to facilitate recording of brainstem responses. FFRs were elicited from each participant by monaural stimulation of the right ear at a level of 80 dB SPL (rarefaction polarity; 2.43/s repetition rate) through a magnetically shielded insert earphone (ER-3A). Presentation order was randomized within/across participants and controlled by a signal generation and data acquisition system (Intelligent Hearing Systems).

FFRs were obtained using a vertical electrode montage, the optimal configuration for recording neural activity in rostral brainstem [8]. Ag-AgCl scalp electrodes placed on the midline of the forehead at the hairline (~Fpz) and right mastoid (A2) served as the inputs to a differential amplifier. Another electrode placed on the mid-forehead served as common ground. The raw EEG was amplified by 200,000 and filtered online (30–5000 Hz). Inter-electrode impedances were maintained ≤ 1 kΩ. Individual sweeps were recorded using an acquisition window of 320 ms at a sampling rate of 10 kHz. Neural responses were further band-pass filtered offline (80–2500 Hz). In total, each FFR waveform represents the average of 3000 artifact-free stimulus presentations (see also, Supplementary methods).

2.3.2 FFR data analysis

We defined three 40-ms time segments of interest (Fig. 1) along the span of each stimulus pitch contour directly before (Pre), during (On), and after (Post) the RE passing tone in the DO-RE-MI sequence. To quantify FFR encoding of F0, FFTs were computed within each of the three time segments per stimulus: 145–185 ms (Pre), 186–226 ms (On), and 227–267 ms (Post) for both the STD and UP pitch sweeps and 75–115 ms (Pre), 116–156 ms (On), and 157–197 ms (Post) for the DOWN sweep. For each subject per condition, the magnitude of FFR F0 was measured as the peak in the response FFT, above the noise floor (mean energy in surrounding bins ± 50 Hz from F0). F0 locations were determined by the expected frequency range according to the input stimulus.

3. RESULTS

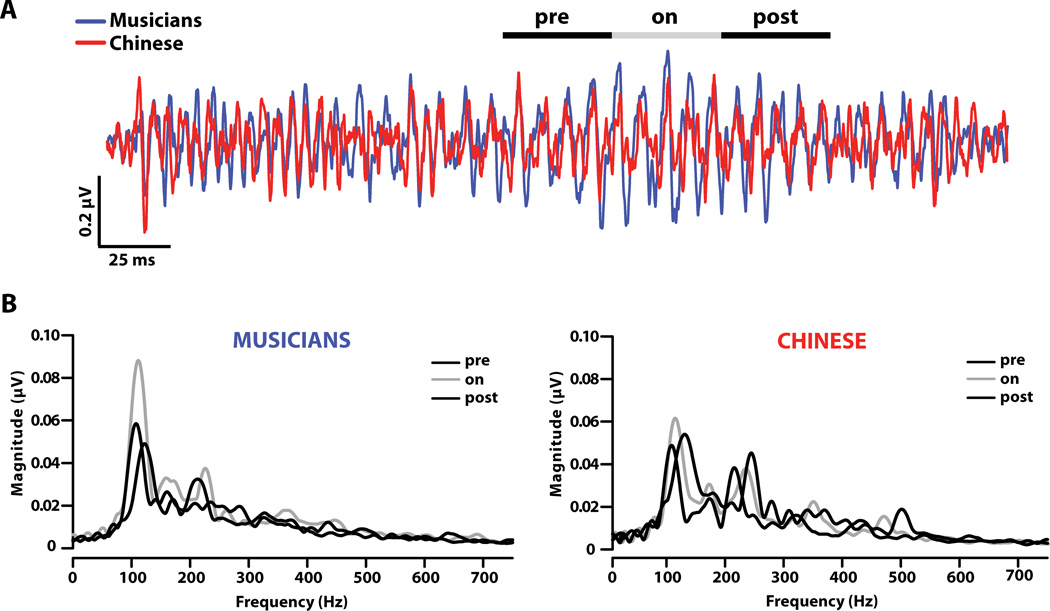
Representative brainstem FFRs and their corresponding FFTs (computed within each segment of interest) are shown in Fig. 2 for the standard (STD) pitch sweep. Relative to Chinese, the musician FFR time waveform shows more robust periodicity only in the temporal segment corresponding to the musical passing tone (On), but not in the segments immediately preceding (Pre) or following (Post) this musical event (Fig. 2A). Response FFTs computed within each segment of the FFR show selective enhancement of F0 (~110 Hz) for musicians, relative to Chinese, but only during the On region of the stimulus corresponding to the location of the musical passing tone (Fig. 2B).

Figure 2.

Group comparisons of FFR response properties for the standard (STD) condition. (A) FFR waveforms of a representative subject from each group. Relative to Chinese, musician FFR time waveforms show more robust periodicity encoding of the tonal sweep during the musical passing tone (On segment) but not immediately preceding (Pre) or following (Post) this musical event. (B) Response spectra (FFTs) computed in each time segment per group. Note the selective enhancement of F0 (~110 Hz) for musicians, relative to Chinese, during the On segment (i.e., the passing tone). No group differences in F0 magnitude are observed immediately preceding (Pre) or following (Post) this musical event.

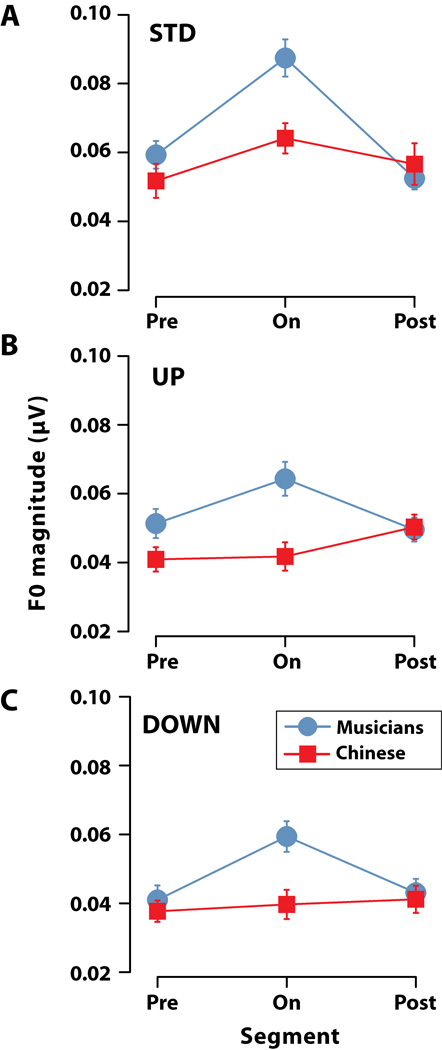
Brainstem encoding of F0 within each segment is shown in Fig. 3 for the three stimuli: (A) STD, (B) UP, and (C) DOWN. For each of the stimulus conditions, an omnibus ANOVA on F0 magnitudes revealed a significant group × segment interaction [STD: F_{2, 52} = 5.91, p = 0.0049; UP: F_{2, 52} = 6.71, p = 0.0026; DOWN: F_{2, 52} = 4.12, p = 0.0218]. By segment, Bonferroni adjusted contrasts revealed that regardless of the direction or absolute height of the pitch sweep, musicians and Chinese did not differ in their encoding of F0 during Pre and Post regions immediately before or after the passing tone, respectively (p > 0.1 in all cases). Yet, importantly, group contrasts for the On segment revealed that musicians had larger F0 magnitudes relative to Chinese listeners during the musical passing tone (p < 0.01 in all cases).

Figure 3.

Group comparisons of brainstem “pitch” encoding computed from FFRs. F0 magnitudes are shown for segments within the response before (Pre), during (On), and after (Post) the location of the passing tone for the (A) standard (STD), (B) UP, and (C) DOWN tonal sweeps (see Fig. 1). Despite their continuous nature, musicians show enhanced encoding, relative to Chinese, in that portion of the stimulus contour localized to this prominent musical event (i.e., RE). Error bars = ±1 SE.

By group, Bonferroni-adjusted multiple comparisons revealed that musicians’ F0 magnitudes in the On segment was greater than that of either the Pre or Post. The two off segment (Pre, Post) did not differ from one another. This pattern (i.e., On > Pre=Post) was true for musicians in all three stimuli regardless of the direction or absolute height of the pitch sweep. In contrast, F0 magnitudes did not differ between segments for Chinese listeners (i.e., Pre=On=Post) indicating no enhancement to the musical passing tone (RE). Taken together, these results suggest that musicians show selective enhancement to discrete notes along the diatonic musical scale during otherwise continuously gliding pitch. This effect held regardless of the passing tone’s position in time or overall pitch height (i.e., transpositional invariance). In addition, such effects were restricted to musically-trained individuals as linguistic pitch experience (Chinese) did not yield these same enhancements.

4. DISCUSSION

By measuring brainstem responses to tonal sweeps in musicians and Chinese listeners we found that musicians show selective subcortical enhancement during intermediate pitches along a continuous glide which correspond to notes of the diatonic musical scale. Musicians apparently “fill in” the major third (i.e., do-RE-mi). This effect was observed regardless of the specific height/transposition of the pitch sweep (low vs. high: STD vs. UP), its direction (rising vs. falling: STD vs. DOWN), or where in time the passing tone occurred (early vs. late: DOWN vs. STD). In contrast to musicians, no enhancements were observed for the passing tone in Chinese listeners indicating that pitch experience alone does not produce this effect, but rather, is limited to musical pitch experience.

4.1 Acoustic account of brainstem enhancement of musical scale tones

One explanation for musicians’ greater F0 magnitudes during the On regions (Figs. 2–3) may involve their superior ability to accurately encode rapid, fine-grained changes in pitch. Indeed, the most rapid changes in F0 across stimuli co-occur with the location of the passing tone RE (B♭2 for STD and DOWN; C3 for UP) (see On regions, Fig. 1).

The rates of F0 change (derivative of F0 contours expressed as Hz/ms) within each time segment of interest are displayed for the three stimuli in Table 1. Regardless of stimulus, On regions contain a faster pitch “acceleration” (i.e., rate of change) than their corresponding Pre or Post segments. Thus, one possible explanation for musicians' enhanced F0 magnitudes during the On segment (i.e., the passing tone) may be a heightened ability to encode rapidly changing pitch [cf. 1]. This type of encoding scheme might be advantageous for a musician given the fact that musical notes can often occur very rapidly in time while spanning the range of many octaves. An encoding scheme of this nature is also consistent with our recent behavioral and neurophysiological data demonstrating that musicians detect minute (~ 4% detuning) variations in pitch during rapidly-changing sequences otherwise undetectable by non-musicians [2].

Table 1.

Pitch rate of change (expressed as Hz/ms) per time segment of interest within each sweep

	Pitch acceleration (Hz/ms)
Stimulus	PRE	ON	POST
STD	0.1721	0.2138	0.1854
UP	0.1920	0.2381	0.2051
DOWN	−0.1636	−0.1944	−0.1760

Based on this type of acoustic explanation, one may posit that musicians exploit rapidly changing portions of pitch glides to “hear out” scale tones during music performance or listening. While the current experimental paradigm does not allow us to fully address this hypothesis, at first glance, this seems unlikely given the predominantly discrete nature of music and ipso facto, musicians’ relative inexperience with continuously sweeping pitch [3, 7]. Thus, while the observed “musician advantage” occurs at a location within a pitch pattern containing maximally changing F0, this is likely to be merely coincidental. Moreover, if an explanation based solely on “pitch acceleration” were true, it might be expected that the contiguous segments in the stimuli (Fig. 1) be perceptually distinguishable from one another in terms of their rates of pitch change. Just noticeable differences (JNDs) for discriminating changes in pitch glide rate range from 0.20 to 0.96 Hz/ms [5, 14, 15]. This JND is larger than any difference in rate between consecutive segments in our stimuli (Table 1). Thus, differences in pitch rate of change cannot be used to distinguish the segments, as these differences are imperceptible to listeners (i.e., below JND threshold). It is unlikely then that musicians’ enhancement during each On segment can be ascribed simply to a selectivity for higher rates of pitch change.

4.2 Experience-dependent explanations underlying brainstem enhancement of musical scale tones

An alternative and perhaps more parsimonious explanation for musicians’ greater F0 magnitudes in the On segment (Figs. 2–3) hinges on the fact that these sections straddle a time position where the curvilinear pitch contour of each sweep moves through the musical passing tone of the major third. Despite their unfamiliarity with curvilinear pitch, musicians seem to extract elements of the fixed, hierarchical scales of music embedded in otherwise continuously changing pitch patterns. All three stimuli spanned a frequency range of a major third, providing a diatonic context for each stimulus (key of A♭ for STD and DOWN; key of B♭ for UP). By the very nature of establishing diatonic context, an intermediate passing tone could be defined within each sweep (A♭-B♭2-C3 for STD and DOWN; B♭2-C3-D3 for UP; Fig. 1). Though none of the sweeps truly realize the passing note in the physical stimulus (i.e., they traverse through without pause), musicians nevertheless “fill in” the major third interval (i.e., DO-RE-MI), selectively enhancing the intermediate diatonic pitch of the scale sequence. Diatonic passing tones supply an important, active ingredient to musical melodies and help establish organizational grouping in music [13]. Musicians’ selective enhancements for these scale features are likely to be a direct reflection of their unique experience with the discrete pitches of composition and the importance of these characteristics to music listening. Indeed, we did not observe such effects in Chinese listeners probably because they lack the exposure and long-term experience with such music-specific attributes. The specific enhancements we observe must be attributed to music experience alone. They are a consequence of the fact the discrete pitches of the musical scale are likely an overlearned property during music acquisition and continued training. Additionally, we note these effects cannot be simply attributed to passive exposure to Western music as English-speaking non-musicians do not show this selective scale-tone enhancement [cf. Fig. 4, reference 1].

We did not observe an enhancement for any of the other chromatic notes (A. or B. for STD and DOWN; B♮ or C# for STD) within the analysis segments nor did we detect group differences during the initial (DO) and final (MI) pitches of the major third sweep (see Fig. 2A). The absence of any musician enhancement for the chromatic pitches may be due to the fact that these “off scale” notes are less probable in the major/minor (i.e., diatonic) musical contexts examined herein. Indeed, behavioral data indicates that musicians are especially sensitive to features of standard music scales and show a propensity for diatonic over chromatic pitch relationships [4, 12]. Thus, it is likely that in the present work, musicians’ enhancement was limited to the diatonic passing tone given its stronger relevance to music than chromatic scale tones.

5. CONCLUSIONS

Our findings suggest that musicians extract features perceptually relevant to the musical scale. Their brainstem responses show more sensitivity to pitches that correspond to discrete notes along the diatonic musical scale than to those falling between them. These enhancements likely result from their many years of active engagement and hours of practice on an instrument. The musician’s brainstem appears to be tuned by long-term exposure to the discrete pitch patterns inherent to musical scales and melodies.