Grid cells and theta as oscillatory interference: Theory and predictions

Abstract

The oscillatory interference model (Burgess, Barry, & O’Keefe, 2007) of grid cell firing is reviewed as an algorithmic level description of a path integration and as an implementation level description of grid cells and their inputs. New analyses concern the relationships between the variables in the model and the theta rhythm, running speed and the intrinsic firing frequencies of grid cells. New simulations concern the implementation of velocity-controlled oscillators (VCOs) with different preferred directions in different neurons. To summarize the model, the distance travelled along a specific direction is encoded by the phase of a VCO relative to a baseline frequency. Each VCO is an intrinsic membrane potential oscillation whose frequency increases from baseline as a result of depolarisation by synaptic input from speed modulated head-direction cells. Grid cell firing is driven by the VCOs whose preferred directions match the current direction of motion. VCOs are phase-reset by location-specific input from place cells to prevent accumulation of error. The baseline frequency is identified with the local average of VCO frequencies, while EEG theta frequency is identified with the global average VCO frequency and comprises two components: the frequency at zero speed, and a linear response to running speed. Quantitative predictions are given for the inter-relationships between a grid cell’s intrinsic firing frequency and grid scale, the two components of theta frequency, and the running speed of the animal. Qualitative predictions are given for the properties of the VCOs, and relationship between environmental novelty, the two components of theta, grid scale and place cell remapping.

Introduction

The discovery of grid cells in layer II of the medial entorhinal cortex (mEC) of freely moving rats (Hafting, Fyhn, Molden, Moser, & Moser, 2005) has sparked enormous theoretical interest. In brief, these cells fire in an array of locations describing the vertices of a regular triangular array across the environment. Neighboring grid cells describe identical but spatially offset arrays. As the recording location moves down the dorso-ventral axis of the medial EC the spatial scale of the grids increases (Hafting et al., 2005), and appears to do so in quantized steps while the orientation of the grids remains the same (Barry, Hayman, Burgess, & Jeffery, 2007). The resulting attempts to understand the function supported by the grid cells, and the mechanisms underlying their striking spatial firing patterns can be thought of in terms of Marr’s three levels of analysis (Marr, 1975; Marr & Poggio, 1977): ‘computational’ - the problem to be solved; ‘algorithmic’ - the algorithm by which it is solved; ‘implementational’ - how the algorithm is implemented in the brain.

There has been a surprisingly rapid and general agreement that the computational problem to which grid cells provide a solution is ‘path integration’ within an allocentric reference frame (Hafting et al., 2005; McNaughton, Battaglia, Jensen, Moser, & Moser, 2006; Fuhs & Touretzky, 2006). More specifically, the entorhinal grid cells and hippocampal place cells (O’Keefe & Dostrovsky, 1971) may together provide an internal representation of the animal’s location within its environment, with the grid cells enabling self-motion information to cause an appropriate translation of the represented location while place cells enable the association of the representation to sensory input specific to particular locations and environments (O’Keefe & Burgess, 2005). Such an arrangement would be consistent with suggestions as to the relationship between these regions which precede consideration of the nature of grid cell firing (Redish & Touretzky, 1998).

Two basic solutions have been proposed at the algorithmic level. First, grid cell firing and its updating by self-motion may result from ‘continuous attractor’ dynamics imposed on neuronal activation by the recurrent connections between grid cells (McNaughton et al., 2006; Fuhs & Touretzky, 2006). These models have two critical features. Finely tuned symmetrical recurrent connections which ensure that the ensemble of connected grid cells maintain grid-like patterns of firing. In addition, an asymmetrical interaction between grid cells causes their pattern of activity to move so as to track the actual movements of the animal. This model extends previous models of place cell firing (Zhang, 1996; McNaughton et al., 1996; Samsonovich & McNaughton, 1997).

The second algorithmic level solution is that grid cell firing, and its updating by self-motion, may result from the interference between two or more oscillations whose frequencies differ according to the velocity of the animal (Burgess et al., 2007). The key insight is that the phase difference between two oscillations, which determines the amplitude or ‘envelope’ of the interference pattern they generate, is the time integral of their frequency difference. This allows the amplitude of neuronal activity to be modulated by the displacement of the animal, since displacement is the time integral of velocity. If different pairs of oscillators are sensitive to the components of velocity in specific directions, grid-like firing patterns can be the net result, see below. This model extends a model of the temporal characteristics of hippocampal place cell firing (O’Keefe & Recce, 1993; Lengyel, Szatmary, & Erdi, 2003). Both oscillations are assumed to be in the theta band (7-11Hz in adult freely-moving rats), and the difference between them is assumed to be due to a change in frequency of one of the oscillators caused by depolarization by a velocity-dependent synaptic input i.e., it operates as a velocity-controlled oscillator.

Evidence for the implementation of the continuous attractor solution in mEC comes from the finding of grid cells in the deeper layers (III and V) whose firing rate is modulated by the direction and speed of running. These cells might mediate the required asymmetrical interaction between the grid cells in layer II (Sargolini et al., 2006) which must effectively connect grid cells whose grids are spatially offset in the direction of motion with connections whose strength reflects the animal’s speed of running in that direction.

Here I review the operation of the oscillatory interference model at the algorithmic and implementational levels, and focus on how it might be implemented by the neurons in mEC, and the testable predictions it generates, extending previous discussion of this (Burgess et al., 2007). Jeewajee et al., (2008a) consider the extracellular evidence for implementation of the model in mEC, while (Giocomo, Zilli, Fransen, & Hasselmo, 2007; Giocomo & Hasselmo, 2008) consider intracellular evidence in slices. I briefly consider the relationship between the oscillatory interference and continuous attractor models in the discussion.

Although accounts of grid cell firing naturally focus on mEC, since the over-whelming majority of data comes from this region, I note that grid cell firing may actually be generated in areas projecting into mEC, such as the presubiculum (Sargolini, Boccara, Witter, Moser, & Moser, 2006). For this reason, and for reasons of clarity, I attempt to identify the testable predictions of the model at a level of abstraction suitable for application beyond mEC.

The algorithm for path integration by velocity-controlled oscillators

Linear path integration a velocity-controlled oscillator

The phase of an oscillation is the time integral of its frequency, i.e. given an initial phase φ(0), an oscillation with time varying frequency f(τ) will have phase at time t given by:

$$\phi \left(t\right)=\phi \left(0\right)+{\int }_0^{t}2\pi f\left(\tau \right)d\tau$$ (1)

Similarly, the phase difference between two oscillations is the time integral of their difference in frequency. This provides a useful mechanism for temporal integration (see also, Huhn, Orban, Erdi, & Lengyel, 2005).

In the context of considering the relative phases of the two oscillations it is convenient to think of one of them as providing a “baseline” frequency f_b(t), and the other as providing an “active” frequency f_a(t) which can vary relative to the baseline frequency. The relationship of the baseline frequency to the EEG theta rhythm is considered in detail in a following section. The frequency of the active oscillation (or oscillations, see below) is assumed to be generated by an intrinsic membrane potential oscillation (MPO) whose frequency f_a(t) varies relative to the baseline frequency f_b(t) according to the depolarisation of the membrane.

More generally, both oscillations could be “active” and the difference between their frequencies is what matters. The following sections consider the implementation of the model in more detail, including how it relates to MPOs, neural firing and the theta rhythm. See Table 1 for a glossary of symbols and acronyms used.

Table 1.

Glossary of symbols and acronyms

Symbol	Meaning	Notes
Measurable extra-cellular quantities
ø(t)	running direction
s(t)	running speed
ν(t)	running velocity
G	spatial scale of the grid	Distance between adjacent firing fields.
fi(t)	intrinsic firing frequency	Estimated from spike-train autocorrelogram. Assumed to reflect neuron’s MPO frequency.
fθ(t)	theta frequency	Measured from the extra-cellular EEG. Assumed to vary with running speed.
f0	theta frequency extrapolated to zero running speed	Intercept of the plot of theta freq. fθ(t) (or intrinsic freq. fi(t)) versus running speed s(t).
Symbols and acronyms describing the model
MPO	membrane potential oscillation
VCO	velocity-controlled oscillator	MPO whose frequency (fa) increases with depolarization by a velocity-dependent synaptic input.
d, ød	‘preferred’ direction	Running direction producing the VCO’s maximum frequency. Shown as a unit vector d or angle ød as convenient.
fb(t)	‘baseline’ frequency
fa(t)	‘active’ frequency	Frequency of VCO: fa(t) = fb(t)+βv(t).d.
β	free parameter	The gain of the VCO response to depolarization. Spatial scale G=2/√3β.
T	time constant for leaky integration of grid cell inputs	T and F set so that roughly coincident inputs from ≥2 VCOs are required for firing.
F	firing threshold on grid cell MPO

The main assumption of the model is that the frequency of the MPO f_a(t) is controlled by synaptic input from a cell or cells whose net firing rate (and thus depolarizing effect) reflects running speed in a “preferred” direction:

$$f_a\left(t\right)=f_b\left(t\right)+\beta \underset{¯}{v}\left(t\right).\underset{¯}{d}$$ (2)

where ν is velocity, d is a unit vector indicating the preferred direction, β is a positive constant and “.” indicates the vector dot product. An alternative formulation of the same equation would be:

$$f_a\left(t\right)=f_b\left(t\right)+\beta s\left(t\right)\cos (ø(t)-{ø}_d)$$ (3)

where s(t) is running speed, ø(t) is running direction and ø_d is the preferred direction. Examples of cells whose firing rate reflects running speed in a particular direction (speed-modulated head-direction cells) can be found in the presubiculum (Jeewajee, 2008) and mEC (Sargolini et al., 2006).

Now, since the frequency difference between the two oscillations is proportional to speed of running in a particular direction, their difference in phase at a given time T, referred to as φ_ab(t)= φ_a(t) - φ_b(t), will reflect the rat’s displacement in the preferred direction:

$${\phi }_{ab}\left(t\right)-{\phi }_{ab}\left(0\right)={\int }_0^{t}2\pi \left[f_a\right(\tau )-f_b(\tau \left)\right]d\tau ={\int }_0^{t}2\pi \left[\beta \underset{¯}{v}\right(\tau ).\underset{¯}{d}]d\tau =2\pi \beta \left[\underset{¯}{x}\right(t)-\underset{¯}{x}(0\left)\right].\underset{¯}{d}$$ (4)

where x(t) is the location of the animal at time t. Thus the firing rate code for direction and speed of running of head direction cells is transformed into a phase code in which displacement in the preferred direction is represented by the phase of the active oscillation relative to the baseline oscillation. I refer to the above mechanism for performing this transformation as a velocity-controlled oscillator.

Note that the representation of displacement is cyclical, as expected from a phase code. However, different grid cells with different values of β represent space at different scales, so that actual location can be unambiguously decoded, see (O’Keefe & Burgess, 2005; Fiete, Burak, & Brookings, 2008).

2-D path integration by multiple velocity-controlled oscillators

Path integration can be thought of as estimating the net displacement x(t)-x(0) in the period [0,t] on the basis of a velocity signal over this period {ν(τ), for τ = 0 to t}. To do this in two dimensions requires integrating displacement along more than one preferred direction. The traditional solution is to integrate displacement along two orthogonal directions by separately integrating the sin and cosine components of the velocity signal (Mittelstaedt, 2000; Gallistel, 1990). In general, integration along any two non-parallel directions would suffice.

However, given the rapid accumulation of error in the noisy integration of a noisy velocity signal, there is a distinct advantage to tracking displacement along three rather than two directions. With integration along two orthogonal directions, accumulation of error occurs independently in each process, resulting in drift of the estimate of net displacement which cannot be detected within the path integration system. When integration occurs (redundantly) along more than two directions, independent accumulation of error in each process leads to a lack of consistency in the resulting estimates which could then be detected within the path integration system.

All path integration systems need to be reset with reference to the external sensory world, if possible, to avoid the accumulation of error, e.g. (Cheung, Zhang, Stricker, & Srinivasan, 2007; Etienne et al., 1998). In addition, with a redundant system of integration along more than 2 directions it is also necessary to align the initial states of the integrators to be consistent with each other. Within an oscillatory interference model, these problems are solved by resetting all active oscillations to be in phase with each other and to any common baseline oscillation at appropriate locations. See (Burgess et al., 2007) and discussion below in the context of a specific implementation.

There are many ways in which the algorithmic description of multiple velocity-controlled oscillators whose phases represent displacement along different directions could be implemented in the brain to support 2-D path integration. The next section describes potential implementations consistent with the idea that grid cell firing corresponds to phase integration of displacement along three directions differing by multiples of 60°.

The implementation of path integration by velocity-controlled oscillators

How could the multiple velocity-controlled oscillators described above actually be implemented in the brain so that they interact to signal net displacement in two dimensions? For simplicity I first consider the 1-dimensional problem of signalling displacement along a specific ‘preferred’ direction, for which a single velocity-controlled oscillator should be sufficient. It is not clear whether displacement along a single direction ever needs to be explicitly represented by neural firing, but the exercise is at least a useful step towards understanding the implementation of a 2-D path integration system, which is considered in the following section.

An implicit assumption in the following sections is that the end result of the interaction of velocity-controlled oscillators with each other, and with the baseline oscillation, is the firing of a grid cell. Thus, the top-down implementation of an algorithm for path integration should match with our bottom-up knowledge of the firing of grid cells. I then describe the experimentally testable predictions resulting from these constraints.

Linear path integration by a velocity-controlled oscillator

For a velocity-controlled oscillator to signal displacement along its preferred direction, its phase relative to the baseline oscillation needs to be signalled by neural firing. The simplest model assumes that the baseline oscillation has a sinusoidal shape, and that both oscillations combine to influence the membrane potential at the soma, with spikes being generated at the peaks of the resulting somatic membrane potential oscillation. Even within this simplest model, there are multiple potential implementations corresponding to how the oscillations combine and to the shape of the active oscillation.

The extreme cases for these implementation choices are illustrated in Figure 1. The choices for combining the oscillations range from addition – corresponding to the additive effect of two sources of current on the membrane potential, to multiplication – corresponding to modulation of a more distal velocity-controlled input by baseline-frequency variation of proximal ion channel conductances. The choices for the shape of the active oscillation vary from sinusoidal – corresponding to an intrinsic MPO in the dendrites (see Kamondi, Acsady, Wang, & Buzsaki, 1998) or synaptic input from a neuron or population of neurons with temporally modulated firing in the theta band, to punctate – corresponding to synaptic input from a neuron or population of neurons firing with highly concentrated phase relative to the baseline frequency.

Figure 1.

Oscillatory interference patterns. Effect of addition (a, b) and multiplication (c, d) of a sinusoidal (a, c) or punctate (b, d) “active” 9Hz oscillation (red, frequency f_a=9Hz) with a sinusoidal “baseline” 8 Hz oscillation (blue, frequency f_b=9Hz). Note that all of the combined oscillations (black) have raised areas of similar extents, but the peaks of the combined oscillation occur over different ranges of phase relative to the baseline oscillation (black diamonds) for the two the types of active oscillation (a,b vs c,d). Both interfering oscillations have range [0, 1] before being combined. Sinusoidal oscillations are: V(t)=(1+cos{2πft})/2, with f = 8 or 9. Punctate oscillations are: V(t)⁵⁰. Figure 1a is adapted from Burgess et al. (2007).

In all cases, the resultant oscillation has an amplitude which varies according to the phase difference of the two oscillations: waxing and waning as they go in and out of phase (producing constructive and destructive interference respectively). The distance L moved by the rat between maxima in the interference pattern when running in a constant direction ø is:

$$L(ø-{ø}_d)=s\left(t\right)∕\mid f_a\left(t\right)-f_b\left(t\right)\mid =1∕\beta \mid \cos (ø-{ø}_d)\mid ,$$ (5)

using equation 3. Note that the spacing of the maxima is independent of running speed s and depends only on direction: producing parallel stripes of maximum amplitude with fixed spacing across the environment. See Figure 2.

Figure 2.

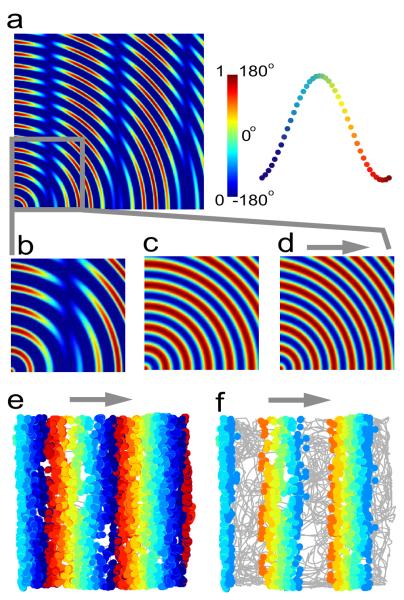
Linear interference patterns in 2D. a) Interference between a velocity-controlled oscillator (VCO) and a baseline oscillation during constant velocity runs from the origin (bottom left). Expanded view (b-d) shows the baseline oscillation (c) and the VCO (d, grey arrow shows preferred direction). Both component oscillations are sinusoidal and the combined oscillation is the thresholded sum (a, b). See Details below and Burgess et al. (2007). e) The firing of a neuronal VCO as the rat follows a 10min foraging path (grey line) in a square box. The VCO fires spikes at the peaks of its membrane potential oscillation (MPO). The locations of spike firing are show colored by the phase of firing relative to the baseline oscillation. See Details below. f) The firing of the neuronal VCO in (e) when its MPO is modulated by the baseline oscillation and a firing threshold of 0.5 is applied. Details: The baseline oscillation is V_b(t)=(1+cos{2πf_bt})/2, the VCO is: V_a(t)=(1+cos{2πf_at})/2, where f_b = 8, f_a= f_b + βv(t).d, β=0.05, and d is a unit vector in the preferred direction (rightwards). In (a-d) ν(t) is a constant 30cm/s to the location of each pixel. The thresholded sum: [V_a(t)+V_b(t)-F]₊ is shown in (a), with threshold F=1. In (e-f) ν(t) is the velocity of the rat, spikes are fired at the peaks of V_a(t) in (e) and colored to show phase of firing relative to V_b(t). In (f) spikes are fired as in (e), but only if V_a(t)*V_b(t) exceeds a firing threshold F=0.5. Color bar (top right) shows amplitude (0-1) and phase. Figure 2a is adapted from Burgess et al. (2007).

Irrespective of the method of combining the oscillations, when the active oscillation has a sinusoidal shape, the frequency of the highest peak in the resultant oscillation per cycle of the baseline oscillation is the mean of the two constituent frequencies, i.e. [f_a(t)+f_b(t)]/2. When the active oscillation has a punctate shape, the frequency of the highest peak in the resultant oscillation per cycle of the baseline oscillation equals the frequency of the active oscillation, f_a(t). Thus, a sinusoidal active oscillation implies a range of firing phases relative to the baseline oscillation of at most 180°, while a more punctate shape allows a range of firing phases of up to 360°. See Figure 1. A more complete model would include an explicit firing threshold, which would further restrict the range of firing phases.

Relation to theta-phase precession of place cell firing

Place cells recorded in the hippocampus of freely moving rats fire whenever the animal enters a specific area of the environment (the ’place field’, O’Keefe, 1976)). Unlike grid cells, firing is usually restricted to a single field or a small number of fields, determined to a large degree by the sensory environment (O’Keefe & Burgess, 1996; Hartley, Burgess, Lever, Cacucci, & O’Keefe, 2000). Whenever the rat is engaged in translational motion, the EEG power spectrum is dominated by a 7-11Hz oscillation of the local field potential – the movement-related “theta” rhythm, see (O’Keefe, 2006) for a review. As the rat runs through a place field the corresponding place cell fires spikes at systematically earlier and earlier phases of the ongoing theta rhythm. This phenomenon is known as theta phase precession and is seen during running on linear tracks (O’Keefe & Recce, 1993) and in open fields, in which phase precession from late to early phases occurs irrespective of running direction (Burgess, Recce, & O’Keefe, 1994; Skaggs, McNaughton, Wilson, & Barnes, 1996; Huxter, Senior, Allen, & Csicsvari, 2008).

The oscillatory interference model was initially proposed to explain theta-phase precession in place cell firing (O’Keefe & Recce, 1993). The baseline frequency was identified with the frequency of the theta rhythm, and the place cell MPO was proposed to increase above this frequency by an amount proportional to running speed. Thus the amplitude of the interference pattern generated by the two frequencies will vary with distance travelled through the firing field (Lengyel et al., 2003), see Figure 1 (top left). I note that the relationship between theta frequency and the baseline frequency is probably more complicated than assumed by this model, as discussed in the section on theta below.

One disadvantage of the application of oscillatory interference to place cell firing is that it predicts multiple repeating firing fields – making it a more appropriate model for grid cell firing (O’Keefe & Burgess, 2005). Nonetheless, substantial evidence suggests that oscillatory interference does contributes to place cell firing, although whether this reflects mechanisms intrinsic to the place cells, or input from grid cells is not yet known. Thus, several predictions of the oscillatory interference model of place cell firing have been verified, as summarized below, see (O’Keefe & Burgess, 2005) for further discussion.

The place cell firing is frequency modulated in the theta band, i.e., the spike train autocorrelogram shows regularly spaced peaks reflecting a regular modulation or ‘intrinsic firing frequency’. This frequency is identified with the MPO frequency and is slightly higher than the concurrent theta frequency, as predicted by the model (O’Keefe & Recce, 1993). In addition, as shown in equation 5, the spatial scale of the firing pattern should be inversely proportional to the difference in intrinsic and theta frequencies, so that place cells with larger firing fields should have lower intrinsic firing frequencies (i.e. closer to theta frequency). This prediction was verified by Maurer et al. (2005); recording place cells at different levels of the hippocampus (fields being smaller in the dorsal hippocampus than more ventrally). It was also indirectly verified by the observation that the rate of phase precession with distance varies with field size so that each field comprises a maximum of 360° of phase shift (Huxter, Burgess, & O’Keefe, 2003; Kjelstrup et al., 2008). Another prediction is that the intrinsic firing frequency of place cells should increase with running speed. This was verified by (Geisler, Robbe, Zugaro, Sirota, & Buzsaki, 2007) who thus refer to place cells as ‘speed-controlled oscillators’, see also (Maurer, Van Rhoads, Sutherland, Lipa, & McNaughton, 2005). I extend this nomenclature to ‘velocity-controlled oscillators’ in the context of grid cells. Finally, phase precession in place cells is unaffected by an NMDA receptor blockade which abolishes any experience-dependent asymmetry in place cell firing (Ekstrom, Meltzer, McNaughton, & Barnes, 2001), ruling out the simplest model by which phase precession and asymmetric firing reflect a common mechanism (Mehta, Lee, & Wilson, 2002).

2-D path integration by multiple velocity-controlled oscillators

How should the different velocity-controlled oscillators (VCOs) be implemented? In our previous paper Burgess et al. (2007) noted that they might be implemented by MPOs either in separate neurons or in separate dendrites. The main difference between these implementations is that a dendritic MPO interacts with other oscillations as a sinusoidal oscillation, while a neuronal MPO only interacts with other oscillations via the firing of spikes, see Figure 3. In practical terms this takes us between the two regimes illustrated in the top and bottom panels of Figure 1.

Figure 3.

Velocity-controlled oscillators (VCOs) could be implemented in dendrites (a, red rectangles) or neurons (b, red circles). In both cases the VCOs are driven by a speed modulated head-direction cell or population of cells (firing rates r_HDCi = v.d_i, where ν is the rat’s current velocity and d_i is the preferred direction for the i^th VCO). (a) An implementation in which dendritic VCOs (sinusoidal dendritic MPOs with frequency f_ai) sum with the baseline input (frequency f_b, blue line) and the interference patterns from different VCOs are multiplied at the grid cell soma (pale blue circle), see equation 6 and Figure 4. (b) An example in which neuronal VCOs (having sinusoidal MPOs with frequency f_ai) fire spikes with frequency f_ai. These spikes affect the membrane potential of the grid cell (modeled as a leaky-integrate and fire neuron, pale blue circle) whose membrane potential is also modulated by the baseline input (frequency f_b, blue line). Figure 3a is adapted from Burgess et al. (2007).

Interference between dendritic velocity-controlled oscillators

Burgess et al. (2007) focussed on the dendritic implementation for the detailed simulations presented. This implementation corresponds to the addition of each sinusoidal active oscillation (interpreted as a dendritic MPO) with a baseline oscillation (related to the theta rhythm), as shown in Figures 1 (top left), 2d and 3 (left). The resulting n linear interference patterns with different preferred directions were combined multiplicatively to give a single value interpreted as the grid cell’s firing rate r(t), i.e., with the above notation, and making explicit the integration of frequency to give phase:

$$\begin{array}{cc}\hfill & r\left(t\right)={\prod }_{i=1}^n{\left[\cos \right\{{\phi }_i\left(t\right)\}+\cos \{{\phi }_b\left(t\right)\left\}\right]}_{+};\hfill \\ \hfill & {\phi }_i\left(t\right)={\phi }_i\left(0\right)+{\int }_0^{t}2\pi \left(f_b\right(\tau )+\beta \underset{¯}{v}(\tau ).{\underset{¯}{d}}_i)d\tau ;\hfill \\ \hfill & {\phi }_b\left(t\right)={\int }_0^{t}2\pi f_b\left(\tau \right)d\tau ,\hfill \end{array}$$ (6)

where [x]₊=x if x>0; [x]₊=0 otherwise, ν(t) is running velocity, d_i indicates the preferred direction of the i^th VCO and φ_i(0) is its initial phase (see Phase re-setting below). See Figure 4, and Burgess et al. (2007) for details¹, and (Hasselmo, Giocomo, & Zilli, 2007) for further simulations.

Figure 4.

Two linear interference patterns with preferred directions differing by 60° (grey arrows, left and middle) combine to produce a triangular grid (right, grid scale = G). The linear interference patterns are the thresholded sum of a velocity-controlled oscillator (VCO) and a baseline oscillation during constant velocity runs from the origin (bottom left), see Figure 2 for details. These patterns are multiplied to produce the grid pattern (right). The colorbar shows amplitude.

Interference between neuronal velocity-controlled oscillators

The principal advantage of the dendritic implementation, above, is the simplicity of equation 6, and the simplicity of the mechanism for phase-resetting (see below). However, it may not be feasible for multiple independent MPOs to exist within a single grid cell, as discussed by Hasselmo (2008). Accordingly, implementations in which separate neurons act as velocity-controlled oscillators, rather than separate dendritic subunits, are explored next.

The outputs of neuronal VCOs are spikes. For simplicity, I assume that each VCO fires one spike at the peaks of its MPO. These spikes must interact at the grid cell with each other, and also with any baseline frequency input, via the excitatory post-synaptic potentials (EPSPs). Two sinusoidal MPOs naturally combine (via addition or multiplication) to produce an interference pattern, and the same is true for the combination of the more punctate EPSPs and sinusoidal MPOs, with some differences, as illustrated in Figure 1. In this Figure, and equations 7 and 11 below, punctate EPSPs are simply modelled as sinusoids normalised to range [0, 1] and raised to the power fifty.

One possibility is that each VCO interacts with the baseline oscillation before spikes are generated and combined with the spikes of other VCOs at the grid cell. This implementation is effectively identical to the dendritic implementation, above, with the exception that the stripy linear interference patterns formed by individual dendritic membrane potentials (see Figure 4) are represented by the firing rates of the neuronal VCOs. This implementation thus predicts neurons showing linear bands of firing across the environment. Here I focus on an alternative neuronal implementation, in which neuronal VCOs output spikes which interact with the spikes from other VCOs at the grid cell, before any interaction with the baseline oscillation. This implementation is similar to that proposed by Hasselmo (2008).

When the spikes from two different VCOs arrive at the grid cell, the EPSPs generated by the two spike trains will also produce an interference pattern in the grid cell’s somatic membrane potential. I assume that the grid cell’s somatic membrane potential performs leaky temporal integration the EPSPs arriving from its dendrites, with a time-constant less than one oscillatory period (i.e. less than 100ms). Then EPSPs arriving at similar phases will summate, while those arriving at different phases will not, i.e. showing constructive interference for small phase differences, or ‘coincidence detection’. See Figure 5, and e.g. Hopfield and Brody (2001) for related discussion. The effect of each train of EPSPs on the grid cell membrane potential is modelled as the convolution of the punctate oscillation in Figure 1 with an exponentially decaying kernel, i.e., the effect of the train of EPSPs from the i^th VCO is:

$$E_i\left(t\right)=C\underset{0}{\overset{t}{\int }}{\left[\right(1+\cos \left\{{\phi }_i\right(t-\tau \left)\right\})∕2]}^{50}\exp (-\tau ∕T)d\tau ,$$ (7)

where the phase of the i^th VCO (φ_i(t); as in equations 1, 2 and 6) is given by:

$${\phi }_i\left(t\right)={\phi }_i\left(0\right)+{\int }_0^{t}2\pi \left(f_b\right(\tau )+\beta \underset{¯}{v}(\tau ).{\underset{¯}{d}}_i)d\tau ,$$ (8)

T is the time constant (see Figure 8 for simulations with T = 6 to 25ms) and C normalises the EPSPs to resemble delta functions, i.e. $C=1∕\underset{-\pi }{\overset{\pi }{\int }}{\left[\right(1+\cos \phi )∕2]}^{50}d\phi$. Note that Leaky temporal integration over these timescales seems like a reasonable assumption for entorhinal neurons, with the possible exception of the “persistent firing” neurons found in deep layers of entorhinal cortex which can integrate over much longer durations (Egorov, Hamam, Fransen, Hasselmo, & Alonso, 2002).

Figure 5.

Illustration of interference between trains of excitatory post-synaptic potentials (EPSPs) during leaky temporal integration within a cell. The effect of individual trains of EPSPs at 9Hz (blue) and 10Hz (red) on the somatic membrane potential, modelled as a leaky integrator with exponential decay (see equations 7 and 8, T= 20ms). The upper plots (black) shows the effect of both trains combined by addition or multiplication. In both cases the higher peaks in the combined oscillation occur at the time of the later of the two contributing peaks, i.e. at the higher frequency prior to the centre of the region of constructive interference and at the lower frequency following it.

Figure 8.

Grid cell firing with directional velocity-controlled oscillator (VCO) inputs and baseline frequency modulation. Each directional VCO fires only when the current running direction matches its preferred direction (within 90°), thus only VCOs firing at above baseline frequency provide the active input f_a to the grid cell. a) 3 clustered directional VCO inputs produces directionally-modulated firing (see polar plot, left). The simulation is as Figure 7b right, but with directional VCOs and a lower firing threshold F=1.3. b-d) 6 directional VCO inputs produces omin-directional firing, showing the effect of varying the time constant T and firing threshold F. Time constant T=25ms and firing threshold F=1.5 in (b); T=12.5ms, F=1.1 in (c) and T=6.25ms, F=1.1 in (d). The size of firing fields decreases with decreasing T and increasing F. To produce grid-like firing patterns the model simply requires the combination of T and F to be such that grid cell firing requires input from VCOs with more than one preferred direction. F must be lower for directional VCOs than non-directional VCOs (Figure 7) since half of them will not be firing spikes at any moment. Baseline frequency f_b= 8Hz. Spike locations are shown on the path of a rat foraging for 10mins in a cylinder, coloured by their phase of firing relative to the baseline oscillation. See main text and Figure 6 for details.

The natural result of this type of interference or coincidence-detection at the grid cell, is for the grid cell’s firing to be concentrated at locations where the inputs from different velocity-controlled oscillators have similar phases. I assume that the grid cell’s firing threshold is set so that coincident inputs from more than one cell are required to make it fire, otherwise spatial bands of firing would be seen. I also assume that the preferred directions of the VCOs differ by multiples of 60° (see below for discussion of this assumption). In this case, the locations of coincident firing from two VCOs, occurring within a particular range of phases, will describe a triangular array across the environment. The locations of coincident firing occurring within different phase ranges describe different grids of identical orientation and spacing (these grids are spatially offset along the mean direction of the two VCO’s preferred directions). See Figure 6.

Figure 6.

Illustration of two neural velocity-controlled oscillators (VCOs, red circles) providing input to a grid cell (blue circle): the configuration shown in Figure 3b. The grid cell’s membrane potential performs leaky temporal integration of the EPSPs from these inputs (time constant T=25ms), and is modulated by a baseline-frequency input (8Hz, blue arrow; sinusoid coloured by phase). The grid cell fires spikes at peaks of its MPO which exceed a firing threshold F=1.5. The above plots show the locations at which the two VCOs with different preferred directions (grey arrow) fired spikes on the path of a rat foraging for 10mins in a cylinder. Spike locations are coloured according to their phase of firing relative to the baseline oscillation (see Figure 2e for details). The grid cell operates as a coincidence detector: firing whenever inputs arrive from both VCOs at the same phase (i.e. locations with spikes in the same colour in the two plots above). Such locations fall at the vertices of a triangular grid, with different firing phases corresponding to grids with different spatial offsets. Modulated by the baseline oscillation selects a specific range of phases for firing and a thus a specific triangular grid (black circles).

For the case of 2 VCO inputs, a modulatory baseline-frequency input to the cell body (as in Figure 3 right) effectively selects the range of phases relative to baseline during which the grid cell will fire, so long as coincident inputs are received. The published data imply a common range of firing phases for layer II grid cells, indicating a common modulatory baseline oscillation (Hafting, Fyhn, Bonnevie, Moser, & Moser, 2008).

If there are three VCO inputs to the grid cell, there is no guarantee that the spikes from all three inputs will arrive coincidently at any phase or location. The need to align the phases of the VCOs whenever there are more than two of them is solved by phase-resetting of all of the oscillators to be in phase at a single location. This reset location will then be the centre of one of the grid nodes, with other nodes in the grid occurring with the same range of phases. However, for three VCOs with evenly spaced preferred directions, coincident firing will also occur at phases ranges shifted by ±120° at the nodes of two other spatially offset grids (if one VCO increases phase by 240° in its preferred direction, the other two VCOs will decrease phase by 120° in their preferred directions, resulting in coincidence). See Figure 7a. Thus a modulatory baseline frequency input is still required to enforce a single range of firing phases, and the reset-signal should occur at the peak of this oscillation so that the VCO inputs are also in phase with it (see Burgess et al., 2007, and Hasselmo et al., 2007, for further discussion).

Figure 7.

Grid cell firing under different configurations of velocity-controlled oscillator (VCO) inputs, without baseline frequency modulation (left), and with baseline frequency modulation (right). a) Three VCO inputs with preferred directions (grey arrows) evenly spaced around 360°. b) Three VCO inputs with grouped preferred directions. c) Six VCO inputs with evenly spaced preferred directions. Notice the three interleaved grids with firing phases differing by ±120° in the simulation without baseline frequency modulation and with three evenly spaced preferred directions (a, left); The location-dependence of firing phase in the case of grouped preferred directions (b); The removal of out-of-field spikes by the baseline frequency modulation (c). Spike locations are shown on the path of a rat foraging for 10mins in a cylinder coloured by their phase of firing relative to the baseline oscillation. Baseline frequency f_b= 8Hz; time constant T=25ms; firing threshold F=2 for three inputs (a, b) and F=3 for six inputs (c). See main text and Figure 6 for details

Although less simple than equation 6, the grid cell’s membrane potential M(t) under the neuronal implementation with n VCO inputs and baseline-frequency modulation can be written in closed form:

$$M\left(t\right)=\frac{1}{2}(1+\cos \{{\phi }_b\left(t\right)\left\}\right)\sum _{i=1}^n{E}_i\left(t\right),$$ (9)

where E_i(t) is the effect on the grid cell membrane potential of the spike train from the i^th VCO, given by equations 7-8, and the phase of the baseline frequency, φ_b(t), is given by:

$${\phi }_b\left(t\right)={\int }_0^{t}2\pi f_b\left(\tau \right)d\tau .$$ (10)

In the simulations shown, I simply assume that a single spike is fired at the time of the peak of M(t) within each theta cycle, so long as the peak value exceeds a firing threshold F. Thus, the intrinsic firing frequency will be the same as the frequency of its MPO.

The final implementational issue I address is the directional tuning of the firing rate of the VCOs. The frequency of VCOs varies around the baseline frequency according to running direction: and their intrinsic firing frequency will too. But this change in firing frequency is slight, and does not result in significant modulation of firing rate by direction. Should the firing rate of a neuronal VCO be modulated by running direction? In the extreme case running directions which depolarise the VCO and lead to above-baseline oscillation frequency might also cause spiking activity, while the opposite directions, which lead to a relative depolarization and below-baseline oscillation frequencies, might not result in spiking activity. In this case, equation 7 becomes:

$$E_i\left(t\right)=CH(\underset{¯}{v}.{\underset{¯}{d}}_i)\underset{0}{\overset{t}{\int }}{\left[\right(1+\cos \left\{{\phi }_i\right(t-\tau \left)\right\})∕2]}^{50}\exp (-\tau ∕T)d\tau ,$$ (11)

where H(x) is the Heaviside function (H(x) =0 if x<0; 1 if x≥0), see equation 6 for definitions of ν and d_i, and equation 7 for definition of C.

Three directional VCO inputs with grouped preferred directions will produce directionally modulated grid cell firing, see Figure 8a. Three or six directional VCO inputs with preferred directions evenly spread around 360° results in omin-directional firing, see Figure 8b. Note that the MPO of directional VCOs maintains phase as the integral of velocity in the preferred direction whether or not the VCO fires a spike see Hasselmo (2008) for discussion of an alternative mechanism.

The main consequence of directional VCO firing is that the VCOs contributing to grid cell firing are always oscillating faster than the baseline frequency, and so the grid cell always shows late-to-early phase precession relative to the baseline frequency. For example, a grid cell with 3 grouped non-directional VCO inputs (with preferred directions 0°, 60°, 120°) will show a late-to-early change in firing phase when the rat runs in the mean preferred direction (60°) within each firing field, but also early-to-late phase precession when it runs in the opposite (240°) direction, see Figure 7b. With 3 grouped directional VCO inputs, the grid cell will only fire when the animal is moving in the mean preferred direction (Figure 8a), thus showing only late-to-early phase precession. For grid cells with six non-directional VCO inputs, there will be no clear net phase precession in grid cell firing, as late-to-early and early-to-late precession will occur simultaneously on runs through the firing fields. By contrast, with six directional VCO inputs, grid cell firing will always be driven by those with above-baseline frequency, and so will show late-to-early phase precession in all directions. See Figure 9.

Figure 9.

Phase of firing on runs in opposing directions (black arrows) through a grid firing field. a) Grid cell with six directional velocity-controlled oscillator (VCO) inputs and baseline frequency modulation (as Figure 8b). Note the late to early phase precession relative to baseline for runs in both directions. b) Grid cell with six non-directionally modulated VCO inputs (as Figure 7c; with F=2 to match the extent of firing in a). Note that no overall phase precession is observed.

Given the consistent late-to-early phase precession and non-directional firing seen in layer II grid cells, the implementation with six directional VCOs seems the most appropriate. To conclude this section I consider the parameters of this model. The six preferred directions (d_i, for i=1 to 6) are assumed to be evenly spaced around 360° and to result from a large-scale developmental process of selection of connections from speed-dependent head-direction cells, given the similar orientation of all grid cells within a hemisphere (Barry et al., 2007). If the preferred directions are chosen randomly, rather than differing by multiples of 60°, irregular grid-like firing patterns result (see Burgess et al., 2007). The initial phases of the VCOs (φ_i(0), for i=1 to 6) have to be set appropriately to produce a grid, with different values producing grids with different spatial offsets. Forcing all VCOs to be in phase at a given location ensures a grid with a firing field at that location. This is taken care of by a phase (re)setting mechanism which is also required to correct the accumulation of error, see below, Burgess et al., 2007, and Hasselmo et al., 2007 for further discussion.

There are three remaining parameters: β, the frequency-voltage gain or spatial scale parameter; T, the leaky integration time constant; F, the firing threshold. How sensitive is the model to the choices of these parameters? To produce grid-like firing patterns the model requires a combination of time constant T and firing threshold F such that input from VCOs with more than one preferred direction is needed for the grid cell to fire. If F is too low or T too long, then spatial bands of firing start to appear, joining together the firing at the grid nodes. As F increases or T becomes shorter, the firing fields shrink (see Figure 8b-d). I assume that the firing threshold, and thus overall firing rate, is actually controlled by feed-back inhibition (not simulated here). This leave one free parameter: β.

Phase re-setting and grid cell - place cell interactions

All path integration mechanisms require re-setting with respect to the sensory environment to prevent the accumulation of error, and this is also true for a model of path integration by grid cells. O’Keefe and Burgess (2005) suggested that the simplest way for grid cells to become associated to environmental stimuli within a familiar environment was via the formation of synaptic connections to grid cells from those place cells whose place field coincided with one of the grid cells firing fields. The firing of place cells, driven by sensory stimuli can then ensure that the connected grid cells maintain their grid fields in the appropriate environmental locations. They argued that place cells can more easily be driven by sensory input as distinct conjunctions of environmental information correspond to different place fields. There is indeed evidence that place cell firing is driven by the conjunctions of distances to environmental boundaries along different allocentric directions (O’Keefe & Burgess, 1996; Hartley et al., 2000; Lever, Burgess, Cacucci, Hartley, & O’Keefe, 2002; Barry et al., 2006). The idea that the association of grid cells to environmental stimuli is learned is consistent with the data of Barry et al. (2007). They showed that manipulation of the shape and size of the boundary of a familiar environment had a similar effect on the spatial firing pattern of grid cells as it has on place cells. However, grid cell firing was unaffected by the shape and size of a new environment.

In the oscillatory interference model the VCO phases will accumulate error as a result of imperfect input from speed-modulated head-direction cells. The effect of noisy VCO phases will be spatially disorganised grid cell firing. In addition, when three or more VCOs input to a grid cell, a reduction in peak firing rates will also occur, as multiple VCOs with arbitrary initial phase offsets will generally fail to coincide precisely at any location. In the model the spatial resetting of grid cells by place cells corresponds to phase resetting of the VCOs driving the firing of a grid cell by input from the place cells whose firing fields coincide with a grid field. This input occurs at the peak firing phase of theta (when the place cells will be most active) and reset the VCO inputs to be in phase with each other and with theta, see (Burgess et al., 2007). An advantage of the dendritic implementation is that resetting the inputs to a grid cell simply involves resetting all of its dendritic MPOs. In the neuronal implementation each VCO might have its own reset location determined by its own place cell inputs. Some local circuitry or plasticity would be required to ensure that the VCOs projecting to a given grid cell have similar reset locations. The model predicts phase precession limited to 180°, see Figure 9. Interestingly, layer II grid cells also appear to show consistent phase precession over the first 180° (‘late’ to ‘medium’ phases), with a much greater variance in the ‘early’ firing phases that occur as the rat exits the firing field (Hafting et al., 2008). It is possible that the phase-reset signal from place cells arrives at the early phase, disrupting the smooth procession of phase, but ensuring that the VCOs are phase-aligned before entry into the next firing field.

While the place cells may serve to reset grid cells in a familiar environment, the grid cells in turn may provide the path integration input to place cells. The subset of grid cells with firing fields coinciding with a place field could form synaptic connections to the corresponding place cell and thus maintain its location-specific firing based on speed and direction information during temporary absences of sensory information. Thus, the combined system supports the interaction between sensory inputs and path integration – with the firing of place cells and grid cells representing a compromise as to the animal’s current location on the basis of both types of information. This corresponds more closely to a mental representation of the environment which includes the animal’s current location (i.e., a cognitive map, O’Keefe & Nadel, 1978) than to a basic path integration system which simply allows return to the start of a trajectory, and which can probably be supported by other brain systems (Alyan & McNaughton, 1999). Note that the association of grid cell firing to environmental sensory input via phase reset may cause deformation of the grids from the spatial pattern predicted by oscillatory interference/path integration alone (Barry et al., 2007). Equally, changes to the spatial scale of grid cell firing may cause remapping of place cell firing, see below.

There are undoubtedly other phase re-setting mechanisms at work, beyond the proposed connections from place cells learned within a familiar environment. First, the most important effect of errors during path integration concerns orientation: orientation is lost rapidly, and once lost renders translational information useless (Cheung et al., 2007). The grid cell path integration system outlined here relies on the head-direction cells for orientational information (strictly speaking these should signal movement direction rather than head direction, although these two signals are at least highly correlated). The head-direction system uses both the integration of internal signals encoding angular velocity, and external sensory information for resetting, see e.g. (Taube, 1998). The independent sensory resetting of the direction signal ensures that the grid cell system will be relatively robust, while still requiring its own sensory resetting to correct translational errors. Second, alternative mechanisms for resetting grid cells must exist to correct translational errors in a new environment. As discussed by Burgess et al. (2007), the phase of theta can be reset by sensory stimuli or actions (Buzsaki, Grastyan, Tveritskaya, & Czopf, 1979; Williams & Givens, 2003). Thus repeating pattern of firing seen in rats running in a maze of hairpin turns (Derdikman, Fyhn, Hafting, Moser, & Moser, 2006) suggests that making a body turn between straight trajectories might provide a reset signal (Burgess et al., 2007), see also (Hasselmo, 2008). The different firing patterns for running in different directions, both in the hairpin maze and on linear tracks (Hafting et al., 2005), indicate that the phase reset is affected by the allocentric direction of the turn. Thus, it is possible that the ‘boundary vector cells’ proposed to drive place cell firing (O’Keefe & Burgess, 1996; Burgess, Jackson, Hartley, & O’Keefe, 2000; Hartley et al., 2000; Barry et al., 2006) may relate to directional phase resetting within mEC, see (Burgess et al., 2007; Savelli, Yoganarasimha, & Knierim, 2008; Hasselmo, 2008) for further discussion.

Relating the model to experimentally measurable quantities (predictions)

In this section I attempt to relate the variables describing the oscillatory interference model to experimentally measurable quantities with the hope of producing clear experimentally testable predictions. One prediction follows directly from the preceding discussion of phase resetting. That is, removal of the place cell input to grid cells will allow the accumulation of translational error, at least within an open-field environment without local sensory or body-turn cues for phase resetting, while correction of directional errors will continue within the head direction system. In this situation, grid cell firing will lose its spatial stability without changing its intrinsic firing frequency. Other predictions require further work to identify the link between the variables in the model and measurable quantities such as the intrinsic firing frequency of the grid cell, grid scale and theta frequency, see below.

Relationship to the theta rhythm and place cell remapping

It is important to understand the context in which reliable and accurate phase representations are proposed. This context is set by extra-cellular recording of EEG in freely-moving rats, which is dominated by a high amplitude and very narrowly tuned movement-related theta rhythm, with mean frequency around 8-9Hz in adult rats. Note that this contrasts with the situation in most in vitro slice preparations in which oscillations tend to show a much broader range of frequencies, but see (Manseau, Goutagny, Danik, & Williams, 2008). Thus we cannot necessarily use standard in vitro data to infer how noisy MPO frequencies will be in vivo (cf. Giocomo & Hasselmo, 2008).

The theta rhythm results from a complex interaction between multiple regions, with generators in both entorhinal cortex and the hippocampus proper, and with a critical contribution from the medial septum, see (Blair, Kishan, & Zhang, 2008) for a model. Two components of theta have been identified, one of them is cholinergically mediated (atropine sensitive) and relates to arousal, the other is the movement-related (atropine resistant) component referred to above. The arousal-related component typically has a lower frequency when measured in the absence of the movement-related component (around 6-7Hz in adult rats), but its contribution during motion is not clear. For example, there is no 6-7Hz sub-peak to the movement-related 8-9Hz peak in the EEG power spectrum (see e.g. Jeewajee, Lever, Burton, O’Keefe, & Burgess, 2008b). Significantly, the movement related component is abolished by lesions of the entorhinal cortex, while both components are abolished by lesions of the medial septum. See O’Keefe (2006) and Buzsaki (2002) for recent reviews. I speculate below, that the mechanisms contributing to these two types of theta may be separately responsible for the intercept and the slope of the relationship between theta frequency and running speed.

The recorded movement-related theta rhythm undoubtedly reflects locally aligned oscillatory current flows, while the influence of larger-scale coupling can also be seen in the constant frequency found throughout the hippocampal formation and medial septum (Bullock, Buzsaki, & McClune, 1990; Maurer et al., 2005), generated in part by the EC, see above. Thus, we cannot simply assume that theta provides the ‘baseline’ frequency (f_b), or that it is independent of the active frequencies of the VCOs (f_a). The implication of an active (VCO) frequency f_a and independent baseline frequency f_b in equation 3 also has the following problem: the synaptic input to a VCO from a speed modulated head-direction cell (or cells) must vary from excitatory (when running in the preferred direction) to inhibitory (when running in the opposite direction) so that its frequency varies above and below the baseline frequency. This appears to violate Dale’s law that a single type of neuron cannot release both excitatory and inhibitory neurotransmitters.

A potential solution is provided by the following two assumptions: a) The synaptic input to each VCO is solely positive (i.e., depolarizing); b) The baseline frequency f_b is the average of the frequencies of the local VCOs (which have preferred directions evenly spread around 360°). Thus, all VCOs increase in frequency with running speed, but those whose preferred directions match the current running direction (and thus drive grid cell firing, in the directional VCO implementation) increase most rapidly. Assumption a) implies:

$$f_a\left(V\right(t\left)\right)=f_0+\beta V\left(t\right),$$ (12)

where

$$V\left(t\right)=s\left(t\right)(1+\cos \{ø\left(t\right)-{ø}_d\left\}\right).$$ (13)

V(t) is the VCO’s depolarization due to velocity-dependent synaptic input, and f₀ is the VCO’s MPO frequency at zero speed, i.e., f_a(V(t)=0). Note that the effect of synaptic input is always positive. The full description of f_a is then:

$$f_a\left(\mathrm{s}\right(t),ø(t),\beta ,{ø}_d)=f_0+\beta s\left(t\right)(1+\cos \{ø\left(t\right)-{ø}_d\left\}\right),$$ (14)

Now assumption b), averaging over all preferred directions ø_d, implies:

$$f_b\left(\mathrm{s}\right(t),\beta )={<f_a\left(\mathrm{s}\right(t),ø(t),\beta ,{ø}_d)>}_{{ø}_d}=f_0+\beta s\left(t\right)$$ (15)

This solves the problem of Dale’s law, without affecting how the model generates spatial patterns, since the difference f_a(t) - f_b(t), and thus equation 3, does not change: we have effectively just added βs(t) to both frequencies f_a(t) and f_b(t). See (Burgess et al., 2007) for an alternative solution in which linear interference patterns are produced by pairs of VCOs with opposing preferred directions and synaptic input equal to [s(t)cos{ø(t)-ø_d})]₊. In this ‘rectified’ model the phase difference between each pair of VCOs produces a linear interference pattern (Figure 2a), with the grid pattern resulting from the combination of multiple linear interference patterns in the usual way (see Figure 4). Unlike the other implementations, the phases of the VCOs in this ‘rectified’ version do not maintain any fixed relationship to the theta rhythm.

How does the (local) baseline frequency f_b for a given grid cell relate to the (global) theta frequency f_θ? Since theta frequency is constant throughout the system, it must reflect a global property of all of the VCOs in mEC. The simplest assumption is that it reflects the mean frequency of all VCOs, averaging over preferred directions and the spatial scale factor β (which varies dorso-ventrally, Hafting et al., 2005), i.e.:

$$f_{\theta }\left(\mathrm{s}\right(t\left)\right)={<f_b\left(\mathrm{s}\right(t),\beta )>}_{\beta }={<f_a\left(\mathrm{s}\right(t),ø(t),\beta ,{ø}_d)>}_{{ø}_d,\beta }=f_0+<\beta >s\left(t\right)$$ (16)

where <β> is the mean β found throughout the dorso-ventral extent of the mEC.

A model in which theta frequency is the mean frequency of neuronal MPOs or intrinsic firing frequencies is still consistent with the phase precession of the individual neurons relative to this ‘theta rhythm’ (as shown for simulations of place cell phase precession, Burgess, O’Keefe, & Recce, 1993). Nonetheless, questions remain regarding the effect of differences between the (local) baseline frequency f_b and the (global) theta frequency f_θ. Thus, phase resetting of VCOs by theta-modulated input (e.g., from place cells) will allow grid cell firing to show phase precession within a fixed range of phases of theta as occurs in layer II, or to fire within a fixed range of phases with or without precession as occurs in some layer III cells (Hafting et al., 2008). However, the relationship to theta described above implies that, between phase resets, the baseline frequency will be higher than theta for cells with small grids (showing accelerated phase precession), equal to theta for cells with median size grids (i.e. with β = <β>, see equations 16 and 19, these will show linear 180 degree phase precession) and slower than theta for cells with very large grids (i.e., with β > 2<β>, so these will show late-to-early phase precession).

Next I consider the effect of manipulations which change the observed theta frequency. Since the theta frequency is not an independent variable, but reflects the mean VCO frequency, a change in the observed theta frequency implies a concomitant change in the frequencies of all VCOs. There are two parameters governing theta frequency: f₀ and <β>. If the observed change in theta frequency reflects a change in <β>, then we assume a simple scaling of all local values of β. In this case, if f’_θ(s(t)) = γf_θ(s(t)), then f’_b(s(t), β) = γ f_b(s(t), β) and f’_a(s(t), ø(t), β, ø_d) = γ f_a(s(t), ø(t), β, ø_d). Since, grid scale G is inversely proportional to the difference f_a - f_b,, equation 5, grid scale will change according to:

$$G^{\prime }=\frac{G}{\gamma }.$$ (17)

Conversely, if the observed change in theta frequency reflects a change in f₀, there will be no change in grid scale. Thus, when theta frequency changes due to changes in arousal, environmental novelty, pharmacology, behavior, age etc, it will be important to measure both f₀ and <β> from a plot of theta frequency versus running speed to predict the effect on grid size. These two parameters may correspond to the two types of theta, i.e., the value of f₀ may be atropine-sensitive and related to arousal, while the increase with running speed is atropine-resistant and, obviously, related to movement. Both components will depend on the medial septum, the movement-related component also depends on mEC.

I assume that place cells receive two types of information (O’Keefe & Burgess, 2005), one conveying sensory information via ‘boundary vector cells’ (O’Keefe & Burgess, 1996; Hartley et al., 2000; Barry et al., 2006), the other path integrative information via grid cells, and these inputs must coincide at the place field. A consequence of this is that a global change to the spatial scale of grids, reflecting a change in <β> (as observed in a plot of theta frequency versus speed), will disrupt place cell firing. Thus, the initial rapid and coherent remapping of place cell firing reflecting extreme environmental novelty (Wills, Lever, Cacucci, Burgess, & O’Keefe, 2005) may be caused by a global increase in grid scale and concomitant drop in theta frequency (Jeewajee et al., 2008b). Conversely, the slower independent (cell-by-cell) remapping of place cell firing (Lever, Wills, Cacucci, Burgess, & O’Keefe, 2002) likely reflects an on-going process of re-aligning place fields with the firing fields of grid cells as they return to their familiar scale as the effects of an environmental manipulation wear off (Barry et al., 2007).

Different implementations may correspond to different types of grid cell

The firing of neuronal velocity-controlled oscillators can be successfully combined as inputs to a grid cell so as to produce grid cell firing in several different ways. In the experimental data, the firing rate of layer II grid cells is not modulated by running direction, but does show theta modulation and phase precession, with only late-to-early phase precession observed on the linear track. In addition, these cells appear to have a fixed range of initial firing phases when the rat enters one of the firing fields of the grid (Hafting et al., 2008). These grid cells would correspond to six directional VCO inputs and theta modulation in the neuronal implementation (see Figures 8b-d, 9a).

By contrast, most layer III grid cells tend to have directionally modulated firing (‘conjunctive’ cells, Sargolini et al., 2006), around 50% do not have theta-modulated firing rates; 25% fire within a fixed range of phases of theta without showing a relationship between phase and location within the firing field; and 25% show phase precession (Hafting et al., 2008). The layer III theta-modulated grid cells which do show phase precession would correspond to 3 directional VCO inputs with grouped preferred directions, in which case they should also show directional modulation of firing along the direction of phase precession, and spatially constant phases of firing (see Figure 8a). The theta-modulated grid cells which do not show phase precession might correspond to three or six non-directional VCO inputs with evenly spaced preferred directions (see Figure 7a,c and 9b), although these would not have directionally modulated firing in the model. The non-theta-modulated grid cells would not be generated by the oscillatory interference mechanism, in which cells fire rhythmically, even if not with fixed phase relative to baseline in the ‘rectified’ version of the model (see above, and Burgess et al., 2007).

Testing these predictions of the origin of the different types of grid cell observed in mEC will depend on identifying the VCOs themselves, which is addressed below.

Velocity-controlled oscillators

The fundamental property of a VCO is that it has a MPO obeying equations 2-3. Intracellular recording of MPOs in freely moving animals remains a technical challenge, but see (Giocomo et al., 2007; Giocomo & Hasselmo, 2008) for an in vitro approach. Nonetheless, the neuronal implementation described above predicts that the intrinsic firing frequency of neuronal VCOs relative to theta should be modulated by running velocity according to equations 2-3. In addition, in implementations other than the ‘rectified’ model (see above), the neuronal VCOs should show spatially constant parallel bands of firing phases, as in Figure 6. See also (Hasselmo, 2008).

Outside of analyses of firing phase or intrinsic firing frequency and running velocity, neuronal VCOs would resemble hippocampal ‘theta cells’ (Ranck, Jr., 1973): showing theta modulated firing with no obvious spatial modulation. In the case of the directional VCO implementation (equation 11), their firing rate would be modulated by running direction, resembling theta-modulated head-direction cells. Thus VCOs might be present among the cell types other than grid cells in medial EC, see e.g., Sargolini et al. (2006). With respect to directional VCOs, it may be worth noting that, although neurons with directionally modulated firing are found at all stages along the head direction circuit (Taube, 1998), the earliest stages in which firing modulated by both theta and head direction has been reported are retrosplenial cortex (Cho & Sharp, 2001) and presubiculum (Cacucci, Lever, Wills, Burgess, & O’Keefe, 2004). In addition, recordings in the medial septum reveal cells with theta-modulated firing which is phase-locked to hippocampal theta and increases in frequency with running speed (King, Recce, & O’Keefe, 1998). The rhythmicity of firing of a small proportion of these cells depended on the direction of running. See Blair et al. (2008) for further discussion, and a related model.

Two other possibilities are worth considering. First, if neuronal VCOs interact with theta prior to combining with other VCO inputs at the grid cell then, as noted above, a linear interference pattern would be visible as linear bands of firing across the environment. Second, it is possible that there is no distinction between neuronal VCOs and grid cells, rather that grid firing patterns arise from the interconnection of multiple neuronal VCOs. In this case, grid cells would revert to neuronal VCOs if their interconnections were disabled. In terms of the contributions of different layers to the network provision of grid cell firing, the layer II stellate cells or layer V pyramidal cells, in which intrinsic oscillations have been identified, might provide the VCOs, while the layer III pyramidal cells, which do not show intrinsic oscillations, might provide the coincidence detection function. See (Erchova, Kreck, Heinemann, & Herz, 2004; Dickson, Mena, & Alonso, 1997; Klink & Alonso, 1993; Hamam, Kennedy, Alonso, & Amaral, 2000; Alonso & Llinas, 1989; Giocomo et al., 2007; Yoshida & Alonso, 2007) for the intrinsic oscillatory properties of entorhinal neurons, and Hasselmo (Hasselmo, 2008) for a specific implementation of VCOs as ‘persistent firing’ cells found in layer V of mEC in-vitro (Egorov et al., 2002).

Relationship between intrinsic frequency, theta frequency, grid size, and running speed

The grid peaks fall along a lines at 30° to the preferred directions of the VCOs, see Figure 4, see also (Burgess et al., 2007; Giocomo et al., 2007). So, following equation 5, the distance between peaks, or grid spacing, G is given by:

$$G=L(\pi ∕6)=\frac{2}{\sqrt{3}\beta }.$$ (18)

Equation 16 tells us how theta frequency f_θ depends on running speed s(t), the average value of β throughout mEC, and the VCO’s MPO frequency at zero speed f₀. Reported grid cells vary in spatial scale from 30cm dorsally (Hafting et al., 2005) to at least 400cm ventrally (Brun et al., 2008). So equation 18 indicates a range of β between 0.039 dorsally and 0.003 ventrally, with a dorsal weighting due to the dorso-ventral wider extent of mEC at dorsal than ventral locations, and indications that grid scale increases more rapidly in the ventral mEC (Brun et al., 2008). The mean value of β depends on the density of representation of different grid scales, ρ(G), i.e.:

$$<\beta >=\underset{30}{\overset{400}{\int }}\frac{2\rho \left(G\right)dG}{\sqrt{3}G},$$ (19)

if ρ(G) is uniform, i.e. ρ(G)=1/370, then <β> ≈ 0.008. However, a uniform density of representation across scales seems unlikely in terms of efficiency. A density inversely proportional to grid scale, i.e. ρ(G)=1/(log(400/30)G), so that the number of cells with grids below a maximum scale is logarithmic in the maximum scale, predicts <β> ≈ 0.014. The observation that grid scales increase in jumps of a fixed factor of around 1.7 (Barry et al., 2007) implies that ρ(G) might decrease exponentially with grid scale, i.e. ρ(G) proportional to exp(−G/γ). This gives the uniform density result for very large γ, and larger values of <β> for smaller values of γ, e.g., <β> ≈ 0.001 for γ = 400cm; <β> ≈ 0.023 for γ = 30cm.

In terms of intra-cellular recording, equations 12 and 18 indicate that:

$$f_a\left(V\right(t\left)\right)=f_0+\frac{2}{\sqrt{3}G}V\left(t\right)$$ (20)

where V(t) is the VCO’s depolarization level and f₀ can be found as the intercept of a plot of theta frequency versus running speed, see equation 16 and the discussion of f₀ and β following it.

In terms of extra-cellular recording, as well as theta frequency, we can measure the intrinsic firing frequency f_i(t) resulting from a grid cell’s VCO and baseline inputs by examining the autocorrelogram of the grid cell’s firing. Replacing f_a and f_b in equation 3 can then produce a relationship between intrinsic firing frequency, aspects of theta frequency, grid scale and running speed, as follows. In the model of layer II grid cells (equations 8-11), peaks occur in the grid cell membrane potential as a result of the multiple directional VCO inputs to it, and I assume that the intrinsic firing frequency equals the frequency of these peaks. The VCOs contribute inputs oscillating at above baseline frequency when the rat is running in the VCOs preferred direction (i.e., ø_d −90° < ø(t) < ø_d +90°) and do not contribute when it runs in the opposite direction. The mean frequency of the contributing VCOs is found by averaging equation 3 over all running directions ø(t):

$${<f_a\left(t\right)>}_{\varphi \left(t\right)}=f_b\left(t\right)+\frac{\beta s\left(t\right)}{\pi }\underset{-\pi ∕2}{\overset{\pi ∕2}{\int }}\cos \left(\varphi \right)d\varphi =f_b\left(t\right)+\frac{2\beta s\left(t\right)}{\pi }.$$ (21)

The VCO frequencies also interact with the baseline frequency, bringing the frequency of the combined MPO closer to the baseline frequency according to the shape of the combined MPO (resulting in little change if it is sufficiently punctate, or resulting in the mean of the two frequencies if it is sinusoidal, see Figure 1). Assuming a sinusoidal oscillation results from multiple VCO inputs (the effect of multiple EPSPs from multiple VCOs in the neuronal implementation; or the smooth MPOs in the dendritic implementation), implies that the grid cell’s combined MPO frequency will be the mean of the contributing VCO inputs (equation 21) and the baseline frequency, giving:

$${<f_i\left(t\right)>}_{\varphi \left(t\right)}=f_b\left(t\right)+\frac{\beta s\left(t\right)}{\pi }.$$ (22)

Substituting for f_b using equation 15 gives:

$${<f_i\left(t\right)>}_{\varphi \left(t\right)}=f_0+(1+\frac{1}{\pi })\beta s\left(t\right),$$ (23)

and substituting for β using equation 18 gives:

$${<f_i\left(t\right)>}_{\varphi \left(t\right)}=f_0+\frac{2(\pi +1)}{\sqrt{3}\pi G}s\left(t\right)$$ (24)

Note that all of the variables in equations 16 and 24 can be measured by recording grid cell firing and EEG in freely moving animals: speed, s(t); grid scale, G; average intrinsic firing frequency, <f_i(t)>; theta frequency, f_θ(t); theta frequency extrapolated to zero speed, f₀; see Table 1. These predictions are examined by Jeewajee et al. (2008a).

Discussion

Evidence for the oscillatory interference model comes from in vitro intracellular recordings in slices taken from medial EC. The membrane potential of layer II stellate cells is known to naturally oscillate at a frequency close to the EEG theta frequency (7-11Hz), see (Alonso & Llinas, 1989; Erchova et al., 2004; Alonso & Klink, 1993). Significantly, this MPO frequency increases with increasing depolarization (Giocomo et al., 2007; Giocomo & Hasselmo, 2008), consistent with equation 20. In addition, equation 20 predicts that the slope of the frequency versus depolarisation curve should be inversely proportional to grid scale G. Giocomo and Hasselmo (2008) showed that this is the case, by measuring f_a as a function of the dorso-ventral location of the slice, and using the known dependence of grid scale on dorso-ventral location to infer the grid scale.

In terms of recording in freely moving animals, evidence so far is indirect. The original suggestion (O’Keefe & Burgess, 2005) that layer II grid cells would show theta phase precession has recently been verified (Hafting et al., 2008). In addition, Burgess et al. (2007) noted reports that grid cell firing shows a slight increase in spatial scale when the rat is put into a novel environment (Fyhn, Hafting, Treves, Moser, & Moser, 2007 supplementary online material). We therefore predicted that environmental novelty would produce a global change in grid scale, reflected in a concomitant change in theta frequency (equation 17). Subsequent work demonstrated that environmental novelty does indeed result in a reduction in theta frequency (Jeewajee et al., 2008b).

The model makes specific prediction relating changes in the response of theta frequency to running speed to changes in grid scale (equations 16 and 17) in response to environmental or pharmacological manipulations. Related predictions concerning place cell remapping can be made, given the disruption to place cell inputs caused by changes in grid scale. These predictions remain the subject of current investigation. In addition, the characteristics of the proposed velocity-controlled oscillators have been well described. Locating these neuronal or dendritic processes constitute another set of predictions, see also (Hasselmo, 2008; Blair et al., 2008).

Jeewajee et al. (2008a) explore the quantitative predictions of equations 16 and 24 by investigating the intrinsic firing frequency f_i(t), theta frequency f_θ(t), grid scale G and running speed s(t) in extra-cellular recordings of grid cells in freely moving rats. Their findings provide the first direct extra-cellular evidence for the model: confirming the increase of theta frequency and grid cell’s intrinsic firing frequency with running speed and the decrease in intrinsic firing frequency with grid scale, consistent with equations 16 and 24.

Relationship to recurrent connectivity and ‘attractor’ models

The oscillatory interference model provides a mechanism to explain the firing pattern of individual grid cells. As such it does not address the likely interactions between different grid cells, but nor does it deny them. Given the anatomy of mEC (see e.g., Witter & Moser, 2006) it is likely that there are functionally relevant recurrent connections between grid cells which affect their firing. And the major alternative model for grid cell firing (the continuous attractor model) is that the grid patterns result directly from this recurrent connectivity (Fuhs & Touretzky, 2006; McNaughton et al., 2006).

To consider how recurrent connectivity and the oscillatory interference model would interact, it is worth distinguishing two types of interaction between neurons: symmetrical, i.e. having an equal effect on the neurons at either end of a functional connection; and asymmetrical. The continuous attractor model, as originally proposed for head-direction cells and place cells, assumes that each member of a population of neurons have similar desired spatial patterns of firing with different offsets, as is the case with head-direction, place or grid cells (Zhang, 1996; McNaughton et al., 1996; Samsonovich & McNaughton, 1997) see also (Droulez & Berthoz, 1991; Ben-Yishai & Sompolinsky, 1995). This model proposes distinct roles for symmetric and asymmetric interactions between neurons, as follows.

The strengths of (symmetric) connections between pairs of neurons are arranged to precisely reflect the spatial proximity of their firing patterns. These connections ensure that the firing of individual neurons follows the desired spatial firing pattern and that the pattern of activity across the population is coherent (i.e. the relative firing rates of neighboring neurons are consistent with each other, and with a single location of direction for the animal). Thus, for grid cells, firing patterns with a poor grid structure will be “cleaned up” to follow the desired grid pattern, and the firing rates of different neurons will correspond to the desired spatial offset between their grids. See (Fuhs & Touretzky, 2006; McNaughton et al., 2006) for details.

By contrast, asymmetric connections between neurons allows the pattern of activity across the population of neurons to move smoothly so as to track the actual movement of the animal. The rate of movement of the location represented by the population activity is proportional to the strength of the asymmetric interaction compared to the symmetric interaction (Zhang, 1996). For this to accurately track actual movement requires precise tuning. First, the symmetric connection strengths between neurons must be perfectly balanced, to prevent drift unrelated to actual movement. Second, asymmetric connections are required between each neuron and other neurons with firing patterns offset in all directions around it, and the strengths of these connections must precisely follow actual motion (they are assumed to be mediated by neurons whose firing rates reflect movement velocity). The presence of asymmetric connections has also been argued to provide an explanation for the phase precession effect (Tsodyks, Skaggs, Sejnowski, & McNaughton, 1996).

There is good evidence for symmetrical recurrent connections between grid cells. Thus the grid cells in one hemisphere all appear to have similarly oriented grids. In addition, while the grid scales increase with the dorso-ventral location of the grid cell in mEC, the scale appears to increases in quantized jumps. See Barry et al. (2007). Both of these findings indicate that populations of grid cells form a coherent representation of the type supported by symmetrical recurrent connectivity.

The oscillatory interference model is not necessarily incompatible with the continuous attractor model. The addition of symmetrical recurrent connectivity between cells individually following the oscillatory interference model would likely improve the stability and coherence of all of the cells in the population. In addition, the constraint that VCOs have preferred directions differing by multiples of 60° indicates the presence of developmental plasticity following an unsupervised learning rule (Burgess et al., 2007; see also Rolls, Stringer, & Elliot, 2006). The presence of recurrent connectivity could ensure that a coherent set of preferred directions was present in the whole population. In return, the oscillatory interference model could provide the firing patterns required to develop the appropriate symmetrical connection strengths in the first place.

The oscillatory interference model does provide a clearly different mechanism to that proposed for the asymmetric connections under the continuous attractor model, i.e., the use of oscillatory phase to perform the temporal integration of a (rate coded) velocity signal to give displacement. Even so it is still possible that, as with symmetrical connections, asymmetric connections between neurons could act in parallel to the proposed oscillatory interference mechanism in driving the firing of individual neurons. Rather than attempting to have a ‘beauty contest’ between the rival models, I hope that these two distinct models signal a more mature era of computational modelling in which the focus is making testable predictions which drive forward the theory-experiment cycle by which science progresses.

Conclusion

I have reviewed the oscillatory interference model (Burgess et al., 2007) from the perspective of providing an algorithm for path integration and of being implemented by grid cells. I have focussed on a specific implementation corresponding to grid cells in layer II of mEC. Briefly, proposed ‘velocity-controlled oscillators’ (VCOs) have a membrane potential oscillation which increases with depolarisation and receive synaptic input from speed-modulated head-direction cells. The phase of each VCO relative to a baseline oscillation will then correspond to distance travelled along the preferred direction of it head-direction cell input. Several VCOs with preferred directions differing by multiples of 60° combine to produce grid cell firing. The VCOs whose preferred directions are with 90° of the current direction of motion drive the firing of the grid cell, while the modulatory baseline oscillation corresponds to the average frequency of the local VCOs (i.e, with all preferred directions). The grid scale is inversely proportional to the gain of the VCO’s frequency response to depolarization, β. The global average frequency of all VCOs in mEC is identified with theta, and comprises two components: the frequency extrapolated to zero speed (f₀) and an increase in frequency with running speed (with the mean gain of all mEC VCOs: <β>). Cumulative error is corrected by phase reset, which is determined by input from place cells in a familiar environment.

I derived quantitative predictions relating theta frequency, grid cell intrinsic firing frequency, grid scale and running speed. I also derived predictions relating changes in the response of theta frequency to running speed to changes in grid scale (equations 16 and 17) in response to environmental or pharmacological manipulations. These predictions can be extended to place cell remapping, given the disruption to place cell inputs caused by changes in grid scale. In addition, I have spelled out the characteristics of the proposed VCOs, which might be instantiated in individual neurons, or in dendritic sub-compartments. Although the specific implementations described here will undoubtedly be wrong in detail, the strength of the oscillatory interference model lies in the experimentally testable predictions that it has made, and continues to make, which I have outlined here.