Sparse High Dimensional Models in Economics

Abstract

This paper reviews the literature on sparse high dimensional models and discusses some applications in economics and finance. Recent developments of theory, methods, and implementations in penalized least squares and penalized likelihood methods are highlighted. These variable selection methods are proved to be effective in high dimensional sparse modeling. The limits of dimensionality that regularization methods can handle, the role of penalty functions, and their statistical properties are detailed. Some recent advances in ultra-high dimensional sparse modeling are also briefly discussed.

1 INTRODUCTION

1.1 High Dimensionality in Economics and Finance

High dimensional models recently have gained considerable importance in several areas of economics. For example, vector autoregressive (VAR) model (Sims (1980), Stock & Watson (2001)) is the key technique to analyze the joint evolution of macroeconomic time series, and can deliver a great deal of structural information. Because the number of parameters grows quadratically with the size of model, standard VARs usually include no more than ten variables. However econometricians may observe hundreds of data series. In order to enrich the model information set, Bernanke et al. (2005) proposed to augment standard VARs with estimated factors (FAVAR) to measure the effects of monetary policy. Factor analysis also plays an important role in forecasting using large dimensional data sets. See Stock & Watson (2006) and Bai & Ng (2008) for reviews.

Another example of high dimensionality is large home price panel data. To incorporate cross-sectional effects, price in one county may depend upon several other counties, most likely its geographic neighbors. Since such correlation is unknown, initially the regression equation may include about one thousand counties in US, which makes direct ordinary least squares (OLS) estimation impossible. One technique to reduce dimension is variable selection. Recently, statisticians and econometricians have developed algorithms to simultaneously select relevant variables and estimate parameters efficiently. See Fan & Lv (2010) for an overview. Variable selection techniques have been widely used in financial portfolio construction, treatment effects models, and credit risk models.

Volatility matrix estimation is a high dimensional problem in finance. To optimize the performance of a portfolio (Campbell et al. (1997), Cochrane (2005)) or to manage the risk of a portfolio, asset managers need to estimate the covariance matrix or its inverse matrix of the returns of assets in the portfolio. Suppose that we have 500 stocks to be selected for asset allocation. There are 125,250 parameters in the covariance matrix. High dimensionality here poses challenges to estimate matrix parameters, since small element-wise estimation errors may result in huge error matrix-wise. In the time domain, high frequency financial data also provide both opportunities and challenges to high dimensional modeling in economics and finance. On a finer time scale, the market microstructure noise may no longer be negligible.

1.2 High Dimensionality in Science and Technology

High dimensional data have commonly emerged in other fields of sciences, engineering, and humanities, thanks to the advances of computing technologies. Examples include marketing, e-commerce, and warehouse data in business; genetic, microarray and proteomics data in genomics and heath sciences; and biomedical imaging, functional magnetic resonance imaging, tomography, signal processing, high resolution images, functional and longitudinal data, among many others. For instance, for drug sales collected in many geographical regions, cross-sectional correlation makes the dimensionality increase quickly; the consideration of 1000 neighborhoods requires 1 million parameters. In meteorology and earth sciences, temperatures and other attributes are recorded over time and in many regions. Large panel data over a short time horizon are frequently encountered. In biological sciences, one may want to classify diseases and predict clinical outcomes using microarray gene expression or proteomics data, in which tens of thousands of expression levels are potential covariates but there are typically only tens or hundreds of subjects. Hundreds of thousands of SNPs are potential predictors in genome-wide association studies. The dimensionality of the feature space grows rapidly when interactions of such predictors are considered. Large scale data analysis is also a common feature of many problems in machine learning such as text and document classification and computer vision. See, e.g., Donoho (2000), Fan & Li (2006), and Hastie et al. (2009) for more examples.

All of the above examples exhibit various levels of high dimensionality. To be more precise, relatively high dimensionality refers to the asymptotic framework where the dimensionality p is growing but is of a smaller order of the sample size n (i.e., p = o(n)), moderately high dimensionality to the asymptotic framework where p grows proportionately to n (i.e., p ~ cn for some c > 0), high dimensionality to the asymptotic framework where p can grow polynomially with n (i.e., p = O(n^α) for some α > 1), and ultra-high dimensionality to the asymptotic framework where p can grow non-polynomially with n (i.e., log p = O(n^α) for some α > 0), the so-called NP-dimensionality. The inference and prediction are based on high dimensional feature space.

1.3 Challenges of High Dimensionality

High dimensionality poses numerous challenges to statistical theory, methods, and implementations in those problems. For example, in linear regression model with noise variance σ², when the dimensionality p is comparable to or exceeds sample size n, the ordinary least squares (OLS) estimator is not well behaved or even no longer unique due to the (near) singularity of the design matrix. Regression model built on all regressors usually has prediction or forecast error of order (1 + p/n)^1/2σ when p ≤ n rather than (1 + s/n)^1/2σ when there are only s intrinsic predictors. This reflects two well-known phenomena in high dimensional modeling: the collinearity or spurious correlations and the noise accumulation. The spurious correlations among the predictors is an intrinsic difficulty of high dimensional model selection. There are two sources of collinearity: the population level and the sample level. There can be high spurious correlation even for independent and identically distributed (i.i.d.) predictors when p is large compared with n (see, e.g., Fan & Lv (2008), Fan & Lv (2010), Fan et al. (2010)). In fact, conventional intuition might no longer be accurate in high dimensions. Another example is the data piling problems in high dimensional space shown by Hall et al. (2005). There are issues of overfitting and model identifiability in presence of high collinearity.

Noise accumulation is a common phenomenon in high dimensional prediction. Although it is well known in regression problems, explicit theoretical quantification of the impact of dimensionality on classification was not well understood until the recent work of Fan & Fan (2008). Fan & Fan (2008) showed that for the independence classification rule, classification using all features has misclassification rate determined by a quantity $C_p/\sqrt{p}$, which trades off between the dimensionality p and overall signal strength C_p. Although the signal contained in the features increases with dimensionality, the accompanying penalty on dimensionality $\sqrt{p}$ can significantly deteriorate the performance. They showed indeed that classification using all features can be as bad as random guessing because of the noise accumulation in estimating the population centroids in high dimensions. Hall et al. (2008) considered a similar problem for distance-based classifiers and showed that the misclassification rate converges to zero when $C_p/\sqrt{p}\to \infty$, which is a specific result of Fan & Fan (2008). See, e.g., Donoho (2000), Fan & Li (2006), and Fan & Lv (2010) for more accounts of challenges of high dimensionality.

As clearly demonstrated above, variable selection is fundamentally important in high dimensional modeling. Bickel (2008) pointed out that the main goals of high dimensional modeling are

• to construct as effective a method as possible to predict future observations;

• to gain insight into the relationship between features and response for scientific purposes, as well as, hopefully, to construct an improved prediction method.

Examples of the former goal include portfolio optimization and text and document classification, and the latter is important in many scientific endeavors such as genomic studies. In addition to the noise accumulation, the inclusion of spurious predictors can prevent the appearance of some important predictors due to the spurious correlation between the predictors and response (see, e.g., Fan & Lv (2008) and Fan & Lv (2010)). In such cases, those predictors help predict the noise, which can be a rather serious issue when we need to accurately characterize the contribution from each identified predictor to the response variable.

Sparse modeling has been widely used to deal with high dimensionality. The main assumption is that the p-dimensional parameter vector is sparse with many components being exactly zero or negligibly small, and each nonzero component stands for the contribution of an important predictor. Such assumption is crucial in ensuring the identifiability of the true underlying sparse model especially given relatively small sample size. Although the notion of sparsity gives rise to biased estimation in general, it has been proved to be very effective in many applications. In particular, variable selection can increase the estimation accuracy by effectively identifying the important predictors and improve the model interpretability. There has been a huge literature contributed to statistical theory, methods, and implementation for high dimensional sparse models. Sparsity should be understood in a wider sense as a reduced complexity. For example, we may want to apply some grouping or transformation of the input variables guided by some prior knowledge and to add interactions and higher order terms for reducing the model bias. These lead to transformed or enlarged feature spaces. The notion of sparsity carries over naturally. Another example of dimensionality reduction is to introduce a sparse representation to reduce the number of effective parameters. For instance, Fan et al. (2008) used the factor model to reduce the dimensionality for high dimensional covariance matrix estimation.

The rest of the article is organized as follows. In Section 2, we survey some developments of the penalized least squares estimation and its applications to econometrics. Section 3 presents some further applications of sparse models in finance. We provide a review of more general likelihood based sparse models in Section 4. In Section 5, we review some recent developments of sure screening methods for ultra-high dimensional sparse inference. Conclusions are given in Section 6.

2 PENALIZED LEAST SQUARES

Assume that the collected data are of the form ${({\mathbf{x}}_i^T,y_i)}_{i=1}^n$, in which y_i is the i-th observation of the response variable and x_i is the associated p-dimensional predictors vector. The data are often assumed to be a random sample from the population (x^T, y), where conditional on the predictor vector x, the response variable y has mean depending on a linear combination of predictors β^Tx with β = (β₁, ⋯ , β_p)^T. In high dimensional sparse modeling, we assume ideally that most parameters β_j are exactly zero, meaning that only a few of the predictors contribute to the response. The objective of variable selection is identifying all important predictors having nonzero regression coefficients and giving accurate estimates of those parameters.

2.1 Univariate PLS

We start with the linear regression model

$$\mathbf{y}=\mathbf{X}\mathit{\beta }+\mathit{\epsilon },$$ (2.1)

where y = (y₁, ⋯ , y_n)^T is an n-dimensional response vector, X = (x₁, ⋯ , x_n)^T is an n × p design matrix, and ε is an n-dimensional noise vector. Consider the specific case of canonical linear model with rescaled orthonormal design matrix, i.e., X^TX = nI_p. The penalized least squares (PLS) problem is

$$\underset{\mathit{\beta }\in {\mathbf{R}}^p}{\text{min}}\left\{\frac{1}{2n}{\Vert \mathbf{y}-\mathbf{X}\mathit{\beta }\Vert }_2^2+{\displaystyle \sum _{j=1}^p{p}_{\lambda }(|{\beta }_j|)}\right\},$$ (2.2)

where ‖ · ‖₂ denotes the L₂ norm and p_λ(·) is a penalty function indexed by the regularization parameter λ ≥ 0. By regularizing the conventional least squares estimation, we hope to simultaneously select important variables and estimate their regression coefficients with sparse estimates.

In the above canonical case of X^TX = nI_p, the PLS problem (2.2) can be transformed into the following componentwise minimization problem

$$\underset{\mathit{\beta }\in {\mathbf{R}}^p}{\text{min}}\left\{\frac{1}{2n}{\Vert \mathbf{y}-\mathbf{X}\widehat{\mathit{\beta }}\Vert }_2^2+\frac{1}{2}{\Vert \widehat{\mathit{\beta }}-\mathit{\beta }\Vert }_2^2+{\displaystyle \sum _{j=1}^p{p}_{\lambda }(|{\beta }_j|)}\right\},$$ (2.3)

where β̂ = n⁻¹X^Ty is the ordinary least squares estimator or more generally the marginal regression estimator. Thus we consider the univariate PLS problem

$$\widehat{\theta }(z)=\underset{\theta \in \mathbf{R}}{\text{arg min}}\left\{\frac{1}{2}{(z-\theta )}^2+p_{\lambda }(|\theta |)\right\}.$$ (2.4)

For any increasing penalty function p_λ(·), we have a corresponding shrinkage rule in the sense that |θ̂(z)| ≤ |z| and θ̂(z) = sgn(z)|θ̂(z)| (Antoniadis & Fan (2001)). It was further shown in Antoniadis & Fan (2001) that the PLS estimator θ̂(z) has the following properties:

1. sparsity if ${\text{min}}_{t\ge 0}\{t+p_{\lambda }^{\prime }(t)\}>0$, in which case the resulting estimator automatically sets small estimated coefficients to zero to accomplish variable selection and reduce model complexity;

2. approximate unbiasedness if $p_{\lambda }^{\prime }(t)=0$ for large t, in which case the resulting estimator is nearly unbiased, especially when the true coefficient β_j is large, to reduce model bias;

3. continuity if and only if arg ${\text{min}}_{t\ge 0}\{t+{p\prime }_{\lambda }(t)\}=0$, in which case the resulting estimator is continuous in the data to reduce instability in model prediction (see, e.g., the discussion in Breiman (1996)).

Here p_λ(t) is nondecreasing and continuously differentiable on [0, ∞), the function $-t-p_{\lambda }^{\prime }(t)$ is strictly unimodal on (0, ∞), and $p_{\lambda }^{\prime }(0)$ represents $p_{\lambda }^{\prime }(0+)$. Generally speaking, the singularity of the penalty function at the origin, i.e., $p_{\lambda }^{\prime }(0+)>0$, is necessary to generate sparsity for the purpose of variable selection and its concavity is needed to reduce the estimation bias when the true parameter is nonzero. In addition, the continuity is to ensure the stability of the selected models.

There are many commonly used penalty functions such as the L_q penalties p_λ(|θ|) = λ|θ|^q for q > 0 and I(|θ| ≠ 0) for q = 0. The uses of L₀ penalty $p_{\lambda }(t)=\frac{{\lambda }^2}{2}I(t\ne 0)$ and L₁ penalty in (2.4) give the hard-thresholding estimator θ̂_H(z) = zI(|z| > λ) and the soft-thresholding estimator θ̂_S(z) = sgn(z)(|z| − λ)₊, respectively. It is easy to see that the convex L_q penalty with q > 1 does not satisfy the sparsity condition, the convex L₁ penalty does not satisfy the unbiasedness condition, and the concave L_q penalty with 0 ≤ q < 1 does not satisfy the continuity condition. Thus none of the L_q penalties simultaneously satisfies all the above three conditions. As such, Fan (1997) and Fan & Li (2001) introduced the smoothly clipped absolute deviation (SCAD) penalty, whose derivative is given by

$$p_{\lambda }^{\prime }(t)=\lambda \left\{I(t\le \lambda )+\frac{{(a\lambda -t)}_{+}}{(a-1)\lambda }I(t>\lambda )\right\}\text{\hspace{1em}for some}a>2,$$ (2.5)

where p_λ (0) = 0 and a = 3.7 is often used. It satisfies the aforementioned three properties and in particular, ameliorates the bias problems of convex penalty functions. A closely related minimax concave penalty (MCP) was proposed in Zhang (2010), whose derivative is given by

$$p_{\lambda }^{\prime }(t)={(a\lambda -t)}_{+}/a.$$ (2.6)

It is easy to see that the SCAD meets the L₁ penalty around the origin and then gradually levels off, and MCP translates the flat part of the derivative of SCAD to the origin. In particular, when a = 1,

$$p_{\lambda }(t)=\frac{1}{2}[{\lambda }^2-{(\lambda -t)}_{+}^2]$$ (2.7)

is called the hard-thresholding penalty by Fan & Li (2001) and Antoniadis (1996), who showed that the solution of (2.4) is the hard-thresholding estimator θ̂_H(z). Therefore, the MCP produces discontinuous solutions with potential of model instability.

2.2 Multivariate PLS

Consider the multivariate PLS problem (2.2) with general design matrix X. The goal is to estimate the true unknown sparse regression coefficients vector β₀ = (β_0,1, ⋯ , β_0,p)^T in linear model (2.1), where the dimensionality p can be comparable with or even greatly exceed the sample size n. The L₀ regularization naturally arises in many classical model selection methods, e.g., the AIC (Akaike (1973, 1974)) and BIC (Schwartz (1978)). It amounts to the best subset selection and has been shown to have nice sampling properties (see, e.g., Barron et al. (1999)). However, it is unrealistic to implement exhaustive search over the space of all submodels in even moderate dimensions, not to mention in high dimensional econometric endeavors. Such computational difficulty motivated various continuous relaxations of the discontinuous L₀ penalty. For example, the bridge regression (Frank & Friedman (1993)) uses the L_q penalty, 0 < q ≤ 2. In particular, the use of the L₂ penalty is called the ridge regression. The non-negative garrote was introduced in Breiman (1995) for variable selection and shrinkage estimation. The L₁ penalized least squares method was termed as Lasso in Tibshirani (1996), which is also collectively referred to as the L₁ penalization methods in other contexts. Other commonly used penalty functions include the SCAD (Fan & Li (2001)) and MCP (Zhang (2010)) (see Section 2.1). A family of concave penalties that bridge the L₀ and L₁ penalties was introduced in Lv & Fan (2009) for model selection and sparse recovery. A linear combination of L₁ and L₂ penalties was called an elastic net in Zou & Hastie (2005), with the L₂ component encouraging grouping of variables.

What kind of penalty functions are desirable for variable selection in sparse modeling? Some appealing properties of the regularized estimator were first outlined in Fan & Li (2001). They advocate penalty functions that give estimators with three properties mentioned in Section 2.1. In particular, they considered penalty functions p_λ(|θ|) that are nondecreasing in |θ|, and provided insights into these properties. As mentioned before, the SCAD penalty satisfies the above three properties, whereas the Lasso (the L₁ penalty) suffers from the bias issue.

Much effort has been devoted to developing algorithms for solving the PLS problem (2.2) when the penalty function p_λ is folded-concave, although it is generally challenging to obtain a global optimizer. Fan & Li (2001) proposed a unified and effective local quadratic approximation (LQA) algorithm by locally approximating the objective function by a quadratic function. This translates the nonconvex minimization problem into a sequence of convex minimization problems. Specifically, for a given initial value ${\mathit{\beta }}^{*}={({\beta }_1^{*},\cdots ,{\beta }_p^{*})}^T$, the penalty function p_λ can be locally approximated by a quadratic function as

$$p_{\lambda }(|{\beta }_j|)\approx p_{\lambda }(|{\beta }_j^{*}|)+\frac{1}{2}\frac{p_{\lambda }^{\prime }(|{\beta }_j^{*}|)}{|{\beta }_j^{*}|}[{\beta }_j^2-{({\beta }_j^{*})}^2]\text{\hspace{1em}for }{\beta }_j\approx {\beta }_j^{*}.$$ (2.8)

With quadratic approximation (2.8), the PLS problem (2.2) becomes a convex PLS problem with weighted L₂ penalty and (2.8) admits a closed-form solution. To avoid numerical instability, it sets the estimated coefficient β̂_j = 0 if ${\beta }_j^{*}$ is very close to 0, that is, deleting the j-th covariate from the final model. One potential issue of LQA is that the value 0 is an absorbing state in the sense that once a coefficient is set to zero, it remains zero in subsequent iterations. Recently, the local linear approximation (LLA)

$$p_{\lambda }(|{\beta }_j|)\approx p_{\lambda }(|{\beta }_j^{*}|)+p_{\lambda }^{\prime }(|{\beta }_j^{*}|)(|{\beta }_j|-|{\beta }_j^{*}|)\text{\hspace{1em}for }{\beta }_j\approx {\beta }_j^{*}.$$ (2.9)

was introduced in Zou & Li (2008), after the LARS algorithm (Efron et al. (2004)) was proposed to efficiently compute LASSO. Both LLA and LQA are convex majorats of concave penalty function p_λ (·) on [0, ∞), but LLA is a better approximation since it is the minimum (tightest) convex majorant of concave function on [0, ∞). For both approximations, the resulting sequence of target values is always nonincreasing, which is a specific feature of minorization-maximization (MM) algorithms (Hunter & Lange (2000)) and Hunter & Li (2005).. This can easily be seen by the following argument. If at the kth iteration L_k(β) is a convex majorant of the target function Q(β) such that L_k(β_k) = Q(β_k) and β_k+1 minimizes L_k(β), then

$$Q({\mathit{\beta }}_{k+1})\le L_k({\mathit{\beta }}_{k+1})\le L_k({\mathit{\beta }}_k)=Q({\mathit{\beta }}_k).$$

For Lasso (L₁ PLS), there are powerful algorithms for convex optimization. For example, Osborne et al (2000) cast the L₁ PLS problem as a quadratic program. Efron et al. (2004) proposed a fast and efficient least angle regression (LARS) algorithm for variable selection, which, with a simple modification, produces the entire LASSO solution path {β̂(λ) : λ > 0}. It uses the fact that the LASSO solution path is piecewise linear in λ (see also Rosset & Zhu (2007) for more discussions on piecewise linearity of solution paths). The LARS algorithm starts with a sufficiently large λ which picks only one predictor that has the largest correlation with the response and decreases the λ value until the second variable is selected, at which the selected variables have the same absolute correlation with the current working residual as the first one, and so on. By the Karush-Kuhn-Tucker (KKT) conditions, a sign constraint is needed for obtaining the Lasso solution path. See Efron et al. (2004) for more details. Zhang (2010) extended the idea of LARS algorithm and introduced the PLUS algorithm for computing the PLS solution path when the penalty function p_λ(·) is a quadratic spline such as the SCAD and MCP.

With linear approximation (2.9), the PLS problem (2.2) becomes a PLS problem with weighted L₁ penalty, say, the weighted Lasso

$$\underset{\mathit{\beta }\in {\mathbf{R}}^p}{\text{min}}\left\{\frac{1}{2n}{\Vert \mathbf{y}-\mathbf{X}\mathit{\beta }\Vert }_2^2+{\displaystyle \sum _{j=1}^p{w}_j|{\beta }_j|}\right\},$$ (2.10)

where the weights are $w_j=p_{\lambda }^{\prime }(|{\beta }_j^{*}|)$. Thus algorithms for Lasso can easily be adapted to solve such problems. Different penalty functions give different weighting schemes, and in particular, Lasso gives a constant weighting scheme. In this sense, the nonconvex PLS can be regarded as an iteratively reweighted Lasso. The weight function is chosen adaptively to reduce the biases due to penalization. The adaptive Lasso proposed in Zou (2006) uses the weighting scheme $w_j={|{\beta }_j^{*}|}^{-\gamma }$ for some γ > 0. However, zero is an absorbing state. In contrast, penalty functions such as SCAD and MCP do not have such an undesirable property. In fact, if the initial estimate is zero, then w_j = λ and the resulting estimate is the Lasso estimate. Fan & Li (2001), Zou (2006), and Zou & Li (2008) suggested to use a consistent estimate such as the un-penalized estimator as the initial value, which implicitly assumes that p ≪ n. When dimensionality p exceeds n, it is not applicable. Fan & Lv (2008) recommended using ${\beta }_j^{*}=0$, which is equivalent to using the LASSO estimate as the initial estimate. The SCAD does not stop here. It further reduces the bias problem of LASSO by assigning an adaptive weighting scheme. Other possible initial values include estimators given by the stepwise addition fit or componentwise regression. They put forward the recommendation that only a few iterations are needed.

Coordinate optimization has also been widely used for solving regularization problems. For example, for the PLS problem (2.2), Fu (1998), Daubechies et al. (2004), and Wu & Lang (2008) proposed a coordinate descent algorithm that iteratively optimizes (2.2) one component at a time. Such algorithm can also be applied to solve other problems such as in Meier et al. (2008) for the group LASSO (Yuan & Lin (2006)), Friedman et al. (2008) for penalized precision matrix estimation, and Fan & Lv (2009) for penalized likelihood(see Section 4.1 for more details).

There have been many studies of the theoretical properties of PLS methods in the literature. We give here only a very brief sketch of the developments due to the space limitation. A more detailed account can be found in, e.g., Fan & Lv (2010). In a seminal paper, Fan & Li (2001) laid down the theoretical framework of nonconcave penalized likelihood and introduced the oracle property which means that the estimator enjoys the same sparsity as the oracle estimator with asymptotic probability one and attains an information bound mimicking that of the oracle estimator. Here the oracle estimator β̂^O means the infeasible estimator knowing the true subset S ahead of time, namely, the component ${\widehat{\mathit{\beta }}}_{S^c}^O=0$ and ${\widehat{\mathit{\beta }}}_S^O$ is the least-squares estimate using only the variables in S. They showed that for certain penalties, the resulting estimator possesses the oracle property in the classical framework of fixed dimensionality p. In particular, they showed that such conditions can be satisfied by SCAD, but not the Lasso, which suggests that the Lasso estimator generally does not have the oracle property. This has indeed been shown in Zou (2006) in the finite parameter setting. Fan & Peng (2004) later extended the results of Fan & Li (2001) to the diverging dimensional setting of p = o(n^1/5) or o(n^1/3). Recently, extensive efforts have been made to study the properties with NP-dimensionality.

Another L₁ regularization method that is related to Lasso is the Dantzig selector recently proposed by Candes & Tao (2007). It is defined as the solution to

$$\text{min}{\Vert \mathit{\beta }\Vert }_1\text{\hspace{1em}subject to\hspace{1em}}{\Vert n^{-1}{\mathbf{X}}^T(\mathbf{y}-\mathbf{X}\mathit{\beta })\Vert }_{\infty }\le \lambda ,$$ (2.11)

where λ ≥ 0 is a regularization parameter. Under the uniform uncertainty principle (UUP) on the design matrix X, which is a condition on the bounded condition number for all submatrices of X, they showed that, with large probability, the Dantzig selector β̂ mimics the risk of the oracle estimator up to a logarithmic factor log p, specifically

$${\Vert \widehat{\mathit{\beta }}-{\mathit{\beta }}_0\Vert }_2\le C\sqrt{(2\text{ log }p)/n}{({\sigma }^2+{\displaystyle {\sum }_{j\in \text{supp}({\mathit{\beta }}_0)}}{\beta }_{0,j}^2\wedge {\sigma }^2)}^{1/2},$$ (2.12)

where β₀ = (β_0,1, ⋯ , β₀,_p)^T is the true regression coefficients vector, C > 0 is some constant, and $\lambda ~\sqrt{(2\text{ log }p)/n}$. The UUP condition can be stringent in high dimensions (see, e.g., Fan & Lv (2008) and Cai & Lv (2007) for more discussions). The oracle inequality (2.12) does not tell the sparsity of the estimate. In a seminal paper, Bickel et al. (2009) presented a simultaneous theoretical comparison of the LASSO and the Dantzig selector in a general high dimensional nonparametric regression model

$$\mathbf{y}=\mathbf{f}+\mathbf{\epsilon },$$ (2.13)

where f = (f(x₁), ⋯ , f(x_n)^T with f an unknown function of p-variates, and y, X = (x₁, ⋯ , x_n)^T, and ε are the same as in (2.1). Under a sparsity scenario, Bickel et al. (2009) derived parallel oracle inequalities for the prediction risk for both methods, and established the asymptotic equivalence of the LASSO estimator and the Dantzig selector. They also considered the specific case of linear model (2.1), i.e., (2.13) with true regression function f = Xβ₀, and gave bounds under the L_q estimation loss for 1 ≤ q ≤ 2.

For variable selection, we are concerned with the model selection consistency of regularization methods in addition to the estimation consistency under some loss. Zhao & Yu (2006) gave a characterization of the model selection consistency of the LASSO by studying a stronger but technically more convenient property of sign consistency: P(sgn(β̂) = sgn(β₀)) → 1 as n → ∞. They showed that the weak irrepresentable condition

$${\Vert {\mathbf{X}}_2^T{\mathbf{X}}_1{({\mathbf{X}}_1^T{\mathbf{X}}_1)}^{-1}\text{sgn}({\mathit{\beta }}_1)\Vert }_{\infty }<1$$ (2.14)

(assume covariates have been standardized) is a necessary condition for sign consistency of the LASSO, and the strong irrepresentable condition stating that the left-hand side of (2.14) is uniformly bounded by a constant 0 < C < 1, is a sufficient condition for sign consistency of the LASSO, where β₁ is the subvector of β₀ on its support supp(β₀), and X₁ and X₂ denote the submatrices of the n × p design matrix X formed by columns in supp(β₀) and its complement, respectively. However, the irrepresentable condition is very restrictive in high dimensions. It requires the L₁-norm of all regression coefficients of all variables in X₂ regressed on X₁ bounded by 1. See, e.g., Lv & Fan (2009) and Fan & Song (2010) for a simple illustrative example. This demonstrates that in high dimensions, the LASSO estimator can easily select an inconsistent model, which explains why the LASSO tends to include many false positive variables in the selected model. The latter is also related to the bias problem in Lasso, which requires a small penalization λ whereas the sparsity requires choosing a large λ.

Three questions of interest naturally arise for regularization methods. What limits of the dimensionality can PLS methods handle? What is the role of penalty functions? What are the statistical properties of PLS methods when the penalty function p_λ is no longer convex? As mentioned before, Fan & Li (2001) and Fan & Peng (2004) provided answers via the framework of oracle property for fixed or relatively slowly growing dimensionality p. Recently, Lv & Fan (2009) introduced the weak oracle property, which means that the estimator enjoys the same sparsity as the oracle estimator with asymptotic probability one and has consistency, and established regularity conditions under which the PLS estimator given by folded-concave penalties has nonasymptotic weak oracle property when the dimensionality p can grow non-polynomially with sample size n. They considered a wide class of concave penalties including SCAD and MCP, and the L₁ penalty at its boundary. In particular, their results show that concave penalties can be more advantageous than convex penalties in high dimensional variable selection. Later, Fan & Lv (2009) extended the results of Lv & Fan (2009) to folded-concave penalized likelihood in generalized linear models with ultra-high dimensionality. Fan & Lv (2009) also characterized the global optimality of the regularized estimator. See, e.g., Kim et al. (2008) and Kim & Kwon (2009), who showed that the SCAD estimator equals the oracle estimator with probability tending to 1. Other work on PLS methods includes Donoho et al. (2006), Meinshausen & Bühlmann (2006), Wainwright (2006), Huang et al. (2008), Koltchinskii (2008), and Zhang (2010), among many others.

2.3 Multivariate Time Series

High-dimensionality arises easily from vector AR models. A p-dimensional time series with d lags gives dp² autoregressive parameters. As an illustration, we focus on an application of PLS to home price estimation and forecasting.

The study of housing market and its relation to broader macroeconomic environment has received considerable interest, especially during the past decade. The empirical relationship between property price and income, interest rate, unemployment, size of labor force, and other variables are widely examined. Iacoviello & Neri (2010) report strong effect of monetary policy on house prices in the more recent periods using a DSGE model. Leamer (2007) noted the importance of housing sector in U.S. business cycles. Bernanke (2010) argues direct linkage between accommodative fed policy rate and home price appreciation is weak, though they coexisted during 2001–2006. Instead, exotic mortgages and deteriorating lending standards contributed much more to the housing bubble.

Forecasting housing prices locally is important, because price dynamics over regions, states, counties, ZIPs behave quite differently, especially for the past two decades. First, prices in the “bubble” states, such as California, Florida and Arizona, experience more appreciation during the booming period of 2001–2006 than other states, and subsequently much more decline during 2007–2009. For some non-bubble states, e.g. northeast states like Massachusetts and New Jersey experience solid price increase during boom, but only moderate decline afterwards, whereas Texas and Ohio have calm markets throughout the period. Second, the seasonality variation across states are different. In all northeast and west coast states, seasonality is pronounced, whereas in most southern states and southwestern inland states, such as NV and AZ, the seasonality amplitude is weak. Most econometric analysis on housing market is based on state-level panel data. Calomiris et al. (2008) performs panel VAR regression to reveal the strong effect of foreclosure on home prices. Stock & Watson (2008) use a dynamic factor model with stochastic volatility to examine the link between housing construction and the decline in macro volatility since mid-1980s. Rapach & Strass (2007) consider combination of individual VAR forecasts, with each equation consisting of only one macroeconomic variable, in forecasting home price growth in several states. Ng & Moench (2010) perform a hierarchical factor model consisting of regions and states to draw a linkage between housing and consumption.

An issue of factor models in forecasting local housing prices is that it cannot explicitly model cross-sectional correlation. For example, to predict the home price appreciation (HPA) in Nevada, the 2-factor equation contains only a national factor component and a state-specific component. It does not include house prices in California and Arizona, both of which can also provide predicting power. In finer scales such as county and ZIP level, local effect can be more pronounced and heterogeneous. For instance, suburbs are sensitive to price changes in city centers, but not vise versa. In a sense, lags variables of other equations may contribute additional predicting power even conditioning on national or aggregated state factors.

Adding neighborhoods variables into regression equation results the problem of high-dimensionality, and standard regression techniques often fail to estimate. Let $y_t^i$ be the HPA in county i, an s-period ahead county-level forecast model writes

$$y_{t+s}^i={\displaystyle \sum _{j=1}^p{b}_{ij}{y}_t^j+{\mathbf{X}}_t{\mathit{\beta }}_i+{\epsilon }_{t+s}^i,i=1,\cdots ,p,}$$

where X_t are observable factors, $y_t^j$ are the HPA of other counties, and b_ij and β_i are regression coefficients. Since p is large (around 1000 counties in US), such model cannot be estimated by OLS simply because of not long enough time series. On the other hand, we expect that conditional on national factors, only a small number of counties are useful for prediction, which gives rises to the notion of sparsity. Penalized least-squares can be used to estimate b_ij and obtain sparse solutions (and hence neighborhood selection) at the same time. A simple solution is to minimize for each given target region i the following object:

$${\text{min}}_{\{b_{ij},j=1,\cdots ,N,{\mathit{\beta }}_i\}}{\displaystyle \sum _{t=1}^{T-s}{\left(y_{t+s}^i-{\mathbf{X}}_t^i{\mathit{\beta }}_i-{\displaystyle \sum _{j=1}^N{b}_{ij}{y}_t^j}\right)}^2+\lambda {\displaystyle \sum _{j=1}^N{w}_{ij}{p}_{\lambda }(|b_{ij}|),}}$$

where the weights w_ij are chosen according to the geographical distances between counties i and j. Counties far away from the target county receive larger penalty, and the lag variable of target county gets zero penalization and will be included in the estimated equation. This choice of penalty reflects the intuition that if two counties are far away, their correlation is more naturally explained by national factors, which are already included in X.

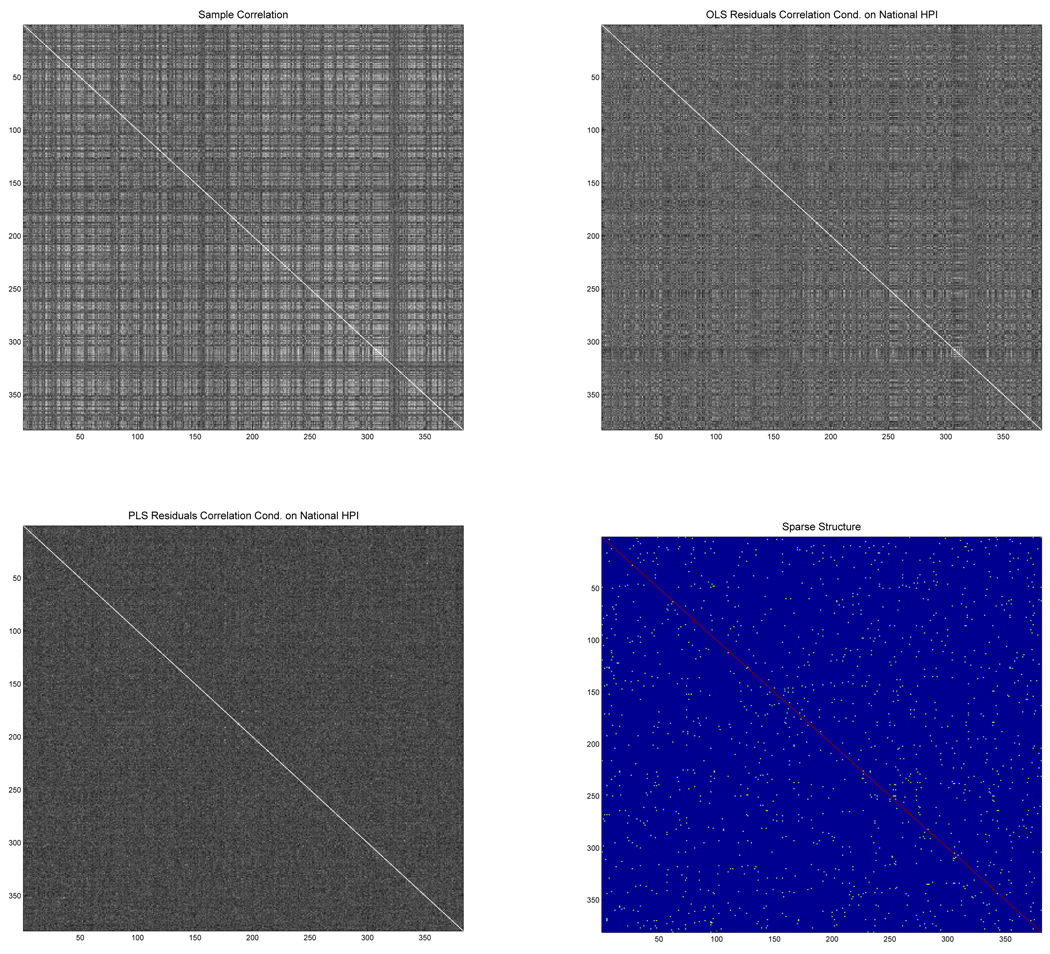
We use monthly HPA data in 352 largest counties of US in terms of monthly repeated sales from January 2000 to December 2009 to fit the model. The measurements of HPAs are more reliable for those counties. As an illustration, the market factor is chosen to be national HPA. Therefore it is a reduced-form forecasting model of county level HPA, taking national HPA forecast as an input. Figure 1 shows how cross-county correlation is captured by a sparse VAR. The top-left panel is the sample correlation of 352 HPA data series, showing heavy spatial-correlation. Top-right panel depicts the residual correlation of an OLS using only the national factor, without using neighboring HPAs. While spatial-correlation is reduced significantly in the residuals, the national factor can not fully capture the local dependence. The bottom left panel shows correlations of residuals using penalized least-squares after considering neighborhood effects. The residual correlations look essentially white noise, indicating that the national HPA along with the neighborhood selection captures the cross-dependence of regional HPAs. Bottom-right panel highlights the selected neighborhood variables. For each county, only 3–4 neighboring counties are chosen on average. The model achieves both parsimony and in-sample estimation accuracy.

Figure 1.

Top left: Spatial-correlation of HPAs. Top right: Spatial-correlation of residuals using only national HPA as the predictor. Bottom left: Spatial-correlation of residuals with national HPA and neighborhood selection. Bottom right: Neighborhoods with non-zero regression coefficients.

The sparse cross-sectional modeling translates into more forecasting power. This is illustrated by an out-of-sample test. Periods 2000.1–2005.12 are now used as training sample, and 2006.1–2009.12 are testing periods. We propose the following scheme to carry out prediction throughout next 3 years. For the short-term prediction horizons s from 1 to 6 months, each month is predicted separately using a sparse VAR with only lag s variables. For moderate time horizon of 7–36 months, we forecast only the average HPA over 6 months, instead of individual months, due to stability concerns. We use discounted aggregated squared error as a measure of overall performance for each county:

$${\text{Forecast Error}}_i={\displaystyle \sum _{s=1}^{\tau }{\rho }^s{({\widehat{y}}_{T+s}^i-y_{T+s}^i)}^2,\rho =0.95.}$$

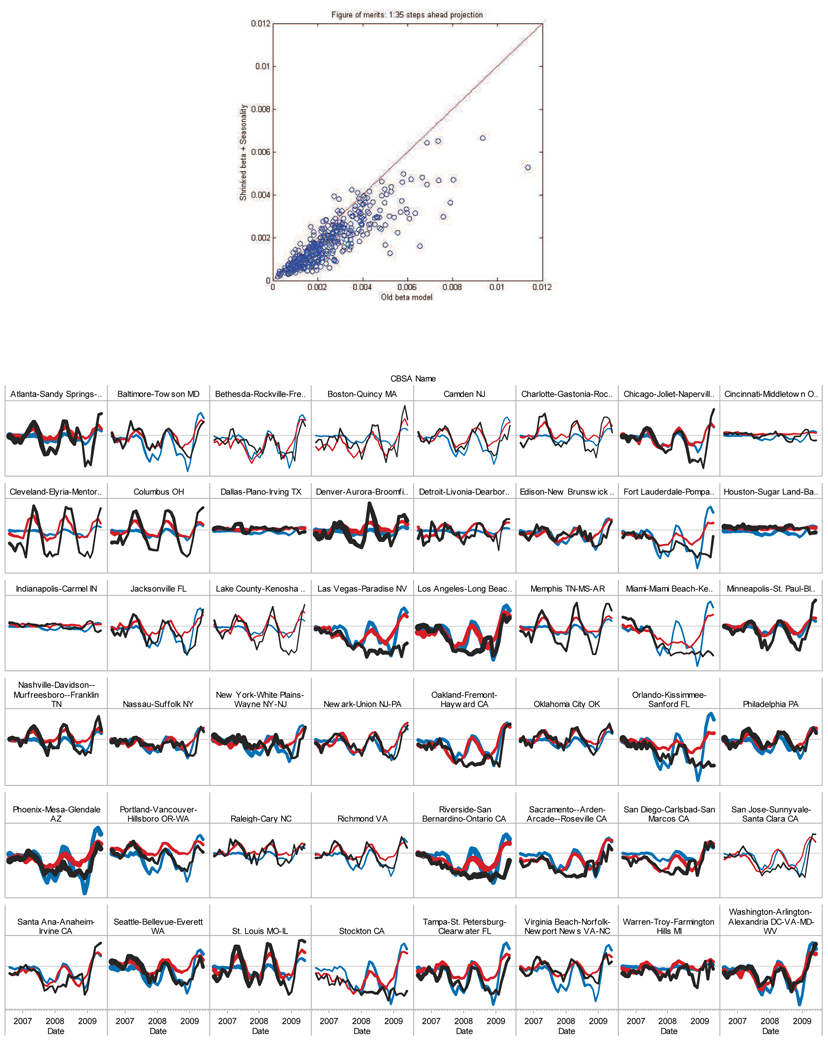
The results shows that over 352 counties, the sparse VAR with neighborhood information performs on average 30% better in terms of prediction error than the model without using the neighborhood information. Details of improvements are seen from the top panel of Figure 2. The bottom panel compares backtest forecasts using OLS with only the national HPA (blue) and PLS with additional neighborhood information (red) for the largest counties with the historical HPAs (black).

Figure 2.

Top: Forecast error comparison over 352 counties. For each dot, the x-axis represents error by OLS with only national factor, y-axis error by PLS with additional neighborhood information. If the dot lies below the 45 degree line, PLS outperforms OLS. Bottom: Forecast comparison for the largest counties during test period. Blue: OLS. Red: PLS. Black: Acutal. Thickness: Proportion to repeated sales.

2.4 Benchmark of Prediction Errors and Spurious Correlation

How good is a prediction method? The ideal prediction is to use the true model and the residual variance σ² provides a benchmark measure of prediction errors. However, in high dimensional econometrics problems, as mentioned in Section 1.3, the spurious correlations among realized random variables are high and some predictors can easily be selected to predict the realized noise vector. Therefore, the residual variance can substantially underestimate σ², since the realized noises can be predicted well by these predictors. Specifically, let 𝒮̂ and 𝒮₀ be the sets of selected and true variables, respectively. Fan et al. (2010) argued that the variables in $\widehat{𝒮}\cap {𝒮}_0^c$ are used to predict the realized noise. As a result, in the linear model (2.1), the residual sum of squares substantially underestimates the error variance. Thus it is important and necessary to screen variables that are not truly related to the response and reduce their influences.

One effective way of handling spurious correlations and their influence is to use the refitted cross-validation (RCV) proposed by Fan et al. (2010). The sample is randomly split into two equal halves, and a variable selection procedure is applied to both subsamples. For each subsample, a variance estimate is obtained by regressing the response on the set of predictors selected based on the other subsample. The average of those two estimates gives a new variance estimate. Specifically, let Ŝ₁ be the selected variables using the first half of the data, then refit the regression coefficients of variables in Ŝ₁ using the second half data and compute the residual variance ${\widehat{\sigma }}_1^2$. A similar estimate ${\widehat{\sigma }}_2^2$ can be obtained and the final estimate is simply ${\widehat{\sigma }}^2=({\widehat{\sigma }}_1^2+{\widehat{\sigma }}_2^2)/2$ or its weighted version using the degrees of freedom in the computation of two residual variances. Fan et al. (2010) showed that when the variable selection procedure has the sure screening property: S₀ ⊂ Ŝ₁ ∩Ŝ₂ (see Section 5.1 for more discussion), the resulting estimator can perform as well as the oracle variance estimator, which knows S₀ in advance. This is because that the probability that a spurious predictor has high correlation with the response in two independent samples is very small, and hence the spurious predictors in the first stage have little influence on the second stage of refitting. This idea of RCV can be applicable to the variance estimation and variable selection in more general high dimensional sparse models.

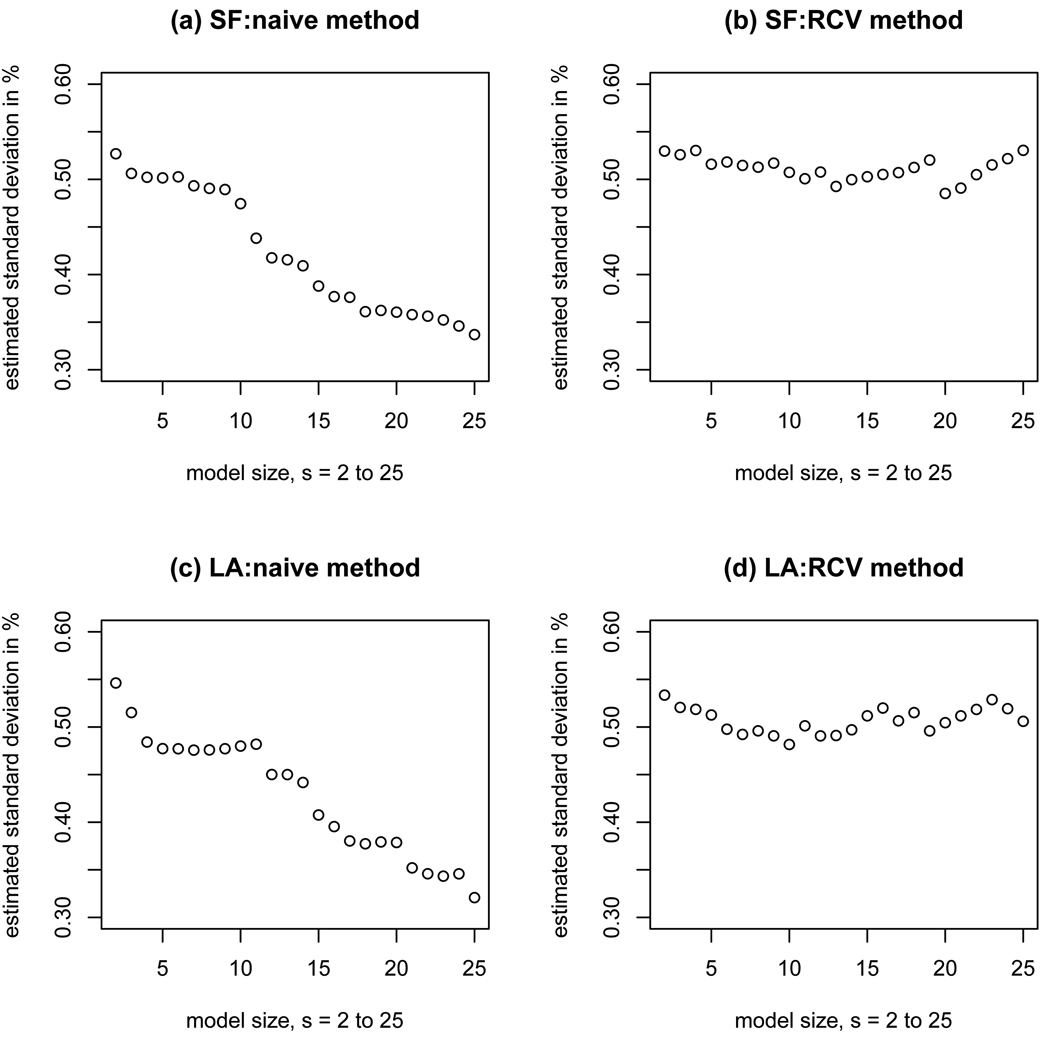
As an illustration, we consider the benchmark one-step forecasting errors σ² in San Francisco and Los Angeles, using the HPA data from January 1998 to December 2005 (96 months). Figure 3 shows the estimates as a function of the selected model size s. Clearly, the naive estimates of directly computing residual variances decrease steadily with the selected model size s due to spurious correlation, whereas the RCV gives reasonably stable estimates for a range of selected models. The benchmark for both regions are about .53%, whereas the standard deviations of month over month variations of HPAs are respectively 1.08% and 1.69% in San Francisco and Los Angeles areas. To see how penalized least-squares method works in comparison with the benchmark, we compute rolling one-step prediction errors over 12 months in 2006. The prediction errors are respectively .67% and .86% for San Francisco and Los Angeles areas, respectively. They are clearly larger than the benchmark as expected, but considerably smaller than the standard deviations, which use no variables to forecast.

Figure 3.

Estimated standard deviation as a function of selected model size s in both San Francisco (top panel) and Los Angeles (bottom panel) using both naive (left panel) and RCV (right panel) methods.

The penalized least-squares with SCAD penalty selects 7 predictors for both areas. National HPA and 1-month lag HPA for each area are selected in both equations. All other predictors are based in California, though the pool of regressors contains all county-level areas in United States. In Los Angeles equation, for example, other selected areas are: Ventura, Riverside-San Bernardino, Tuolumne, Napa, and San Diego. Among them Ventura, Riverside-San Bernardino and San Diego are southern California areas which are geographically adjacent/close to Los Angeles. Other two areas lie in Bay area/inner northern CA and are likely to be spurious predictors.

3 SPARSE MODELS IN FINANCE

In this section, we consider some further applications of PLS methods with focus on sparse models in finance.

3.1 Estimation of High-dimensional Volatility Matrix

Covariance matrix estimation is a fundamental problem in many areas of multivariate analysis. For example, an estimate of covariance matrix Σ is required in financial risk assessment and longitudinal studies, whereas an inverse of the covariance matrix, called the precision matrix Ω = Σ⁻¹, is needed in optimal portfolio selection, linear discriminant analysis, and graphical models. In particular, estimating a p × p covariance or precision matrix is very challenging when the number of variables p is large compared with the number of observations n as there are p(p + 1)/2 parameters in the covariance matrix that need to be estimated. The traditional covariance matrix estimator, the sample covariance matrix, is known to be unbiased and is invertible when p is no larger than n. The sample covariance matrix is a natural candidate when p is small, but it no longer performs well for moderate or large dimensionality (see, e.g., Lin & Perlman (1985) and Johnstone (2001)). Additional challenges arise when estimating the precision matrix when n < p.

To deal with high dimensionality, two main directions have been taken in the literature. One is to remedy the sample covariance matrix estimator using approaches such as eigen-method and shrinkage (see, e.g., Stein (1975) and Ledoit & Wolf (2004)). The other one is to impose some structure such as the sparsity, factor model, and autoregressive model on the data to reduce the dimensionality. See, for example, Wong et al. (2003), Huang et al. (2006), Yuan & Lin (2007), Bickel & Levina (2008a), Bickel & Levina (2008b), Fan et al. (2008), Bai & Ng (2008), Levina et al. (2008), Rothman et al. (2008), Lam & Fan (2009), and Cai et al. (2010). Various approaches have been taken to seek a balance between the bias and variance of covariance matrix estimators (see, e.g., Dempster (1972), Leonard & Hsu (1992), Chiu et al. (1996), Diggle & Verbyla (1998), Pourahmadi (2000), Boik (2002), Smith & Kohn (2002), and Wu & Pourahmadi (2003)).

The PLS and penalized likelihood (see Section 4.1) can also be used to estimate large scale covariances effectively and parsimoniously (see, e.g., Huang et al. (2006), Li & Gui (2006), Yuan & Lin (2007), Levina et al. (2008), and Lam & Fan (2009)). Assuming the covariance matrix has some sparse parametrization, the idea of variable selection can be used to select nonzero matrix parameters. Lam & Fan (2009) gave a comprehensive treatment on the sparse covariance matrix, sparse precision matrix, and sparse Cholesky decomposition.

The negative Gaussian pseudo-likelihood is

$$\text{tr}(\mathbf{S}\mathbf{\Omega })-\text{log}|\mathbf{\Omega }|,$$ (3.1)

where S is the sample covariance matrix. Therefore, the sparsity of the precision matrix can be explored by the penalized pseudo-likelihood

$$\text{tr}(\mathbf{S}\mathbf{\Omega })-\text{log}|\mathbf{\Omega }|+{\displaystyle \sum _{i\ne j}{p}_{\lambda }(|{\omega }_{i,j}|),}$$ (3.2)

penalizing only the off-diagonal elements ω_i,j of the precision matrix Ω, since the diagonal elements are non-sparse. This allows us to estimate the precision matrix even when p > n. Similarly, the sparsity of the covariance matrix can be explored by minimizing

$$\text{tr}(\mathbf{S}{\mathbf{\Sigma }}^{-1})+\text{log}|\mathbf{\Sigma }|+{\displaystyle \sum _{i\ne j}{p}_{\lambda }(|{\sigma }_{i,j}|),}$$ (3.3)

again penalizing only the off-diagonal elements σ_i,j of the covariance matrix Σ. Various algorithms have been developed for optimizing (3.2) and (3.3). See, for example, Friedman et al. (2008) and Fan et al. (2009). A comprehensive theoretical study of properties of these approaches has been given in Lam & Fan (2009). They showed that the rates of convergence for these problems under the Frobenius norm are of order (s log p/n)^1/2, where s is the number of nonzero elements. This demonstrates that the impact of dimensionality p is through a logarithmic factor. Their also studied the sparsistency of the estimates, which is a property that all zero parameters are estimated as zero with asymptotic probability one, and showed that the L₁ penalty is restrictive in that the number of nonzero off-diagonal elements s′ = O(p), whereas for fold-concave penalties such as SCAD and hard-thresholding penalty, there is no such a restriction.

Sparse Cholesky decomposition can be explored similarly. Let w = (W₁, ⋯ , W_p)^T be a p-dimensional random vector with mean zero and covariance matrix Σ. Using the modified Cholesky decomposition, we have LΣL^T = D, where L is a lower triangular matrix having diagonal elements 1 and off-diagonal elements −ϕ_t,j in the (t, j) entry for 1 ≤ j < t ≤ p, and $\mathbf{D}=\text{diag}\{{\sigma }_1^2,\cdots ,{\sigma }_p^2\}$ is a diagonal matrix. Denote by e = Lw = (e₁, ⋯ , e_p)^T. Since D is diagonal, e₁, ⋯ , e_p are uncorrelated. Thus, for each 2 ≤ t ≤ p,

$$W_t={\displaystyle \sum _{j=1}^{t-1}{\varphi }_{tj}{W}_j+e_t.}$$ (3.4)

This shows that the W_t is an autoregressive (AR) series, which gives an interpretation for elements of matrices L and D and enables us to use the PLS for covariance selection. Suppose that w_i = (W_i1, ⋯ , W_ip)^T, i = 1, ⋯ , n, is a random sample from w. For t = 2, ⋯ , p, covariance selection can be accomplished by solving the following PLS problems:

$$\underset{{\varphi }_{tj}}{\text{min}}\{\frac{1}{2n}{\displaystyle \sum _{i=1}^n}{(W_{it}-{\displaystyle \sum _{j=1}^{t-1}}{\varphi }_{tj}{W}_{ij})}^2+{\displaystyle \sum _{j=1}^{t-1}{p}_{{\lambda }_t}(|{\varphi }_{tj}}|)\}.$$ (3.5)

With estimated sparse L, the diagonal elements can be estimated by the sample variance of the components of L̂w_i. Hence, the sparsity of loadings in (3.4) is explored.

When the covariance matrix Σ admits sparsity structure, other simple methods can be exploited. Bickel & Levina (2008b) and El Karoui (2008) considered the approach of directly applying entrywise hard thresholding on the sample covariance matrix. The thresholded estimator has been shown to be consistent under the operator norm, where the former considered the case of (log p)/n → 0 and the latter considered the case of p ~ cn. The optimal rates of convergence of such covariance matrix estimation were derived in Cai et al. (2010). Bickel & Levina (2008a) studied the methods of banding the sample covariance matrix and banding the inverse of the covariance via the Cholesky decomposition of the inverse for the estimation of Σ and Σ⁻¹, respectively. These estimates have been shown to be consistent under the operator norm for (log p)²/n → 0, and explicit rates of convergence were obtained. Meinshausen & Bühlmann (2006) proved that Lasso is consistent in neighborhood selection in high dimensional Gaussian graphical models, where the sparsity in the inverse covariance matrix Σ⁻¹ amounts to the conditional independency between the variables.

3.2 Portfolio Selection

Markowitz (1952, 1959) laid down the seminal framework of mean-variance analysis. In practice, a simple implementation is to construct the mean-variance efficient portfolio using sample means and sample covariances matrix. However, due to accumulation of estimation errors, the theoretical optimal allocation vector can be very different from the estimated one, especially when the number of assets under consideration is large. As a result, such portfolios often suffer poor out-of-sample performance, although they are optimal in-sample. Recently a number of works focus on improving the performance of Markowitz portfolio using various regularization and stabilization techniques. Jagannathan & Ma (2003) consider the minimum variance portfolio with no short sale constraints: They show that such a constrained minimum variance portfolio outperforms the global minimum variance portfolio in practice when unknown quantities are estimated. They try to explain the puzzle why no short-sale constraints help. To bridge the no-short constraints on one extreme and no constraints on short sales on the other extreme, Fan et al. (2008) introduce a gross-exposure parameter c and examine the impact of c on the performance of the minimum portfolio. They show that with gross-exposure constraint the empirically selected optimal portfolios based on estimated covariance matrices have similar performance to the theoretical optimal portfolios, and there is little error accumulation effect from estimation of vast covariance matrices when c is modest.

The portfolio optimization problem is

$$\begin{array}{r}\hfill {\text{max}}_{\mathbf{w}}{\mathbf{w}}^T\mathbf{\Sigma }\mathbf{w}\\ \hfill s.t.{\mathbf{w}}^T\mathbf{1}=1,{\Vert \mathbf{w}\Vert }_1\le c,\mathbf{A}\mathbf{w}=\mathbf{a},\end{array}$$

where Σ is the true covariance matrix. The side constraints Aw = a can be on the expected returns of the portfolio, as in the Markowitz (1952, 1959) formulation. They can also be the constraints on the allocations on sectors or industries, or the constraints on the risk exposures to certain known risk factors. They make the portfolio even more stable. Therefore, they can be removed from theoretical studies. Let

$$R(\mathbf{w})={\mathbf{w}}^T\mathbf{\Sigma }\mathbf{w}\text{\hspace{1em}and\hspace{1em}}{R}_n(\mathbf{w})={\mathbf{w}}^T\widehat{\mathbf{\Sigma }}\mathbf{w}$$

be the theoretical and empirical portfolio risk with allocation w, where Σ̂ is an estimator of covariance matrix with sample size n. Let

$${\mathbf{w}}_{\mathit{\text{opt}}}={\text{argmin}}_{{\mathbf{w}}^T\mathbf{1}=1,{\Vert \mathbf{w}\Vert }_1\le c}R(\mathbf{w})\text{\hspace{1em}and\hspace{1em}}{\widehat{\mathbf{w}}}_{opt}={\text{argmin}}_{{\mathbf{w}}^T\mathbf{1}=1,{\Vert \mathbf{w}\Vert }_1\le c}{R}_n(\mathbf{w}).$$

The following theorem shows the theoretical minimum risk R(w_opt) (also called the oracle risk), the actual risk R(ŵ_opt) and empirical risk R_n(ŵ_opt) are approximately the same for a moderate c and a reasonable covariance matrix estimator.

Theorem 1 Let a_n = ‖Σ̂ − Σ‖_∞. Then, we have

$$\begin{array}{l}|R({\widehat{\mathbf{w}}}_{opt})-R({\mathbf{w}}_{opt})|\le 2a_n{c}^2,\hfill \\ |R({\widehat{\mathbf{w}}}_{opt})-R_n({\widehat{\mathbf{w}}}_{opt})|\le a_n{c}^2,\hfill \\ |R({\mathbf{w}}_{opt})-R_n({\widehat{\mathbf{w}}}_{opt})|\le a_n{c}^2.\hfill \end{array}$$

Theorem 1, due to Fan et al. (2008), gives the upper bounds on the approximation errors of risks. The following result further controls a_n.

Theorem 2 Let σ_ij and σ̂_ij be the (i, j)th element of the matrices Σ and Σ̂, respectively. If for a sufficiently large x,

$$\underset{i,j}{\text{max}}P\{\sqrt{n}|{\sigma }_{ij}-{\widehat{\sigma }}_{ij}|>x\}<\text{exp}(-C{x}^{1/a})$$

for two positive constants a and C, then

$${\Vert \mathbf{\Sigma }-\widehat{\mathbf{\Sigma }}\Vert }_{\infty }=O_P\left(\frac{{(\text{ log }p)}^a}{\sqrt{n}}\right).$$ (3.6)

Fan et al. (2008) give further elementary conditions under which Theorem 2 holds. The connection between portfolio minimization with gross exposure constraint and L₁ constrained regression problem enables fast statistical algorithms. The paper uses least-angle regression, or LARS-LASSO algorithm to solve for optimal portfolio under various gross exposure limits c. When c = 1, it is equivalent to no short sale constraint; as c increases the constraint becomes less stringent and becomes the global minimum variance problem when c = ∞. Empirical studies find when c is around 2 the portfolio achieves best out of sample performance in terms of variance and Sharpe ratio, when low-frequency daily data are used.

Another important feature of gross exposure constraint is that it yields sparse portfolio selection, meaning that there are only a fraction of active positions, while most other assets receive exactly zero position. This greatly reduces transaction cost, research and tracking cost. This feature is also noted in Brodie et al. (2009). DeMiguel et al. (2009) consider other norms to constrain portfolio; Carrasco & Noumon (2010) propose generalized cross-validation to optimize the regularization parameters.

3.3 Factor Models

In Section 3.1, we discussed large covariance matrix estimation via penalization methods. In this section, we focus on a different approach of using a factor model, which provides an effective way of sparse modeling. Consider the multi-factor model

$$Y_i=b_{i1}{f}_1+\cdots +b_{iK}{f}_K+\epsilon ,i=1,\cdots ,p,$$ (3.7)

where Y_i is the excess return of the i-th asset over the risk-free asset, f₁, ⋯ , f_K are the excess returns of K factors that influence the returns of the market, b_ij’s are unknown factor loadings, and ε₁, ⋯ , ε_p are idiosyncratic noises that are uncorrelated with the factors. The factor models have been widely applied and studied in economics and finance. See, e.g., Engle & Watson (1981), Chamberlain (1983), Chamberlain & Rothschild (1983), Bai (2003), and Stock & Watson (2005). Famous examples include the Fama-French three-factor model and five-factor model (Fama & French (1992, 1993)). Yet, the use of factor models on volatility matrix estimation for portfolio allocation was poorly understood until the work of Fan et al. (2008).

Thanks to the multi-factor model (3.7), if a few factors can completely capture the cross-sectional risks, the number of parameters in covariance matrix estimation can be significantly reduced. For example, using the Fama-French three-factor model, there are 4p instead of p(p + 1)/2 parameters. Despite the popularity of factor models in the literature, the impact of dimensionality on the estimation errors of covariance matrices and its applications to optimal portfolio allocation and portfolio risk assessment were not well studied until recently. As is now common in many applications, the number of variables p can be large compared to the size n of available sample. It is also necessary to study the situation where the number of factors K diverges, which makes the K-factor model (3.7) better approximate the true underlying model as K grows. Thus, it is important to study the factor model (3.7) in the asymptotic framework of p → ∞ and K → ∞.

Rewrite the factor model (3.7) in matrix form

$$\mathbf{y}=\mathbf{B}\mathbf{f}+\mathbf{\epsilon },$$ (3.8)

where y = (Y₁, ⋯ , Y_p)^T, B = (b₁, ⋯ , b_p)^T with b_i = (b_i1, ⋯ , b_iK)^T, f = (f₁, ⋯ , f_K)^T, and ε = (ε₁, ⋯ , ε_p)^T. Denote by Σ = cov(y), X = (f₁, ⋯ , f_n), and Y = (y₁, ⋯ , y_n), where (f₁, y₁), ⋯ , (f_n, y_n) are n i.i.d. samples of (f, y). Fan et al. (2008) proposed a substitution estimator for Σ,

$$\widehat{\mathbf{\Sigma }}=\widehat{\mathbf{B}}\widehat{\text{cov}}(\mathbf{f}){\widehat{\mathbf{B}}}^T+{\widehat{\mathbf{\Sigma }}}_0,$$ (3.9)

where B̂ = YX^T(XX^T)⁻¹ is the matrix of estimated regression coefficients, $\widehat{\text{cov}}(\mathbf{f})$ is the sample covariance matrix of the factors f, and Σ̂₀ = diag(n⁻¹ÊÊ^T) is the diagonal matrix of n⁻¹ÊÊ^T with Ê = Y–B̂X the matrix of residuals. With true factor structure, the substitution estimator Σ̂ is expected to perform better than the sample covariance matrix estimator Σ̂_sam. They derived the rates of convergence of the factor-model based covariance matrix estimator Σ̂ and the sample covariance matrix estimator Σ̂_sam simultaneously under the Frobenius norm ‖ · ‖ and a new norm ‖ · ‖_Σ, where ‖A‖_Σ = p^−1/2 ‖Σ^−1/2AΣ^−1/2‖ for any p × p matrix A. This new norm was introduced to better understand the factor structure. In particular, they showed that Σ̂ has a faster convergence rate than Σ̂_sam under the new norm. The inverses of covariance matrices play an important role in many applications such as optimal portfolio allocation. Fan et al. (2008) also compared the convergence rates of Σ̂⁻¹ and ${\widehat{\mathbf{\Sigma }}}_{\text{sam}}^{-1}$, which illustrates the advantage of using the factor model. Furthermore, they investigated the impacts of covariance matrix estimation on some applications such as optimal portfolio allocation and portfolio risk assessment. They identified how large p and K can be such that the error in the estimated covariance is negligible in those applications. Explicit convergence rates of various portfolio variances were established.

In many applications, the factors are usually unknown to us. So it is important to study the factor models with unknown factors for the purpose of covariance matrix estimation. Constructing factors that influence the market itself is a high dimensional variable selection problem with massive amount of trading data. One can apply, e.g., the sparse principal component analysis (PCA) (see Johnstone & Lu (2004) and Zou et al. (2006)) to construct the unobservable factors. It is also practically important to consider dynamic factor models where the factor loadings as well as the distributions of the factors evolve over time. The heterogeneity of the observations is another important aspect that needs to be addressed.

4 LIKELIHOOD BASED SPARSE MODELS

Sparse models arise frequently in the likelihood based models. Penalization methods provide an effective approach to explore the sparsity. This section gives a brief overview on the recent development.

4.1 Penalized Likelihood

The ideas of the AIC (Akaike (1973, 1974)) and BIC (Schwartz (1978)) suggest a common framework for model selection: choose a parameter vector β that maximizes the penalized likelihood

$${\mathit{\ell }}_n(\mathit{\beta })-\lambda {\Vert \mathit{\beta }\Vert }_0,$$ (4.1)

where ℓ_n(β) is the log-likelihood function and λ ≥ 0 is a regularization parameter. The computational difficulty of the combinatorial optimization in (4.1) stimulated many continuous relaxations of the discontinuous L₀ penalty, leading to a generalized form of penalized likelihood

$$n^{-1}{\mathit{\ell }}_n(\mathit{\beta })-{\displaystyle \sum _{j=1}^p{p}_{\lambda }(|{\beta }_j|),}$$ (4.2)

where ℓ_n(β) is the log-likelihood function and p_λ(·) is a penalty function indexed by the regularization parameter λ ≥ 0 as in PLS (2.2). It produces sparse solution when λ is sufficiently large.

It is nontrivial to maximize the penalized likelihood (4.2) when the penalty function p_λ is folded concave. In such case, it is also generally difficult to study the global maximizer without the concavity of the objective function. As is common in the literature, the main attention of theory and implementations has been on local optimizers that have nice statistical properties. Many efficient algorithms have been proposed for optimizing nonconcave penalized likelihood when p_λ is a folded concave function. Fan & Li (2001) introduce the LQA algorithm by using the Newton-Raphson method and a quadratic approximation in (2.8) and Zou & Li (2008) propose the LLA algorithm by replacing the quadratic approximation with a linear approximation in (2.9). See Section 2.2 for more detailed discussions on those and other algorithms. Consider the SCAD as an example. The use of the trivial zero initial value for LLA gives exactly the Lasso estimate. In this sense, the folded-concave regularization methods such as SCAD and MCP can be regarded as iteratively reweighted Lasso.

Coordinate optimization has gained much interest recently for implementing regularization methods for high dimensional variable selection. It is fast to implement when the univariate optimization problem has an analytic solution, which is the case for many commonly used penalty functions such as Lasso, SCAD, and MCP. For example, Fan & Lv (2009) introduced the iterative coordinate ascent (ICA) algorithm, a path-following coordinate optimization algorithm, for maximizing the folded concave penalized likelihood (4.2) including PLS (2.2). It maximizes one coordinate at a time with successive displacements for the penalized likelihood (4.2) with regularization parameters λ in decreasing order. More specifically, for each coordinate within each iteration, it uses the second order approximation of ℓ_n(β) at the current p-vector along that coordinate and maximizes the univariate penalized quadratic approximation

$$\underset{\theta \in \mathbf{R}}{\text{max}}\left\{-\frac{1}{2}{(z-\theta )}^2-\mathrm{\Lambda }{p}_{\lambda }(|\theta |)\right\},$$ (4.3)

where Λ > 0. It updates each coordinate if the maximizer of the above univariate penalized quadratic approximation makes the penalized likelihood (4.2) strictly increasing. Thus the ICA algorithm enjoys the ascent property that the resulting sequence of values of the penalized likelihood is increasing for a fixed λ. Fan & Lv (2009) demonstrated that the coordinate optimization works equally well and efficiently for producing the entire solution paths for concave penalties.

A natural question is what the sampling properties of penalized likelihood estimation (4.2) are when the penalty function p_λ is not necessarily convex. Fan & Li (2001) studied the oracle properties of folded concave penalized likelihood estimators in the finite-dimensional setting, and Fan & Peng (2004) generalized their results to the relatively high dimensional setting of p = o(n^1/5) or o(n^1/3). Let ${\mathit{\beta }}_0={({\mathit{\beta }}_1^T,{\mathit{\beta }}_2^T)}^T$ be the true regression coefficients vector with β₁ and β₂ the subvectors of nonsparse and sparse elements, respectively, and s = ‖β₀‖₀. Denote by $\mathbf{\Sigma }=\text{diag}\{p_{\lambda }^{″}(|{\mathit{\beta }}_1|)\}$ and ${\overline{p}}_{\lambda }({\mathit{\beta }}_1)=\text{sgn}({\mathit{\beta }}_1)○p_{\lambda }^{\prime }(|{\mathit{\beta }}_1|)$, where ○ denotes the the Hadamard (componentwise) product. Under some regularity conditions, they showed that with probability tending to 1 as n → ∞, there exists a ${(n/p)}^{\frac{1}{2}}$ consistent local maximizer $\widehat{\mathit{\beta }}={({\widehat{\mathit{\beta }}}_1^T,{\widehat{\mathit{\beta }}}_2^T)}^T$ of (4.2) satisfying the following

1. (Sparsity) β̂₂ = 0;

2. (Asymptotic normality)

$$\sqrt{n}{\mathbf{A}}_n{\mathbf{I}}_1^{-1/2}({\mathbf{I}}_1+\mathbf{\Sigma })[{\widehat{\mathit{\beta }}}_1-{\mathit{\beta }}_1+{({\mathbf{I}}_1+\mathbf{\Sigma })}^{-1}{\overline{p}}_{\lambda }({\mathit{\beta }}_1)]\stackrel{𝓓}{\to }N(\mathbf{0},\mathbf{G}),$$ (4.4)

where A_n is a q × s matrix with ${\mathbf{A}}_n{\mathbf{A}}_n^T\to \mathbf{G}$, a q × q symmetric positive definite matrix, I₁ = I(β₁) is the Fisher information matrix knowing the true model supp(β₀), and β̂₁ is a subvector of β̂ formed by components in supp(β₀). In particular, the SCAD estimator performs as well as the oracle estimator knowing the true mode in advance, whereas the Lasso estimator generally does not since the technical conditions are incompatible.

A long-lasting question in the literature is whether the penalized likelihood methods possess the oracle property (Fan & Li (2001)) in ultra-high dimensions. Fan & Lv (2009) recently addressed this problem in the context of generalized linear models (GLMs) with NP-dimensionality: log p = O(n^a) for some a > 0. With a canonical link, the conditional distribution of y given X belongs to the canonical exponential family with the following density function

$$f_n(\mathbf{y};\mathbf{X},\mathit{\beta })\equiv {\displaystyle \prod _{i=1}^n{f}_0(y_i;{\theta }_i)={\displaystyle \prod _{i=1}^n\left\{c(y_i)\text{ exp }\left[\frac{y_i{\theta }_i-b({\theta }_i)}{\varphi }\right]\right\},}}$$ (4.5)

where β = (β₁, ⋯ , β_p)^T is an unknown p-dimensional vector of regression coefficients, {f₀(y; θ) : θ ∈ R} is a family of distributions in the regular exponential family with dispersion parameter ϕ ∈ (0, ∞), and (θ₁, ⋯ , θ_n)^T = Xβ. Well-known examples of GLMs include the linear, logistic, and Poisson regression models. They proved that under some regularity conditions, there exists a local maximizer $\widehat{\mathit{\beta }}={({\widehat{\mathit{\beta }}}_1^T,{\widehat{\mathit{\beta }}}_2^T)}^T$ of the penalized likelihood (4.2) such that β̂₂ = 0 with probability tending to 1 and ${\Vert \widehat{\mathit{\beta }}-{\mathit{\beta }}_0\Vert }_2=O_P(\sqrt{s}{n}^{-1/2})$, where β̂₁ is a subvector of β̂ formed by components in supp(β₀) and s = ‖β₀‖₀. They also established asymptotic normality and thus the oracle property. Their studies demonstrate that the technical conditions are less restrictive for folded concave penalties such as SCAD. A natural and important question is when the folded concave penalized likelihood estimator is a global maximizer of the penalized likelihood (4.2). Fan & Lv (2009) gave characterizations of such a property from two perspectives: global optimality (for p ≤ n) and restricted global optimality (for p > n). In addition, they showed that the SCAD penalized likelihood estimator can meet the oracle estimator under some regularity conditions. Other work on penalized likelihood methods includes Meier et al. (2008) and van de Geer (2008), among many others.

4.2 Penalized Partial Likelihood

Credit risk is a topic that has been extensively studied in finance and economics literature. Various models have been proposed for pricing and hedging credit risky securities. See Jarrow (2009) for a review of credit risk models. Cox (1972, 1975) introduced the famous Cox’s proportional hazards model

$$h(t|\mathbf{x})=h_0(t)e^{{\mathbf{x}}^T\mathit{\beta }}$$ (4.6)

to accommodate the effect of covariates in which h(t|x)is the conditional hazard rate at time t, h₀(t) is the baseline hazard function, and β = (β₁, ⋯ , β_p) is a p-dimensional regression coefficients vector. This model has been widely used in survival analysis for modeling the time-to-event data, in which censoring occurs because of the termination of the study. Such a model can naturally be applied to model credit default. Lando (1998) first addressed the issue of default correlation for pricing credit derivatives on baskets, e.g., collateralized debt obligation (CDO), by using the Cox processes. The default correlations are induced via common state variables that drive the default intensities. See Section 4 of Jarrow (2009) for more detailed discussions of the Cox model for credit default analysis.

Identifying important risk factors and quantifying their risk contributions are crucial aims of survival analysis. Thus variable selection in the Cox model is an important problem, particularly when the dimensionality of the feature space p is large compared to sample size n. It is natural to extend the regularization methods to the Cox model. Tibshirani (1997) introduced the Lasso method (L₁ penalization method) to this model. To overcome the bias issue of convex penalties, Fan & Li (2002) extended the nonconcave penalized likelihood in Fan & Li (2001) to the Cox model for variable selection. The idea is to use the partial likelihood introduced by Cox (1975). Let $t_1^0<t_2^0<\cdots <t_N^0$ be N ordered observed failure times (assuming no common failure times for simplicity). Denote by x_(k) the covariates vector of the subject with failure time $t_k^0$ and $R_k=\{i:y_i\ge t_k^0\}$ the risk set right before time $t_k^0$. Fan & Li (2002) considered the penalized partial likelihood

$$n^{-1}{\displaystyle \sum _{k=1}^N\left[{\mathbf{x}}_{(k)}^T\mathit{\beta }-\text{log}\left\{{\displaystyle \sum _{i\in R_k}\text{exp}({\mathbf{x}}_i^T\mathit{\beta })}\right\}\right]-{\displaystyle \sum _{j=1}^p{p}_{\lambda }(|{\beta }_j|).}}$$ (4.7)

They proved the oracle properties for folded concave penalized partial likelihood estimator. Later, Zhang & Lu (2007) introduced the adaptive Lasso for Cox’s proportional hazards model, and Zou (2008) proposed a path-based variable selection method by using penalization with adaptive shrinkage (Zou (2006)) for the same model, both of which papers have shown the asymptotic efficiency of the methods.

5 SURE SCREENING METHODS

Ultra-high dimensional modeling is a more common task than before due to the emergence of ultra-high dimensional data sets in many fields such as economics, finance, genomics and health studies. Existing variable selection methods can be computationally intensive and may not perform well — the conditions required for those methods are very stringent when the dimensionality is ultrahigh. How to develop effective procedures and what are their statistical properties?

5.1 Sure Independence Screening

A natural idea for ultra-high dimensional modeling is applying a fast, reliable, and efficient method to reduce the dimensionality p from a large or huge scale (say, log p = O(n^a) for some a > 0) to a relatively large scale d (e.g., O(n^b) for some b > 0) so that well-developed variable selection techniques can be applied to the reduced feature space. This powerful tool enables us to approach the problem of variable selection in ultrahigh dimensional sparse modeling. The issues of computational cost, statistical accuracy, and model interpretability will be addressed when the variable screening procedures retain all the important variables with asymptotic probability one, the so-called sure screening property introduced in Fan & Lv (2008).

Fan & Lv (2008) recently proposed the sure independence screening (SIS) methodology for reducing the computation in ultra-high dimensional sparse modeling, which has been shown to possess the sure screening property. It also reduces the correlation requirements among predictors. The SIS uses independence learning with the correlation ranking that ranks features by the magnitude of its sample correlation with the response variable. More generally, the independence screening means ranking features with marginal utility, i.e., each feature is treated as an independent predictor for measuring its effectiveness for prediction. Independence learning has been widely used in dealing with large-scale data sets. For example, Dudoit et al. (2003), Storey & Tibshirani (2003), Fan & Ren (2006), and Efron (2007) apply two-sample tests to select significant genes between the treatment and control groups in microarray data analysis.

Assume that the n × p design matrix X has been standardized to have mean zero and variance one for each column and let ω = (ω₁, ⋯ , ω_p)^T = X^T y be a p-dimensional vector of componentwise regression estimator. For each d_n, Fan & Lv (2008) defined the submodel consisting of selected predictors as

$${\widehat{ℳ}}_d=\{1\le j\le p:|{\omega }_j|\text{ is among the first }{d}_n\text{ largest of all}\}.$$ (5.1)

This reduces the dimensionality of the feature space from p ≫ n to a (much) smaller scale d_n, which can be below n. This correlation learning screens variables that have weak marginal correlations with the response and retains variables having stronger correlations with response. The correlation ranking amounts to selecting features by two-sample t-test statistics in classification problems with class labels Y = ±1 (see Fan & Fan (2008)). It is easy to see that SIS has computational complexity O(np) and thus is fast to implement. To better understand the rationale of SIS (correlation learning), Fan & Lv (2008) also introduced an iteratively thresholded ridge regression screener (ITRRS), which is an extension of the dimensionality reduction method SIS. ITRRS provides a very nice technical tool for understanding the sure screening property of SIS and other methods.

To demonstrate the sure screening property of SIS, Fan & Lv (2008) provided a set of regularity conditions. Denote by ℳ_* = {1 ≤ j ≤ p : β_j ≠ 0} the true underlying sparse model and s = |ℳ_*| the nonsparsity size. The other p – s noise variables are allowed be correlated with the response through links to the true predictors. Fan & Lv (2008) studied the ultra-high dimensional setting of p ≫ n with log p = O(n^a) for some a ∈ (0, 1 – 2κ) (see below for the definition of κ) and Gaussian noise ε ~ N(0, σ²). They assumed that var(Y) = O(1), and that λ_max(Σ) = O(n^τ),

$$\underset{j\in {ℳ}_{*}}{\text{min}}|{\beta }_j|\ge c{n}^{-\kappa }\text{\hspace{1em}and\hspace{1em}}\underset{j\in {ℳ}_{*}}{\text{min}}|\text{cov}({\beta }_j^{-1}Y,X_j)|\ge c,$$ (5.2)

in which Σ = cov(x), κ, τ ≥ 0, and c > 0 is a constant. One technical condition is that the p-dimensional covariates vector x has an elliptical distribution and the random matrix XΣ^−1/2 has a concentration property, which they proved to hold for Gaussian distributions. Under those regularity conditions, Fan & Lv (2008) showed that as long as 2κ + τ < 1, there exists constant θ ∈ (2κ + τ, 1) such that when d_n ~ n^θ, we have for some C > 0,

$$P({ℳ}_{*}\subset {\widehat{ℳ}}_d)=1-O(e^{-C{n}^{1-2\kappa }/\text{log}n}).$$ (5.3)

This shows that SIS has the sure screening property even in ultra-high dimensions. Such a property also entails the sparsity of the model: s ≤ d_n. With SIS, we can reduce exponentially growing dimensionality to a relatively large scale d_n ≪ n, while all the important variables are contained in the reduced model ℳ̂_d with a significant probability.

The above results have been extended by Fan & Song (2010) to cover non-Guassian covariates and/or non-Gaussian response. In the context of generalized linear models, they showed that independence screening by using marginal likelihood ratio or marginal regression coefficients possesses a sure screening property with the selected model size explicitly controlled. In particular, they do not impose elliptical symmetry of the distribution of covariates nor conditions on the covariance Σ of covariates. The latter is a huge advantage over the penalized likelihood method, which requires restrictive conditions on the covariates.

There are other related methods of marginal screening. Huang et al. (2008) introduced marginal bridge regression, Hall & Miller (2009) proposed a generalized correlation for feature ranking, and Fan et al. (2010) developed nonparametric screening using B-spline basis. All of these need to choose a thresholding parameter. Zhao & Li (2010) proposed using an upper quantile of marginal utilities for decoupled (via random permutation) responses and covariates, called PSIS, to select the thresholding parameter in the context of the Cox proportional hazards model. The idea is to randomly permute the covariates and response so that they have no relation and then to compute the marginal utilities based on the permuted data and to select the upper α quantile of the marginal utilities as the thresholding parameter. The choice of α is related to the false selection rate. A stringent screening procedure would take α = 0, namely, the maximum of the marginal utilities for the randomly decoupled data. Hall et al. (2009) presented independence learning rules by tilting methods and empirical likelihood, and proposed a bootstrap method for assessing the accuracy of feature ranking in classification.

5.2 A Two Scale Framework

When the dimensionality of the feature space is reduced to a moderate scale d with a sure screening method such as SIS, the well-developed variable selection techniques, e.g., the PLS and penalized likelihood methods, can be applied to the reduced feature space. This provides a powerful tool of SIS based variable selection methods for ultra-high dimensional variable selection. The sampling properties of such methods can easily be derived by combining the theory of SIS and those penalization methods. This suggests a two scale learning framework, that is, large scale screening followed by moderate scale selection.

By its nature, the SIS only uses the marginal information of predictors without looking at their joint behavior. Fan & Lv (2008) noticed three potential issues of the simple SIS that can make the sure screening property fail to hold when the technical assumptions are not satisfied. First, it may miss an important predictor that is marginally uncorrelated or very weakly correlated but jointly correlated with the response. Second, it may select some unimportant predictors that are highly correlated with the important predictors and exclude important predictors that are relatively weakly related to the response. Third, the issue of collinearity among predictors is an intrinsic difficulty of the variable selection problem. To address these issues, Fan & Lv (2008) proposed an iterative SIS (ISIS) which iteratively applies the idea of large-scale screening and moderate-scale selection. This idea was extended and improved by Fan et al. (2009) as follows.

Suppose that we wish to find a sparse β to minimize the objective

$$Q_n(\mathit{\beta })=n^{-1}{\displaystyle \sum _{i=1}^{n}L(Y_i,{\beta }_0+{\mathbf{X}}_i^T\mathit{\beta }),}$$ (5.4)

where L is the loss function which can be the quadratic loss, robust loss, log-likelihood, or quasi-likelihood. It is usually convex in β. The first step is to apply the marginal screening, using the marginal utilities

$$L_j=\underset{{\beta }_0,{\beta }_j}{\text{min}}{n}^{-1}{\displaystyle \sum _{i=1}^{n}L(Y_i,{\beta }_0+X_{i,j}{\beta }_j)}$$ (5.5)

or the magnitude |β̂_j| of the minimizer of (5.5) itself (assuming covariates are standardized in this case) to rank the covariates. This results in the active set 𝒜₁. The thresholding parameter can be selected by using the permutation method of Zhao & Li (2010) mentioned in Section 5.1. Now, apply a penalized likelihood method

$$n^{-1}{\displaystyle \sum _{i=1}^{n}L(Y_i,{\beta }_0+{\mathbf{X}}_{i,{𝒜}_1}^T{\mathit{\beta }}_{{𝒜}_1})+{\displaystyle \sum _{j\in {𝒜}_1}{p}_{\lambda }(|{\beta }_j|)}}$$ (5.6)

to further select a subset of active variables, resulting in ℳ₁. The next step is the conditional screening. Given the active set of covariates ℳ₁, what are the conditional contributions of those variables that were not selected in the first step? This leads to define the conditional marginal utilities:

$$L_{j|{ℳ}_1}=\underset{{\beta }_0,{\mathit{\beta }}_{{ℳ}_1},{\beta }_j}{\text{min}}{n}^{-1}{\displaystyle \sum _{i=1}^{n}L(Y_i,{\beta }_0}+{\mathbf{X}}_{i,{ℳ}_1}^T{\beta }_{{ℳ}_1}+X_{ij}{\beta }_j).$$ (5.7)

Note that for the quadratic loss, when β_ℳ1 is fixed at the minimizer from (5.6), such method reduces to the residual based approach in Fan & Lv (2008). The current approach avoids the generalization of the concept of residuals to other complicated models and uses fully the conditional inference, but it involves more intensive computation in the conditional screening. Recruit additional variables by using the marginal utilities L_j|ℳ1 or the magnitude of the minimizer (5.7). This is again a large-scale screening step giving an active set 𝒜₂ and the thresholding parameter can be chosen by the permutation method. The next step is then the moderate-scale selection. The potentially useful variables are now in the set ℳ₁ ∪ 𝒜₂. Apply the penalized likelihood technique to the problem:

$${\displaystyle \sum _{i=1}^n{n}^{-1}L(Y_i,{\beta }_0+{\mathbf{X}}_{i,{ℳ}_1}^T{\mathit{\beta }}_{{ℳ}_1}+{\mathbf{X}}_{i,{𝒜}_2}^T{\mathit{\beta }}_{{𝒜}_2})+{\displaystyle \sum _{j\in {ℳ}_1\cup {𝒜}_2}{p}_{\lambda }(|{\beta }_j|).}}$$ (5.8)

This results in the selected variables ℳ₂. Note that some variables selected in the previous step ℳ₁ can be deleted in this step. This is another improvement of the original idea of Fan & Lv (2008). Iterate the conditional large-scale screening followed by the moderate-scale selection until ℳ_ℓ−1 = ℳ_ℓ or the maximum number of iterations is reached. This takes account of the joint information of predictors in the selection and avoids solving large scale optimization problems. The success of such a two-scale method and its theoretial properties are documented in Fan & Lv (2008), Fan et al. (2009), Fan & Song (2010), Zhao & Li (2010) and Fan et al. (2010)

6 CONCLUSIONS

We have briefly surveyed some recent developments of sparse high dimensional modeling and discussed some applications in economics and finance. In particular, the recent developments in ultra-high dimensional variable selection can be widely applicable to statistical analysis of large-scale economic and financial problems. Those sparse modeling problems deserve further studies both theoretically and empirically. We have focused on regularization methods including penalized least squares and penalized likelihood. The role of penalty functions and the impact of dimensionality on high dimensional sparse modeling have been revealed and discussed. Sure independent screening has been introduced to reduce the dimensionality and the problems of collinearity. It is a fundamental element of the promising two-scale framework in ultrahigh dimensional econometrics modeling.

Sparse models are ideal and generally biased. Yet, they have been proved to be very effective in many large-scale applications. The biases are typically small since variables are selected from a large pool to best approximate the true model. High dimensional statistical learning facilitates undoubtedly the understanding and derivation of the often complex nature of statistical relationship among the explanatory variables and the response. In particular, the key notion of sparsity which helps reduce the intrinsic complexity at little cost of statistical efficiency and computation provides powerful tools to explore relatively low-dimensional structures among huge amount of candidate models. It expects to have huge impact on econometric theory and practice, from econometric modeling to fundamental understanding of economic problems. New novel modeling techniques are needed to address the challenges in the frontiers of economics and finance, and other social science problems.