2DIR spectroscopy of human amylin fibrils reflects stable β-sheet structure

Abstract

The aggregation of human amylin to form amyloid contributes to islet β-cell dysfunction in type 2 diabetes. Studies of amyloid formation have been hindered by the low structural resolution or relatively modest time resolution of standard methods. Two-dimensional infrared (2DIR) spectroscopy, with its sensitivity to protein secondary structures and its intrinsic fast time resolution, is capable of capturing structural changes during the aggregation process. Moreover, isotope labeling enables the measurement of residue-specific information. The diagonal line widths of 2DIR spectra contain information about dynamics and structural heterogeneity of the system. We illustrate the power of a combined atomistic molecular dynamics simulations and theoretical and experimental 2DIR approach by analyzing the variation in diagonal line widths of individual amide I modes in a series of labeled samples of amylin amyloid fibrils. The theoretical and experimental 2DIR line widths suggest a “W” pattern, as a function of residue number. We show that large line widths result from substantial structural disorder, and that this pattern is indicative of the stable secondary structure of the two β-sheet regions. This work provides a protocol for bridging MD simulation and 2DIR experiments for future aggregation studies.

Introduction

Amylin, also known as islet amyloid polypeptide or IAPP, is a 37-residue peptide cosecreted with insulin by the pancreatic β-cells. Amyloid plaques formed from human-IAPP (hIAPP) are commonly found in the islet cells of patients with type 2 diabetes.^1–4 The mechanism of amyloid formation and the molecular basis for cell death are not clear, in part because existing experimental methods are either low in structural resolution or have limited time resolution or both.

The sequence of hIAPP is shown in Figure 1. Amyloid fibrils formed from hIAPP adopt the classic cross-β structure, in which continuous β-strands run perpendicular to the fibril axis and form inter-strand hydrogen bonds that are aligned with the fibril axis.⁵ The hIAPP peptides form in-register parallel β-sheets, as revealed by electron paramagnetic resonance (EPR)⁶ and solid-state nuclear magnetic resonance (NMR) measurements.⁷ Based on solid-state NMR and scanning transmission electron microscopy (STEM) experiments, Tycko and coworkers propose that the protofilament, which is the elementary structure of the fibril, contains two columns of hIAPP monomers with C₂ rotational symmetry.⁷ The existing experimental data are not sufficient for an unambiguous protofilament structure. Instead, based on experimental constraints and molecular dynamics (MD) simulations, two possible structural models with two-fold symmetry are proposed, in which the protofilament consists of four layers of parallel β-strands with two symmetric columns of hIAPP molecules, as shown in Figure 2(a).⁷ The two models differ mainly in the side chain arrangements, and thus for example certain side-chain atoms that are buried in one model get exposed to solvent in the other. Their cross sections are shown in Figure 2(b) and 2(c), and we refer to them as models I and II in the following.

Fig. 1.

The primary sequences of hIAPP and rIAPP. Differences between the two are shown in red for rIAPP. Both peptides have an amidated C-terminus and a disulfide bond between residues 2 and 7.

Fig. 2.

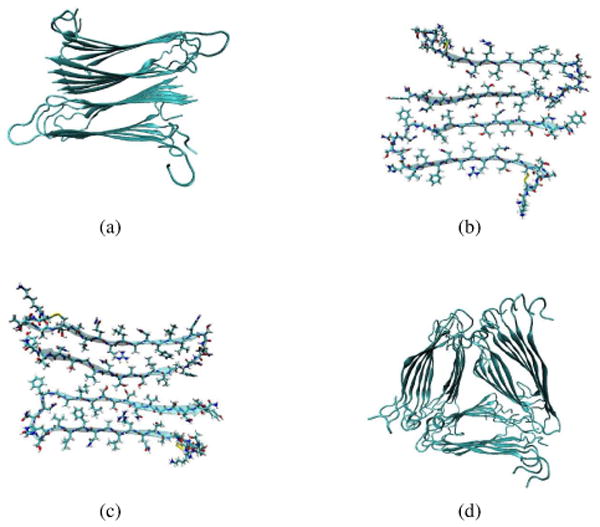
(a) The overall backbone arrangement of the two-fold protofilament structural models.⁷ (b) The cross section of the two-fold model I, which corresponds to the structure depicted in Figure 11C of reference 7. (c) The cross section of the two-fold model II, which corresponds to the structure depicted in Figure 11D of reference 7. (d) The overall backbone arrangement of the three-fold protofilament model.⁹² In each diagram, for each peptide the inner strand ends with the C-terminus (and the outer strand ends with the N-terminus).

There is increasing evidence that intermediates populated during the process of amyloid formation may be the most cytotoxic species, but the exact nature of these species is controversial.^8–14 Lipid membranes may play a role in this context, as they can greatly accelerate the formation of amyloid fibers in vitro, although it is not completely clear how these studies translate to aggregation in vivo.^12,15–18 Concomitantly, membranes can be disrupted during aggregation and membrane failure might be the origin of hIAPP toxicity.^8–14,19 Therefore, understanding the aggregation process of hIAPP both in the absence and presence of lipid membranes is of crucial importance to the understanding of hIAPP cytotoxicity.

A wide variety of experimental and theoretical techniques have been applied to the study of hIAPP aggregation.^{5–7,13,15–17,20–36} X-ray diffraction and solid-state NMR experiments have the capability to provide high-resolution structures.^{5,7,24,26,28,29} However, they lack the required time resolution to study aggregation kinetics. EPR, in conjunction with site-specific spin labeling techniques, has revealed structural information about the aggregation process,^6,25 but the bulky spin label necessarily perturbs the system, and in the case of hIAPP, the necessity of attaching the spin labels via a Cys mutation has meant that the native disulfide bond is replaced with a pair of Ala residues. Optical techniques such as circular dichroism (CD) and fluorescence spectroscopy are able to monitor the in-situ aggregation kinetics,^{13,15–17,20–23,33} although they provide low structural resolution.

Infrared (IR) spectroscopy is a powerful tool for studying the structure and dynamics of the aggregation process. It is readily applicable to small amounts of sample in a variety of conditions, such as in aqueous solution and lipid membranes. IR experiments on peptides usually focus on the amide I band, which shows distinct spectral features for different protein secondary structures.^37–39 Recent development of time-resolved two-dimensional IR (2DIR) spectroscopy enables sub-picosecond time resolution, and provides detailed information on correlations between chromophores.^40–53 Moreover, residue-specific information can be revealed by the use of isotope labeling techniques.^{48,51,52,54–64} For example, labeling a particular carbonyl with ¹³C and ¹⁸O lowers its frequency by ∼70 cm⁻¹ and spectrally isolates it from the rest of the peptide signal.^{46–52,55,56,59,61} Since isotope-labeling simply replaces an atom with its isotope, it has a minimal perturbation to the system.

In this work we describe a study of the structure and dynamics of hIAPP fibrils by means of theoretical and experimental 2DIR spectroscopy, combined with atomistic molecular dynamics (MD) simulations. MD simulations show that model I is more stable than model II. 2DIR spectra for each residue in model I are calculated, from which properties such as peak positions and diagonal line widths are extracted. Using our recently improved backbone and side-chain frequency maps,⁶⁵ we were able to achieve good agreement between theory and experiments, validating both the Tycko model⁷ and our theoretical approach for 2DIR calculations. The line widths suggest a “W” pattern, as a function of residue number, which results from different structural stabilities within the fibril. Small line widths in the two β-sheet regions reveal that they are very stable, which indicates that they are potential targets for drugs designed to inhibit amyloid formation.

Materials and Methods

A. MD Simulations

Naturally occurring hIAPP contains a disulfide bridge between Cys2 and Cys7 and an amidated C-terminus (see Figure 1).⁶⁶ The coordinate files of models I and II were generously provided by Dr. Tycko, and were modified such that the C-terminal of the peptide is capped with an -NH₂ group. The GROMOS96 53a6 force field^67–69 was used to model the peptides, and the SPC model⁷⁰ was used for water molecules. This force field has been used extensively for protein simulations,^71,72 and was shown to provide good agreement with experiment in our recent studies of IAPP monomers^73,74 and peptide aggregation.^75,76 The ionization states of the amino acid side chains were assigned on the basis of their intrinsic pKa values. Our model of the amyloid protofilament has five stacked pairs of hIAPP, as in Figure 2(a), and has a net positive charge of +30 (+3 on each peptide). Thirty Cl⁻ ions were added to neutralize the system. The initial configuration was generated such that water fully solvates the peptides, existing both outside and inside the fibril. MD simulations were performed with the GROMACS molecular simulation package.^77–80 Long-range electrostatic interactions were treated with a particle-mesh Ewald sum.^81,82 All simulations were performed with rigid bonds (using the linear constraint solver method) and with an integration time step of 2 fs. Once at equilibrium, production runs were performed at a temperature of 298 K using the Nose-Hoover thermostat^83,84 and a pressure of 1 bar using the Parinello-Rehman barostat.⁸⁵

To validate our approach of solvating the peptides, we ran a second set of simulations, where we removed water molecules within 0.4 nm of all the peptides, ensuring the absence of water molecules in all the cavities of the aggregate structure. After such artificial removal of water, the energy of the system was minimized using a Polak-Ribier conjugate gradient scheme⁸⁶ without any constraints, and then the system was equilibrated as described above. We refer to such simulations as the dehydrated simulations.

Experimental and computational studies have shown that the hIAPP fibril has polymor­phic features.^21,87–89 We took the basic structural unit of the two-fold model and constructed two of the possible morphology alternates, for the purpose of studying the effect of polymorphism on 2DIR spectral features. Structural polymorphism is better studied for the amyloid beta (Aβ) peptide, which is associated with the Alzheimer's disease and shares sequential and structural similarity with hIAPP.^{6,7,21,24,87–91} For example, utilizing solid state NMR, Tycko and coworkers proposed two distinct structural models for the Aβ_1–40 fibril, with either two-fold or three-fold symmetry about the fibril axis.^92–94 The two-fold model of the hIAPP fibril, as shown in Figure 2(a), resembles that of the two-fold Aβ_1–40 fibril, and considering their structural similarity, we postulate that hIAPP might also adopt a three-fold morphology. Based on the Aβ_1–40 model provided by the Tycko group,⁹² we have constructed a three-fold symmetric model for the hIAPP protofilament. This model contains three columns forming a triangular shape and each column contains six hIAPP monomers, as shown in Figure 2(d). Specifically, this model was generated by replacing the Aβ_1–40 monomer by the hIAPP monomer while maintaining the backbone configuration of the three-fold Aβ_1–40 fibril. The side chains of hIAPP monomers were constructed as elongated chains, with similar inter-strand arrangement as the two-fold model I.

Experimental and computational evidence also suggests a single-column structure for the Aβ fibrils.^95,96 We took one column from model I as a plausible model. Both the 3-fold and the single-column model were energy minimized using the steepest descent algorithm followed by a 1 ns MD run, with the backbone atoms constrained. The peptides were then solvated and equilibrated for 10 ns without any constraints. Production runs with the same parameters as the two-fold model were performed for 100 ns.

B. Calculation of the 2DIR Spectra

In a typical 2DIR experiment, three pulses with time intervals t₁ and t₂ interact with the sample. A photon echo is generated and detected after time t₃. The measured echo signal is Fourier transformed with respect to both t₁ and t₃ to obtain 2DIR spectra.

To calculate 2DIR line shapes for each isolated chromophore, one needs the instantaneous frequency along the MD trajectory. Wang et al.⁶⁵ recently developed frequency maps for protein backbone and side-chain chromophores, which relate the amide I frequencies to the local electric fields. These frequency maps, in conjunction with established nearest-neighbor frequency shift (NNFS)⁹⁷ and coupling schemes,^97,98 have been applied to peptides of vari­ous secondary structures, including hIAPP monomers, and have been shown to reproduce experimental FTIR spectra well.⁶⁵ The frequency maps are utilized here for the frequency calculations. Specifically, for the i^th residue, the electric fields in the C=O bond direction on the amide C and N atoms, i.e. E_Ci and E_Ni, are calculated within a cutoff of 20 Å. E_Ci and E_Ni come from nearby water molecules, counter-ions and peptide atoms that are more than three covalent bonds away. For residues 1 through 36, the backbone frequency map⁶⁵ is used to calculate the local-mode frequencies from E_Ci and E_Ni,

$${\omega }_{ib}=\left\{1684+7729E_{Ci}-3576E_{Ni}\right\}{\text{cm}}^{-1}.$$ (1)

E_Ci and E_Ni are both in atomic units. For residue 37 with the chromophore -CONH₂, the side-chain frequency map is used for its frequencies⁶⁵

$${\omega }_{is}=\left\{1714+2154E_{Ci}+3071E_{Ni}\right\}{\text{cm}}^{-1}.$$ (2)

For all chromophores on the backbone, covalent through-bond effects from nearest-neighbor amide groups (termed as Δω_N and Δω_C) depend on the Ramachandran (ϕ,ψ) angles and are accounted by the NNFS maps developed by Jansen and coworkers.⁹⁷ Therefore, for residues 1 through 36 the total frequencies are

$${\omega }_i={\omega }_{ib}+\Delta {\omega }_N({\varphi }_{i-1},{\psi }_{i-1})+\Delta {\omega }_C({\varphi }_{i+1},{\psi }_{i+1}).$$ (3)

The first residue does not have a nearest-neighbor amide group on its N-terminal side, thus the Δω_N correction is zero. For residue 37,

$${\omega }_i={\omega }_{is}+\Delta {\omega }_N({\varphi }_{i-1},{\psi }_{i-1}).$$ (4)

The frequencies are used to calculate the frequency time-correlation function (FTCF)

$$C\left(t\right)=\langle \delta \omega \left(t\right)\delta \omega \left(0\right)\rangle .$$ (5)

δω(t) is the fluctuation of the instantaneous frequency from its average value, δω(t) = ω_i – 〈ω〉. The line shape function g(t) is defined as

$$g(t)\equiv {\int }_0^{t}d\tau \left(t-\tau \right)C\left(\tau \right).$$ (6)

We set the “waiting time” t₂ to zero, consistent with experiment, and assume infinitely short pulses, and the rephasing and non-rephasing response functions become^52,99–101

$$R_R\left(t_1,0,t_3\right)\sim e^{-2g\left(t_1\right)-2g\left(t_3\right)+g\left(t_1+t_3\right)}{e}^{-\left(t_1+t_3\right)/2T_1}[e^{i\langle \omega \rangle \left(t_1-t_3\right)}-e^{i\langle \omega \rangle t_1-i\langle {\omega }_{21}\rangle t_3}{e}^{-t_{3/}{T}_1}],$$ (7)

$$R_{NR}\left(t_1,0,t_3\right)\sim e^{-g\left(t_1+t_3\right)}{e}^{-\left(t_1+t_3\right)/2T_1}[e^{-i\langle \omega \rangle \left(t_1+t_3\right)}-e^{-i\langle \omega \rangle t_1-i\langle {\omega }_{21}\rangle t_3}{e}^{-t_{3/}{T}_1}].$$ (8)

〈ω〉 and 〈ω₂₁〉 are the average transition frequencies between the ground and the first-excited vibrational state, and between the first and the second excited states, respectively. They differ by the vibrational anharmonicity, which is taken to be 14 cm^−1.63 T₁ is the lifetime of the first excited state of an isolated amide I vibration, and the terms e^{−(t₁+t₃)/2T₁} and e^−t₃/T₁ are added phenomenologically to include lifetime broadening.¹⁰⁰ We are aware that vibrational population relaxation might involve multiple lifetime constants,^65,102 and that T₁ might vary from residue to residue. However, we choose to set uniformly T₁ to be 600 fs,⁵⁹ since there is no systematic experimental lifetime study for every amino acid, and the possible error of using this single lifetime for the line width calculation is within 5 cm⁻¹. Note that we have made several approximations in order to obtain Eqs. 7 and 8. We have used the second-cumulant expansion, made the Condon approximation and neglected orientational dynamics. We also assumed that the frequency gaps are strictly correlated (δω₂₁(t) = δω(t)).

The rephasing and non-rephasing spectra are obtained from the double Fourier transforms of their corresponding response functions,

$$S_R\left({\omega }_1,0,{\omega }_3\right)\sim {\int }_0^{\infty }d{t}_1{e}^{-i{\omega }_1{t}_1}{\int }_0^{\infty }d{t}_3{e}^{i{\omega }_3{t}_3}Re\left\{R_R\left(t_1,0,t_3\right)\right\},$$ (9)

and

$$S_{NR}\left({\omega }_1,0,{\omega }_3\right)\sim {\int }_0^{\infty }d{t}_1{e}^{i{\omega }_1{t}_1}{\int }_0^{\infty }d{t}_3{e}^{i{\omega }_3{t}_3}Re\left\{R_{NR}\left(t_1,0,t_3\right)\right\}.$$ (10)

Both the rephasing and non-rephasing signals have phase-twisted features, which complicate the spectra analysis.¹⁰³ A nicer spectrum can be obtained by summing the above two spectra, which gives the absorptive spectrum

$$I\left({\omega }_1,0,{\omega }_3\right)\sim Re\left\{S_R\left({\omega }_1,0,{\omega }_3\right)+S_{NR}\left({\omega }_1,0,{\omega }_3\right)\right\}.$$ (11)

To calculate the 2DIR spectrum, MD simulations were performed with the GROMACS molecular simulation package using the same parameters described in Section A.^{77–79,104,105} The MD package was modified to report the local-mode frequencies using Eqs. 1 and 2. The local-mode frequencies and coordinate trajectories were saved every 2 fs for a total of 2 ns for each simulation. The latter were used to get corresponding (ϕ, ψ) angles and calculate NNFS. To sample better the configurations of the fibril, a total of 12 simulations were performed for the two-fold model I, each starting from configuration 10 ns apart in the 110 ns MD simulations. Notice that an ideal fibril involves an infinite number of hIAPP chains stacked along the fibril axis, and each peptide chain forms hydrogen bonds with residues in its nearest two chains. Such an environment is well represented by the two central chains (one in each column) in the two-fold structural models, while all the other chains have edge effects. 2DIR spectra were calculated based on the simulations, and representative spectra are shown in Figure S1. In each spectrum, a pair of peaks appear near the diagonal. The positive peak corresponds to a transition from the first to the second excited state, while the negative peak results from the transition from the ground state to the first vibrational exited state and its minimum is defined as the fundamental peak. Note that the fundamental peak is near, if not along, the diagonal and its ω₃ value was used as its position ω_p. As ω_p and the diagonal line widths Γ_d are two of the most characteristic features of a 2DIR spectra,^{49,51,52,101,106,107} we have extracted values of ω_p and Γ_d to compare with experiments. Their final values, as reported below, were averaged over the central 2 chains for each simulation and then over the 12 simulations.

For the three-fold model, 5 simulations were performed from configurations spanning the first 50 ns MD simulation. The results were averaged over the central two chains of each of the three columns, and then over the 5 simulations. Similarly, for the single-column model, 6 simulations were performed from configurations spanning the 100 ns simulation. The results were averaged over all 6 simulations.

C. Peptide Preparation and 2DIR Measurements

Amylin peptides were synthesized using previously reported methods.^108,109 Amino acids labeled with ¹³C=¹⁸O isotopes were prepared as previously reported.¹¹⁰ Lyophilized peptides were dissolved to 1 mM concentration stock solutions in deuterated hexafluoroisopropanol. A 5 µL aliquot of the stock solution was dried under nitrogen and then reconstituted in 5 µL of 20 mM phosphate D₂O buffer solution (pD ∼7.4) to initiate aggregation. The sample was then immediately transferred to a CaF₂ IR sample cell with a 56 µm Teflon spacer and kept under dry air to prevent hydrogen exchange from ambient water vapor. Dilute labels were prepared by mixing stock solutions of labeled and unlabeled peptides in a 1:3 labeled:unlabeled ratio before drying under nitrogen.

2DIR absorptive spectra were measured and processed as previously described.¹¹¹ Briefly, mid-IR pulses (60 fs FWHM) were generated using a femtosecond laser system and optical parametric amplifier. Mid-IR pulses were split into pump and probe paths and then spatially and temporally overlapped in the sample. A mid-IR pulse shaper¹¹² in the pump path was used to create two pump pulses with a computer-controlled time delay which was scanned on a shot-by-shot basis. The probe beam was detected and digitized using a 64-element linear MCT array. The polarization of the pump pulses was set perpendicular to the probe pulse.

For each sample, 2DIR absorptive spectra were collected continuously until satisfactory signal-to-noise was achieved. Then the average and standard deviation of the spectral amplitude were calculated as a function of pump and probe frequencies. Diagonal slices through the average and standard deviation contours were obtained via 2D interpolation. The slice amplitude was fit to a sum of two Gaussians: one for the label peak and one for the unlabeled β-sheet peak. In some cases a small baseline offset was included in the fit but was held at the experimental value. The slice standard deviations were used as weighting factors in the nonlinear least-squares fitting procedure. The resulting fit line widths and uncertainties (twice the standard deviation) are reported.

Results and Discussion

In both models I and II, the N-terminal half of each hIAPP chain faces water, while the less-hydrophilic C-terminal half forms the fibril core (Figure 2(a)). Each monomer contains two β-strands, one in the C-region and one in the N-region of the chain, which are connected by a flexible turn. Due to the constraints from the disulfide bond, the N-terminal end is frayed.

MD simulations of the two-fold models I and II were performed for 110 ns. Model II underwent large structural fluctuations and had not equilibrated by the end of the simulation. On the other hand, model I remained stable during the entire simulation. From our previous study on rat IAPP (rIAPP), we found that different force fields did not alter the structural stability.⁷³ Therefore, we expect that this phenomenon is due to the intrinsic instability of model II, which is not force-field dependent. A snapshot of model I is shown in Figure 3(a). In the dehydrated simulations, model II also shows the unstable behavior, while model I gradually opens up, allows water to re-enter and finally resembles the structure in the normal simulation. Two snapshots of model I in the dehydrated simulation are taken, at the beginning of the simulation and after 100 ns. They are shown in Figure 3(b) and 3(c) to demonstrate the incorporation of water molecules. This result justifies our approach of solvating the fibril structure with water initially existing in the interior of the fibril. Since we cannot obtain reliable 2DIR spectra from the unstable model II trajectory, we will not consider this model further.

Fig. 3.

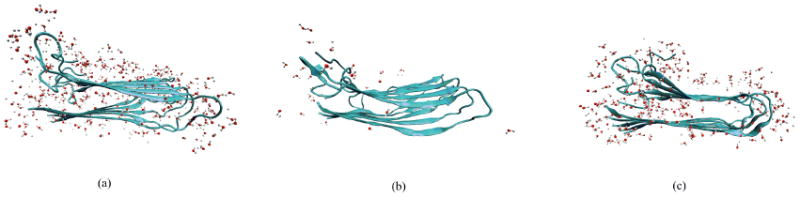
Snapshots of model I: (a) in the normal simulation, (b) at 0 ns and (c) at 100 ns in the dehydrated simulation. One peptide column is shown for clarity.

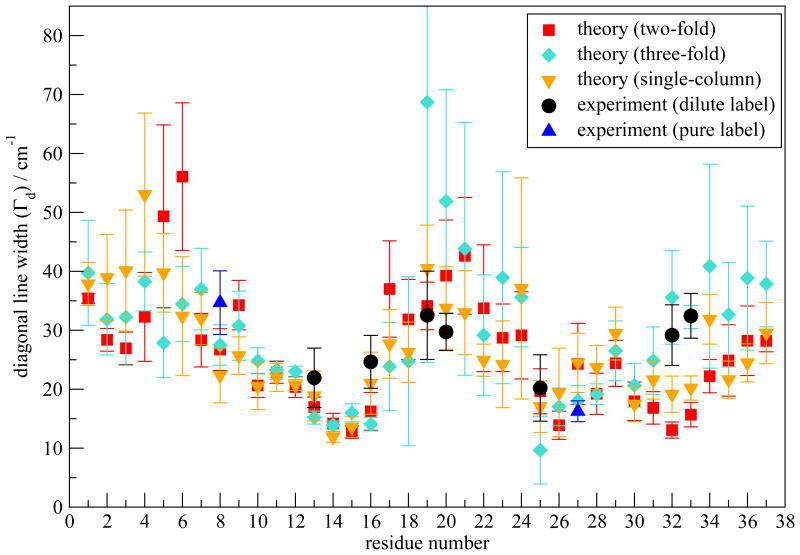
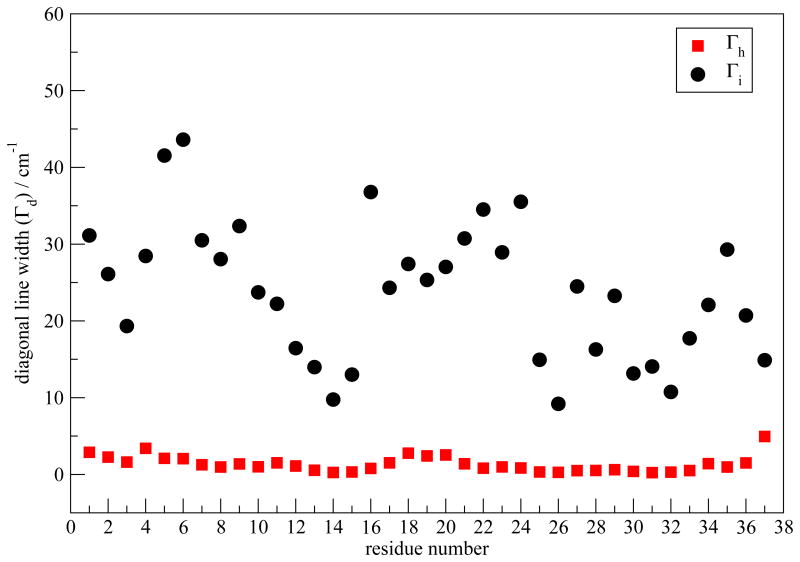
2DIR spectra were measured for the mature hIAPP fibril. A single ¹³C=¹⁸O label was placed at residues Ala13, Leu16, Ser19, Ser20, Ala25, Val32 or Gly33, one at a time. In each experiment, the singly-labeled hIAPP monomers are diluted by unlabeled monomers and we refer to such experiments as dilute-label cases. After the aggregates are fully formed, 2DIR experiments are performed and representative spectra are shown in Figure 4. At the top of each 2D spectrum are the corresponding diagonal slice through the 2D contour (black) and the result of fitting the slice to two Gaussians (red). All spectra have three features in the spectral region shown. (1) A diagonal peak pair is observed at a pump frequency of ∼1620 cm⁻¹. It is a characteristic peak due to the antisymmetric stretching of a parallel β-sheet, and is created by the unlabeled residues incorporated into the β-sheets of the mature fibril.^48,49 This feature is not fully visible in Figure 4 because the chosen amplitude scale emphasizes the label peaks and therefore shows amplitude that is too strong in the unlabeled region. (2) A diagonal peak pair at pump frequency ∼1595 cm⁻¹ which is assigned to the respective ¹³C=¹⁸O isotope labeled residue. (3) A cross-peak pair at a pump frequency of ∼1595 cm⁻¹ and probe frequency of ∼1620 cm⁻¹, which has also been previously discussed.^48,49 The focus of this work is on the variations of the diagonal slice of the label peaks, which are characterized by ω_p and Γ_d. These two quantities are shown as black circles in Figures 5 and 6, respectively. ω_p is generally close to 1595 cm⁻¹ and their variation shows no discernable pattern. On the other hand, Γ_d shows a greater variation from residue to residue. For example, residues Ala13 and Ala25 have relatively narrow label peaks with Γ_d of 22 ± 5 and 20 ± 6 cm⁻¹, respectively, while residues Ser19 and Val32 have much broader label peaks with Γ_d of 33 ± 7 and 29 ± 5 cm⁻¹, respectively. Figure 6 shows that more generally, residues near the C terminus and at the purported turn region have larger line widths than residues in regions thought to form β-sheets. We are aware that more data points and more accurate error bars are desirable in order to show a more convincing trend. However, at the current stage we are limited to certain residues that we can perform isotope label. The label peaks overlap with the background of the strong unlabeled peak, which leads to certain uncertainties we are not able to reduce. As an on-going project, we have also performed “pure-label” experiments, where a particular residue is ¹³C=¹⁸O isotope labeled on every chain to study the spectral changes due to couplings between them. Preliminary results show that, for the seven residues studied in this work, couplings alter ω_p by as much as 10 cm⁻¹, but the corresponding Γ_d is similar to the dilute case (Figure S2). Assuming this is also true for other residues, we have presented Γ_d for residues Ala8 and Leu27 from the pure-label experiments in Figure 6, for comparison purposes.

Fig. 4.

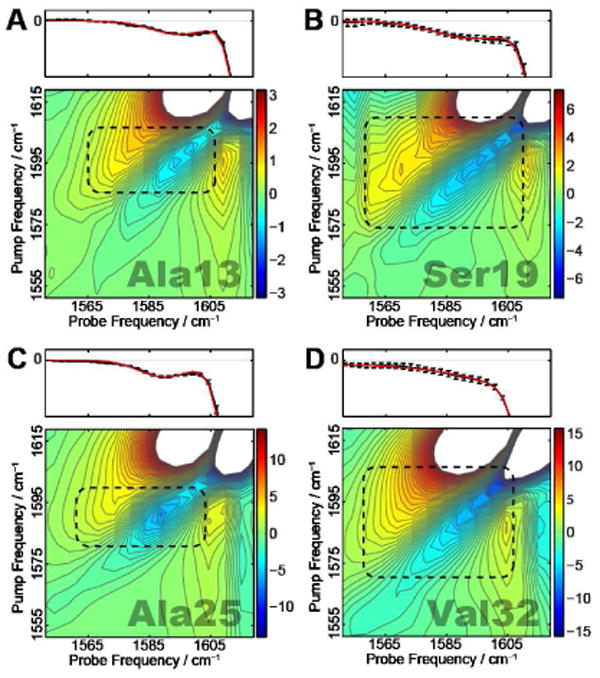
Experimental 2DIR spectra for (A) Ala13, (B) Ser19, (C) Ala25 and (D) Val32. The label peaks are identified with black boxes. The top panels show diagonal slices (with error bars) of the 2DIR spectra and the fit to the label peaks.

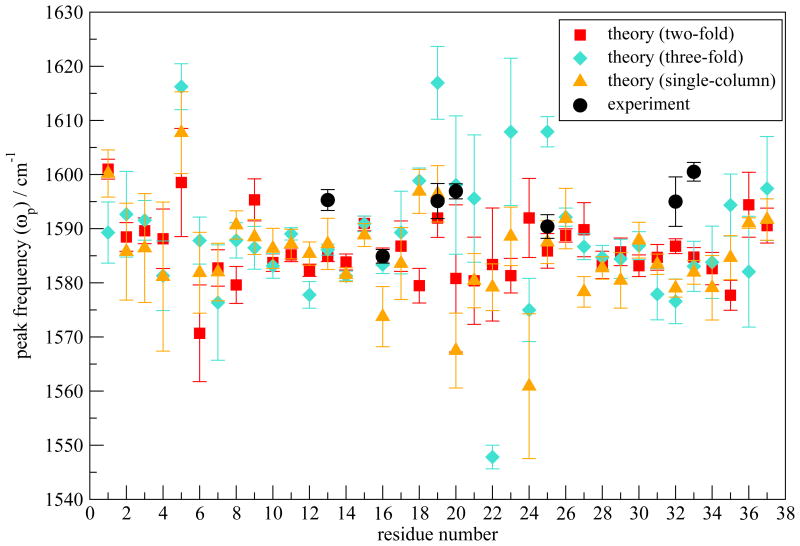
Fig. 5.

ω_p (in cm⁻¹) as a function of residue number calculated for the two-fold model I and the three-fold and the single-column models. The isotope shift is taken to be −70 cm⁻¹. Experimental values are shown as black circles.

Fig. 6.

Γ_d (in cm⁻¹) as a function of residue number calculated for the two-fold model I and the three-fold and single-column models. Experimental values for the dilute labels are shown as black circles. Experimental values for the pure labels are shown as blue triangles.

In the dilute-label experiments, the labeled residues can be well assumed to be local oscillators, uncoupled from the other amide modes. 2DIR calculations have been performed on every residue, assuming that the specific residue is isotope labeled. The ¹³C=¹⁸O isotope shift is taken to be −70 cm^{−1. 55–57,60,65,113} ω_p as a function of residue number are plotted in Figure 5. Error bars are shown as twice the standard deviation of the mean calculated from the 12 simulations. The theoretical ω_p are in the correct range (around 1585 cm⁻¹) compared to experiment, which validates our theoretical approach. As discussed above, ω_p does not show a particular pattern and therefore is not indicative of the fibril structure.

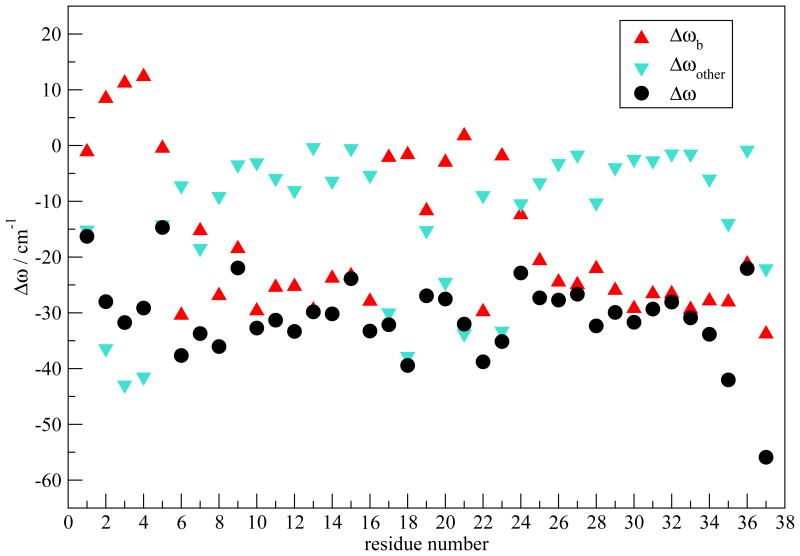
Theoretical values of Γ_d as a function of residue number are plotted in Figure 6, which are in good agreement with experiments. A characteristic “W” shape appears for both theory and experiment. To understand the relation between the W pattern and the fibril structure, we have first decomposed the average frequency shift (from the frequency map intercept value ω₀) for each residue in order to determine the key contributing components. The frequency shift is defined as Δω_i ≡ ω_i – ω₀. For residues 1-36, ω_i is calculated from Eqs. 1 and 3, with ω₀ = 1684. For residue 37, ω_i is calculated from Eqs. 2 and 4, with ω₀ = 1714. Factors that contribute to Δω_i include the through-bond NNFS (Δω_C and Δω_N) and the electric fields E_Ci and E_Ni due to the surrounding charged groups. E_Ci and E_Ni can further be separated into contributions from peptide backbone and side-chain atoms, as well as those from solvent molecules and counter-ions. As regular arrangement of backbone atoms is characteristic of ordered secondary structures, it is of interest to separate the backbone contribution from all other factors and study their effect individually, especially in the β-sheet regions. Note that electric fields decay rapidly with distance, and so backbone atoms far away from the chromophore of interest have a small effect. Therefore, for a residue in the i^th chain we have combined NNFS and the electrostatic interactions from backbone atoms in the (i-1)^th, i^th and (i+1)^th chains into the “backbone” contribution Δω_b. Contributions due to all the other factors are summed as “other” contribution Δω_other. The average frequency shift is 〈Δω_i〉 ≡ Δω = Δω_b+Δω_other. Δω is plotted in Figure 7 as a function of residue number. The overall Δω as a function of residue number closely resembles the ω_p pattern shown in Figure 5 (red squares). The deviation of the calculated 2DIR absorption peak frequencies from the average frequency is due to the distortion of adding up the rephasing and non-rephasing spectra, as well as the cancelation of the positive and the negative peaks. Δω_b dominates the frequency shift in the β-sheet regions, i.e. residues 8-16 and 25-36. In these regions, the fibril structure is characterized by inter-strand hydrogen bonds. Therefore, backbone atoms in the nearby strands that are directly hydrogen bonded to the chromophore of interest produce the largest electrostatic field along the C=O bond direction, and therefore lead to the biggest frequency shift. NNFS are close to zero due to the extended β-sheet conformation in these regions.⁹⁷ On the other hand, towards the N-terminal between residues 1 and 7 and at the turn region from residues 17 to 24, Δω_other dominates. Water forms hydrogen bonds to peptide atoms, replacing the inter-strand interactions and directly exerting forces on the chromophores. In addition, peptides adopt random configurations, leading to a reduction of the backbone electrostatic effect, a non-zero NNFS contribution, and an increase in the side-chain contributions. These factors combine to make Δω_other, rather than Δω_b, the dominant contribution. Note that for residue 37 both Δω_b and Δω_other have large magnitude, leading to an overall big frequency shift. As the terminal residue has an ω₀ of 1714 cm⁻¹, its total frequency is comparative to the other residues.

Fig. 7.

Decomposition of Δω (in cm⁻¹) for model I.

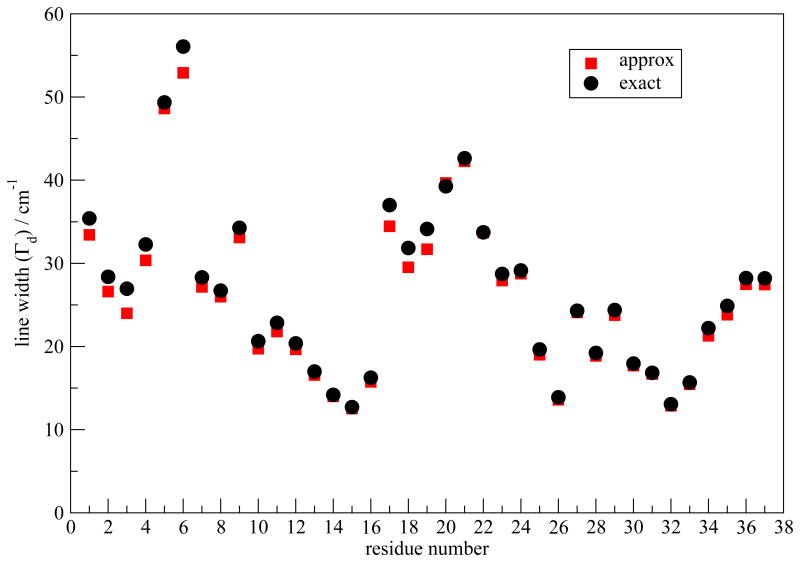
To study the contributions to Γ_d, we decompose the FTCFs. It is observed that the FTCFs generally consist of a fast component, followed by a slow decay. We approximate C(t) by a generalized Kubo model^101,114

$$C\left(t\right)=C_f\left(t\right)+{\Delta }^2{e}^{-t/\tau }.$$ (12)

C_f (t) decays sufficiently fast that it leads to a homogeneous contribution to the line widths, from ${\Gamma }_h=2{\int }_0^{\infty }dt{C}_f\left(t\right)$, while the slowly decaying exponential leads to an inhomogeneous contribution, from ${\Gamma }_i=2\sqrt{2\text{ln}2}\Delta$.¹⁰¹ The C(t) data after 0.5 ps are fitted to an exponential form to obtain the slow part, and C_f (t) is calculated by subtracting the slow part from C(t). Γ_d with the approximate C(t) are compared to the exact results in Figure 8. The good agreement between the two validates the approximation. Γ_h and Γ_i for the peptides in the centers of the two columns are similar and the results for one column are shown in Figure 9. From the figure, Γ_i dominates the contribution, and it closely follows the W-trend observed in the overall Γ_d. Those two factors suggest that in this case Γ_d is dominated by inhomogeneous frequency distributions, which in turn are due to structural inhomogeneity. The small values of Γ_i in the β-sheet regions indicates their structural stability. In contrast, the Γ_i are large at the terminal and in the turn regions, indicating structural disorder and frequency modulation by water molecules. Recently, Kim et al. utilized 2DIR spectroscopy to study the Aβ fibril.¹¹⁵ By varying t₂, they observed fast frequency variations for residues that are in direct contact with water molecules. For the hIAPP fibril, it is expected that the spectral features in the terminal and the turn regions will similarly show significant changes with variations in the t₂ time.

Fig. 8.

Γ_d (in cm⁻¹) calculated from the approximate and exact C(t) for model I.

Fig. 9.

Theoretical inhomogeneous (Γ_i) and homogeneous (Γ_h) contributions (in cm⁻¹) to the absorption line widths, calculated for model I. The results for one column are shown.

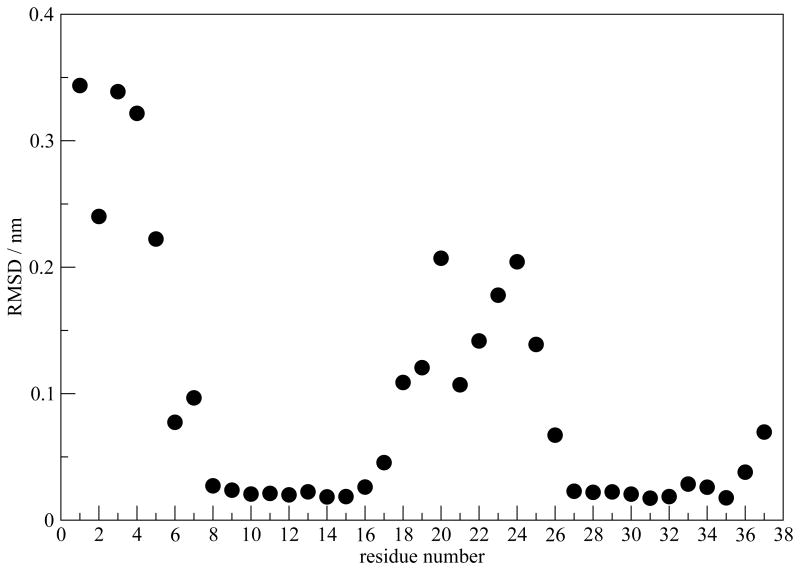
Next we illustrate directly the stability of the β-sheet regions. Distances between the i^th C_α in the central peptide chain and the i^th C_α's in the nearest two chains are chosen to represent the backbone structure. Root-mean-square deviations (RMSDs) of the distances (from their average values) are reported in Figure 10, as a measure of structural fluctuations. Once again, the result is averaged over the two columns in each simulation and then averaged over the 12 simulations. As shown in Figure 10, the backbone structure fluctuates along the MD simulation, but the β-sheet regions of residues 8-16 and 27-36 stay stable, consistent with the small Γ_d values.

Fig. 10.

RMSD of the C_α distance between the central peptide chain and nearest two chains, calculated for model I.

Based on the above analysis, a spectrum-structure relation is proposed to explain the W pattern in Γ_d. Structurally, each hIAPP monomer contains two β-strands connected by a turn, with the terminal and the turn regions particularly disordered. Residues within these regions are also in close contact with water molecules. The large structural fluctuations, combined with fast water dynamics, manifest themselves as enhanced diagonal line width. In contrast, the two β-sheet regions are well ordered and do not exhibit significant static or dynamic disorder and therefore have smaller line widths.

We have also analyzed the effect of polymorphism on 2DIR spectral features. The threefold model stays stable within the first 50 ns. Its triangular arrangement of the β-sheets causes the ends of the C-terminus to fray and allows a water channel to exist in the central cavity, in agreement with a recent simulation study of the three-fold Aβ fibril.⁹¹ It becomes less stable in the following simulations. Two of the columns slowly rotate towards each other and tend to form a two-fold-like structure. A snapshot of the model at 100 ns is shown in Figure 11. A full structural rearrangement might take microseconds or longer, and we will not focus on that in this study. As for the single-column model, the central three chains stay in the β-sheet conformation within the 100 ns simulation. The outer two chains lack the stabilization effect of neighboring β-sheet and become more random-like, similar to a recent simulation of the Aβ fibril.⁹⁶

Fig. 11.

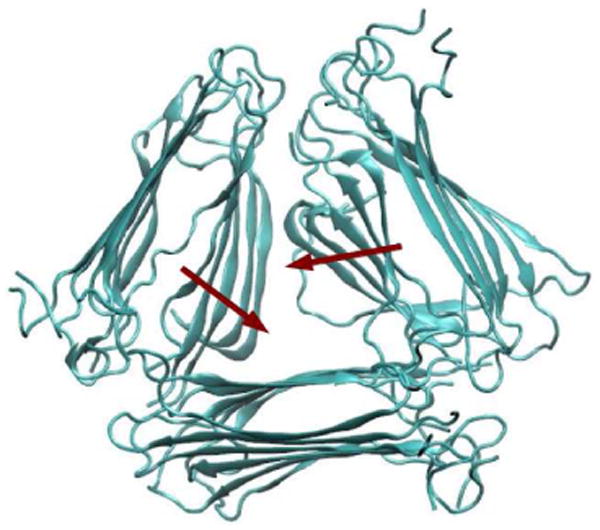
A snapshot of the three-fold structure after 100 ns of simulation. Red arrows show the most prominent structural changes from the initial configuration.

2DIR spectra of the two alternative morphologies are calculated. Their ω_p and Γ_d are shown in Figures 5 and 6, respectively. Compared with model I, ω_p of the three-fold and single-column models show larger fluctuation. For example, residue 22 in the three-fold model has a particularly low ω_p, due to its strong interaction with the surrounding water molecules and with the terminal regions of another column. Γ_d of all three morphologies show the W pattern, because they share the same β-sheet structural unit. Note that Γ_d at residues 19 and 20 of the three-fold model are abnormally large. This is mostly related to poor sampling. The three-fold structure is not dynamically stable enough for sufficient sampling, which leads to multiple peaks in the averaged spectra and consequently very broad line widths.

One might notice the discrepancy between experimental Γ_d and the theoretical results for model I near the C-terminus. The two-fold model I has a well-defined C-terminus, consistent with the small theoretical line width values, while the large experimental Γ_d at residues Val32 and Gly33 indicate possible structural disorder in that region. The fact that both the three-fold and single-column models show larger Γ_d at residues 32 and 33 indicates that such discrepancy might be due to polymorphism, although we do not see evidence for polymorphism in the TEM experiments (data shown in Figure S3).

The fibril structure has been classified at different levels, with the primary structure being the amino acid sequence, secondary structure being the configuration of each peptide monomer, tertiary structure referring to the organization of β-strands within the β-sheet, and quaternary structure being the positions and orientations of β-sheets relative to one another.^24,92,93,116 The possible polymorphism discussed above might come from the secondary structure level, with fibrils sharing the two-fold symmetry but with different stability in the C-terminus. In addition, the fact that the three-fold and the single-column models provides better agreement with experimental Γ_d in the C-terminus indicates possible polymorphism at the quaternary structure level.

Conclusions

In this paper, we present a study of hIAPP fibril by theoretical and experimental 2DIR spectroscopy, combined with atomistic MD simulations. ω_p and Γ_d have been chosen to quantify the 2DIR spectra for each isolated chromophore. Our theoretical approach of calculating the amide I frequencies,⁶⁵ in conjunction with MD simulation using the GROMOS96 53a6 force field, are able to capture experimental features of both quantities. Γ_d as a function of residue number indicates a W pattern. The spectral analysis reveals that Γ_d is dominated by an inhomogeneous distribution of frequencies. Large Γ_d towards the terminals and the turn regions reflects large structural fluctuations and the modulation by surrounding water molecules. On the other hand, the small values of Γ_d in the two β-sheet regions reveal that they form robust, rigid structures, consistent with structural analysis.

This work provides a protocol for directly connecting 2DIR experiments with MD simulations by theoretical calculations. 2DIR experiments, with their structural sensitivity and intrinsic fast time resolution, have the capability to study the in-situ aggregation dynamics of hIAPP both in the absence and presence of lipid membranes.^46–50 This and other frameworks that provide such connections will enable the analysis of the complex experimental spectra in atomistic detail. We are currently working on applying the combined MD simulation, theoretical and experimental 2DIR method to study the hIAPP aggregation process.

Theoretical 2DIR calculations on model I are in good agreement with experiments. The discrepancy in Γ_d near the C-terminus is possibly due to polymorphism of the fibril.^21,87–89 We have taken the structural unit of model I and constructed two other morphologies, based on the the Aβ structures.^93,95,96 All three models show the “W” pattern in Γ_d, in agreement with experiment, validating the structural unit of the model proposed by Tycko and coworkers.⁷ Note that the generally good agreement between theoretical and experimental 2DIR spectra indicates that different morphologies might share similar structural behavior in the N-terminal and turn regions, with the C-terminal the main polymorphic region. Besides, the fact that model I, the three-fold and single-column models differ in Γ_d at the C-terminus raises the possibility of utilizing 2DIR, in conjunction with the isotope labeling technique, to distinguish between different fibril morphologies.

The β-sheet-forming regions have been identified as amyloidogenic.^117–119 Mutations in these regions often reduce the aggregation propensity. For example, rIAPP differs from hIAPP at only six positions and four of the mutations occur in the β-sheet region, as shown in Figure 1(b). rIAPP is known not to form amyloid aggregates. When interacting with lipid membranes, both hIAPP and rIAPP initially form an α-helical structure at the N-terminal.^16,17,120 It is proposed that for hIAPP, assembly of the α-helical N-termini increase the local concentration of the highly amyloidogenic regions between residues 20 and 29, which promotes the formation of β-sheet oligomers.^{12,16,17,121,122} On the other hand, for rIAPP proline mutations in the C-terminal region reduce its β-sheet-forming propensity and possibly reduce its toxicity to membranes. The β-sheet regions are therefore of great importance in the aggregation process and are closely related to cytotoxicity.

The possibility of designing inhibitors for hIAPP amyloid formation has gained much attention in the past decade.^33,123–129 It has been proposed that hIAPP with N-methylation or a single mutation in the C-terminal β-sheet region dramatically inhibits the aggregation process.^124,125,127 In addition, rIAPP is also an effective inhibitor.¹²⁶ The importance of the β-sheet regions in hIAPP fibril formation and inhibition, and their great stability in the mature fibril, as revealed in the present work, indicate that they might be potential drug binding targets for treating amyloid formation in type 2 diabetes.