Needle-Tissue Interaction Forces for Bevel-Tip Steerable Needles

Abstract

The asymmetry of a bevel-tip needle results in the needle naturally bending when it is inserted into soft tissue. As a first step toward modeling the mechanics of deflection of the needle, we determine the forces at the bevel tip. In order to find the forces acting at the needle tip, we measure rupture toughness and nonlinear material elasticity parameters of several soft tissue simulant gels and chicken tissue. We incorporate these physical parameters into a finite element model that includes both contact and cohesive zone models to simulate tissue cleavage. We investigate the sensitivity of the tip forces to tissue rupture toughness, linear and nonlinear tissue elasticity, and needle tip bevel angle. The model shows that the tip forces are sensitive to the rupture toughness. The results from these studies contribute to a mechanics-based model of bevel-tip needle steering, extending previous work on kinematic models.

I. Introduction

Needle insertion into soft tissues is probably the most common invasive surgical procedure used for either therapeutic drug delivery or tissue sample removal from deep within the body. Inaccurate needle placement may result in malignancies not being detected during biopsy, radioactive seeds not being in the correct location to destroy cancerous lesions during brachytherapy, and traumatic or even fatal effects while performing anesthesia. Thus, for medical diagnoses and treatments, the needle must reach its intended target. But tissue inhomogeneity and anisotropy, organ deformation, and physiological processes, such as respiration and flow of fluids, cause the needle to deviate from its intended path. A possible method to mitigate needle targeting errors is to use a needle that can be robotically steered in the body to reach the intended target.

Several groups have examined the use of robotically steered flexible needles through tissue [3], [8], [9], [16], [18], [19], [20], [21]. Planning such procedures requires an accurate model of the needle-tissue interaction. One of the methods to steer needles through the body uses needles with standard bevel tips that naturally cause the needle to bend when interacting with soft tissue [20]. This phenomenon is attributed to the asymmetry of the bevel edge, which results in bending forces at the needle tip. Ideally, a mechanics-based model of the tip forces would be used to predict needle behavior based on information about geometry and material properties.

Several research groups have developed physics-based needle and soft tissue interaction models that are not specific to bevel-tip needles [2], [6], [7], [11], [12], [15]. A summary of these studies and other non-physics-based needle-tissue interaction models is provided in [14]. In all these studies, the objective of the researchers was to develop models to render simulation of needle-tissue interaction for real-time applications without specifically focussing on the interaction forces at the needle tip. Experimental work has identified forces (due to puncture, cutting, and friction) developed during needle insertion through tissue [13], [17]. Further, in [21] a kinematic model specifically for bevel-tip needles was presented whose parameters were fit using experimental data, but this model did not consider the interaction of the needle with an elastic medium. None of these studies focused on relating the tip forces to the amount of needle deflection based on the fundamental principles of continuum and fracture mechanics.

In this research we study the effect of tissue material and needle tip geometric parameters on tip forces. Using finite element (FE) simulations, we show the relationship between the bevel angle and the forces generated at the needle tip. Using needle insertion experimental studies with gels and tissue, we extract the material properties. We incorporate these physical values into an FE simulation. The FE model includes contact between the needle tip and tissue, and also incorporates a cohesive zone model to simulate the tissue cleavage process.

This paper is organized as follows: Section II presents the mathematical preliminaries required to obtain the tissue elasticity and toughness values. Section III describes the experiments to measure tissue elasticity and toughness. Section IV provides details on the FE simulations and sensitivity studies. Finally, Section V summarizes the work done and provides possible directions for future work.

II. Tissue Elasticity and Toughness

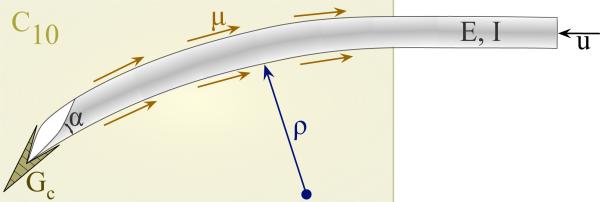
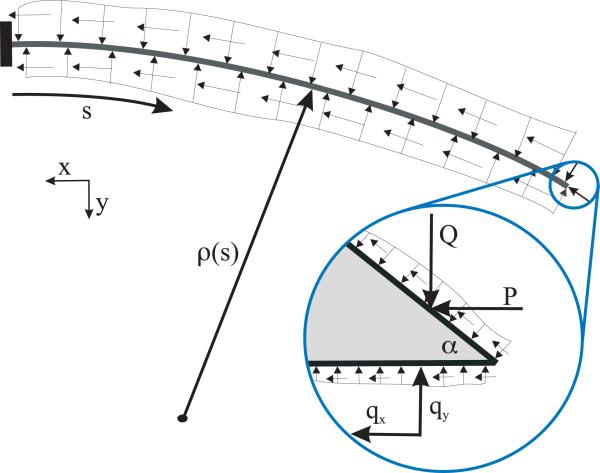
The deflection of a bevel-tip needle is a function of several parameters (Figure 1): the needle's Young's modulus $\left(E,\text{units}:\frac{N}{m^2}\right)$, second moment of inertia (I, units: m⁴), and tip bevel angle (α); the tissue's nonlinear (hyperelastic) material property $\left(C_{10},\text{units}:\frac{N}{m^2}\right)$, rupture toughness $\left(G_c,\text{units}:\frac{N}{m}\right)$, and coefficient of friction (μ); and input displacement from the robot controller (u, units: m). Dimensional analysis provides an organized method to group dimensionally similar variables [5]. Thus, the radius of curvature of the needle (ρ, units: m) can be written as a function, f, of these parameters

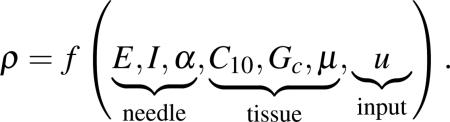(1)

Performing dimensional analysis and invoking Buckingham's Π theorem on this system results in the following Π-groups, for primary variables E, C₁₀, and G_c:

$${\Pi }_1=\frac{\rho C_{10}^2}{E{G}_c},{\Pi }_2=\frac{I{C}_{10}^5}{E{G}_c^4},\text{and}{\Pi }_3=\frac{u{C}_{10}^2}{E{G}_c}.$$ (2)

Thus, the non-dimensional form of (1), for some function, g, is given by

$$\frac{\rho C_{10}^2}{E{G}_c}=g\left(\frac{I{C}_{10}^5}{E{G}_c^4},\frac{u{C}_{10}^2}{E{G}_c},\alpha ,\mu \right).$$ (3)

From (3) it is observed that the radius of curvature is dimensionally scaled by both the tissue elasticity (global parameter) and also the tissue rupture toughness (local parameter), which tells us that in additon to α and μ, the effect of both of these parameters (C₁₀ and G_c) needs to be investigated. In this section, we present a mathematical formulation to evaluate the tissue elasticity and toughness to be incorporated in an FE simulation framework.

Fig. 1.

Schematic of a bevel-tip needle interacting with a soft elastic medium.

A. Tissue Elasticity

The deformation of materials under strains greater than 1%-2% is described by the theory of nonlinear elasticity, and hyperelastic models are commonly used. For a hyperelastic material, the Cauchy stress tensor, σ, can be derived from a strain energy density function, W [10]. There are various formulations for the strain energy density function depending on the material. The material parameters associated with the hyperelastic model are experimentally derived using tensile, compression, shear, or biaxial tests. In this study, uniaxial compression experimental data was used and it fit the Neo-Hookean model well.

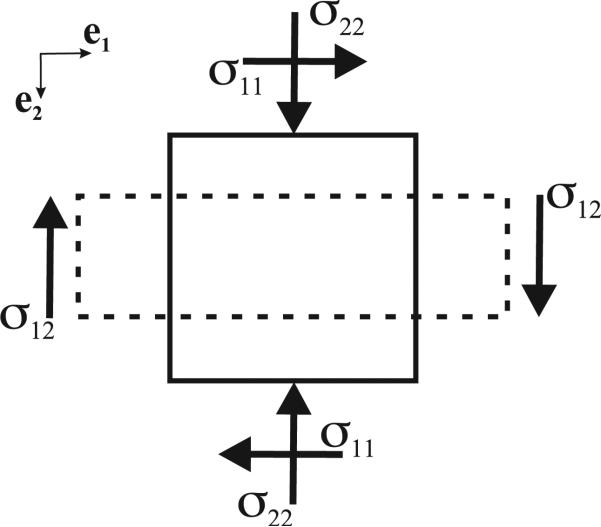
In order to fit the experimental data to a nonlinear elastic constitutive relation, we proceed to derive the stress-strain relationship. For a body under uniaxial compression (Figure 2), if y represents the position after deformation of a material reference initially located at X, we can describe compression by

$$\mathbf{y}={\lambda }_1{X}_1{\mathbf{e}}_1+{\lambda }_2{X}_2{\mathbf{e}}_2+{\lambda }_3{X}_3{\mathbf{e}}_3,$$ (4)

where e_i and λ_i, for i = 1 to 3, are the Cartesian base vectors and stretch ratios, respectively. From (4), the matrix of the deformation gradient tensor, F, for axisymmetric (λ₁ = λ₃ and λ = λ₂) and incompressible $\left({\lambda }_1={\lambda }_3=\frac{1}{\sqrt{\lambda }}\right)$ materials is computed as

$$\mathbf{F}=\frac{\partial \mathbf{y}}{\partial \mathbf{X}}=\left[\begin{array}{ccc}\hfill \frac{1}{\sqrt{\lambda }}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \lambda \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{1}{\sqrt{\lambda }}\hfill \end{array}\right].$$ (5)

Fig. 2.

Stresses acting on body under uniaxial compression, where the solid and dashed lines represent the body before and after compression, respectively.

Using the Representation Theorem [10], σ for an isotropic, homogenous, and incompressible hyperelastic material can be derived as

$$\sigma =-p\mathbf{I}+2\left\{\left(\frac{\partial W}{\partial I_1}+I_1\frac{\partial W}{\partial I_2}\right)\mathbf{B}-\frac{\partial W}{\partial I_2}{\mathbf{B}}^2\right\},$$ (6)

where I₁ and I₂ are the principal invariants, B is the left Cauchy-Green tensor, and p is the Lagrange multiplier (essentially a pressure). The Neo-Hookean strain energy density function is given by

$$W=C_{10}(I_1-3),$$ (7)

where C₁₀ is a material parameter specific to the tissue. In (7), the principal invariant, I₁, can be evaluated from B = FF^T as

$$I_1=\mathbf{B}:\mathbf{I}=\frac{2+{\lambda }^3}{\lambda }.$$ (8)

The Lagrange multiplier, p, in (6) can be evaluated from the boundary condition

$${\sigma }_{11}={\sigma }_{12}=0\Rightarrow p=\frac{2C_{10}}{\lambda }.$$ (9)

From (5) and (7) we can compute B² and $\frac{\partial W}{\partial I_1}$, respectively, and using (6) and (9), the compressive stress, σ₂₂, is computed as

$${\sigma }_{22}=\frac{2C_{10}}{\lambda }({\lambda }^3-1),$$ (10)

where stretch ratio is, λ = 1 – strain. (10) is used to fit experimental stress-strain data to obtain C₁₀.

B. Tissue Toughness

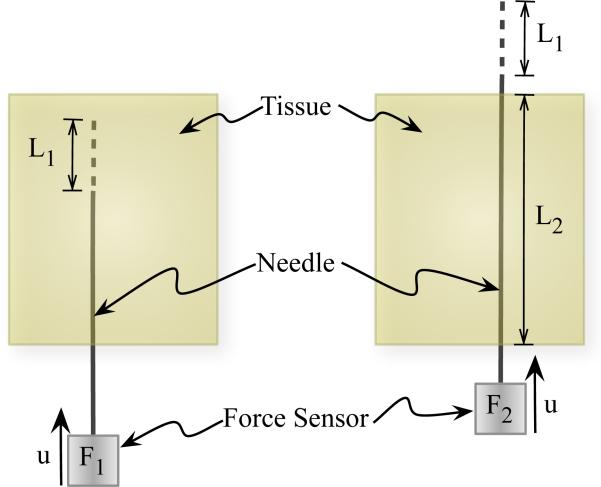
As the needle penetrates through material, the insertion force during this phase includes the force to overcome friction and resistance due to tissue elasticity, and the force needed to cut through tissue. Figure 3 provides a schematic representation of the method we use to extract the toughness. A similar method has been employed to extract fracture toughness during needle insertion in [4]. The insertion force recorded for some distance, L₁, travelled by the needle is F₁. The work done, divided by the needle cross-sectional area, A, to overcome friction and tissue resistance, and to cut through tissue, G_ftc, is given by

$$G_{ftc}=\frac{1}{A}{\int }_0^{L_1}{F}_{1}dL.$$ (11)

Fig. 3.

Schematic describing the procedure to calculate the rupture toughness of an elastic material during needle insertion.

Once the needle tip has completely passed through the material, there is no cutting force. The force recorded during this phase, for a distance L₁ travelled by the needle, is given by F₂. The work done, divided by the needle cross-sectional area, A, to overcome friction and tissue resistance, G_ft, is given by

$$G_{ft}=\frac{1}{A}{\int }_0^{L_1}{F}_2^{\prime }dL,$$ (12)

where L₂ is the length of the needle shaft within the material and $F_2^{\prime }=F_2\frac{L_1}{L_2}$. In order to account for the differences in frictional force along the needle shaft when the needle tip has completely passed through the material versus the case when the needle tip is interacting with the elastic medium, F₂ is scaled by $\frac{L_1}{L_2}$. This scaling assumes that frictional force varies linearly along the length of the needle shaft. The work done per unit needle cross-section area, G_c, to rupture and cut through tissue, is the rupture toughness (effective) of the tissue and is given by

$$G_c=G_{ftc}-G_{ft},$$ (13)

where G_ftc and G_ft are calculated for various materials using needle insertion experiments.

III. Tissue Parameter Acquisition

Experimental studies on phantom tissues (gels) and real tissue were performed in order to obtain both tissue elasticity and toughness parameters. Specifically, we found the Neo-Hookean model material parameter C₁₀ given in (10) and the rupture toughness derived in (13). Experiments were conducted with two variants of plastisol gel (soft and hard versions), porcine gel, and chicken breast tissue. All tests were performed at room temperature and the chicken samples were thawed from freezer prior to the experiments.

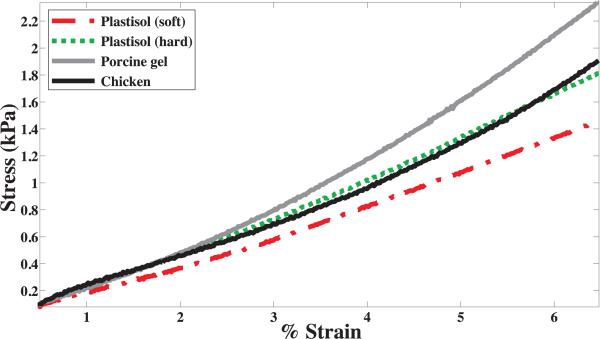
In order to obtain values for C₁₀, uniaxial compression tests were performed on the soft materials using a Rheo-metrics Solids Analyzer (RSA) II, as shown in Figure 4. Three 1 cm³ cube samples of each material were prepared and tested. The compression tests were performed at a strain rate of 0.001 s^–1. Representative stress versus strain curves for various materials are shown in Figure 5. The experimental data were fit to the constitutive equation given in (10) to obtain C₁₀, and Table I provides the mean values of the tissue elasticity for various materials. Linear elastic models were also fit to the experimental data and Table I gives the mean values of the Young's modulus, E_tissue, for the various materials.

Fig. 4.

Tissue elasticity measurement performed on several materials via uniaxial compression tests using the RSA II, where ① and ② are the actuator and load cell, respectively.

Fig. 5.

Representative compressive stress versus strain curves for various materials recorded using the RSA II.

TABLE I.

Measured material elasticity and rupture toughness properties for gels and tissue.

Material	C10 (kPa)	Etissue (kPa)	Gc (kN/m)	tc (MPa)
Plastisol (soft)	3.6	21.5	39.3	110.6
Plastisol (hard)	4.0	24.2	46.8	131.8
Porcine	4.9	29.6	114.4	322.2
Chicken	3.7	22.1	24.2	68.2

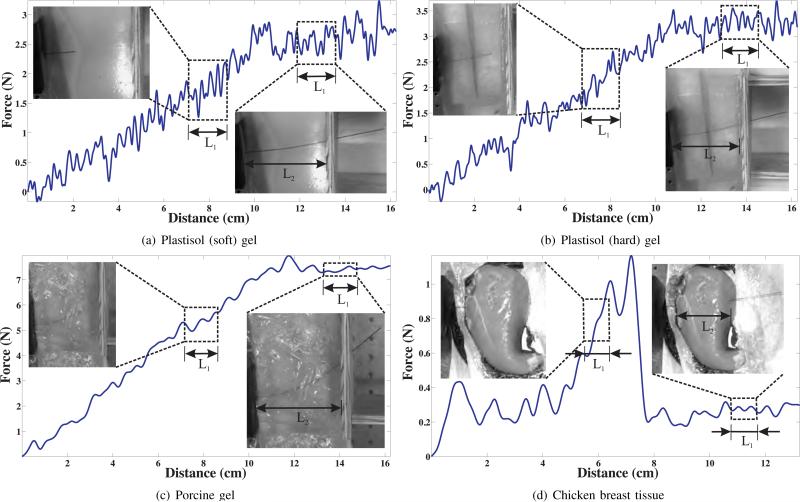
In addition to tissue elasticity, the rupture toughness of several materials were evaluated using the needle steering robot shown in Figure 6 [20]. The nitinol needle had a diameter of 0.71 mm and a tip bevel angle of 55°. As the needle penetrated through the material, the insertion force was recorded using an ATI Nano 17 force sensor. The material toughness was evaluated for soft and hard versions of plastisol gel, porcine gel, and chicken breast tissue using the expression given in (13). Figure 7 shows the insertion force recorded as the needle travels through different materials. The needle was driven at a constant insertion velocity of 0.125 cm/sec and the length, L₂, for all gels was 10.2 cm except for the chicken tissue, which was 7.5 cm. Also shown in Figure 7 are representative snapshots during which the toughness measurements were made. The length of the window when the needle tip is interacting and outside the tissue is given by L₁. During the phase when the needle tip is outside the tissue and only the needle shaft interacts with tissue, the insertion force is fairly constant. The rupture toughness for the various materials are provided in Table I.

Fig. 6.

Experimental setup used to robotically steer a flexible needle though soft elastic materials and used for toughness measurement.

Fig. 7.

Insertion force versus distance travelled by needle used for rupture toughness measurement. The representative snapshots show the needle tip interacting and outside the tissue samples. Data collected in the windows during which the needle tip travelled L₁ are used to calculate G_ftc and G_ft.

IV. Sensitivity Studies

The material parameters obtained from the experiments in the previous section were incorporated into FE simulations using ABAQUS [1] in order to evaluate the forces at the needle tip. Figure 8 shows the various forces acting on the needle interacting with an elastic medium. The needle is subjected to compressive and frictional forces along its needle shaft, and forces due to tip asymmetry. In this paper, we investigate the effect of rupture toughness, bevel angle, and tissue elasticity on the forces at the bevel tip.

Fig. 8.

Distributed load (compresssive and frictional forces) acting on a needle shaft as it interacts with an elastic medium. Inset: Forces acting on the bevel tip, where P and Q are the resultant forces along the bevel edge. q_x and q_y are the resultant forces along the bottom edge of the needle tip.

A. Sensitivity to Tissue Rupture Toughness

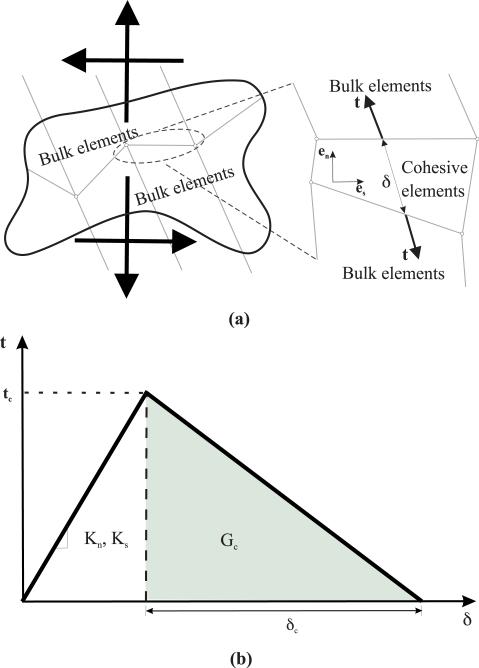
In order to simulate the interaction of the needle tip deforming and rupturing tissue as it travels, we employ a cohesive zone model (Figure 9). Cohesive zone modeling techniques are commonly used to simulate interface failure in composite structures. The cohesive zone is a mathematical approach to modeling the fact that work must be done to separate the two surfaces at an interface. This work is described in terms of a prescribed relationship between the tractions, t, required to separate the surfaces and the relative strains, δ, of those surfaces. A detailed explanation of the numerical implementation of cohesive zone models is presented in [22]; cohesive zone elements are placed between bulk elements, as shown in Figure 9(a).

Fig. 9.

The cohesive zone model used to simulate tissue cleavage process. (a) A sketch depicting application of cohesive zone elements along the bulk element boundaries, where tensile/compressive (normal) and shear strains result in deformation and rupture of the cohesive elements. (b) Linear traction-separation laws where values for K_n, K_s, G_c, and t_c are obtained from experiments and given in Table I.

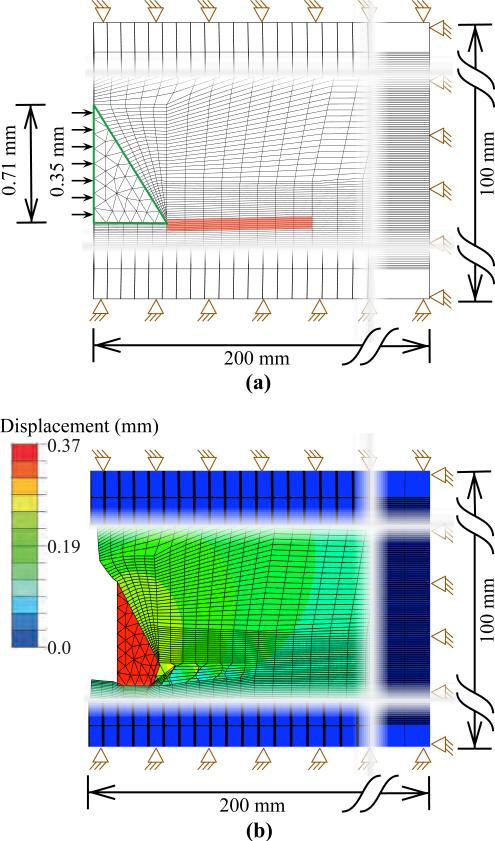
The cohesive zone elements are placed between continuum (bulk) elements and are defined in a small region (1 mm long and 0.072 mm wide) near the needle tip, as shown in Figure 10(a). In our FE simulation models, the cohesive zone is implemented using quadrilateral elements (ABAQUS element COH2D4), while the bulk elements are a mixture of quadrilaterals (ABAQUS element CPE4H) and triangular elements (ABAQUS element CPE3H). The bulk elements are assigned the nonlinear material properties (C₁₀) given in Table I, in addition to having geometric nonlinearity. As the needle tip deforms the tissue and the cleavage process is initiated, the cohesive zone elements open up in order to simulate this behavior. All of the cohesive elements use a traction-separation law (Figure 9(b)), which defines the relationship between the vectorial tractions (force density vectors), t, and strains, δ, across the element. The tractions and strains are given by

$${\mathbf{t}}_c=K_n{\delta }_n{\mathbf{e}}_n+K_s{\delta }_s{\mathbf{e}}_s,$$ (14)

where K_s, K_n and δ_s, δ_n are stiffnesses and strains in the shear and normal directions, respectively. The description of the deformation and the traction evolution in these elements is governed by a linear traction-separation law, as shown in Figure 9(b). The damage evolution and subsequent cleavage of the tissue is given by the rupture toughness, G_c. In order to define the traction-separation law, inputs to the FE simulation model are: K_n, K_s, t_c, and G_c. We assume the stiffness in the normal and shear directions are the same and given by the elastic modulus of the tissue, as provided in Table I, i.e. K_n = K_s = E_tissue. G_c values are also provided in Table I. For unit original constitutive thickness of the cohesive element, d_c is taken to be the same order of magnitude as the diameter of the needle i.e. δ_c = 0.71 mm, so for G_c being the area of the shaded region (Figure 9(b)), $t_c=\frac{2G_c}{{\delta }_c}$. The frictionless contact surfaces and the cohesive zone are highlighted in Figure 10(a) with an applied displacement of 0.35 mm.

Fig. 10.

FE simulation setup used to model needle and tissue interaction for a needle with 55° bevel angle and 0.71 mm diameter. The needle tip was made of nitinol (E = 50 GPa, ν = 0.3). (a) The green border used to signify contact surfaces and the elements in red are assigned to be the cohesive zone. (b) Magnitude of nodal displacement contour plot for the needle tip penetrating the tissue.

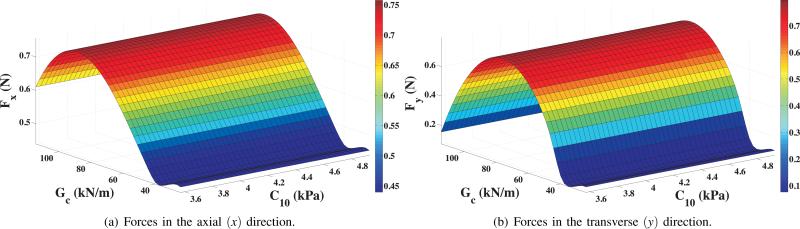
Figure 10(b) shows the contour of the magnitude of nodal displacement in the vicinity of the needle tip and cohesive zone. Also shown is the needle tip penetrating through the tissue elements and the initiation of cleavage. The tissue rupture process is simulated as the cohesive zone elements open up, which in turn is governed by the traction-separation law. The resultant tip forces in the axial and transverse directions are given by F_x and F_y, respectively, where F_x = q_x + P and F_y = q_y + Q. Figure 11 shows the variation in F_x and F_y as the rupture toughness, G_c, and the material elasticity, C₁₀, changes for the different tested materials. G_c and C₁₀ varied from 24.22 $\frac{kN}{m}$ to 114.4 $\frac{kN}{m}$ i.e. 372.3% change, and 3.57 kPa to 4.93 kPa, i.e. 38% change, respectively. This resulted in a 38% (0.44 N to 0.61 N) and 260.2% (0.11 N to 0.39 N) variation in F_x and F_y, respectively. Also, as seen in Figure 11, changes in tip forces are dominated by the variations in G_c, and not C₁₀. The overall bending of the needle is due to a combination of forces along the needle shaft and at the tip. The results of this study indicate that the tip forces are primarily governed by the rupture toughness. But in order to predict the path the needle will follow, the structural stiffness of the needle shaft needs to be included in the model.

Fig. 11.

FE simulation results for needle tip forces with variation in nonlinear material elasticity and rupture toughness.

B. Sensitivity to Needle Tip Bevel Angle and Tissue Elasticity

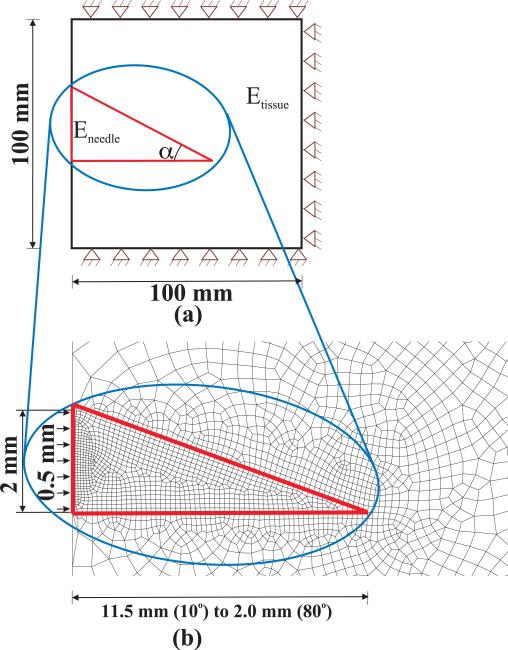
In addition to studying the effect of rupture toughness, FE calculations were also performed to assess the effect of bevel angle and tissue elasticity. Figure 12 shows the simulation setup with boundary conditions and input displacement. Also shown is an example FE mesh used for the study. The associated elements used in this study are a combination of quadrilateral (ABAQUS element CPE8) and triangular (ABAQUS element CPE6 and CPE6M) elements. Unlike the study presented in Section IV-A in which contact was simulated between the needle tip and the elastic medium, here we model the tissue and needle tip as one body but assign different material properties to signify the needle and tissue.

Fig. 12.

(a) FE simulation model for performing tip force versus bevel angle and tissue elasticity sensitivity studies. (b) Example FE mesh for a 20° bevel angle where the elements within the red border have been assigned needle material properties.

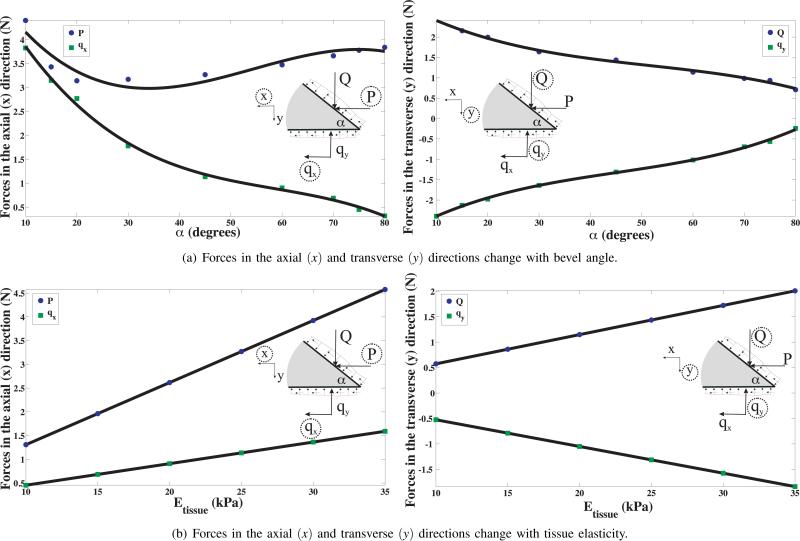
To study the effect of bevel angle, a was varied from 10° to 80°, while the tissue Young's modulus and Poisson's ratio were kept constant at E_tissue = 25 kPa and ν_tissue = 0.45, respectively. In order to study the sensitivity of tip forces to tissue elasticity, E_tissue was varied from 10 kPa to 35 kPa with ν_tissue = 0.45 and α = 45°. It should be noted that a variation in bevel angle entails changing the geometry of the model, and requries re-meshing the model, unlike the cases in which the elastic property of the tissue is changed. For all studies, needle tip Young's modulus and Poisson's ratio were set to E = 2 × 10¹¹ Pa and ν = 0.3, and the needle diameter was 2 mm with applied displacement of 0.5 mm. Also, though the constitutive behavior of the elements is linear, geometric nonlinearity of the elements has been incorporated. Figure 13(a) provides the variation of the needle tip forces in the axial (P, q_x) and transverse (Q, q_y) directions as bevel angle is changed. q_x decreases in a nonlinear manner with increase in bevel angle, while P decreases to a minimum value at approximately 35° and then begins to rise for increase in bevel angle. It is seen that Q monotonically decreases with increase in bevel angle, while q_y monotonically increases (decreases in the opposite direction) with increase in bevel angle. The trends observed for q_x, q_y, and Q could be explained as follows: With the increase in bevel angle, for constant needle diameter, the length of the bevel and bottom edges decrease and hence the sum of the nodal forces along these edges also decrease. In Figure 13(b), Q and q_y linearly increase and decrease (increases in the negative direction) with increase in tissue elasticity, respectively. Also, P and q_x increase linearly with increase in tissue elasticity. The trend followed by the tip forces could be explained as follows: With the increase in Young's modulus (linear elasticity), the tissue resistance increases and thus, the tip forces linearly increase for the same input displacement of 0.5 mm.

Fig. 13.

FE simulation results depicting the sensitivity of tip forces to changes in bevel angle and tissue elasticity, where the solid lines show the trend in the tip forces.

V. Conclusions and Future Work

This study determined bevel-tip needle and tissue interaction forces using FE simulations. We demonstrated a technique to extract physically relevant tissue properties (tissue rupture toughness and nonlinear elasticity) and incorporated them into a FE simulation model in order to simulate the tissue cleavage process.

Tissue properties for several materials were measured experimentally and the sensitivity of the needle tip forces to these parameters were shown using FE simulations. The needle tip forces were observed to be sensitive to the rupture toughness. A 38% variation in nonlinear material elasticity did not produce significant changes in tip forces. For most applications, in which the needle would be steered through soft tissue, large variations in tissue elasticity are not expected. Further, sensitivity of needle tip forces to changes in the bevel angle were also studied through FE simulations. In general, smaller bevel angles resulted in larger axial and transverse tip forces. Possible extentions to this work include refining the toughness experiments and performing simulations with contact and cohesive zone models for various bevel angles. Also, including the needle shaft within the simulation model is essential to predict the needle curvature. Further, the validation of such FE simulation models which include the complete needle-tissue interaction, both along the needle shaft and also at the bevel tip, is integral for planning needle insertion procedures. Validation studies need to be done with independent experimental data, where comparison metrics might include needle insertion forces, tip deflection, or radius of curvature. Currently there only exists a kinematic model that predicts the needle deflection for a user-defined position input [21]. The parameters of this kinematic model must be determined experimentally and are not related to needle geometry or material properties. One of the primary goals within the domain of robotically steered bevel-tip needles is to have an analytical and/or simulation model that would take inputs as the tissue and needle material properties, and needle geometry, and predict the interaction forces and deflection of the needle. Our future work is to develop such a model to estimate the bending needed to robotically steer needles through tissue and also, to choose feasible clinical applications and optimize needle design.