Hippocampal Surface Mapping of Genetic Risk Factors in AD via Sparse Learning Models

Abstract

Genetic mapping of hippocampal shape, an under-explored area, has strong potential as a neurodegeneration biomarker for AD and MCI. This study investigates the genetic effects of top candidate single nucleotide polymorphisms (SNPs) on hippocampal shape features as quantitative traits (QTs) in a large cohort. FS+LDDMM was used to segment hippocampal surfaces from MRI scans and shape features were extracted after surface registration. Elastic net (EN) and sparse canonical correlation analysis (SCCA) were proposed to examine SNP-QT associations, and compared with multiple regression (MR). Although similar in power, EN yielded substantially fewer predictors than MR. Detailed surface mapping of global and localized genetic effects were identified by MR and EN to reveal multi-SNP-single-QT relationships, and by SCCA to discover multi-SNP-multi-QT associations. Shape analysis identified stronger SNP-QT correlations than volume analysis. Sparse multivariate models have greater power to reveal complex SNP-QT relationships. Genetic analysis of quantitative shape features has considerable potential for enhancing mechanistic understanding of complex disorders like AD.

1 Introduction

Recent advances in brain imaging and high throughput genotyping techniques enable new approaches to study the influence of genetic variation on brain structure and function. Existing imaging genetics studies employ summary statistics (e.g., volume, thickness) [7] and detailed voxel-wise measures [8] as phenotypes to discover genetic risk factors. Genetic mapping of hippocampal shape, an under-explored area, has strong potential as a neurodegeneration biomarker for Alzheimer’s disease (AD) and mild cognitive impairment (MCI). The present study investigates genetic effects of top candidate single nucleotide polymorphisms (SNPs) on hippocampal shape features in a large cohort.

Massive univariate analyses are often used in imaging genetics [7, 8], and can quickly identify important associations between individual SNPs and imaging quantitative traits (QTs). However, it treats SNPs and QTs as independent units, and overlooks relationships in which multiple SNPs jointly effect multiple QTs. In this work, two multivariate sparse models, the elastic net and sparse canonical correlation analysis, are used to study genetic effects on hippocampal shape and are expected to have greater power to reveal complex SNP-QT relationships. These models could enable discovery of a small set of relevant features which may provide potential surrogate biomarkers for therapeutic trials.

2 Materials and Methods

Magnetic resonance imaging (MRI) and genotype data were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database [7]. ADNI is a landmark investigation sponsored by the NIH and industrial partners designed to collect longitudinal neuroimaging, biological and clinical information from over 800 participants that will track the neural correlates of memory loss from an early stage. Further information can be found at www.adni-info.org. 582 non-Hispanic Caucasian participants (166 Healthy Control (HC), 287 MCI, 129 AD participants) with segmented hippocampal data and quality controlled (QC) genotype data were included in this study (Table 1).

Table 1.

Participant characteristics

Category	HC	MCI	AD	p-value
Gender (M/F)	91/75	184/103	68/61	0.041
Baseline Age (years; Mean±STD)	76.18±4.91	74.99±7.21	75.36±7.78	0.198
Education (years; Mean±STD)	16.20±2.63	15.71±2.98	15.07±3.04	< 0.005
Handedness (R/L)	155/11	260/27	121/8	0.411

Hippocampal Shape

Hippocampi were segmented from the baseline MRI scans by applying probabilistic-based FreeSurfer and Large Deformation Diffeo-morphic Metric Mapping (FS+LDDMM) [3]. This fully-automated segmentation pipeline first uses FreeSurfer subcortical labeling to provide information for initialization, and then employs LDDMM to generate a diffeomorphic transformation so that anatomical structures can be mapped consistently and smoothly. To remove size effect, total intracranial volume (ICV) was adjusted to a constant (i.e., mean ICV of all HCs) and each hippocampus was scaled accordingly. Rigid body transformation was then applied to register each hippocampus to a template (defined as the mean of all HCs) in a least square fashion. Surface signals were extracted as the deformation along the surface normal direction of the template, and were adjusted for baseline age, gender, education, and handedness using the regression weights derived from the HC participants (Table 1).

Candidate SNPs

The SNP data were genotyped using the Human 610-Quad BeadChip (Illumina, Inc., San Diego, CA). We focused on top AD genetic risk factors, including top 23 SNPs from the AlzGene database [1] as of 09/01/2010, and a SNP from the TOMM40 gene adjacent to the APOE gene. The TOMM40 SNP was included because it was unclear whether the SNP played a unique role in AD or served solely as an APOE marker. Four SNPs were excluded due to failed imputation or quality check. Among the remaining 20 SNPs (Fig. 1(a)), 10 SNPs were available from the ADNI data and 10 SNPs were successfully imputed using MACH v1 [4] and IMPUTE v2 [6] software packages. The QC criteria for the SNP data include (1) call rate check per subject and per SNP marker, (2) gender check, (3) sibling pair identification, (4) the Hardy-Weinberg equilibrium test, (5) marker removal by the minor allele frequency and (6) population stratification. The selected 20 SNPs were numerically coded to test additive genetic effect, i.e., dose dependent effect of the minor allele.

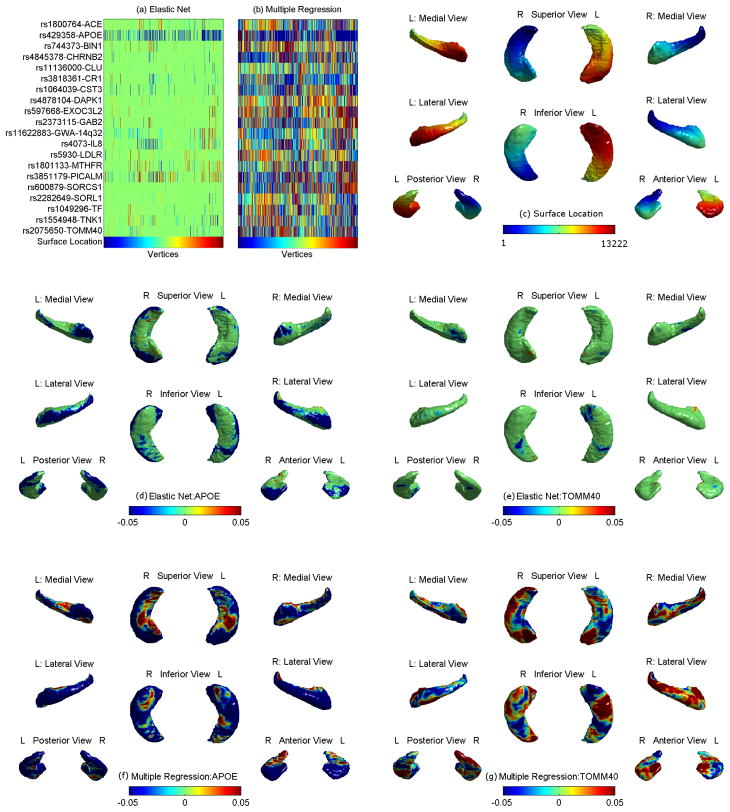
Fig. 1.

(a–c) Heat maps of regression coefficients for elastic net (a) and multiple regression (b), where the hippocampal surface location (bottom row in (a,b)) is color-coded and mapped in (c). (d–e) Surface map of genetic effects of the APOE and TOMM40 SNPs estimated by elastic net (d,e) and multiple regression (f,g).

Overall Strategy

For comparative analysis, multiple regression models were fit using all 20 SNPs to predict the hippocampal volume (mean of left and right, covaried for age, gender, education, handedness and ICV) and, in addition, the surface signal at each location or vertex on the hippocampal surface. The elastic net regression was then applied to identify a small set of relevant SNPs for each surface location. Finally, sparse canonical correlation analysis was used to examine more complex relationships between SNP sets and surface regions.

Multiple Regression

Under the additive model, the surface signals are linearly related to the number of minor alleles. This implies, assuming no interactions between SNPs, the multiple regression model S_i,j = β_0,j + β_1,jSNP_i,1 + … + β₂₀SNP_i,20 + ∈_i,j, where S_i,j is the surface signal at vertex j for subject i. The model utility F test was used to test the null hypothesis of no relationship between S_j and the 20 SNPs for the j = 1, …, 13222 vertices. Gaussian random field theory (RFT) methods [13], implemented in SurfStat [12], were used to ensure the family-wise error rate did not exceed 0.05. While this procedure can detect any linear relationship between S_j and the SNPs this flexibility comes at the cost of reduced power to detect a relationship between a specific SNP and S_j. Sparse regression methods, which seek to accurately predict the response variable using a minimal number of predictors, address this and other regression shortcomings by integrating variable selection and model estimation.

Elastic Net Regression

The ability of sparse regression methods to detect and model genetic relationships was investigated by estimating the above model at each hippocampal location using elastic net (EN). EN produces sparse solutions by adding a coefficient magnitude penalty to the least squares objective function [14]. More specifically, the EN coefficient estimates minimize the penalized least squares objective function ${\text{ElNet}}_j({\beta }_0,{\beta }_1,\dots ,{\beta }_{20})={\sum }_{i=1}^n{(S_{i,j}-{\widehat{S}}_{i,j})}^2+\lambda P_{\alpha }({\beta }_1,\dots ,{\beta }_{20})$, in which Ŝ_i,j = β_0,j + β_1,jSNP_i,1 + … + β_20,jSNP_i,20 and the penalty ${\widehat{P}}_{\alpha }({\beta }_1,\dots ,{\beta }_{20})=\alpha {\sum }_{k=1}^{20}\mid {\beta }_k\mid +(1-\alpha ){\sum }_{k=1}^{20}{\beta }_k^2$ is a convex combination of the L₁ lasso and L₂ ridge penalties. This objective function has two parameters: λ controls the amount of shrinkage; and α adjusts the trade-off between lasso and ridge to capitalize on their strengths and minimize their weaknesses. The preceding regression analysis was duplicated using the Glmnet [2, 9] implementation of EN with α = 0.5 and λ chosen using 10-fold cross-validation.

Sparse Canonical Correlation Analysis

The surface signals represent samples of a smooth function defined on the hippocampus. Methods which capitalize on the resulting correlation between surface signals at neighboring vertices by modeling the joint relationship between multiple surface signals and SNPs should provide increased power to detect any relationships present [10]. To investigate this possibility for linear relationships, sparse canonical correlation analysis (SCCA) was used. Let X_i = (SNP_i,1, SNP_i,2, …, SNP_i,20)′ be the vector of the 20 SNPs for subject i and Y_i = (S_i,1, S_i,2, …, S_i,m)′ be the vector consisting of the surface signals at the m = 13, 222 vertices. Canonical correlation analysis (CCA) produces linear combinations (canonical variates) $U_j=A_j^{\prime }Y$ and $V_j=B_j^{\prime }X$, j = 1, …, 20, such that the correlation between Uj and Vj is maximized subject to orthogonality constraints. Two major weaknesses of CCA are that it requires the number of observations n to exceed the combined dimension of Y and X (here 13,242) and that it produces nonsparse A_j and B_j which are difficult to interpret. The SCCA method employed here ameliorates these weaknesses using the penalized matrix decomposition approach [11]. This method maximizes the correlation between U and V subject to the coefficient vector constraints P₁(A) ≤ c₁ and P₂(B) ≤ c₂. Here the L₁ penalty $P(A)={\sum }_{k=1}^p\mid A(k)\mid$ was used for both P₁ and P₂. Values for c₁ and c₂ were chosen using Witten and Tibshirani’s permutation tuning procedure. The SCCA analyses were computed using the R package PMA (Penalized Multivariate Analysis v.1.0.7.1).

3 Results

In the volumetric analysis of 20 SNPs, only APOE SNP (rs429358) has a significant (p ≤ 0.0004) effect on the hippocampal volume. The Pearson correlation coefficient between the APOE SNP and hippocampal volume was −0.159.

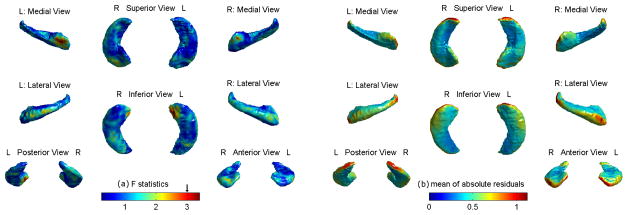
Fig. 2(a) shows the map of F-statistics of multiple regression (MR). Regions with F ≥ 3.0 and spatial extent ≥ 2.4 resels have a random field theory adjusted p-value ≤ 0.05. Fig. 2(b) shows the mean of the absolute residuals (fitted errors) over all subjects. The residual map of elastic net (EN) is almost identical to Fig. 2(b), showing similar predictive power between EN and MR.

Fig. 2.

(a) F-map of multiple regression. (b) Mean of absolution residuals.

However, the predictors selected by EN are much more sparse than those of MR (see Fig. 1(a–c)). Combining Fig. 1(c) with (a) and (b), we can extract the coefficient map for a specific SNP and examine localized genetic effects on the surface. Shown in Fig. 1(d–g) are examples of the APOE and TOMM40 SNPs, which elucidate the benefit of sparsity achieved in EN compared to MR. While MR indicates a global effect on the surface (f,g), EN identifies localized regional effects (d,e) and yields useful information for biomarker discovery.

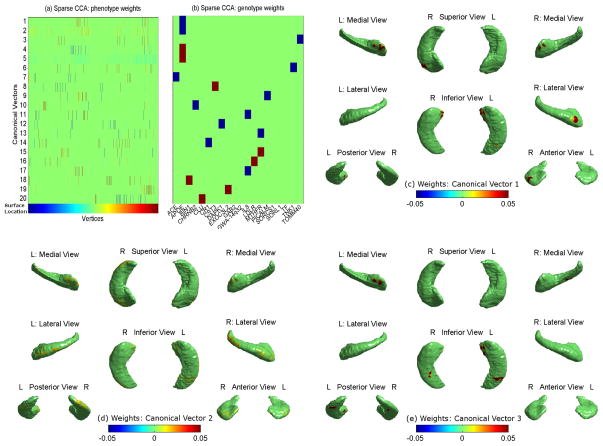
Fig. 3 shows the results of SCCA. Weights of 20 canonical vectors for vertex-based surface signals (a) and SNPs (b) were color-coded as heatmaps. The top three rows in (a) were mapped onto the hippocampal surface and shown in (c–e), respectively. In (a–b), canonical vector pairs (i.e., corresponding rows in (a–b)) were ordered by descending correlation between surface signals and SNPs; and the correlation coefficients of all 20 pairs ranged from 0.26 to 0.17 in descending order. This clearly demonstrated the increased power of shape analysis, since the strongest correlation between each of 20 SNPs and hippocampal volume in our volumetric analysis was between the APOE SNP and hippocampal volume with a magnitude of 0.159. This was corroborated by the fact that the maximum absolute correlation between the surface signal and APOE SNP was 0.20 among all vertices and was 0.19 among the vertices with F ≥ 3.0.

Fig. 3.

(a–b) Weights of canonical vectors ordered by descending correlations between surface signals (a) and SNPs (b). (c–e) Surface maps of the top three canonical vectors: the first three rows in (a) are mapped onto the surface.

In addition, the parameters for SCCA were automatically tuned by 100 permutations to increase the sparsity and smoothness. As a result, the identified surface locations, correlated with each SNP were more sparse than those for the same SNP from EN (see Fig. 3(a–b) vs Fig. 1(a)). Interestingly, the sparsity was maximized for SNPs, since each canonical SNP vector selected exactly one SNP (Fig. 3(b)), yielding a simple model easy to interpret (i.e., multi-SNP-multi-location associations became single-SNP-multi-location ones).

Fig. 3(c–d) show surface regions related with the APOE SNP (rs429358) at different correlation levels. The correlated vertices in Fig. 3(c–d) have non-zero weights as in Fig. 1(d,f), but they are localized to smaller regions in Fig. 3(c–d). Fig. 3(e) shows surface regions related with the TOMM40 SNP (rs2075650). All vertices with non-zero weights in Fig. 3(e) also have non-zero weights in Fig. 1(e,g). However, compared to Fig. 1(e,g), vertices with non-zero weights in Fig. 3(e) are highly sparse and spatially localized to smaller areas. These two types of patterns are complimentary: the associations derived from EN are multi-SNP-single-location, while those found in SCCA are single-SNP-multi-location.

Five-fold cross-validation of SCCA yielded equally sparse SNP-QT patterns. The most consistent canonical component identified in all five trials is similar to the top finding using the entire data: the genetic vector contains only APOE, and the phenotype vector shows a pattern like Fig. 3(c). Training and testing correlation coefficients are 0.279± 0.017 (mean ± SD) and 0.175± 0.068, respectively, while the magnitudes of correlation coefficients between APOE and hippocampal volume in the same data are 0.159 ± 0.012 and 0.163 ± 0.056, respectively.

4 Discussion

Detailed surface mappings of localized genetic effects were identified from our hippocampal shape analysis. Different from existing massive univariate analyses [7, 8], this study is among the first to simultaneously use multiple response variables with multiple predictors for analyzing real neurogenomic data [5, 10] and may be the first for studying genetic influences on hippocampal morphom-etry using this paradigm. In our analyses, we combined two promising sparse multivariate models with a typical morphometric method. Investigation of other statistical models (e.g., [10]) and surface metrics, coupled with pathway analyses, will be important future topics to potentially yield new discoveries. As the best known AD genetic risk factor, APOE was the most prominent signal in all of our analyses, which to some extent validated the efficacy of our methods. Replication in independent large samples will be important to confirm the imaging genetic findings. Genetic analysis of quantitative shape features has considerable potential for examining disease mechanisms from a novel perspective that can inform selection of imaging biomarkers for early detection and therapeutic trials.