Sensitivity and ex vivo validation of finite element models of the domestic pig cranium

Abstract

A finite element (FE) validation and sensitivity study was undertaken on a modern domestic pig cranium. Bone strain data were collected ex vivo from strain gauges, and compared with results from specimen-specific FE models. An isotropic, homogeneous model was created, then input parameters were altered to investigate model sensitivity. Heterogeneous, isotropic models investigated the effects of a constant-thickness, stiffer outer layer (representing cortical bone) atop a more compliant interior (representing cancellous bone). Loading direction and placement of strain gauges were also varied, and the use of 2D membrane elements at strain gauge locations as a method of projecting 3D model strains into the plane of the gauge was investigated. The models correctly estimate the loading conditions of the experiment, yet at some locations fail to reproduce correct principal strain magnitudes, and hence strain ratios. Principal strain orientations are predicted well. The initial model was too stiff by approximately an order of magnitude. Introducing a compliant interior reported strain magnitudes more similar to the ex vivo results without notably affecting strain orientations, ratios or contour patterns, suggesting that this simple heterogeneity was the equivalent of reducing the overall stiffness of the model. Models were generally insensitive to moderate changes in loading direction or strain gauge placement, except in the squamosal portion of the zygomatic arch. The use of membrane elements made negligible differences to the reported strains. The models therefore seem most sensitive to changes in material properties, and suggest that failure to model local heterogeneity in material properties and structure of the bone may be responsible for discrepancies between the experimental and model results. This is partially attributable to a lack of resolution in the CT scans from which the model was built, and partially due to an absence of detailed material properties data for pig cranial bone. Thus, caution is advised when using FE models to estimate absolute numerical values of breaking stress and bite force unless detailed input parameters are available. However, if the objective is to compare relative differences between models, the fact that the strain environment is replicated well means that such investigations can be robust.

Introduction

Finite element analysis has become an established technique in functional morphology and palaeontology for its potential to elucidate functional stresses and strains in complex musculoskeletal geometries (Richmond et al. 2005; Rayfield, 2007). The technique works by discretising the structure of interest into a large but finite number of simple shaped elements, which are interconnected and solved simultaneously to produce a representation of the continuum solution. A number of initial conditions (including magnitude and directions of loading, material properties and constraints) must also be specified to produce the final model. Provided these conditions are modelled appropriately, finite element (FE) models can potentially yield information on biomechanical performance (such as stress, strain and deformation), and the wider relationship between function and form. For palaeontologists in particular, finite element analysis (FEA) allows a unique opportunity to ascertain possible functions and behaviours from extinct taxa, and the ability to observe how mechanical performance may have changed within a lineage through time.

In biological problems, FE input variables may be incredibly complex: for instance, material properties of bone are known to be variable depending on location in the skull and to vary in orientation, i.e. they are not isotropic (Peterson & Dechow, 2003; Wang & Dechow, 2006; Dechow et al. 2010). It is potentially easy to be misled by FEA because analyses will always produce quantitative results, but if the assumptions used to build the models are inaccurate, then the results will be inaccurate also. In order to accurately use FEA, it is important to establish how sensitive models are to variation in the input parameters that may be present within the specimen, as well as intra- and inter-specifically, and to test how accurately FE models represent reality.

To address these issues, validation studies compare FE models with strain data gathered experimentally from actual bone. Most comparative morphological and palaeontological applications of FEA are concerned with the mechanics of the skull, and this is where most validation studies have focused. The skull is an incredibly complex structure, and many of its inherent variables have begun to be validated, including material properties (Strait et al. 2005; Panagiotopoulou et al. 2010; Davis et al. 2011), muscle loadings (Ross et al. 2005), dentition and periodontal ligament (PDL; Marinescu et al. 2005; Panagiotopoulou et al. 2011), and the presence of cranial sutures (Kupczik et al. 2007). Additionally, sensitivity tests have varied the model parameters to assess the manner in which they affect results, but without comparison with experimental strain data (Grosse et al. 2007; Wroe et al. 2007; Curtis et al. 2008; Wang et al. 2010; Gröning et al. 2011a). All of the studies mentioned above were undertaken on primates. There is a remarkable paucity of validation or sensitivity data for other taxa [only alligators (Metzger et al. 2005; Reed et al. 2011), Uromastyx (Moazen et al. 2008, 2009), Komodo dragons (Moreno et al. 2008) and ostriches (Rayfield, 2011)]. Of course, in palaeontology, direct validation of extinct taxa is impossible. Thus, it is important to perform validation studies on a range of modern taxa, so as to establish an estimate of the likely errors encountered by using input data from modern analogues that are functionally and/or phylogenetically closely related to the extinct taxa of interest.

The aims of this study were to determine whether FE models of a modern domestic pig would match with experimental strain data obtained from the same animal ex vivo. Then, from this establish which variables the model was most sensitive to, and how variations in the input parameters affected results. To the authors’ knowledge, this represents the first FE validation of a non-primate mammalian cranium. Pigs present an ideal model for validation: they are generalised, omnivorous artiodactyls with no behavioural or dietary specialisations that obviously influence skull morphology, and there is an extensive literature on pig cranial anatomy and in vivo strains (Herring, 1972; Herring & Scapino, 1973; Herring et al. 2001; Rafferty et al. 2003). Moreover, it will be interesting to compare the results of this study with previous FE validation work, to determine any common results; similarities between pigs and macaques may be indicative of broader mammalian trends if results differ from those found in reptilian taxa. Similarities between all validated taxa may demonstrate more general biomechanical rules.

The initial FE model was set up to be as simple as possible, with isotropic homogeneous material properties, simplified muscle loading, and no sutures or PDL. This would establish a baseline of error likely to be encountered in the absence of detailed data, such as would be the case in a palaeontological investigation. The input parameters were then varied to determine how sensitive the model was to a particular parameter, and whether these alterations resulted in a more accurate model when compared with the experimental strain. Previous validation studies report varying degrees of success replicating measured strain (Marinescu et al. 2005; Metzger et al. 2005; Ross et al. 2005, 2011; Strait et al. 2005; Kupczik et al. 2007; Gröning et al. 2009; Panagiotopoulou et al. 2010, 2011; Rayfield, 2011). However, in practice the threshold for what is an acceptable amount of error between the two datasets will, to an extent, depend on the question that the analysis seeks to address. For example, whether it is sufficient to merely replicate the patterns of strain or stress, or are absolute magnitudes and bite force estimates a desired outcome?

Materials and methods

Ex vivo experiment

Strain gauges are electrical components that experience changes in length as changes in resistance. This property can be used to measure strain on a surface. In order to accurately measure the orientation of maximum principal strain, a strain gauge must comprise of multiple measuring grids. Rectangular rosette gauges have three grids orientated at 45 ° to one another, and are available in stacked or planar configurations. Because of their larger size, planar rosettes are rarely used in vivo as they are more invasive (Herring et al. 2001; Thomason et al. 2001; Ross et al. 2011), and obviously their size prohibits their use on smaller specimens (Rayfield, 2011). However, in this experiment, where the bones are large and invasion is not an issue, planar rosettes are preferred for two reasons, as follows. (i) Resistance is also affected by heat. Bone is a poor thermal conductor, and gauges in a stacked configuration may overheat, causing their reporting of strain to drift (Tech Note TN-515; Vishay Measurements Group, Basingstoke, UK). (ii) Bone is a heterogeneous material. Larger gauges will average strain over a larger area, meaning that small heterogeneities in the bony material will not overtly influence the reporting of local strain. In this experiment, 16 planar rosette gauges (C2A-06-062LR-350; Vishay Micro-Measurements, Basingstoke, UK) were used.

Gauges were attached to locations on the skull of a modern domestic pig (Sus scrofa; Fig. 1A). The skull was manually defleshed with a scalpel, and the gauge sites prepared: periosteum was removed with pumice powder and the site cleaned with alcohol, before applying the gauges with cyanoacrylate adhesive (M-Bond 200; Vishay Micro-Measurements, Basingstoke, UK). The gauges were then covered with a waterproof silicon rubber coating for protection (3140 RTV Coating; Dow Corning, Midland, MI, USA). Strain was recorded by the 16 gauges using an amplifier (5100B; Vishay Micro-Measurements, Basingstoke, UK), and converted to principle strains and orientations using StrainSmart 4.01 software (Vishay Measurements Group, Basingstoke, UK). Preliminary drift tests were conducted for all gauges before loading. When each new gauge was connected, it was left unloaded for 30 min, to assess whether the gauges were thermally drifting. Over 30 min, the average thermal drift on the gauges was 11.58 με. The standard deviation from the mean unloaded strain gives an indication of the noise on the gauges, which was 2.00 με. During these drift tests, it was noticed that one of the strain grids on G1 (on the dorsal premaxilla) was drifting by 59 με and, as a result, the gauge had trouble zeroing and reporting stable strain. For this reason, results from G1 were not considered further.

Fig. 1.

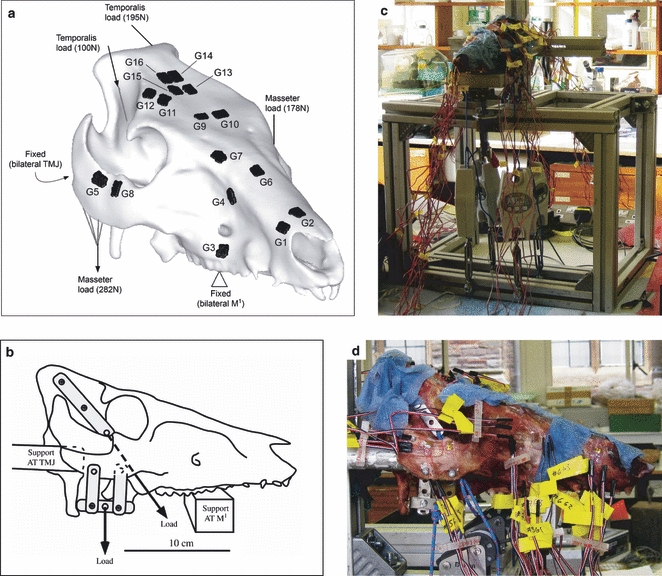
(A) A CT-derived 3D model of the pig specimen showing gauge locations, and FE loading and constraints simulating (B) diagram of loading details in experiment. (C) Photograph of experimental set-up, and (D) closer photo of load application. G, gauge; M¹, 1st molar tooth; TMJ, temporomandibular joint.

A custom-built aluminium testing rig was designed to apply loads representing the temporalis and the combined masseter/zygomaticomandibularis muscles (Fig. 1). Mastication is a complex muscular process (Herring & Scapino, 1973), which would be impossible to replicate accurately ex vivo. As a validation, the objective of the model was not to replicate in vivo loading, but to test how accurately FE reported experimentally derived strains; hence it was decided that a simpler approximation would provide a scenario that is easy to replicate both experimentally and in the computational analysis, while also applying a similar load to that which the structure is adapted for. As a static load was applied here, the intricacies of muscle activation patterns were not considered, nor were the presence of functional units within the muscles that do not all activate contemporaneously. Despite being active with the masseter during jaw adduction in vivo, the medial pterygoid was not included for practical reasons, as attaching experimental loading to the pterygoid tubercle from which the muscle arises was problematic. It has been shown that the dominant source of masticatory loading in the pig skull is from the masseter (Herring et al. 2001), thus this omission was considered justifiable.

The specimen was supported bilaterally by aluminium bars at the temporomandibular joints (TMJ) and bilaterally at the 1st molar teeth (M¹). Loads were applied to the attachment sites of the masseter and temporalis muscles. Thin (1 mm) steel strips were attached to the zygomatic arch with 3.5-mm bolts, and to the temporal bone using 3.5-mm self-tapping screws. These steel strips were tied with non-slipping bowline knots to hanging balances [HCB 100K200 (masseter) and HCB 50K100 (temporalis), Kern & Sohn GmbH, Balingen, Germany] using 3-mm low-stretch polyester cord (3 mm Magic Speed, LIROS GmbH, Berg, Germany). In the case of the loads from the temporalis, these passed over low-friction pulleys (Size 1 upright block, Barton Marine Equipment, Kent, UK) to apply the desired line-of-action determined from dissection. The hanging balances were then attached to rigging screws (6 mm Fork Bottlescrew; Sea Sure, Hampshire, UK). Manually tightening the screws applied tension without twisting, which was recorded by the hanging balances to a precision of 1 N. During the experiment, the specimen was kept moist by applying a 50 : 50 mixture of glycerine and water between each loading.

The load was applied with the right masseter (RM)/left temporalis (LT) pair ‘active’, and the left masseter (LM)/right temporalis (RT) pair ‘balancing’. The desired load was RM = 300 N; LT, LM = 200 N, RT = 100 N. This load was an idealised one, based on bite force measurements from pigs of a similar age and weight to the specimen (Bousdras et al. 2006), and the observation from electromyography that, although pigs bite bilaterally, their muscle activation is not symmetrical, with the working-side master and balancing-side temporalis acting together to close the jaw (Herring & Scapino, 1973; Herring & Teng, 2000).

Because there was only space on the amplifier for four rosette gauges to be tested at any time, the gauges were divided into four groups of four (G1–G4, G5–G8, G9–G12 and G13–G16) and the experiment repeated three times for each group, to assess error in the repetition of loading. Gauges were zeroed, and the screws were tightened one at a time by approximately 50 N increments, in the following order: RM, LT, LM, RT. Once the final load was achieved, it was allowed to stabilise for 1 min, then strain was recorded for 2 min. After unloading, the specimen was allowed to recover for 15 min to allow any residual strain to dissipate.

Upon unloading, it was noticed that the hanging balances reported a load still present (mean RM = 20 ± 4 N, LT = 5 ± 2 N, LM = 24 ± 6 N, RT = 2 ± 2 N). Whilst every effort had been made to reduce these effects, this probably represented load that was lost to friction, elasticity and knot-tightening in the cords, as the strain gauges returned to zero following unloading, suggesting that plastic deformation of the bone had not occurred. For each loading, the lost load was recorded and deducted from the experimental load to determine the true load applied by each screw.

FEA

The pig specimen (Large White Breed, age approximately 6 months, skull dimensions 247 × 141 × 133 mm) was CT scanned at the Royal Veterinary College on a Picker PQ5000 medical scanner (0.55 mm pixel size, 2 mm slice thickness, 120 kV, 200 mA). Scan data were imported into amira 4.1 (Mercury Computer Systems, USA), and the bony and dental materials were segmented out, generating a stereolithography surface that was imported into HyperMesh 10.0 (Altair Engineering, USA) to generate a specimen-specific FE model.

The surface was ‘cleaned’ to remove mesh errors (free edges, holes, T-connections), and the HyperMesh‘shrink-wrap’ function was used to generate a mesh of good aspect ratio, evenly sized elements (as tested using standard element quality checks in HyperMesh and Abaqus). Following a convergence test (Bright & Rayfield, 2011), a model with 1 749 149 second-order (quadratic 10-noded) tetrahedral elements [modal element size of 0.92 mm, with 10 nodes per element (TET10)] was confirmed to report strain at all gauge sites within 5% (except G7, which was within 12%), and was selected for the analysis. From this mesh, 23 models were created to test sensitivity and validity. These models are summarised in Table 1, and described in detail below.

Table 1.

Material properties and loading assignments for all models in the analysis

		E (GPa)		ν
Model	Element type	Cortical	Cancellous	Cortical	Cancellous	Alteration of masseter (°)	Alteration of temporalis (°)
HOM	TET10	12.5	N/A	0.35	N/A	0	0
LOAD_antmass2.5	TET4	12.5	N/A	0.35	N/A	2.5 anterior	0
LOAD_antmass5	TET4	12.5	N/A	0.35	N/A	5 anterior	0
LOAD_antmass10	TET4	12.5	N/A	0.35	N/A	10 anterior	0
LOAD_postmass2.5	TET4	12.5	N/A	0.35	N/A	2.5 posterior	0
LOAD_postmass5	TET4	12.5	N/A	0.35	N/A	5 posterior	0
LOAD_postmass10	TET4	12.5	N/A	0.35	N/A	10 posterior	0
LOAD_latmass2.5	TET4	12.5	N/A	0.35	N/A	2.5 lateral	0
LOAD_latmass5	TET4	12.5	N/A	0.35	N/A	5 lateral	0
LOAD_latmass10	TET4	12.5	N/A	0.35	N/A	10 lateral	0
LOAD_medmass2.5	TET4	12.5	N/A	0.35	N/A	2.5 medial	0
LOAD_medmass5	TET4	12.5	N/A	0.35	N/A	5 medial	0
LOAD_medmass10	TET4	12.5	N/A	0.35	N/A	10 medial	0
LOAD_lattemp2.5	TET4	12.5	N/A	0.35	N/A	0	2.5 lateral
LOAD_lattemp5	TET4	12.5	N/A	0.35	N/A	0	5 lateral
LOAD_lattemp10	TET4	12.5	N/A	0.35	N/A	0	10 lateral
LOAD_venttemp2.5	TET4	12.5	N/A	0.35	N/A	0	2.5 ventral
LOAD_venttemp5	TET4	12.5	N/A	0.35	N/A	0	5 ventral
LOAD_venttemp10	TET4	12.5	N/A	0.35	N/A	0	10 ventral
HET_6	TET10	12.5	6	0.35	0.35	0	0
HET_1	TET10	12.5	1	0.35	0.35	0	0
HET_6ν	TET10	12.5	6	0.35	0.2	0	0
HET_1ν	TET10	12.5	1	0.35	0.2	0	0

TET4, 1st order linear (4-noded) tetrahedra; TET10, 2nd order quadratic (10-noded) tetrahedra.

Initial model (HOM model)

Material properties were assigned initially as isotropic and homogenous. In the absence of data for pigs, the average properties of muscle-bearing human cortical bone from the cranial vault were used (E = 12.5 GPa, ν = 0.35; Peterson & Dechow, 2003). The teeth were modelled as being continuous with bone, and were assigned the same material properties. Debate persists on whether it is necessary to include the PDL in FE models. A validation study by Panagiotopoulou et al. (2011) demonstrated that models of the macaque mandible are relatively insensitive to the presence of the PDL beyond the immediate vicinity on the alveolar region. Conversely, other validation and sensitivity tests (Marinescu et al. 2005; Gröning et al. 2011a) have found that neglecting to model the PDL can result in models that are too stiff and deform differently to models with a PDL. In this study, CT resolution was insufficient to precisely resolve the position of the tooth roots, meaning that the PDL could not be incorporated accurately.

Loads and constraints were applied to replicate the conditions of the ex vivo experiment. Repetition of loading introduced some variation into the experiment, as it was difficult to consistently apply the same load, given that not all the load was successfully transferred to the specimen as mentioned earlier. For this reason, the loads applied to the model were averages of the experimental loads. The final load applied to the model was RM = 282 N [experimental standard deviation (ESD) = 4 N], LT = 195 N (ESD = 2 N), LM = 178 N (ESD = 6 N), RT = 100 N (ESD = 3 N), giving a total model load of 755 N.

Constraints were applied to 25 nodes bilaterally at the TMJ, preventing translation in the x-, y- and z-axes, and to 20 nodes bilaterally at the 1st molar teeth preventing translation in the dorso-ventral (y) axis. Muscle vectors were defined to simulate the lines of action of the cords in the experiment, and the corrected experimental loads were applied via rigid body elements (RBE3 in Abaqus; Fig. 1A).

Loading direction (LOAD models)

To assess the effects of loading direction, the vector of load application was varied by 2.5 °, 5 ° and 10 ° in the anterior-posterior and medio-lateral directions in the RM, and in the lateral and ventral directions in the RT, resulting in 18 further models (LOAD models, Table 1). Loading was not varied medially in the temporalis because the position of the bone meant that it was not possible for the load to be applied more medially in the experiment. Similarly, the load was not varied dorsally because doing so would have produced a line of action equivalent to the ropes of the experiment intersecting the zygomatic arch. In an earlier paper, Bright & Rayfield (2011) demonstrated that, because of its high resolution, this model could be run satisfactorily using first-order [4-noded (TET4)] elements without notably affecting strains. As models with first-order elements take significantly less time to run, the load sensitivity models were run with 4-noded elements to save time. All other boundary conditions were kept the same as in the HOM model.

Cancellous bone (HET models)

It is recognised that the structure of cancellous bone is less stiff than that of cortical bone, a factor that may be relevant in FEA. Although cortical and cancellous bone could be identified in the CT scans, the fact that these were of relatively low resolution meant that consistently distinguishing cancellous from cortical bone was not possible at all locations, nor could the internal architecture of the cancellous bone be seen. A higher resolution scan, though desirable, was not possible due to the large size of the specimen. To assess the effects of a stiffer cortex surrounding cancellous bone, the outermost layer of elements in the model were defined as a cortical bone shell with the properties of the solid model (E = 12.5 GPa, ν = 0.35) one element thick (0.92 mm), and the remaining internal elements were assigned less stiff material properties to determine whether this would affect the patterns or magnitudes of strain. Bone was over 2 mm thick in all locations. The thinnest bone was in the palate and anterior to the orbit (2.5 mm), and the thickest bone was located around the braincase (10.5–36 mm). Gauges were located on bone at least 5 mm thick. Cortical bone is not universally thick over the whole skull, but these idealised models remove any ambiguity from the results that may be caused by the uneven distribution of real bony material. Currey (2002) cites cancellous bone properties ranging from 0.004 to 0.35 GPa in humans and 0.035 to 7 GPa in non-humans. To encompass this range, values of 6 and 1 GPa were tested, with Poisson's ratio kept at ν = 0.35. Six gigapascals represents the higher range of values, and is roughly half the stiffness of the cortical bone value used. The value of 1 GPa is closer to the values reported for humans, and was shown by Panagiotopoulou et al. (2010) to give good validation results when using a similar technique on a macaque mandible.

Cancellous bone is also believed to have a lower Poisson's ratio than cortical bone (ν = 0.2; Dalstra et al. 1993). To test the effects of varying cancellous bone Poisson's ratio, the HET models were run again, but this time with ν = 0.2. All models used second-order elements, assumed isotropy, and loading was kept as in the HOM model.

Other variables

Orthotropy is well known from long bones and the mandible across several taxa, and has been demonstrated to be present in the cranium to varying degrees as well (O'Mahony et al. 2000; Zapata et al. 2010; Chung & Dechow, 2011). As material properties vary throughout the skull, and may not be aligned with a standard anatomical axis (Peterson & Dechow, 2003; Wang & Dechow, 2006; Dechow et al. 2010), defining cranial orthotropy in an FE model is considerably difficult, even with detailed measurements of material properties (which were unavailable for this study). For this reason, the effects of orthotropy are not modelled here.

Based on numerous studies of modern mammals, cranial sutures are suspected to play a functional role in the pig (Herring & Mucci, 1991; Rafferty & Herring, 1999; Herring & Teng, 2000; Herring et al. 2001; Rafferty et al. 2003; Popowics & Herring, 2007) and other animals (Jaslow, 1990; Jaslow & Biewener, 1995; Thomason et al. 2001; Kupczik et al. 2007; Moazen et al. 2009). It is therefore desirable to investigate whether ex vivo and in silico strains are comparable without the added modelling complexity of introducing cranial sutures. The study presented here sets up a further investigation into the effects of cranial sutures on FE model validation, and will be considered in a future paper.

Data extraction

Node sets representing the positions of 16 strain gauges were defined. This allowed the models to be queried precisely for comparison with the experiment, as well as amongst each other. The placement of the gauge sites on the experimental specimen was measured with calipers, and those measurements were repeated in HyperMesh to confirm gauges were positioned correctly. To ensure that sampling of the node sets was not affecting results, these ‘virtual gauges’ were widened by 1 and 2 mm on each edge and compared with the other results.

Membrane elements (M3D6 in Abaqus) were also constructed in the positions of the gauges. These are two-dimensional elements that share nodes with the original node sets, and were constructed with negligible thickness (0.001 mm) and material properties (E = 0.001 GPa, ν = 0.35), so they would move with the underlying model without affecting its results by introducing additional stiffness. This technique allows the reporting of in-plane stresses and strains, to accommodate the fact that FEA applied here is a 3D technique, whereas strain gauges are 2D and only report a projection of 3D strain that could lead to errors in the calculation of principal strains and their orientations. Principal strains and strain orientations from the membrane elements were compared with results from the node sets to assess differences between the two practices. The issue of 3D vs. 2D strain conversions has only been directly addressed once before in the FE validation literature (Ross et al. 2011), using custom-written matlab software for use with strain output from Strand7.

The model was solved in Abaqus 6.8.2 (Dassault Systèmes Simulia, Providence, RI, USA) on desktop PC (Windows 64-bit Vista Business, Intel Xeon x5450 3.00 GHz CPU, 64 GB RAM).

Results

Ex vivo experiment

Results from the ex vivo experiment are presented in Table 2. Gauge 1 drifted during preliminary tests, making it unreliable. The results of G1 show high standard errors (SE) in the measurements of compressive strain and strain ratio, and as such are unsuitable for further comparison with the FE models. Gauge 6 also reports a SE higher than the mean for ε_max and strain ratio. This is because G6 recorded maximum principal strains of −23.3 με; +21.3 με; −23.3 με during the three repetitions of loading. The reason for this flip from compressive to tensile strain and back again is unclear, as the loading was consistent, and other gauges recording at the same time do not show this phenomenon (G5, G7, G8). The lack of repeatability in G6 means that it too is unreliable. The other 14 gauges were stable, giving SE ≤ 14% of the grand mean for ε_max, ε_min, maximum shear strain (γ_max) and strain ratio. Strain orientation (as measured from gauge grid 1 to the maximum principal strain axis) is very stable, showing SE ≤ 1 ° in most locations.

Table 2.

Experimental grand means over three repeated loadings, ± standard error

	G1	G2	G3	G4	G5	G6	G7	G8	G9	G10	G11	G12	G13	G14	G15	G16
Tension (εmax)	108 ± 10	52 ± 5	388 ± 22	264 ± 5	456 ± 33	−8.4 ± 15	485 ± 13	68 ± 5	81 ± 3	40 ± 3	60 ± 3	151 ± 5	17 ± 1	21 ± 3	23 ± 2	120 ± 17
Compression (εmin)	−6 ± 6	−84 ± 2	−375 ± 33	−107 ± 6	−288 ± 17	−54 ± 4	−196 ± 12	−606 ± 18	−122 ± 9	−84 ± 12	−132 ± 6	−196 ± 5	−176 ± 11	−74 ± 6	−57 ± 7	−40 ± 4
Orientation (angle from grid 1 to εmax axis)	−78 ± 3	−49 ± 0.8	45 ± 0.4	46 ± 0.3	−85 ± 0.6	24 ± 9	28 ± 0.8	−28 ± 1	−24 ± 1	−26 ± 3	−53 ± 2	−85 ± 1	44 ± 0.9	70 ± 5	57 ± 2	87 ± 1
Strain ratio (εmax/|εmin|)	14 ± 5	0.62 ± 0.05	1.04 ± 0.04	2.48 ± 0.16	1.58 ± 0.02	−0.11 ± 0.29	2.45 ± 0.23	0.11 ± 0.01	0.67 ± 0.02	0.49 ± 0.06	0.46 ± 0.04	0.77 ± 0.02	0.10 ± 0.004	0.28 ± 0.01	0.42 ± 0.10	2.94 ± 0.17
Shear (γmax = εmax−εmin)	115 ± 8	135 ± 7	763 ± 55	371 ± 7	743 ± 50	46 ± 11	681 ± 4	674 ± 14	202 ± 12	125 ± 14	192 ± 4	347 ± 9	193 ± 12	94 ± 9	80 ± 5	160 ± 21

As expected, principal strains are highest in the zygomatic arch (G5, G8) in close proximity to the application of loading. High strains were also observed in the maxilla (G4), dorsal to the loaded tooth (G3) and in the frontal bone near the naso-frontal suture (G7). The right parietal bone also experienced relatively high strains (G12, G16). Maximum shear strain is also highest at these locations (Table 2). Strains are lowest elsewhere in the cranial vault (G9, G10, G11, G13, G14, G15) and in the rostrum (G2).

Strain ratio (ε_max/|ε_min|) is an indicator of the strain regime: values > 1 indicate that tension is greater than compression, and values < 1 indicate that compression is greater than tension. Tension is observed in G4, G7 and G16 and, to a lesser extent, G5. Compression is observed in G8 and G13. The state of strain at the other gauge sites is more complicated, with neither tension nor compression dominating the strain regime. Approximately equal but opposite strains, such as are present in G3 and G12, are indicative of shearing. Figure 2 shows how these axes of tension and compression are aligned with the skull.

Fig. 2.

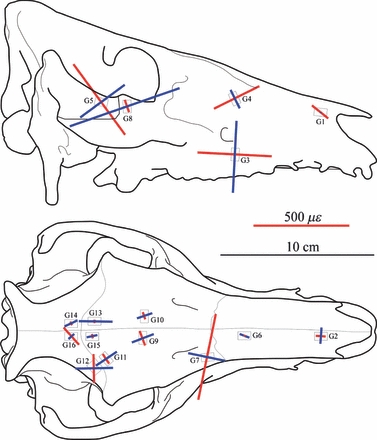
Principal strain orientations recorded during ex vivo experimentation. Red lines indicate ε_max (tension) and blue lines indicate ε_min (compression). Lengths of lines are scaled to show strain magnitude.

FEA

Material properties

The most obvious result that can be seen when comparing the absolute experimental strain magnitudes to the homogeneous (HOM) and heterogeneous (HET) model results (Fig. 3) is that the models are too stiff, by approximately an order of magnitude. Nevertheless, it can be seen that many gauges are in general agreement between the experiment and the model, especially in the frontal and parietal bones (G9–G16). Additionally, it can be seen that, although the magnitudes are underestimated, the model creates peaks of strain at G3, G5 and ε_min G8 that are comparable with the experiment. In some locations, the model recognises peaks of strain that were absent in the experiment (ε_max G8) or vice versa (ε_max G7, G12, G16). The model also appears to be appropriately estimating patterns of maximum shear strain, following the experimental peaks in most locations (Fig. 4; although absolute magnitudes are again low), but does fail to replicate peaks of shear at G7 and G12. Strain orientations between the experiment and both the HOM and HET models, however, are remarkably consistent, with most model gauges differing from the experiment by < 10 °, and falling easily within the experimental range (Fig. 5). Gauges 9, G10 and G15 are within 12 ° of the experiment but outside of the 2 SE range; G8, G11, G14 and G16 fall between 25 ° and 40 ° of the experiment.

Fig. 3.

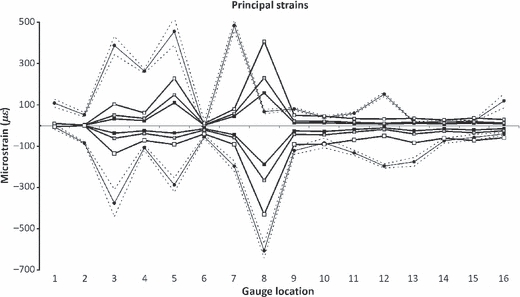
Principal strain magnitudes, comparing experimental results (black circular markers), with HOM (black squares), HET_6 (grey squares) and HET_1 (white squares). Dashed lines show 2 SE of the experimental mean. G1 and G6 gave unstable experimental results, and should be disregarded.

Fig. 4.

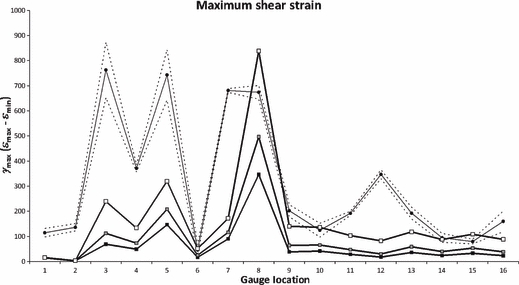
Maximum shear strains (γ_max), comparing experimental results (circular markers), with HOM (black squares), HET_6 (grey squares) and HET_1 (white squares). Dashed lines show 2 SE of the experimental mean. G1 and G6 gave unstable experimental results, and should be disregarded.

Fig. 5.

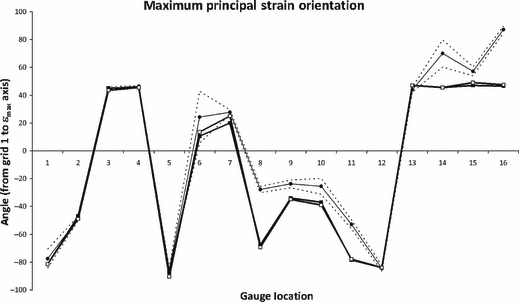
Principal strain orientations, comparing experimental results (circular markers), with HOM (black squares) and HET_6 (white squares). Dashed lines show 2 SE of the experimental mean. G1 and G6 gave unstable experimental results, and should be disregarded.

Because strain ratios remove the effects of magnitude, they are a useful method for determining whether the models and experiment are deforming in a comparable manner (Fig. 6). In half the locations (G3, G9, G10, G11, G12, G14, G15), the models and the experimental strain ratios match well. In the other half (G2, G4, G5, G7, G8, G13, G16), they do not.

Fig. 6.

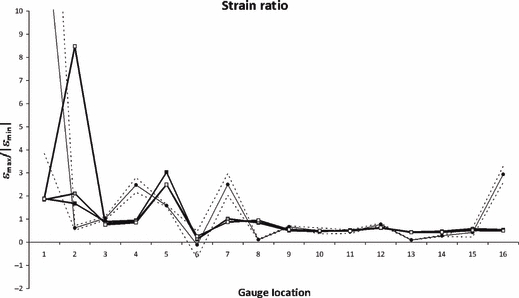
Strain ratios, comparing experimental results (circular markers), with HOM (black squares), HET_6 (grey squares) and HET_1 (white squares). Dashed lines show 2 SE of the experimental mean. G1 and G6 gave unstable experimental results, and should be disregarded.

In Figs 3–6, we see that decreasing the Young's modulus of the cancellous interior in the HET models increases the principal and shear strains in the model, but barely affects the strain ratios or orientations. This lack of change is also reflected qualitatively in contour plots of the skull (Fig. 7). However, strain ratios are increased and decreased, respectively, in G2 and G5 and, in the case of G2, this increase takes the models further from the experimental results; HET_1ν dramatically so. Decreasing the Poisson's ratio of the cancellous interior to ν = 0.2 makes principal strains very slightly lower than when ν = 0.35, which in turn makes strain ratios slightly higher, but this effect is very small (Table S1).

Fig. 7.

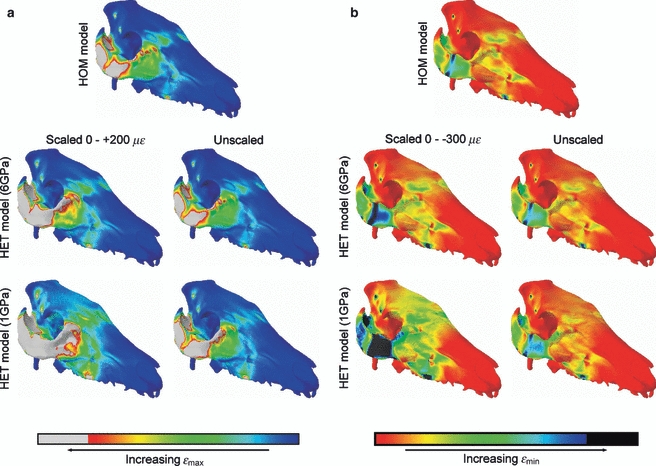
The effects of varying material properties on contours of ε_max (A) and ε_min (B). When the contours are scaled to the same values, values above +200 με (A) and below −300 με (B) are displayed as white and black areas, respectively. Higher strain magnitudes are evident in the less stiff HET models, but when left unscaled it can be seen that the contour patterns are barely affected.

Membrane elements

Membrane elements are 2D elements that were placed in the model to accommodate the fact that, while the FEA applied here is 3D, strain gauges are planar, and thus only able to report a 2D projection of 3D strains. It was found that the use of membrane elements in this model made negligible differences to the output strains in most locations (< 1%; Table 3). Large percentage differences between models with and without membranes in principal strains, and hence strain ratios and γ_max, were noted in G2 (ε_min = 9.99%), G5 (ε_min = 64.48%) and G6 (ε_max = 75.12%). Strain orientations were affected by < 3 ° in all locations. When strain ratios are plotted (Fig. 8), the lack of difference between models with and without membranes is clearly apparent.

Table 3.

Comparison between HOM models with and without membrane elements

	G1	G2	G3	G4	G5	G6	G7	G8	G9	G10	G11	G12	G13	G14	G15	G16
εmax
NO	9.38	1.72	32.39	23.95	115.19	7.19	45.53	156.94	12.99	13.14	9.76	6.76	11.05	7.72	12.11	8.21
MEM	9.40	1.70	32.49	23.91	110.01	1.79	45.50	158.23	12.96	13.11	9.79	6.78	11.03	7.73	12.14	8.17
% difference	0.31	0.84	0.29	0.16	4.50	75.12	0.06	0.82	0.21	0.25	0.31	0.28	0.17	0.10	0.20	0.40
εmin
NO	−4.93	−1.12	−36.54	−25.29	−59.74	−15.14	−44.28	−189.57	−25.73	−28.54	−18.64	−10.91	−24.99	−16.39	−20.91	−15.15
MEM	−4.98	−1.01	−36.51	−25.24	−36.32	−15.06	−44.73	−188.37	−25.64	−28.44	−18.71	−10.89	−25.11	−16.41	−20.91	−15.13
% difference	1.08	9.99	0.07	0.19	64.48	0.54	1.02	0.64	0.33	0.33	0.39	0.20	0.46	0.12	0.02	0.13
Strain ratio
NO	1.90	1.54	0.89	0.95	1.93	0.47	1.03	0.83	0.50	0.46	0.52	0.62	0.44	0.47	0.58	0.54
MEM	1.89	1.68	0.89	0.95	3.03	0.12	1.02	0.84	0.51	0.46	0.52	0.62	0.44	0.47	0.58	0.54
% difference	0.76	8.32	0.36	0.03	36.33	74.99	1.08	1.45	0.12	0.08	0.07	0.47	0.62	0.02	0.17	0.27
γmax
NO	14.30	2.83	68.93	49.23	174.93	22.33	89.81	346.51	38.72	41.68	28.39	17.67	36.04	24.11	33.02	23.36
MEM	14.38	2.72	68.99	49.15	146.33	16.85	90.24	346.60	38.61	41.56	28.50	17.66	36.14	24.14	33.05	23.30
% difference	0.57	4.09	0.10	0.17	16.35	24.55	0.47	0.03	0.29	0.31	0.36	0.01	0.27	0.11	0.09	0.23
Orientation
NO	−81.00	−45.50	42.50	45.00	−88.00	9.00	20.00	−67.00	−33.00	−38.00	−78.50	−84.00	47.00	44.00	48.00	47.00
MEM	−81.50	−47.00	45.00	45.50	−87.50	10.50	20.00	−67.50	−34.00	−37.00	−78.50	−84.00	47.00	45.50	47.00	46.50
Absolute difference (°)	0.50	1.50	2.50	0.50	0.50	1.50	0.00	0.50	1.00	1.00	0.00	0.00	0.00	1.50	1.00	0.50

Fig. 8.

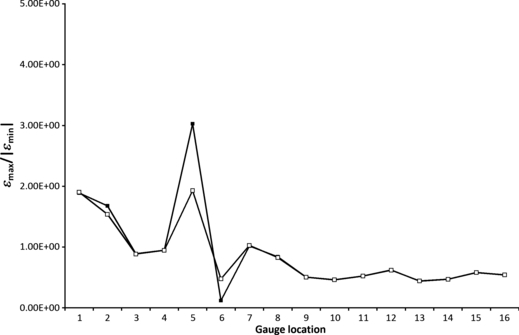
Strain ratio comparing HOM models with (filled squares) and without (open squares) membrane elements.

Virtual gauge sampling

To examine the effects that virtual strain gauge size may be having on model results, additional nodes were selected around the gauge circumference for one (+1) or two (+2) elements, corresponding to an increase of the dimensions of the virtual gauges by 1 or 2 mm, respectively. The effects of this sensitivity test on strain ratio are shown in Table 4 and Fig. 9, which shows that only G2, G5 and G6 are affected by gauge size. In all cases, expanding the area of the gauge brings the strain ratio closer to 1. In the case of G5, this expansion gives a result that is comparable to the experimental result.

Table 4.

Comparison between strain ratios in HOM models at original gauge sizes (+0), and the expanded gauge sizes (+1, +2)

	G1	G2	G3	G4	G5	G6	G7	G8	G9	G10	G11	G12	G13	G14	G15	G16
Ex vivo	14.10	0.62	1.04	2.48	1.58	−0.11	2.50	0.11	0.67	0.49	0.46	0.77	0.10	0.28	0.42	2.94
+0	1.90	1.54	0.89	0.95	1.93	0.47	1.03	0.83	0.50	0.46	0.52	0.62	0.44	0.47	0.58	0.54
+1	1.93	1.44	0.88	0.96	1.73	0.47	1.03	0.82	0.51	0.46	0.52	0.61	0.45	0.47	0.58	0.54
+2	1.94	1.37	0.87	0.98	1.56	0.48	1.01	0.82	0.51	0.46	0.52	0.61	0.46	0.46	0.58	0.55

Fig. 9.

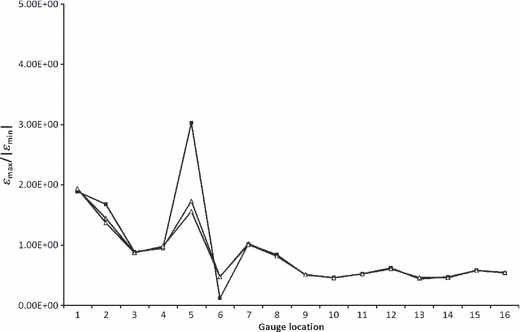
Strain ratio comparing HOM models at original (filled squares), +1 (grey triangles) and +2 (open triangles) gauge placements.

Loading direction

Figure 10 illustrates the sensitivity of the model to changes in loading direction. Most locations seem largely insensitive to alterations in masseter load direction, usually resulting in absolute differences between strain ratios on the order of 0.01. Gauge 5 seems highly sensitive to loading direction from the masseter; however, moving the masseter to pull more anteriorly (Fig. 10a) or posteriorly (Fig. 10b) both seem to improve the fit of the model results to the experimental data, as does pulling it more ventrally (Fig. 10c). Pulling the masseter more laterally (Fig. 10d) has the greatest effect on model strain ratios, and seems to improve the model fit for G2 and G8, but reverse the strain environment in G5 from one of tension to one of compression if this change is > 5 °. Moving the masseter anteriorly slightly improves the fit of G11, but worsens the fit of G2 and G3. Moving it posteriorly improves G12, but worsens G11 and G15. Moving it medially improves G7 and G12, but worsens the fit of G3 and G8.

Fig. 10.

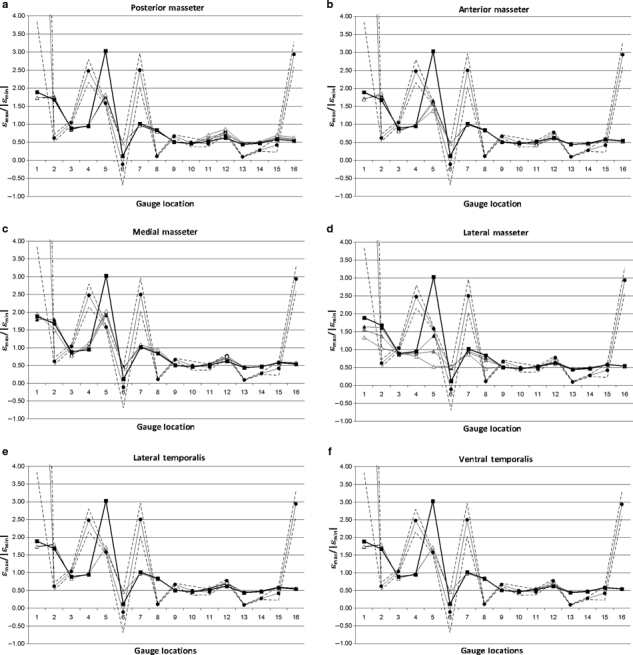
Sensitivity of the model strain ratios to changes in loading to the masseter (a–d) and the temporalis (e, f) in the (a) posterior; (b) anterior; (c) medial; (d, e) lateral; and (f) ventral directions. Circular markers show the experimental results and dashed lines indicate 2 SE of the mean. Square markers show the original HOM model configuration. Triangular markers show the LOAD models modified by 2.5 ° (black), 5 ° (grey) and 10 ° (white) in the indicated direction. G1 and G6 gave unstable experimental results, and should be disregarded.

The model is even less sensitive to alterations in the direction of the temporalis load, although the gauges closest to the temporalis (G11 and G12) show some small changes (Fig. 10e,f). Interestingly, G5 seems to improve under altered temporalis loading as well, in the same way that it improves when masseter loading is altered.

As G5 was the only gauge notably affected by loading, principal strain orientation was compared at this location between all the altered masseter load models. For all but three models, the principal strain orientations were within 1 ° of the HOM model. The models LOAD_postmass10 and LOAD_latmass5 were within 5 ° of the HOM model. The model LOAD_latmass10 was 12 ° from the HOM model in projected strain; however, the principal strain axis appeared to be directed out of plane. These results again illustrate the models’ insensitivity to small changes in loading direction.

Discussion

The aim of this study was to determine the influence of input parameters on the accuracy of FEA performed on a non-primate mammal. The paucity of material properties data from pigs provides an interesting insight into the potential errors that may be encountered in a palaeontological study.

Even in this well controlled set-up, it was difficult to replicate ex vivo strain magnitudes. Firstly, the models are too stiff. The assumption that material properties of isotropic cortical bone are applicable throughout the cranium is incorrect, and models with a stiff outer shell around a more flexible interior (representing cortical and cancellous bone respectively) show a move towards ex vivo magnitudes of strain as the overall stiffness of the specimen is reduced. However, strain ratios in most locations are barely affected, indicating that when (as here) a universally thick layer of cortical bone atop cancellous bone is modelled, the strain distribution of the homogeneous model is maintained. Thus, it appears that the introduction of this basic heterogeneity is the equivalent of simply reducing the overall stiffness of the model, i.e. the magnitudes of strain change, but the patterns do not. This is a similar result to those of Wroe et al. (2007) and Moreno et al. (2008), who both found that incorporating heterogeneous material properties derived from Hounsfield Units tended to result in higher magnitudes but broadly similar patterns of strain. Other potential explanations for the over-stiffness in the model could be found in consideration of the model practices used. Over-constraints at the TMJ could have caused the model to be too stiff. However, we relaxed constraints to reduce the number of nodes and degrees of freedom that were constrained, and found no differences between the models (data not shown). Alternatively, it is possible that a cortical layer that was only one element layer thick may not have fully accommodated bending in the model. The use of quadratic elements should have mitigated this effect, but a full sensitivity test into the appropriate number of elements to be included in a cortical bone layer, though outside of the scope of this study, would be useful.

The consistency in strain orientation between the models and experiments suggests that the model is correctly replicating the loading conditions. However, it is failing to correctly estimate the absolute magnitudes of strain and, because of this, strain ratios and γ_max may be incorrect in places. Similarities between strain orientations are often reported, even when the strain magnitudes/ratios show less correspondence (Ross et al. 2005, 2011; Strait et al. 2005). The most likely explanation for this observation is local heterogeneity in material properties, and structural differences within the skull that were not incorporated in the model due to a lack of CT resolution, and the absence of detailed material properties data for pig bone. If cancellous bone was modelled accurately, it is possible that local variations in the thickness of the overlying cortical bone material would reduce or increase local strain accordingly, as has been shown for the human pelvis (Anderson et al. 2005). Gauge 2 is dramatically affected by the inclusion of cancellous bone, showing a large increase in strain ratio. A possible explanation for this is its location on the anterior nasal bone, which is particularly thin, and thus potentially has a different distribution of cancellous to cortical bone compared with the other locations in the study.

Similarly, complex orthotropy may be present, perhaps increasing bone stiffness parallel to muscle lines of action or the tooth row, or to withstand joint reaction forces. Strait et al. (2005) found that strain ratios in most facial locations could be improved by refining the material properties of the model, and that a model incorporating both intracranial variation in Young's modulus and orthotropy provided the best match. It is tempting to speculate that, if orthotropy in the zygomatic arch was aligned to be stiffer parallel to the muscle force, then perhaps the models would have not overestimated tension in G8 in the dramatic way that they did. Although orthotropic properties could be introduced to test this possibility, this was outside of the scope of this study, given that the correct cortical bone thickness in our specimen was also unknown. Although there were only minor differences between 2D and 3D strains in this isotropic model, it is possible that this would not be the case if anisotropic material properties were included. Thus, there is scope for further investigation of this technique as a convenient means of projecting 3D to 2D strains, particularly if multiple models or anisotropic properties are to be investigated.

There is currently debate as to whether including the PDL in FE models is necessary. On the one hand, Panagiotopoulou et al. (2011) found that the presence of a PDL only affects strains locally in the alveolar bone, and therefore could be left out of the model unless these alveolar strains were of particular interest. Conversely, Marinescu et al. (2005) found that their edentulous model of a macaque jaw was more valid than one incorporating the dentition even when the teeth were not load-bearing. They suggested that their failure to incorporate the PDL had resulted in a dentate model that was too stiff because there was no interface between the teeth and alveolar bone, which changed the axis of bending. The same scenario was found by Gröning et al. (2011a) in a sensitivity study where they demonstrated that including a PDL not only reduces model stiffness, but can alter the deformation regime of the whole mandible. The PDL could not be modelled here because the CT resolution was insufficient to accurately visualise the roots of the teeth. It is possible that introducing a PDL to the pig models would decrease the model stiffness or alter the deformation regime, but this remains to be tested.

The experimental results show that, when moving from one bone to an adjacent bone across a cranial suture, strain magnitudes and strain orientations can be very different (compare G5 and G8 on the zygomatic arch, or G13–16, located within 5 mm of each other on four different bones). This is in line with previous studies, which have led to the hypothesis that cranial sutures may act as strain sinks or shock absorbers (Jaslow, 1990; Herring & Mucci, 1991; Jaslow & Biewener, 1995; Rafferty & Herring, 1999; Herring & Teng, 2000; Herring et al. 2001; Thomason et al. 2001; Rafferty et al. 2003; Popowics & Herring, 2007). Wang et al. (2010) found that the introduction of sutures into a model of a macaque cranium made little difference to the in silico results, and other macaque models without sutures show a reasonable match with in vivo strain ratios and orientations (Strait et al. 2005; Ross et al. 2011), although Kupczik et al. (2007) found that strains in the macaque zygomatic arch improved when suture material was included. Models of an alligator cranium (Metzger et al. 2005) and ostrich mandibles without sutures (Rayfield, 2011) found good approximation of strain orientation only in certain bones, and sensitivity tests on the mandible of an alligator (Reed et al. 2011) have shown that changing sutural stiffness causes significant differences in the strain regime of the model, which also differs between bones. Moazen et al. (2009) have suggested that the role of cranial sutures is to distribute strains more evenly throughout the skull, and thus their true function may only become apparent when multiple or dynamic loading scenarios are considered. Thus, previous studies of sutures in FE models seem divided on whether the inclusion of cranial sutures in FE models is necessary, although it is possible that this division may represent inherent differences between the studied taxa (e.g. the role of sutures in reptiles vs. mammals), or the maturity of the individuals under study, as sutures often fuse during ontogeny. Cranial sutures are not included in this model, and given the patterns of experimental strain, it will be interesting to observe the effects of their introduction.

The models are generally very insensitive to changes in loading condition. However, it is interesting that the in silico strain ratio of G5 (located on the zygomatic arch) seems to improve in all the alternative loading situations, even when the loadings modelled are direct opposites of one another. This is particularly interesting as the strain orientations of G5 matched the experiment well under unaltered loading, suggesting the loading regime was being modelled accurately. Gauge 5 is also sensitive to the nodes chosen to represent the gauge. The zygomatic arch experiences the highest strains in the model and the gradients of strain are high, meaning that G5 averages strain over a large range of values (Bright & Rayfield, 2011). These high-strain gradients mean that discrepancies in the positioning of the gauge between the experiment and the model are likely to affect validity: because a large range of strain values exist within a small distance of bone, sampling error in the virtual gauge would result in failure to precisely capture the experimental result. Additionally, small alterations in loading may cause the position of the strain gradients to move slightly, which will similarly affect results. Therefore, because of its location, G5 seems to be highly susceptible to small changes in loading.

Implications for morphological and palaeontological applications of FEA

The primary conclusion of this study is that estimates of absolute numerical values from zoological FEA (such as strain, breaking stress and bite force) should be approached with extreme caution unless input parameters have been accurately measured (e.g. Strait et al. 2005). The models described above seem most sensitive to changes in material properties, and these are the hardest to estimate from palaeontological data (and indeed are problematic even in extant taxa due to the variation encountered even in one specimen). Other sensitivity studies have similarly shown that strain magnitudes are very sensitive to changes in material properties in macaques (Strait et al. 2005; Kupczik et al. 2007), alligators (Reed et al. 2011) and ostriches (Rayfield, 2011), suggesting that this variable is of modelling importance across a disparate range of taxa. More studies on the distribution of cranial material properties within and between modern specimens are desirable.

It is interesting to compare the patterns of strains in this study of the pig (see Fig. 7) with those in previous studies of the skulls of other taxa. Comparisons with macaques (Strait et al. 2005; Kupczik et al. 2007) show that strains in both taxa are high in the zygomatic arches, and extending anteriorly beneath the orbit toward the maxilla. This is presumably due to high loading experienced in this region from the masseter. In the pig, strains are high in the frontal bones, whereas in the macaque they are high in the nasals, a difference that likely reflects how bending is accommodated differently in the faces of the two animals (the pig having an elongated snout and the macaque's face being relatively flat). Further investigation of other mammalian taxa highlighting notable similarities and differences in strain across different morphologies may provide insight on how the mammalian skull has adapted to fill different ecological niches. The future combination of FEA with geometric morphometrics studies will offer a robust method of investigating further the association between function and form (e.g. Pierce et al. 2008; and see O'Higgins et al. 2011).

The main limitation currently in FE validation studies is that they focus on only one specimen. Subject-specific validations, such as the one presented here, are useful in that one can be confident that the geometry of the specimen is accurate, and therefore not confounding the results. However, more generally the objective is to use FEA to investigate morphological traits. It is therefore crucial that future works address the effects of intra-specific variation on the results of FEA (e.g. Rayfield, 2011).

Unless such data are available from a living relative or suitable analogue, caution is advised about using FEA to make absolute numerical predictions for palaeontological specimens. However, FE studies in palaeontology and functional morphology to date have focused more on assessments of the relative structural performance of different skulls, setting out to perform an analysis of shape rather than make predictions about in vivo performance (Rayfield et al. 2007; Farke, 2008; Pierce et al. 2008; Slater & Van Valkenburgh, 2009; Stayton, 2009; Fletcher et al. 2010; Dumont et al. 2011; Gröning et al. 2011b; Nakashige et al. 2011). In such studies, it is the differences between the models that are informative, rather than the absolute values. Apart from some local perturbations, the overall nature of deformation in the models described here was correct when compared with the ex vivo data, and contours of strain were barely affected by the changes in material properties. Thus, comparisons of stress or strain patterns amongst palaeontological models can be robust, provided that: (i) they are appropriately converged (Bright & Rayfield, 2011); and (ii) the same assumptions are made about all specimens (for example appropriate scaling; Dumont et al. 2009).

Conclusions

The results of several FE models were compared with data collected from a pig skull ex vivo. The results indicate that the models correctly estimate the loading conditions of the experiment, yet fail to accurately report principal strain magnitudes in all measured locations. The models are particularly sensitive to changes in material properties, and the results imply that caution should be exercised in using FEA to estimate absolute numerical values, such as breaking stress and bite force. However, the fact that the models can accurately reproduce the overall strain environment suggests that comparative studies (such as are often undertaken in palaeontological investigations) can be robust.

Supporting Information

Additional Supporting Information may be found in the online version of this article:

Table S1. Principal strains in models using ν = 0.35 (HET_6; HET_1), and ν = 0.2 (HET_6ν; HET_1ν).

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer-reviewed and may be re-organized for online delivery, but are not copy-edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.