Abstract
Carboxy-fluorescein diacetate succinimidyl ester (CFSE) labeling is an important experimental tool for measuring cell responses to extracellular signals in biomedical research. However, changes of the cell cycle (e.g., time to division) corresponding to different stimulations cannot be directly characterized from data collected in CFSE-labeling experiments. A number of independent studies have developed mathematical models as well as parameter estimation methods to better understand cell cycle kinetics based on CFSE data. However, when applying different models to the same data set, notable discrepancies in parameter estimates based on different models has become an issue of great concern. It is therefore important to compare existing models and make recommendations for practical use. For this purpose, we derived the analytic form of an age-dependent multitype branching process model. We then compared the performance of different models, namely branching process, cyton, Smith-Martin, and a linear birth-death ordinary differential equation (ODE) model via simulation studies. For fairness of model comparison, simulated data sets were generated using an agent-based simulation tool which is independent of the four models that are compared. The simulation study results suggest that the branching process model significantly outperforms the other three models over a wide range of parameter values. This model was then employed to understand the proliferation pattern of CD4+ and CD8+ T cells under polyclonal stimulation.
Keywords: CFSE-labeling, Cell Cycle, Age-dependent Multitype Branching Process, Cyton Model, Smith-Martin Model, Differential Equation Model, Agent-based Model, Hybrid Optimization, Parameter Estimation
1 Introduction
Carboxy-fluorescein diacetate succinimidyl ester (CFSE) labeling studies have been widely used to measure the responses of a population of cells to different receptor-mediated signals (Lyons, 2000; Hawkins et al., 2007). Under ideal conditions, the CFSE dye bound to intracellular proteins of progenitor cells will be equally partitioned into two daughter cells after a successful division; therefore, the intensity of CFSE dye of a cell population directly suggests the number of divisions that its ancestors have gone through. At a specific time point, the number of cells of different generations can thus be measured by CFSE dye intensity clusters (e.g., using a Gaussian mixture model). Such measurements conducted at multiple time points allow one to determine the time to division or death of each generation as well as variations in division and death time. Thus CFSE labeling experiments have significantly advanced our understanding of the regulation of the cell cycle, particularly of lymphocytes (Hodgkin et al., 1996; Hasbold et al., 1998; Deenick et al., 1999; Gett and Hodgkin, 2000; Deenick et al., 2003; Asquith et al., 2006).
The characteristics of the CFSE labeling data structure have been thoroughly discussed by Hyrien and Zand (2008). To model such data, the ideal mathematical model should be able to account for the following facts: 1) within a time window of interest, only one of the three events will occur: a cell proliferates, dies or remains quiescent; 2) the time to division or death of the first generation cells is usually different from that of the later generations, mainly due to an activation delay (Gett and Hodgkin, 2000; Bonnevier and Mueller, 2002; Deenick et al., 2003; Hawkins et al., 2007); 3) the lifetimes of sibling cells are positively correlated; 4) different types of cells may interact with each other (e.g., CD4+ T helper cells and CD8+ T effector cells). Usually the correlations among sibling cells cannot be observed in CFSE labeling experiments and a single cell type instead of multiple cell types has been considered in mathematical models. To account for the first two facts, a number of independent studies have proposed different mathematical models for CFSE data analysis. For example, Revy et al. (2001) and Asquith et al. (2006) proposed linear birth-death type ordinary differential equation (ODE) models. Although such models have the advantage of simplicity, their performance is questionable due to their neglect of the delays inherent in the cell cycle (De Boer and Perelson, 2005), i.e., a cell that has just divided cannot divide again instantly. To incorporate such delays in a simple manner, the Smith-Martin cell cycle model (Smith and Martin, 1973), which divides the cell cycle into a variable length A phase and a fixed length B phase, has been used in a number of modeling studies (Nordon et al., 1999; Bernard et al., 2003; Deenick et al., 2003; Pilyugin et al., 2003; Leon et al., 2004; De Boer and Perelson, 2005; Ganusov et al., 2005; De Boer et al., 2006; Ganusov et al., 2007; Lee and Perelson, 2008; Lee et al., 2009; Zilman et al., 2010). In the original Smith-Martin model, the length of the A phase was described by an exponential distribution (Smith and Martin, 1973); Lee and Perelson (2008) generalized this by using a delayed gamma distribution to describe the length of the A phase of a cell that has never divided. They then derived the analytical solution of this generalized Smith-Martin model, which significantly extended the flexibility of the Smith-Martin model. In another approach, Hawkins et al. (2007) proposed the cyton model in which the time to division and death of cells in each generation was described using independent continuous probability distributions (e.g., lognormal or gamma). The derived cyton model takes the form of integral equations involving multifold convolutions and has been successfully applied to experimental data with biologically reasonable parameter estimates obtained (e.g., Hawkins et al., 2007). Kimmel (1980) used stochastic point processes to model the proliferation of leukemia cells taking into consideration the need to progress through the various stages of the cell cycle. Other approaches have used age-structured models that can be shown to be formally equivalent to the cyton model or Smith-Martin model (Zilman et al., 2010). Lee et al. (2009) studied another form of the generalized Smith-Martin model, in which they allowed the death rate of cells to vary with the number of divisions they had undergone, and verified that the solution of the delay differential equation model with inhomogeneous death rates was consistent with the solution of the cyton model proposed by Hawkins et al. (2007). For Smith-Martin type models in which the cell cycle is divided into A and B phases, the length of the B phase is unknown and cannot be directly determined from experiments. One modeling approach is to arbitrarily fix the length of the B phase, which avoids the unidentifiability problem (Miao et al., 2011), but this could directly introduce bias into estimates of the average length of the A phase.
Hyrien and Zand (2008) proposed a branching process model for the interpretation of CFSE data and showed that the branching process model significantly outperformed the linear birth-death type ODE models and the Smith-Martin type models in the sense of obtaining more accurate parameter estimates in simulation studies. However, Hyrien and Zand (2008) restricted their analysis to situations in which cell death could be ignored and thus the branching process model for CFSE data is not adequately developed. A relative concern is that, like the cyton model, the branching process model in Hyrien and Zand (2008) did not explicitly distinguish the subtypes of cells such that estimated parametric distributions (e.g., the mean of the time to division distribution) could be biased, especially when a large portion of cells die and the average time to death is significantly different from the average time to division. Such a concern is conceptually straightforward considering the fact that the mean of a cell population can be very different from the means of its distinctive sub-populations. In this study, we explicitly classify cells into different subtypes and derive a multitype branching process model in analytical form with careful considerations of model assumptions in Section 2. For completeness, we also briefly describe the cyton model, the Smith-Martin model and the linear birth-death ODE model. In Section 3, an agent-based model used for generating simulated data is described; then numerical algorithms important to the reliability of simulation results are discussed; finally, the performance of four types of models is compared and summarized. In Section 4, we apply the proposed branching process model to understand the cell cycle regulation of CD4+ and CD8+ T cells subjected to polyclonal stimulation. Finally, we summarize and discuss our findings in Section 5.
2 Mathematical Models
Details of four different mathematical models for analyzing CFSE data are described in this section; important model assumptions and critical model construction procedures are also illustrated. These details also form the basis for model comparison and discussion later.
2.1 Age-dependent Multitype Branching Process
A branching process is a suitable mathematical tool to describe a system of individuals that have offspring or of cells that have progeny. A number of studies have employed branching process models to investigate cell kinetics with particular attention paid to cell proliferation or differentiation (Jagers, 1975; Macken and Perelson, 1988; Yakovlev and Yanev, 1989; Yakovlev et al., 1998; Kimmel and Axelrod, 1991, 2002; Hyrien et al., 2005; Yakovlev and Yanev, 2006; Hyrien and Zand, 2008; Yakovlev et al., 2008). Consider a cell of age zero, it may undergo apoptosis, proliferate or remain quiescent. It is also possible that a proliferating cell fails to accomplish the division process and starts dying instead. Considering such complexity in a cells’ behavior, we classify cells into three subtypes according the events that will occur at the end of a time period equal to a cell cycle time instead its current status
Type I: cells that will eventually die;
Type II: cells that stay resting;
Type III: cells that will successfully divide into two daughter cells.
Such a classification ignores the actual processes that a cell undergoes before its eventual death or division, which is a reasonable simplification since it is usually not tracked in CFSE labeling studies whether individual cells are proliferating, dying, resting or switching from proliferation to apoptosis. Also, Type II cells do not represent a stable phenotype since all cells will eventually die or divide; however, for a short time window of interest, we can treat quiescent cells, which survive sufficiently long, as being of this type. We will further discuss the influence of Type II cells on model formulation later. By definition, a Type I cell no longer exists at the end of its lifetime; a Type II cell stays resting and makes no contribution to the total cell number change; a Type III cell divides into two independent daughter cells, each of which then randomly belong to one of the three subtypes. A multitype branching process is suitable for modeling such populations (Athreya and Ney, 1972; Kimmel and Axelrod, 2002).
Macken and Perelson (1988) and Kimmel and Axelrod (1991) proposed multitype Galton-Watson process models for describing cell populations. However, this process is discrete in time and cannot accommodate the continuous time nature of CFSE labeling experiments and asynchrony of cell division among cells. Instead, age-dependent processes are more appropriate to model the randomness in the time to division or time to death of cells. Age-dependent processes are usually non-Markovian unless some conditions can be satisfied (e.g., when the distribution of particle lifetime follows an independent exponential distribution). Non-Markovian age-dependent processes were first introduced and studied by Bellman and Harris (1952), and are thus called the Bellman-Harris process. The Bellman-Harris process has been widely used to describe various biological processes (e.g., Cowan and Morris, 1986; Kimmel and Traganos, 1986; Yakovlev et al., 1998; Hyrien et al., 2005; Yakovlev and Yanev, 2006; Yakovlev et al., 2008). Hyrien and Zand (2008) employed the Bellman-Harris process to analyze CFSE data without considering cell quiescence and death. Here a Bellman-Harris process with three types of particles is formulated based on the following assumptions or facts:
The process starts at time 0 with N(1)(0) Type I progenitors of age zero, N(2)(0) Type II progenitors, and N(3)(0) Type III progenitors;
Cells of any type from any generation evolve independently;
At the end of the lifetime of a Type I cell, the cell vanishes;
The lifetime of a Type II cell is beyond the experimental end point. Because a cell cycle length is not imposed in this continuous time model, a Type II cell is defined as a cell that survives and remains quiescent throughout the experiment;
At the end of the lifetime of a Type III cell, the cell divides into two daughter cells of Type I, Type II or Type III, and the two daughter cells can be of different types;
The lifetime of cells of the same type from the same generation follows the same distribution with the same distribution parameters; however, the lifetime of the same type of cells of different generations may follow the same distribution with different distribution parameters. For example, the lifetime of the first generation of Type III cells may follow a lognormal distribution with mean 10 and variance 100; however, the lifetime of the second generation of Type III cells may follow a lognormal distribution with mean 5 and variance 64.
It should be emphasized that the fates of sister cells could strongly correlate with each other such that assumption (b) may seem invalid. For example, Powel (1955) reported such positive correlations between sibling bacterial cells in in vitro experiments and Hawkins et al. (2009) showed this for B cells stimulated by TLR9 ligands in vitro. However, such correlations or dependences have no effect on the expected number of cells at an arbitrary time point (Crump and Mode, 1969); therefore, assumption (b) is a valid mathematical simplification. Hyrien and Zand (2008) further discussed the validity of this assumption in the context of age-dependent branching processes. It is possible to incorporate such a dependence into a mathematical model (Wellard et al., 2010); however, for the data sets considered in this study, no information on such a dependence has been obtained experimentally, so the incorporation of such a dependence into the model is premature and would result in unnecessary complexity.
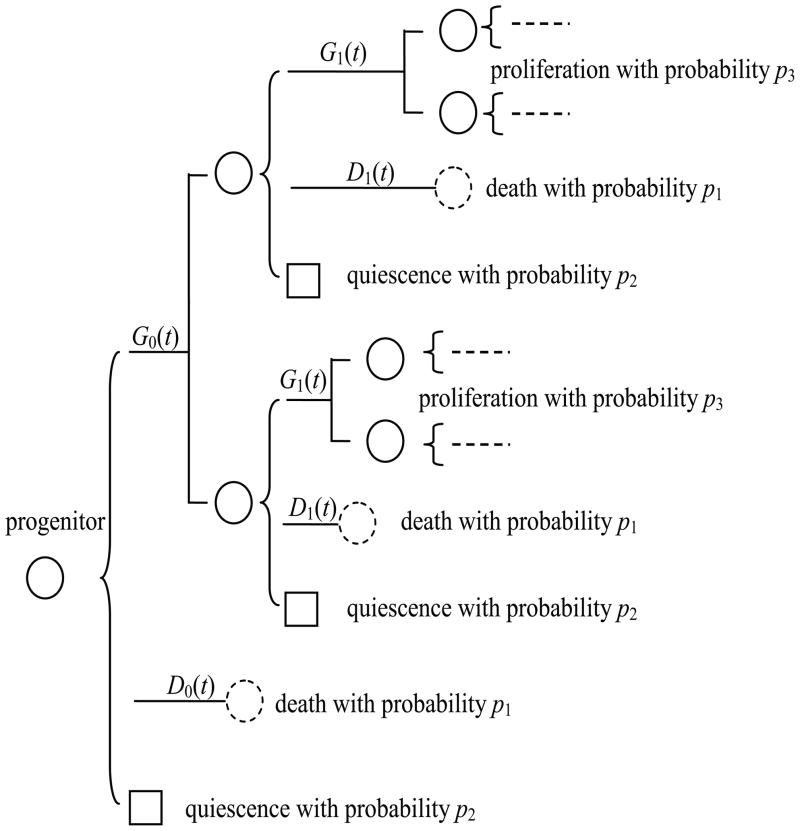
To better illustrate the model under consideration, these assumptions are summarized and represented in Fig. 1. In Fig. 1, the cell population starts with a single progenitor. This progenitor of age zero is of Type I with probability p1, Type II with probability p2, and Type III with probability p3, with p1 + p2 + p3 = 1. At the end of the lifetime of a Type III progenitor, two offspring of age zero are generated and they are assumed to have the same probabilities to be of Type I, II or III as their progenitor. Thus, in our system, there are no other directions of “differentiation” except for from Type III to Type I or Type II. For convenience, the lifetime distribution of a Type I progenitor, i.e., a cell destined to die, is denoted by a cumulative distribution function (c.d.f.) D0(t); and the lifetime distribution of a Type III progenitor, i.e., a cell destined to divide, is denoted by G0(t), where the subscript 0 indicates that a cell has experienced zero divisions.
Figure 1.
A schematic illustration of the branching process model with death and quiescence.
We consider the d-type Bienayme-Galton-Watson (BGW) process (Heyde and Seneta, 1977) embedded in the Bellman-Harris process. Such an embedded BGW process with d types of cells can be defined by the following recurrence relation (p. 1362 in Yakovlev et al., 2008)
| (2.1) |
where denotes the number of cells of type j in the (n+1)-th generation descended from the k-th cell of type i in the n-th generation, and is the number of cells, both dead and alive of type j which were or currently are in the n-th generation (that is, Type III cells in the n-th generation that already divided are also counted although their daughter cells are now in the (n + 1)-th generation). For , define
| (2.2) |
Then the number of living cells of type j in the n-th generation at time t is just
| (2.3) |
which connects the embedded multitype BGW process and the multitype Bellman-Harris process.
If one considers a single Type III progenitor, we can follow the argument on pages 143–144, chapter 3 in Athreya and Ney (1972) to obtain
| (2.4) |
and
| (2.5) |
where Gn(t) denotes the distribution of time to division of the n-th generation and the asterisk denotes convolution. If we assume the distribution of times to division of all the non-first generation cells are the same, denoted by G(t), then Eq. (2.4) becomes
| (2.6) |
where G*n(t) denotes the n-fold convolution of G(t). For simplicity, the later formula derivations are based on this assumption.
Eq. (2.5) follows according to the properties of BGW process. Also, Eq. (2.6) follows because
| (2.7) |
where denotes the lifetime of Type III cells in the h-th generation. In other words, a Type III cell in the n-th generation still remains in the n-th generation at time t only when the sum of the lifetimes of its ancestors is less than or equal to t and the sum of the lifetimes of its ancestors and its own is greater than t, as argued in Athreya and Ney (1972). Combine Eq. (2.6) and Eq. (2.5) and recall Assumption (a), the expected number of Type III cells in the n-th (n ≥ 1) generation at time t is finally given by
| (2.8) |
By following the same argument, we can obtain the cell numbers of different types at time t as follows
| (2.9) |
where and denote the expectation of the number of dead cells at time t in generation 0 and generation n (n ≥ 1), respectively.
When deriving the model above, cells are classified into 3 subtypes, including Type II cells which neither divide nor die and thus survive forever. The practical concerns about this classification are: 1) as mentioned before, all cells will eventually die or divide. Thus, Type II cells do not exist in reality; 2) if a cell of Type I (or Type III) is born, say, 1 minute before the experimental end point, and it survives beyond the end point, it can be mistaken as Type II although it is in the process of apoptosis (or division). Therefore, instead of classifying cells into 3 subtypes, one may want to simply consider two subtypes: Type I or Type III. Now model (2.9) becomes
| (2.10) |
It should be noted that this simplified model may not determine distributions as accurately as model (2.9) when the number of quiescent cells is large.
Note that in the derivations above, the only requirement for the distribution functions Gi(t) and Di(t) (i = 0, 1, 2, …) is continuity since the time to division or death is a continuous random variable. Therefore, gamma, lognormal or even exponential distributions can be plugged into the branching process models above. However, as in Hawkins et al. (2007), we will only consider the gamma distribution in this study due to its flexibility in shape (e.g., it could be non-bell shaped) and the comparison of different distribution functions are outside of the scope of this study. Finally, although a number of parameter estimation methods (e.g., the pseudo-likelihood estimator) have been proposed for branching process model fitting, the nonlinear least squares (NLS) estimator turns out to be the most robust one (Hyrien and Zand, 2008) and therefore is employed in this study for all types of models. Note that numerous alternative methods, such as the approximate Bayesian computation (ABC) (Toni et al., 2009), can also be used for parameter estimation, but a thorough comparison and evaluation of all applicable estimation methods is out of the scope of this study.
2.2 Cyton Model
Gett and Hodgkin (2000) proposed a simple mathematical model for CFSE data analysis. This model was then compared with a relatively simple branching process model in Hyrien and Zand (2008) and the key model assumption in Gett and Hodgkin (2000) of a normal distribution of the time to first division turned out to be likely inappropriate. The recent work of Hawkins et al. (2007) extended the work of Gett and Hodgkin (2000) by directly modeling the time to division and time to death of cell generations using independent single mode continuous distributions. This is called the cyton model. Thus, the cyton model does not require the assumption of a normal distribution and it is flexible enough to model different generations with different kinetic parameter values (e.g., different proliferation or death rates for different cell generations). In this section, the cyton model is briefly reviewed and discussed.
Let n = 0, 1, 2, … denote the n-th generation of cells. For the n-th generation, a continuous distribution φn(t) is assigned to model the distribution of the time to divide, and ψn(t) is assigned to model the distribution of time to die. To calculate the cell number in each generation at time t, we start from the first generation. Given N(0) cells of age zero at time zero, then at time t, the rates of cell division or death in the first generation are given by
| (2.11) |
| (2.12) |
where f0 denotes the probability that a cell will divide in response to the given stimulus. Then for later generations, the rates of cell dividing or dying are given by
| (2.13) |
| (2.14) |
Thus, the number of cells in each generation can be calculated as follows
| (2.15) |
The construction of the model above is straightforward. For detailed explanation, the reader is referred to Hawkins et al. (2007).
Note that, φn(t) and ψn(t) in the cyton model are the probability density functions (PDF) of some continuous distributions.
2.3 Smith-Martin and Linear Birth-Death Model
In this section, we describe two differential equation models for CFSE data. First, the simple Smith-Martin model is described and discussed. This model is based on the cell cycle model proposed by Smith and Martin (1973). Then a linear birth-death ODE model is described to overcome the identifiability problem of the Smith-Martin model. Although ODE models have been criticized for poorly fitting CFSE data (e.g., De Boer and Perelson, 2005), it is worth evaluating their relative performance compared with other types of models.
More specifically, the Smith-Martin model divides the four phases (G1, S, G2, M) of the cell division cycle into an A phase and a B phase. The A phase approximately corresponds to the G1 phase, and the B phase includes S, G2, M, and possibly a portion of G1. In the Smith-Martin model, the duration of the A phase is thought to be extremely variable but the duration of the B phase is usually assumed fixed. Therefore, the A phase becomes the main contributor to cell asynchrony. Based on the Smith-Martin model, several investigations have developed mathematical models for the purpose of CFSE data analysis (Nordon et al., 1999; Bernard et al., 2003; Pilyugin et al., 2003; Leon et al., 2004; De Boer and Perelson, 2005; Ganusov et al., 2005; Lee and Perelson, 2008), including deterministic ODE models as well as stochastic models. However, the Smith-Martin model has been criticized for its simplicity and inaccuracy (Smith et al., 1981; Cooper, 1982; Koch, 1999; Tyrcha, 2001; Hyrien and Zand, 2008) and more complicated cell cycle models have been proposed (Tyson, 1991; Novak and Tyson, 1995, 1997, 2004; Clyde et al., 2006). The recent work of Lee and Perelson (2008) greatly extended the Smith-Martin model by introducing the gamma distribution for the A phase duration, generation-dependent death rates, and variable length of the B phase. Three models were developed in Lee and Perelson (2008), including the time-to-first-division (TFD) model, generalized Smith-Martin (GSM) model and the heterogeneous generalized Smith-Martin (HGSM) model. Although the GSM and HGSM models are more flexible to accommodate variations from generation to generation, some assumptions in Lee and Perelson (2008) have been made to simplify the analysis of models, which may not hold in practice. For example, it was assumed that after the first division, cells of different ages have the same average A and B phase lengths. Also, more complex Smith-Martin models were shown to be comparable to the cyton model (Lee et al., 2009). In this study, we focus on the following simple Smith-Martin model instead of the more complex Smith-Martin models since the cyton model will also be directly compared,
| (2.16) |
| (2.17) |
| (2.18) |
| (2.19) |
| (2.20) |
where and (n = 0, 1, 2, …) denote the number of cells in the A-phase and the B-phase in the n-th generation, respectively, λ0 and λ the rates cells leave the A phase and enter the B phase, d0 and d the death rates, and Δ the length of the B phase. However, since it is usually not feasible to distinguish the A-phase cells from B-phase cells in experiments, we re-write the model as follows
| (2.21) |
where is the number of cells in the n-th generation. We assume initially only cells of generation 0 are present and they are all in the A phase.
The biggest problem of the Smith-Martin model is that the distinction between the A phase and the B phase is not clear. Although it is possible to experimentally determine whether a cell is in the B phase using a DNA binding dye (De Boer and Perelson, 2005), such information is not collected in most of CFSE labeling experiments as well as in the experimental portion of this study. This suggests that the A phase duration and the length of the B phase may not be distinguishable from each other due to lack of information, and the corresponding statistical inferences are likely to be unreliable. Furthermore, for slowly dividing cells the length of the A phase may be very small compared with the total cell cycle length. In such circumstances, it is also worth considering the following linear birth-death type ODE model (DE Boer and Perelson, 2005)
| (2.22) |
where all generations except for the first one are assumed to have the same proliferation rate and death rate.
3 Simulation Studies
3.1 Simulated Data from Agent-based Model
An agent-based simulation tool was developed to generate simulated data, which will be fit by the four formula-based mathematical models considered in this study. The simulation follows a set of rules and one can be concerned that the rules will generate data more compatible with one model than another. We will first describe the simulation model and then address the compatibility issue.
In our agent-based model, each cell of the zeroth generation has a probability pa to be activated; then for each cell of this generation, a random number between [0, 1] is drawn from a uniform distribution. If this number is smaller than pa, this cell will be activated; otherwise, it will remain inactivated or die. Cells once activated enter the process of apoptosis with probability pad or proliferation with probability (1 − pad). The unactivated cells of the zeroth generation stay resting until the end of the experiment. We assume that the time to activation of the zeroth generation cells follows a gamma distribution, denoted by Γ(μa, va), where μ denotes the mean and v the variance of the gamma distribution. Also, for the activated and proliferating cells of the zeroth generation, let Γ(μp0, vp0) denote the distribution of times to division; for the activated and dying cells of the zeroth generation, let Γ(μd0, vd0) denote the distribution of times to death. For cells of the first and subsequent generations, we assume that the time to division follows a common gamma distribution Γ(μp, vp), and the time to death follows a common gamma distribution Γ(μd, vd). As mentioned in Section 2, when a proliferating cell divides, two independent daughter cells are generated; and each of the two daughter cells with probability p1 enters apoptosis and with probability p3 enters proliferation. Thus, the probability of quiescence is (1 − p1 − p3).
Since the agent-based model has parameters, such as p1 and p3, that are similar to those in the branching process model, one may be concerned that the data produced would be best-fit by a branching process model. Since a cell can clearly die or proliferate, we believe it is appropriate to have as parameters in the agent-base model that a cell has a probability p1 to enter apoptosis and a probability p3 to enter proliferation. Since the branching process model describes the same biological process, it is natural and necessary for the branching model to have these two parameters, too. If we look at the other three formulas-based models, we see that the parameters rdie and rdiv in the cyton model, d and λ in the Smith-Martin model and the linear birth-death model are similar parameterizations to p1 and p3. Therefore, we do not think similar parameterization will bias the data generated by the agent-based model so as to favor one model over another.
We start each simulation from one million cells (that is, N(0) = 106) to achieve a low noise-signal ratio in simulated data. To efficiently conduct simulations, an event-based updating strategy instead of the time-stepping strategy was employed (Guo and Tay 2008). During each simulation run, the number of cells in each generation is recorded at hours 0, 24, 36, 48, 60, 66, 72, 80, 88, 96, 104, 112, and 120, which comes from one of our actual schedules for experimental data collection. Since most CFSE labeling experiments only collect the number of living cells of multiple generations, only the numbers of living cells generated from the agent-based simulation tool are used for model evaluation. More specifically, the default parameter values used in the simulation are N(0) = 106 cells, pa = 0.95, pad = 0.90, p1 = 0.35, p3 = 0.30, μa = 16 hours, va = 32 hours2, μp0 = 24 hours, vp0 = 48 hours2, μd0 = 44 hours, vd0 = 88 hours2, μp = 8 hours, vp = 8 hours2, μd = 60 hours, and vd = 60 hours2, which are chosen based on previous studies (e.g., Hawkins et al. (2007)). Since the true parameter values can vary significantly for different types of cells under different stimulations, 500 simulated data sets are produced for 500 parameter value sets randomly generated around the default values. For convenience, the procedure for generating simulated data is give below:
-
Fix N(0) = 106 cells, pa = 0.95, and pad = 0.90. For the other twelve parameters (p1, p3, μa, va, μp0, vp0, μd0, vd0, μp, vp, μd, vd), five sets of boundaries are considered:
±5% of the default values as the boundaries;
±10% of the default values as the boundaries;
±20% of the default values as the boundaries;
±30% of the default values as the boundaries;
±50% of the default values as the boundaries;
Generate uniformly-distributed parameter values within these boundaries until 100 sets of parameter values are obtained for each set of bounds; therefore, 500 sets of parameter values are generated in total;
For each set of parameter values, run the simulation from hour 0 to 120 and record the cell numbers of each generation at hours 0, 24, 36, 48, 60, 66, 72, 80, 88, 96, 104, 112, and 120. Although the maximum number of cell generations is not limited during a simulation, when recording the cell counts, cells after the 10-th generation are added to the 10-th generation cell counts.
We call the simulation study described above Scenario 1. Although the agent-based simulation tool used in Scenario 1 is independent of all the four models to be compared, one may question the fairness of the simulated data: first, gamma distributions are used to generate the simulated data, and such distributions are also used by the branching process model and the cyton model; second, the ODE model does not explicitly classify the cells into subtypes and thus may not be able to correctly interpret the simulated data generated in Scenario 1, where a large portion (p2 = 35%) of cells stay resting. Therefore, we further consider Scenario 2 in which: i) exponential distributions are used to model the time to division or death for all cell generations when generating simulated data; ii) cells can only die or divide and thus no Type II cells exist. Since both the Smith-Martin and the linear birth-death ODE models do not include an explicit activation delay for cells in the zeroth cell generation, the sum of the time to activation and the time to first division is assumed to follow a single exponential distribution, denoted by Exp(μa+p0), where μa+p0 denotes the mean. Similarly, we use Exp(μa+d0) to model the length of time to death for cells in the zeroth generation. The default parameter values used in Scenario 2 are: N(0) = 106 cells, pa = 1, p1 = p3 = 0.5, μa+p0 = 40 hours, μp = 8 hours, μa+d0 = 60 hours, μd = 60 hours. The means of the exponential distributions in Scenario 2 are chosen to be as the same as those of the gamma distributions in Scenario 1. Note that Scenario 2 is a hypothetical situation that we intentionally designed to favor the ODE models. Therefore, we used exponential distributions. This does not imply that the time to division or death will necessarily follow an exponential distribution in real biological data.
3.2 Numerical Algorithms
The purpose of the simulation study is to compare the performance of the four different models, therefore, it is necessary to employ appropriate numerical algorithms to rule out the possibility of misleading results due to unreliable numerical algorithms. Our main concerns are the algorithms for the calculation of the n-fold convolution of the gamma distribution and the optimization algorithms for parameter estimation.
The convolution of multiple independent random variables is of great interest in applications in various disciplines (e.g., Thom 1968; Fleurant et al. 2004). Here, let Xi(i = 1, 2, …, n) denote the independent random variable of interest, which follows the gamma distribution Γ(αi, βi), where αi denotes the shape parameter and βi the scale parameter. Also, let Y = X1 + X2 + … + Xn. It is easy to show that Y’s distribution function is the convolution of the distributions of Xis (Karlin and Taylor 1975). It is known that if all scale parameters βis are the same, Y simply follows the gamma distribution . However, when any two of βis are different, there exists no exact expression for the n-fold convolution of the gamma distribution. A number of independent studies have investigated this problem (Thom 1968, Mathai 1982, Moschopoulos 1985, Sim 1992, Akkouchi 2005, Stewart et al. 2007, Vellaisamy and Upadhye 2009). For computing efficiency, the expression derived by Sim (1992) is used in this study when the scale parameters are close to each other. Sim’s expression was also used in Stewart et al. (2007) as a benchmark for validating a simpler approximation to the n-fold convolution of gamma distributions. The probability density function (pdf) of Y given by Sim (1992) is:
| (3.1) |
accordingly, the cumulative distribution function (cdf) of Y is
| (3.2) |
However, when the scale parameters are very different from each other, we use the approximation (Stewart et al. 2007).
To obtain reliable parameter estimates, a hybrid optimization algorithm called DESQP, which combines the Differential Evolution (Storn 1997) and Sequential Quadratic Programming (SQP) (Ye 1987; Nocedal 1999), is employed in this study. Differential evolution (DE) is an evolutionary optimization algorithm proposed by Storn (1997). The DE algorithm randomly generate parameter candidates by mimicking the inheritance, mutation, selection, and crossover of genes to cover the whole parameter space such that the global minima/maxima of an objective function (e.g., the residual sum of squares or the likelihood function) can be located. Many studies including our previous work (Miao et al. 2008, 2009) have shown that the DE algorithm performs much better than gradient methods when the objective function is ill-behaved (e.g., crowded with multiple peaks and nadirs). However, the main problem of global optimization algorithms such as DE is the associated expensive computing cost. To solve this problem, Rodriguez-Fernandez et al. (2006) made an attempt to combine the scatter search method (Glover 1977, Laguna and Marti 2003, 2005) with the SQP algorithm, and such a hybrid algorithm reduced the computing cost significantly when fitting a simple HIV dynamic model to noisy data, compared with the pure DE algorithm. However, the work of Moles et al. (2004) verified that the differential evolution method is superior to the scatter search method and six other global methods in the sense of computational cost and convergence rate. Therefore, in this study, the differential evolution algorithm was combined with SQP and employed for parameter estimation. For more details about DESQP, see Liang et al. (2010).
3.3 Model Performance Comparison
After fitting models to simulated data, we can calculate the average relative errors (ARE) in parameter estimates defined as follows (Miao et al. 2009)
where θ̂i is the estimate of the true parameter θi used to generate the j-th simulation data set and N (e.g., equal to 500) is the total number of simulation runs. By definition of ARE, the smaller the ARE, the better the model performance is.
Note that the four models under consideration only share four parameters in common (average time to division or death of cells in the zeroth generation and later generations); therefore, we can only compare model performance based on these parameters, as shown in Tables 1 and 2. First, for all the four models, no strong correlations between AREs and the parameter value ranges can be observed. For example, for the branching process model in Table 1, the ARE of time to division of the zeroth generation stays around 8% for different parameter value ranges. This observation suggests that the model performance comparison based on AREs are not heavily dependent on the parameter range. Therefore, the model performance comparison discussed below will be solely based on ARE values corresponding to the largest parameter range (±50% of the default parameter values).
Table 1.
Average relative error (ARE) in model fitting to cell counts simulated in Scenario 1.
| Model | Parameter range | ARE(%) of time to division of gen. 0 | ARE(%) of time to division of gen. ≥1 | ARE(%) of time to death of gen. 0 | ARE(%) of time to death of gen. ≥1 |
|---|---|---|---|---|---|
| Branching Process (2.9) | ±5% | 7.73 | 4.26 | 0.56 | 21.9 |
| ±10% | 9.06 | 5.58 | 0.69 | 27.6 | |
| ±20% | 7.76 | 6.93 | 0.67 | 39.7 | |
| ±30% | 7.66 | 7.71 | 0.59 | 49.8 | |
| ±50% | 7.52 | 18.2 | 1.03 | 84.6 | |
| overall | 7.95 | 8.53 | 0.71 | 44.7 | |
|
| |||||
| Branching Process (2.10) | ±5% | 8.20 | 18.6 | 24.4 | 131 |
| ±10% | 7.75 | 23.0 | 24.6 | 101 | |
| ±20% | 9.42 | 34.9 | 24.1 | 195 | |
| ±30% | 12.1 | 30.3 | 23.4 | 194 | |
| ±50% | 22.7 | 64.1 | 21.3 | 206 | |
| overall | 12.3 | 34.2 | 23.5 | 166 | |
|
| |||||
| Cyton | ±5% | 6.24 | 26.4 | 29.0 | 59.2 |
| ±10% | 8.59 | 26.2 | 25.5 | 64.9 | |
| ±20% | 12.9 | 29.7 | 19.9 | 79.8 | |
| ±30% | 19.5 | 27.6 | 19.0 | 80.0 | |
| ±50% | 24.2 | 42.2 | 27.1 | 103 | |
| overall | 14.3 | 30.4 | 24.1 | 77.4 | |
|
| |||||
| Simple ODE | ±5% | 527 | 406 | 1.92 × 1010 | 5.65 × 1011 |
| ±10% | 556 | 427 | 1.00 × 1010 | 3.76 × 1011 | |
| ±20% | 629 | 485 | 2.44 × 1010 | 5.62 × 1011 | |
| ±30% | 694 | 474 | 2.07 × 1010 | 2.40 × 1011 | |
| ±50% | 899 | 640 | 5.27 × 1010 | 1.03 × 1012 | |
| overall | 661 | 486 | 2.54 × 1010 | 9.86 × 1011 | |
|
| |||||
| Smith-Martin | ±5% | 321 | 155 | 1.68 × 1016 | 4.82 × 1015 |
| ±10% | 297 | 168 | 1.30 × 1016 | 1.38 × 1015 | |
| ±20% | 315 | 178 | 5.52 × 1016 | 1.04 × 1015 | |
| ±30% | 352 | 171 | 1.37 × 1016 | 2.25 × 1015 | |
| ±50% | 406 | 227 | 7.34 × 1016 | 7.22 × 1015 | |
| overall | 338 | 180 | 3.44 × 1016 | 3.34 × 1015 | |
Table 2.
Average relative error (ARE) in model fitting to cell counts simulated in Scenario 2.
| Model | Parameter range | ARE(%) of time to division of gen. 0 | ARE(%) of time to division of gen. ≥1 | ARE(%) of time to death of gen. 0 | ARE(%) of time to death of gen. ≥1 |
|---|---|---|---|---|---|
| Branching Process (2.9) | ±5% | 57.0 | 17.6 | 14.9 | 54.4 |
| ±10% | 59.9 | 15.5 | 7.80 | 53.0 | |
| ±20% | 62.0 | 22.4 | 11.6 | 54.7 | |
| ±30% | 62.9 | 19.2 | 14.9 | 60.7 | |
| ±50% | 61.5 | 40.2 | 50.8 | 91.4 | |
| overall | 60.7 | 23.0 | 20.0 | 62.8 | |
|
| |||||
| Branching Process (2.10) | ±5% | 25.0 | 15.1 | 85.7 | 40.7 |
| ±10% | 26.3 | 17.9 | 78.4 | 41.8 | |
| ±20% | 34.8 | 28.6 | 174 | 59.0 | |
| ±30% | 32.8 | 44.7 | 118 | 55.7 | |
| ±50% | 39.4 | 83.7 | 94.1 | 200 | |
| overall | 31.6 | 38.0 | 110 | 79.4 | |
|
| |||||
| Cyton | ±5% | 73.1 | 24.8 | 12.9 | 57.0 |
| ±10% | 73.4 | 27.6 | 12.0 | 59.6 | |
| ±20% | 72.3 | 31.5 | 13.6 | 54.2 | |
| ±30% | 72.9 | 42.8 | 12.5 | 55.3 | |
| ±50% | 68.0 | 60.1 | 19.0 | 67.7 | |
| overall | 71.9 | 37.4 | 14.0 | 58.8 | |
|
| |||||
| Simple ODE | ±5% | 8.40 | 66.5 | 1.66 × 1011 | 71.0 |
| ±10% | 4.10 | 59.9 | 7.61 × 1010 | 72.9 | |
| ±20% | 13.4 | 71.2 | 4.30 × 1010 | 69.5 | |
| ±30% | 9.80 | 66.5 | 7.01 × 1010 | 70.0 | |
| ±50% | 22.4 | 80.3 | 4.44 × 1010 | 6.46 × 107 | |
| overall | 11.6 | 68.9 | 7.99 × 1010 | 1.29 × 107 | |
|
| |||||
| Smith-Martin | ±5% | 10.6 | 60.8 | 2.34 × 1016 | 7.13 × 109 |
| ±10% | 12.9 | 63.0 | 3.90 × 1016 | 72.0 | |
| ±20% | 13.9 | 60.1 | 1.50 × 1016 | 2.01 × 1012 | |
| ±30% | 15.6 | 61.4 | 1.33 × 1016 | 6.46 × 107 | |
| ±50% | 26.7 | 74.5 | 2.29 × 1016 | 1.46 × 109 | |
| overall | 16.0 | 64.0 | 2.27 × 1016 | 4.04 × 1011 | |
In Table 1 for Scenario 1, the branching process model (2.9) that includes Type II cells is found to have the smallest ARE values and therefore performs the best, the performance of the branching process model (2.10) that excludes Type II cells and the cyton model are close to each other and therefore the second, the Smith-Martin model the third, and the linear birth-death ODE model the last. More specifically, for the time to division of the zeroth generation, the branching process model (2.9) has an ARE of 7.52%, the branching process model (2.10) has an ARE of 22.7%, the cyton model has an ARE of 24.2%, the Smith-Martin model has an ARE of 406%, and the linear birth-death ODE model has an ARE of 899%. Therefore, fitting the branching process model (2.10) and the cyton model to data can produce reasonable estimates, but these are less accurate than those from fitting the full branching process model (2.9). This is mainly because the branching process model (2.9) explicitly accounts for Type II cells and there exist 35% Type II cells in the simulated data. The estimates from the Smith-Martin model or the linear birth-death ODE model are much worse. As discussed in Lee et al. (2009), more complex Smith-Martin models are equivalent to cyton models with appropriate choices of birth and death probability density functions. But, even so they will not outperform the branching process model according to Table 1. Finally, if only counts of living cells are used for model fitting, the ARE of time to death of the first and later generations can be as high as 84.6% even for the branching process model (2.9); however, if dead cell counts are also available for model fitting, the ARE dramatically drops to only 8.9%. Therefore, to obtain more precise estimates of the time to death, methods need to be developed to measure the dead cell counts of each generation at multiple time points.
In Table 2 for Scenario 2, we found that when the simulated data are generated in favor of ODE models, the Smith-Martin model and the linear birth-death model now both perform well and better than the branching process models and the cyton model when determining the estimate of the time to first division; for example, the linear birth-death model has the smallest ARE of 22.4%. However, the Smith-Martin model and the linear birth-death model perform much worst than the other three models when determining estimates of the time to death; for example, the AREs of the time to death in the zeroth generation are 2.29 × 1016% and 4.44×1010% for the Smith-Martin model and the linear birth-death model, respectively. Such extremely large AREs are generated because time to death is calculated using ln2/d, and when d cannot be reliably estimated the estimates usually get close to zero. Therefore, the ODE model and Smith-Martin models are still not recommended. Since there are no Type II cells in the simulated data generated in Scenario 2, the branching process model (2.9) now does not perform uniformly better than model (2.10) and the cyton model. For example, when determining the estimates of the time to first division, the branching process model (2.9) has a larger ARE 61.5% than the ARE 39.4% of model (2.10); however, for the other three parameters, model (2.9) and the cyton model have close AREs and these are smaller than those of model (2.10).
In summary, the branching process models and the cyton model based on gamma distributions are found robust to the distribution assumptions on the time to division or death: first, when an activation delay is considered in the simulated data generated in Scenario 1, the branching process models and the cyton models still perform well although such a delay is not explicitly incorporated in these models; second, when exponential distributions are used to model time to division and death in the simulated data generated in Scenario 2, the branching process models and the cyton model based on gamma distributions still perform better than the ODE and Smith-Martin models in general. Also, when fitting the branching process models to data, the model performance may become worse if the model assumptions do not exactly match those used to generate the data (e.g., apply model (2.10) to data with a large number of Type II cells). Note that it is difficult to tell whether the percentage of Type II cells is large from CFSE data alone; for example, even if a large number of cell in generation 0 are observed at the end of a CFSE-labeling experiments, most of them may successfully divide or die within one hour after the experimental end point, and are thus not of Type II by definition. So in practice, it is recommended to fit both models (2.9) and (2.10) to data and then select the better one using model selection criteria, as described in the next section. Finally, according to Tables 1 and 2, the branching process models perform as well as or better than the cyton model and thus are recommended for practical use.
4 Applications
In this section, we apply the branching process models (2.9) and (2.10) and the cyton model to a data set collected in humans for understanding CD4+ and CD8+ cell responses to polyclonal (e.g., PHA) stimulation (Liu et al., 2006). In this study, heparinized blood was obtained from anonymous healthy human volunteer donors for research purposes (New York blood center). For local blood donors, a signed informed consent form was obtained from each volunteer. State and Federal human subject study regulations and guidelines were strictly followed in all studies. CD4+ and CD8+ T cells from these blood samples were isolated and labeled with CFSE, and then stimulated with PHA. At hours 0, 24, 48, 72, 96, 108 and 120, the counts of CD4+ and CD8+ T cells of different generations were obtained based on CFSE profiles. More experimental details are given in Liu et al. (2006).
We fitted the branching process models (2.9) and (2.10) and the cyton model to the experimental data described above. We then used AIC, BIC and AICc criteria (Akaike, 1973; Schwarz, 1978; Burnham and Anderson, 2004) to select the best model, where
| (4.1) |
| (4.2) |
| (4.3) |
Here L is the likelihood, N the number of observations, and K the number of unknown parameters. Under the normality assumption of measurement errors, these model selection criteria become
| (4.4) |
| (4.5) |
| (4.6) |
where RSS is the residual sum of squares obtained from least squares model fitting. Briefly, the smaller the model selection score the better the model. The model comparison and selection results are summarized in Table 3. From this table, it is clearly seen that the branching process model (2.10) has the smallest AIC, BIC and AICc scores for both the CD4+ and CD8+ data sets and thus is the best model. For example, for the CD8+ data set, model (2.10) has a AICc score 21.5, which is notably smaller than the AICc scores 28.6 and 29.4 for model (2.9) and the cyton model, respectively. Therefore, discussions below are mainly based on model (2.10).
Table 3.
Model comparison and selection for real data using AIC, BIC and AICc. Residual sum of squares (RSS) are also listed for completeness.
| Data | Model | RSS | AIC | BIC | AICc |
|---|---|---|---|---|---|
| CD4 | Branching Process Model (2.9) | 59.0 | 35.1 | 59.7 | 45.1 |
| Branching Process Model (2.10) | 59.9 | 31.8 | 52.6 | 38.8 | |
| Cyton Model | 60.2 | 32.1 | 52.9 | 39.1 | |
|
| |||||
| CD8 | Branching Process Model (2.9) | 42.1 | 18.6 | 43.2 | 28.6 |
| Branching Process Model (2.10) | 42.0 | 14.5 | 35.3 | 21.5 | |
| Cyton Model | 49.4 | 22.4 | 43.2 | 29.4 | |
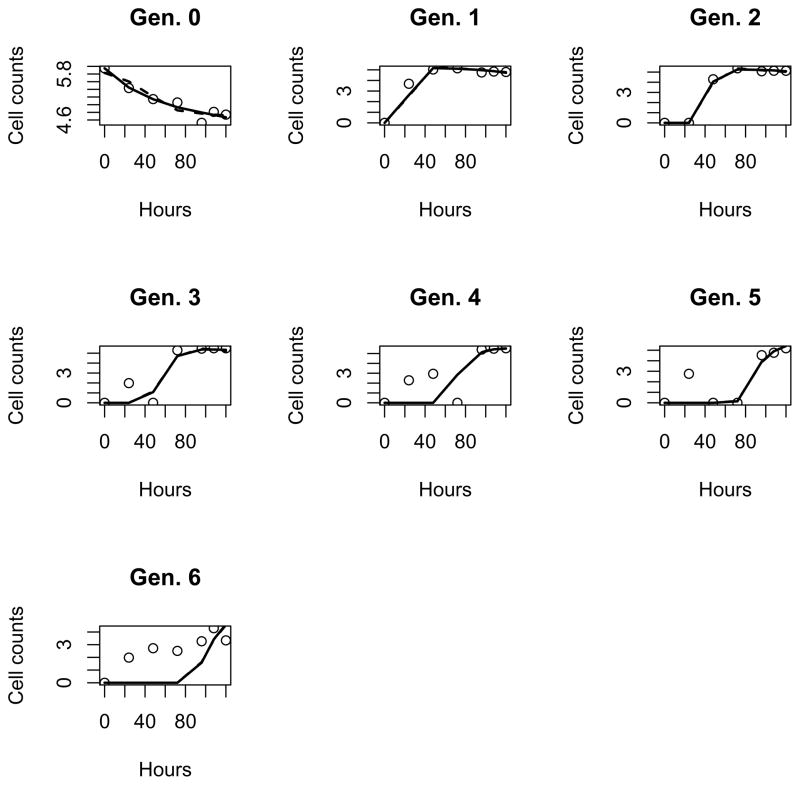
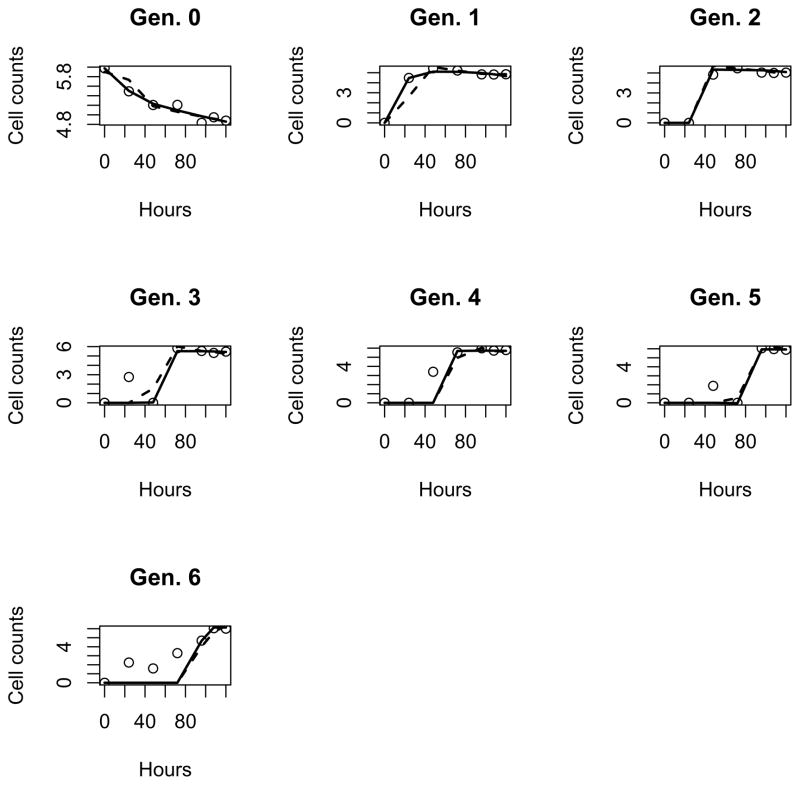
For comparison purpose, the parameter estimates for both the branching process model (2.10) and the cyton model are summarized in Table 4 and the fitted curves in log10 scales are given in Figs. 2 and 3 for the CD4+ and CD8+ cell data sets, respectively. As suggested in Table 4, the branching process model (2.10) fits both data sets better than the cyton model. Specifically, the RSS of model (2.10) is 59.9 and 42.0 for the CD4+ and CD8+ data sets, respectively, which are less than the RSS of the cyton model (60.2 and 49.4, respectively). Also, the estimates of the mean of time to division from model (2.10) and the cyton model are close to each other with a relative difference less than 16%. However, the difference in the estimates of the mean of time to death from the two models can be as large as 46%, mainly due to the lack of information about dead cells.
Table 4.
Parameter estimates and 95% confidence intervals via bootstrap for fitting the branching process model (2.10) and the Cyton model to real data. The lower bound for some highly-skewed parameters in the Cyton model are not available.
| Model | Parameter | CD4 PHA | CD8 PHA | |||||
|---|---|---|---|---|---|---|---|---|
| symbol | unit | est. | lower bound | upper bound | est. | lower bound | upper bound | |
| Branching Process Model (2.10) | N(1)(0) | cells | 7.99 × 105 | 1.10 × 105 | 8.57 × 105 | 8.63 × 105 | 6.86 × 104 | 9.09 × 105 |
| N(3)(0) | cells | 9.17 × 104 | 5.12 × 104 | 4.62 × 105 | 7.92 × 104 | 4.24 × 104 | 8.96 × 105 | |
| p3 | % | 31.3 | 0 | 71.2 | 19.6 | 0 | 88.2 | |
| μa+p0 | hours | 41.7 | 24.3 | 151 | 24.4 | 24.0 | 102 | |
| va+p0 | hours2 | 52.8 | 5.15 × 10−4 | 6.38 × 103 | 0.246 | 0 | 1.77 × 103 | |
| μp | hours | 19.3 | 4.73 | 70.7 | 15.1 | 11.3 | 29.9 | |
| vp | hours2 | 19.2 | 0 | 7.74 × 103 | 0.839 | 0 | 485 | |
| μa+d0 | hours | 25.5 | 0.78 | 76.4 | 34.1 | 20.0 | 299 | |
| va+d0 | hours2 | 3.52 × 103 | 1.51 × 10−3 | 1.00 × 105 | 5.26 × 103 | 0.39 | 1.00 × 105 | |
| μd | hours | 74.7 | 15.0 | 3.87 × 103 | 88.3 | 6.26 | 358 | |
| vd | hours2 | 689 | 0 | 5.41 × 104 | 638 | 0 | 1.50 × 103 | |
|
| ||||||||
| Cyton Model | N(0) | cells | 6.75 × 105 | 2.09 × 105 | 9.26 × 105 | 7.95 × 105 | 2.68 × 105 | 1.69 × 106 |
| f0 | % | 73.9 | 17.2 | 100 | 60.9 | 18.7 | 100 | |
| fn | % | 61.6 | - | 100 | 78.0 | 40.0 | 100 | |
| μa+p0 | hours | 48.6 | 33.6 | 145 | 29.0 | - | 131 | |
| va+p0 | hours2 | 77.5 | 0.05 | 5.73 × 103 | 1.97 | 0.39 | 4.63 × 103 | |
| μp | hours | 18.8 | 10.6 | 42.1 | 16.0 | 9.92 | 22.2 | |
| vp | hours2 | 17.3 | 3.38 | 996 | 4.60 | 2.11 | 90.2 | |
| μa+d0 | hours | 36.4 | 21.7 | 440 | 52.0 | 23.6 | 464 | |
| va+d0 | hours2 | 1.23 × 103 | 14.0 | 1.03 × 105 | 4.01 × 103 | 6.78 | 1.56 × 105 | |
| μd | hours | 80.9 | 24.6 | 8.71 × 103 | 47.3 | 21.0 | 9.00 × 103 | |
| vd | hours2 | 702 | 0.48 | 1.87 × 105 | 105 | 9.54 | 1.85 × 105 | |
Figure 2.
Fit the branching process model (2.10) (solid) and the Cyton model (dashed) to raw data (circle) in log10 scale for CD4+ cells under PHA stimulation.
Figure 3.
Fit the branching process model (2.10) (solid) and the Cyton model (dashed) to raw data (circle) in log10 scale for CD8+ cells under PHA stimulation.
Based on the results obtained from model (2.10), we found several major distinctions between the PHA-stimulated proliferation of human CD4+ and CD8+ cells: (1) The average time to first division is significantly longer for CD4+ than that of CD8+ cells (41.7 and 24.4 hours, respectively); (2) After the first division, the average time to division of CD4+ and CD8+ cells are only slightly different (19.3 and 15.1 hours, respectively); (3) The average time to death for cells in the first generation are very different: CD4+ cells die significantly slower than CD8+ cells (25.5 and 34.1 hours, respectively); after the first division, they die at much reduced rates (74.7 hours for CD4+ T cells and 88.3 hours for CD8+ T cells).
During infections, CD8+ T cells expand to much larger population sizes than CD4+ T cells, in both animal and human studies (Whitmire and Ahmed 2000). The mechanistic interpretation of this observation, however, is still in debate. Results from studying Listeria infection in mice lead to the suggestion that CD4+ and CD8+ T cells are programmed differently for expansion after antigenic stimulation (Foulds et al. 2002). By mathematically modeling LCMV infection data, De Boer et al. (2003) have concluded that CD4+ and CD8+ T cells are programmed similarly for proliferation, contraction and long term memory, except that CD8+ T cells have a faster kinetics than CD4+ T cells in all phases of the immune response.
Our current study shows that the differential division of human CD4+ and CD8+ T cells in vitro is likely the result of multiple interacting factors, the major ones of which are the different delay time to first cellular division and different death rates of undivided cells. This might have something to do with divergence in the surface molecular display and signaling pathways between CD4+ and CD8+ T cells. Of note, by modeling B cell division, it was shown that variability in time to first division (i.e., delay time) contributes most significantly to asynchronizing cellular divisions, while the doubling time and the death rate are relatively constant for each subsequent cell division (Hawkins et al. 2007).
5 Discussion and Conclusion
CFSE labeling experiments have played an important role in quantifying and understanding the role of various signals in regulating immune cell proliferation. Although a number of mathematical models have been proposed to analyze CFSE experimental data, it is not clear how accurately such models can determine the kinetic parameters governing cell life cycles. In this study, we proposed an age-dependent multitype branching process model for CFSE labeling data. This model considers three types of cell behavior (successful proliferation, apoptosis and quiescence). Also, under certain assumptions (e.g., no quiescent cells), this model can be simplified as we illustrated in Section 2. For comparison purpose, we also briefly described three other mathematical models, including the cyton model, Smith-Martin model and a linear birth-death type ODE model. It turns out that the proposed branching process model has a cleaner structure and is easier to implement in comparison with the previous models such as the Smith-Martin models in Lee and Perelson (2008) and Lee et al. (2009). We then developed an agent-based simulation tool to generate simulated data that were used to evaluate the performance of the four models. We found that the proposed branching process models significantly outperformed the ODE models and perform at least as well as the cyton model in two scenarios. The branching process models and the cyton model were then applied to CFSE data collected in vitro for human CD4+ and CD8+ T cells under PHA stimulation; and the simplified branching process model (no quiescent cells) was found the best according to model selection scores. We estimated that, the average time to first division of CD4+ T cells is almost double of that of CD8+ T cells (41.7 and 24.4 hours, respectively). After the first division, the average division time of CD4 T cells is about 28% longer than that of CD8+ cells (19.3 and 15.1 hours, respectively). Based on the parameter estimates we obtained, the variation in division time of CD8+ T cells is much smaller than that of CD4+ T cells.
Note that although the agent-based model used for simulation data generation does not explicitly employ mathematical formula, the way it is constructed is similar to that of the branching process model and the cyton model. However, to verify the robustness of the model comparison conclusions, the simulated data were generated in two scenarios, the first of which is in favor of the branching process model and the cyton model and the second is in favor of the ODE models. In the first scenario, we found that the cyton model performance was inferior to that of the branching process models, mainly because it does not divide living cells into subtypes (see discussion in Section 2). In the second scenario, the ODE and Smith-Martin models perform much better but still worse than the branching process models and the cyton model; also, the branching process models perform close to or slightly better than the cyton model. Thus, the branching process models are recommended for practical use.
The choice of a distribution for describing the time to division or death deserves further discussion. One particular concern is that using a gamma distribution in the branching process model may leave the possibility for cells to accomplish divisions within a very short time; therefore, a shifted gamma distribution may be preferred instead. While it is not expected for cells to complete their divisions very quickly, in an in vitro experiment, we cannot rule out the possibility that there may exist some cells that are not of age zero at the start of the experiment and will complete a division after a very short time. Also, although a shifted gamma distribution was not used when generating simulated data in this study, an activation procedure was considered before cells go into the division or apoptosis procedure. This is equivalent to using a shifted gamma distribution and we think an activation procedure may better reflect our knowledge of cell cycles. Furthermore, different from the simulated data in which an activation procedure was incorporated, a gamma distribution without an explicit activation phase was intentionally used in our model to reduce the number of model parameters. As we expected, the simulation results suggest that the gamma distribution without an explicit shifting or activation can still describe the time to first division (that is, the summation of the duration of activation and the duration of cell division) because the gamma distribution (density function) can have a long left tail.
In conclusion, we have constructed and validated two branching process models for CFSE labeling data analysis. Our simulation studies suggest that the two models together with model selection criteria can be used to better estimate the kinetic parameters which are critical to understanding cell cycles and their regulation. By applying this model to human CD4+ and CD8+ T cells under PHA stimulation, we successfully determined the difference in proliferation between CD4+ and CD8+ T cells.
Acknowledgments
We would like to acknowledge the excellent and dedicated technical support of Huiyuan Chen, Rahel Bezabhie, and Julianne Nelson for the experiments. This research was supported by the NIAID/NIH grants AI50020, AI052765, AI055290, AI065217, AI27658, AI28433, P30-AI078498, P01-AI071195, PHY05-51164 and 1P01 AI078907-01A.
References
- Akaike H. Information theory as an extension of the maximum likelihood principle. In: Petrov BN, Csaki F, editors. Second International Symposiumon Information Theory. Budapest: Akademiai Kiado; 1973. pp. 267–281. [Google Scholar]
- Akkouchi M. On the convolution of gamma distributions. Soochow Journal of Mathematics. 2005;31(2):205–211. [Google Scholar]
- Asquith B, Debacq C, Florins A, Gillet N, Sanchez-Alcaraz T, Mosley A, Willems L. Quantifying lymphocyte kinetics in vivo using carboxyfluorescein diacetate succinimidyl ester (CFSE) Proc R Soc B. 2006;273:1165–1171. doi: 10.1098/rspb.2005.3432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Athreya KB, Ney PE. Branching Processes. Springer; Berlin: 1972. [Google Scholar]
- Bellman R, Harris T. On age-dependent binary branching processes. Ann of Math. 1952;55(2):280–295. [Google Scholar]
- Bernard S, Pujo-Menjouret L, Mackey MC. Analysis of cell kinetics using a cell division marker: mathematical modeling of experimental data. Biophys J. 2003;84:3414–3424. doi: 10.1016/S0006-3495(03)70063-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonnevier JL, Mueller DL. Cutting edge: B7/CD28 interactions regulate cell cycle progression independent of the strength of TCR signaling. J Immunol. 2002;169(12):6659–6663. doi: 10.4049/jimmunol.169.12.6659. [DOI] [PubMed] [Google Scholar]
- Burnham KP, Anderson DR. Multimodel inference: understanding AIC and BIC in model selection. Sociological Methods Research. 2004;33:261–304. [Google Scholar]
- Clyde RG, Bown JL, Hupp TR, Zhelev N, Crawford JW. The role of modelling in identifying drug targets for diseases of the cell cycle. J Roy Soc Interface. 2006;22:617–627. doi: 10.1098/rsif.2006.0146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper S. The continuum model: statistical implications. J Theor Biol. 1982;94:783–800. doi: 10.1016/0022-5193(82)90078-9. [DOI] [PubMed] [Google Scholar]
- Cowan R, Morris VB. Cell population dynamics during the differentiation phase of tissue development. Journal of Theoretical Biology. 1986;122:205–224. doi: 10.1016/s0022-5193(86)80082-0. [DOI] [PubMed] [Google Scholar]
- Crump KS, Mode CJ. An age-dependent branching process with correlations among sister cells. Journal of Applied Probability. 1969;6:205–219. [Google Scholar]
- Deenick EK, Hasbold J, Hodgkin PD. Switching to IgG3, IgG2b, and IgA is division linked and independent, revealing a stochastic framework for describing differentiation. J Immunol. 1999;163:4707–4714. [PubMed] [Google Scholar]
- Deenick EK, Gett AV, Hodgkin PD. Stochastic model of T cell proliferation: a calculus revealing IL-2 regulation of precursor frequencies, cell cycle time, and survival. J Immunol. 2003;170(10):4963–4972. doi: 10.4049/jimmunol.170.10.4963. [DOI] [PubMed] [Google Scholar]
- De Boer RJ, Perelson AS. Estimating division and death rates from CFSE data. J Comput Appl Math. 2005;184:140–164. doi: 10.1007/s11538-006-9094-8. [DOI] [PubMed] [Google Scholar]
- De Boer RJ, Homann D, Perelson AS. Different dynamics of CD4+ and CD8+ T cell responses during and after acute lymphocytic choriomeningitis virus infection. J Immunol. 2003;171(8):3928–3935. doi: 10.4049/jimmunol.171.8.3928. [DOI] [PubMed] [Google Scholar]
- De Boer RJ, Ganusov VV, Milutinovic D, Hodgkin PD, Perelson AS. Estimating lymphocyte division and death rates from CFSE data. Bull Math Biol. 2006;68:1011–1031. doi: 10.1007/s11538-006-9094-8. [DOI] [PubMed] [Google Scholar]
- Fleurant C, Duchesne J, Raimbault P. An allometric model for trees. J Theor Biol. 2004;227(1):137–147. doi: 10.1016/j.jtbi.2003.10.014. [DOI] [PubMed] [Google Scholar]
- Foulds KE, Zenewicz LA, Shedlock DJ, Jiang J, Troy AE, Shen H. Cutting edge: CD4 and CD8 T cells are intrinsically different in their proliferative responses. J Immunol. 2002;168:1528–1532. doi: 10.4049/jimmunol.168.4.1528. [DOI] [PubMed] [Google Scholar]
- Ganusov VV, Pilyugin SS, De Boer RJ, Murali-Krishna K, Ahmed R, Antia R. Quantifying cell turnover using CFSE data. J Immunol Methods. 2005;298:183–200. doi: 10.1016/j.jim.2005.01.011. [DOI] [PubMed] [Google Scholar]
- Ganusov VV, Milutinovic D, De Boer RJ. IL-2 regulates expansion of CD4+ T cell populations by affecting cell death: insights from modeling CFSE data. J Immunol. 2007;179:950–957. doi: 10.4049/jimmunol.179.2.950. [DOI] [PubMed] [Google Scholar]
- Gett AV, Hodgkin PD. A cellular calculus for signal integration by T cells. Nat Immunol. 2000;1(3):239–244. doi: 10.1038/79782. [DOI] [PubMed] [Google Scholar]
- Glover F. Heuristics for integer programming using surrogate constraints. Decision Sciences. 1977;8:156–166. [Google Scholar]
- Guo Z, Tay JC. Multi-timescale event-scheduling in multi-agent immune simulation models. BioSystems. 2008;91:126–145. doi: 10.1016/j.biosystems.2007.08.007. [DOI] [PubMed] [Google Scholar]
- Hasbold JA, Lyons AB, Kehry MR, Hodgkin PD. Cell division number regulates IgG1 and IgE switching of B cells following stimulation by CD40 ligand and IL-4. Eur J Immunol. 1998;28:1040–1051. doi: 10.1002/(SICI)1521-4141(199803)28:03<1040::AID-IMMU1040>3.0.CO;2-9. [DOI] [PubMed] [Google Scholar]
- Hawkins ED, Turner ML, Dowling MR, van Gend C, Hodgkin PD. A model of immune regulation as a consequence of randomized lymphocyte division and death times. Proc Natl Acad Sci USA. 2007;104(12):5032–5037. doi: 10.1073/pnas.0700026104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hawkins ED, Markham JF, McGuinness LP, Hodgkin PD. A single-cell pedigree analysis of alternative stochastic lymphocyte fates. Proceedings of the National Academy of Sciences. 2009;106(32):13457–13462. doi: 10.1073/pnas.0905629106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heyde CC, Seneta E. IJ Bienayme: Statistical Theory Anticipated. Berlin, Germany; 1977. [Google Scholar]
- Hodgkin PD, Lee JH, Lyons AB. B cell differentiation and isotype switching is related to division cycle number. J Exp Med. 1996;184:277C281. doi: 10.1084/jem.184.1.277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyrien O, Mayer-Pröschel M, Noble M, Yakovlev A. A stochastic model to analyze clonal data on multi-type cell populations. Biometrics. 2005;61:199–207. doi: 10.1111/j.0006-341X.2005.031210.x. [DOI] [PubMed] [Google Scholar]
- Hyrien O, Zand MS. A mixture model with dependent observations for the analysis of CFSE-labeling experiments. Journal of the American Statistical Association. 2008;103(481):222–239. [Google Scholar]
- Jagers P. Branching Processes with Biological Applications. London: Wiley; 1975. [Google Scholar]
- Karlin S, Taylor HM. A first course in stochastic processes. 2. San Diego: Academic Press; 1975. [Google Scholar]
- Kimmel M. Cellular population dynamics. I. Model construction and reformulation. Mathematical Biosciences. 1980;48(3–4):211–224. [Google Scholar]
- Kimmel M, Axelrod DE. Unequal cell division, growth regulation and colony size of mammalian cells: a mathematical model and analysis of experimental data. Journal of Theoretical Biology. 1991;153:157–180. doi: 10.1016/s0022-5193(05)80420-5. [DOI] [PubMed] [Google Scholar]
- Kimmel M, Axelrod DE. Branching Processes in Biology. New York: Springer-Verlag; 2002. [Google Scholar]
- Kimmel M, Traganos F. Estimation and prediction of cell cycle specific effects of anticancer drugs. Mathematical Biosciences. 1986;80:187–208. [Google Scholar]
- Koch AL. The re-incarnation, re-interpretation and re-demise of the transition probability model. J Biotech. 1999;71:143–156. doi: 10.1016/s0168-1656(99)00019-x. [DOI] [PubMed] [Google Scholar]
- Laguna M, Marti R. Scatter search: Methodology and implementations in C. Boston: Kluwer Academic Publishers; 2003. [Google Scholar]
- Laguna M, Marti R. Experimental testing of advanced scatter search designs for global optimization of multimodal functions. Journal of Global Optimization. 2005;33:235–355. [Google Scholar]
- Lee HY, Perelson AS. Modeling T cell proliferation and death in vitro based on labeling data: generalizations of the Smith-Martin cell cycle model. Bulletin of Mathematical Biology. 2008;70(1):21–44. doi: 10.1007/s11538-007-9239-4. [DOI] [PubMed] [Google Scholar]
- Lee H, Hawkins E, Zand MS, Mosmann T, Wu H, Hodgkin PD, Perelson AS. Interpreting CFSE obtained division histories of B cells in vitro with Smith-Martin and cyton type models. Bulletin of Mathematical Biology. 2009;71(7):1649–1670. doi: 10.1007/s11538-009-9418-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leon K, Faro J, Carneiro J. A general mathematical framework to model generation structure in a population of asynchronously dividing cells. J Theor Biol. 2004;229:455–476. doi: 10.1016/j.jtbi.2004.04.011. [DOI] [PubMed] [Google Scholar]
- Liang H, Miao H, Wu H. Estimation of constant and time-varying dynamic parameters of HIV infection in a nonlinear differential equation model. Annals of Applied Statistics. 2010 doi: 10.1214/09-AOAS290. accepted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu D, Yu J, Chen H, Reichman R, Wu H, Jin X. Statistical determination of threshold for cellular division in the CFSE-labeling assay. Journal of Immunological Methods. 2006;312(1–2):126–136. doi: 10.1016/j.jim.2006.03.010. [DOI] [PubMed] [Google Scholar]
- Lyons AB. Analyzing cell division in vivo and in vitro using flow cytometric measurement of CFSE dye dilution. J Immunol Methods. 2000;243:147–154. doi: 10.1016/s0022-1759(00)00231-3. [DOI] [PubMed] [Google Scholar]
- Macken CA, Perelson AS. Lecture Notes in Biomathematics. Vol. 76. Springer Verlag; New York: 1988. Stem Cell Proliferation and Differentiation: A Multi-type Branching Process Model. [Google Scholar]
- Mathai A. Storage capacity of a dam with gamma type inputs. Annals of the Institute of Statistical Mathematics. 1982;34(1):591–597. [Google Scholar]
- Miao H, Dykes C, Demeter LM, Cavenaugh J, Park SY, Perelson AS, Wu H. Modeling and estimation of kinetic parameters and replicative fitness of HIV-1 from flow-cytometry-based growth competition experiments. Bull Math Biol. 2008;70(6):1749–1771. doi: 10.1007/s11538-008-9323-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miao H, Dykes C, Demeter LM, Wu H. Differential equation modeling of HIV viral fitness experiments: model identification, model selection, and multi-model inference. Biometrics. 2009;65(1):292–300. doi: 10.1111/j.1541-0420.2008.01059.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miao H, Xia X, Perelson AS, Wu H. On identifiability of nonlinear ODE models with applications in viral dynamics. SIAM Review. 2011;53(1):3–39. doi: 10.1137/090757009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moles CG, Banga JR, Keller K. Solving nonconvex climate control problems: pitfalls and algorithm performances. Applied Soft Computing. 2004;5(1):35–44. [Google Scholar]
- Moschopoulos PG. The distribution of the sum of independent gamma random variables. Annals Instit Statist Math. 1985;37(3):541–544. [Google Scholar]
- Nocedal J, Wright SJ. Numerical Optimization. New York: Springer Verlag; 1999. [Google Scholar]
- Nordon RE, Nakamura M, Ramirez C, Odell R. Analysis of growth kinetics by division tracking. Immunol Cell Biol. 1999;77:523–529. doi: 10.1046/j.1440-1711.1999.00869.x. [DOI] [PubMed] [Google Scholar]
- Novak B, Tyson JJ. Quantitative analysis of a molecular model of mitotic control in fission yeast. J Theor Biol. 1995;173:283–305. [Google Scholar]
- Novak B, Tyson JJ. Modeling the control of DNA replication in fission yeast. Proc Natl Acad Sci USA. 1997;94:9147–9152. doi: 10.1073/pnas.94.17.9147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novak B, Tyson JJ. A model for restriction point control of the mammalian cell cycle. J Theor Biol. 2004;230:563–579. doi: 10.1016/j.jtbi.2004.04.039. [DOI] [PubMed] [Google Scholar]
- Pilyugin SS, Ganusov VV, Murali-Krishna K, Ahmed R, Antia R. The rescaling method for quantifying the turnover of cell population. J Theor Biol. 2003;225:275–283. doi: 10.1016/s0022-5193(03)00245-5. [DOI] [PubMed] [Google Scholar]
- Powell EO. Some features of the generation times of individual bacteria. Biometrika. 1955;42(1–2):16–44. [Google Scholar]
- Revy P, Sospedra M, Barbour B, Trautmann A. Functional antigen-independent synapses formed between T cells and dendritic cells. Nat Immunol. 2001;2(10):925–931. doi: 10.1038/ni713. [DOI] [PubMed] [Google Scholar]
- Rodriguez-Fernandez M, Egea JA, Banga JR. Novel metaheuristic for parameter estimation in nonlinear dynamic biological systems. BMC Bioinformatics. 2006;7:483. doi: 10.1186/1471-2105-7-483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwarz G. Estimating the dimensions of a model. Annals of Statistics. 1978;6:461–464. [Google Scholar]
- Sim CH. Point processes with correlated gamma interarrival times. Statistics & Probability Letters. 1991;15(2):135–141. [Google Scholar]
- Smith JA, Martin L. Do cells cycle? Proc Natl Acad Sci USA. 1973;70:1263–1267. doi: 10.1073/pnas.70.4.1263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith JA, Laurence DJR, Rudland PS. Limitations of cell kinetics in distinguishing cell cycle models. Nature. 1981;293:648–50. doi: 10.1038/293648a0. [DOI] [PubMed] [Google Scholar]
- Stewart T, Strijbosch LWG, Moors JJA, Van Batenburg P. A Simple Approximation to the Convolution of Gamma Distributions. Tilburg University, Center for Economic Research; 2007. [Google Scholar]
- Storn R, Price K. Differential evolution - a simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization. 1997;11:341–359. [Google Scholar]
- THOM HCS. Approximate convolution of the gamma and mixed gamma distributions. Monthly Weather Review. 1968;96(12):883–886. [Google Scholar]
- Toni T, Welch D, Strelkowa N, Ipsen A, Stumpf MPH. Approximate Bayesian computation scheme for parameter inference and model selection in dynamical systems. Journal of The Royal Society Interface. 2009;6(31):187–202. doi: 10.1098/rsif.2008.0172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tyrcha J. Age-dependent cell cycle models. J Theor Biol. 2001;213(1):89–101. doi: 10.1006/jtbi.2001.2403. [DOI] [PubMed] [Google Scholar]
- Tyson JJ. Modeling the cell division cycle: cdc2 and cycling interactions. Proc Natl Acad Sci USA. 1991;88:7328–7332. doi: 10.1073/pnas.88.16.7328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vellaisamy P, Upadhye NS. On the sums of compound negative binomial and gamma random variables. J Appl Prob. 2009;46:272–283. [Google Scholar]
- Wellard C, Markham J, Hawkins ED, Hodgkin PD. The effect of correlations on the population dynamics of lymphocytes. Journal of Theoretical Biology. 2010;264(2):443–449. doi: 10.1016/j.jtbi.2010.02.019. [DOI] [PubMed] [Google Scholar]
- Whitmire JK, Ahmed R. Costimulation in antiviral immunity: differential requirements for CD4(+) and CD8(+) T cell responses. Curr Opin Immunol. 2000;12(4):448–455. doi: 10.1016/s0952-7915(00)00119-9. [DOI] [PubMed] [Google Scholar]
- Yakovlev AY, Yanev NM. Transient processes in cell proliferation kinetics. Heidelberg: Springer; 1989. [Google Scholar]
- Yakovlev AY, Mayer-Pröschel M, Noble M. A stochastic model of brain cell differentiation in tissue culture. Journal of Mathematical Biology. 1998;37:49–60. doi: 10.1007/s002850050119. [DOI] [PubMed] [Google Scholar]
- Yakovlev AY, Yanev NM. Branching stochastic processes with immigration in analysis of renewing cell pupulations. Mathematical Biosciences. 2006;203:37–63. doi: 10.1016/j.mbs.2006.06.001. [DOI] [PubMed] [Google Scholar]
- Yakovlev AY, Stoimenova VK, Yanev NM. Branching processes as models of progenitor cell populations and estimation of the offspring distributions. Journal of the American Statistical Association. 2008;103(484):1357–1366. [Google Scholar]
- Ye Y. PhD thesis. Dept. of ESS, Stanford University; 1987. Interior algorithms for linear, quadratic and linearly constrained non-linear programming. [Google Scholar]
- Zilman A, Ganusov VV, Perelson AS. Stochastic models of lymphocyte proliferation and death. PLoS ONE. 2010;5(9):e12775. doi: 10.1371/journal.pone.0012775. [DOI] [PMC free article] [PubMed] [Google Scholar]