Tradeoffs between hydraulic and mechanical stress responses of mature Norway spruce trunk wood

Summary

We tested the effects of growth characteristics and basic density on hydraulic and mechanical properties of mature Norway spruce (Picea abies (L.) Karst.) wood from six 24-year-old clones, grown on two sites in southern Sweden differing in water availability. Hydraulic parameters assessed were specific hydraulic conductivity at full saturation (k_s100) and vulnerability to cavitation (Ψ₅₀), mechanical parameters included bending strength (σ_b), modulus of elasticity (MOE), compression strength (σ_a) and Young’s modulus (E). Basic density, diameter at breast height, tree height, and hydraulic and mechanical parameters varied considerably among clones. Clonal means of hydraulic and mechanical properties were strongly related to basic density and to growth parameters across sites, especially to diameter at breast height. Compared with stem wood of slower growing clones, stem wood of rapidly growing clones had significantly lower basic density, lower σ_b, MOE, σ_a and E, was more vulnerable to cavitation, but had higher k_s100. Basic density was negatively correlated to Ψ₅₀ and k_s100. We therefore found a tradeoff between Ψ₅₀ and k_s100. Clones with high basic density had significantly lower hydraulic vulnerability, but also lower hydraulic conductivity at full saturation and thus less rapid growth than clones with low basic density. This tradeoff involved a negative relationship between Ψ₅₀ and σ_b as well as MOE, and between k_s100 and σ_b, MOE and σ_a. Basic density and Ψ₅₀ showed no site-specific differences, but tree height, diameter at breast height, k_s100 and mechanical strength and stiffness were significantly lower at the drier site. Basic density had no influence on the site-dependent differences in hydraulic and mechanical properties, but was strongly negatively related to diameter at breast height. Selecting for growth may thus lead not only to a reduction in mechanical strength and stiffness but also to a reduction in hydraulic safety.

Introduction

In conifers, such as Norway spruce (Picea abies (L.) Karst.), with growth rates inversely related to wood density (Johansson 1993, Rozenberg and Cahalan 1997, Hannrup et al. 2004), rapid growth rate is the principal criterion for tree breeding and high density is of only secondary importance (Zobel and Jett 1995). Nevertheless, in some conifers, density is strongly related to mechanical and hydraulic wood functions important for tree survival (Evans and Ilic 2001, Hacke and Sperry 2001, Hacke et al. 2001, Rosner et al. 2007). Selection for breeding, without considering the relationships between wood structure and tree survival, may result in trees with enhanced growth but lower survival prospects (Booker and Sell 1998, Domec and Gartner 2002a, Rozenberg et al. 2002). In the present study, we tested the effects of growth traits on hydraulic and mechanical properties and determined how these biological functions of wood are related in the trunk of mature Norway spruce.

Much is known about heritability of growth parameters and wood properties in spruce species (Rozenberg and Cahalan 1997, Hannrup et al. 2004). Heritabilities for growth parameters and specific gravity tend to be higher than for other traits, and both are genotypically and phenotypically negatively correlated in Norway spruce wood (Hannrup et al. 2004). There is, however, a lack of information on how growth and density are related to hydraulic and mechanical properties in the mature Norway spruce trunk. Recently, Rosner et al. (2007) investigated the structural properties influencing hydraulic and mechanical properties in the juvenile Norway spruce trunk, but the relationships found may be inapplicable to the mature trunk. Mechanical stiffness is strongly related to density in both juvenile and mature Norway spruce wood (Rozenberg and Cahalan 1997, Lundström et al. 2007); however, hydraulic conductivity and vulnerability to cavitation are unrelated to density in juvenile wood, which can be explained by the complex density structure of the first annual rings (Mayr and Cochard 2003, Mayr et al. 2003, Rosner et al. 2007). In past studies, much effort has focused on relating wood structural traits to the hydraulic properties of mature conifer trunk wood (Mencuccini et al. 1997, Domec and Gartner 2002a, 2003, Bouffier et al. 2003, Jagels et al. 2003, Jagels and Visscher 2006). Vulnerability to cavitation and implosion are strongly negatively related to wood density at the cellular level (Hacke and Sperry 2001, Hacke et al. 2001) and at the tissue level, as shown for pine species (Domec and Gartner 2002a, 2003, Bouffier et al. 2003). Wood density depends on wall thickness, lumen diameter and latewood percentage (Zobel and van Buijtenen 1989, Wimmer 1995). Higher vulnerability to cavitation of wider tracheids is the result of both increased susceptibility to cavitation and decreased capability for embolism removal (Zwieniecki and Holbrook 1998, Holbrook and Zwieniecki 1999).

Rapid growth depends on less densely structured wood to guarantee efficient water transport. Hydraulic effectiveness and safety are conflicting wood functions: the most conductive tissues are the most vulnerable to cavitation (Cochard 1992, Piñol and Sala 2000, Domec and Gartner 2001, 2003, Tyree and Zimmermann 2002, Bouffier et al. 2003). Larger and more numerous pit membranes in earlywood facilitate water transport, but may require thicker secondary cell walls to compensate for a potential weakening of walls (Gartner 1995, Hacke and Sperry 2001, Domec and Gartner 2002b). Little is known, however, about genetic versus environmental controls on cavitation resistance and xylem conductivity (Hacke and Sperry 2001). High biomass allocation aboveground demands an increase in mechanical strength and stiffness to support the crown, and height influences the magnitude of the bending moment under conditions of dynamic wind loading (Mattheck 1998, Spatz and Bruechert 2000). Wood density is considered the best predictive trait for mechanical properties (Niklas 1992). Mechanical strength and stiffness increase with increasing wood density, therefore a tradeoff between mechanical stiffness and hydraulic efficiency (maximum sap flow rate) should be expected (Hacke and Sperry 2001, Roderick and Berry 2001, Domec and Gartner 2002a). In some conifer species, however, no such tradeoff between mechanical stiffness and hydraulic conductivity was found (Mencuccini et al. 1997, Jagels et al. 2003, Jagels and Visscher 2006), because mechanical stiffness can be modified not only by increasing whole-wood density but also by varying latewood percentage, tracheid length, microfibril angles, arrangement of cell wall layers or cell wall chemistry (Mencuccini et al. 1997, Ezquerra and Gil 2001, Gindl 2001, Jagels et al. 2003, Jagels and Visscher 2006).

To test the effects of growth rate on hydraulic and mechanical properties of mature wood we investigated Norway spruce clones differing in growth rates on two sites with different water availability. Given the negative relationship between growth and wood density, we expected clonal as well as site differences in hydraulic and mechanical properties. We predicted that density is positively related to hydraulic safety but negatively related to hydraulic conductivity, because wood structure is less complex in mature tree stems than in juvenile tree stems or branches (Mayr and Cochard 2003, Mayr et al. 2003, Rosner et al. 2007). We hypothesized that a possible tradeoff between hydraulic vulnerability and conductivity (hereafter termed wood density-based tradeoff) involves a negative relationship between mechanical strength and hydraulic vulnerability as well as hydraulic conductivity.

Materials and methods

Site and trial description

Wood specimens came from 24-year-old Norway spruce trees (Picea abies (L.) Karst.) of two clonal trials in southern Sweden, Tönnersjöheden and Vissefjärda. In 1982, two-season-old rooted cuttings were randomly planted as 1.4 × 1.4 m spaced tree plots in a randomized block design. In total, 325 clones with nine replicates were planted within 0.7-ha areas at both sites. Tönnersjöheden has almost twice as much precipitation during the growth season and more than three times higher humidity (difference between precipitation and evaporation) than Vissefjärda, especially during the growth period (Table 1). Therefore, Tönnersjöheden (hereafter denoted wet site) should have higher water availability than Vissefjärda (hereafter denoted dry site). Based on a screening in 2002, we selected six clones differing in growth characteristics with five replicates per site.

Table 1.

Description of study sites.

	Tönnersjöheden	Vissefjärda
Site type	Wet	Dry
Latitude (N)	56°67′	56°54′
Longitude (E)	13°07′	15°53′
Altitude (m a.s.l.)	60	120
Slope (°)	< 5	< 5
Wind exposure	Low	Low
Precipitation during growth period (mm)	600	350
Available water during growth period1 (mm)	> 150	< 50
Soil description	Sandy loam till	Sandy loam till
Soil type2	Orthic podzol	Orthic podzol
Site index (H100)3	G32	G28
Field vegetation type	Narrow grass	Bilberry (Vaccinium myrtillus)
Tree survival until 2002 (%)	65	61

¹Difference between precipitation and evaporation.

²FAO-UNESCO 1981.

³Height of dominant trees at age 100 years estimated according to Hägglund and Lundmark (1981).

Sample harvesting and storage

Trees were harvested during a wet period in mid-June 2004, when plant water stress was minimal. Tree height (H) was divided by stem diameter outside bark (D) measured at breast height (1.3 m) to determine the H/D ratio. Wood bole segments, 20–30 cm in length, were taken immediately after felling at 1.3-m height from the ground. During transport, samples were kept wet in plastic bags containing some fresh water. In the laboratory, bole segments were debarked and split along the grain. An outer sapwood zone of 20 mm was separated from the split samples and put in plastic zip bags together with fresh water containing 0.01% (v/v) Micropur (Katadyn Products), a source of silver chloride, to prevent microbial growth. Samples were sent within 24 h to BOKU Vienna (Austria) and stored frozen at −18 °C until processed (Mayr et al. 2003, Rosner et al. 2006).

Preparation of standard beams for flow experiments and mechanical testing

Wood samples were thawed in fresh water. Outer sapwood specimens with a transverse surface area of about 9 × 9 mm were isolated by splitting the wood along the grain with a chisel. Tangential and radial faces of the beams used for hydraulic testing were planed on a sliding microtome. Specimens were shortened on a band saw, and specimen ends were re-cut with a razor blade. During all these steps the specimens were kept wet. They were then soaked in distilled water under vacuum for at least 48 h to refill embolized tracheids and then stored in degassed water containing 0.01% Micropur. The final standard dimensions of the specimens were 6 mm in the tangential and radial planes and 110 mm in length. Standard beams were produced from specimens taken at 1.3 m from the ground containing annual rings 17–19. Additional wood beams with the same final dimensions were prepared with a saw. Specimens were kept wet during all preparation steps and stored for three days at 4 °C in fresh tap water containing 0.01% Micropur until mechanical tests were performed.

Hydraulic method to assess hydraulic vulnerability

Hydraulic conductivity was measured under a hydraulic pressure head of 5.4 kPa with distilled, filtered (0.22 μm) and degassed water containing 0.005% Micropur. Conductivity data were corrected to 20 °C to account for the temperature dependence of fluid viscosity. Vulnerability curves were obtained as described by Spicer and Gartner (1998) and Domec and Gartner (2001). After determination of saturated mass and conductivity at full saturation (k_s100), air overpressure (P) was applied to the sides of the specimens, while the ends protruded from a double-ended pressure chamber (PMS Instruments, Corvallis, OR), to induce cavitation. After the pressure treatment, the specimens were weighed and put in distilled water for about 30 min. Hydraulic conductivity (k_s(P)) was measured again after recutting the specimens. Initially, the pressure chamber was pressurized to 0.5 MPa, and the pressure was subsequently increased after each conductivity measurement in steps of 0.5 or 1.0 MPa until more than 95% loss of conductivity (PLC) occurred. The PLC at a given P was calculated as:

$$\mathrm{PLC}=\left(\frac{k_{\mathrm{s}100}-k_{\mathrm{s}\left(P\right)}}{k_{\mathrm{s}100}}\right)100$$ (1)

where k_s100 is the flow rate at full saturation.

In some specimens, specific conductivity was up to 10% higher after exposure to low pressures between 0.5 and 1 MPa than at full saturation (Domec et al. 2007). As a reference value for constructing vulnerability curves, the initial conductivity at full saturation was chosen and values higher after the first pressure increases were excluded from the analysis (Rosner et al. 2006). Hydraulic vulnerability curves were fitted by the least square method based on a sigmoidal function to calculate Ψ₅₀, the potential at which 50 PLC occurred (Pammenter and Vander Willigen 1998).

Relative water loss (RWL; %) caused by the air overpressure was calculated as:

$$\mathrm{RWL}=\left(1-\frac{\text{actual fresh mass}-\text{dry mass}}{\text{saturated mass}-\text{dry mass}}\right)100$$ (2)

Dry mass was obtained by drying wood specimens at 103 °C to constant mass. The RWL was related to the pressure applied with a cubic function, and the overpressure resulting in 50% RWL was calculated (Ψ_RWL50) (Rosner et al. 2006).

Mechanical properties

Mechanical traits comprised bending strength (σ_b; Pa) and bending stiffness (MOE, modulus of elasticity; Pa) as well as compression strength (σ_a; Pa) and compression stiffness in the axial direction (E, Young’s modulus; Pa) of saturated green wood.

Mechanical testing was performed with a Zwick/Roell Z100 SW5A universal testing machine (Ulm, Germany) at ambient temperature (~22 °C). A crosshead speed of 1 mm min⁻¹ was chosen for the compression tests and 3 mm min⁻¹ for the bending tests, respectively. The span width for the 3-point bending tests was 80 mm. An 80-mm span width means that deflection of the beam was mainly influenced by the axial stiffness of the material, and less so by shear deformation. Because of the design of the test set-up, measured MOE was mainly determined by the axial stiffness of the specimens. Specimens were loaded up to fracture and unloaded after a force drop of 10% of the maximum force (F_max; N). We calculated σ_b as the maximum bending moment divided by the section modulus of the specimens. We calculated σ_a as F_max divided by the cross-sectional area of the specimens (m²). Values of MOE and E were derived from the stress–strain curves between 10 and 40% and between 35 and 50% of F_max, respectively.

Basic density

Basic density was determined as dry mass after drying at 103 °C to constant mass divided by the volume in the fully saturated green state.

Sample numbers and statistics

Hydraulic tests were performed on 5–6 sapwood specimens per tree and bending and compression testing was made on 7–10 sapwood specimens per tree taken from randomly chosen positions around the circumference. Compression wood (if present) was excluded from the measurements. Sixty trees were investigated.

Values are given as means ± standard error (SE). All traits followed a normal distribution. Significant differences for clones, sites and their interaction were tested by factorial analysis of variance (ANOVA). Clones and sites were assumed to be fixed effects. Associations between two variables were examined by linear or nonlinear regression analyses. Nonlinear regression models were quadratic and S-models, where y = e^{(b0 + b1/x)}. The Pearson correlation coefficient was used to associate traits on a single tree basis as well as on a clonal mean basis. We investigated relationships between two variables on a single tree (each site n = 30) as well as on a clonal mean basis at each site (each site n = 6) and on a clonal mean basis across sites (n = 6 and n = 12 for regression lines in the figures). Regression slopes were analyzed by the Student’s t-test for site-specific differences. Differences between mean values and regression slopes were accepted as significant if P ≤ 0.05.

Results

Growth, wood density and hydraulic and mechanical parameters: site and clonal effects

Mean tree height and DBH were significantly smaller at the dry than at the wet site. Crown percent was higher at the dry site than at the wet site, whereas there were no significant differences in H/D ratio and basic density between sites (Table 2). Hydraulic conductivity at full saturation and mechanical properties had significantly higher values at the wet site than at the dry site. Only two of the six clones studied—the two fast-growing clones—showed significantly lower hydraulic vulnerabilities at the dry site than at the wet site (P < 0.05, Figure 1a), whereas hydraulic vulnerability in the slowest-growing clone was slightly (but not significantly) higher at the dry site than at the wet site. Therefore, mean hydraulic vulnerability (Ψ₅₀) of single trees did not differ between sites (Table 2). All traits investigated showed clone-specific differences, with the exception of crown percent (Table 1). Clone × site interactions were found for wood density, hydraulic vulnerability, and all mechanical properties assessed, except Young’s modulus.

Table 2.

General linear models (fixed factors: clone and site (Tönnersjöheden, Vissefjärda)) of growth factors, basic density and wood biological functions. Abbreviations: DBH = diameter at breast height, H = tree height; H/D = height/diameter at breast height; CP = crown percentage; BD = basic density; Ψ₅₀ = applied air pressure causing 50% loss of conductivity; Ψ_RWL50 = applied air pressure causing 50% loss of relative water content; k_s100 = specific hydraulic conductivity at full saturation; E = Young’s modulus; σ_a = compression strength; MOE = modulus of elasticity; σ_b = bending strength; SS = sum of squares; and SE = standard error.

Trait	Site	Mean (SE)	Clone			Site			Clone × Site
			SS	F	P > F	SS	F	P > F	SS	F	P > F
DBH (cm)	Wet	11.81 (0.52)	117.59	5.22	0.001	21.12	4.68	0.035	53.38	2.37	0.053
	Dry	10.62 (0.42)
H (m)	Wet	10.81 (0.27)	37.20	4.12	0.003	36.35	20.11	0.000	13.64	1.51	0.205
	Dry	9.26 (0.29)
H/D	Wet	94.89 (3.27)	1112.68	6.61	0.000	534.42	3.18	0.081	1498.60	1.78	0.134
	Dry	88.92 (2.58)
CP (%)	Wet	72.51 (1.09)	179.19	1.34	0.264	468.02	17.52	0.000	153.21	1.15	0.349
	Dry	78.72 (0.93)
BD (g cm−3)	Wet	0.39 (0.01)	246.83	8.90	0.000	9.24	1.67	0.203	81.36	2.93	0.022
	Dry	0.38 (0.01)
Ψ50 (MPa)	Wet	−2.42 (0.05)	0.88	8.45	0.000	0.07	3.15	0.082	0.46	4.45	0.002
	Dry	2.48 (0.03)
ΨRWL50 (MPa)	Wet	−3.05 (0.07)	2.38	5.54	0.001	0.03	0.41	0.526	0.82	1.91	0.111
	Dry	−3.00 (0.05)
ks100 (10−4 m2 s−1 MPa−1)	Wet	29.65 (1.93)	3763.56	11.00	0.000	1035.51	15.14	0.000	260.60	0.76	0.582
	Dry	21.4 (2.22)
E (GPa)	Wet	1.03 (0.02)	0.31	6.32	0.000	0.13	12.85	0.001	0.04	0.90	0.490
	Dry	0.94 (0.02)
σa (MPa)	Wet	21.09 (0.46)	87.93	5.74	0.000	33.56	10.95	0.002	63.79	4.16	0.003
	Dry	19.59 (0.36)
MOE (GPa)	Wet	8.99 (0.19)	15.08	4.13	0.003	12.22	16.73	0.000	10.46	0.86	0.024
	Dry	8.09 (0.18)
σb (MPa)	Wet	41.19 (0.70)	275.00	7.92	0.000	91.89	13.23	0.001	115.56	3.33	0.012
	Dry	38.72 (0.59)

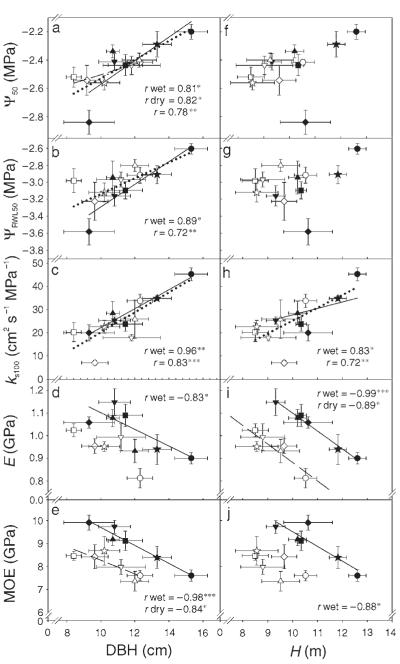
Figure 1.

Clonal means of diameter at breast height (DBH) and tree height (H) as functions of clonal means of the air overpressure causing 50% loss of hydraulic conductivity (Ψ₅₀), the air overpressure causing 50% relative water loss (Ψ_RWL50), the specific hydraulic conductivity at full saturation (k_s100), the compression stiffness (E) and the bending stiffness (MOE). Filled symbols denote trees from the wet site (Tönnersjöheden); open symbols denote trees from the dry site (Vissefjärda); each symbol denotes a different clone. Error bars represent one standard error. Significant relationships are indicated by solid regression lines for the wet site and by dashed regression lines for the dry site. Dotted lines indicate significant relationships across sites (n = 12), in cases where the regression slopes did not differ between sites. The significance of the correlation coefficients of the linear model equations are indicated by asterisks: *, P < 0.05; **, P < 0.01; and ***, P < 0.001.

Relationships between growth, wood density and hydraulic and mechanical parameters

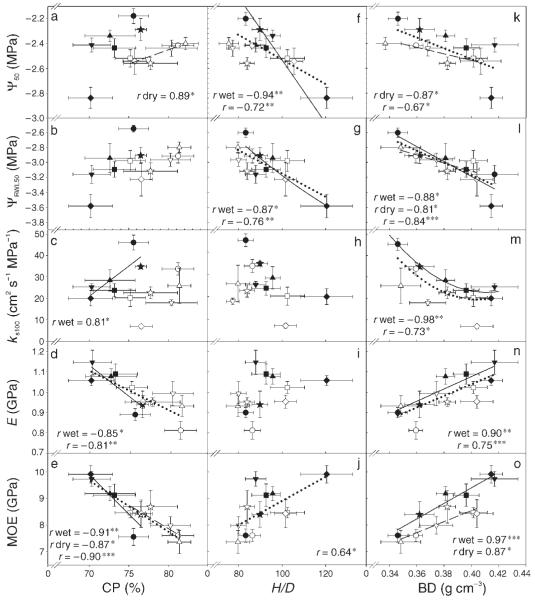
Vulnerability to cavitation and hydraulic conductivity increased with DBH (Figures 1a–c) and crown percent (Figures 2a–c), but decreased with the H/D ratio (Figures 2f–h). Values of k_s100 increased with increasing height growth (Figure 1h). Relationships between hydraulic wood functions and growth traits were generally stronger at the wet site than at the dry site (Table 3). Mechanical properties tended to increase with H/D ratio (Figures 2i–j), but decrease with growth (Figures 1d, 1e, 1i and 1j) and crown percent (Figures 2d and 2e). Basic density was significantly lower in trees with rapid growth and high crown percentage, but higher in trees with high H/D ratios (Table 3). Vulnerability to cavitation and hydraulic conductivity were negatively related to basic density (Figures 2k–m), whereas mechanical strength and stiffness increased significantly with increasing basic density (Figures 2n and 2o). The site-specific relationships assessed were mainly significant on a single tree basis (Table 3), but less often on a clonal mean basis (Figures 1 and 2).

Figure 2.

Clonal means of crown percentage (CP), height/diameter ratio (H/D) and basic density (BD) as functions of clonal means of the air overpressure causing 50% loss of hydraulic conductivity (Ψ₅₀), the air overpressure causing 50% relative water loss (Ψ_RWL50), the specific hydraulic conductivity at full saturation (k_s100), the Young’s modulus (E) and the modulus of elasticity (MOE). Filled symbols denote trees from the wet site (Tönnersjöheden); open symbols denote trees from the dry site (Vissefjärda); each symbol denotes a different clone. Error bars represent one standard error. Significant relationships are indicated by solid regression lines for the wet site and by dashed regression lines for the dry site. Dotted lines indicate significant relationships across sites (n = 12), in cases where the regression slopes did not differ between sites. The significance of the correlation coefficients of the linear or quadratic (3g, 3m) equations are indicated by asterisks: *, P < 0.05; **, P < 0.01; and ***, P < 0.001.

Table 3.

Relationships between growth traits, wood density and wood biological functions of single trees; upper right:wet site (Tönnersjöheden, n = 30); lower left: dry site (Vissefjärda, n = 30). Abbreviations: DBH = diameter at breast height; H = tree height; H/D = height/diameter at breast height; CP = crown percentage; BD = basic density;Ψ₅₀ = applied air pressure causing 50% loss of conductivity; Ψ_RWL50 = applied air pressure causing 50% loss of relative water content; k_s100 = specific hydraulic conductivity at full saturation; E = Young’s modulus; σ_a = compression strength; MOE = modulus of elasticity; and σ_b = bending strength.

	DBH	H	H/D	CP	BD	Ψ50	ΨRWL50	ks100	E	σa	MOE	σb
DBH		0.810***	−0.788***	0.270	−0.747***	0.677***	0.748***	0.702**	−0.591***	−0.772**	−0.772***	−0.739***
H	0.733***		−0.343	0.380*	−0.626***	0.358	0.537***	0.638***	−0.586***	−0.673***	−0.612***	−0.501***
H/D	−0.582***	0.107		−0.147	0.500**	−0.786***	−0.714***	−0.538**	0.318	0.503**	0.636***	0.662***
CP	0.715***	0.567***	−0.379*	−0.097	0.134	−0.022	0.	132	−0.146	−0.183	−0.215	−0.192
BD	−0.699***	−0.202	0.792***	−0.527***		−0.740***	−0.750***	−0.698***	0.823***	0.928***	0.798***	0.878***
Ψ50	0.531**	0.318	−0.456*	0.505**	−0.708***		0.857***	0.703***	−0.537***	−0.648***	−0.713***	−0.835***
ΨRWL50	0.471**	0.148	−0.542**	0.401*	−0.624***	0.768***		0.705***	−0.556***	−0.692***	−0.752***	−0.806***
ks100	0.385*	0.113	−0.420*	0.406*	−0.577***	0.457*	0.401*		−0.575***	−0.696***	−0.681***	−0.706***
E	−0.630***	−0.381*	0.472**	−0.295	0.719***	−0.495**	−0.323	−0.398*		0.909***	0.788***	0.786***
σa	−0.736***	−0.240	0.778***	−0.513***	0.954**	−0.678***	−0.599***	−0.449**	0.764***		0.846***	0.871***
MOE	−0.507**	−0.144	0.589***	−0.436*	0.808***	−0.687***	−0.547**	−0.338	0.593***	0.781***		0.882***
σb	−0.529**	−0.007	0.770***	−0.362*	0.857***	−0.599***	−0.482**	−0.397*	0.468**	0.789***	0.785***

^*The significance of the correlation coefficients of the linear or quadratricmodel equations are indicated as: P < 0.05;

^**The significance of the correlation coefficients of the linear or quadratricmodel equations are indicated as: P < 0.01;

^***The significance of the correlation coefficients of the linear or quadratricmodel equations are indicated as: P < 0.001.

Relationships between wood biological functions, growth traits and basic density became stronger when the analysis was performed for clonal means across sites (n = 6 clones). Clonal means of k_s100 were significantly positively correlated with DBH (r = 0.97, P < 0.01) and negatively correlated with basic density (r = −0.94, P < 0.05), but not with tree height. Clonal means of Ψ₅₀ were positively correlated with DBH (r = 0.82, P < 0.01) and to crown percent (r = 0.87, P < 0.05), but negatively correlated with H/D ratio (r = −0.93, P < 0.01) and basic density (r = −0.85, P < 0.01). Clonal means of the mechanical properties σ_b, σ_a and E decreased with increasing DBH (r = −0.89, −0.95 and −0.83, respectively, P < 0.05). Clones with denser wood had significantly higher σ_a, σ_b (r = 0.96 and −0.88, respectively, P < 0.05) than clones with less dense wood. Regression slopes for the relationships between tree height and E (Figure 1i), DBH and MOE (Figure 1e) and between MOE and basic density (Figure 2o) differed significantly between sites (P < 0.01). Basic density at breast height was strongly negatively related to DBH (r = −0.91, P < 0.01) and to crown percent (r = −0.98, P < 0.001). The mechanical properties σ_a, MOE and σ_b were therefore also negatively correlated with crown percent (r = −0.95, −0.93 and −0.92, respectively, P < 0.01). The H/D ratio was significantly positively correlated to σ_b (r = 0.95, P < 0.01).

Tradeoffs between wood functions

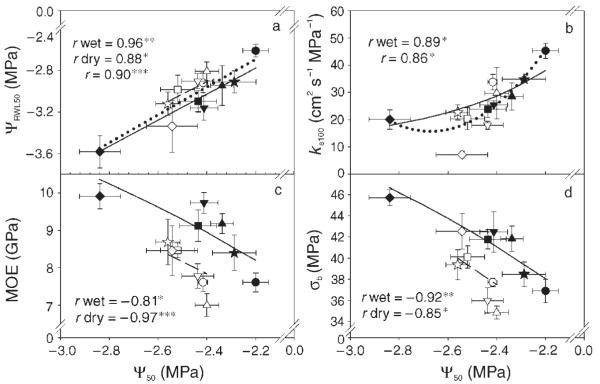
Hydraulic vulnerability was significantly positively related to hydraulic conductivity on a single tree basis (Table 3), as well as on a clonal mean basis at the wet site (Figure 3b). Across sites, clonal means of Ψ₅₀ and k_s100 were strongly related to each other (r = 0.89, P < 0.05, n = 6). Hydraulic vulnerability was negatively related to bending strength and stiffness (Table 3), but regression lines of the clonal means differed significantly between sites (P < 0.05, Figures 3c and 3d). The overpressure resulting in 50% RWL was a good predictive trait for hydraulic vulnerability (Figure 3a), with the relationship reaching maximum values when calculated for clonal means across sites (r = 0.98, P < 0.001, n = 6). Hydraulic conductivity was negatively related to mechanical strength and stiffness at both sites (Table 3). Across sites, clonal means of k_s100 increased with decreasing σ_a, MOE and σ_b (r = −0.93, −0.97 and −0.92, respectively, P < 0.01, n = 6).

Figure 3.

Clonal means of the air overpressure causing 50% loss of hydraulic conductivity (Ψ₅₀) as a function of clonal means of the air overpressure causing 50% relative water loss (Ψ_RWL50), the specific hydraulic conductivity at full saturation (k_s100), the modulus of elasticity (MOE) and the bending strength (σ_b). Filled symbols denote trees from the wet site (Tönnersjöheden); open symbols denote trees from the dry site (Vissefjärda); each symbol denotes a different clone. Error bars represent one standard error. Significant relationships are indicated by solid regression lines for the wet site and by dashed regression lines for the dry site. Dotted lines indicate significant relationships across sites (n = 12) in cases where the regression slopes did not differ between sites. The significance of the correlation coefficients of the linear (3a), quadratic (3b across sites) or S-model (3b wet, 3c, 3d) equations are indicated by asterisks: *, P < 0.05; **, P < 0.01; and ***, P < 0.001.

Discussion

Genetic and environmental determination of wood biological functions

In accordance with the study of Hannrup et al. (2004), we found high variability in basic density among clones (Table 2) and strong positive relationships between basic density and mechanical strength and stiffness (Niklas 1992, Rozenberg and Cahalan 1997). Vulnerability to cavitation and hydraulic conductivity of mature wood also varied considerably among clones, as has been shown for juvenile wood of Norway spruce (Rosner et al. 2007) and other species (Cochard et al. 2007). Trees with high growth efficiency had higher hydraulic conductivity (Mencuccini and Grace 1996, Rosner et al. 2007) but also higher hydraulic vulnerability to cavitation (Domec and Gartner 2003, Cochard et al. 2007). Clonal variability in hydraulic properties of mature Norway spruce wood was more strongly influenced by DBH than by tree height (Figures 1a–c and 1f–h). The linear relationship between vulnerability to cavitation and tree height at the wet site was distorted by one clone, the trees of which had high H/D ratios and thus the growth characteristics of a suppressed tree (Figures 2f and 2g). The strong negative relationship between vulnerability and H/D ratio suggests that sociability affects hydraulic vulnerability. Because of this clone, Ψ₅₀ showed a clone × site interaction, whereas clonal ranking for k_s100 was similar at both sites (Table 2). Site conditions had a significant effect on hydraulic conductivity, but only the two fastest-growing clones showed less vulnerability to cavitation at the dry site than at the wet site. This result is in accordance with the studies of Kavanagh et al. (1999) and Bouffier et al. (2003), who found lower hydraulic conductivities in Douglas-fir and ponderosa pine populations growing on drier sites, but no site-specific differences in the vulnerability parameter Ψ₅₀. However, Bouffier et al. (2003) observed that another vulnerability parameter, the PLC induced by 3 MPa overpressure, showed site-specific differences.

We calculated PLC for several pressures, but found no differences between sites (data not shown). Bouffier et al. (2003) also reported that ponderosa pines had enhanced height growth at wetter sites. We also found more significant differences in tree height than in diameter between the dry and wet site. The most striking difference between sites was in crown percent, a parameter hardly influenced by genetics (Table 2), but altered by physiological age and by stand density (Deleuze et al. 1996, Kantola and Mäkelä 2004). We suppose that the Norway spruce trees were in a physiologically younger stage at the dry site than at the wet site because of their higher crown percentages and slightly lower H/D ratios (Table 2). Tree shape has a profound effect on the mechanical stress distribution in the tree stem. In young, moderately tapered trees (lower H/D ratios), stress is maximum in the lowest third of the stem. If the stem becomes a regular cylinder, the largest bending stresses occur at the stem base (Milne and Blackburn 1989, Gartner 1995, Mattheck 1998, Lundström et al. 2007). Clonal ranking of the mechanical parameters was significantly influenced by site effects (Table 2). Higher mechanical strength in trees at the wet site than at the dry site might be an adaptation to better growth conditions, because high biomass allocation demands increased wood strength and stiffness to support the crown. Bending stiffness (MOE) showed two separate, site-dependent regression lines when related to DBH (Figure 1e) or basic density (Figure 2o), but one similar line across sites when related to crown percentage (Figure 2e). Mechanical strength and stiffness were significantly lower at the dry site than at the wet site, although basic density, the best indicator of mechanical properties in wood (Niklas 1992), did not differ between sites. Mechanical properties can, however, also be modified by cell geometry, tracheid length and the microfibril angle of the cell walls (Evans and Ilic 2001, Ezquerra and Gil 2001, Jagels et al. 2003, Jagels and Visscher 2006).

Tradeoffs between wood biological functions

Basic density was a good predictor of hydraulic properties of mature Norway spruce wood: clonal variability in k_s100 and Ψ₅₀ were strongly dependent on basic density (r = −0.94 and −0.85, respectively). Maximum hydraulic conductivity and vulnerability to cavitation are supposed to be conflicting wood functions and if both functions are strongly related to wood density we expect a density-based tradeoff between them. In contrast to our results for juvenile trunkwood (Rosner et al. 2007), we found a density-based tradeoff between hydraulic vulnerability and hydraulic conductivity in mature Norway spruce trunk wood (Table 3, Figure 3b). Density-based tradeoffs in hydraulics are present within branch systems or within a tree trunk of the same species (Sellin 1991, Cochard 1992, Domec and Gartner 2001, 2002a, 2003, Bouffier et al. 2003, Rosner et al. 2006). The smallest and usually youngest branches tend to be less vulnerable than the largest branches. There is a tradeoff between efficiency and safety when comparing tracheids within a tree, where the most efficient conduits are also the most vulnerable (Boyer 1985, Lewis and Tyree 1985, Sellin 1991, Hargrave et al. 1994, Tyree et al. 1994, Tyree and Zimmermann 2002). Hydraulic tradeoffs in juvenile wood have been found across species (Piñol and Sala 2000, Hacke and Sperry 2001), but rarely in wood of the same cambial age originating from the same species (Kavanagh et al. 1999, Bouffier et al. 2003, Cochard et al. 2007). We suppose that there is a density-based tradeoff between k_s100 and Ψ50 (r = 0.89 across sites) in mature wood because of its higher uniformity compared with juvenile wood. Other than in juvenile wood, a hydraulic tradeoff was not masked by structural compromises, such as light bands, or mechanical demands, such as spiral grain and production of compression wood (Mayr and Cochard 2003, Mayr et al. 2003, 2005, Rosner et al. 2007).

Mature conifer wood is supposed to adjust its resistance to embolism by increasing density at the cost of reducing hydraulic conductivity (Domec and Gartner 2003), and thus growth. In the clones we investigated, wood density was strongly negatively related to DBH (r = −0.91), implying that the slower-growing Norway spruce clones are able to compensate for their lower growth rate by producing a safer xylem, thus high resistance to cavitation is genetically determined, but at the cost of growth (Hacke and Sperry 2001, Roderick and Berry 2001). Domec and Gartner (2002a) found hydraulic safety factor values less than half those for mechanical safety factors in Douglas-fir and concluded that wood structure in conifers has evolved primarily in response to requirements for hydraulic safety rather than for mechanical safety. Our Norway spruce clones with higher hydraulic safety had lower growth rates (Figures 1a and 1b), implying lower mechanical strength and stiffness to support the crown; however, basic density and stiffness were higher in the slower-growing clones (Figures 2d, 2e, 2i and 2j). Thus, we did not find a simultaneous increase in hydraulic conductivity and mechanical stiffness as reported for other conifer species (Mencuccini et al. 1997, Jagels et al. 2003, Jagels and Visscher 2006): mechanical strength and stiffness were negatively related to hydraulic vulnerability (Figures 3c and 3d) and to hydraulic conductivity (Table 3). Larger and more frequent pit membranes facilitate water transport, but require thicker secondary cell walls to compensate for a potential weakening of walls. Larger tracheids and thin cell walls increase flow rates, but raise the risk of implosion (Hacke and Sperry 2001).

Within a tree stem, a simultaneous increase in hydraulic efficiency and mechanical strength is advantageous, because an increase in height influences both the distance water must travel to transpiring leaves, and the magnitude of the bending moment of dynamic wind loading (Mencuccini et al. 1997). We found a simultaneous increase in mechanical stiffness and k_s100 within a Norway spruce trunk. Values of MOE measured in annual rings 1–3 were only half those measured in annual rings 17–19 (despite the higher density of the first annual rings), but k_s100 was much lower in annual rings 1–3 than in annual rings 17–19 (Rosner et al. 2007). The hydraulic and mechanical demands of a young trunk or the tree top (e.g., high hydraulic safety, flexibility, keeping the upright position by formation of compression wood) are, however, quite different from those of mature wood at breast height (Gartner 1995, Mattheck 1998). Although hydraulic conductivity was negatively related to mechanical strength and stiffness at both sites (Table 3) and across sites, we found indications of structural compromises that guarantee both hydraulic efficiency and mechanical strength. For example, trees at the wet site had significantly higher k_s100 and thus higher growth rates, but also higher mechanical strength and stiffness values than trees at the dry site. Although we found no significant differences in density between sites, high k_s100 and mechanical stiffness can be obtained simultaneously by modifying pit pore size, latewood density, microfibril angle or cell wall chemistry (Mencuccini et al. 1997, Gindl 2001, Ezquerra and Gil 2001, Jagels et al. 2003, Jagels and Visscher 2006). Mechanical properties were strongly negatively correlated to Ψ₅₀, but the relationship varied significantly between sites (Figures 3c and 3d). Structural compromises induced by differences in crown length and stem taper might also explain why regression lines between Ψ₅₀ and mechanical properties differed between the wet and dry sites.

Consequences for tree breeding

Wood density was a good indicator of hydraulic vulnerability in mature Norway spruce wood, but not in juvenile wood (Rosner et al. 2007). Another easily measured vulnerability indicator, Ψ_RWL50, was strongly negatively related to Ψ₅₀ and to density. Wood density is genetically negatively related to growth in spruce species and both properties are highly heritable (Rozenberg and Cahalan 1997, Hannrup et al. 2004). Our results suggest that mechanical properties and vulnerability to cavitation are under strong genetic control. Selecting for growth may thus lead not only to a reduction in mechanical strength and stiffness but also to a reduction in hydraulic safety if adequate precautions are not taken (Booker and Sell 1998, Domec and Gartner 2002a, Rozenberg et al. 2002, Cochard et al. 2007).