Statistical Analysis of Daily Smoking Status in Smoking Cessation Clinical Trials

Abstract

Aims

Smoking cessation trials generally record information on daily smoking behavior, but base analyses on measures of smoking status at the end of treatment (EOT). We present an alternative approach that analyzes the entire sequence of daily smoking status observations.

Methods

We analyzed daily abstinence data from a smoking cessation trial, using two longitudinal logistic regression methods: A mixed-effects (ME) model and a generalized estimating equations (GEE) model. We compared results to a standard analysis that takes as outcome abstinence status at EOT. We evaluated time-varying covariates (smoking history and time-varying drug effect) in the longitudinal analysis and compared ME and GEE approaches.

Results

We observed some differences in the estimated treatment effect odds ratios across models, with narrower confidence intervals under the longitudinal models. GEE yields similar results to ME when only baseline factors appear in the model, but gives biased results when one includes time-varying covariates. The longitudinal models indicate that the quit probability declines and the drug effect varies over time. Both the previous day’s smoking status and recent smoking history predict quit probability, independently of the drug effect.

Conclusion

When analysing outcomes of studies from smoking cessation interventions, longitudinal models with multiple outcome data points, rather than just end of treatment, can makes efficient use of the data and incorporate time-varying covariates. The generalized estimating equations approach should be avoided when using time-varying predictors.

INTRODUCTION

Smoking cessation trials typically record daily smoking behavior but base analyses on summary outcome measures of abstinence at selected time points. For example, point-prevalence abstinence, a popular primary endpoint, is defined as abstinence status during a window (typically 7 days) immediately preceding the assessment (often the end of treatment or 6 or 12 months of follow-up) [1, 2]. The use of such outcomes simplifies analysis but ignores intermediate daily outcomes and the information they contain [3, 4].

Strategies that exploit the full series of daily cigarette consumption data can model either the raw daily counts, the lengths of abstinent and smoking episodes (in days), or the daily binary smoking status indicators. The first method is subject to the problem of heaping, because smokers typically self-report cigarette counts as round numbers (particularly multiples of 20, 10 or 5), which can bias analyses [5]. The second method simplifies matters by analyzing only binary indicators of daily smoking status, but can lead to complicated modeling that requires specialized statistical programming [6]. This paper will focus on the third method, which avoids the heaping issue but permits more detailed modeling of the data series, including the time dependence of treatment effects.

A conventional analysis of smoking cessation data uses end-of-treatment (EOT) smoking status as the outcome in a logistic regression model, estimating the odds ratio (OR) for treatment with adjustment for predictors of quit probability. Acknowledged influential predictors include race, sex, the Center for Epidemiologic Studies Depression (CESD) scale [7], and the Fagerström Test for Nicotine Dependence (FTND) score [8]. The impact of race and CESD on abstinence is controversial, but previous studies suggest consistently that male sex and a lower FTND score predict successful abstinence [9–11].

A longitudinal analysis can provide a detailed description of quit probability over time (by using time as a predictor) and of treatment differences over time (using time-by-treatment interactions). Moreover, it can be of interest to evaluate how the evolution of smoking behavior during treatment influences later success. For example, Wileyto et al. demonstrated that the occurrence of small lapses during treatment predicted subsequent relapse [12]. And even when treatment effects are uncomplicated, the longitudinal analysis is potentially more powerful simply because it includes more data in the analysis.

We present here a detailed analysis of a smoking cessation trial using mixed-effects (ME) [13] and generalized estimating equations (GEE) models [14]. We compare these methods to each other and to a conventional analysis of EOT abstinence, and demonstrate links between the longitudinal and conventional analyses.

METHODS

Data Source

The data (n=555) are from a randomized trial of bupropion for smoking cessation conducted at the University at Buffalo and Georgetown University [15]. Briefly, subjects who reported smoking at least 10 cigarettes per day were randomized to receive 10 weeks of either twice-daily bupropion or placebo. All subjects received seven sessions of in-person behavioral group counseling. The studies collected a range of baseline predictors of smoking behavior, including FTND, CESD, race and sex.

Participants began taking assigned medication on the day of the first counseling session, and all were to quit smoking on the target quit date (TQD), two weeks later. Prior to each counseling session between TQD and EOT (eight weeks later), participants reported numbers of cigarettes smoked each day since the previous assessment, using a timeline followback (TLFB) questionnaire. From the reported daily consumption we constructed daily smoking status, designating a day as a smoking day if the subject reported consuming one or more cigarettes. At EOT, subjects were asked if they had smoked in the last 7 days. Self-reported quits were verified by assays for smoking by-products in the breath or saliva.

Statistical Analysis

In the standard analysis, the primary outcome was quit status at EOT, with the data for subject i coded as Y_i=1 for smoke-free and Y_i=0 for smoking; the treatment effect was estimated via logistic regression, possibly including covariates. In the longitudinal analysis, the primary outcome for subject i was daily smoking status Y_ij, where j indexes days within subjects. We use P(Y_ij=1) to denote the probability that subject i is smoke-free on day j, X_i to denote a baseline factor, e.g. the treatment assignment for subject i, and Z_ij to denote a time-varying covariate, e.g. the smoking status of subject i on the day preceding day j.

A mixed-effects (ME) logistic model with a subject random effect takes the form

$$log\left(\frac{P(Y_{ij}=1)}{1-P(Y_{ij}=1)}\right)=\alpha +\beta \times X_i+\gamma \times Z_{ij}+b_i,$$

where α is the intercept and β and γ are coefficients for baseline and time-varying covariates. With the predictors as described above, exp(β) represents the odds ratio (OR) for the treatment effect, and exp(γ) represents the OR for smoking yesterday vs. not. The term b_i is a subject-specific random effect, which we assume to follow a normal distribution with mean 0 and variance σ². The random effect describes between-subject heterogeneity, not otherwise captured in predictors, that gives rise to correlation within subjects’ repeated daily outcomes.

An alternative is the marginal modeling approach, in which one makes minimal assumptions about the distribution of the outcome given the predictors. One such model is

$$log\left(\frac{P(Y_{ij}=1)}{1-P(Y_{ij}=1)}\right)=\alpha +\beta \times X_i+\gamma \times Z_{ij},\text{corr}(Y_{ij},Y_{ik})=\rho \text{for}j\ne k;$$

that is, we assume a logistic regression of the smoking outcomes Y on X and Z, with the repeated outcomes within subjects having a correlation ρ. This correlation structure is called “exchangeable”, as it assumes that all pairs of repeated observations have equal correlation. Many other possible correlation models are in use, such as the independence, autoregressive, m-dependence, unstructured, and so on. Note that the parameters of the marginal and ME models are not the same, even if the two models include identical predictors.

A popular method for estimating marginal models is the generalized estimating equations (GEE) approach [14]. With GEE, correct specification of the correlation ensures efficiency of estimation (minimum standard errors for estimates, maximum power for tests) but is not required to achieve consistency of estimation (lack of bias in large samples) [1414]. Although strictly the term “GEE” pertains to a method for fitting marginal models, we henceforth use it to refer to both the model and the method.

Our analyses considered the baseline factors treatment group, race, sex, FTND, CESD and center. Following previous practice, we dichotomized FTND and CESD using cutoffs of 6 and 16, respectively [1615]. To describe potential differences between recruitment centers we included an indicator variable for the Buffalo site. In some analyses we included as time-varying covariates the week of the study and two summaries of individual smoking history: the previous day’s smoking status as a summary of recent history, and the number of smoking days in the last week as a summary of longer-term smoking behavior. We also included a drug-by-week interaction to examine variation in the drug effect over time.

We present results computed with the procedures NLMIXED (for ME) and GENMOD (for GEE) of SAS version 9.2 (SAS Institute; Cary, NC). In the Appendix we provide sample code for analyses in both SAS and Stata (StataCorp LP; College Station, TX).

RESULTS

Analysis with baseline factors only

We base analyses on 540 subjects, excluding 15 who were missing baseline data or verified EOT outcomes. Table 1 shows descriptive characteristics by treatment arm. Baseline factors were balanced across arms, except that the fraction of whites was significantly larger in the bupropion arm. More subjects in the bupropion group achieved success at TQD (73% vs. 58%). On average, subjects on bupropion smoked 35% of days during the treatment phase and those on placebo smoked 54% of days. Both self-reported and verified EOT quit rates were higher on bupropion.

Table 1.

Subject characteristics by treatment arm.

Characteristic	Bupropion (n=274)	Placebo (n=266)	P value1
Sex: female	158 (57.7%)	148 (55.6%)	0.6349
Race: white	226 (82.5%)	198 (74.4%)	0.0228
FTND score: ≥6	114 (41.6%)	125 (47.0%)	0.2077
CESD scale: ≥16	90 (32.9%)	70 (26.3%)	0.0966
Subjects quit on TQD	200 (73.0%)	154 (57.9%)	0.0002
Fraction of smoking days in treatment	0.35 (SE 0.024)	0.54 (SE 0.026)	<0.0001
Self reported EOT quit	139 (51.1%)	91 (34.7%)	0.0001
Verified EOT quit	94 (34.3%)	56 (21.1%)	0.0006

Note:

¹P value is for comparing the bupropion and placebo arms. It is based on t test for the continuous variable fraction of smoking days, and on the chi-squared test for all other variables, which are binary.

We first analyzed the quit status at EOT using logistic regression, with and without baseline covariates. We then analyzed daily quit status using longitudinal logistic models: ME with a random subject effect and GEE with exchangeable and independent correlations. For comparability with standard analyses, we excluded time-varying covariates from the longitudinal models. Moreover, as the ORs of ME models have a different interpretation from the ORs of GEE models [17], we applied a scale factor to render the results comparable [18, 19].

Results appear in Table 2. Treatment effect ORs are similar for models with and without baseline covariates, and for the two standard logistic models using self-reported and verified EOT quit. The three longitudinal models yield similar ORs, as expected. Compared to the standard analysis, the longitudinal ORs are higher, and the corresponding 95% confidence intervals (CIs) are narrower. For example, in the standard analysis using self-reported EOT quit, the adjusted OR is 2.06 (95% CI 1.44–2.96), whereas in the GEE model with exchangeable correlation the adjusted OR is 2.26 (95% CI 1.67–3.05).

Table 2.

Summary of treatment effects in different models with baseline factors only (n=540).

Models	OR (95% CI)	Adjusted1 OR (95% CI)
Standard Logistic Model2
Self-reported EOT quit	1.96 (1.39, 2.78)	2.06 (1.44, 2.96)
Verified EOT quit	1.96 (1.33, 2.88)	2.02 (1.36, 2.99)
Longitudinal Logistic Model3
ME model: Raw	15.74 (5.62, 44.07)	16.30 (5.95, 44.63)
ME model: Scaled4	2.23 (1.65, 3.00)	2.30 (1.70, 3.11)
GEE exchangeable	2.19 (1.64, 2.94)	2.26 (1.67, 3.05)
GEE independent	2.20 (1.64, 2.95)	2.26 (1.67, 3.06)

Notes:

¹Adjusted for baseline factors sex, race, FTND, CESD and site.

²The standard logistic models use the single outcome at EOT.

³The longitudinal models (ME and GEE) analyze daily smoking outcomes.

⁴We applied a scale factor to make ORs from ME models comparable to those from GEE models and standard logistic models. $\text{Scale}\text{factor}=\sqrt{0.346{\sigma }^2+1}$, where σ² is the estimated variance of the random effects. ln(OR^scaled) = ln(OR^raw)/scale factor.

⁵P<0.001 for all ORs in this table.

To explain the difference between standard and longitudinal analyses, we plotted daily ORs (from a series of univariate logistic regressions using day j smoking outcomes) and their 95% CIs (Figure 1), and the quit fractions over time (Figure 2). Figure 1 suggests that the drug effect is larger in the middle of the treatment phase than at the end; because the longitudinal OR represents an average of drug effects across time, it is unsurprising that it is higher than the EOT OR from the standard analysis. This is also illustrated in Figure 2, where the two curves diverge somewhat in the middle weeks of treatment, implying that there was less relapse in the drug group during that period.

Figure 1.

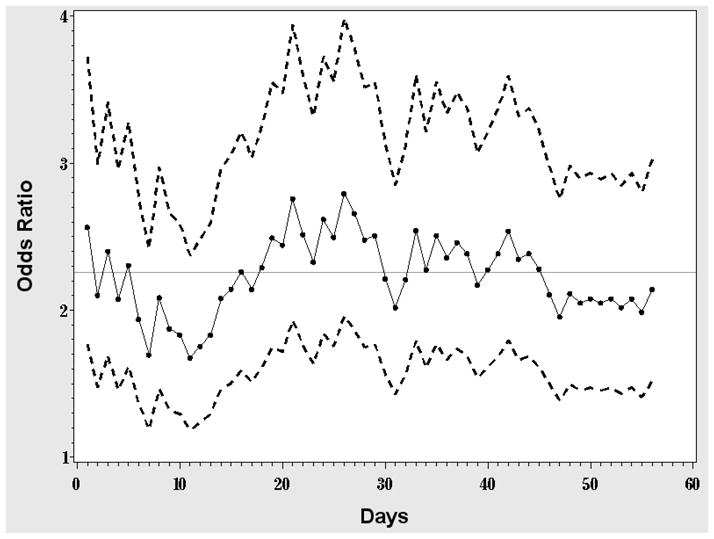
Daily OR of the drug effect. Each dot represents the estimated OR from a simple logistic regression of the smoking status data from day j with only drug in the model. Points are connected by a solid line to illustrate the trend over time; dashed lines represent the corresponding 95% CIs. The horizontal line represents the estimated OR from the corresponding GEE exchangeable model.

Figure 2.

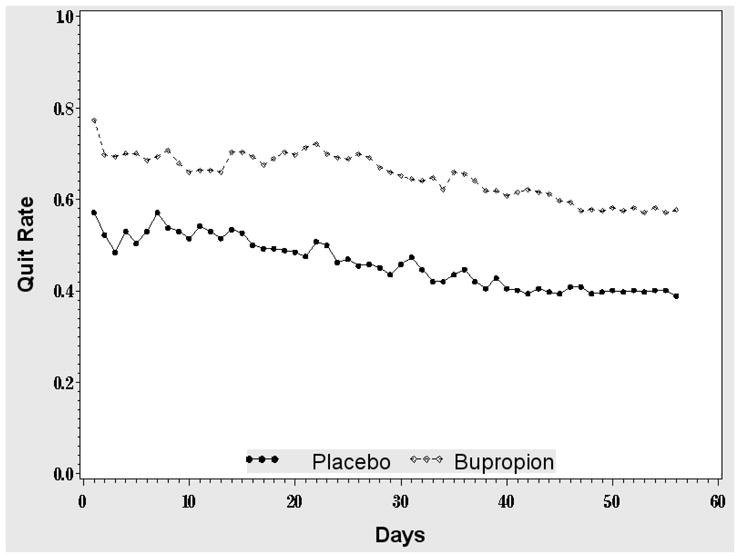
Daily quit rate by treatment arm. The solid (dashed) line is the fraction of subjects who are smoke-free in the placebo (bupropion) arm.

The CIs from the longitudinal models are not dramatically narrower than those from the standard analysis. This is because of the strong within-subject correlation (ρ=0.7) among the daily outcomes, which diminishes the potential efficiency gain in a longitudinal analysis involving between-subjects comparisons [20]. Increasing intra-subject correlation improves the precision of estimates of within-subject contrasts (such as time trends and changes from baseline) but only harms the efficiency of between-subject contrasts (such as randomization group ORs). For example, when ρ=0, each new measurement adds independent information of equivalent value to the first measurement, whereas when ρ=1 taking additional measurements adds no new information.

Longitudinal analyses with time-varying predictors

We also conducted analyses including the time-varying predictors daily and weekly smoking history, a time effect, and a drug-by-time interaction. We first compared the results under ME and GEE, for simplicity treating week as continuous and excluding the drug-by-week interaction. The results (Table 3) show a substantial difference between ME and GEE, reflecting problems with including time-varying covariates in a marginal model [21, 22] (essentially, the incorporation of a time-varying covariate can vitiate the basic assumption of the marginal model’s mean outcome). Moreover, estimates differ substantially between the two GEE models. GEE typically yields consistent estimates regardless of the working correlation structure, as long as the mean model is correctly specified and the missing observations are missing completely at random [23]. With few missing observations, the discrepancy between the two GEE models must indicate a problem in the mean model itself. Thus we henceforth use the ME model to evaluate history and time effects on daily quit probability.

Table 3.

Comparison of longitudinal models that include time-varying covariates (n=540).

	ME model scaled1	GEE exchangeable	GEE independent
Parameters2	OR (95% CI)	OR(95% CI)	OR(95% CI)
Bupropion	2.14 (1.62, 2.82)	1.75 (1.38, 2.21)	1.32 (1.16, 1.50)
Week3	0.89 (0.88, 0.90)	0.90 (0.89, 0.91)	0.83 (0.81, 0.84)
Previous day’s smoking status	0.34 (0.32, 0.37)	0.17 (0.14, 0.21)	0.08 (0.06, 0.10)
Number of smoking days in the last week	0.79 (0.78, 0.80)	0.74 (0.73, 0.76)	0.53 (0.51, 0.54)

Notes:

¹The variance of the random effect in the ME model was 6.06; estimates and their CIs were adjusted by the scale factor (see Table 2).

²Adjusted for baseline factors sex, race, FTND, CESD and site.

³Week analyzed as a continuous variable, with no drug-by-week interaction.

In an elaborated ME model, we included a categorical week variable (taking the final week [week8] as the reference) and a drug-by-week interaction. Results (Table 4) suggest that female sex and elevated FTND and CESD scores decreased the daily quit probability (OR= 0.63 for female vs. male, 95% CI 0.48–0.82; OR=0.58 for high vs. low FTND, 95% CI 0.44–0.76; OR=0.73 for high vs. low CESD, 95% CI 0.54–0.98). Recent history of smoking significantly influenced current quit probability; subjects who smoked yesterday were less likely to abstain today (OR=0.35, 95% CI 0.33–0.38), as were subjects who smoked more in the last week (OR=0.76 for one additional smoking day in the last week, 95% CI 0.74–0.77).

Table 4.

The elaborated ME model¹ for predicting daily quit probability (n=540).

Predictor2	OR	95% CI	P value
Sex: female	0.63	(0.48, 0.82)	0.0008
FTND score: ≥6	0.58	(0.44, 0.76)	<0.0001
CESD: ≥16	0.73	(0.54, 0.98)	0.0340
Previous day smoking status	0.35	(0.33, 0.38)	<0.0001
Number of smoking days in the last week	0.76	(0.74, 0.77)	<0.0001
Week1 vs. week8	2.37	(1.98, 2.84)	<0.0001
Week2 vs. week8	1.44	(1.19, 1.75)	0.0002
Week3 vs. week8	1.19	(0.98, 1.45)	0.0782
Week4 vs. week8	1.20	(0.98, 1.46)	0.0770
Week5 vs. week8	1.05	(0.86, 1.29)	0.6169
Week6 vs. week8	0.92	(0.75, 1.12)	0.4085
Week7 vs. week8	0.99	(0.81, 1.22)	0.9606
Bupropion in week1	2.04	(1.52, 2.74)	<0.0001
Bupropion in week2	1.81	(1.32, 2.47)	0.0002
Bupropion in week3	2.64	(1.92, 3.63)	<0.0001
Bupropion in week4	2.29	(1.65, 3.17)	<0.0001
Bupropion in week5	1.94	(1.41, 2.69)	<0.0001
Bupropion in week6	2.27	(1.64, 3.15)	<0.0001
Bupropion in week7	1.75	(1.26, 2.44)	0.0010
Bupropion in week8	1.91	(1.37, 2.67)	0.0002

Notes:

¹The estimated variance of the random effect in the ME model was 5.51; estimates and CIs were adjusted by the scale factor (see Table 2).

²Analysis adjusted for other baseline factors: race and site.

Results moreover indicate that quit probability gradually decreased over time, with the quit probability significantly higher in the first two weeks compared to the last week, and eventually leveling off in the final three weeks. The drug effect is statistically significant in all weeks, varying somewhat in the first several weeks and becoming stable in the last two. A likelihood ratio test for equality of the ORs in all eight weeks gives P=0.036. Contrasts for the specific elements of the drug-by-week interaction show that the drug effect in week3 is significantly larger than that in week8 (P=0.023).

DISCUSSION

We have presented longitudinal models for binary daily abstinence data in smoking cessation trials. Our approach uses the finest-level data on quit history commonly available and provides a nuanced description of the evolution of the outcomes. By comparison, the standard approach of summarizing the point prevalence abstinence at a single designated time ignores the bulk of the available information, calling into question the common practice of collecting daily smoking data [24].

The standard analysis of point-prevalence abstinence is subject to the arbitrary choice of assessment time. Although most studies conduct the assessment at EOT, the length of the recommended treatment phase varies by drug [25], and therefore the reported point prevalence abstinence could refer to 8, 10 or 12 weeks of treatment. Although meta-analysis suggests that the treatment effect is insensitive to study duration [26], because quit rates generally decline over time this practice can diminish cross-trial comparability. In contrast, longitudinal analysis models the daily quit probability, rendering the interpretation independent of other elements of the study design.

As the longitudinal analysis uses all time points in the treatment period, the drug effect OR represents an effect averaged across time, whereas the standard analysis reflects the effect only at EOT. Our data analysis revealed higher ORs with the longitudinal models, suggesting some variation of drug effect over time. Regardless of the estimated ORs, the corresponding CIs from longitudinal models are generally narrower than those from simple logistic models, with the size of the difference depending on the within-subject correlation [20].

A randomized longitudinal study with repeated outcomes collected at k>1 times can reduce sample size requirements compared to a design with the outcome collected at a single time. Neuhaus and Segal [20] found that to achieve the same power for detecting a designated OR, the sample size N₁ in a longitudinal design is smaller than the sample size N₀ in a conventional design, in the ratio $N_1=\frac{1+\rho (k-1)}{k}{N}_0$, here ρ is the within-subject correlation. The saving is greatest when ρ=0 and declines with increasing ρ, until there is no saving at all when ρ=1.

A longitudinal analysis of daily smoking status has greater potential efficiency gain when some observations are missing, because it can include the available data from all randomized subjects, even those lost to follow-up, whereas the standard approach has to either exclude the drop-outs or assume that they continued to smoke. Although such an assumption is held to be conservative, there is an increasing awareness that its indiscriminate use may lead to bias and lack of comparability between studies [26, 2726]. Fortunately our example had few missing observations.

An important advantage of longitudinal modeling is its ability to incorporate time-varying predictors. In some studies, treatment (such as drug dose) changes over time by design [28]. Even if the treatment is constant, including the treatment-by-time interaction allows us to test whether its effects change over time, as in our example. We investigated the influence of smoking history on later success by coding summary measures of history as time-varying predictors. Our results suggest that history is an important independent predictor of future outcome. Generally, there is concern that including outcome history may over-adjust and thereby attenuate treatment main effects. In our results, the drug effect OR in the ME model was 2.30 before adjusting for history, declining to 2.14 after adjustment. Possibly the history variable absorbed some of the treatment effect, resulting in the decreased OR. Still, the large size and strong statistical significance of the adjusted effect suggests that bupropion continues to have an effect no matter how long one has been taking it and regardless of its effect to date.

Although the ME and GEE models work similarly in many cases, one must bear in mind that their regression coefficients have different interpretations [17]. The drug effect OR in the ME model represents the odds of the outcome for a person taking the drug compared to the same person not taking the drug. In contrast, the GEE OR represents the average OR of the drug group compared to the placebo group. Estimates from GEE are generally smaller than those from ME, and the attenuation increases with the between-subjects variability. After applying the scale factor as we illustrated, the two estimates are comparable [18, 19].

A marginal approach like GEE is problematic when one wishes to model time-varying effects [21, 22]. As shown in our example, GEE is unreliable when one includes the outcome histories as predictors. Moreover, ME is preferable when there is substantial dropout, because one can estimate it consistently with weaker assumptions on the missing-data mechanism [29].

A potential limitation of our analysis is that we used treatment phase data only. Given the logarithmic nature of relapse curves [30], outcomes at later follow-ups such as 6 or 12 months are considered superior indicators of treatment success. Commonly, however, daily smoking data are either not collected or are unreliable after EOT, limiting the use of daily data beyond that point. Nevertheless, the analysis we presented provides a way to evaluate the dynamic process in the treatment period using all the available information; one may conduct separate analyses on later outcomes using standard methods.

Another limitation of our analysis is its use of TLFB data, which are self-reported and thus may be inaccurate in a fraction of subjects who falsely report abstinence [31]. Nevertheless, our data suggest that the drug effect is similar whether we use self-reported or verified EOT point prevalence abstinence as the outcome (Table 2). One possible reason is that subjects in both arms are equally likely to report false abstinence and therefore any biases are offsetting. Models for daily abstinence would not be biased by subjects who under-report cigarette counts, as long as they do not claim abstinence on smoking days.

TLFB data are typically collected every one or two weeks and are therefore potentially subject to recall bias, which may affect estimates of within-subject correlation if the subjects incorrectly report the same or very similar counts for all the days being recorded at each visit. To address this possibility, we repeated the analysis using only data from the last day of each week (results not shown), giving us a single day’s data from each weekly TLFB questionnaire. We observed the same large correlation, suggesting that it is real and not simply an artifact of recall bias. Moreover, the drug effect OR was similar to that from the daily data, with a slightly wider CI. This is expected because the efficiency gain from using daily vs. weekly data is substantial only if the correlation is small. Even if efficiency gain is minimal, analyzing daily data reveals changes occurring at scales less than a week, as illustrated by Figure 1 and 2. The advent of electronic diaries, allowing collection of cigarette counts by ecological momentary assessment, may obviate the need for daily summarization of cigarette counts.

One could in principle obtain a more efficient analysis from the series of daily cigarette counts. Because such data are subject to severe heaping, in the form of over-reporting of round numbers of cigarettes smoked [5], there is substantial potential for bias in such analyses, and it has been considered preferable to use the daily abstinence indicators. As we have suggested, another approach is to model the duration of abstinent and smoking episodes, incorporating the possibility of permanent recovery and relapse [6]. Such models, when estimated exclusively from treatment-period data, can make excellent predictions for remote long-term outcomes [32]. With current types of data, the day is still the smallest time interval, but as electronic recording devices become more common, it will be possible to measure inter-cigarette intervals to the second, providing for an even finer analysis.

SUMMARY

We have presented a strategy to model longitudinal daily smoking status data from smoking cessation trials. Compared to the standard analysis of EOT abstinence status, our approach permits more detailed modeling and more precise estimation of effects. We compared ME and GEE models, illustrating problems with GEE in modeling time-varying covariates such as outcome history. In our example study a strong drug effect persisted in the treatment period, with its magnitude varying across time. A subject’s recent history of smoking independently predicted later quit probability.

APPENDIX

The data set ‘daily’ stores the longitudinal daily smoking data. Column variables are ‘id’ (the unique identification number for subjects), ‘day’ (the study day from 1 to 56), ‘abstinent’ (binary smoking outcome on each day), and ‘drug’ (the treatment assignment). Each subject can have up to 56 rows of data.

Examples of SAS code for a GEE model:

proc genmod data=daily desc;
 class id;
 model abstinent = drug/link=logit dist=bin;
 repeated subject=id/type=exch;
run;

Example of SAS code for a ME model:

proc nlmixed data=daily qpoints=12;
 parms int=0 beta=0 logvar=0;
 eta = int + beta*drug + u;
 p = exp(eta)/(1 + exp (eta));
 model abstinent ~ binary(p);
 random u ~ normal(0, exp(logvar)) subject=id;
run;

Examples of Stata code for a GEE model:

xtgee abstinent drug, i(id) family(binomial) link(logit) corr(exch)

Examples of Stata code for a ME model:

xtlogit abstinent drug, i(xid)