Evolution of Tumor Invasiveness: The Adaptive Tumor Microenvironment Landscape Model

Abstract

Interactions between cancer cells and their microenvironment are crucial for promoting tumor growth and invasiveness. In the tumor adaptive landscape model, hypoxic and acidic microenvironmental conditions reduce the fitness of cancer cells and significantly restrict their proliferation. This selects for enhanced motility as cancer cells may evolve an invasive phenotype if the consequent cell movement is rewarded by proliferation. Here, we used an integrative approach combining a mathematical tumor adaptive landscape model with experimental studies to examine the evolutionary dynamics that promote an invasive cancer phenotype. Computer simulation results hypothesized an explicit coupling of motility and proliferation in cancer cells. The mathematical modeling results were also experimentally examined by selecting Panc-1 cells with enhanced motility on a fibroblast-derived 3D matrix for cells that move away from the unfavorable metabolic constraints. After multiple rounds of selection, the cells that adapted through increased motility were characterized for their phenotypic properties compared to stationary cells. Microarray and gene depletion studies demonstrated the role of Rho-GDI2 in regulating both cell movement and proliferation. Together, this work illustrates the partnership between evolutionary mathematical modeling and experimental validation as a potentially useful approach to study the complex dynamics of the tumor microenvironment.

Introduction

The tumor microenvironment is not an idle bystander, but actively participates in tumor progression and metastasis (1, 2). It consists of many components including endothelial, mesenchymal cells, extracellular matrix (EM), and physical parameters such as gradients of oxygen, glucose, pH, and interstitial pressure. An accumulation of evidence has shown that interactions between cancer cells and their surrounding stroma are crucial for promoting the growth and invasiveness of tumor (3–5). Tumor cells promote the development of a tumor-permissive stroma via the aberrant expression of paracrine factors that induce an altered stromal compartment. In turn, alterations in the stromal microenvironment, including enhanced vasculature, modified EM composition, inflammatory responses, and imbalanced protease activity, are essential regulatory factors of tumor growth and invasion (6–8). Thus, it is critical to understand and predict the multistage, non-linear dynamics of tumor-microenvironment interactions to facilitate the clinical development of novel therapeutic targets that may disrupt the stromal influences on tumor invasion and growth.

It is generally understood that cancers arise through a process characterized as “somatic evolution”. These Darwinian dynamics consist of competition among evolving tumor phenotypes within environmental selection forces that govern fitness. Although tumor cells are continuously evolving through accumulative genetic and epigenetic changes, it is microenvironmental selection forces that may determine the optimal phenotypic properties, i.e. the cellular characteristics that result in the greatest fitness. These selection pressures are dynamically changed as a result of tumor population growth and evolution (9). The disordered tumor-stroma interactions typically result in reduced and chaotic blood flow that produces hypoxic and acidic microenvironmental conditions. Acidic pH, hypoxia, and fluctuations in nutrition exert strong selection pressures on tumor growth and progression (10).

The evolutionary dynamics of carcinogenesis have been described through a quantitative mathematical model to predict the bidirectional interactions of tumor cells and their surrounding environment during cancer progression (10–12). Our mathematical model demonstrates that evolution of invasiveness occurs by coupling proliferation and motility (9). That is, cancer cell invasiveness can evolve if it is rewarded by proliferation as enhanced motility allows the cell to escape to a more favorable microenvironment that permits greater proliferation. We hypothesize that enhanced motility is selected as an adaptive mechanism to escape harsh microenvironmental conditions that reduce the cancer cell fitness.

Several studies have demonstrated that a fibroblast-derived 3D-matrix system can be utilized to study the influence of the stromal landscape on cell motility (13–15). Fibroblast activation protein (FAP), a serine protease selectively expressed on tumor stromal fibroblasts but not on carcinomas (16), was used as a platform for studying tumor-stromal interactions. FAP expressing fibroblast-derived matrix was used as an in vivo-like in vitro setting to evaluate the motility phenotype of cancer cells. In this study, we tested the hypothesis predicted from the mathematical model that cancer cell proliferation is rewarded when enhanced motility is selected by the tumor landscape.

Materials and Methods

In silico system

Each cell was represented as a cubic volume with a 25μm side, or a volume of 15,625μm³. Cell metabolism was modeled as anaerobical or aerobical glycolysis (17). Outside cover slip, media contain 0.15mM oxygen corresponding to 100mmHg pO2, 5mM glucose, and 24mM bicarbonate, pH 7.4. Species diffused with coefficients of 1.46×10⁻⁵ cm²/s for O₂ (18), 5×10⁻⁶ cm²/s for Glucose (19), 5×10⁻⁶ cm²/s for bicarbonate and 1.5×10⁻⁵ cm²/s for CO₂ (20). Glucose uptake by cells was calculated by the expression 6×10⁻⁵x[Glu]_e, where [Glu]_e represents the extracellular glucose concentration, adapted from (17) for cells with metabolic rate arbitrarily set at 5-fold that of a normal epithelial cell. Oxygen uptake was modeled as simple diffusion by the expression 0.1×O₂ (17). Cell metabolism, diffusion of species and pH buffering effects were calculated as described previously (21). The model implementation is further detailed in the Supplemental Material with the physical and biological constants used (22–24).

Selection of subpopulations in the computational model (in silico system)

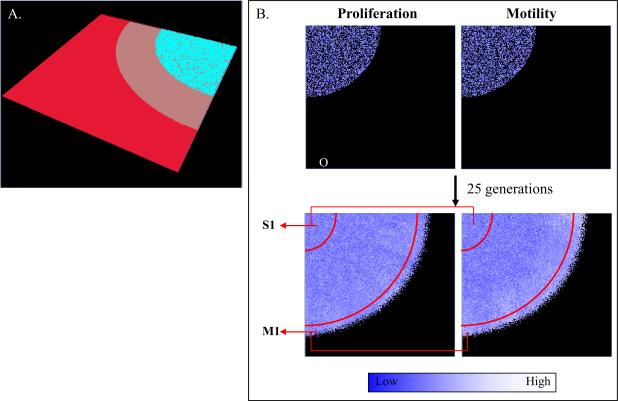
In order to study the evolutionary dynamics occurring in vitro, we built a computational model that reproduces the geometry of the cover slip. This computational model allowed us to study the fate of thousands of cells individually, and better understand how and which phenotypes are selected as they replicate and move under the cover slip. The computational model was built as a 3D structure with two layers of cells trapped under a cover slip. The simulation model was delimited by a volume with dimensions 200×200×3 cell. The cover slip was a disc with a radius of 150 cells (μ4mm). The original population (O, 10,000 cells) was grown under the center of cover slip in 50% confluence until they reached the distance of 20 cells away from the outer edge of the cover slip and the first two subpopulations were collected. In all simulations, the cells selected for the motile population (M) were collected from a distance of 10–20 cells from the edge of the cover slip and the stationary population (S) was collected from those closest to the center of cover slip (3,000 cells each). These subpopulations were independently re-seeded in the center of new cover slips for each new simulation and selected 4 more times. The first simulation lasted 25 generations while the four others required 40 generations to reach the same distance limit, due to their smaller initial population size (3,000 vs. 10,000).

Motility and proliferation in the computational model

The starting population was initialized with random values for motility and proliferation according to a normal distribution with mean 0.5 and standard deviation 0.1, corresponding to a probability between 0 and 1 of moving or proliferating at every time step. We considered that each cell has a cell cycle of 1 day and can move 25 μm (a cell length in this model) every 2 hours. This estimation was obtained from the observed motility in the Panc-1 cell line (ATCC, Manassas, VA) used in this experiment (between 13 and 18 μm/hour). Due to the fixed-lattice limitation of our computational model, it is not possible to represent a distance smaller than 25 μm, thus a time step of 2 hours was used instead. The simulation flow thus consisted of one cycle of replication for every 12 events of movement (one cell long), resulting in a minimum theoretical cell cycle of 24 hours, or a 48 hours cell cycle for the original tumor population (motility value 0.5), which matched the cell cycle in vitro for the Panc-1 cell line used in this experiment (52 hours). No mutations were considered in the cover slip model, thus the only force acting on population phenotypic values is selection.

A second model representing the growth of a solid tumor in vivo, described in the “Appendix B” of the supplemental material, was used to study if the evolution of these two phenotypes observed in the cover slip model, would also be valid in an actual tumor. In this model, we seeded tumors at different densities and allowed mutations to occur with a 1% probability at every replication.

Cell motility was modeled as a dislocation to an empty space randomly chosen immediately next to it. Cell duplication occurred only if three conditions were met simultaneously: (a) at every generation the cell would be tested for duplication depending on its proliferation phenotype (0 ≤ duplication phenotype ≤ 1.0 results in a probability between 0 and 1); (b) there must be at least one empty space available next to the mother cell to be occupied by the new cell; (c) the cell was tested for its energy production rate and the probability of duplication was represented as a linear function with value 0 for an ATP production rate equal to or below 8.6×10⁻⁷ M/s (lower values lead to cell death) and 1 for an ATP production rate equal to or higher than 8.6×10⁻⁶ M/s (19) as described in equation 1:

$$\begin{array}{cc}\hfill p_{\mathit{DUPLICATION}}=& \frac{(\mathit{ATP}-0.1\times {\mathit{ATP}}_0)}{0.9\times {\mathit{ATP}}_0}\text{If}0.1\times \text{ATP}0\le \text{ATP}\le \text{ATP}0;\hfill \\ \hfill p_{\mathit{DUPLICATION}}=& 0\text{If ATP}\le 0.1\times \text{ATP}0;\hfill \\ \hfill p_{\mathit{DUPLICATION}}=& 1\text{If ATP}0\le \text{ATP};\hfill \end{array}$$ (1)

Where p_duplication is the probability for cell division, ATP is the ATP production rate, and ATP₀ is

the minimum energy production rate for 100% probability of cellular division (8.6×10⁻⁶ M/s).

All the parameters used in this model and their literature sources are listed in Supplemental Tables 1 and 2. A further description of the computational model implementation can be found in the “Appendix B: Computational Model Implementation” in the supplemental material.

Production of a fibroblast-derived 3D matrix

Matrices were produced by FAP expressing fibroblasts that were co-transfected with murine fap gene under the Tet-responsive promoter and rtTA regulatory element into NIH-3T3 cells. The NIH-3T3 cell line was obtained from the American Type Culture Collection (ATCC). ATCC has verified the identity of this cell line by methods including short tandem repeat profiling. As described (25), fibroblasts (7×10⁵) were seeded onto gelatin-coated glass cover slips (18mm), and confluent fibroblastic cultures were treated with media supplemented with ascorbic acid (50μg/ml) and Doxycycline (2μg/ml) every other day for 8 days. Alkaline detergent treatment (0.5% Triton X-100, 20mM NH₄OH in PBS) gave rise to cell-free in vivo-like 3D matrices.

Speciation of motile Panc-1 cells by enhanced cell migration

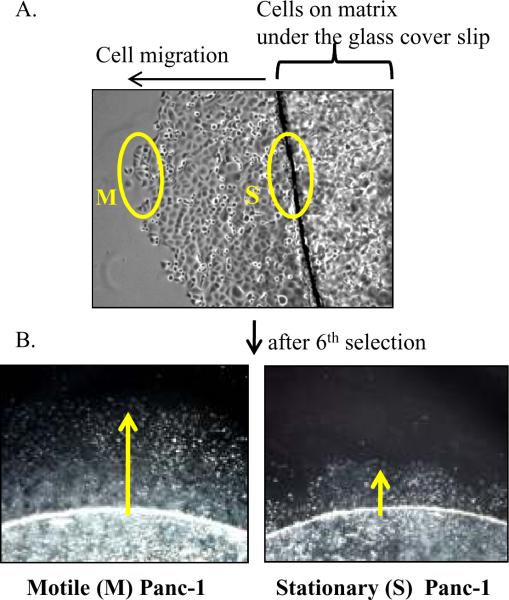
The Panc-1 cell line was obtained from the American Type Culture Collection (ATCC). ATCC has verified the identity of this cell line by methods including short tandem repeat profiling. Panc-1 cells (1×10⁴) were incubated onto matrix-coated glass cover slip for 3 hours to allow for attachment to the matrix. Then glass cover slips were placed upside down onto a plate for allowing cells to grow between cover slip and plate, resulting in the metabolic constraints by limited diffusion of nutrients (26). After 2 weeks incubation, motile (M) cells, migrated out and away from underneath the cover slip vs. stationary (S) cells, resided near the cover slip, were isolated using Cloning Disks (Labcor Products, MD). These cells were independently re-plated and re-selected over six times. Speciated cells from the 5^th (M5 and S5) or 6^th (M6 and S6) selections were further analyzed the following studies.

Cell migration assay

Speciated Panc-1 cells (5×10⁴) in DMEM with 1% FBS were plated onto a Transwell system insert (8μm pore size, Falcon) in a 24 well-plate. The lower chamber was filled with DMEM supplemented with 10% FBS in the presence or absence of recombinant human HGF (100ng/ml) (27). After 24 hours incubation, un-migrated cells were removed from the upper surface of the insert membrane with cotton swab, and migrated cells on the lower membrane were stained using DiffQuick stain kit (IMEM Inc., CA). Cells from 5 regions per filter were randomly selected and counted under the microscope. Each experiment was conducted in triplicate and repeated 3 times.

Invasion assay within 3D matrices

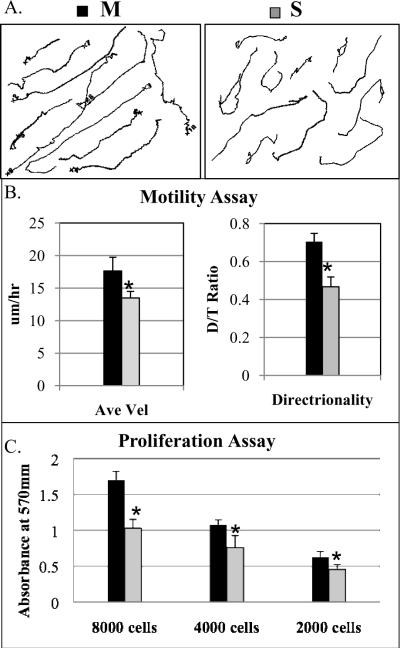
As described (15, 28), speciated Panc-1 cells (1×10⁴/24well-plate) were re-plated onto the matrices and incubated overnight. Approximately 10~15 cells were selected under inverted microscope (Nikon TE-2000U) and images acquired every 10 minutes for 12 hours. Individual cell dynamics were analyzed using the MetaMorph program following factors: (a) the net path distance (D, μm) by calculating the number of μm/pixel, (b) the path trajectory (T, μm) of the individual cell during the recording period, (c) average velocity (AV, μm/hr) is the path distance divided by the elapsed time, and (d) directionality (D/T ratio) is the ratio of the net distance divided by trajectory path and determines random (<0.5) versus directional invasion (close to 1) of individual cells.

MTT assay for cell proliferation

Speciated Panc-1 cells (2000, 4000, and 8000 cells/well) were grown on a 96 well-plate in triplicates for 4 days. Cells were incubated with MTT solution (40μl of 5mg/ml, Sigma) for 2 hours at 37°C in the dark and lysed by SDS solution (100μl of 20%) overnight. A color change from yellow to purple caused by metabolically active cells was detected in the Multiskan plate reader at 570 nm.

Differential gene expression profile by microarray analysis

The Agilent Expression array was performed at the Microarray facility in Fox Chase Cancer Center. Briefly, 500ng of total RNA from speciated Panc-1 cells (the 5^th and 6^th selections) was labeled using the Agilent Low RNA input linear amplification kit following the manufacturer's instructions. 825ng of labeled targets were hybridized onto Agilent 4×44k whole genome arrays for 17 hours at 65°C. Microarray scan images were processed using Feature Extraction software (Agilent) and subjected to further statistical analysis. To avoid dye bias, RNA samples were performed as dye-flip replicates.

Gene profile analysis

Agilent Human 4×44K Whole Genome arrays were preprocessed with Agilent Feature Extraction (FE), version 9.5. Expression measurements used for analysis were the FE Processed Signal values, which are background-corrected and dye-normalized. Probes were removed if they lacked a valid Entrez gene identifier or Gene Ontology (GO) annotations, or if they had intensities near background across more than 75% of all channels. Differential expression was assessed using empirical Bayes moderated one-sample t-statistics implemented in the Bioconductor (29) package limma (linear modeling of microarray data) (30). P-values were adjusted for multiple testing using the method of Benjamini and Hochberg (31) to estimate False Discovery Rates (FDR). Lists of differentially expressed probes were generated separately for the two sets of samples, M5 vs. S5 and M6 vs. S6.

Gene depletion by siRNA transfection

Speciated Panc-1 cells (2×10⁵ cells/6 well-plate) grown in antibiotic-free DMEM overnight were transfected with 80 pmol of siRNA duplexes of RhoGDI2 (Rho GDP dissociation inhibitor2, Rho-GDIβ), Amphregulin, SgII (secretogranins), SPARC (Secreted Protein Acidic and Rich in Cysteine), and scrambled control siRNA following the manufacture's instruction (Santa Cruz Biotechnology, CA). Levels of gene expression knocked down by each siRNA confirmed by Onestep RT-PCR kit (Qiagen, Valencia, CA) (32).

Results

Selection of subpopulations in silico system

In a 3D computer structure with cells trapped under a cover slip, oxygen and nutrients flowed from the media surrounding the cover slip and diffused to the cells (Fig. 1A). As oxygen and nutrients were metabolized by cells under the cover slip, a gradient was formed through the outer regions by decreasing oxygen and glucose concentrations and increasing acidity generated by anaerobic glucose metabolism in the hypoxic regions of the model. In these simulations, the M population was collected a distance of 10–20 cells from the edge of the cover slip and the S population was collected from cells closer to the center of the cover slip (Fig. 1B). These two subpopulations were re-seeded in the center of the cover slip for each new simulation and selected 5 additional times.

Figure. 1.

In silico system. (A) The 3D computational model was built with cells trapped under a cover slip. Cyan, gray and red layers represent cells, cover slip, and the surface of media, respectively. (B) The original (O) population is seeded at 50% confluence and grown under a cover slip (top panel). In all simulations, subpopulations were selected from the regions delimited by the red arcs in the figure (bottom panel) and independently re-seeded in the center of cover slips for each simulation and selected 4 more times. Proliferation and motility values are graphically represented by white (higher) and blue (lower).

Computer simulation results hypothesized an explicit coupling of motility and proliferation in cancer cells

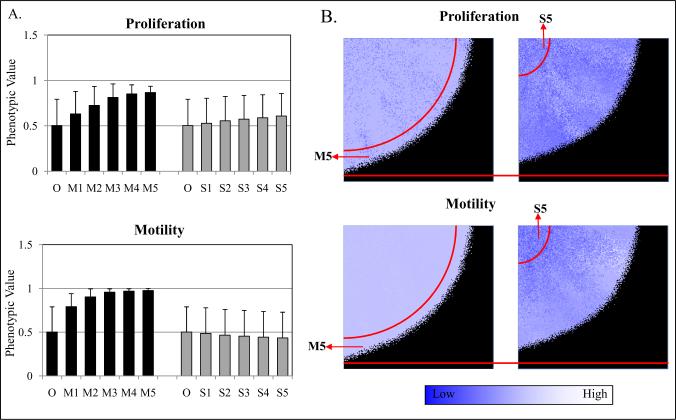
The original (O) population was initialized with random values for motility and proliferation according to a normal distribution with mean 0.5 and standard deviation 0.1, corresponding to a probability from 0 to 1 of moving or proliferating. Each simulation was run 5 times. The computer simulations showed that the M5 final subpopulation had higher proliferative values than the O cells (M5=0.7 ± 0.07, S5=0.52 ± 0.1, and O=0.5) (Fig. 2A, top panel). While M5 cells also had increased motility (0.76 ± 0.01) compared to the O (0.5), S5 cells did not demonstrate enhanced motility (0.48 ± 0.1) (Fig. 2A, bottom panel). These results suggest that proliferation and motility are selected by environmental pressures by M5 cells leaving the acidic and hypoxic environment of the cover slip, resulting in greater proliferation. The selection for proliferation of M cells as compared to S cells is likely due to the lower metabolic and spatial restrictions (gaps of up to 20 cells) which allow the M5 cells to grow unrestrained. In the interval evaluated, cells that have higher proliferative potential outgrow their competitors as 3D-simulations after 5 selection rounds make explicit the difference in progression and phenotype distribution between the two populations (Fig. 2B). The results suggest that the invasive phenotype and proliferative phenotype may not be able to be separated in populations growing in a spatially confined area such as a solid tumor or in our experimental model.

Figure. 2.

Computer simulation predicted an explicit coupling of motility and proliferation. (A) Proliferation and motility values (0 to 1) are randomly attributed to each cell in initial populations through a normal distribution with mean 0.5 (standard deviation=0.1), corresponding to a probability from 0 to 100% of moving or proliferating. M subpopulation has higher proliferative values (0.7) than both S (0.52) and O cells (0.5). Also, M5 cells had increased motility (0.76) as compared to O (0.5) and S5 cells (0.48). (B) 3D-simulations after 5 selections explicit the difference in progression and phenotype distribution between the two populations.

The simulations with the solid tumor model, where no re-seeding was allowed, led to cells with increased values for proliferation and motility in the tumor-host interface: 0.54 ± 0.01 for proliferation and 0.58 ± 0.003 for motility when no mutations were allowed, and 0.68 ± 0.02 for proliferation and 0.75 ± 0.01 for motility for a mutation rate of 1%. No significant differences were observed when the original tumor was seeded at a density of 20% when compared to a fully confluent original tumor.

The mathematical modeling results were experimentally examined by selecting motile Panc-1 cells

We tested our mathematical modeling experimentally by selecting Panc-1 cancer cells for enhanced motility/invasion on a 3D matrix away from the metabolic constraints of limited diffusion imposed by a glass cover slip over multiple iterations (Fig. 3A). Speciation was accomplished by serially selecting M cells that migrated away from the glass cover slip, as opposed to S cells that were viable but did not migrate. After six consecutive rounds of selections, M6 cells traveled greater distances away from the cover slip compared to S6 cells (Fig. 3B).

Figure. 3.

Panc-1 cells were experimentally speciated by enhanced motility. (A) Panc-1 cells plated on the matrix-coated glass cover slips were placed upside down onto plates to allow cells to grow in between the cover slip and plate, resulting in metabolic constraints imposed by limited diffusion of nutrients under the cover slip. After 10 days culture, the distinct cell populations (yellow circles) were isolated and independently re-plated. (B) After six consecutive selections, M6 and S6 cells visually demonstrate cell motility differences. Yellow arrows indicate the direction of cell movement away from the cover slip where the cells were seeded.

Speciated M Panc-1 cells retain enhanced motility/invasion in vitro and in 3D matrix

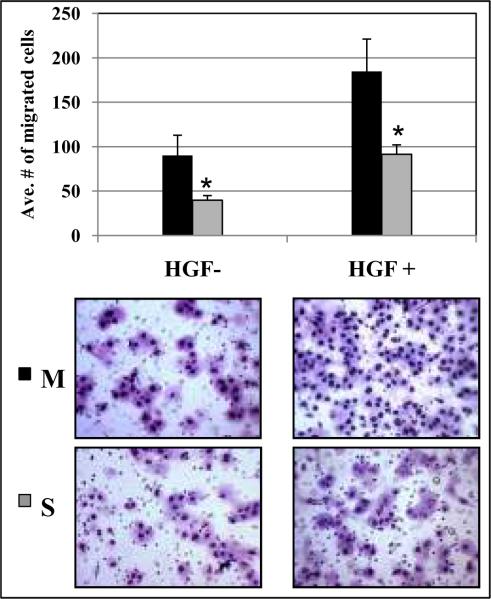
To characterize the invasive phenotype, chemoattractant induced migration of M6 and S6 cells was measured using a Transwell assay. As shown in Figure 4, there was a two-fold increase in the number of M6 cells migrated into the lower chamber due to a FBS gradient (1% FBS in top chamber and 10% FBS in lower chamber, p=0.014). Consistent results were also seen with HGF supplementation in the lower chamber as an additional chemoattractant (p=0.001). These observations suggest that speciated Panc-1 cells could be selected that retain enhanced motility in vitro.

Figure. 4.

Speciated M cells showed enhanced motility/invasion in vitro. Serum-starved speciated cells were characterized the invasive phenotype plated onto a Transwell insert. After 24 hours incubation, migrated cells on the lower membrane were counted under the microscope (20× magnifications). Both FBS (1 to 10%) and HGF chemoattractant gradient (0 to 100ng/ml) led to a two fold increase in M6 migration compared to S6 cells (p=0.014 and p=0.001, respectively). Statistical significances were marked with asterisks.

To further assess the motility phenotype of speciated Panc-1 cells in an in vivo-like setting, 3D matrices were generated by culturing FAP expressing fibroblasts for 8 days prior to denuding the confluent fibroblasts leaving an acellular extracellular matrix. These matrices contain a meshwork of long fibronectin fibrils that can be utilized as roadways by tumor cells (14). Random vs. directional motility of individual cells was quantified by determining the ratio of the net distance over trajectory path (D/T). In this analytical method, the range is 0–1 with a ratio of 1 representing the maximum value for ideal directional motility, while ratios significantly less than 0.5 are cells migrating in a random pattern. Figure 5A and 5B are representative examples of migration/invasion tracks of Panc-1 cells over 12 hours and quantified for average velocity and directionality, respectively. M6 cells had greater velocity and directional motility compared to S6 cells (velocity=17.6 ±2.1 vs. 13.4 ±1.0μm/hr, p=0.04; directionality=0.70 ±0.04 vs. 0.46 ±0.05, p<0.001 for M6 and S6 cells, respectively). In addition, speciated M6 cells demonstrated greater average velocity and directional invasion compared to parental Panc-1 cells (velocity=11 ±1.8, directionality=0.66 ±0.02).

Figure. 5.

Motile Panc-1 cells had greater directional motility and enhanced proliferation. (A) Speciated cells within matrix were monitored cell behaviors for 12 hours. Randomly selected individual tracks were combined into a single figure. (B) Individual cell dynamics were measured for average velocity and directionality. M6 cells have greater velocity and directionality compared with S6 cells (p=0.04 and p=0.001, respectively). (C) Cells were tested for the growth rate by MTT assay. M6 cells had a two fold greater proliferation rate compared with S6 cells (p=0.001). Statistical significances were marked with asterisks.

Speciating M Panc-1 cells have greater intrinsic proliferative phenotype

Given the mathematical model prediction of an intrinsic relationship between motility and proliferation, a cell proliferation assay was performed of the speciated Panc-1 cells in an MTT assay (Fig. 5C). After 4 days incubation, M6 cells had a nearly two fold greater intrinsic proliferation rate compared to S6 cells (p<0.001). Speciated M6 cells also had a 2-fold greater proliferation rates compared to parental Panc-1 cells. Thus, speciating M6 cells resulted in greater intrinsic proliferative phenotype that was coupled with its enhanced motility, providing experimental evidence confirming the mathematical model prediction.

Identification of altered gene expression in speciated subpopulations

To characterize the potential molecular mechanism regulating the observed coupling of cell motility and proliferation in speciated M cells, gene-expression profiles of two independent samples (5^th and 6^th selections) were analyzed using an Agilent Expression Microarray. From the 34,127 genes in the microarray, genes that showed a statistically significant difference were identified as described in method. The resulting set (~2400 genes) having more than two-fold differential expression between M and S cells was analyzed by Gene Ontology enrichment process for clustering genes within the cell motility and proliferation categories. After adjusting p-values of differential expression to an estimated FDR <1%, a list of 23 differentially expressed genes was generated (Supplemental Table 3). Four candidate genes up-regulated in M Panc-1 cells were selected for further study. These candidate genes are rho-GDI2, sparc, amphiregulin, and sgII.

Rho-GDI2 plays a role in regulating both cell movement and proliferation

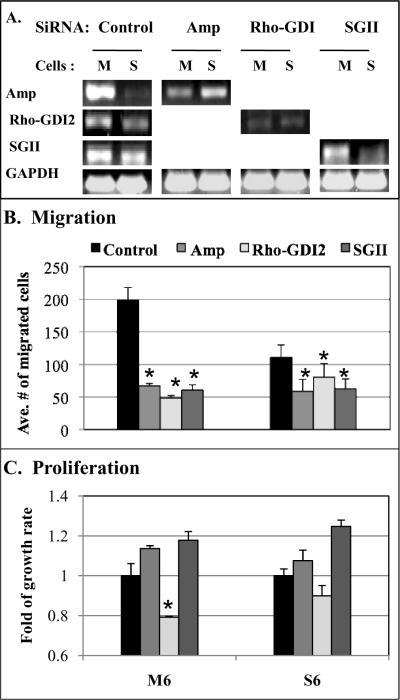
To test the role of candidate genes in regulating cell migration and proliferation, transcripts of candidate genes were knocked down in speciated cells using RNA interference with siRNA, and the transfected cells analyzed for in vitro migration and proliferation assays in three independent experiments. Endogenous RNA levels of each gene in M6 and S6 cells were analyzed by quantitative RT-PCR (Fig. 6A). Compared to control transfection with scrambled RNA duplexes, each siRNA was able to down-regulate gene expression by ~70% for amphiregulin, ~60% for rho-GDI2, and ~50% for sgII. However, only minor depletion was seen in sparc siRNA transfected cells (<10 %, data not shown).

Figure. 6.

Rho-GDI2 plays a role in regulating both cell migration and proliferation. (A) The endogenous level of each gene in speciated cells was analyzed by RT-PCR after control siRNA transfection. Levels of gene expression knocked down by each siRNA confirmed depletion of targeted genes. (B) In Transwell assay, amphiregulin, rho-GDI2, and sgII depletion made a significant reduction in the cell migration of both M and S cells (all p<0.001) compared to control transfection. (C) Cell proliferation assay showed a significant decrease in rho-GDI2 depleted M cells (p=0.02) but had minimal effect on S cells (p=0.15). Statistical significances were marked with asterisks.

In a Transwell experiment to analyze the effects of specific gene depletion on cell migration (Fig. 6B), consistent results across multiple experiments demonstrated amphiregulin, rho-GDI2, and sgII depletion caused a significant reduction in the cell migration of both M6 and S6 cells (all p<0.001) compared to control transfection.

siRNA-transfected cells were further analyzed the functional role that may play in cell proliferation (Fig. 6C). Depletion of amphiregulin and sgII had no significant inhibitory effect on cell proliferation. In contrast, rho-GDI2 depletion caused a significant decrease in cell proliferation in M6 cells (p=0.02), but had minimal effect on S6 cells (p=0.15). These results suggest that since Rho-GDI2 positively regulates both the cell migration and proliferation of motile pancreatic cancer cells, it may be the mechanism by which tumor cells invade and proliferate to escape the harsh microenvironment.

Discussions

Mathematical modeling of the adaptive tumor microenvironment landscape is helpful, because non-linear dynamics of tumor-microenvironment interactions are difficult to predict intuitively. Mathematical models can assist in devising multiple new strategies aimed at targeting the stroma and their interactions with the tumor population. This work is novel because it utilizes mathematical modeling of the tumor microenvironment to quantify these interactions, and begins to identify new concepts that may disrupt the stromal influences on tumor invasion and growth.

In this study, we utilized a mathematical model to examine the complex balance of tumor phenotypic properties that may impact tumor growth. Cell proliferation in normal tissue under physiologic conditions is controlled by biological constraints. However in abnormal physiologic states such as in tumors with its abnormal vasculature and chaotic blood flow, proliferation will at times be limited by the availability of key substrates such as oxygen and glucose. Distinct tumor microenvironmental forces can exert strong selection pressures, and enhanced motility to escape this harsh environment may be selected as an optimal phenotypic property (9, 12, 33), resulting in enhanced fitness or proliferation. Thus, our mathematical modeling predicts a coupling of proliferation and motility, as cancer cell proliferation is rewarded when enhanced motile phenotype is selected by the tumor microenvironment landscape. Here, we have validated the predictions of the adaptive tumor landscape concept experimentally by speciating cells for enhanced motility on computer simulation and in vitro 3D matrix system.

Computer simulation setting up an in silico system demonstrates that phenotypic adaptation to the cover slip experiments proceeds in two steps. First, escape from the harsh environment under the cover slip is possible only for cells with increased motility. Second, cells that escape the cover slip enter a normal in vitro environment in which they must compete for space. In this adaptive landscape, a phenotype with high proliferation rate will be selected. Therefore, the results suggest that the invasive and proliferative phenotypes cannot be separated. In fact, increased invasiveness by itself is insufficient to change the heritable phenotype unless it also increases proliferation. That is, the Darwinian dynamics that promote invasiveness must also promote proliferation to establish increased motility as a heritable trait within the population.

The conclusions obtained from the computational model used in this experiment are limited by the simplifications inherent to it. For instance in this model, cell replication was limited only by the availability of metabolic substrates and pH, as well as “free space” for growth. In reality, cell-cell interactions inhibit replication in cell lines to different degrees (34), which is also likely the case for cancers in vivo. Cell growth is also dependent on growth factors produced by the stroma, which must diffuse through layers of avascular tumors before reaching the innermost layers of the tumor. We believe that these two limitations, however, do not compromise the conclusions drawn from these simulations because: (A) While actual cells are elastic and may deform under pressure allowing for regions of higher cell density and prolonged replication, these cells eventually will reach a maximum density that will induce quiescence. Computational models that have modeled the mechanic process of cell division and its importance for solid tumors have shown that these tumors have an initial exponential growth phase that later is replaced by a more linear growth (35, 36). This is what is observed in our proposed model, with only cells in the outer shell being able to replicate, thus reinforcing the natural selection for not only proliferation but also for being at the tumor-host interface. Thus highly proliferative but poorly motile cells will similarly become trapped in both models, although ours may underestimate the density at which this happens. (B) Although this model implementation does not account for stroma-produced growth factors, however, the diffusion of these species is ruled by the same dynamics as the diffusion of oxygen and glucose. Thus the cells in the inner core of the tumor would still likely become quiescent or die with a probability that increases by their distance from the tumor-host interface.

Our simulation results and in vitro studies confirm prior studies that have used evolutionary game theory to determine the outcome of a “game” played by cancer cells with different degrees of proliferative and motile strategies. Basanta et al. (37, 38, 39) have shown that motility is rewarded when cells are in a harsh environment (closer to the tumor inner core), while proliferation is the optimal strategy when cells are closer to the tumor-host interface, and that cells alternate between strategies during tumor growth. In the current model, cells are randomly seeded with different values for both phenotypes or strategies, and we observe that our model predicts the selection of cells capable of implementing both.

We also examined the evolutionary dynamics that promote invasive cancer phenotypes experimentally by speciating Panc-1 cancer cells for enhanced motility using the metabolic constraints of limited diffusion imposed by a glass cover slip. We have characterized speciated Panc-1 cells for motility/invasion, migration, proliferation, and gene expression profile. The motile Panc-1 cells have enhanced directional motility/invasion, and a nearly two-fold greater intrinsic proliferation rate compared to stationary Panc-1 cells. This confirmed in vitro that speciated Panc-1 cells demonstrated a coupling of enhanced motility with the resultant greater proliferation.

To characterize the molecular mechanism of microenvironment facilitated cell motility/invasion and proliferation, gene-expression profiles of speciated Panc-1 cells were analyzed by microarray. The analysis revealed an essential role of Rho-GDI2 in regulating cell movement and proliferation. Depletion of rho-GDI2 expression suppressed both motile Panc-1 cell motility and cell proliferation in vitro, suggesting that Rho-GDI2 functions as a positive regulator of tumor motility in this pancreatic cancer cell line. Rho-GDIs are guanine nucleotide dissociation inhibitors, and one of the key components in controlling the biological activities of Rho GTPases via a tightly regulated GDP/GTP cycle of cytosol/membrane alterations (40). Several studies have investigated the level of expression of Rho-GDI2 in various cancer cells compared with normal cells, revealing distinct phenotypes depending on the tumor cell context as well as the tumor stage. In human bladder cancer cells, Rho-GDI2 was found to be a negative regulator of Rho family GTPase and potential suppressor of tumor metastasis (41). In contrast, in breast cancer and ovarian adenocarcinoma, rho-GDI2 mRNA levels were associated with tumor growth and invasiveness (42, 43). Recently, rho-GDI2 expression was found to be positively correlated with tumor progression and metastasis in human gastric tumor tissues and cell lines (32). In this context, overexpression of rho-GDI2 caused a significant increase in cell invasion in vitro, tumor growth, angiogenesis, and metastasis in vivo, whereas rho-GDI2 depletion demonstrated opposite effects.

The complex interaction of the tumor with its microenvironment is best studied in its biological context and as a tumor “organ”, with its integrated constituents and competing requirements and rewards. The use of evolutionary game theory in partnership with biological experimentation is an attractive approach to model the complex dynamical system of the tumor microenvironment, and may lend itself to evaluating the therapeutic impact in-silico of stromal alterations in future preclinical studies. Our study demonstrates the potential utility of an in-silico system that can mimic experiment designs for predictive comparisons of experimental results.