Anomaly Detection Using an Ensemble of Feature Models

Abstract

We present a new approach to semi-supervised anomaly detection. Given a set of training examples believed to come from the same distribution or class, the task is to learn a model that will be able to distinguish examples in the future that do not belong to the same class. Traditional approaches typically compare the position of a new data point to the set of “normal” training data points in a chosen representation of the feature space. For some data sets, the normal data may not have discernible positions in feature space, but do have consistent relationships among some features that fail to appear in the anomalous examples. Our approach learns to predict the values of training set features from the values of other features. After we have formed an ensemble of predictors, we apply this ensemble to new data points. To combine the contribution of each predictor in our ensemble, we have developed a novel, information-theoretic anomaly measure that our experimental results show selects against noisy and irrelevant features. Our results on 47 data sets show that for most data sets, this approach significantly improves performance over current state-of-the-art feature space distance and density-based approaches.

1 Introduction

We present a new approach to semi-supervised anomaly detection, which involves learning a classifier from only one class of training example. That is, we are given a sample from one distribution (i.e., “normal” examples¹), and our goal is to differentiate in the future between these normal examples and those that do not appear to come from the same distribution (“anomalies”). This task is distinct from unsupervised anomaly detection, where we are given one sample that is a mixture of examples from two distributions, and the task is to differentiate them, and from supervised anomaly detection, where we are given a sample of labeled examples from both distributions. For a survey of anomaly detection problems and current approaches, see [3].

Most current approaches make judgments based on the distance among examples. For example, one-class support vector machines (SVMs) [12] attempt to separate the training examples from the rest of feature space and rank anomalies according to their distance from this region The local outlier factor method (LOF) [2] compares the distance between a point and its nearest neighbors to the distances between other nearby points and their nearest neighbors. It identifies anomalies as points relatively far from local clusters. That is, LOF is a density-based approach that has the advantage of distinguishing between a point near the boundary of a sparse cluster and a point that does not appear to be part of any cluster or distribution.

We hypothesize that features have more complex relationships to one another than preserved locations in feature space, and that these relationships can be learned using standard supervised learning techniques. As a concrete example from anomaly detection in computer security [6], consider the normal behavior for the TCP protocol. A connection is initialized by a three-way handshake—the sender sends a TCP packet, the receiver sends a SYN packet, and the sender replies with an ACK packet. Thus we can anticipate a fairly stable relationship between the frequency of these packet types during normal protocol behavior. In contrast, consider the Neptune attack, which is an example of TCP SYN Flooding [5]. During a Neptune attack, the sender sends the TCP packet, but does not send the ACK packet to complete the three-way handshake. Sending the initial TCP packet initiates a TCP connection, and the server allocates resources to handle it. The objective of the Neptune attack is to cause a denial-of-service by creating many “half-open” connections and, in turn, exhausting server resources. During the attack, the number of TCP, SYN and ACK packets are all issued in typical frequencies when examined individually, and the distance in feature space between attacks and the normal examples is comparable to the distance between pairs of normal examples (especially considering that in a network anomaly detection method there are typically several additional features derived from packet header data that affect the distance). Thus, it is difficult to identify Neptune attacks from points in feature space. However, if we use normal traffic to train a model that can predict the number of ACK packets based on the number of TCP and SYN packets, then we will identify the Neptune attack as anomalous because it issues many connections that do not complete the TCP three-way handshake, and therefore has fewer ACK packets than would be expected, given the number of TCP and SYN packets.

In this paper we explore the idea that the distribution of normal examples is marked by a preserved relationship among a few key features. Based on this insight we present an approach to the anomaly detection problem that discovers these relationships. Specifically, we attempt to learn accurate models that can predict feature values from other feature values. That is, we hold aside one feature (e.g., the number of ACK packets in the example above) as the “target” feature, then use supervised learning methods to learn to predict the value of this target from some of the other features (e.g., the number of TCP and SYN packets). After holding aside and learning predictors (i.e., classifiers or regression models, depending on whether a feature is discrete or continuous) for each of a set of features in turn, we estimate the evidence of an anomaly conferred by each feature’s predictor and combine the evidence into a final judgment.

This framework, using supervised learning to infer models for each of a set of features, has been used in previous approaches for noise-reduction [15], feature construction [11], and has even been applied in a specific anomaly detection application with discrete features [9]. However, the key to making the approach work for general anomaly detection problems is the way that the ensemble of feature predictors are combined together to make a decision. Our experiments suggest that this must be done in such a way as to eliminate unreliable predictors and irrelevant or noisy features. We present a novel approach for the analysis and contribution of each feature predictor and show with thorough experimentation that (i) our approach is generally applicable to a variety of data sets, and (ii) that our approach is more robust to noisy or irrelevant features than existing state-of-the-art anomaly detection methods.

In the sections that follow, we explain how we train and evaluate the predictors, demonstrate how we interpret their output, and show that their accuracy is generally better than either one-class SVMs and LOF over 47 anomaly detection tasks of various size and difficulty. Because our approach involves feature regression and classification, we refer to it as FRaC.

2 Approach: Feature Regression and Classification

Formally, we are given a training set of N examples χ = {x⃗₁, x⃗₂, …, x⃗_N}, all assumed to be of the same class (i.e., “normal”). Each example x⃗_j is a fixed-length vector of D features x⃗_j = 〈x_j1, x_j2, …, x_jD〉 of types t⃗ = 〈t₁, t₂, …, t_D〉. In this paper, we assume that these types are either nominal, in which case we know the set of possible feature values, or continuous, in which case we know the feasible range of real values. However, our approach extends to online learning by simply updating these domains and retraining, and it can be used with complex feature types, provided the appropriate comparison operators are defined.

Our goal is to learn a function f : x⃗ → ℝ that maps a query vector x⃗_q to a real-valued score. We can use these scores to rank examples by how likely each is to come from a different distribution than the training set. Our approach involves three key design choices. The first is which features we will attempt to predict, and which other features to use as the predictor features. In our experiments, we learn a predictor for each feature, using all remaining features as the predictor features. Note that it may be possible to optimize these sets for specific tasks, particularly if we have prior knowledge about the relationships among features. When we learn a predictor for a target feature, our set of selected predictor features are only potential predictors—whether or not they are used to predict the target value depends on our choice of predictor model, learning algorithm and training set (for example, a decision tree will only use those features necessary to correctly predict the target feature).

The second choice is which supervised learning algorithm to use to predict feature values. Of course, we want choose a hypothesis space and learning algorithm appropriate for our feature set and problem domain, but any choice may be appropriate for our approach, provided the algorithm learns a regression model if the target feature has continuous feature values and a classifier if it has nominal values. We may also choose to learn multiple predictors for each feature. In general, we use P independent underlying prediction models and learning algorithms to learn P prediction models for each feature. Formally, let ρ_i refer to the set of (potential) predictor features used to predict target i, and let ρ_i(x⃗_j) refer to just these values in a vector x⃗_j, i.e., if we use all features apart from i itself, then

$${\rho }_i({\overrightarrow{x}}_j)=\langle x_{j1},x_{j2},\dots ,x_{j,i-1},x_{j,i+1},\dots ,x_{jD}\rangle$$ (1)

We learn a regression or classification predictor of type C_p,i : ρ_i(t⃗) → t_i, where t⃗ are the feature types, and p ∈ {1, 2, …, P} indicates the underlying supervised model.

The third design choice is how we will combine the ensemble of feature predictors into f : x⃗ → ℝ to produce the real-valued anomaly score for a previously unseen example. The intuition behind our approach is that predictors that are accurate on the training set will continue to be accurate when predicting the feature values of examples that come from the same distribution as the training set, and they will make more mistakes when predicting the feature values of examples that come from a different distribution.

Thus, we expect the total error of a test set example x⃗_q

$$\mathit{\text{error}}({\overrightarrow{\mathrm{x}}}_q)={\displaystyle \sum _{p=1}^P{\displaystyle \sum _{i=1}^D\mathit{\text{distance}}(x_{qi},C_{p,i}({\rho }_i({\overrightarrow{\mathrm{x}}}_q)))}}$$ (2)

(assuming the distance function is defined for each feature type) to be higher if x⃗_q is an anomaly than if x⃗_q is normal. Equation (2) does not account for the accuracy of each predictor C_p,i. For example, if C_p,i is no better than random guessing, even on the training examples, and makes an incorrect prediction half the time, then (2) will randomly penalize half the test set examples that come from the same distribution as the training set. Therefore, we use an information-theoretic metric to evaluate each prediction. Specifically, for a test example x⃗_q, and a feature i, we estimate the likelihood of observing the feature value x_qi, given the prediction C_p,i(ρ_i(x⃗_q)) (implicitly assuming x⃗_q comes from the “normal” training set distribution). We then take the amount of self-information [13], or surprisal, in this likelihood to be the amount of evidence we have that x⃗_q comes from a different distribution than the training set:

$$\mathit{\text{surprisal}}(p)=-\mathit{\text{log}}(p).$$ (3)

To calculate p(x_qi|C_p,i(ρ_i(x⃗_q))), we first evaluate C_p,i using cross-validation over the training set. This gives us A_p,i, a sample of (observed value, predicted value) pairs,

$$A_{p,i}=\{(x_{1i},C_{p,i}({\rho }_i({\overrightarrow{\mathrm{x}}}_1))),\dots ,(x_{Ni,}{C}_{p,i}({\rho }_i({\overrightarrow{\mathrm{x}}}_N)))\}.$$ (4)

For nominal features, we use A_p,i to construct a confusion matrix which gives us an estimate of the likelihood of each feature value for each predicted value.² For example, suppose that feature i has two values, v₁ and v₂, and that C_p,i is very accurate on the training set: when it predicts v₁, it is correct 99% of the time. When it predicts v₁ on a test set example, but the value is v₂, the surprisal is −log(0:01) = 6:64 (bits, if we use log base 2). Note that if C_p,i is a poor predictor, say 50% accurate on a binary feature, then the surprisal is only −log(0:5) = 1 (bit, in log base 2) when the predictor is incorrect, but we are equally surprised when it is correct, thus the correctness of such a classifier has no effect on surprisal.

If feature i is continuous, we use A_p,i to construct a sample of error values,

$$E_{p,i}=\{x_{1i}-C_{p,i}({\rho }_i({\overrightarrow{\mathrm{x}}}_1)),\dots ,x_{Ni}-C_{p,i}({\rho }_i({\overrightarrow{\mathrm{x}}}_N))\}$$ (5)

and we use the sample to estimate the error density distribution. In our experiments, we discretize the values in E_p,i into $\lfloor \sqrt{N}\rfloor$ bins, where each bin contains a sample of values from E_p,i that are all approximately the same. We then smooth the resulting histogram of error values with a Gaussian-shaped kernel with a standard deviation of one bin [10]. Given a test example x⃗_q, we estimate p(x_qi|C_p,i(ρ_i(x⃗_q))) as the probability mass in the bin corresponding to the error x_qi − C_p,i(ρ_i(x⃗_q)).

Finally, we add the evidence provided by all features to produce the surprisal anomaly score,

$$S({\overrightarrow{\mathrm{x}}}_q)={\displaystyle \sum _{p=1}^P{\displaystyle \sum _{i=1}^D\mathit{\text{surprisal}}(p(x_{qi}|C_{p,i}({\rho }_i({\overrightarrow{\mathrm{x}}}_q)),A_{p,i})).}}$$ (6)

The surprisal anomaly score tends to be higher for features with high-entropy value distributions (e.g., features with many possible values) even if all classifiers are relatively accurate. We account for this by subtracting the entropy (i.e., the expected surprisal) of the training set feature value distribution.

If feature i is a nominal feature with V values 𝒱 = {v₁, v₂, …, v_V}, then we estimate the likelihood of each possible feature value from its frequency in the training set i.e., if feature value v_k occurs n_k times in N training set examples, then we estimate that $p(v_k)=\frac{n_k}{N}$. We then estimate the entropy of the feature value distribution as

$$\mathit{\text{entropy}}(\{x_{1i},x_{2i},\dots ,x_{Ni}\})={\displaystyle \sum _{k=1}^V-p(v_k)\mathit{\text{log}}(v_k).}$$ (7)

If feature i is a continuous feature, then we model the probability density with a smoothed histogram of discretized feature values (just as we do for calculating the prediction error distributions above), and calculate entropy with Equation (7).

Our last issue is how to handle missing values in the calculation of surprisal. Note that the contribution of a feature i is zero if the surprisal of a prediction is exactly the expected surprisal without regard to any classifier. This makes zero a natural value to use when the feature value x_qi is missing i.e., when we have no evidence for or against its value being anomalous.

This gives us an alternative anomaly score which handles missing data that we call normalized surprisal,

$$NS({\overrightarrow{\mathrm{x}}}_q)={\displaystyle \sum _{p=1}^P{\displaystyle \sum _{i=1}^D\{\begin{array}{c}0\text{if}{x}_{qi}\text{is missing},\text{otherwise}:\\ \mathit{\text{surprisal}}(p(x_{qi}|C_{p,i}({\rho }_i({\overrightarrow{\mathrm{x}}}_{\mathrm{q}})),A_{p,i}))\\ -\mathit{\text{entropy}}(\{x_{1i,\dots ,}{x}_{Ni}\})\end{array}}}$$ (8)

Normalized surprisal has the advantage of treating all features equally by taking their (potentially imbalanced) feature value distributions into account. Note that normalized surprisal is negative if a predictor makes an observed value likely enough to be less surprising than the entropy of the feature. This effect is more pronounced for high-entropy features, which means that normalized surprisal has properties that are intuitive for anomaly detection: the score is high for incorrect predictions, especially when the predictors are accurate, and the score is low (or negative) for correct predictions, especially when the prediction is nontrivial.

3 Experiments on UCI Data Sets

We hypothesize that learning feature predictors is a superior general approach to the semi-supervised anomaly detection task than current state-of-the-art approaches based on measuring distance between examples in feature space.

We test this hypothesis using 47 classification datasets from the UCI Repository [1].³ For each data set, we consider the most-represented class to be “normal.” We take 75% of the normal examples for training. The remaining 25% of the normal examples and all “anomalous” examples are held aside for testing.

We compare our approach to local outlier factor (LOF) [2], which we believe to be the current state-of-the-art general-purpose approach to anomaly detection. Density-based approaches such as LOF model the distance between examples (computed from all features), and can fail to detect anomalies when they appear in entirely distinct regions of feature space, provided their distances are comparable to training examples. Thus, we also compare against a one-class SVM [12], another popular approach to anomaly detection, which is less susceptible to this weakness. One-class SVMs learn from numerically-valued features, thus when using SVMs, we replace k-valued nominal features with k binary features, each set to 0, except for the one corresponding to the feature’s value, which is set to 1. We use the LIBSVM implementation [4] of one-class SVMs with a radial basis kernel (RBF).

LOF is a density-based approach, fundamentally based on a feature distance metric. For our experiments, we use the Euclidean distance between feature vectors, where the distance for a single continuous feature is the difference in value divided by the range of that feature’s value (i.e., the maximum distance is 1.0), and the distance for a nominal feature is the Hamming distance (i.e., 1 if the feature values are different, 0 if they are identical). We compute the LOF separately for each test set example, such that a test set example cannot receive a low LOF score due to other test set examples in the same neighborhood. LOF has one parameter, MinPts, which is the size of the neighborhood. Following a suggestion in Breunig et al. [2], we calculate the anomaly score by taking the maximum LOF over a range of values.

For our approach using feature regression and classification (FRaC), we combine multiple underlying feature prediction methods: (i) support vector machines (SVMs) using a linear kernel, (ii) SVMs using a radial basis function kernel, and (iii) decision trees. We choose these methods because they represent a variety of hypothesis spaces. We use the LIBSVM implementation for multi-class SVMs and support vector regression [4,7]. When learning SVM models, we replace the nominal predictor features with multiple binary features as described above. We use the WEKA implementation for C4.5 classification decision trees and decision/regression trees [8]. We use normalized surprisal as our anomaly detection score, and we calculate this as the sum of the normalized surprisal for each of the three underlying prediction models.

A key decision in learning support vector machines is the setting of parameters C (the cost of misclassifying a training example), γ (a parameter of the radial basis function), and for regression models, ε, which is part of the loss function. We use a log-scale grid search to select these parameters for accuracy (classification of nominal features) or mean squared error (continuous features) over 10-fold cross-validation on the training data. We do not use a grid search for one-class SVMs, because, with no labeled anomalies in the training data, we do not have a similar objective to optimize.

Some feature values in some of the UCI datasets are missing. We try to handle missing data as simply as possible. When learning SVMs, we replace the missing values of continuous features with a mid-range value, and we set all binary features corresponding to a missing nominal feature value to zero. For FRaC, we discard examples from the training set when they are missing a target feature value (and the contribution to normalized surprisal of a test set example with a missing the target feature value is zero by definition).

The output of each method (LOF, one-class SVM, FRaC) is a real number, which we use to rank each test set example. We then evaluate the resulting rank order by constructing an ROC curve [14] and reporting the area under the curve (AUC).⁴ The results on 47 datasets are reported in Table 1. The results include a estimated upper-bound, which is a classifier (SVM) trained on labeled examples (75% of the anomalous examples are moved from the test set to the training set and labeled “anomalous”). This is meant to judge the difficulty of the learning task—we expect the AUC of the supervised classifier to be a rough estimate of the upper-bound for any anomaly detection approach. The training and test sets for each row in Table 1 are identical across the three anomaly detection methods.

Table 1.

Test set area under the ROC curve (AUC) on UCI classification datasets that have been modified to be anomaly detection tasks. The highest AUC score among the three anomaly detection methods is shown in bold. The estimated upper-bound reports the AUC score for the corresponding supervised classification task, i.e., when training on both “normal” and “anomalous” examples.

Data Set	Estimated Upper-Bound	One-Class SVMs	LOF	FRaC
abalone	0.60	0.56	0.49	0.42
acute	1.00	0.96	0.87	1.00
adult	0.63	0.62	0.47	0.59
annealing	0.95	0.64	0.83	0.83
arrhythmia	0.82	0.61	0.73	0.76
audiology	0.96	0.78	0.77	0.83
balance-scale	1.00	0.95	0.94	0.97
blood-transfusion	0.70	0.56	0.55	0.51
breast-cancer-wisconsin	0.95	0.52	0.92	0.95
car	1.00	0.97	0.76	0.98
chess	1.00	0.71	0.89	0.94
cmc	0.74	0.42	0.45	0.41
connect-4	0.97	0.52	0.86	0.75
credit-screening	0.83	0.72	0.72	0.86
cylinder-bands	0.50	0.91	0.71	0.81
dermatology	1.00	0.94	1.00	1.00
echocardiogram	0.71	0.68	0.73	0.70
ecoli	0.99	0.99	0.99	0.95
glass	0.86	0.58	0.71	0.66
haberman	0.69	0.65	0.60	0.65
hayes-roth	0.69	0.51	0.63	0.78
hepatitis	0.67	0.51	0.58	0.87
horse-colic	0.77	0.72	0.74	0.84
image	1.00	0.85	0.98	1.00
internet ads	0.97	0.79	0.79	0.95
ionosphere	0.98	0.86	0.93	0.97
iris	1.00	1.00	1.00	1.00
letter-recognition	1.00	0.99	0.99	1.00
libras	1.00	0.68	0.68	0.94
magic	0.87	0.78	0.81	0.86
mammographic-masses	0.90	0.78	0.59	0.77
mushroom	1.00	0.95	1.00	1.00
nursery	1.00	1.00	1.00	1.00
ozone	0.52	0.39	0.46	0.33
page-blocks	0.96	0.57	0.96	0.94
parkinsons	0.94	0.72	0.65	0.64
pima-indians-diabetes	0.81	0.64	0.73	0.70
poker	0.71	0.52	0.52	0.54
secom	0.50	0.50	0.54	0.59
spambase	0.96	0.77	0.59	0.86
statlog (german)	0.55	0.55	0.61	0.66
tae	0.74	0.45	0.40	0.66
tic-tac-toe	1.00	0.84	0.99	0.99
voting-records	0.98	0.97	0.87	0.93
wine	0.96	0.80	0.84	0.94
yeast	0.77	0.72	0.74	0.74
zoo	1.00	1.00	1.00	1.00
Number of data sets with the maximum AUC score		8	7	23

On average, the AUC scores for FRaC are better than those of LOF and one-class SVMs. Indeed, the AUC scores for FRaC are better than the maximum of AUC scores for LOF and one-class SVMs on a majority of the data sets. We run one experiment per data set (training on 75% of one class, testing on the remaining 25% and the other classes), and there is doubtless some variance that we are not measuring in the the AUC scores reported in Table 1. However, each column in Table 1 represents 47 independent samples, and according to a two-tailed, paired Student’s t-test, the superiority of the AUC scores in Table 1 for FRaC over those of LOF and one-class SVMs is statistically significant (Table 2).

Table 2.

The average improvement and the probabilities associated with a two-tailed, paired Student’s t-test comparing the AUC scores shown in Table 1 of FRaC with (i) LOF, (ii) one-class SVMs, and (iii) the better of LOF and one-class SVMs for each data set.

Approach	Average improvement in AUC score using FRaC	p-value
One-class SVM	0.082	0.000038
LOF	0.051	0.00062
max(LOF,One-class SVM)	0.022	0.088

4 Why does FRaC work?

Based on the comparison in Table 1, we believe that FRaC is the superior general approach to semi-supervised anomaly detection. In this section, we test a hypothesis to explain, in part, why it is so successful.

In any learning task, there are many potentially irrelevant features that distort the feature space, affecting the shapes of clusters and the relative distance between examples. LOF and one-class SVMs treat all features equally, but by using normalized surprisal to combine the output of feature predictors, FRaC implicitly selects features, because normalized surprisal is only very high (or very low) for accurate predictors.

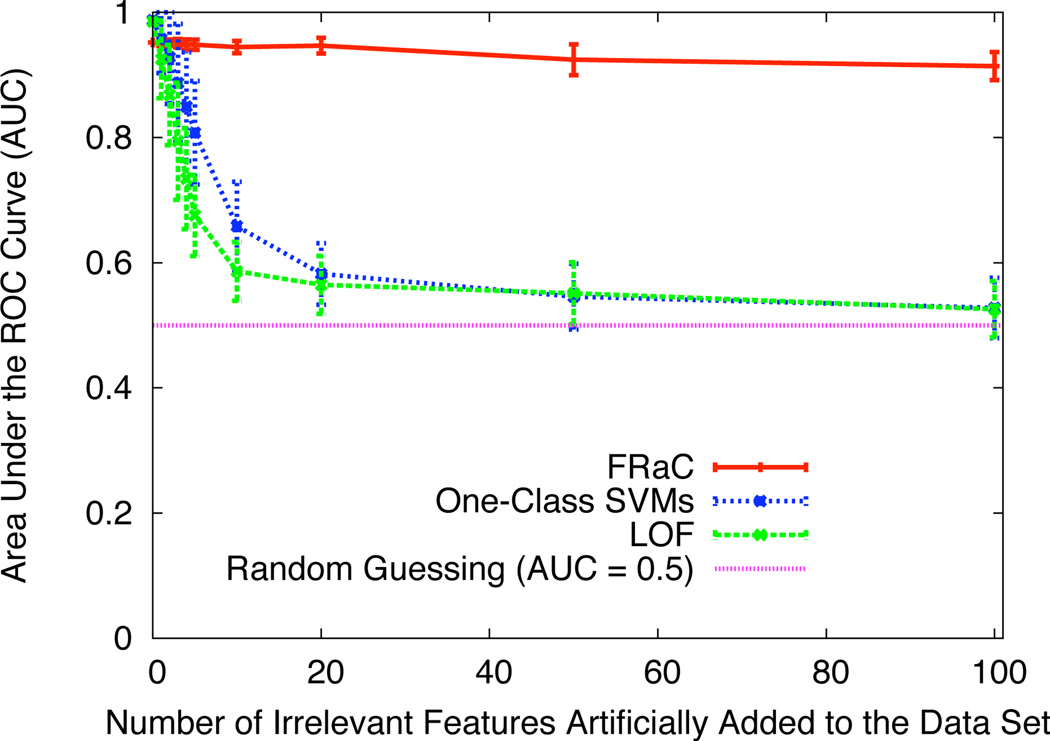
To show that FRaC is robust to irrelevant features, we perform the following experiment. We first select a data set from Table 1, and then add stochastically-generated irrelevant features to the data set and track the predictive accuracy of the anomaly detection methods. We choose the data set ecoli because it has a relatively small number of features and all three anomaly detection methods have high AUC scores. We start with the existing set of seven features in the ecoli data set, and generate additional irrelevant features as follows. For each additional feature i, we first choose the parameter of a Bernoulli distribution p_i from a uniform distribution. Next, for each of N examples j, we set x_j,i to 1 with probability p_i or to 0 with probability 1 − p_i. Because the AUC scores vary with the skewness of the Bernoulli distributions, we replicate the experiment 40 times to determine the distribution of AUC scores for each number of additional irrelevant features. Figure 1 shows the average AUC scores of FRaC, one-class SVMs, and LOF after adding between zero to 100 irrelevant features to the ecoli data set and repeating the anomaly detection experiments. The AUC scores of one-class SVMs and LOF quickly degrade with the dimensionality of the feature space, eventually approaching performance that is no better than random guessing. The AUC score for FRaC, on the other hand, never drops below 0.9, even when (at least) 93% of the features are completely irrelevant. We believe that running this test on other data sets would yield similar results.

Figure 1.

The effect of additional irrelevant features on three anomaly detection methods for the data set ecoli.

5 Conclusion

FRaC is a new, general purpose approach to the semi-supervised anomaly detection problem. It works because it implicitly reduces feature space to those features that, through conserved learned relationships among features, characterize the distribution of “normal” examples. It can then recognize anomalies as examples whose features do not conform to those patterns. It is therefore robust to high-dimensional learning tasks, which are difficult to characterize using the current state-of-the-art feature space distance and density-based approaches.