HEALTH CARE SPENDING GROWTH AND THE FUTURE OF U.S. TAX RATES

Abstract

The fraction of GDP devoted to health care in the United States is the highest in the world and rising rapidly. Recent economic studies have highlighted the growing value of health improvements, but less attention has been paid to the efficiency costs of tax-financed spending to pay for such improvements. This paper uses a life cycle model of labor supply, saving, and longevity improvement to measure the balanced-budget impact of continued growth in the Medicare and Medicaid programs. The model predicts that top marginal tax rates could rise to 70 percent by 2060, depending on the progressivity of future tax changes. The deadweight loss of the tax system is greater when the financing is more progressive. If the share of taxes paid by high-income taxpayers remains the same, the efficiency cost of raising the revenue needed to finance the additional health spending is $1.48 per dollar of revenue collected, and GDP declines (relative to trend) by 11 percent. A proportional payroll tax has a lower efficiency cost (41 cents per dollar of revenue averaged over all tax hikes, a 5 percent drop in GDP) but more than doubles the share of the tax burden borne by lower income taxpayers. Empirical support for the model comes from analysis of OECD country data showing that countries facing higher tax burdens in 1979 experienced slower health care spending growth in subsequent decades. The rising burden imposed by the public financing of health care expenditures may therefore serve as a brake on health care spending growth.

I. Introduction

Health care spending in the United States is now 17.6 percent of GDP, and if unchecked it is expected to account for 26 percent of GDP by as early as 2035 (Congressional Budget Office 2010). Public expenditures account for almost half of health care spending. Beyond the aging of the population, rising health care costs per person account for the majority of the projected increase in government spending on health. Federal spending on Medicare, expanded Medicaid and SCHIP, and newly enacted exchange subsidies is anticipated to grow from 5.5 percent of GDP now to almost 14 percent on more in 2060. Unchecked, these increases in entitlement spending would double the federal budget (as a share of GDP), necessitating some combination of tax increases, the elimination of other public spending, or public debt levels that would far exceed those currently observed in Greece.

The bipartisan National Commission on Fiscal Responsibility and Reform has recognized that health care spending growth represents “our single largest fiscal challenge over the longrun” (National Commission on Fiscal Responsibility and Reform 2010). While the Commission proposed a variety of cost-saving mechanisms, ultimately it concludes that health care expenditures cannot grow in excess of 1 percent above GDP if the long-term deficit is to be brought under control, although it does not offer a concrete plan for achieving this goal. In this paper, we consider the implications of the failure to achieve this moderation in spending, necessitating a sharp increase in taxation to avoid explosive deficits. Indeed, one prominent New York Times columnist helpfully translated the circumspect language of U.S. senators voicing concerns about future fiscal imbalances: “Like having Medicare? Then taxes must rise.” (Leonhardt 2009).

While this prospect made rising health care spending a topic of considerable concern and focus during the 2010 reform debate, a recent literature is more sanguine, suggesting that the share of GDP devoted to health care in the U.S. is not inefficiently high, and might optimally rise to one-third of GDP in the future as demand for better health rises more than proportionately with income growth (Hall and Jones, 2007; Fogel, 2008). These findings are driven by the argument that the benefits of additional years of good health arising from technological improvements in health care are large and increase as income rises. However, these studies pay little attention to how society pays for this additional health care. Aside from the broad recognition that taxes are sure to rise in the future, there has been little discussion of how such sharply rising tax rates might affect the social value of health care spending or the non-health sectors of the economy. This paper takes a first look at this larger question by focusing on the economic and distributional implications of the projected increases in tax revenue necessary to pay for rising health care costs.

We develop a macroeconomic model based on choices about working, consumption, and saving. Included in the model is a government sector that imposes taxes, some of which it uses to pay for health care that improves longevity. We then use this model to evaluate the effects of the rising tax rates that finance rising health care spending on economic growth and the well-being of different segments of the population. We focus on a benchmark case in which marginal income tax rates rise by enough to finance an increase in health spending by 2060 of roughly 8 percentage of GDP and in which the share of taxes paid by the top and bottom parts of the income distribution are held constant. We also look at alternative scenarios in which increases in health spending are financed by a less progressive payroll tax and in which increases in health care productivity mitigate the required tax increase.

Consistent with an important Congressional Budget Office study (Orszag, 2007), we find that in our benchmark case that maintains the share of taxes paid by different income groups, rising health spending results in sharp tax hikes, with marginal rates of 70 percent for the very highest income group and marginal efficiency costs of up to $1.48 per dollar of revenue collected. These in turn imply an 11 percent decline in estimated GDP by 2060 relative to baseline, suggesting that estimated future marginal benefits of health care spending could be attenuated by the large efficiency costs of a progressive tax system. These efficiency costs are highly dependent on the way in which revenues are raised however: less progressive financing generates smaller efficiency costs. Increasing payroll taxes by a flat rate generates a more modest 5 percent relative decline in GDP, but leads to a doubling of average tax rates paid by the lowest-income households.

Our results reconcile the popular dismay over rising health care spending with the more positive findings of Hall and Jones and others. We too find that the assumed improvement in longevity is “worth it” on average. However, previous studies based on evaluating the utility of representative agents do not incorporate the costs of the partial public financing of the health care system, the redistribution from rich to poor and from healthy to sick. Our model includes heterogeneous agents, and it is the marginal cost of redistribution through the tax system that leads to a more-than-proportional decline in the non-health sector (Browning and Johnson 1984).

The implicit costs of redistribution in a system partly funded by public dollars may affect the aggregate demand for health care. Getzen (1992) suggested that health care spending at the country level is driven in large part by the ability to finance health care, as opposed to factors such as the health care needs of an aging population. We test a related hypothesis by asking a simple empirical question: do countries with higher marginal costs of raising revenue – as proxied by their average tax-to-GDP ratio – experience slower subsequent growth rates in health care spending? Using OECD country data for higher-income countries, we find that countries with a higher tax-to-GDP ratio in 1979 experienced significantly slower growth in health care spending between 1980 and 2008, a result consistent with our model. Even if health care reform fails to tame health care spending growth, the rising political and economic costs of taxation may ultimately serve as a brake (albeit an inefficient one) on health care spending growth.

II. Background

There is a vast literature exploring the internal organization and efficiency of health care, but there is limited evidence on how rising growth rates and the public financing of health care might affect the non-health-care sector of the economy and overall economic growth, or how different tax policies to pay for more expensive health care might affect the distribution of the burden of financing health care and consequent deadweight loss imposed on the economy.

Health Spending in the Economy

Stories of the toll of rising health care costs on wages and employment abound in the popular press. While these pressures have been present for many years – resulting in stagnant net wage growth (after health insurance payments) over the last decade as an increasing share of compensation is devoted to health insurance benefits – the current recession and debate over health care reform have cast the rising burden of health care costs in a much starker outline (Fletcher 2008). These consequences are particularly dire for low-income populations, who may be at greatest risk of losing jobs when the costs of benefits rise (Baicker and Levy 2008).

Rising health care costs also threaten to erode the risk pooling that occurs in private insurance markets. The majority of private health insurance in the U.S. today is obtained through employer-sponsored plans, which cover more than 170 million lives (compared with under 20 million covered through private non-group insurance plans) (America’s Health Insurance Plans 2007). Economic theory suggests that in the long run the cost of these benefits is borne entirely by workers (as long as they value the benefits) (Summers 1989), but in the short run there are constraints that affect the ability of firms to shift costs to workers, and thus rising costs can result in fewer people covered by group policies (Cutler and Madrian 1998; Currie and Madrian 2000; Carrington, McCue K. et al. 2002; Baicker and Chandra 2006). While the vast majority of large employers offer health benefits, over the last 10 years the share of small firms offering health benefits has dropped from 69 percent to 61 percent and rising costs are cited as one of the main factors influencing firms’ decisions to discontinue offering benefits (Kaiser Family Foundation and Health Research and Education Trust 2008). Health care spending growth has also been shown to reduce private health insurance coverage and exacerbate adverse selection (Currie and Madrian 2000; Baicker and Chandra 2006).

Rising health care costs thus seem to present obvious challenges to the U.S. economy, but a more recent set of economic studies provides a far more sanguine perspective, suggesting that the share of GDP devoted to health care in the U.S. is not inefficiently high and, indeed, might optimally be substantially higher still in the future. One study by Robert Hall and Charles Jones suggests that given the productivity of health spending relative to other forms of consumption, we might optimally spend as much as a third of GDP on health by mid-century (Hall and Jones 2007; Fogel 2008). Kevin Murphy and Robert Topel find that health care spending in the last century has generated massive improvements in health and longevity, worth more than $3.2 trillion annually – well in excess of the cost of care (Murphy and Topel 2006). Their research argues that health care is a valuable good, and that we should not be surprised that we are devoting a large and growing share of our national resources to living longer and healthier lives.

There are two approaches to reconciling these two views of health care costs. First, the productivity of health care spending may be overstated because of a failure to distinguish between average and marginal returns to health spending (Garber and Skinner, 2008). Second, and the main focus of this paper, the financing of health spending through redistributive taxation may affect the true social cost of spending an ever-rising fraction of GDP on health care.

The Productivity of Health Spending

The literature above finds large gains to health care spending, but the distinction between average returns to health care spending and marginal returns to the last dollar spent is important but often lost (Weinstein, 2005). It may be difficult to identify the last marginal dollar, or to develop health care reforms that would leave the valuable health care services but get rid of the waste.

Garber and Skinner document differences in spending and outcomes between the U.S. and other developed countries (Garber and Skinner 2008), and suggest that much of the high apparent average benefits of health care spending were generated not by the expenditures at the margin, but instead by the very low-cost innovations such as the use of aspirin and beta blockers for cardiovascular disease, and by important risk factors having little to do with health care intensity per se such as better diet and lower smoking rates (Cutler and Lleras-Muney 2006; Cutler, Rosen et al. 2006). Other studies have found some evidence of high productivity, such as for surgery for spinal stenosis (Tosteson, Skinner et al. 2008) or for the intensive treatment of tourists (but not residents) in Florida admitted to the hospital through emergency rooms (Doyle 2010). In other cases, spending at the margin yielded little value, as in a study of changes over time in expenditures and outcomes for acute myocardial infarction (heart attack) patients (Skinner, Staiger et al. 2006). In the case of Cesarean sections, increases in the use of the procedure were likely to result in utilization of dwindling value (Baicker, Buckles et al. 2006). This suggests a more nuanced view of health care productivity, with some treatments having very large benefits but others exhibiting near-zero benefits but very large costs (Chandra and Skinner 2011). While we do not model these marginal (versus average) productivity effects explicitly in this study, it is important to note that the incremental effects of increasing spending by 8 percent of GDP rather than by 7 percent of GDP are likely to be modest relative to the average improvements in health considered below.

The Financing of U.S. Health Care Expenditures

A second source of worry about rising health spending comes from the fact that a substantial share of health spending is financed by public dollars. These public programs are fundamentally about redistribution from high income to low income, and from healthy to sick. Figure 1 shows the growing share of U.S. health care financed by public dollars. (These figures are in real 2007 millions of dollars, calculated from national health expenditures from CMS deflated by CPI (Centers for Medicare and Medicaid Services and Office of the Assistant Secretary for Planning and Evaluation 2008)). All told, public dollars account for half of national health expenditures. This share is even higher when one includes not only Medicare and the federal and state shares of Medicaid and a host of other government insurance and direct care programs (such as care for veterans and care provided through community health centers), but the tax subsidization of private health insurance through the exclusion of employment-based insurance policy premiums from payroll and income tax bases. This tax expenditure is as large as Federal spending on Medicaid (Kleinbard 2008).

Figure 1. Health Spending by Source in the U.S.

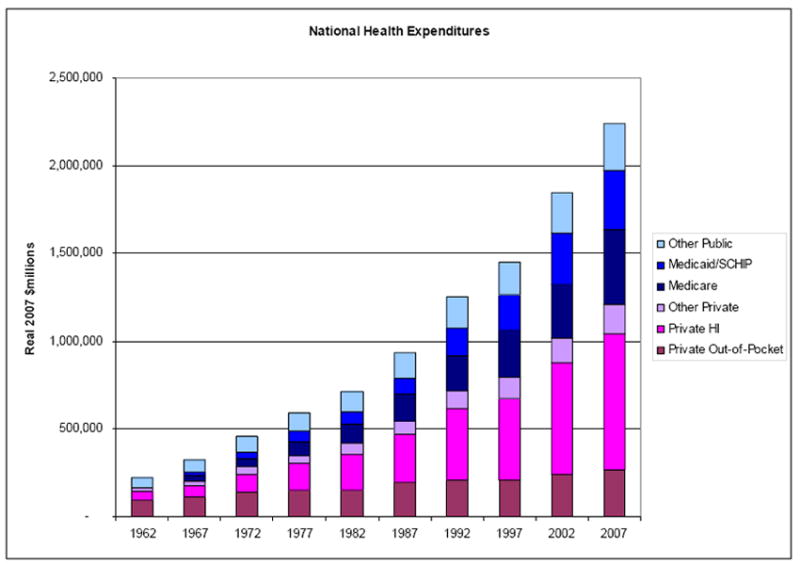
Source: National Health Expenditures, CMS

The deadweight loss generated by the behavior changes induced by the taxes necessary to finance these programs must be added to their direct costs when evaluating their cost-effectiveness. At first blush, these tax distortions may appear to be static in nature (they result in lower economic activity at a point in time), but as Engen and Skinner have demonstrated, tax rate distortions can also have implications for economic growth rates by distorting investment decisions (Engen and Skinner 1996). More importantly, in a dynamic framework there are strong implications for economic growth when tax rates rise.

There is a substantial body of research exploring the size of the incremental deadweight burden in the U.S., based on the existing tax structure. Many estimates cluster around 0.3 – meaning that every dollar of public spending comes with an additional cost of 30 cents in the form of reduced economic activity (Feldstein 1973; Fullerton and Henderson 1989; Poterba 1996; Feldstein 1999; Feldstein 2006; Gahvari 2006). Saez, Slemrod, and Giertz (2009) provide a comprehensive framework and review of the substantial empirical literature on the elasticity of taxable income with respect to tax rates, including evidence from both the U.S. and abroad (Saez, Slemrod et al. 2009). They note that it is not clear whether changes in taxable income are a sufficient statistic to gauge the inefficiency introduced by taxes, but that there are advantages to collapsing the many dimensions of potential response (from hours worked to form of compensation to use of tax shelters) into this summary measure. Liebman, Luttmer, and Seif (2009) similarly find that both hours worked and retirement decisions are sensitive to changes in the social security tax rate (Liebman, Luttmer et al. 2009).

The Congressional Budget Office has produced estimates of the effect of rising health care spending on marginal tax rates and the distribution of taxes paid if increases in revenues come from income taxes (Orszag 2007). They show that, assuming public spending is valued by workers and health spending grows 1 percent faster than GDP, the increase in income taxes necessary to finance public health spending would reduce GDP by 1-6 percent if revenues were raised by maintaining the current tax structure without indexing or by 3-16 percent if revenues were raised by increasing marginal income tax rates across the board. They show the effects of such increases on the taxes paid by taxpayers at 4 different points in the income distribution, focusing on steady-state (rather than transition paths) and on the distribution of the tax burden (rather than changes in income distribution). While this study provides a key contribution in projecting future marginal tax rates under a scenario of increasing health care spending, it did not consider the longer-term impact of such taxes on GDP growth and the welfare of individual taxpayers.

III. Simulation Methods

The distributional implications of the tax-finance of almost half of health care spending depend crucially on both how quickly spending grows and the progressivity of the tax system. In this section, we sketch out the model used to characterize the impact of projected tax growth on overall economic activity and the distribution of the burden of paying for health spending under different stylized revenue systems and different scenarios about the growth in health care spending. (See the Appendix for technical details.)

We use a life cycle model where individuals get utility from consumption and leisure in each period they are alive. They live up to age 95, with the probability of survival depending on aggregate investment in health care. They work during the first part of their lives, generating income that they can consume but taking away from their leisure. Their wages grow at a steady rate each year. They retire exogenously in the last part of their lives, during which they live off of savings from their working years and Social Security benefits. They can borrow, but must repay the loans during their lifetimes. For the sake of simplicity, there is no bequest motive.

Their wage income is subject to payroll taxes and the interest on their savings is subject to interest income taxation. The tax schedule is progressive, with an exemption and with higher income groups paying higher marginal tax rates. Public health care financing involves transfers from high income households to low income households; indeed, the growth in per capita health care expenditures may within the decade make it impossible for lower income households to bear the full cost of their health care (Baicker and Levy, 2009).

Using data from 2007 taxpayers from the IRS, we categorize individuals on the basis of the marginal tax rate that they face under federal tax rules to create a stylized, simplified tax schedule. We create four separate groups The sizes of these groups were determined by the fraction of taxpayers facing marginal federal tax rates of 10 percent or less (low income), 15 percent (middle), 25 to 28 percent (averaged to 26 percent; high), and 33 or 35 percent (averaged to 34 percent; very high).¹ We also assume that each income group faces an additional constant 8 percent marginal tax rate from other taxes. For the lower income group, this increment reflects the phase-out of the Earned Income Tax Credit and Social Security and Medicare taxes. For higher income groups, the taxes reflect state- or city-level income taxes or corporate taxes on interest income. The marginal tax rates at the baseline (2010) are thus assumed to be 18, 23, 34, and 42 percent. The annual interest-income tax is assumed to be half of the marginal tax rate, reflecting the often preferential treatment of investments through capital gains and the use of tax-preferred accounts. The top panel of Table 1 summarizes the percentage of the population in each bracket, average taxes, and tax shares. These match closely to the actual 2007 data from the Internal Revenue Service Statistics of Income; see Appendix Table A for details.²

Table 1.

Tax Rates and Taxes Paid Under Different Scenarios

	Low	Middle	High	Very High
Baseline Simulation (2010 values) (2060 per-household GDP = $149,400)
Share of Households	.256	.468	.251	.025
Share of Income	.076	.336	.350	.236
Marginal Tax Rate	.180	.230	.340	.420
Average Tax Rate	.083	.143	.228	.347
Share of Taxes Paid	.030	.223	.369	.378
Scenario 1: 8% GDP Raised through Income Tax (2060 per-household GDP = $133,900)
Marginal Tax Rate	.218	.318	.550	.700
Average Tax Rate	.117	.206	.359	.590
Share of Taxes Paid	.030	.224	.382	.364
Increase in taxes paid (present value $1000)	7.4	29.6	104.7	900.8
Utility loss per dollar increase in taxes	1.18	1.70	2.79	2.65
Scenario 2: 8% GDP Raised through Payroll Tax (2060 per-household GDP = $141,700)
Marginal Tax Rate	.304	.354	.464	.544
Average Tax Rate	.171	.234	.327	.450
Share of Taxes Paid	.042	.254	.367	.337
Increase in taxes paid (present value $1000)	21.8	52.2	110.3	743.8
Utility loss per dollar increase in taxes	1.20	1.23	1.32	1.45
Scenario 3: 8% GDP Raised through Income Tax, Gini Constant (2060 per-household GDP = $140,900)
Marginal Tax Rate	.280	.340	.450	.528
Average Tax Rate	.171	.238	.329	.450
Share of Taxes Paid	.042	.256	.366	.336
Increase in taxes paid (present value $1000)	19.1	47.5	99.4	662.0
Utility loss per dollar increase in taxes	1.24	1.35	1.41	1.51
Scenario 4: 4% GDP Raised through Income Tax (2060 per-household GDP = $141,900)
Marginal Tax Rate	.198	.274	.4300	.562
Average Tax Rate	.100	173	.286	.464
Share of Taxes Paid	.029	.223	.370	.378
Increase in taxes paid (present value $1000)	3.5	14.8	49.8	559.2
Utility loss per dollar increase in taxes	1.17	1.66	2.27	1.89

Notes:

All values below the first baseline panel are values for 2060. The marginal tax rate shown is the tax rate on earned income. For the income tax, the tax on interest income is one-half the earned income tax rate. The progressive tax schedule has an $2400 exemption that rises with productivity growth (1.3% annually). The average tax rate is the total tax paid as a share of adjusted gross income for each group. Change in utility is measured as the change in the present discounted value of utility times the marginal utility of first-period consumption in each income group.

Government programs that are financed by these taxes include both health spending and other programs including Social Security. We hold constant these other programs, relative to underlying growth in the macroeconomy. We further assume productivity growth of 1.3 percent annually, estimated per capita income growth since 1993 for the bottom 99 percent of the economy (Saez, 2009).

We assume that a combination of technological progress and investment in health care produces increases in longevity of 1.8 years by 2060. While individuals value the increase in longevity that health spending provides, the key assumption is that their individual increase in longevity is not tied to the increase in what they pay – whether through taxes (as in this case) or in other financing mechanisms designed to pay for future Medicare benefits.

The baseline is the case in which tax revenues do not need to rise to achieve this gain. Implicitly, this would assume that all future medical expenditures are being funded by deficit spending (and where this spending does not have an adverse impact on U.S. bond credit ratings or other economic conditions), or that other government spending is reduced to pay for the extra health care expenditures, or that all future health gains are financed by reducing waste in U.S. health care.

A more realistic scenario is one in which increases in longevity come in part through increased federal expenditures on health care. We consider four scenarios. The first increases marginal income taxes enough to raise addition revenue of 8 percent of baseline GDP, an estimate consistent with CBO forecasts (Congressional Budget Office 2010) while maintaining the share of taxes paid by the top two income groups, the middle income group, and the bottom income group.³ It is worth noting that because taxes are rising faster than GDP, holding tax shares constant means that the share of income going to taxes for higher income groups will rise by more. The second scenario increases payroll taxes by a flat percentage across the board that is enough to raise the same revenue. The distributional effects of a flat payroll tax – a fixed percentage decrease in after-tax wages – therefore places a larger tax burden on low-income households.

The third scenario raises income tax rates, but rather than trying to keep tax shares constant over time, it instead adjusts marginal tax increases to keep the after-tax-income Gini coefficient constant. The final scenario assumes that gains in health care productivity are enough that income taxes need only raise additional revenue of 4 percent of GDP, using the same distribution across income groups as in the first case.

We assume a separable utility function with respect to leisure and consumption, with an elasticity of substitution of 1.0 (equivalent to a Cobb-Douglas labor supply curve). This means that hours of work are insensitive to a purely proportional tax that is used to finance health care improvements. However, labor supply does respond to changes in taxes in a progressive tax system, as does savings behavior. We further assume that each income group is subject to a single marginal tax rate (that is, they do not jump from one marginal tax bracket to another).

A fully-dynamic model would incorporate overlapping generations, each of which has been affected by its past economic conditions and each of which will ultimately be affected by future fiscal and tax policies. One disadvantage of these models is that individuals’ labor market choices are sensitive to the very large differences between current and future tax rates, making them very unstable when there is the prospect of dramatic increases in tax rates. (The instability arises because the prospect of higher marginal tax rates in the future leads to a large jump in labor supply today.)

Here however we adopt a simpler model to explore different tax structures (with potentially very high future tax rates) when public spending on health care spending rises. In this model people assume, myopically, that current tax rates are likely to persist (Fullerton, Shoven et al. 1983). We also do not model here the complex interaction between private insurance coverage and public programs. We calibrate this model using existing data on interest rates, wages and wage growth, and mortality at different ages; and estimates of discount rates, elasticities and health care productivity, described more fully in the Appendix.

IV. Simulation Results

This section presents results from the model to shed light on how aspects of financing health growth and the productivity of health care spending affect welfare costs and macroeconomic effects of rising health spending.

Lifecycle Consumption

We begin by showing the spending and savings patterns over a lifetime implied by the baseline model. Figure 2 shows average income (including non-wage income), consumption, and assets by age for the middle-income group. Income rises over time before a sharp reduction at retirement; income further declines as the household spends down their retirement wealth. Similarly, assets exhibit an increase until peaking at retirement, at which point they are depleted by age 95. Consumption exhibits a “hump” shape, with an increase early on because the aftertax rate of return exceeds the discount rate (plus the risk of dying early), but declines at later years as individuals account for the smaller probability of actually reaching age 90. While a more complex model accounts for additional effects of children and spouses on household spending patterns, these patterns of simulated consumption and wealth accumulation are broadly consistent with the empirical evidence.

Figure 2. Baseline Earnings, Consumption, and Wealth Accumulation (in $1,000).

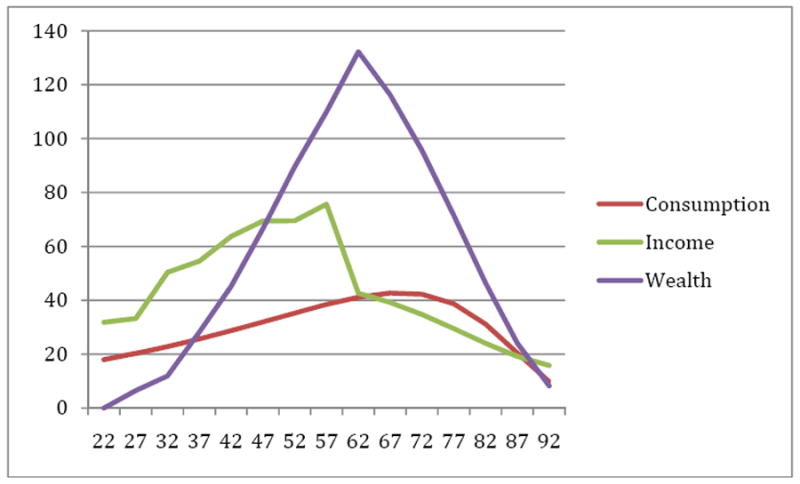
Note: Results of baseline simulation model described in text and Appendix.

Health

We assume a very simple health sector that absorbs all of the new revenue generated by these taxes and in turn “produces” additional health outcomes, measured here as rising survival rates. This approach thus considers both the costs of the taxes and the value of the spending financed by those taxes. For the purposes of this exercise, we assume a robust health care production function that yields estimates of health care productivity consistent with the trends estimated in Cutler et al. (2006). We begin with a survival curve for 2010 based on U.S. vital statistics from 2004), with slightly less than 100 percent of the population surviving to age 20 and successively less from that age forward. By proportionately reducing the conditional mortality rates at every age, survival improves by 2060, as shown in Figure 3, with a resulting increase in life expectancy from 79.0 to 80.8 years, or an increase of 1.8 years at a cost of approximately $140,000 per (undiscounted) life year in 2060.

Figure 3. Survival Curves for Age 20+; Assumed for 2010 and 2060.

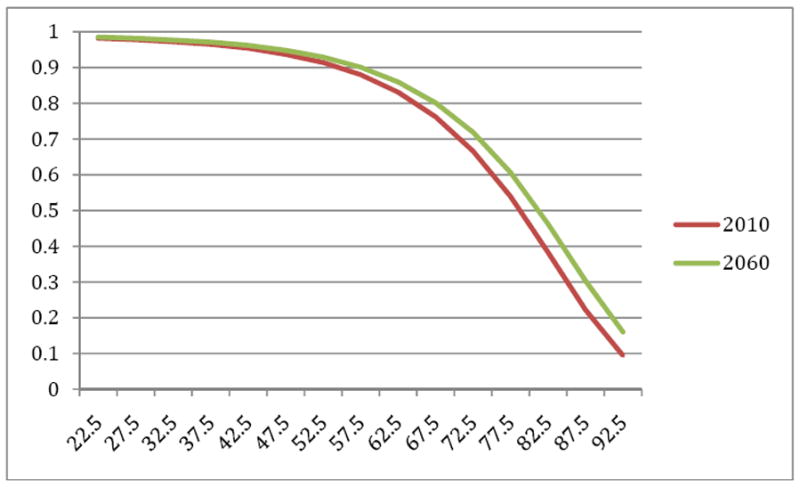
Notes: Results of simulation described in text and Appendix. Assumed 2010 survival curve is equal to the 2004 Vital Statistics survival curve; thus both may be understated. Life expectancy is simulated to rise from 79 years to 80.8 years.

Taxes, Economic Activity, and Well-being

Baseline Simulation

As noted above, the top panel of Table 1 summarizes the 2010 values of taxes paid and tax share. While the lowest income category comprises 25.6 percent of households, they pay 3 percent of combined tax payments. By contrast, the highest income category consists of 2.5 percent of households, but accounts for 38 percent of total taxes paid. Figure 4 shows projected growth in GDP per household, from $77,300 in 2010 to $149,400 in 2060, under the baseline assumption that there is an increase in longevity of 1.8 years, but no corresponding increase in tax rates. This rise in living standards is driven by the assumed 1.3 annual growth in wages. In this scenario, however, we have not specified how the revenue necessary for the increased projected longevity would be generated. We consider four scenarios below.

Figure 4. GDP Per Household (in thousands) Under Alternative Finance Scenarios.

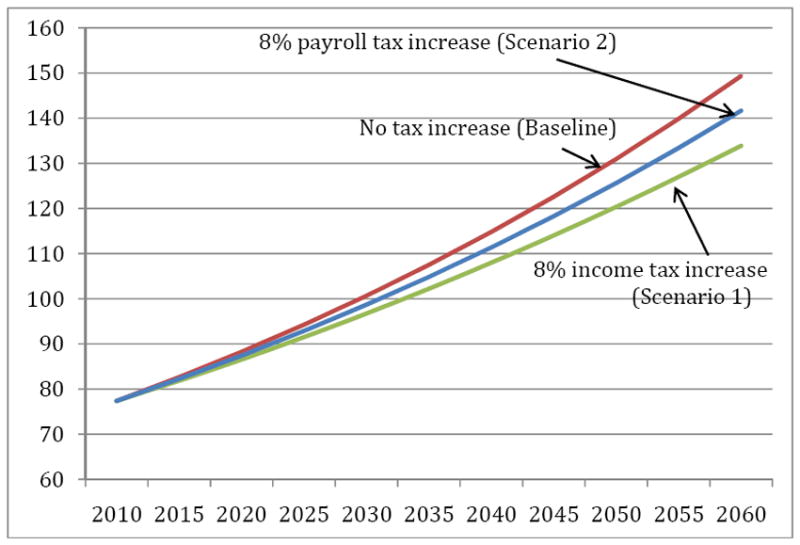
Notes: Results of simulation model. Wages are assumed to grow at a rate of 1.3% annually. See Appendix for details.

Scenario 1: Raising Income Tax Revenue by 8 percent of GDP, Keeping Tax Shares Constant

In this scenario, we increase rates such that the share of taxes paid by the top two brackets relative to the bottom two brackets remains the same. This also implies that the share of income devoted to taxes (or the average tax rate) for the top two groups increases by more than the share for the bottom two groups. Results are summarized in the second panel of Table 1, with the time-path of predicted marginal tax rates shown in Figure 5. Marginal tax rates are predicted to increase from 18 to 21.8 percent for the lowest income group, and from 42 to 70 percent for the highest income group. As noted above, the implicit interest income taxes for the highest income group are equal to half of the wage tax, for a maximum tax rate of 35 percent. (Results were not sensitive to specifying higher tax rates for interest income.) Figure 5 compares predicted GDP growth for this scenario with the baseline in which tax rates are unchanged over time. By 2060, per-household GDP is $133,900, or 11 percent below the baseline of $149,400.

Figure 5. Predicted Marginal Tax Rates by Income Group Under Income Tax Increases (Scenario 1), 2010-2060.

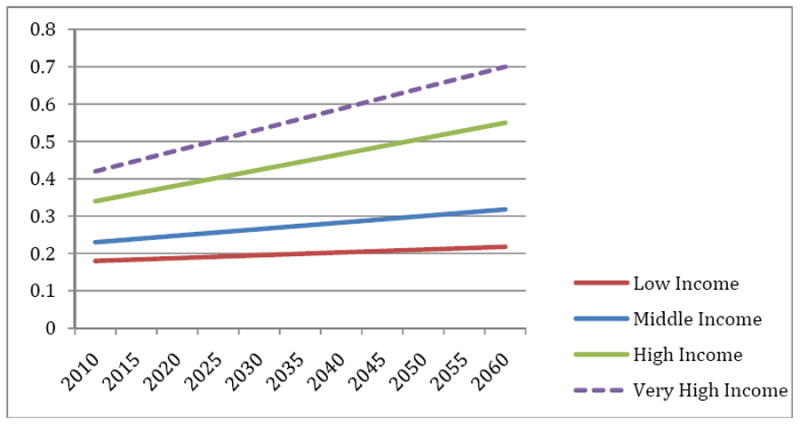
Notes: Results of simulation model. The marginal tax rates increase so as to raise 8% of (baseline) GDP in additional revenue for the funding of public health care spending. The share of taxes paid by the top two groups combined, and each of the lower two groups, is held constant.

Note that the per-household increase in the tax burden resulting from the higher costs for health care results in an average (present value) increase of $64,500. Table 1 also shows the dollar-equivalent loss in lifetime utility arising from the higher taxes, by income group, which ranges from $1.18 loss in utility per $1 of revenue collected for the lowest income group, to $2.79 loss in utility for every $1 in revenue for the high income group.⁴ Given the very high share of new tax revenue paid by higher income groups, the average loss in utility is roughly $2.48 per every dollar increase in tax revenue, yielding a net cost to society (or efficiency cost) of $1.48.

These estimated distortionary effects of taxes on GDP are somewhat larger than have been estimated using traditional measures, e.g. (Gahvari 2006), but reflect the impact of raising already high marginal tax rates, particularly in the highest income group where no revenue is raised at the margin. Estimates of the deadweight loss imposed in systems with much higher tax rates (such as Sweden) are substantially higher, ranging from 50 cents to more than $2 (Blomquist 1983; Rosen 1997; Hansson 2007). Saez, Slemrod, and Giertz review estimates of the elasticity of taxable income across several different countries, finding that those in higher tax brackets seem to be more sensitive generally to tax policy changes (Saez, Slemrod et al. 2009). In other words, over time we can expect an ever-larger distortionary effect arising not so much from raising taxes per se, but from the transfer of tax revenue from one group to another (Kaplow 2008).

Another way to see the extent of this distortion is to note that the annual increase in health care spending as a percentage of GDP – as distinct from the present value calculations above – is $12,000 per household in 2060. Raising that revenue through higher progressive taxes leads to a decline in 2060 per-household GDP equal to $15,500 ($149.4 thousand minus $133.9 thousand). In other words, for every one-dollar increase in the tax-financed health sector, there is a $2.29 decline in non-health-sector GDP – a one-dollar shift into a different sector, plus a $1.29 decline in overall GDP.

Scenario 2: Raising Tax Revenue by 8 percent of GDP with a Flat Increase in Payroll Tax

We next model a scenario in which necessary taxes are raised via a flat increase in the payroll tax (levied on earned income but not interest income). Because taxes are levied on a smaller base (excluding interest income), the increase in the labor tax rate for each bracket is 12.4 percentage points to increase total tax revenues by 8 percent of GDP. These results are also presented in Figure 4 and Table 1. As the columns in Table 1 show, this results in a much less progressive distribution of the burden of financing rising health spending, with an average tax burden in 2060 of 17.1 percent of income instead of 11.7 percent for the lowest income group. This approach also illustrates the tradeoff between equity and efficiency. While the burden of taxes are shifted in part to lower income groups, growth in marginal tax rates for the highest income group is to 54.4 percent instead of 70.0 percent as in the first scenario. For the payroll tax – and, we expect, a value-added tax which would exert similar effects – the average excess burden is much lower, $0.41 per one dollar of revenue raised. And as shown in Figure 5, the decrement to GDP is considerably smaller, with a decline of 5.2 percent. However, the tax change more than doubles the average tax rate for the lowest income group.

Scenario 3: Raising Income Tax Revenue by 8 percent of GDP, Holding the Gini Coefficient Constant

A third case would hold constant the after-tax income distribution across the four income groups. We measure this distribution using the Gini coefficient, a standard measure of inequality. This is in fact less progressive than holding the share of taxes paid by the bottom two and top two income groups constant because, as noted above, when taxes rise faster than income, holding tax shares constant means that the share of income devoted to taxes rises more for high income groups than low ones. Holding the Gini coefficient constant at 0.48 yields a top marginal tax rate of 52.8 percent, comparable to the tax structure in Scenario 2 (Table 1, Panel 4), and therefore has similar effects as the payroll tax modeled there.

Scenario 4: Raising Income Tax Revenue by 4 percent of GDP, Keeping Tax Shares Constant

A fourth case is the possibility that increases in health care productivity allow the same increase in longevity to be financed by an increase in revenues of only 4 percent of GDP, rather than the 8 percent in Scenarios 1-3. This case, Scenario 4 in the bottom panel of Table 1, illustrates the large potential gains – beyond simply the money saved – in effecting cost savings that do not adversely affect health outcomes. Under this scenario, the top tax bracket of 56.2 percent is more similar to Scenarios 2 and 3 than it is to Scenario 1 (which uses the same tax structure but raises twice the revenue), with a resulting loss of 5.1 percent of GDP relative to baseline. When the 4 percent increase in revenue is generated by a payroll tax (as in Scenario 2) rather than the constant tax-share income tax here (as in Scenario 1), simulated GDP is just 2.7 percent below the baseline in 2060.

Together, these scenarios illustrate the trade-off between progressivity of the tax structure and the efficiency with which revenues are raised. For the same loss in economic activity, twice the revenue can be gained from the stylized less progressive payroll tax than the more progressive one. These simulations also illustrate the magnitude of potential gains from scaling back on waste in health care. It’s not just the health care dollar saved – it’s also avoiding distortionary taxes that would otherwise reduce economic activity by an additional $1.29. Finally, it is important to note that even in the most distortionary tax system, overall utility is still higher because the highest-income individuals – those subject to the greatest tax distortions – also place the greatest dollar value on extended lifespan.

The results are sensitive to assumptions made about a variety of parameters. First, varying γ has a large impact on GDP growth estimates. If γ = 2, there is a backward-bending supply curve, so that GDP is little affected; the consequent rise in longevity if anything leads to even greater lifetime labor supply. Conversely, when γ =.5 and labor supply is far more sensitive to tax rates, GDP is predicted to decline by 20 percent relative to the benchmark case, with correspondingly larger welfare effects.

We did not model the effects of using other revenue sources, such as property taxes or sales taxes. Nor did the simulations explicitly distinguish between the income tax base and GDP, which means that future tax distortions could be even higher than we estimate. Based on aggregate data from the IRS and the Bureau of Economic Analysis, adjusted gross income (AGI) is roughly 60 percent of GDP. Thus if the federal income tax were the sole source of the rise in federal spending for Medicare and Medicaid, an increase of 8/.6 or 13 percentage points would be necessary to fund the assumed additional health care spending, thus placing more stress on the current tax system. Simulations imposing this larger proportional revenue gain lead to marginal efficiency cost measures of $1.72 per dollar of revenue collected, and a nearly 14 percent decline in GDP relative to trend. Applying the augmented higher average tax burden using the payroll tax implies a 9 percent reduction in GDP and marginal tax rates ranging from 40 to 62 percent depending on the income group. These calculations point to the importance of funding sources such as sales or value-added tax that are levied on a broader base.

V. Empirical Evidence on the Link Between Taxes and Health Expenditures

Governments making coverage and budgetary decisions about expanding health care should in theory consider the marginal costs of redistributing resources to the health care sector (Getzen 1992). To test this hypothesis, we consider a simple empirical comparison of tax-to-GDP ratios and the subsequent rise in health care spending as a percentage of GDP. Using data from the OECD, we evaluate the association between government revenues as a share of GDP in 1979 and the increase in health care spending as a share of GDP from 1980 to 2008 (or the most recent year available).

As shown in Figure 6, there is a wide range in the extent to which health care spending as a percentage of GDP has increased since 1980.⁵ The U.S. leads the way, with a growth of 7 percentage points, while in Sweden, Denmark, and Ireland the share grew by less than one percentage point. Tax revenues as a share of GDP in 1979 are shown on the horizontal axis. Here, too, there is substantial variation, with Sweden, Belgium, Denmark, Norway, the Netherlands, and Luxembourg above 50 percent, while Australia, Turkey, Japan, and Spain were under 30 percent.

Figure 6.

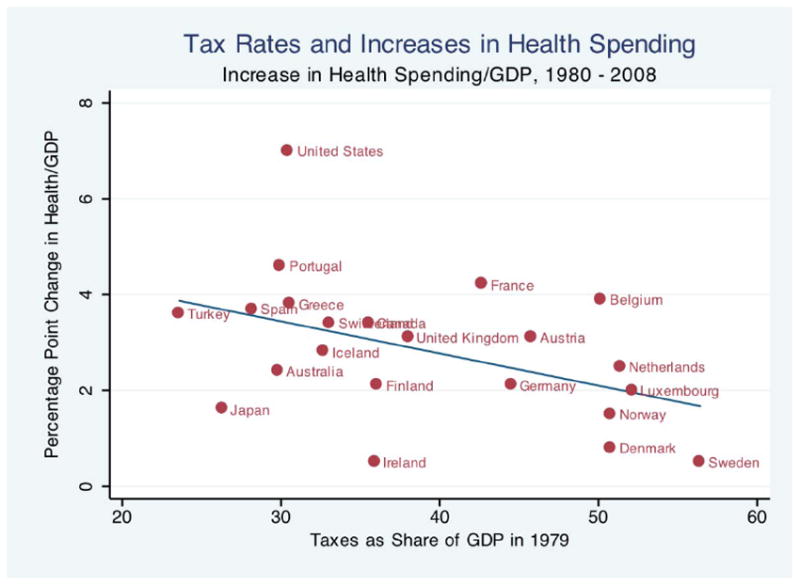
Notes:

Correlation coefficient = -0.44, regression coefficient = -0.067, p-value = .039. Health growth rates shown for 1980-2007 for Australia, Denmark, Greece, Japan, and Turkey; and for 1980-2006 for Luxembourg and Portugal.

Sources:

Health as a share of GDP from OECD Health Data, June 2010 (OECD 2010); Revenues as a share of GDP from OECD Report (Oxley and Martin 1991)

The growth of health spending as a share of GDP over the next decades is negatively and significantly associated with this initial level of tax effort. The correlation coefficient is -0.44 (p-value = 0.04). The regression coefficient of -0.07 suggests that in countries where revenues as a share of GDP were 10 percentage points higher in 1979, health care spending as a share of GDP grew by 0.7 percentage points less in the next 30 years. This association is consistent with the hypothesis that high tax rates limit the further growth of public contributions to health spending because of the much larger economic costs (as shown in the simulation model above) and because of political pressures against high tax rates, a result also found in a cross-country study of health care expenditure growth (Getzen 1992).

VI. Conclusions

With almost half of health expenditures publicly financed and the prospect of further government subsidization of health insurance under health care reform, the rising burden of health care spending during the next half-century will most likely necessitate large increases in tax rates. In this paper, we have estimated the efficiency costs of such tax increases and their effects on economic activity. Our results suggest a large attenuation in economic growth, with estimated GDP in 2060 11 percent below the baseline estimates in the absence of the distortionary impact of the tax-financing of rising health care costs. This efficiency cost is lower when the tax revenue is raised less progressively, or when it takes less revenue to generate the same health gains.

Most models of health care spending growth, such as those of CBO and the CMS Office of the Actuary, assume that there must be a break in current trends, as the current growth of health care spending in excess of GDP cannot continue unabated. This is consistent with the Deficit Commission’s call for a similar slowdown in spending growth; otherwise, the deficit could be tamed only through an unpalatably large increase in taxes. However, it is not clear what policy or condition would change to effect that slowdown. Our empirical analysis across countries suggests that strains on the revenue-raising system may exert a natural brake on health care spending, and may thus be a key (albeit inefficient) mechanism for constraining overall health care spending growth.

There are several limitations to this analysis. First, a stylized model of labor supply and a simple linear approximation to a progressive tax may not do justice to the very complex U.S. tax code. Second, the model considers sequenced equilibrium, and thus will not capture the potentially dynamic reactions of individuals who may choose to work more today if they foresee future tax hikes. Third, we have not explicitly considered non-tax finance reforms and mechanisms to reduce demand. While there are a variety of proposals involving demand-side mechanisms to reduce spending, tax-financed public insurance programs (like Medicare and Medicaid) or public subsidization of private plans (such as vouchers or tax credits) are likely to continue to play a key role in financing health insurance and health care. And finally, the model does not simultaneously determine the optimal level and growth rate of health care spending, as do Hall and Jones (2007). Complementary analysis would develop such a model with dynamic feedback between GDP growth and publicly financed health care spending, and with endogenous choice of government and privately provided health insurance. Still, this paper shows that, absent the success of health reform in substantially slowing spending growth, the steeply rising efficiency cost of tax distortions (and political opposition to further tax hikes) may ultimately temper health care spending growth in the coming decades.

Technical Appendix: The Simulation Model

We use a life cycle model with leisure, consumption, and saving, as well as uncertain lifetimes. The tax distortions arise from income taxation in the form of a payroll tax on wages and an interest income tax. For simplicity, there are five-year time periods, so that people live from age 20-24 (i = 1) to at most age 90-94 (i = 15). Lifetime utility is:

$$U_k=\sum _{i=1}^D\left[\frac{S_{\mathit{it}}}{{(1+\delta )}^{i-1}}\right]U(C_{\mathit{it}},{\ell }_{\mathit{it}})$$ (1)

Utility in each period is a function of leisure ℓ and consumption C, discounted at the rate δ, and weighted by the expected value of survival S_it. To ensure stability in the model we specify a separable utility function for consumption and leisure with a intertemporal and intratemporal elasticity of substitution parameter 1/γ.

$$\begin{array}{lll}U(C_{\mathit{it}},{\ell }_{\mathit{it}})& =& B+\left[\frac{C_{\mathit{it}}^{1-\gamma }+\alpha {\ell }_{\mathit{it}}^{1-\gamma }}{1-\gamma }\right]\mathit{if}\gamma \ne 1\\ & =& B+\ln (C_{\mathit{it}})+\alpha \ln ({\ell }_{\mathit{it}})\mathit{if}\gamma =1\end{array}$$ (2)

We have assumed away retirement decisions, but instead assume exogenous retirement at age R, which corresponds to leisure comprising all of the time endowment (that is, (θ − 1). The presence of the term B > 0 ensures that utility is everywhere positive even when γ > 1, with the second term on the right-hand side of Equation (2) everywhere negative. (Utility arising from being retired simplifies to α/(1-γ), but we write it in its expanded version to show that the utility function is common across the life-cycle.) We set B to ensure that on average, the discounted value of a life is equal to roughly 5 million dollars. Except for measuring the dollar benefit of additional lifespan, the value of B does not affect labor supply or saving behavior

Structure of the dynamic model

The standard approach for using life cycle models with dynamic transition paths is to construct an overlapping-generations model, so that different cohorts are alive at a point in time, each of which has been affected by its past economic shocks (think of the depression generation) and each of which will ultimately be affected by future fiscal and tax policies. One disadvantage of these models is that they are forward-looking with regard to policy variables, so that people who are today age 20 should – in theory – anticipate the very high tax rates necessary to pay for health care in 2060. Given the logic of the dynamic model, younger workers will step up labor supply today to avoid the onerous future taxes. (Of course, if taxes on saving rise, they might also go on a spending spree today to avoid the future taxes.)

While we have explored this overlapping generations approach, here we adopt a simpler model of “sequenced” steady state equilibria, where in the initial benchmark year (2010), individuals make plans as if those 2010 tax rates were going to persist into the future. Similarly, as tax rates rise, we reevaluate steady-state consumption, work effort, savings, and tax revenue under the assumption that the 2020 tax regime will persist not just in 2020, but also going forward. This assumption is similar to “myopic” sequenced equilbria, as in Fullerton, Shoven, et al. (1983).

We assume a productivity growth rate in wages of 1.3 percent. This is a more conservative estimate than the 2.3 percent growth in Hall and Jones (2007), and captures average growth rates among the bottom 99^th percentile of the income distribution between 1993-2008 (Saez, 2009).

Different income groups

There are four different income groups, categorized according to the marginal tax rates they face: 10 percent or less, 15 percent, 25 to 28 percent, and 33 percent or more. The very highest income group as shown in the Statistics of Income showed adjusted gross income levels roughly 14 times the middle-income group, but they comprised only 2.5% of the household population.

The individual’s budget constraint

The present value of earnings and transfers constrain total the present value of consumption:

$$\sum _{i=1}^D[{\mathrm{\Gamma }}_{\mathit{ijt}}+{\mu }_{\mathit{ijt}}+w_{\mathit{ijt}}(1-{\tau }_{\mathit{wjt}})(1-{\mathrm{l}}_{\mathit{ijt}})]R_{\mathit{ijt}}\ge \sum _{i=1}^D{C}_{\mathit{ijt}}{R}_{\mathit{ijt}}$$ (3)

where the discount rate R_ijt = (1+ r(1 − τ_rjt))¹⁻ⁱ, j represents the income group, and w_ijt is the full hourly compensation, while (1-ℓ_ijt) is the fraction of time spent working. We allow for a positive marginal tax rate on labor income, τ_wjt that varies across income groups, an interest income tax rate τ_rt and a credit (or exemption) μ_it to reflect the progressivity of the tax system. The interest rate is assumed to be constant, as would be the case in an open-economy model.

The interest income tax τ_r is assumed to be half of the wage tax τ_w, reflecting the variety of tax benefits available from 401k and IRA accounts, capital gains taxes, and stepped-up basis at death for the revaluation of assets. Social Security income, equal to Γ_it, is zero for ages less than 65 but equal to empirical measures of Social Security payments for ages 65 and up. By income group, Social Security payments are 75%, 100%, 150% 150% of the average $14,000 annual payment, and they are assumed to grow at the rate of productivity growth across generations. Income interest is taxed fully (at their original tax rate) while retired;. given their receipt of social security, retirees do not receive an exemption amount μ_ijt. Finally, there are no explicit borrowing constraints in the model.

It is also useful to define assets:

$$A_{(i+)1\mathit{jt}}=A_{\mathit{ijt}}(1+r(1-{\tau }_{\mathit{rjt}}))+[Y_{\mathit{ijt}}-T_{\mathit{ijt}}-C_{\mathit{ijt}}]$$ (4)

where T is the total taxes paid in that year (defined below), and we impose a lifecycle model by setting initial assets equal to zero. Hence there are no transfers to subsequent generations when people die with existing balances in their savings accounts.

The government budget constraint

Taxes paid at each age and for each year are written

$$T_{\mathit{it}}=w_{\mathit{it}}(1-{\mathrm{l}}_{\mathit{it}}){\tau }_{\mathit{wt}}-{\mu }_{\mathit{it}}+{\tau }_{\mathit{rt}}r{A}_{\mathit{it}}$$ (5)

We measure marginal efficiency costs in the following way. The numerator is ΔU divided by the marginal utility of income, to give the “money-metric” change in utility, evaluated at the marginal utility consistent with 2060 consumption absent tax hikes. The denominator is the present value of taxes on a lifetime basis (weighted by the probability of survival). While this comparison is not unique – one could also evaluate initial utility at the after-tax level rather than the pre-tax level – this provides a convenient approach to comparing the relative efficiency costs of different tax instruments.

Health care and health

Rather than developing an explicit health care sector, we instead consider simulations with gradually rising survival rates over time. This is implemented by decreasing the period-specific mortality rate by a constant proportion. The conditional probability of dying at age i in year t is:

$$m_{\mathit{it}}=\frac{S_{\mathit{it}-1}-S_{\mathit{it}}}{S_{\mathit{it}-1}}$$ (6)

Technological improvement in health care is assumed to take the form m_it = m_i1/(1+g_s)^t-1. Assuming an annual improvement of 0.3 percent per annum yields an increase in life expectancy of 1.8 years, a number that, coupled with an assumed increase of 8 percent of GDP in government-based health care spending, and an equivalent increase of 8 percent of GDP in private health care spending, yields an average cost of just under $150,000 per life-year in 2060. (Note that this value discounts spending but not life expectancy, and thus the simulated effects can be compared directly to the estimates in Cutler, Rosen, et al., 2006.)

What the model is missing

As noted above, we do not implement a full-blown overlapping-generations model, nor do we allow for changes in asset accumulation to affect interest rates or gross wages. (We thereby assume an open economy model.) The U.S. is a combination of both private and public health insurance, and that mix might be expected to evolve over time. However, we do not model the more complex interaction between private insurance coverage and potential crowding out effects of public programs as private premiums continue to rise. Finally, we do not include uncertainty in the model, either about income, uninsured medical expenses, or the direction of future tax policy in the U.S.

Calibrating the model

The model is calibrated using 15 five-year age groups from age 20-25 to age 90-95. We set the real (after-inflation) annualized gross interest rate r equal to .04, (Council of Economic Advisers 2008) and convert all annualized growth rates and parameters into their equivalent 5-year counterparts. Although it is difficult to observe, we choose a value of δ = .01, which, coupled with the influence of uncertain lifespan, ensures an empirically plausible time-path of consumption. Consistent with other simulation studies, we assume γ = 1 (or intertemporal elasticity of substitution of 1), primarily because we want to get the labor supply elasticity right. Because the intratemporal and intertemporal elasticities of substitution are assumed equal in this model, we are also assuming an intertemporal elasticity equal to 1, which is at the low end of the values of gamma (De Nardi, French et al. 2006). Using larger labor supply elasticities would lead to even larger incentive effects in this model.

Age-specific earnings data are drawn from Census data on earnings and Bureau of Labor Statistics data on hours – with the “full wage” calculated as the hourly rate of compensation times the number of full hours available for work (Bureau of Labor Statistics 2008; Bureau of the Census 2008). Benchmark survival data S_a1 at five year intervals comes from Vital Statistics data (National Center for Health Statistics 2008; U.S. Census Bureau 2008). Tax rates for each income group are described in the text. The virtual “intercept” of the linear tax rate is determined by integrating through to the minimum inflection point in their tax schedule – that is, where the marginal tax rate changes, and then backing out the implicit intercept term consistent with the marginal tax rate. Thus changes in marginal tax rates at lower income brackets will have inframarginal effects on the taxes paid by higher-income taxpayers.

The inflection points were determined to best match the parameters of the model – such as tax shares and average taxes paid by income group. (They were $25,000 between income groups one and two, $75,000 between groups 2 and 3, and $300,000 between 3 and 4.) These are different from actual inflection points because they also reflect differences across income groups in deductions and credits. Table A show the match between actual income and tax parameters from the 2007 Statistics of Income (www.irs.gov/pub/irs-soi/07in01tr.xls). Note that both marginal and average tax rates have been increased by 8 percentage points to reflect state, local, corporate, and Social Security and Medicare taxes, as discussed in the text.

Table A.

Baseline Parameters of the Simulation Model

	Low	Middle	High	Very High
Share of Taxable Income (Actual)	.070	.325	.357	.248
Share of Taxable Income (Simulated)	.076	.336	.350	.238
Average Tax Rate (Actual)	.093	.150	.216	.318
Average Tax Rate (Simulated)	.083	.143	.228	.347
Share of Taxes Paid (Actual)	.031	.231	.365	.373
Share of Taxes Paid (Simulated)	.030	.223	.369	.378

Note: Average household adjusted gross income (AGI) (actual) is $77,089 in 2007. The simulated average income is $77,385.