Hydraulic and mechanical properties of young Norway spruce clones related to growth and wood structure

Summary

Stem segments of eight five-year-old Norway spruce (Picea abies (L.) Karst.) clones differing in growth characteristics were tested for maximum specific hydraulic conductivity (k_s100), vulnerability to cavitation and behavior under mechanical stress. The vulnerability of the clones to cavitation was assessed by measuring the applied air pressure required to cause 12 and 50% loss of conductivity (Ψ₁₂, Ψ₅₀) and the percent loss of conductivity at 4 MPa applied air pressure (PLC_4MPa). The bending strength and stiffness and the axial compression strength and stiffness of the same stem segments were measured to characterize wood mechanical properties. Growth ring width, wood density, latewood percentage, lumen diameter, cell wall thickness, tracheid length and pit dimensions of earlywood cells, spiral grain and microfibril angles were examined to identify structure–function relationships. High k_s100 was strongly and positively related to spiral grain angle, which corresponded positively to tracheid length and pit dimensions. Spiral grain may reduce flow resistance of the bordered pits of the first earlywood tracheids, which are characterized by rounded tips and an equal distribution of pits along the entire length. Wood density was unrelated to hydraulic vulnerability parameters. Traits associated with higher hydraulic vulnerability were long tracheids, high latewood percentage and thick earlywood cell walls. The positive relationship between earlywood cell wall thickness and vulnerability to cavitation suggest that air seeding through the margo of bordered pits may occur in earlywood. There was a positive phenotypic and genotypic relationship between k_s100 and PLC_4MPa, and both parameters were positively related to tree growth rate. Variability in mechanical properties depended mostly on wood density, but also on the amount of compression wood. Accordingly, hydraulic conductivity and mechanical strength or stiffness showed no tradeoff.

Introduction

Wood serves several functions required for tree survival, such as water, carbon and nutrient transport, mechanical support and storage of water and photosynthates. The optimum wood structure likely differs for each of these functions (Baas 1983, Gartner 2001). Several recent studies dealing either with mechanical (Färber et al. 2001, Müller et al. 2003, Gindl et al. 2004, Burgert et al. 2005) or hydraulic properties (Mayr et al. 2003, Mayr and Cochard 2003, Mayr et al. 2005, Rosner et al. 2006) have increased knowledge of structure–function relationships in Norway spruce (Picea abies (L.) Karst.). No study, however, has focused on the relationships between the hydraulic and mechanical properties of spruce wood. We studied structure–function relationships in young Norway spruce clones with different growth characteristics, thus allowing assessment of the genetic determination of biological wood functions.

Juvenile trunk wood of young Norway spruce stems seems to be designed for low hydraulic vulnerability, as indicated by its high density, which guarantees a high degree of protection against cavitation and implosion (Gartner 1995, Hacke and Sperry 2001, Hacke et al. 2001, 2004). Branches or juvenile wood from the upper canopy are more resistant to cavitation than mature trunk wood (Rosner 2004, Rosner et al. 2006). High hydraulic vulnerability is associated with high hydraulic conductivity within (Gartner 1995, Kavanagh et al. 1999, Domec and Gartner 2002a, Rosner et al. 2006) and across species (Piñol and Sala 2000, Maherali et al. 2004).

Studies in Norway spruce shoots and branches suggest, however, that a wood-density-based tradeoff can be masked by mechanical demands (Mayr and Cochard 2003, Mayr et al. 2003). Keeping the stem upright by formation of compression wood is an important biomechanical task in young trees (Lindström et al. 1998); therefore, juvenile trunk wood contains variable amounts of compression wood (Zobel and Sprague 1998). Although compression wood is dense, it is more vulnerable to cavitation than opposite wood because of the structural characteristics of its bordered pits. The lower hydraulic conductivity of compression wood is compensated for by the formation of light bands (Mayr et al. 2005). If the high density of normal young trunk wood is compensated for by similar highly conductive structures, there will be a density-based tradeoff between hydraulic conductivity and mechanical strength at the level of the tracheid (Hacke et al. 2001, Hacke and Sperry 2001), but not the whole stem.

Structural compromises between wood hydraulic and mechanical functions might complicate the search for structure–function relationships. Dense wood is costly, but high biomass allocation to foliage demands an increase in mechanical support of the crown (compression) and height growth increases the stem bending moment that must be resisted under dynamic wind loading (Mencuccini et al. 1997, Mattheck 1998, Spatz and Bruechert 2000). Mechanical support can be enhanced by increasing whole-wood density or by varying latewood percentage, tracheid length, microfibril angles, arrangement of the cell wall layers or cell wall chemistry (Gil 2001, Mencuccini et al. 1997, Ezquerra and Gindl 2001, Jagels et al. 2003, Jagels and Visscher 2006).

Dense wood reduces the risk of drought-induced tracheid implosion (Hacke et al. 2001, Hacke and Sperry 2001) in young trees which have a shallow root system, and which are, therefore, prone to experience low tissue water potentials. Nevertheless, stems also have to be flexible to cope with heavy wind and snow loads. Flexibility is achieved by high microfibril angles (Meylan and Probine 1969, Lindström et al. 1998, Lichtenegger et al. 1999). In juvenile spruce wood, microfibril angles are reportedly similar in normal and compression wood (Gorišek and Torelli 1999), which might obscure the positive relationship between cavitation resistance and mechanical strength.

Another strategy to cope with heavy snow loads and deflection by strong winds is spiral grain, which reaches its highest values in the first annual rings (Danborg 1994, Eklund et al. 2003, Harris 1989, Eklund and Säll 2000, Hannrup et al. 2002). Under bending and torsional strains, spiral grain improves the bending strength of stems when directed in the same direction as the torque, whereas in the other direction the bending strength is reduced (Skatter and Kucera 1997). Other studies have underlined the physiological importance of spiral grain for the efficient distribution of sap throughout the crown (Vité and Rudinsky 1959, Kubler 1991).

In this study, we searched for structural traits in the trunk wood of young Norway spruce trees that might be strongly related to specific conductivity at full saturation, vulnerability to cavitation, and strength and stiffness under compression and bending strains. Structure–function relationships are used to interpret possible tradeoffs between hydraulic and mechanical properties in young spruce trunk wood. We hypothesize that a wood-density-based tradeoff between hydraulic and mechanical wood functions is obscured in juvenile wood of young spruce trees by structural compromises. The expected complex structure–function relationships within young spruce stems required consideration of a wide range of wood structural parameters. We therefore assessed wood structural aspects at the levels of cell walls, pits, tracheids and tissues. By studying Norway spruce clones, we were able to predict survival prospects based on broad-sense heritabilities and genotypic correlations of wood functions and structural traits.

Materials and methods

Plant material

The clonal material originated from Forstamt Schongau (Germany) and was raised in the forest nursery Pflanzgarten Laufen (Bavaria, Germany). Clones were raised outdoors under similar environmental conditions. Clones were planted separately in blocks of 1 × 3 m within an area of 35 m². In early spring 2003, randomly selected 5-year-old ramets of the eight clones were planted in pots (30-cm diameter). In May 2003, the pots were transported to Vienna (Austria) and placed outdoors in the botanical garden of the University of Natural Resources and Applied Life Sciences (BOKU, Vienna). The trees remained there untill they were sequentially harvested during summer 2003. Only healthy undamaged trees were investigated. The final sample set comprised eight clones with five to nine ramets per clone.

Hydraulic traits

Trees were harvested in the early morning. Segments of 3-year-old stems were debarked in the laboratory and 13-cm-long wood samples were recut under water with a razor blade to a length of 11 cm and soaked in distilled water under vacuum for at least 48 h to refill embolized tracheids (Domec and Gartner 2001).

Assessed hydraulic parameters were specific hydraulic conductivity at full saturation (k_s100), the negative of the applied air pressure that caused 12% (Ψ₁₂) and 50% (Ψ₅₀) loss of conductivity and the percent loss of conductivity induced by 4 MPa applied air pressure (PLC_4MPa). According to the air seeding hypothesis, the positive pressure needed to blow air through the largest water-filled pores should be the same in magnitude but opposite in sign to the xylem tension initiating drought-induced embolism (Tyree and Sperry 1989). Parameter Ψ₁₂ is termed the air entry point and is an estimate of the xylem tension when the resistance to air entry of the pit membranes within the conduits is overcome and cavitation and embolism begin (Domec and Gartner 2001).

Specific hydraulic conductivity (k_s; m² s⁻¹ MPa⁻¹) is the permeability of a wood segment following Darcy’s Law and is defined as:

$$k_{\mathrm{s}}=Ql{A_{\mathrm{s}}}^{-1}\Delta P^{-1}$$ (1)

where Q is volume flow rate (m³ s⁻¹), l is length of the segment (m), A_s is sapwood cross-sectional area (m²) and ΔP is pressure difference between the ends of the segment (MPa). Calculated conductivity data were corrected to 20 °C for fluid viscosity. Conductivity measurements were carried out under a hydraulic pressure head of 0.008 MPa with distilled, filtered (0.22 μm) and degassed water containing 0.005% (v/v) Micropur (Katadyn Produkte AG, Wallisellen, Switzerland) to prevent microbial growth. Vulnerability curves (VCs) were constructed by plotting the percent loss of conductivity (PLC; %) versus the pressure in a double-ended pressure chamber (PMS Instruments, Corvallis, OR) (Cochard 1992b, Domec and Gartner 2001). The measuring procedure is described by Rosner et al. (2006). Hydraulic VCs were fitted by the least square method based on a sigmoidal function (Pammenter and Vander Willigen 1998):

$$\mathrm{PLC}=\frac{100}{1+\exp \left(a\right(-\mathrm{OP}-b\left)\right)}$$ (2)

where a is the slope of the linear part of the curve, b is the pressure at which 50 PLC occurred (Ψ₅₀) and OP is the corresponding applied air pressure. Equation 2 was also used to calculate Ψ₁₂ (Domec and Gartner 2001).

The loss of conductivity induced by identical air pressure application on fully saturated samples (PLC_4MPa) is a directly assessed (i.e., not a modeled) vulnerability parameter. Although we used only vulnerability curves (Equation 2) with r² > 0.95 for estimating Ψ₁₂ and Ψ₅₀, the curves rarely passed through all the data points directly (Bouffier et al. 2003). We chose the PLC induced by 4 MPa because differences among clones were most apparent at this pressure and PLC values covered the physiologically interesting range between 12% (Ψ₁₂) and 50% (Ψ₅₀).

Mechanical traits

Assessed mechanical traits were bending strength (σ_b) and bending stiffness (MOE, modulus of elasticity) as well as compression strength (σ_a) and compression stiffness in the axial direction (E, Young’s modulus). Stem sections (10-cm-long, 6.2 ± 0.2 mm diameter, cambial age = 3 years) assessed for hydraulic characteristics were resaturated in distilled water under vacuum, and mechanical tests for σ_b and MOE were performed. Water was expressed in the double-ended pressure chamber until around 95 PLC, indicating that the fiber saturation point (Berry and Roderick 2005) had not been reached. Generally, no changes in mechanical properties (absolute values) at water contents above the fiber saturation point are observed (Kollmann 1982). We suppose, therefore, that absolute values of σ_b and MOE of the resaturated samples were similar to those of the trunk wood in living trees.

We tested σ_a and E on small wood cylinders, 7 mm in height, sawn from each end of the bending test samples. Surface roughness of the small wood cylinders was minimized by planing the transverse cut surfaces on a sliding microtome (Wolcott et al. 1989) and equilibrium water content of 12% was achieved by storing the samples in a standard climate of 20 °C and 65% RH. Compression test samples were dried to 12% water content because determination of the amount of compression wood (CW, see below in the text) gave clearer results for dried wood and its measurement had to be done before compression testing. Behavior under compression stress in dried wood is related to the behavior in the fully saturated state (Kollmann 1982, Gindl 2001). We assumed that σ_a and E measured on dried wood are reliable relative parameters to assess the mechanical behavior of wood under compression stress in living trees.

Mechanical testing was performed with a Zwick/Roell Z100 SW5A universal testing machine (Ulm, Germany) at ambient temperature (~22 °C). Crosshead speeds of 1 and 3 mm min⁻¹ were chosen for the compression and bending tests, respectively. The span width for the 3-point bending tests was 7 cm. Samples were loaded to the point of fracture and unloaded after a force drop of 10% of the maximum force (F_max). We calculated σ_b (Pa) as the maximum bending moment divided by the section modulus of the samples. To calculate σ_a (Pa), F_max (N) was divided by the area of the cross section of the samples (m²). Parameters MOE and E (Pa) were derived from the stress–strain curves between 20 and 40% and between 10 and 40% of F_max, respectively.

Growth traits

Assessed growth traits were the total aboveground dry biomass (BM), tree height (H), stem diameter at the base of the trunk (D) and ring width (RW). After harvesting and preparation of the stem segments for hydraulic testing (3-year-old stem segments, 13-cm-long), the aboveground dry biomass of the remaining plant material was obtained by drying at 103 °C to constant mass. Basic density (mass per volume in the green state) obtained on the bending test samples was used to calculate the oven-dry biomass of the 3-year-old stem segments on which the hydraulic and mechanical tests were performed. Dry biomass was obtained from the sum of the weighed and the calculated (3-year-old stem segments) aboveground biomass. Ring width (RW) of the 2nd and 3rd annual rings was measured on transverse sections (25-μm thick) cut on a sliding microtome (preparation see below).

Wood density

Wood density (dry mass per volume) was measured on the compression test samples after drying at 103 °C to constant mass.

Wood structural traits

Structural traits comprised characteristics of the first earlywood cells, such as the lumen diameter (L_EW), thickness of the double cell walls (W_EW), tracheid length (TL_EW), dimensions and frequencies of bordered pits, and microfibril angle (MFA_EW), as well as the microfibril angle of latewood cells (MFA_LW), latewood percentage (LWP), percentage of compression wood (CP) and spiral grain angle (SG).

Lumen diameters and W_EW were obtained for the first 5–7 earlywood cell rows only. Structure is complex in the first annual rings of trunk wood because the amount of compression wood and the density of earlywood is highly variable. Therefore, we obtained tracheid dimensions of defined wood regions, instead of measuring all tracheids of a transverse cut face. The first 5–7 earlywood cell rows have a more uniform wood structure around the circumference compared with the later earlywood and the latewood. They resemble the highly conductive light bands observed in Norway spruce branches (Mayr et al. 2005). Their structural aspects might therefore influence whole-stem conductivity.

Transverse sections (25-μm thick) were cut on a sliding microtome from the fully saturated pieces of the bending test samples and RW, LWP, L_EW and W_EW measured. Sections were stained with methylene blue, dehydrated and mounted in Entellan (Merck, Darmstadt, Germany). Radial lumen diameter (L_EW) and tangential wall thickness (W_EW) were measured along radial reference lines that were drawn from pith to bark.

Compression test samples were radially split in half. From one half, 2-mm-thick radial wood sections were prepared with razor blades. To measure the tracheid length of the first earlywood tracheids, annual rings were separated with the aid of a microscope and the samples macerated in Jeffreys solution (Jeffrey 1917).

Radial sections (20-μm thick) cut from the other half of each compression test sample were stained with methylene blue, dehydrated and mounted in Entellan (Merck, Darmstadt, Germany). The microfibril angle of the S2 layer of the tracheid wall was measured as the angle between the longitudinal cell axis and micro-cracks in the cell wall induced by rapid dehydration as performed by Hannrup et al. (2004). The MFA_EW was obtained in the first earlywood cell rows and MFA_LW in the last latewood cell rows.

We measured LWP, L_EW, W_EW, TL_EW, MFA_EW and MFA_LW for the 2nd and the 3rd annual rings separately by means of National Institute of Health (NIH) Image software (freely available from http://rsb.info.nih.gov). An annual mean value was calculated from 40 measurements in each tree ring, which were made for L_EW and W_EW at randomly selected positions around the stem.

Dimensions of bordered pits were measured on a Leica DM4000 M microscope equipped with a Leica DFC320 R2 digital camera and Leica IM 500 Image Manager image analyzing software (Leica, Wetzlar, Germany). Pit dimensions were measured on earlywood of the 2nd and the 3rd annual rings of the remainders of the bending test samples radially split along the grain. Traits assessed were the diameter of the bordered pits (membrane diameter, D_m), the pit aperture diameter (D_a) (Hacke et al. 2004) and the ratio of the pit aperture diameter to the pit diameter (PP, pit aperture percentage) (Mayr et al. 2002). Mean pit dimensions were calculated from 40 single measurements in each annual ring. The shapes of bordered pits and pit apertures were mainly circular in normal wood; where they were ellipsoid, mean diameters were calculated from the minor and major diameters.

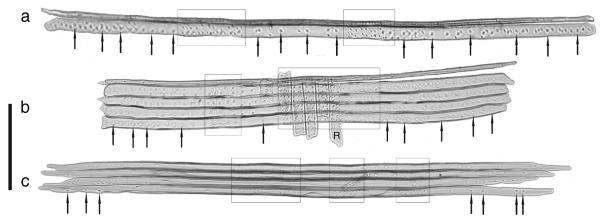
Bordered pit frequency (PF), defined as the number of bordered pits along 1 mm of the radial cell wall of the first earlywood tracheids, was measured on radially cut, 20-μm-thick wood sections (see preparation above). The number of bordered pits was counted in each of the first five earlywood cell rows within a longitudinal distance of 5 mm, including areas of cross-field pitting. The parameter PF represents the mean value of the pit frequencies of the first five earlywood cell rows. Counting the bordered pits along the first earlywood tracheids did not require maceration of the wood samples, because bordered pits occurred along the entire length of the tracheid and tracheids had rounded tips (Figures 1a and 1b). In later-formed earlywood tracheids, bordered pits were situated near the tapered tips, where they could be counted only after separation of the tracheids (Figure1c).

Figure 1.

Macerated wood samples of Norway spruce showing tracheids of the last latewood cell row (upper side) and the adjacent first earlywood cell row(s) formed in the following growing season (a, b) and tracheids of the earlywood formed later in the growing season (c). Tracheid samples shown here were taken from different trees, which explains the difference in sizes. Selected bordered pits are indicated by arrows. Cross-field pittings are marked by frames. The letter R marks a ray cell. The reference bar represents 200 μm.

Transverse surfaces of the wood cylinders (dried to 12% water content) were scanned at a resolution of 1000 × 1000 dpi before axial compression testing. The scanned surfaces were analyzed with NIH Image software to determine the area of compression wood relative to the whole transverse surface area excluding the pith (CP).

Spiral grain angle (GA) was measured with a precision of 0.5° on the radially split pieces of the bending test samples as the angle between the axis of the stem and the inclination of the longitudinal tracheids of the outermost annual ring (Harris 1989).

Statistics

Numbers are given as means ± standard error (SE). With the exception of biomass, tree height and microfibril angles, all traits followed a normal distribution. To meet the requirement of normality in the statistical analysis, the three traits were transformed into normal scores by logarithmic transformation. The significance of relationships between traits was evaluated by one-way analysis of variance (ANOVA). Associations between two variables were also examined by linear or nonlinear regression analyses. The Pearson correlation coefficient (r_P) was used to associate traits on a single tree as well as on a clonal mean base and to test single tree and clonal mean model equations for their predictive quality. Differences between mean values and relationships were accepted as significant if P was < 0.05.

Genetic parameters

Variance components were estimated by univariate ANOVA, where variance components for each trait were estimated, and by multivariate ANOVA, where variances and covariances between pairs of traits were estimated. For the univariate analysis, the following linear model was used:

$$y_{ij}=\mu +c_i+e_{ij}$$ (3)

where y_ij is an observation of each trait of the ij^th tree, μ is the overall mean, c is the random clone effect and e is the random residual. The random effects were assumed to be normally distributed with an expected mean value of zero, and to be independent of each other.

The following model, expressed in matrix notation, was used for the multivariate analysis:

$${\mathbf{y}}_i={\mathbf{Z}}_i{\mathbf{c}}_i+{\mathbf{e}}_i$$ (4)

where i pertains to traits 1 and 2, y is the vector of individual tree observations, c is the vector of random clone effects, e is the vector of random residuals and Z is the design matrix of the clone effects. The random effects are assumed to have a multivariate normal distribution with an expected mean value of zero, and may be summarized as $\mathbf{c}=({\mathbf{c}}_1,{\mathbf{c}}_2^{\prime })$ and ${\mathbf{c}}^{\prime }=({\mathbf{e}}_1^{\prime },{\mathbf{e}}_2^{\prime })$.

Variances and covariances were estimated using the Average Information algorithm (Gilmour et al. 1995) for restricted maximum likelihood estimates (Schaeffer et al. 1978), as implemented in the ASReml software (Gilmour et al. 1999).

Genotypic (${\widehat{\sigma }}_{\mathrm{G}}^2$) and phenotypic (${\widehat{\sigma }}_{\mathrm{P}}^2$) variance components were estimated as ${\widehat{\sigma }}_{\mathrm{G}}^2={\widehat{\sigma }}_{\mathrm{c}}^2$ and ${\widehat{\sigma }}_{\mathrm{P}}^2={\widehat{\sigma }}_{\mathrm{c}}^2+{\widehat{\sigma }}_{\mathrm{e}}^2$, where ${\widehat{\sigma }}_{\mathrm{c}}^2$ and ${\widehat{\sigma }}_{\mathrm{e}}^2$ are the estimated clonal and residual variances, respectively. The estimates of broad-sense heritability (${\widehat{H}}^2$) were obtained by ${\widehat{H}}^2={\widehat{\sigma }}_{\mathrm{G}}^2∕{\widehat{\sigma }}_{\mathrm{P}}^2$. Genotypic correlations (${\widehat{r}}_{\mathrm{G}}$) between traits were estimated as ${\widehat{r}}_{\mathrm{G}}={\widehat{\sigma }}_{{\mathrm{G}}_1{\mathrm{G}}_2}∕{\widehat{\sigma }}_{{\mathrm{G}}_1}{\widehat{\sigma }}_{{\mathrm{G}}_2}$, where ${\widehat{\sigma }}_{{\mathrm{G}}_1{\mathrm{G}}_2}$ is the genotypic covariance between two traits. Estimates of the standard errors of the genetic parameters were calculated from a Taylor series approximation, performed with ASReml software.

Because the plants were not randomized within the experiment, the clonal effects may to some extent be confounded with environmental effects. We assumed, however, that such effects can be neglected.

Results

Vulnerability to cavitation

Of the vulnerability parameters, the loss of conductivity induced by 4 MPa (PLC_4MPa) showed the highest variability among clones, whereas no significant clonal differences could be found for Ψ₅₀ (Table 1). The air entry point (Ψ₁₂, Figure 2) was reached at lower pressures and PLC_4MPa was higher in single trees (Table 1) or clones with higher biomass production (r = 0.75, P < 0.05) and stem diameters (r = 0.80, P < 0.05). Genotypic correlations between these vulnerability parameters and growth parameters were stronger than phenotypic correlations (Table 1). Parameter Ψ₅₀ was unrelated to tree growth.

Table 1.

Mean wood trait values, heritabilities and relationships of wood functions to growth and density. Mean and standard error (SE), significant differences between clones tested by one way ANOVA (P), broad sense heritabilities (H²) of all hydraulic, mechanical, tree growth and wood structural traits assessed, and their correlation (Pearson correlation coefficient, r_P) and genotypic correlation (r_G) to the total above ground biomass, tree height, stem diameter and wood density. Bold numbers indicate significant relationships (P < 0.05) between the traits. Values are missing where heritabilities or genotypic correlations could not be estimated. Abbreviations: EW, earlywood; and LW, latewood.

Trait	Abbrev.	n	Mean (SE)	P	H2(SE)	Trait × BM		Trait × H		Trait × D		Trait × WD
						r P	r G	r P	r G	r P	r G	r P	r G
Negative of applied air pressure  causing 12% loss of conductivity	Ψ 12	49	3.14 (0.11)	0.024	0.20 (0.14)	0.33		0.19	0.71	0.34	1.12	0.25	0.00
Negative of applied air pressure  causing 50% loss of conductivity	Ψ 50	49	4.71 (0.06)	0.073	0.14 (0.16)	0.09	0.42	0.06	0.34	0.17	0.47	0.07	−0.66
Slope of the linear part of the  vulnerability curves	a	49	1.48 (0.09)	0.066	0.15 (0.13)	−0.28		−0.14	−0.59	−0.23	−1.01	−0.25	−0.62
Percent loss of conductance at 4 MPa	PLC4MPa	47	30.49 (1.96)	0.007	0.26 (0.15)	0.37	1.00	0.18	0.46	0.42	0.92	0.19	−0.08
Specific hydraulic conductivity at full  saturation (m2s−1MPa−1 × 10−4)	k s100	51	2.56 (0.16)	0.002	0.31 (0.16)	0.51	0.81	0.39	0.47	0.48	0.99	−0.05	−0.27
Wood density (g cm−3)	WD	60	0.58 (0.01)	0.004	0.24 (0.14)	0.00	0.09	0.02	0.15	0.04	0.02
Compression stiffness (GPa)	E	56	1.35 (0.05)	0.003	0.26 (0.15)	−0.11	−0.15	−0.05	0.13	−0.17	−0.09	0.41
E / WD (GPa g−1)	E WD	56	2.33 (0.08)	0.180	0.08 (0.10)	−0.09	−0.22	−0.03	0.23	−0.17	−0.05	−0.02
Compression strength (MPa)	σ a	55	51.93 (0.86)	0.000	0.36 (0.17)	−0.12	−0.09	−0.06	0.07	−0.10	−0.03	0.76	1.00
σa / WD (MPa g−1)	σ aWD	55	89.93 (1.02)	0.367		0.01		0.03	0.65	−0.04		−0.34	-
Bending stiffness (GPa)	MOE	53	3.48 (0.12)	0.000	0.56 (0.16)	0.15	0.23	0.31	0.55	0.24	0.29	0.31	1.02
MOE / WD (GPa g−1)	MOEWD	53	6.03 (0.21)	0.004	0.29 (0.17)	0.20	0.38	0.34	0.75	0.23	0.48	−0.24
Bending strength (MPa)	σ b	56	58.03 (1.17)	0.001	0.33 (0.16)	0.01	0.20	0.06	0.34	0.12	0.27	0.53
σb / WD (MPa g−1)	σ bWD	52	100.90 (1.56)	0.328	0.04 (0.10)	−0.14	−0.50	−0.06	−0.22	0.01	0.08	−0.09
Total aboveground biomass (g)	BM	59	63.70 (4.71)	0.000	0.76 (0.11)
Tree height (cm)	H	60	59.66 (2.22)	0.000	0.83 (0.08)	0.78	0.85
Stem diameter at tree base (cm)	D	59	1.44 (0.04)	0.000	0.65 (0.14)	0.85	0.93	0.72	0.82
Ring width (mm)	RW	60	0.96 (0.03)	0.000	0.44 (0.16)	0.45	0.42	0.51	0.40	0.46	0.58	−0.37	−0.69
Latewood percentage (%)	LWP	57	18.39 (1.24)	0.000	0.58 (0.15)	0.58	0.95	0.46	0.77	0.56	0.85	0.36	0.36
Compression wood percentage (%)	CP	58	6.61 (0.69)	0.000	0.38 (0.16)	−0.18	−0.18	−0.15	−0.27	−0.33	−0.24	−0.22	−0.76
Cell wall thickness (μm)	W EW	58	5.13 (0.08)	0.000	0.34 (0.16)	0.01	0.14	−0.13	−0.19	0.07	0.16	0.07	0.35
Lumen diameter (μm)	L EW	56	11.57 (0.24)	0.121	0.11 (0.11)	0.15		0.22	0.60	0.21	1.00	−0.12	0.65
Tracheid length (mm)	TLEW	60	1.20 (0.01)	0.000	0.72 (0.12)	0.64	0.86	0.62	0.74	0.70	0.88	0.18	0.39
Pit aperture diameter (μm)	D a	59	3.38 (0.04)	0.000	0.54 (0.16)	0.40	0.34	0.38	0.31	0.53	0.47	−0.01	−0.18
Pit membrance diameter (μm)	D m	59	10.67 (0.10)	0.015	0.21 (0.15)	0.08	−0.14	0.09	−0.04	0.24	0.14	−0.02	−0.03
Pit aperture percentage (%)	PP	59	31.75 (0.30)	0.000	0.49 (0.16)	0.42	0.55	0.38	0.44	0.46	0.59	−0.05	−0.22
Pit frequency (no. mm−1)	PF	58	21.55 (0.36)	0.000	0.51 (0.17)	−0.16	−0.17	−0.34	−0.34	−0.11	−0.05	−0.24	−0.56
Microfibril angle of earlywood (°)	MFAEW	58	31.43 (0.34)	0.000	0.72 (0.12)	0.13	0.06	0.14	0.15	−0.06	−0.32	−0.14	−0.13
Microfibril angle of latewood (°)	MFALW	60	24.79 (0.34)	0.000	0.56 (0.16)	0.26	0.33	0.30	0.46	−0.03	0.08	0.04	−0.06
Spiral grain angle (°)	GA	60	2.51 (0.18)	0.000	0.61 (0.15)	0.64	0.71	0.50	0.43	0.60	0.83	−0.13	−0.05

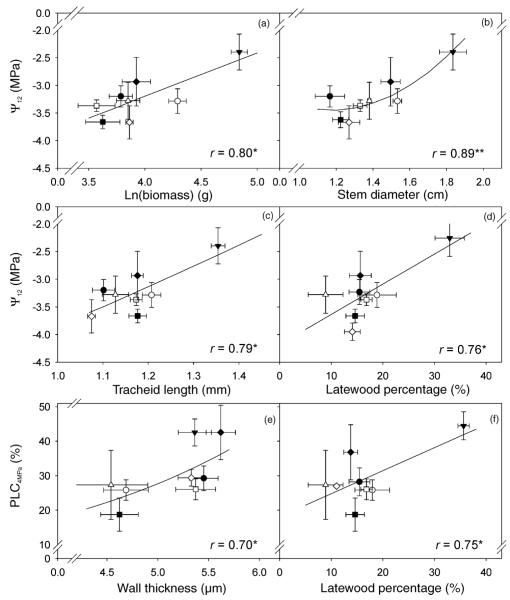
Figure 2.

Clonal means of the negative of the applied air pressure that caused 12% loss of hydraulic conductivity (Ψ₁₂) related to clonal means of total above-ground biomass (BM; a), stem diameter (SD; b), tracheid length (TL_EW; c) and latewood percentage (LWP; d). Clonal means of the percent loss of conductivity induced by an applied air pressure of 4 MPa (PLC_4MPa) related to clonal means of the thickness of tangential cell walls of the first earlywood tracheids (W_EW; e) and latewood percentage (f). Different symbols indicate different clones and error bars represent one standard error. The correlation coefficients of the linear or quadratic model equations are marked with a single asterisk (*) if significant at the 5% level and with two asterisks (**) if at the 1% level.

Wood structural traits positively related to growth parameters (Table 1), such as W_EW, TL_EW, PP, LWP and GA, showed the highest values in trees that were most vulnerable to cavitation (Table 2). Stem wood density was unrelated to the vulnerability to cavitation. For the parameters Ψ₅₀ and Ψ₁₂, no model equations could be found that exceeded the predictive quality of correlations with single structural traits. Variability of PLC_4MPa in single trees could be explained best by Equation 5, where TL_EW, W_EW, PD_m and PF were the independent variables. Independent variables showed no significant intraspecific relationships.

$$\begin{array}{cc}\hfill {\mathrm{PLC}}_{4\mathrm{MPa}}=& -79.676+66.11{\mathrm{TL}}_{\mathrm{EW}}+11.931{\mathrm{W}}_{\mathrm{EW}}\hfill \\ \hfill & -5.799{\mathrm{PD}}_{\mathrm{m}}+1.502\mathrm{PF}\hfill \\ \hfill & \hfill \\ \hfill r=0.81,P& <0.001,n=47\hfill \end{array}$$ (5)

Table 2.

Relationships between wood functions and structural traits. Specific hydraulic conductivity at full saturation (k_s100), applied air pressure causing 12% (Ψ₁₂) and 50% (Ψ₅₀) loss of hydraulic conductivity, the slope parameter a, percent loss of conductivity induced by 4MPa applied air pressure (PLC_4MPa), axial compression stiffness (E), compression strength (σ_a), bending stiffness (MOE) and bending strength (σ_b) related by Pearson correlation coefficient (r_P) and genotypic correlation (r_G) to wood structural traits. Full names of wood structural traits are given in Table 1. Bold numbers indicate significant relationships (P < 0.05) between the traits. Values are missing where genotypic correlations could not be estimated.

Trait	k s100		Ψ 12		Ψ 50		a		PLC4MPa		E		σ a		MOE		σ b
	r P	r G	r P	r G	r P	r G	r P	r G	r P	r G	r P	r G	r P	r G	r P	r G	r P	r G
RW	0.52	0.90	−0.05	0.31	−0.12	−0.05	0.02	−0.24	−0.03	0.27	−0.30	−0.43	−0.45	−0.68	−0.17	−0.40	−0.27	−0.56
LWP	0.30	0.55	0.66	1.09	0.39	0.40	−0.48	−1.01	0.59	0.88	−0.07		0.14	0.31	0.20	0.51	0.40	0.41
CP	−0.15	−0.41	0.00	0.11	0.06	0.82	0.01	0.44	0.05	0.19	−0.26	−0.76	−0.15	−0.65	−0.44	−0.54	−0.35	−0.63
W EW	0.11	−0.21	0.38	0.67	0.39	0.65	−0.25	−0.41	0.59	0.68	−0.09	−0.04	0.00	0.44	0.05	0.14	0.22	0.44
L EW	0.44	0.93	0.13	-	0.09	−0.14	0.03	-	0.19	0.95	−0.11	0.12	−0.09	0.20	0.13	0.27	0.20	0.39
TLEW	0.42	0.48	0.41	1.02	0.23	0.52	−0.25	−1.01	0.46	0.77	0.04	0.04	0.17	0.21	0.33	0.51	0.29	0.48
D a	0.68	0.93	−0.01	0.09	−0.09	−0.53	−0.08	−0.31	0.10	0.09	−0.04	0.10	−0.20	−0.13	0.11	−0.11	−0.03	−0.11
D m	0.32	0.33	−0.17	−0.17	−0.16	0.02	0.02	0.45	−0.22	−0.09	−0.01	0.24	0.01	0.37	0.23	0.18	0.04	0.25
PP	0.57	1.00	0.15	0.25	0.02	−0.68	−0.13	−0.82	0.34	0.21	−0.04	−0.03	−0.24	−0.39	−0.07	−0.24	−0.01	−0.28
PF	0.14	0.72	−0.04	−0.28	−0.15	−0.55	−0.04	0.09	0.02	0.26	−0.07	−0.34	−0.17	−0.32	−0.31	−0.75	−0.18	−0.49
MFAEW	−0.28	−0.54	−0.07	0.16	0.07	0.51	−0.08	0.09	−0.07	0.09	−0.19	−0.34	−0.17	−0.22	−0.04	−0.01	−0.18	−0.17
MFALW	−0.11	−0.35	0.14	0.34	0.09	0.49	−0.10	0.19	0.07	0.19	−0.09	−0.22	−0.05	−0.21	−0.02	0.16	−0.09	−0.06
GA	0.71	-	0.23	0.77	−0.13	−0.28	−0.36	−1.12	0.33	0.76	−0.21	0.02	−0.18	−0.21	−0.14	−0.14	0.11	−0.05

Predictive structural traits for the clonal variability in Ψ₁₂ were LWP and TL_EW (Figure 2). Clonal mean values of Ψ₅₀ showed no significant relationships to any structural trait assessed. The slope parameter a was genotypically negatively related to LWP, TL_EW, PP and GA (Table 2). Clonal variability in PLC_4MPa depended on LWP and W_EW (Figure 2). About 86% of the variability in PLC_4MPa could be explained by variation in W_EW and PP, which were weakly negatively related to each other (r_P = –0.22, P > 0.05, n = 57; r_G = –0.65, P < 0.05), and by TL_EW (Equation 6).

$$\begin{array}{cc}\hfill {\mathrm{PLC}}_{4\mathrm{MPa}}=& -176.858+19.034{\mathrm{W}}_{\mathrm{EW}}+2.703\mathrm{PP}\hfill \\ \hfill & +19.963{\mathrm{TL}}_{\mathrm{EW}}\hfill \\ \hfill & \hfill \\ \hfill r=0.93,P& <0.05,n=8\hfill \end{array}$$ (5)

Specific hydraulic conductivity

Specific hydraulic conductivity (k_s100) varied considerably among clones and showed the highest genetic determination of all the hydraulic traits assessed (Table 1). Single trees or clones with high growth rates had higher k_s100 (Figure 3).

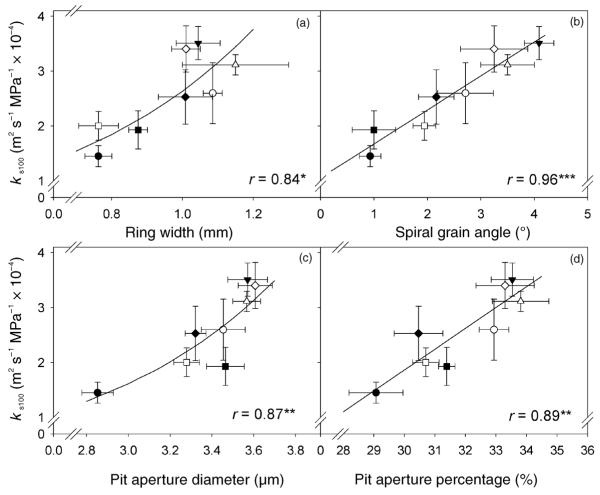
Figure 3.

Clonal means of specific hydraulic conductivity at full saturation (k_s100) related to clonal means of spiral grain angle (GA; a), ring width (RW; b), pit aperture diameter (D_a; c) and pit aperture percentage (PP; d). Different symbols indicate different clones and error bars represent one standard error. The correlation coefficient of the linear or quadratic equations is marked with a single asterisk (*) if significant at the 5% level, with two asterisks (**) if at the 1% level and with three asterisks (***) if at the 0.1% level.

Specific hydraulic conductivity was positively related to GA, TL_EW, L_EW, D_a, PP and LWP (Table 2). Lumen diameter was positively related to TL_EW (r_P = 0.50, P < 0.001, n = 56), D_a (r_P = 0.29, P < 0.05, n = 56; r_G = 0.79, P < 0.05) and PP (r_P = 0.32, P < 0.01, n = 56; r_G = 0.92, P < 0.01). Tracheid length corresponded positively to LWP (r_P = 0.59, P < 0.001, n = 57; r_G = 0.98, P < 0.01), D_a (r_P = 0.40, P < 0.01, n = 59; r_G = 0.36, P > 0.05) and PP (r_P = 0. 41, P < 0.001, n = 59; r_G = 0.36, P > 0.05).

Relationships between k_s100 and anatomical traits became more obvious when investigated by genotypic correlations. Genotypic correlation between k_s100 and GA could not be estimated because of high within-clone correlations. Variability of k_s100 in single trees could be explained best by the linear Equation 7 based on GA and D_a. The independent variables, GA and D_a, were positively related to each other (r_P = 0.55, P < 0.001, n = 59; r_G = 0.75, P < 0.05). Spiral grain was also positively related to L_EW (r_P = 0.32, n = 56, P < 0.001, r_G = 1.02, P < 0.01), TL_EW (r_P = 0.51, n = 60, P < 0.001, r_G = 0.50, P > 0.05) and PP (r_P = 0.60, n = 59, P < 0.001, r_G = 0.97, P < 0.001).

$$\begin{array}{cc}\hfill & k_{s100}=-3.273+0.393\mathrm{GA}+1.439D_a\hfill \\ \hfill & \hfill \\ \hfill & r=0.78,P<0.001,n=51\hfill \end{array}$$ (7)

Clonal means of k_s100 were positively related to GA, D_a and PP (Figure 3). Variation in GA and PF explained 98% of the clonal variation in K_s100 (Equation 8). Values of GA and PF showed no significant relationship, and PF was negatively related to H (Table 1) and TL_EW (r_P = −0.28, P < 0.05, n = 58; r_G = −0.39, P > 0.05).

$$\begin{array}{cc}\hfill & k_{s100}=-0.510+0.566\mathrm{GA}+0.077\mathrm{PF}\hfill \\ \hfill & \hfill \\ \hfill & r=0.99,P<0.001,n=8\hfill \end{array}$$ (8)

Mechanical traits

Mechanical properties varied considerably among clones and showed high genetic determination (Table 1). Parameters σ_a, σ_b, E and MOE depended mostly on variations in WD (Table 1). Wood density was unrelated to BM, H or D, but was negatively related to RW and CP (Table 1). Percentage of compression wood and PF had a slight negative effect on mechanical strength and stiffness (Table 2). Parameters σ_a, σ_b and E were also negatively related to RW, whereas MOE was positively related to H and TL_EW. Density-specific MOE corresponded positively to TL_EW (r_P = 0.28, P < 0.05, n = 52; r_G = 0.62, P < 0.05) and negatively to PF (r_P = −0.21, P > 0.05, n = 52; r_G = −0.85, P < 0.05), and σ_b was negatively related to MFA_LW (r_P = −0.29, P < 0.05, n = 53, r_G = −0.89, P > 0.05).

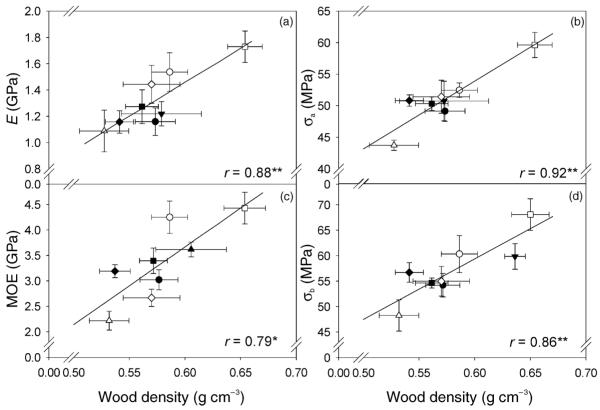
Wood density explained up to 85% of the variation in mechanical traits on a clonal mean basis (Figures 4a–d), and genotypic correlations were stronger than those of single trees (Table 1). Mean clonal variation of MOE was explained best by Equation 9.

$$\begin{array}{cc}\hfill & \mathrm{MOE}=-1.603+13.060\mathrm{WD}-0.117\mathrm{PF}\hfill \\ \hfill & \hfill \\ \hfill & r=0.87,P<0.05,n=8\hfill \end{array}$$ (9)

Figure 4.

Clonal means of the axial compression stiffness (E; a), axial compression strength (σ_a; b) at 12% of water content, bending stiffness (MOE; c) and bending strength (σ_b; d) at full saturation related to clonal means of wood density. Different symbols indicate different clones and error bars represent one standard error. Correlation coefficient of the linear equations is marked with a single asterisk (*) if significant at the 5% level and with two asterisks (**) if at the 1% level.

Relationships between biological wood functions

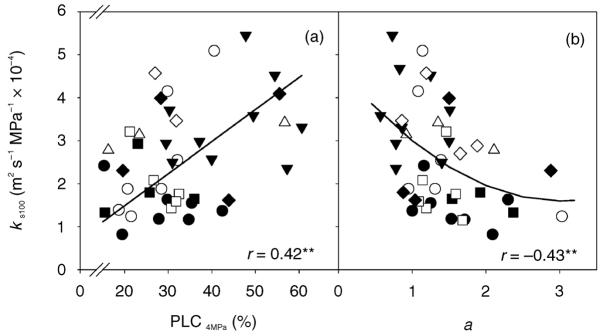
Trees that were most sensitive to cavitation had the highest specific conductivities, as demonstrated by the positive relationship between k_s100 and PLC_4MPa (Figure 5, r_G = 0.83, P < 0.05). Parameters Ψ₁₂ and Ψ₅₀ showed no significant relationship to hydraulic conductivity. The slope parameter a was negatively correlated to hydraulic conductivity (Figure 5, r_G = −0.97, P < 0.01) as well as to Ψ₁₂ (r_P = −0.65, P < 0.001, n = 49; r_G = −0.69, P > 0.05). The k_s100 and hydraulic vulnerability parameters (Ψ₁₂, Ψ₅₀, PLC_4MPa) showed no significant relationships to the mechanical traits assessed (E, σ_a, MOE, σ_b).

Figure 5.

Specific hydraulic conductivity (k_s100) related to the percent loss of conductivity induced by 4 MPa applied air pressure (PLC_4MPa; a) and to the slope parameter a (b). Different symbols indicate different clones according to Figures 2–4. The correlation coefficients of the linear or quadratic equations are marked with two asterisks (**) if significant at the 1% level.

Discussion

Vulnerability to cavitation

Despite the structural heterogeneity of young spruce trunk wood, we found some anatomical traits that were related to hydraulic vulnerability. Vulnerability to cavitation correlated with anatomical properties of the first earlywood tracheids, such as tracheid length, pit aperture percentage and wall thickness, and with the percentage of latewood (Table 2, Figure 2).

The positive relationship between tracheid length and hydraulic vulnerability was driven by the properties of the fastest growing clone. The bigger (wider or longer) the conduit, the more likely it is that the water column will break (Sellin 1991, Cochard 1992a, Sperry 1995). We failed to find relationships between hydraulic vulnerability and lumen diameter, probably because our data were restricted to a distinct part of the earlywood.

In accordance with Mayr et al. (2002), hydraulic vulnerability was positively related to pit aperture percentage (pit aperture diameter was related to pit membrane diameter). Bordered pits with a higher pit aperture percentage are seemingly more prone to pit aspiration and air seeding by membrane stretching or rupture than bordered pits with a lower pit aperture percentage. The pitted fraction of the wall (ligament efficiency) is assumed to be a function of the pit aperture percentage (Hacke et al. 2004). When scaled to the whole-tracheid level, a smaller pitted fraction of the cell wall results in increased wall strength. Stronger walls are required to avoid wall collapse when resistance to embolism, set by individual pit structure and functioning, is high.

Latewood percentage was positively related to earlywood tracheid length. Its statistical linkage with hydraulic vulnerability may therefore not be causal, unless we assume that cavitation starts in latewood (Mayr and Cochard 2003). Conifer earlywood and latewood have different mechanisms for achieving hydraulic safety from xylem cavitation (Gartner 1995, Domec and Gartner 2002b): relatively mild water stress leads to pit aspiration in earlywood tracheids, whereas in latewood, mild water stress leads to air seeding through pit membrane pores rather than in torus closure of the pits (Liese and Bauch 1967, Gregory and Petty 1973). Air seeding in earlywood occurs when the torus is forced out of its sealing position enough to allow air leakage (Sperry and Tyree 1990, Hacke and Sperry 2001). Despite its greater vulnerability to embolism at moderate xylem tension (Ψ₁₂), some latewood parts are reported to remain conductive at low (more negative) water potentials (Domec and Gartner 2002b, Mayr and Cochard 2003). We found that trees more vulnerable to cavitation at moderate applied pressures tended to be less vulnerable at higher applied pressures (negative correlation between Ψ₁₂ and the slope parameter a), probably because they had more latewood (Mayr and Cochard 2003). Accordingly, latewood percentage was negatively correlated with the slope parameter a (Table 2).

Latewood contributions to the overall stem conductivity at full saturation are minor, but juvenile spruce trunk wood contains variable amounts of compression wood (Zobel and Sprague 1998), which might account for differences in hydraulic vulnerability (Domec and Gartner 2002b). Nevertheless, the percentage of distinct compression wood zones showed no relationship to the overall hydraulic vulnerability of the stem segment, and was negatively related to wood density (Table 1). We did not assess the density variations in earlywood, but whole-wood density of 3-year-old stem segments resembled latewood density values of mature Norway spruce wood (Rozenberg et al. 2002, Hannrup et al. 2004). The positive relationship between earlywood wall thickness and vulnerability to cavitation (Table 2) suggested that air seeding through the margo of the bordered pits may occur in young juvenile earlywood as well. Pit membranes of earlywood cells with thicker walls may be less flexible, so they are not easily deflected to seal off the pit aperture completely (Sperry and Tyree 1990), as proposed for compression wood and latewood (Domec and Gartner 2002b, Mayr and Cochard 2003).

The model explaining 86% of the clonal variability in vulnerability to cavitation (Equation 6) presumably contains information about air seeding both through margo pores of tracheids (wall thickness) and owing to stretching or rupture of the pit membrane (pit aperture percentage, tracheid length). The positive relationship between wood density and hydraulic safety found across species and in mature conifer wood (Domec and Gartner 2002a, Hacke and Sperry 2001, Bouffier et al. 2003) was therefore not evident for juvenile wood of young trees (Domec and Gartner 2003, Mayr et al. 2003).

Specific hydraulic conductivity

Because high biomass production requires high water transport efficiency (Mencuccini and Grace 1996, Domec and Gartner 2003), wood anatomical traits positively correlated with growth parameters were also positively correlated with specific hydraulic conductivity (Table 2, Figure 3). We found that high water permeability was more strongly related to larger pit apertures and higher ratios of pit aperture diameters to pit membrane diameters (Schulte and Gibson 1988, Lancashire and Ennos 2002, Tyree and Zimmermann 2002, Mayr et al. 2002, Hacke et al. 2004, Aumann and Ford 2005) than to greater earlywood lumen diameters (Lo Gullo and Salleo 1991, Tyree et al. 1994, Kolb and Sperry 1999) or longer earlywood tracheids (Pothier et al. 1989, Mencuccini et al. 1997, Spicer and Gartner 1998). Recent studies on angiosperms also indicate that flow resistance of pits is more strongly related to the total pit area per conduit than to the individual pit membrane structure (Wheeler et al. 2005, Hacke et al. 2006), which might apply to conifers as well. In accordance with Hacke et al. (2004), pit aperture diameter was a better measure of the total pit area per conduit than pit frequency (pits per mm tracheid length), because pit aperture diameter was more strongly correlated with conductivity than was pit frequency (Table 2).

Hydraulic conductivity also depended strongly on spiral grain angle (Figure 3), because this parameter was positively related to lumen diameter, tracheid length and pit aperture diameter and percentage. Earlier studies (Vité and Rudinsky 1959, Kubler 1991) underlined the physiological importance of spiral grain for the dynamic distribution of sap throughout the crown. Spiral grain angle was positively related to tree growth as well (Table 1), as observed by Danborg (1994) and Eklund et al. (2003), whereas Hannrup et al. (2004) found no such relationships. High spiral grain angle was of minor importance in slower growing trees, probably because different mechanical requirements are associated with slower growth (Skatter and Kucera 1997). The relationship between hydraulic conductivity and spiral grain angle in our samples suggests that the spiral arrangement of tracheids favors water conduction by reducing the flow resistance of bordered pits. Norway spruce pit densities culminate at about 10% of the distance from the tracheid tips and reach low values in the middle part of the tracheid (Sirviö and Kärenlampi 1998). We made similar observations for juvenile earlywood produced later in the growing season. In the first tracheid rows, however, the density of bordered pits was high (Figure 1), as also observed in light bands of branch compression wood (Mayr et al. 2005) and pits were more uniformly distributed along the entire length. The strong correlation between spiral grain angle and hydraulic conductivity might explain the quite uniform distribution of bordered pits along the entire length (Liese and Ammer 1962) and the less tapered tracheid tips of the earliest earlywood tracheids (Figure 1). Spiral grain angle together with pit frequency, which was negatively correlated with tracheid length as found by Hacke et al. (2004), explained 98% of the clonal variation in hydraulic conductivity. In the first annual rings, where spiral grain is generally high (Danborg 1994, Hannrup et al. 2002, Eklund et al. 2003), uniform distribution of bordered pits along the entire tracheid length might reduce flow resistance more than a concentration of pits at the tapered tracheid tips. These highly conductive zones in the first tracheid rows might also explain why we found no relationship between hydraulic conductivity and wood density or percentage of compression wood (Spicer and Gartner 1998, Spicer and Gartner 2002, Mayr et al. 2005) and why whole-stem hydraulic conductance could be explained largely by the structural characteristics of the first earlywood cells (Table 2, Figure 3).

Mechanical strength and stiffness

The mechanical traits assessed were positively correlated with wood density (Table 1, Figure 4). Together with the microfibril angle, wood density is the most predictive trait for wood stiffness (Meylan and Probine 1969, Evans and Ilic 2001). In older juvenile or mature spruce wood, wood density is positively correlated with bending stiffness but negatively with wood growth, on a phenotypic as well as on a genotypic basis (Lindström 1996, Rozenberg and Cahalan 1997, Hannrup et al. 2004). In very wide annual rings, however, the negative relationship between wood density and ring width is reported to vanish (Dutilleul et al. 1998). Wood density was only weakly correlated with ring width and not at all with biomass, height or diameter (Tables 1 and 2), probably because wood density is generally high in the first annual rings and variable amounts of compression wood can occur. The amount of compression wood was negatively correlated with wood density, because compression wood zones contain intercellular spaces (Timell 1986) and demand compensation by less dense, highly conducting wood parts (Mayr et al. 2005). Mechanical strength and stiffness were reduced in samples with a large amount of compression wood (Table 2). Compression wood has lower density-specific compression stiffness but a compressive strength similar to normal wood (Gindl 2001). Microfibril angles of juvenile spruce wood are high and associated with a higher flexibility of young stems (Gorišek and Torelli 1999, Lichtenegger et al. 1999, Lindström et al. 1998). In accordance with Cramer et al. (2005), a negative relationship between density-specific bending strength and microfibril angle was found for latewood only.

Whereas compression stiffness was mainly determined by density and the percentage of compression wood, bending stiffness was also influenced by anatomical characteristics of the first earlywood tracheids (Table 2). Bending stiffness was positively related to tree height growth as found by Mencuccini et al. (1997), which might result from longer tracheids associated with increased height growth (Ezquerra and Gil 2001), but decreased with higher pit frequency of the first earlywood cells, as supposed by Sirviö and Kärenlampi (1998) and Hacke et al. (2004).

Tradeoffs between biological wood functions?

Rapidly growing trees or clones were more sensitive to cavitation but showed higher hydraulic conductivities (Sellin 1991, Domec and Gartner 2003). The relationship was significant only for the parameter PLC_4MPa (Figure 5) and became more apparent in the genotypic correlations (Table 1). Structural traits that caused tradeoffs between hydraulic wood functions were tracheid length (Sellin 1991, Cochard 1992a, Sperry 1995) and pit aperture percentages (Hacke et al. 2004). Vulnerability curves of trees with higher specific hydraulic conductivities and higher values of Ψ₁₂ showed flatter slopes (Figure 5), because higher pressures had to be applied on samples with a higher latewood percentage to result in more than 50% loss of conductivity (Domec and Gartner 2002b, Mayr and Cochard 2003).

We found no relationship between hydraulic and mechanical wood functions because wood density explained most of the variability in mechanical properties, but it was unrelated to the hydraulic properties. A density-based tradeoff between hydraulic wood functions (Gartner 1995, Hacke and Sperry 2001, Hacke et al. 2001, Domec and Gartner 2002a, Bouffier et al. 2003) was presumably influenced by structural compromises associated with mechanical demands of the young trunk. Wood density was not negatively related to hydraulic conductivity, because flow reduction was compensated for by structural characteristics of the first earlywood tracheids (Figure 1). Hydraulic vulnerability of the dense juvenile trunk wood was positively related to the wall thickness of the first earlywood cells (Figure 2), suggesting that air seeding through the margo of the bordered pits may occur in earlywood, as supposed for latewood and compression wood (Domec and Gartner 2002b, Mayr and Cochard 2003). Mechanical support can be achieved not only by increasing density but also by varying latewood percentage, tracheid length, microfibril angles, arrangement of the cell wall layers or by cell wall chemistry (Mencuccini et al. 1997, Gindl 2001, Ezquerra and Gil 2001, Jagels and Visscher 2006). Traits increasing bending stiffness and hydraulic conductivity, e.g., longer tracheids, were, in turn, associated with higher hydraulic vulnerability (Table 2).

Consequences for tree breeding

The number of our samples may have been too small and trees too young to allow us to draw conclusions on the genotypic biomechanical or hydraulic stress behavior of more mature trees. Some genotypic correlations between functional traits and growth or structural traits were, however, quite strong (Tables 1 and 2), and prediction of growth or wood quality traits, such as density, is possible at an early developmental stage (between ages 5 and 7 years, Rozenberg and Cahalan 1997).

Genetic determination of wood density was low in our young wood samples, whereas it is under strong genetic control in mature spruce wood (Rozenberg and Cahalan 1997, Rozenberg et al. 2002, Hannrup et al. 2004). Nevertheless, heritabilities of the mechanical properties assessed were quite high. For example, selection for high bending stiffness, the most heritable functional trait, would not result in decreased growth rate in young trees, because hydraulic conductivity and bending strength were not antagonistic wood functions as found by Mencuccini et al. (1997).

Heritabilities of the hydraulic vulnerability traits were quite low, but their predictive structural traits were under strong genetic control. Most of these traits, such as tracheid length and pit aperture percentage, were positively related to growth. Earlywood wall thickness, one of the most predictive traits for vulnerability to cavitation, was unrelated to growth, although it is in young mature spruce wood (Hannrup et al. 2004). We suppose that the positive relationship between density and hydraulic safety (Hacke and Sperry 2001) becomes more apparent in mature spruce wood. In spruce species, where growth rate is inversely related to wood density, rapid growth is the principal criterion for tree breeding, and density is only second (Zobel and Jett 1995). Selection for high growth rate could thus result in an increased sensitivity to cavitation (Domec and Gartner 2002a).