Assessment of Bias for MRI Diffusion Tensor Imaging Using SIMEX

Abstract

Diffusion Tensor Imaging (DTI) is a Magnetic Resonance Imaging method for measuring water diffusion in vivo. One powerful DTI contrast is fractional anisotropy (FA). FA reflects the strength of water’s diffusion directional preference and is a primary metric for neuronal fiber tracking. As with other DTI contrasts, FA measurements are obscured by the well established presence of bias. DTI bias has been challenging to assess because it is a multi-variable problem including SNR, six tensor parameters, and the DTI collection and processing method used. SIMEX is a modern statistical technique that estimates bias by tracking measurement error as a function of added noise. Here, we use SIMEX to assess bias in FA measurements and show the method provides; i) accurate FA bias estimates, ii) representation of FA bias that is data set specific and accessible to non-statisticians, and iii) a first time possibility for incorporation of bias into DTI data analysis.

1 Introduction

Radiological practice appears to be on the cusp of reliably and routinely using imaging biomarkers as surrogates for traditional tissue biopsy (e.g., virtual biopsy). One promising magnetic resonance imaging (MRI) technique, diffusion tensor imaging (DTI) provides unique, non-invasive contrasts sensitive to tissue micro-architecture, which can be correlated with cellular organization – for example, as seen through histological analysis [1]. However, quantification of observed data is an estimation process and numeric values must be viewed in light of their distributional properties. Extensive research has been invested in characterizing the impacts of noise and study design on DTI contrasts [2–4] and it is well recognized that both lead to changes in precision (variance) as well as accuracy (bias) of diffusion derived measures. Much progress has been made on variability analysis in DTI using Monte Carlo and boot-strap techniques [5], but quantitative post hoc assessment of the bias in diffusion estimated parameters has remained elusive.

Bias is explicitly defined as the difference between the expectation value of an experimentally observed measure, E(Θ_obs), and the true value of that measure, Θ_truth; bias = E(Θ_obs) − Θ_truth. Therefore, bias causes the statistical average of a measured DTI contrast to converge on the wrong value. Bias in DTI is a multi-variable function including imaging noise, field inhomogeneity, DTI experimental parameters, and the underlying biological diffusion parameters. No analytic equation for bias in DTI is known and no published method to account for bias in empirical DTI data has been tried. Herein, we present a statistical approach to estimate the expected level of bias in DTI contrasts on a voxel-wise basis.

In this initial evaluation, we focus on quantifying the bias in the commonly studied and important DTI contrast fractional anisotropy (FA) as measured using the traditional log-linear minimum mean-squared error (LLMMSE) tensor estimation framework. Significant bias in FA has been well documented both experimentally and through computational studies [2, 4, 6]. Within a clinical and research SNR range (~ 15:1 – 40:1), FA bias is generally a monotonic decreasing function, with lower FA values tending to have larger bias than higher FA values.

To estimate FA bias, we test the simulation extrapolation method (SIMEX) which emerged from the statistical literature as a way to compensate for bias due to additive noise within a regression framework [7, 8]. However, it can also be viewed as a general procedure to extrapolate the degree of bias in an estimate given noisy data by studying the sensitivity of the model fitting procedure when additional synthetic noise is added. Two key criterion of SIMEX are (i) the bias as a function of SNR is monotonic and smooth and (ii) the noise level of the observed data is well understood. Fortunately, (i) is generally holds and for (ii), noise estimation has been well-studied in the DTI literature and several robust methods exist to estimate the noise field given empirical data [9–11].

This manuscript is organized as follows. First, we briefly review the diffusion tensor formulation and describe how the SIMEX bias estimation can be applied to bias estimation for FA. Second, we present a simulation based on empirical data which enables knowledge of the true bias level for comparison with the SIMEX estimated bias. Third, we present single and multi-voxel demonstrations of SIMEX estimation of bias in FA. We close with a brief critique and discussion of potential applications for this approach and avenues for continuing research.

2 Theory

2.1 Diffusion Tensor Imaging

In DTI, magnetic gradients (g) are used to label the position of water at the start and end of an experiment. Given the random thermal motions of water, the labels add incoherently and result in an attenuated, diffusion weighted image (dwi). In general, the greater probabilistic movement, the greater the signal attenuation. In the tensor model, the dwi will be a function of the unweighted signal intensity, S_o, diffusion direction and magnitude (encoded in diffusion tensor D), the experimental timing and gradient strength (encoded in parameter b), and the direction of the gradient applied (encoded in g). For a single voxel we write

$${\text{dwi}}_{\text{j}}={\text{S}}_{\text{o}}exp(-b{\mathbf{g}}_{\mathbf{j}}^{\mathbf{T}}·\mathbf{D}·{\mathbf{g}}_{\mathbf{j}}).$$ (1)

Here, j indexes the gradient directions. . For convenience, we define the observed data for a single voxel, X⇀_obs;, as a vector with elements x_i, representing dwi_j for j = 1,2, … m, and S_o.

$${\stackrel{\rightharpoonup }{\text{X}}}_{\text{obs}}=\{\text{dwi}{\mid }_{j=1}^m,{\text{S}}_{\text{o}}\}=\{{\text{x}}_i\mid \begin{array}{c}m+1\\ i\end{array}\}.$$ (2)

D is a 3 × 3 symmetric matrix who’s Eigenvalues, λ₁, λ₂, and λ₃, describe the three principal axis of diffusion. Herein, we consider the FA of the tensor which is the normalized standard deviation of the Eigenvalues and reflects the relative degree of orientation (i.e., 0: no orientation preference = isotropic diffusion, 1: infinite direction preference = 1−D diffusion).

$$\text{FA}=\sqrt{\frac{3}{2}\frac{{({\lambda }_1-\overline{\lambda })}^2+{({\lambda }_2-\overline{\lambda })}^2{({\lambda }_3-\overline{\lambda })}^2}{{\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2}}.$$ (3)

2.2 SIMEX applied to DTI

The premise of SIMEX is simple. Bias can be understood by adding noise to data in incremental amounts and measuring the resulting contrast. The trend in the contrast with added noise should enable prediction of the contrast with ‘removed’ noise. For simplicity, the following description assumes a single DTI experiment is performed (e.g. single subject, one DTI dataset) and describes the single-voxel case, though the analysis can be extended to multiple experiments and multiple voxels.

Let a truth data set be described by zero experimental noise,

$${\stackrel{\rightharpoonup }{X}}_{\text{truth}}=\{{\text{x}}_i{\mid }_{i=1}^{m+1}\}s.t.({\sigma }_{\text{E}}=0),$$ (4)

where σ_E is the standard deviation of the experimental noise. The function T mapping X⇀_truth to FA determines the calculated ground truth FA value, FA_truth.

$${\text{FA}}_{\text{truth}}=\mathbf{T}(\{{\stackrel{\rightharpoonup }{\text{X}}}_{\text{truth}}\}).$$ (5)

The observed data of an actual experiment contains experimental noise and is described by,

$${\stackrel{\rightharpoonup }{\text{X}}}_{\text{obs}}={\stackrel{\rightharpoonup }{\text{X}}}_{\text{truth}}+{\sigma }_{\text{E}}\stackrel{\rightharpoonup }{\text{Z}}.$$ (6)

Here, Z⇀ is a vector of m+1 random drawings from a standard normal distribution. The resulting observed FA from the experiment is then,

$${\text{FA}}_{\text{obs}}=\mathbf{T}(\{{\stackrel{\rightharpoonup }{\text{X}}}_{\text{obs}}\}).$$ (7)

In SIMEX, synthetic normally distributed noise with standard deviation ω^1/2σ_E is added to X⇀_obs, and the new simulated data is written as,

$${\stackrel{\rightharpoonup }{\text{X}}}_{\text{M}.\text{C}.}(\omega )={\stackrel{\rightharpoonup }{\text{X}}}_{\text{obs}}+{\omega }^{1/2}{\sigma }_{\text{E}}\stackrel{\rightharpoonup }{\text{Z}}.$$ (8)

Where M.C. stands for ‘Monte Carlo’ (M.C. replaces ‘b’ and ω replaces ‘λ’ as defined in the SIMEX literature [8]). The simulated FA is then described by,

$${\text{FA}}_{\text{M}.\text{C}.}(\omega )=\text{T}\left(\{{\stackrel{\rightharpoonup }{\text{X}}}_{\text{M}.\text{C}.}(\omega )\}\right).$$ (9)

The variance of the simulated data as a function of ω is

$$\begin{array}{c}var\left({\stackrel{\rightharpoonup }{\text{X}}}_{\text{M}.\text{C}.}(\omega )\right)=\\ var\left({\sigma }_{\text{E}}\stackrel{\rightharpoonup }{Z}+{\omega }^{1/2}{\sigma }_{\text{E}}\stackrel{\rightharpoonup }{Z}\right)=\\ {\sigma }_{\text{E}}^2(1+\omega ).\end{array}$$ (10)

A key observation is to note that at the value ω = −1, (which cannot be simulated) the variance goes to 0. For repeated Monte Carlo simulations of FA_M.C.(ω), a mean value can be calculated, ${\overline{\text{FA}}}_{\text{M}.\text{C}.}$, and the trend approximated by fitting ${\overline{\text{FA}}}_{\text{M}.\text{C}.}(\omega )$ with a standard non-linear equation, $\stackrel{\sim }{\text{FA}}(\omega )$ [8],

$$\stackrel{\sim }{\text{FA}}(\omega )=\text{a}+\frac{\text{b}}{1+\omega }$$ (11)

The FA at zero noise can then be estimated by solving eq. 11 for = −1,

$${\text{FA}}_{\text{SIMEX}}=\stackrel{\sim }{\text{FA}}(-1).$$ (12)

The bias in the data can then be estimated,

$$\text{Estimated}\text{Bias}={\text{FA}}_{\text{obs}}-{\text{FA}}_{\text{SIMEX}}.$$ (13)

The true bias can also be calculated if the truth data is known,

$$\text{True}\text{Bias}=\text{E}({\text{FA}}_{\text{obs}})-{\text{FA}}_{\text{Truth}}.$$ (14)

3 Methods and Results

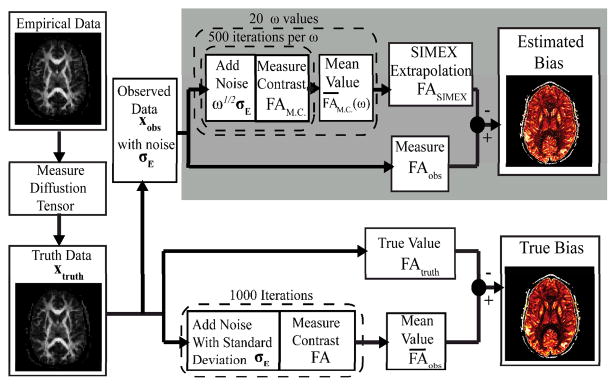
The steps used here to evaluate SIMEX on FA are summarized in the flow chart of Fig. 1 and exampled by individual voxels in Fig. 2. Unless otherwise stated, all processing and analysis was performed in Matlab 2010 (Mathworks, Natick, MA). Diffusion tensor estimates were calculated by fitting the diffusion model (eq.1) to the data using a simple LLMMSE. In all cases, noise was added to data using a Rician distribution, which is approximately Gaussian for SNR > 5:1[12].

Fig. 1.

Flow chart of steps to create SIMEX Estimated Bias and True Bias maps. Variables refer to terms defined explicitly by equations in the Theory section.

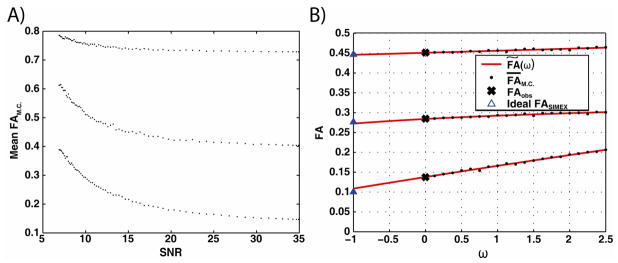
Fig. 2.

(A) Exploratory SIMEX plots of simulated FA_M.C. as a function of SNR for three voxels from the simulated observed data. 1000 Monte Carlo simulations were averaged for each ${\overline{\text{FA}}}_{\text{M}.\text{C}.}$. The FA_obs is the point at the highest SNR value (SNR = 35:1). An upward bias with decreasing SNR is observed for all three voxels. (B) FA_M.C.(ω) and the extrapolation fit for three voxels in the observed data set. The x-axis for extrapolation is ω ~1/SNR and the fit is extrapolated to ω = −1. The ideal FA_SIMEX (blue triangles) represents the extrapolated FA_SIMEX value if the true bias was correctly estimated.

Empirical Data

Empirical data (KKI2009-33-DTI) was downloaded from the Multi-Modal MRI Reproducibility study available online at www.nitrc.org [13]. Full collection details are provided in the reference. Briefly, DTI data was collected using a multi-slice, single-shot, echo planar imaging (EPI) sequence. Thirty two gradient directions were used with b = 700 s/mm² (m = 32, b = 700, eq. 1 & 2). Five S_o images were collected and averaged into a single S_o. The resulting images consisted of sixty-five transverse slices with a field of view = 212 × 212 reconstructed to 256 × 256.

Creating Noiseless Ground Truth (eq. 4)

The 32 dwi images were registered to the single S_o image using FLIRT affine registration (FMRIB, Oxford, UK). For spatial consistency, the resulting affine transformation matrix was applied to the gradient table. A single axial slice of interest was selected and diffusion tensor estimates (D) for that slice were calculated. Using the S_o image, the estimated diffusion tensor, and the given g and b as inputs to eq. 1, dwi images were simulated. The S_o image and the 32 noiseless dwi images make the noiseless ground truth dataset, X⇀_truth.

Creating Observed Data (eq. 6)

To create the observed data, X⇀_obs, noise was added to the ground truth data set such that SNR = 35:1. The signal strength was estimated from the average signal intensity of the masked S_o image. Noise, σ_E = signal/35, was added to the ground truth data to create the 32 dwi images and the single S_o image.

Calculating the Estimated Bias (eq. 13)

To calculate FA_SIMEX, first a plot of ${\overline{\text{FA}}}_{\text{M}.\text{C}.}(\omega )$ needed to be constructed. 500 Monte Carlo simulations for 20 different ω values were performed and ${\overline{\text{FA}}}_{\text{M}.\text{C}.}(\omega )$ calculated from the average. Each simulation consisted of a noise adding step to create X_M.C. (eq. 8), followed by a calculation of FA_M.C.. Example ${\overline{\text{FA}}}_{\text{M}.\text{C}.}(\omega )$ for three voxels are shown in Fig. 2A. $\stackrel{\sim }{\text{FA}}(\omega )$ was fit using the empirical non-linear equation (eq. 11). The fit equation was extrapolated to ω = −1, producing FA_SIMEX (Fig. 2B). The FA_obs from eq. 13 was calculated directly from diffusion tensor fits to the observed data set, X⇀_obs. The difference of FA_SIMEX and FA_obs was taken and the Estimated Bias calculated.

Calculating True Bias (eq. 14)

The average of 1000 iterations was used to estimate the expected value of FA_obs, ${\overline{\text{FA}}}_{\text{obs}}\sim \mathbf{E}({\text{FA}}_{\text{obs}})$. Each simulation consisted of first adding noise (SNR = 35:1) to X⇀_truth followed by calculation of FA. FA_truth was calculated directly from X⇀_truth. The True Bias was calculated from the difference between ${\overline{\text{FA}}}_{\text{obs}}$ and FA_truth. Exploratory M.C. simulations applying SIMEX to different SNR levels of X⇀_obs for a single ground truth voxel are shown in Fig. 3. The True Bias and Estimated Bias are compared in Fig. 4. The results shown in Fig. 4 were typical for multiple test trials (data not shown).

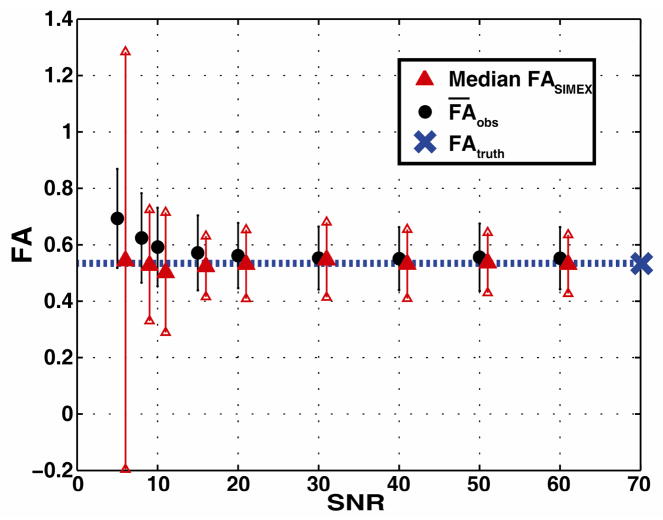
Fig. 3.

Simulated outcomes for SIMEX at several SNR values. ${\overline{\text{FA}}}_{\text{obs}}$ values for each SNR value (circles) were calculated starting from a voxel in the simulated truth data. The ${\overline{\text{FA}}}_{\text{obs}}$ values are shown with the standard deviation (error bars) from 1000 simulations run at each SNR value. 100 observations at each SNR value were randomly chosen for SIMEX. The median FA_SIMEX values (triangles) are shown with the standard deviation(error bars). The median value was chosen due to the decreased robustness of only 100 simulations.

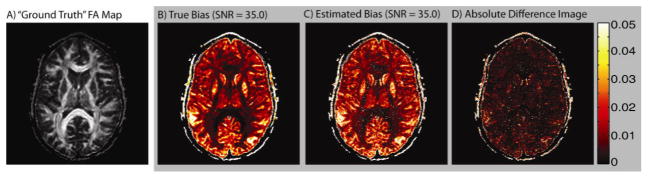
Fig. 4.

(A) The ‘ground truth’ FA map (FA_truth) of the slice selected for data analysis. (B) The True Bias map for an SNR of 35:1 is compared to (C) the absolute value of the Estimated Bias at SNR = 35:1. The absolute value difference map was calculated from the raw bias data (not the difference in the absolute values). For a significant majority of voxels the True Bias is positive and the Estimated Bias is greater than the True Bias.

4 Discussion

Potential systematic differences in distributional properties of tensor-derived contrasts pose serious hazards for statistical analysis. Understanding “statistical artifacts” in DTI has long been an essential challenge in proper interpretation of DTI contrasts [14]. Routine approaches for interpreting contrasts (e.g., regions of interest, voxel-based morphometry, tract-based spatial statistics) hinge upon the assumption of equivalent (or zero) bias between populations. If this assumption is violated then the inferences (and p-values) may be suspect. In any empirical experiment, there will be variations in bias due to subject characteristics, protocols, scanner stability, hardware/software changes, etc. Without a method to estimate bias in measures derived from individual empirical datasets, evaluation of any change requires an extensive simulation study based on a range of potential anatomical models.

With the proposed SIMEX approach, it is possible to estimate bias in contrasts on a voxel-by-voxel level given the empirical data. SIMEX proved a sensitive method for detecting FA bias as evidenced by its success on the high SNR (and therefore relatively low bias) dataset used here (Fig. 4). Although bias may be negligible for some individual cases at high SNR values (such as exampled for high SNR values in Fig. 3), bias may become increasingly important at lower SNR values or in hypothesis test settings where even a small bias can significantly inflate the Type-I error rate. To that end, the individual voxel test case (Fig. 3) suggests SIMEX to be a promising technique for empirical data collected at lower SNR levels (stable median FA_SIMEX values) as well as a reliable method for repeated use on individual datasets within grouped data (stable error bars). The instability of the SIMEX estimate for SNR ≤ 10:1 (Fig. 3) is likely to be a result of the non-monotonic behavior of bias at extremely low SNR values [6].

We note that at these early stages, we are not specifically recommending using the estimated bias measures to correct for voxel-wise bias. Optimization of user input SIMEX parameters (e.g. the approximation function in eq. 11 or the number of Monte Carlo iterations) and repeat testing on empirical data of various SNR levels is underway. Refinements may help decrease the variability in the SIMEX estimate (Fig. 3 red error bars) and mediate some of the isolated outliers seen in Fig. 4D. Additionally, methods for constructing error estimates of the measured SIMEX bias exist and have yet to be tested in the context of DTI [7, 8]. With continued future refinement and careful incorporation of robust/advanced tensor estimators it may be possible to produce unbiased contrast estimates without the disadvantages of direct maximum likelihood methods [15, 16].

In summary, a method for direct, empirical assessment of bias in tensor derived contrasts opens many possibilities for useful statistical assessments and improved analysis approaches. Further investigation is warranted into bias estimation with other tensor contrasts, using advanced tensor fitting methods, and examining quantitative tissue models beyond the tensor formulation.