Estimating the 4D Respiratory Lung Motion by Spatiotemporal Registration and Building Super-Resolution Image

Abstract

The estimation of lung motion in 4D-CT with respect to the respiratory phase becomes more and more important for radiation therapy of lung cancer. However, modern CT scanner can only scan a limited region of body at each couch table position. Thus, motion artifacts due to the patient’s free breathing during scan are often observable in 4D-CT, which could undermine the procedure of correspondence detection in the registration. Another challenge of motion estimation in 4D-CT is how to keep the lung motion consistent over time. However, the current approaches fail to meet this requirement since they usually register each phase image to a pre-defined phase image independently, without considering the temporal coherence in 4D-CT. To overcome these limitations, we present a unified approach to estimate the respiratory lung motion with two iterative steps. First, we propose a new spatiotemporal registration algorithm to align all phase images of 4D-CT (in low-resolution) onto a high-resolution group-mean image in the common space. The temporal consistency is persevered by introducing a concept of temporal fibers for delineating the spatiotemporal behavior of lung motion along the respiratory phase. Second, the idea of super resolution is utilized to build the group-mean image with more details, by integrating the highly-redundant image information contained in the multiple respiratory phases. Accordingly, by establishing the correspondence of each phase image w.r.t. the high-resolution group-mean image, the difficulty of detecting correspondences between original phase images with missing structures is greatly alleviated, thus more accurate registration results can be achieved. The performance of our proposed 4D motion estimation method has been extensively evaluated on a public lung dataset. In all experiments, our method achieves more accurate and consistent results in lung motion estimation than all other state-of-the-art approaches.

1 Introduction

The modern 4D-CT technique is very useful in many clinical applications, which provides the solid way for the researchers to investigate the dynamics of organ motions in the patient. For example, 4D-CT has been widely used in lung cancer treatment for helping the dose planning by delineating the tumor in multiple respiratory phases. However, the respiratory motion is the significant source of error in radiotherapy planning of thoracic tumors, as well as many other image guided procedures [1]. Therefore, there is increasing growth in investigating the methods for accurate estimation of the respiratory motion in 4D-CT [2-4].

Image registration plays an important role in the current motion estimation methods by establishing temporal correspondences, e.g., between the maximum inhale phase and all other phases [3, 4]. However, there are some critical limitations in these methods. The first obvious limitation is the independent registration for different pairs of phase images. In this way, the coherence in 4D-CT is totally ignored in the whole motion estimation procedure, thus making it difficult to maintain the temporal consistency along the respiratory phases. The second limitation is mainly coming from the image quality of 4D-CT. Since the modern CT scanner can only scan a limited region of human body at each couch position, the final 4D-CT has to be assembled by sorting multiple free-breathing CT segments w.r.t. the couch position and tidal volume [3]. However, due to the patient’s free breathing during scan, no CT segment can be scanned exactly at the particular tidal volume. Thus, motion artifacts can be observed in the 4D-CT, including motion blur, discontinuity of lung vessel, and irregular shape of lung tumor. All these artifacts in 4D-CT challenge the registration methods to establish reasonable correspondences. The final limitation is that the motion estimation in the current methods is generally completed with a single step, i.e., registering all phase images to the fixed phase image, without providing any chance to rectify the possible mis-estimation of respiratory motions.

To overcome these limitations, we present a novel registration-based framework to estimate the lung respiratory motion in 4D-CT. Our method consists of two iterative steps. In the first step, a spatiotemporal registration algorithm is proposed to simultaneously align all phase images onto a group-mean image in common space. Particularly, rather than equally estimating the correspondence for each point, we propose to hierarchically select a set of key points in the group-mean image as the representation of group-mean shape, and let them drive the whole registration process by robust feature matching with each phase image. By mapping the group-mean shape to the domain of each phase image, every point in the group-mean shape has several warped positions in different phases, which can be regarded as an ‘artificial’ temporal fiber once assembling them into a time sequence. Thus, the temporal consistency of registration is achieved by requiring the smoothness on all temporal fibers during the registration. In the second step, after registering all phase images, the respiratory motion of lung can be obtained to guide the reconstruction of the high-resolution group-mean image. By repeating these two steps, not only more accurate but also more consistent motion estimation along respiratory phases can be achieved, as confirmed in the experiment on a public lung dataset [2], by comparing to the diffeomorphic Demons [5] and the B-spline based 4D registration method [4].

2 Methods

The goal of our method is to estimate the respiratory motion φ(x, t) at arbitrary location x and time t. In 4D-CT, only a limited number of phase images are acquired. Thus, given the 4D-CT image I ={I_s∣s = 1, … , N} acquired with N phases, we can model the respiratory motion φ(x, t) as a continuous trajectory function with its known landmark at the position x of the phase t_s, i.e., φ(x, t_s) = f_s(x), which is obtained by simultaneously estimating the deformation fields, F = {f_s(x)∣x ∈ Ω_c, s = 1, … , N}, from the common space C to all N phase images.

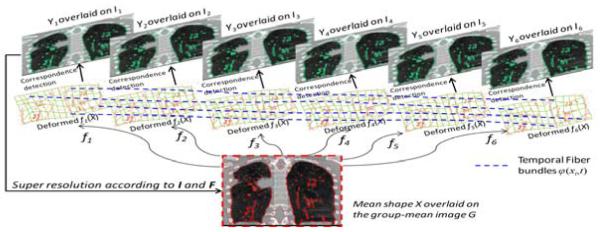
Our method consists of two iterative steps, as shown in Fig. 1. First, we will calculate the deformation field f_s for each phase image I_s w.r.t. the current-estimated group-mean image G in the common space. Generally, G has higher image resolution than all I_s s, since it integrates all information from the aligned I_s s. Thus, the registration can be performed between the high-resolution group-mean image G and the low-resolution phase images I_s, by requiring the respiratory motion φ(x, t) to be temporally smooth across all N phases. Second, after aligning all phase images onto the common space, the procedure of super resolution (SR) is performed to construct a high-resolution group-mean image G based on the latest estimated deformation fields F and the corresponding phase images I. By repeating these two steps, all phase images can be jointly registered onto the common space, with their temporal motions well delineated by φ(x, t). The final super-resolution group-mean image G integrates all image information from all phases, thus it has much clearer anatomical details than any phase image I_s, as will be shown next. Also, it can help resolve the uncertainty in correspondence detection for the case of directly registering different phase images, since, in our method, each point in the phase image I_s can easily find its correspondence in the group-mean image (which has complete image information).

Fig. 1.

The overview of our method in respiratory motion estimation by joint spatiotemporal registration and high-resolution image reconstruction.

Our method differs from the conventional group-wise registration method [6] in several ways: 1) The registration between group-mean image and all phase images is simultaneously performed by exploring the spatiotemporal behavior on a set of temporal fibers, instead of independently deploying the pairwise registrations; 2) The correspondence is always determined between high-resolution group-mean image and low-resolution phase image; 3) The construction of group-mean image considers the alignment of local structures, instead of simple intensity average, thus better alleviating the effect of misalignment. Next, we will explain the proposed spatiotemporal registration and super resolution methods.

2.1 Hierarchical Spatiotemporal Registration of 4D-CT

Before registration, we will first segment each phase image into bone, soft tissue (muscle and fat), and lung. Then, the vessels inside lung will be enhanced by multiscale hessian filters [7], in order to allow the registration algorithm to focus on the alignment of lung vessels during the registration. Meanwhile, instead of using only image intensity, we employ an attribute vector $\stackrel{\rightharpoonup }{a}(x,I_s)$ as the morphological signature for each point x in the image I_s to characterize its local image appearance. The attribute vector consists of image intensity, Canny edge response, and geometric moments of each segmented structure (i.e., bone, soft tissue, lung, and vessel).

In general, simultaneous estimation of deformation fields for all phase images is very complicated and vulnerable of being trapped in local minima during the registration. Since different image points play different roles in registration, we select to focus only on a limited number of key points with distinctive attribute vectors (i.e., obtained by thresholding the Canny edge response in the attribute vector) and let them drive the whole registration. Both key points in the group-mean image, X = {x_i∣i = 1, … , P}, and in each phase image I_s, ${\mathit{Y}}_s=\left\{y_j^s\mid j=1,\dots ,Q_s\right\}$, are extracted, as overlaid in red and green in Fig. 1, respectively, to mutually guide the registration. With use of these key points, we can decouple the complicate registration problem into two simple sub-problems, i.e., (1) robust correspondence detection on the key points and (2) dense deformation interpolation from the key points.

Robust Correspondence Detection by Feature Matching

Inspired by [8], the key points X in the group-mean image G can be considered as the mean shape of the aligned phase images. Similarly, the respective shape in each phase image I_s can be represented by its key point set Y_s. Then, each key point $y_j^s$ in the phase image I_s can be regarded as a random variable drawn from a Gaussian mixture model (GMM) with its centers as the deformed mean shape X in I_s. In order to find the reliable anatomical correspondences, we also require the attribute vector $\stackrel{\rightharpoonup }{a}(x_i,G)$ of the key point x_i in the group-mean image to be similar with the attribute vector of its corresponding point in I_s. Thus, the discrepancy criterion is given as:

$$\eta (x_i,y_j^s)=\beta \cdot {\Vert f_s\left(x_i\right)-y_j^s\Vert }^2+(1-\beta )\cdot {\Vert \stackrel{\rightharpoonup }{a}(x_i,G)-\stackrel{\rightharpoonup }{a}(y_j^s,I_s)\Vert }^2,$$ (1)

where β controls the balance between shape and appearance similarities.

Soft correspondence assignment [8] is further used to improve the robustness of correspondence detection by calculating the matching probability for each candidate. Specifically, we use ${\pi }_{i,j}^s$ to denote the likelihood of $y_j^s$ being the true correspondence of x_i in the phase image I_s. It is worth noting that the correspondence assignment is hierarchically set for soft correspondence detection in the beginning, and turn to one-to-one correspondence in the final registration in order to increase the specificity of correspondence detection results. Accordingly, the entropy of ${\pi }_{i,j}^s$, i.e., ${\pi }_{i,j}^s\mathit{log}\left({\pi }_{i,j}^s\right)$, is set from large to small value with progress of registration. As we will explain later, this dynamic setting is controlled by introducing the temperature r to the entropy degree of ${\pi }_{i,j}^s$, which is widely used in annealing system [8].

Kernel Regression on Temporal Fibers

After detecting correspondence for each key point x_i, its deformed position f_s(x_i) in each phase image I_s can be regarded as the landmark of φ(x_i, t) at time t_s. Here we call this motion function φ(x_i, t) on the key point x_i as the temporal fiber, with the total number of temporal fibers equal to P (i.e., the number of key points in the group-mean image). In the middle of Fig. 1, we show the deformed group-mean shape in the space of each phase image. By sequentially connecting the deformed position f_s(x_i) along respiratory phases, a set of temporal fibers can be constructed, which are shown as blue dash curves in Fig. 1. The advantages of using temporal fibers include: 1) The modeling of temporal motion is much easier on the particular temporal fiber φ(x_i, t) than on the entire motion field φ(x, t); 2) The spatial correspondence detection and temporal motion regularization are unified along the temporal fibers. Here, we model the motion regularization on each temporal fiber as the kernel regression problem with kernel function ψ:

$$\mathit{arg}\underset{\phi }{\min }{L}_T\left(\phi (x,t)\right)={\sum }_{s=1}^N{\left[\phi \right(x,t)-\phi (x,t_s\left)\right]}^2\frac{1}{\sigma }\psi \left(\frac{t-t_s}{\sigma }\right),$$ (2)

Energy Function of Spatiotemporal Registration

The energy function in our spatiotemporal registration method is defined as:

$$E=\sum _{s=1}^N\left\{\sum _{i=1}^P\sum _{j=1}^{Q_s}[{\pi }_{i,j}^s\cdot \eta \left(x_i,y_j^s\right)+r\cdot {\pi }_{i,j}^s\cdot \mathit{log}\left({\pi }_{i,j}^s\right)]+{\lambda }_1{L}_s\left(f_s\right)\right\}+{\lambda }_2\sum _{i=1}^P{L}_t\left(\phi (x_i,t)\right),$$ (3)

where L_s(f_s) is the bending energy for requiring the deformation field f_s to be spatially smooth [8]. λ₁ and λ₂ are the two scalars to balance the strength of spatial smoothness L_s and temporal consistency L_T. The terms in the square bracket measures the alignment between the group-mean shape X and each shape Y_s in the s-th phase image, where r is used similarly as the temperature in annealing system to dynamically control the correspondence assignment from soft to one-to-one correspondence, as explained next.

Optimization of Energy Function

First, the spatial assignment ${\pi }_{i,j}^s$ can be calculated by minimizing E in Eq.3 w.r.t. ${\pi }_{i,j}^s$:

$${\pi }_{i,j}^s=\mathit{exp}\left\{-\frac{\eta \left(x_i,y_j^s\right)}{r}\right\}/{\sum }_{j=1}^{Q_s}\mathit{exp}\left(-\frac{\eta \left(x_i,y_j^s\right)}{r.}\right)$$ (4)

It is clear that ${\pi }_{i,j}^s$ is penalized in the exponential way according to the discrepancy degree $\eta \left(x_i,y_j^s\right)$ defined in Eq. 1. Notice that r is the denominator of the exponential function in Eq. 4. Therefore, when r is very high in the beginning of registration, although the discrepancy between x_i and $y_j^s$ is large, the key point $y_j^s$ still might have the chance to be selected as the correspondence of x_i w.r.t. I_s. In order to increase the registration accuracy, the specificity of correspondence will be encouraged by gradually decreasing the temperature r, until only the key points $y_j^s$ with the smallest discrepancy will be considered as the correspondences of x_i in the end of registration

Then, the correspondence of each x_i w.r.t. the shape Y_s in the s-th phase image can be determined as the weighted mean location of all $y_j^s$s, i.e., $f_s\left(x_i\right)={\sum }_{j=1}^{Q_s}{\pi }_{i,j}^s{y}_j^s$, by discarding all unnecessary terms with f_s(x_i) in Eq. 3. Recall that φ(x_i, t_s) = f_s(x_i), thus a set of temporal fibers can be constructed to further estimate the continuous motion function φ(x_i, t) by performing the kernel regression on a limited number of landmarks φ(x_i, t_s). Here, we use $\widehat{\phi }(x_i,t_s)$ to denote the deformed position of x_i in phase image I_s after kernel regression. The last step is to interpolate each dense deformation field f_s. TPS [8] is used to calculate dense deformation field f_s by considering {x_i} and $\left\{\widehat{\phi }\right(x_i,t_s\left)\right\}$ as the source and target point sets, respectively, which has the explicit solution to minimize the bending energy L_s(f_s). In the next section, we will introduce our super-resolution method for updating of the group-mean image G with guidance of the estimated f_ss. After that, the group-mean shape X can be extracted in the updated group-mean image G again to guide the spatiotemporal registration in next round.

2.2 High-Resolution Group Mean Image

Given the deformation field f_s of each phase image I_s, all image information of 4D-CT in different phases can be brought into the common space. Thus, the highly-redundant information among all registered phase images can be utilized to refine the high-resolution group-mean image by the technique of super resolution [9]. Here, we follow the generalized nonlocal-means approach [9] to estimate G(x) , whose objective function is to minimize the differences of local patches between high-resolution image G and each aligned low-resolution phase image I_s. Before super resolution, we define R_Is (y, d) as a local spherical patch at point y ∈ I_s with radius dmm. Then, the expression $R_{I_s}(y,d)\stackrel{\rightharpoonup }{a}$ results with a array of attribute vectors (in lexicographic ordering) in the local patch of phase image I_s. It is worth noting that we consider both registration and group-mean image construction in the physical space. Thus, given the same radius of dmm, the number of elements in the neighborhood of group-mean image is larger than that of any phase image because the image resolution of group-mean image is higher than each phase image. To be simple, we use R_G(x, d) denote the local spherical patch in the group-mean image space with radius dmm after down-sampled in accordance with the image resolution of each phase image. Thus, R_G(x, d) and R_Is(y, d) have the equal number of elements.

By taking account the possible misalignment, the calculation of G(x) is the weighted intensity average of not only all corresponding points f_s(x) in difference phase images I_s but also their neighboring points in the local spherical patch R_Is (f_s(x), d₁) with the radius d₁mm:

$$G\left(x\right)={\sum }_{s=1}^N{\sum }_{\nu \in R_{I_s}\left(f_s\right(x),d_1)}w(x,G,\nu ,I_s)\cdot I_s\left(\nu \right)/{\sum }_{s=1}^N{\sum }_{\nu \in T_{I_s}\left(f_s\right(x,d_1\left)\right)}w(x,G,\nu ,I_s)$$ (5)

where the weight $w(x,G,\nu ,I_s)=1-{\Vert R_G\left(x,d_2\right)\stackrel{\rightharpoonup }{a}-R_{I_s}\left(\nu ,d_2\right)\stackrel{\rightharpoonup }{a}\Vert }^2$ measures the regional similarity in another local sphere patch with radius d₂mm.

3 Experiments

To demonstrate the performance of our proposed lung motion estimation method, we evaluate its registration accuracy on DIR-lab data [2], by comparison with the pairwise diffeomorphic Demons [5] and B-spline based 4D registration algorithm [4].

Evaluation of Motion Estimation Accuracy on DIR-Lab Dataset

There are 10 cases in DIR-lab dataset, each case having a 4D-CT with six phases. The resolution for intra-slice is around 1mm×1mm, and the thickness is 2.5mm. For each case, 300 corresponding landmarks in the maximum inhale (MI) and the maximum exhale (ME) phases are available with manual delineations, and also the correspondences of 75 landmarks are provided for each phase. Thus, we can evaluate the registration accuracy by measuring the Euclidean distance between the reference landmark positions and those estimated by the registration method. It is worth noting that our registration is always performed on the entire 4D-CT, regardless in the evaluation of 300 landmarks in MI and ME phases or 75 landmarks in all 6 phases. The image resolution of the group-mean image is increased to 1mm×1mm×1mm.

The registration results by Demons, B-splines based 4D registration, and our algorithm on 300 landmarks between MI and ME phases are shown in the left part of Table 1. Note that we show the results only for the first 5 cases, since the authors in [4] reported their results only for these 5 cases. It can be observed that our method achieves the lowest mean registration errors. Also, the mean and standard deviation on 75 landmark points over all six phases by the two 4D registration methods, the B-spline based 4D registration algorithm and our registration algorithm, are shown in the right part of Table 1. Again, our method again achieves the lower mean registration errors.

Table 1.

The mean and standard devidation of registration error (mm) on 300 landmark points between maximum inhale and exhale phases, and on 75 landmark points in all six phases.

	300 landmark points				75 landmark points
#	Initial	Demons	Bspline4D	Our method	Initial	Bspline4D	Our Method
1	3.89(2.78)	2.91(2.34)	1.02 (0.50)	0.64(0.61)	2.18(2.54)	0.92 (0.66)	0.51(0.39)
2	4.34(3.90)	4.09(3.67)	1.06 (0.56)	0.56(0.63)	3.78(3.69)	1.00 (0.62)	0.47(0.34)
3	6.94(4.05)	4.21(3.98)	1.19 (0.66)	0.70(0.68)	5.05(3.81)	1.14 (0.61)	0.55(0.32)
4	9.83(4.85)	4.81(4.26)	1.57 (1.20)	0.91(0.79)	6.69(4.72)	1.40 (1.02)	0.69(0.49)
5	7.48(5.50)	5.15(4.85)	1.73 (1.49)	1.10(1.14)	5.22(4.61)	1.50 (1.31)	0.82(0.71)

Evaluation of High-Resolution Group-Mean Image

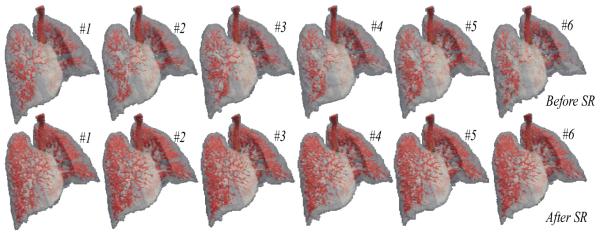
After obtaining the high-resolution group-mean image, we can map it back onto the original phase image space. Since the estimated group-mean image has richer information than any phase image in 4D-CT, some missing anatomical structures in the individual phase image could be recovered after mapping our group-mean image with high resolution onto each phase image space. The upper row in Fig. 2 shows the vessel trees from MI (#1) to ME phases (#6) in the original 4D-CT (Here, No. 4 case (with large lung motion) in DIR-Lab dataset is used as an example). Note that the vessels are extracted by setting threshold (top 10%) on the hessian map and further morphologically processed. Using the same technique, the vessel trees are also extracted from the deformed group-mean images at all phases and shown in the lower row of Fig. 2. It can be observed that (1) more details on vessels have been recovered by employing the super resolution technique in our method, and (2) the vessel trees are temporally consistent along the respiratory lung motion.

Fig. 2.

The vessels tree in all respiratory phases before and after super resolution.

4 Conclusion

In this paper, a novel motion estimation method has been presented to measure lung respiratory motion in 4D-CT. Our method is completed by repeating two iterative steps, i.e., (1) simultaneously aligned all phase images onto the common space by spatiotemporal registration and (2) estimating the high-resolution group-mean image with improved anatomical details by super resolution technique. By using our method, not only the estimated motion accuracy, but also the temporal consistency, has been greatly improved, compared to the other two state-of-the-art registration methods.