Abstract
Meta-analysis of genome-wide association studies involves testing single nucleotide polymorphisms (SNPs) using summary statistics that are weighted sums of site-specific score or Wald statistics. This approach avoids having to pool individual-level data. We describe the weights that maximize the power of the summary statistics. For small effect-sizes, any choice of weights yields summary Wald and score statistics with the same power, and the optimal weights are proportional to the square roots of the sites' Fisher information for the SNP's regression coefficient. When SNP effect size is constant across sites, the optimal summary Wald statistic is the well-known inverse-variance-weighted combination of estimated regression coefficients, divided by its standard deviation. We give simple approximations to the optimal weights for various phenotypes, and show that weights proportional to the square roots of study sizes are suboptimal for data from case-control studies with varying case-control ratios, for quantitative trait data when the trait variance differs across sites, for count data when the site-specific mean counts differ, and for survival data with different proportions of failing subjects. Simulations suggest that weights that accommodate inter-site variation in imputation error give little power gain compared to those obtained ignoring imputation uncertainties. We note advantages to combining site-specific score statistics, and we show how they can be used to assess effect-size heterogeneity across sites. The utility of the summary score statistic is illustrated by application to a meta-analysis of schizophrenia data in which only site-specific p-values and directions of association are available.
Keywords: combining GWAS, effect-size heterogeneity, meta-analysis, noncentrality parameter, score statistics, Wald statistics
Introduction
Combining data from multiple genome-wide association studies (GWAS) of a common outcome has emerged as a major tool for identifying susceptibility loci for human disease and other conditions [Scott et al., 2007; Zeggini et al., 2007; Shi et al., 2009]. The goals are to discover new variants missed by the individual studies, to identify variants for outcomes not considered when the data were collected (e.g. cancer survival), and, for associated variants, to assess effect-size and its possible variation across sites. A challenge to achieving these goals is the need to assess and accommodate inter-site differences in study characteristics, such as demographic attributes of the populations studied, phenotypic aspects such as disease severity and extent of censoring of survival data, the SNPs included in the genotyping platforms used, and the choice and coding of covariates in need of adjustment.
The pooled analysis of individual-level data on phenotypes, genotypes and covariates has several advantages. Quality control can be implemented uniformly for all sites, and SNP genotypes can be imputed using data from all sites. Covariates common to multiple studies can be coded uniformly and their regression coefficients can be estimated with all available data. Optimal likelihood-based methods can be used to test whether SNP regression coefficients are nonzero and whether they vary across study sites. Offsetting these advantages is the labor involved in assembling the raw data from each site and coding common covariates, and privacy issues which could limit the sharing of genotypes.
An alternative to pooled analysis is the meta-analysis of site-specific test statistics, each having approximately a standard normal distribution under the null hypothesis of no association. Here each site types or imputes genotypes for a common set of SNPs, and then calculates a covariate-adjusted statistic for each SNP. The site-specific statistics are either Wald statistics (ratios of regression coefficient estimates to their estimated standard deviations (SDs), or score statistics (ratios of efficient scores to estimates of their null SDs) [Soranzo et al., 2009; Tanaka et al., 2009]. The coordinating center then computes a weighted sum of these statistics as a summary test statistic for the SNP [Cantor et al., 2010]. For reviews of issues in GWAS meta-analysis, see [Ioannidis 2007; Ioannidis et al., 2007; de Bakker et al., 2008; Guan and Stephen, 2008; Zeggini and Ioannidis, 2009; Cantor et al., 2010].
When SNP effect size is constant across sites, the optimal summary Wald statistic is the well-known inverse-variance-weighted combination of estimated regression coefficients, divided by its estimated standard deviation [Cohran 1954]. However there are practical advantages to combining score statistics rather than Wald statistics for GWAS meta-analyses. First, the score statistics do not require iterative parameter estimates for each SNP to be tested. Estimates for the site-specific covariate effects need be calculated just once under the global null hypothesis of no effect for any SNP; thus score statistics provide fast assessment of the statistical significance of large numbers of SNPs. Second, a SNP score statistic can be computed even when the site has provided only the SNP's p-value and direction of association. Third, the summary score statistic may be easier to interpret when the sites differ with respect to the covariates included in their regression models or with respect to their phenotype definition, measurement or coding. For example, a GWAS of nicotine addiction among current and former smokers might include sites whose outcome is a count of smoking cessation attempts, and other sites that simply classified subjects according to presence or absence of a successful cessation attempt. For a meta-analysis such as this, a combination of site-specific score statistics may be easier to interpret than a combination of site-specific Wald statistics, since the SNP regression coefficients in the latter are not comparable. Finally, site-specific score statistics have straightforward extensions to accommodate uncertainty due to imputation of unobserved genotypes, and we shall show that they can be used to assess heterogeneity of effect-size across sites.
Here we focus on optimal weights for combining site-specific statistics to identify new variants and, for associated variants, to assess possible effect-size variation across sites. Asymptotically optimal weights for combining Wald statistics have been known for more than half a century [Cochran 1954; DerSimonian and Laird, 1986]. Surprisingly however, despite their practical advantages, optimal weights for combining score statistics are not well known. In fact, some investigators suggest or use weights proportional to the square roots of the study-specific sample sizes [Soranzo et al., 2009; Willer et al., 2010; Hu et al., 2011]. We show that this strategy can be suboptimal when combining data from sites whose phenotypes have different null distributions. Instead, for the small effect-sizes expected of GWAS meta-analysis, the optimal weights for combining score statistics are essentially the same as those used to combine Wald statistics. We provide explicit forms for the optimal weights for a general class of phenotypes that includes binary outcomes, quantitative traits, counts of events and censored survival outcomes.
In the following Methods section we begin by reviewing the score and Wald statistics for testing the null hypothesis of no SNP-phenotype association at a single site, with application to case-control studies, quantitative traits, count data and censored survival data. We also show how the site-specific score statistics can be extended to handle imputation uncertainties, as noted by Marchini et al., [2007]. Then, for each of these phenotypes, we describe the optimal weights for combining site-specific score or Wald statistics. We also extend the weights to handle SNP effect-sizes that vary across sites, and we show how the site-specific score statistics can be used to assess inter-site heterogeneity. The Methods section is followed by an evaluation of power for various summary score and Wald statistics, based on simulated case-control and censored survival data. An application to schizophrenia data shows that for binary outcomes, the score statistics can be used to assess inter-site effect-size heterogeneity even when only site-specific SNP p-values and direction of association are available. The final section concludes with a brief discussion.
Methods
Score and Wald Statistics for One Site
For simplicity we model the effects of each SNP as additive on an appropriate scale (the so-called trend or gene dosage model), though other genotype models can be used. Let (y, g, x) = {(yj, xj, gj), j = 1, …, n} represent the data for the n study subjects. For subject j, yj is the phenotype, xj is a column vector of covariates whose first component may be one to accommodate an intercept, and gj = (gj1, gj2, …) is a vector of minor allele counts for each of the SNPs under study. We focus on testing association for just one of these SNPs, and omit its subscript. We assume that the loglikelihood ℓ(y∣x, g; θ) for the phenotypes y conditional on covariates x and genotypes g depends on a parameter θ = (α, β). Here α is a s-dimensional vector of parameters corresponding to an intercept and/or any covariates used by the site, and β specifies the trend relating phenotype to SNP minor allele count.
We wish to test the null hypothesis H0: θ = θ0 = (α, 0). To do so, we introduce the Fisher information for θ, given by
| (1) |
Here iαα is the s × s matrix whose entries are the negative expectations of the second derivatives of the loglikelihood function for θ with respect to α, and the other submatrices are defined analogously. Also let denote the (s + 1)-dimensional score vector whose entries are the derivatives of the loglikelihood function with respect to θ = (α, β). The covariate-adjusted efficient score for testing β = 0 is Uβ = Uβ (α̂(0), 0), where α̂(0) satisfies Uα (α̂k (0), 0) = 0. Under H0 and mild regularity conditions [Cox and Hinkley, 1979], Uβ has an asymptotic Gaussian distribution with mean zero and variance
| (2) |
evaluated at (α̂(0), 0).
The score and Wald statistics are
| (3) |
where îβ is a consistent estimate of iβ evaluated at β = 0, β̂ is the maximum likelihood estimate (MLE) of β, and evaluated at β̂. The two statistics are locally asymptotically equivalent, i.e., they are asymptotically equivalent when β = 0 and are approximately so when β is small in absolute value [Cox and Hinkley, 1979]. Their noncentrality parameters (NCPs) are , with iβ evaluated at θ0 = (α, 0) for Zscore and at θ = (α, β) for ZWald. In the following we shall approximate iβ for the Wald statistic by evaluating it at its null value, and refer to a common NCP ξ for both statistics.
We now specialize the score and Wald statistics to specific phenotypes of relevance to GWAS. We first consider phenotypes whose relation to genotypes and covariates can be described by generalized linear models (GLMs) [McCullagh and Nelder, 1989]. Special cases of particular relevance are the binary phenotypes of case-control studies, quantitative traits such as height or weight, and counts of events such as attempts to quit smoking, and censored survival data.
Example: generalized linear models
GLMs assume that the mean but not the dispersion parameter of the phenotype distribution depends on genotypes and covariates, so that their effects can be modeled as a function of a linear predictor ηj = αxj + βgj. The first component of the covariate vector xj may equal one, in order to accommodate an intercept. The loglikelihood is
| (4) |
where a (·), b (·) and c (·) are known functions, and ϕ is the dispersion parameter of the model. The score for β corresponding to (4) is
| (5) |
where μ̂j is the fitted mean of y under H0, and φ̂ is a consistent estimate of ϕ. The null Fisher information (1), with θ = θ0, and ηj = αxj is
| (6) |
In the absence of covariates xj = 1, ηj = α1 where α1 is the intercept, and (6) reduces to
| (7) |
where p = 1 − q is the SNP minor allele frequency (MAF). Using (7) in (2), we find that the null Fisher information for β is
| (8) |
For binary phenotypes yj is coded as one if subject j has the trait and zero otherwise, and the logistic model corresponds to ϕ = a (ϕ) = c (y; ϕ) = 1, and b (ηj) = ln [1 + eηj]. In a case-control study with n1 cases and n0 = n − n1 controls, b″ (α1) can be estimated consistently by n0n1/n2.
Substituting these expressions in (8) gives
| (9) |
For quantitative traits whose distribution is (possibly after transformation) Gaussian with mean μj = ηj and variance ϕ, we have a (ϕ) = ϕ, and . Thus b″ (α1) = 1. Substitution of these values for a (ϕ) and b″ (α1) into (8) gives
| (10) |
where ϕ̂ is a consistent estimate of the phenotype variance.
For Poisson count data, a (ϕ) = 1, b (ηj) = eηj and c (y; ϕ) = 0. Thus b″ (α1) = eα1 = μ, where μ is the null mean of the counts. Substituting these values into (8) gives
| (11) |
Example: censored survival data
Here the data are where for subject j, tj is survival time and εj is a failure indicator. We assume independent times to failure and censoring, each with hazard that may vary across studies. We also assume that the failure distribution follows a proportional hazards model of the form h (t; xj, gj) = h* (t) eαxj+βgj, where h* (t) is the baseline hazard, and that the m failures occur at distinct times. Inferences are based on the log of a partial likelihood function for β, given by , where m is the number of failures, gi1 and xi1 are, respectively, the genotype and covariates of the ith failure, and Ri is the set of subjects at risk just before this failure, i = 1, …, m. The corresponding score for β is
| (12) |
In the absence of covariates, the null Fisher information for β, as given by (2) and (1), is
| (13) |
Accommodating imputed genotypes
Meta-analysis of site-specific statistics requires local imputation at the study sites. This involves calculating posterior probabilities Pjg for each subject's unobserved SNP minor allele count g, with Pj0 + Pj1 + Pj2 = 1. Here Pjg is the conditional probability that subject j has allele count g, given the observed genotype data Obs, and the haplotypes in a reference panel such as HapMap2 [International HapMap Consortium et al., 2007]. Louis [1982] provided a likelihood-based extension to the score statistic to accommodate this imputation. Inferences are based on the probability of phenotypes conditional on observed genotype data Obs, and covariates x:
| (14) |
Here g denotes a vector of genotypes for the nk subjects, and the posterior probabilities Pr (g∣Obs) = Pr(g) / Σg′∈G Pr (g′), where Pr (g) is based on the Hardy-Weinberg MAF, and the sum is taken over genotypes in the set G consistent with the observed data Obs and the haplotypes in the reference panel. The posterior probabilities can be computed using available imputation software [Li and Abecasis 2006; Scheet and Stephens, 2006; Browning BL and Browning SR, 2009; Howie et al., 2009]. As shown by Louis [1982], the score for β is
| (15) |
where is the complete data score and the expectation is taken with respect to the posterior distribution Pr (g∣Obs) for the SNP of interest. The null variance of Uβ is given by (2) and (1), but with the Fisher information for the observed data reduced by a penalty due to the uncertainty in genotypes:
| (16) |
where Jc is the negative of the second derivative matrix for the complete data. The score statistic is Zscore = Uβ/îβ;where îβ is obtained from (2) and (16).
The score Uβ of (5) and (12) for GLMs and survival data depends linearly on the genotypes gj. Thus in the presence of unobserved genotypes, the posterior expectation (15) can be obtained simply by replacing the unobserved allele counts with their posterior means, as noted by Schaid et al., [2002] and Marchini et al., [2007]. In addition, the entries of the information matrix (16) are quadratic forms in the genotypes. Thus their posterior expectations can be computed as functions of the first and second moments of the posterior genotype distributions. In practice however, imputation uncertainties are generally ignored for both score and Wald statistics; instead, subjects' unknown minor allele counts are replaced by their posterior means Pj1 + 2Pj2.
Meta-Analysis of Data from K Sites
Suppose now that each of K sites has computed a score or Wald statistic using a regression model that may include an intercept and/or covariates. We wish to combine these site-specific statistics into a single summary statistic to assess the overall evidence for or against association between a SNP and a given phenotype. We assume that subjects participate in only one study (see [Lin and Sullivan, 2009] for methods applicable to studies with overlapping study subjects). We first describe the weights optimal under the assumption that the SNP effect-size β is common across sites (homogeneous effect-size), and then consider the weights optimal when the effect-sizes β1, …, βK vary across sites (heterogeneous effect-size).
Homogeneous effect-size
Here the null hypothesis to be tested is H0: θ = θ0 = (α1, …, αK, 0), where αk is the sk-dimensional nuisance parameter for study k, k = 1, …, K. The summary statistics used for this purpose in GWAS meta-analysis are weighted sums , where Zk is either a site-specific score statistic or a site-specific Wald statistic, and where the weights wk are nonnegative constants with . Under H0, both summary statistics, Zscore and ZWald, have standard Gaussian distributions asymptotically [Cox and Hinkley, 1979]. The optimal weights wk are defined as those that maximize the summary statistic's NCP, given by ξ = Σkwkξk, where ξk is the NCP for the score and Wald statistics at site k, k = 1, …, K. We have seen that the NCP for both site-specific score and site-specific Wald statistics are ; thus . A straightforward application of the Cauchy-Schwartz inequality shows that the weights wk that maximize ξ under local alternatives are proportional to . Thus the optimal summary score and Wald statistics are given by
| (17) |
They are asymptotically equivalent for testing θ = θ0 under the null hypothesis and under local alternatives. Replacing the the terms Zk:score with the score statistics of (3) in the first equality of (17) shows that the summary Zscore is just the well-known stratified score statistic, i.e., the one obtained from the sum of the K loglikelihood functions:
For case-control data, Zscore is the Mantel-Haenzel test for trend in a 2 × K table [Breslow and Day, 1980]. Moreover, replacing the terms Zk:Wald with the Wald statistics of (3) in the second equality of (17) shows that the summary ZWald is the commonly deemed inverse-variance-weighted summary statistic proposed by Cochran [1954] and given by
| (18) |
The term “inverse-variance-weighted” refers to the fact β̂ is a weighted sum of the site-specific regression coefficients β̂k, weighted in inverse proportion to their estimated variances:
Table 1 gives the optimal weights for case-control data, quantitative trait data, Poisson count data and censored survival data, when the participating sites do not include covariates in the model, and do not adjust for imputation. The weight wk for a given site and phenotype is proportional to the square root of the corresponding estimated null information îkβ for β, as given by the appropriate choice of expressions (9-13). In contrast, the weights based on study size are proportional to . Comparison of these size-based weights to those in Table 1 shows that, even though SNP allele frequencies may be similar across sites, the size-based weights are suboptimal for case-control data from studies with varying case-control ratios, for quantitative trait data with varying trait variances, for count data with varying null expected counts, and for censored survival data with varying numbers of failures. Since the variance of a quantitative trait depends on the covariates included in the regression model which may vary across sites, using a common trait variance may in some circumstances be substantially suboptimal.
Table 1. Optimal Weights in GWAS Meta-analysis without Covariates.
| Phenotype | Optimal Weight wk for kth Studya | |
|---|---|---|
| Case-control Statusb |
|
|
| Quantitative Traitc |
|
|
| Poisson Count Datad | (nkμkpkqk)1/2 | |
| Censored Survival Datae | (mkpkqk)1/2 |
wk are optimal under effect size homogeneity across sites, and are given up to a proportionality factor determined by the constraint . pk = 1-qk is the SNP MAF and nk is the number of subjects in study k.
nkj is the number of cases (j=1) and controls (j=0).
ϕk is the trait variance.
μk is the null expected count
mk is the number of failures.
In the presence of site-specific adjustment for covariates and/or imputation uncertainty, the optimal weights are more complex than those shown in Table 1. According to (17), they are proportional to the square roots of the null SNP information îkβ, which depend on the covariate distributions, covariate effects, and imputation uncertainty specific to each site. In principal, the values îkβ could be provided by the sites. Instead, Zaitlen and Eskin [2010] have suggested accommodating imputation uncertainty by incorporating in each site's weight an estimate of the correlation coefficient rk between true and imputed SNP allele counts. In the following section we use simulations to evaluate the power of this strategy.
Heterogeneous effect-size
Site-specific effect-size variation is plausible for several reasons. First, the studies may have used different genotyping platforms with different numbers and locations of SNPs. This results in differences across sites in levels of genotype measurement error, creating different levels of regression coefficient attenuation across sites. Second, when covariates or their coding differ across sites, different levels of control for confounding can affect SNP effect-sizes. For example, genetic ancestry may be associated with both phenotype and genotypes, and variable control for ancestry may induce differential levels of residual confounding. Third, for survival data, site-specific variation may occur if effect-size changes over time and the studies differ in level and type of censoring. Finally, the SNP of interest may interact with other risk factors whose prevalences vary across sites, which would cause variation in effect-size.
The site-specific Wald statistics have the form Zk:Wald = β̂k/SD (β̂k), where β̂k is the MLE for β and . These quantities lend themselves naturally to evaluating SNP effect-size heterogeneity across sites, using the methods of Cochran [1954] and DerSimonian and Laird [1986]. Here we show that the components of the site-specific score statistics also can be used for this purpose. Specifically, when βk is small in absolute value, the asymptotic mean φk of Ukβ can be approximated as φk∼ βkikβ (see Appendix). This approximation suggests estimating βk by , with SD (β̂k) estimated as , k = 1, …, K. Then Cochran's homogeneity test can be applied with β̂k equal to either the MLE or the quantity .
For either the score-based or Wald-based estimates β̂1, …, β̂K, Cochran's test is based on the statistic Q = Σkîk (β̂k − β̂)2, where β̂ is given by (18). Under the homogeneity hypothesis β1 = … βK = β, Q has a chi-squared distribution on K − 1 degrees of freedom (DF). When homogeneity is rejected, DerSimonian and Laird [1986] propose estimating the inter-site variance τ2 of the βk as
where , r = 1, 2. The overall effect-size is estimated as
Corresponding summary statistics for testing β1 = … = βK = 0 are
| (19) |
and Zk denotes either Zk:score or Zk:Wald. When Cochran's test does not reject homogeneity and τ̂2 is set to zero, the two summary statistics (19) reduce to their usual forms (17) optimal for homogeneous effects.
In conclusion, one can choose between four types of summary statistics, each formed as a weighted sum of site-specific statistics. The four summary statistics differ according to the site-specific statistics (score vs Wald) and whether the weights are chosen to be optimal under effect-size homogeneity (ZHM) or heterogeneity (ZHT).
Simulations
We simulated case-control and survival data to evaluate the performances of the optimal summary score and Wald statistics, and to compare them to that of the size-weighted summary ZSZ, obtained using weights proportional to the square roots of study sizes. For each replication, we generated data assuming both homogeneous and heterogeneous effect-sizes, with and without imputation error, and then computed the various summary statistics. We flagged those exceeding certain thresholds, and then computed for each statistic the proportion of all replications in which it was flagged.
Type-1 Error
To evaluate type 1 error, we compared nominal to empirical type-1 error rates, defined as the proportion of replications in which the summary test statistic exceeded the standard Gaussian threshold for the nominal two-sided p-value. We considered two null hypotheses. The first homogeneity null hypothesis specifies that the true values of the βk satisfy β1 = … = βK = 0 The second heterogeneity null hypothesis specifies that the βk are a random sample from a Gaussian distribution with mean zero and variance τ2 > 0. Under the homogeneity null hypothesis, we found good agreement between nominal and empirical p-values for all summary test statistics considered. In contrast, under the heterogeneity null hypothesis all summary statistics showed inflated empirical error rates relative to their nominal values, with the extent of inflation somewhat attenuated when the summary statistics were heterogeneity-weighted compared to homogeneity-weighted (data not shown). We shall return to this finding after a comparison of test power.
Power
Case-control data
We simulated the meta-analysis of K = 3 case-control studies having the sample sizes shown in Table 2. We generated genotypes for a single SNP assuming Hardy-Weinberg allele frequencies, and then used a logistic regression model with study-specific intercepts (α1, α2, α3) = (−3.0, −2.5, −2.5) and one of three effect-size triples (β1, β2, β3) to generate case and control phenotypes until we had achieved the targeted numbers of cases and controls. Two triples correspond to effect-size homogeneity, as given by β1 = β2 = β3 = ln (1.3) = 0.26, and β1 = β2 = β3 = ln (1.4) = 0.34. The third triple (β1, β2, β3) = (0, 0.34, 0.26) corresponds to effect-size heterogeneity across the three sites. Power was taken as the proportion of the 1000 replications in which the test statistic exceeded the threshold for a p-value of 10−8.
Table 2. Test Powera in Meta-analysis of Three Case-control Studies (α = 10-8).
| Study-site | 1 | 2 | 3 | Summary Test Statistic | |||||
|---|---|---|---|---|---|---|---|---|---|
| Cases | 500 | 1000 | 500 | Score-based | Wald-based | ||||
| Controls | 500 | 1000 | 5000 | ZHMb | ZHTc | ZSZd | ZHM | ZHT | ZSZ |
|
Odds-ratio MAF |
1.3 | 1.3 | 1.3 | ||||||
| 0.2 | 0.2 | 0.2 | 0.356 | 0.349 | 0.301 | 0.348 | 0.343 | 0.291 | |
| 0.3 | 0.3 | 0.3 | 0.638 | 0.632 | 0.563 | 0.634 | 0.629 | 0.555 | |
| 0.3 | 0.3 | 0.2 | 0.543 | 0.537 | 0.426 | 0.530 | 0.527 | 0.418 | |
|
| |||||||||
|
Odds-ratio MAF |
1.4 | 1.4 | 1.4 | ||||||
| 0.2 | 0.2 | 0.2 | 0.887 | 0.886 | 0.840 | 0.886 | 0.885 | 0.836 | |
| 0.3 | 0.3 | 0.3 | 0.974 | 0.974 | 0.951 | 0.974 | 0.974 | 0.949 | |
| 0.3 | 0.3 | 0.2 | 0.953 | 0.950 | 0.908 | 0.951 | 0.950 | 0.904 | |
|
| |||||||||
|
Odds-ratio MAF |
1.0 | 1.4 | 1.3 | ||||||
| 0.2 | 0.2 | 0.2 | 0.188 | 0.086 | 0.170 | 0.185 | 0.086 | 0.164 | |
| 0.3 | 0.3 | 0.3 | 0.457 | 0.230 | 0.420 | 0.452 | 0.221 | 0.409 | |
| 0.3 | 0.3 | 0.2 | 0.323 | 0.168 | 0.260 | 0.309 | 0.166 | 0.254 | |
fraction of 1000 replications rejecting H0 at α = 10-8
homogeneity weights of equation (17)
heterogeneity weights of equation (19)
weights proportional to square root of study size
Table 2 shows power for summary score and Wald statistics with weights determined by assumptions of homogeneous (ZHM) and heterogeneous (ZHT) effect-sizes, and with size-based weights (ZSZ). As expected given their asymptotic equivalence, the score-based and Wald-based summary statistics performed similarly for any given choice of weights. For all types of data, the homogeneity-weighted summary statistics were most powerful. When the data were generated under the homogeneous effect-size assumption, both homogeneity- and heterogeneity-weighted statistics ZHM and ZHT consistently outperformed the size-weighted statistic ZSZ. However when the data were generated according to heterogeneous effect-sizes, the heterogeneity-weighted statistic ZHT performed poorly compared to the other two. This finding, which is consistent with that reported in other applications [Clayton and Hills, 1993], reflects power loss due to sampling error in estimating the inter-site effect-size variance τ2.
Survival data
We also generated censored survival data for a total of 2,483 subjects of European ancestry from Heidelberg Germany, Ontario Canada, and Seattle US who have been genotyped for 600,000 SNPs using the Illumina 610Quad chip as part of an ongoing GWAS of early-onset breast cancer. To mimic a meta-analysis based on K = 6 study sites, we split the subjects from each of the three regions into two subsets, which yielded six sites with the sample sizes shown in Table 3. We focused on 1000 SNPs in a 6-MB region of chromosome 2 (positions 1,000,713 to 6,488,209). To generate subjects' survival times, we assumed independent exponentially distributed times to failure and censoring with site-specific baseline and censoring hazards λk, μk, k = 1, …, 6, independent of nongenetic covariates. These values are shown in Table 3. Subjects who had not failed by time t = 1 were censored at that time. We assumed that the site-specific failure hazards also depend, via a proportional hazards model, on the minor allele counts of SNP rs17360123 at position 5,531,665 (MAF = 0.2) and SNP rs4072375 at position 3,565,156 (MAF = 0.4). Specifically, we assumed that the failure hazard at site k was λk exp(βkgkj), where gkj is the SNP minor allele count for the jth subject at site k, k = 1, …, 6. For the homogeneity model we took the common β to be 0.25, 0.30 and 0.35, and for the heterogeneity model we took β = 0 for sites 1 and 2, and β = 0.35 for the remaining sites.
Table 3. Sample Sizes and Hazard Rates for Data from Six Survival Studies.
| Study | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Sample size | 468 | 470 | 328 | 395 | 296 | 526 |
| λk | 0.105 | 0.127 | 0.223 | 0.274 | 0.510 | 0.693 |
| μk | 2.000 | 1.500 | 1.000 | 0.090 | 0.200 | 0.075 |
| Expected no failures | 20.5 | 23.9 | 63.0 | 90.7 | 108.0 | 254.4 |
λk and μk are failure and censoring hazards, respectively, for study k, k=1, …, 6
Table 4 shows the power of homogeneity-weighted, heterogeneity-weighted and size-weighted summary score and Wald statistics under these generating models. The same patterns found for the case-control data in Table 2 are evident here: the homogeneity weighted summary statistics are consistently most powerful, and when the data were generated with homogeneous SNP effects, the size-weighted statistic is least powerful. In the presence of heterogeneous SNP effects, however, the heterogeneity-weighted test statistic is least powerful, most likely because of power loss associated with error in estimating the variance parameter τ2.
Table 4. Test Powera in Meta-analysis of Six Survival Studies.
| Associated SNP | MAF | Log hazard ratio β | Summary Test Statistic | |||||
|---|---|---|---|---|---|---|---|---|
| Score-based | Wald-based | |||||||
| ZHMb | ZHTc | ZSZd | ZHM | ZHT | ZSZ | |||
| rs17360123 | 0.2 | 0.25 | 0.264 | 0.202 | 0.172 | 0.265 | 0.208 | 0.162 |
| 0.30 | 0.530 | 0.449 | 0.416 | 0.550 | 0.487 | 0.403 | ||
| 0.35 | 0.827 | 0.709 | 0.716 | 0.841 | 0.792 | 0.709 | ||
| Heterogeneous βe | 0.294 | 0.117 | 0.201 | 0.302 | 0.129 | 0.194 | ||
| rs4012375 | 0.4 | 0.25 | 0.463 | 0.422 | 0.333 | 0.465 | 0.429 | 0.318 |
| 0.30 | 0.787 | 0.719 | 0.673 | 0.787 | 0.738 | 0.665 | ||
| 0.35 | 0.954 | 0.884 | 0.910 | 0.956 | 0.904 | 0.907 | ||
| Heterogeneous βe | 0.566 | 0.204 | 0.416 | 0.579 | 0.232 | 0.401 | ||
fraction of 1000 replications in rejecting H0 at α = 10-5
homogeneity weights of equation (17)
heterogeneity weights of equation (19)
weights proportional to square root of study size
β = 0 for sites 1,2, and β = 0.35 for studies 3-6
The poor power of the heterogeneity-weighted test statistics mitigates against their use in GWAS meta-analysis. In general, these statistics are used to guard against false positives when the null hypothesis specifies varying site-specific effect-sizes whose overall mean is zero. However the primary null hypothesis in the GWAS setting specifies zero SNP effect-size at all K sites. This suggests the strategy of testing all SNPs using a homogeneity-weighted summary statistic, and investigating heterogeneity for those SNPs whose p-values suggest departures from this primary null hypothesis.
Finally, we evaluated how imputed genotypes affect the power of the homogeneity-weighted score-based test by masking and imputing some sites' genotypes in regions containing SNPs rs17360123 and rs4072375. These two SNPs were assumed associated with survival with a common effect-size β = 0.35 across the six sites. We masked and imputed either: i) the associated SNPs and their nearest flanking markers (a total of three SNPs imputed); or ii) the associated SNPs and their nearest two flanking markers (a total of five SNPs imputed). SNPs were masked and imputed for: a) one study (study 1); b) three studies (studies 1,3,5); and c) five studies (studies 1-5). We conducted the imputations using the HapMap2 reference panel in an eight megabase region containing 9262 SNPs. The five studies with masked SNPs had estimated correlation coefficients between imputed and actual rs17360123 minor allele counts of (r̂1, …, r̂5) = (0.62, 0.66, 0.57, 0.56, 0.60) when three SNPs were imputed, and (0.59, 0.58, 0.51, 0.52, 0.49) when five SNPs were imputed. The corresponding values for rs4072375 were (0.82, 0.77, 0.57, 0.62, 0.68) and (0.54, 0, 58, 0, 49, 0.46, 0.45). These estimates were obtained as described by Li and Abecasis [2006]. In total, we considered the 12 data sets described in Table 5. We imputed all masked SNPs using the Caucasian data from the HapMap2 reference panel and the imputation software BEAGLE [Browning BL and Browning SR, 2009] (http://faculty.washington.edu/browning/beagle/beagle.html). We evaluated the power of three statistics adapted from the homogeneity-weighted summary score statistic ZHM. The first is the likelihood-based score statistic given by equations (15, 16) that accounts for imputation uncertainty. The second statistic replaces subjects' unobserved SNP minor allele counts by their posterior means, ignoring imputation uncertainties. The third statistic also is based on subjects posterior mean minor allele counts, but with weights proportional to , a strategy similar to that proposed by Zaitlen and Eskin [2010].
Table 5. Test Powera in Score-based Meta-analysis of Six Survival Studies with SNP Imputation.
| Associated SNP | SNPs Imputedb | Sites with Imputed SNPs | Imputation Method | ||
|---|---|---|---|---|---|
| Likelihood-basedb | Posterior Meanc | rbasedd | |||
| rs17360123 MAF = 0.2 | Threee | Site 1 | 0.802 | 0.803 | 0.798 |
| Sites 1,3,5 | 0.777 | 0.768 | 0.722 | ||
| Sites 1-5 | 0.737 | 0.726 | 0.649 | ||
| Fivee | Site 1 | 0.803 | 0.802 | 0.798 | |
| Sites 1,3,5 | 0.767 | 0.757 | 0.692 | ||
| Sites 1-5 | 0.715 | 0.697 | 0.591 | ||
| rs4072375 MAF = 0.4 | Three | Site 1 | 0.947 | 0.945 | 0.942 |
| Sites 1,3,5 | 0.918 | 0.918 | 0.896 | ||
| Sites 1-5 | 0.854 | 0.843 | 0.789 | ||
| Five | Site 1 | 0.934 | 0.933 | 0.933 | |
| Sites 1,3,5 | 0.836 | 0.839 | 0.818 | ||
| Sites 1-5 | 0.654 | 0.647 | 0.601 | ||
fraction of 1000 replications rejecting H0 at α = 10-5, with data generated under a common effect size β = 0.35
obtained from equations (15,16)
masked genotypes replaced by mean of posterior distributions
using posterior means with weights proportional to rkik1/2
masking 3 SNPs (causal SNP plus one flanking SNP each side) or 5 SNPs (causal SNP plus 3 flanking SNPs each side)
Table 5 shows power for each of these three summary statistics as applied to each of the 12 data sets. For comparison, the power for the optimal tests with completely observed data was 0.827 for SNP rs17360123 and 0.954 for SNP rs4012375 (Table 4). Several results are noteworthy. First, as expected, the power of all tests dropped increasingly with the masking of increasingly many SNPs at increasingly many sites. Moreover the rs4012375 SNP suffers more power loss from masking five rather than three SNPs than does rs17360123. This difference mirrors the correspondingly larger loss of imputation accuracy for rs4012375 than rs17360123, as measured by their estimated correlation coefficients, described in the preceding paragraph. Second, substituting posterior means performed as well as the likelihood-based score statistics. In fact, substituting the posterior means for the unobserved genotypes gives exactly the observed data score (15), since the complete data score is a linear function of the unobserved genotypes. Moreover the Fisher information computed by substituting posterior means for unobserved genotypes is an approximation to the Fisher information for the observed data, given by (16), and it accounts for genotype uncertainty by its reduced inter-subject variation for poorly imputed SNPs. So it is not surprising that these two statistics show similar power. Third, the statistic formed by weighting by did not perform as well, most likely due to inaccuracies in the estimates r̂k and sensitivity of the weights to such error. These results contrast with those of Zaitlen and Eskin [2010] who found slightly increased power using this strategy; further investigation of this matter would be useful.
Application to GWAS Meta-Analysis
We illustrate the summary score-statistics by application to the meta-analysis of three case-control GWAS studies of schizophrenia in European-Americans described by Shi et al., [2009]. The three studies are the SGENE Consortium [Stefansson et al., 2009], The International Schizophrenia Consortium [ISC; International Schizophrenia Consortium, 2009] and The Molecular Genetics of Schizophrenia study, [MGS: Shi et al., 2009]. These studies enlisted a total of 8,008 cases and 19,077 controls, as shown in Table 6. For the meta-analysis, only site-specific p-values and the directions of association for the logistic trend test were available for each of a common set of SNPs in six regions containing SNPs satisfying a predetermined threshold for statistical significance in at least one of the three studies. For the meta-analysis the authors converted each p-value to a score statistic determined as the quantile corresponding to the appropriate tail of the standard Gaussian distribution. They then evaluated SNPs using the summary score statistic of (17), with weights proportional to the square roots of the estimates îkβ of (9). GWAS tag SNPs are selected to have common frequencies in different Caucasian populations; thus the authors assumed that the SNP MAFs are approximately the same across the three sites, which gives weights wk proportional to [(nk0nk1) / (nk0 + nk1)]1/2.
Table 6. Sample Sizes in Meta-Analysis of K=3 Schizophrenia Case-control GWASa.
| Study b | MGS | ISC | SGENE | Total | ||||
|---|---|---|---|---|---|---|---|---|
| Cases | Controls | Cases | Controls | Cases | Controls | Cases | Controls | |
| Number of Subjects | 2681 | 2653 | 3322 | 3587 | 2005 | 12,837 | 8008 | 19,077 |
MGS: Molecular Genetics of Schizophrenia; ISC : International Schizophrenia Consortium; SGENE : SGENE Consortium
We computed three test statistics for each of the 28 SNPs in the major histocompatibility complex class I and II identified by the authors as significantly associated with schizophrenia risk. These test statistics are: 1) the homogeneity-weighted statistic (17) used by Shi et al., [2009]; 2) the heterogeneity-weighted statistic (19); and 3) the size-weighted statistic with weights proportional to (nk0 + nk1)1/2. For the heterogeneity-weighted statistic, we found that the estimated inter-study variances τ̂2 were zero for all SNPs, and Cochran's Q test did not reject homogeneity at a significance level of 0.1. (An alternate measure of heterogeneity, defined as I2 = 1 − [(K − 1) /Q], estimates the percentage of total inter-site variation beyond chance, with heterogeneity suggested by values I2 > 0.5 [Ioannidis et al., 2007]. For these data, I2 was negative for all 28 SNPs, showing no evidence of heterogeneity.) Thus the heterogeneity- and homogeneity-weighted score statistics were equal for all 28 SNPs. Figure 1 shows that this summary score statistic yielded smaller p-values than the size-weighted statistic.
Fig. 1.
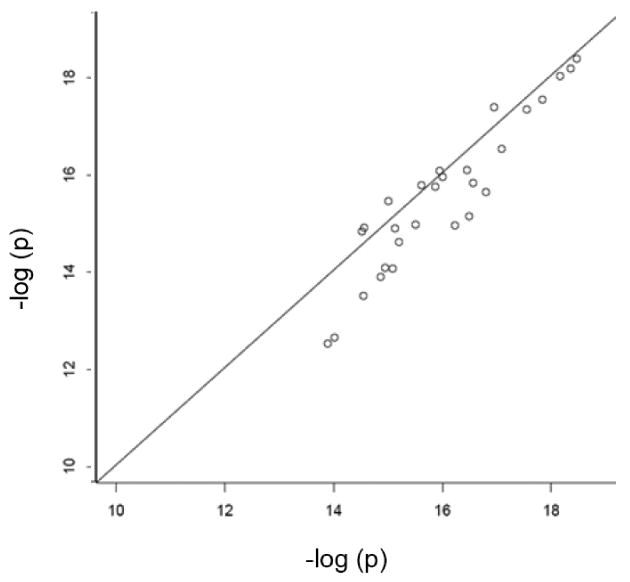
p-values of size-weighted statistics (y-axis) versus summary score statistics with homogeneity weights(x-axis) for 28 top schizophrenia SNPs
This example illustrates three points. First, site-specific data can be combined optimally simply by sharing p-values, the directions of association, and the null information estimates (as obtained from case and control sample sizes). Second, heterogeneity across studies can be evaluated even with such minimal information from the sites. Finally, as expected from the theory and simulations, the optimally-weighted summary score-statistic is more powerful than the size-weighted score-statistic. For case-control data such as these, optimal weighting achieves the greatest power gain relative to size-based weighting when case and control numbers are roughly the same for some studies, but substantially different for others (as in the present example). Power gains also can be substantial for meta-analysis of censored survival data when censoring levels differ among the studies.
Discussion
We have reviewed SNP association tests based on weighted sums of site-specific score and Wald statistics. We have shown that when SNP effect-size β is constant across sites, the optimal weights for both statistics are approximately proportional to the square roots of the sites' null Fisher information for the SNP of interest, and we have described these weights for the phenotypes commonly studied with GWAS. These optimal weights have simple forms in the absence of site-specific differences in covariates and their effects, and in the absence of accommodation for site-specific differences in imputation uncertainty. Their optimality in these circumstances is supported by simulation results. In the presence of covariate adjustment, the simple weights described here should be nearly optimal unless the sites differ strongly in choice of covariates or their effect-sizes. The simulations also suggest little power loss in using weights that ignore imputation uncertainties. This finding is consistent with the similarities in the two statistics noted in the Methods section.
We also have shown how to use the site-specific score statistics to obtain SNP effect-size estimates for assessing inter-site effect-size heterogeneity. An application to schizophrenia data shows that for case-control GWAS meta-analysis, such heterogeneity can be assessed even when only site-specific SNP p-values and directions of association are available. Both simulations and the data application support the conclusion of others that Cochran's test has poor power to detect effect-size heterogeneity, particularly when the number of sites is small [Clayton and Hills, 1993]. Thus we suggest performing GWAS meta-analysis using the homogeneity-weighted summary statistics and examining heterogeneity for the hit SNPs, with the caveat that lack of evidence for heterogeneity can be interpreted only as ruling out very large differences across sites.
A limitation of all meta-analysis is its need for site-specific estimates of regression coefficients for covariates that are common to all or several sites (e.g. age, sex, ancestry). The simulations of Lin and Zeng [2010a; 2010b] suggest that site-specific regression coefficient estimates for such covariates do not produce substantial bias or power loss. Although this conclusion seems plausible unless the covariates are strongly associated with both genotype and phenotype, more evidence would be useful.
Acknowledgments
This research was supported by NIH grants R01 CA094069 and U01 CA122171. The authors are grateful to Habibul Ahsan, Irene Andrulis, Jenny Claude-Chang, Mohammed Kibriya, and Kathi Malone for the use of these genotype data, and to the reviewers of an earlier version of the manuscript for their helpful suggestions.
Appendix: Approximating the Asymptotic Mean of the Score uβ
Let U (θ0) = (Uα (θ0), Uβ (θ0))T denote the vector of efficient scores for θ, evaluated at θ0 = (α, 0). Thus E [U (θ0); θ0] = 0. To approximate this expectation over local alternatives for θ, we evaluate it over a distribution governed by a value near to but not equal to θ0. Thus we write θ = θ0 + δ, where δ = (0, β)T, and β is small in absolute value. Using a multivariate version of the argument given by Cox and Hinkley [1979, p 109]; we can write
where i (θ0) is the Fisher information for θ evaluated at θ0. Similarly, the covariance matrix of U (θ0) is
These results, when used with standard normal theory, show that, conditional on θ0 = (α̂ (0), 0), the asymptotic distribution of Uβ (α̂ (0), 0) = Uβ is normal with mean βiβ + o (|β|) and variance iβ+ O (|β|). Here iβ is given by (2) with i(θ) = i (θ0).
References
- Breslow NE, Day NE. Statistical methods in cancer research, vol 1, the Analysis of Case-control Studies. Lyon: International Agency for Research on Cancer; 1980. [PubMed] [Google Scholar]
- Browning BL, Browning SR. A unified approach to genotype imputation and haplotype-phase inference for large data sets of trios and unrelated individuals. Am J Hum Genet. 2009;84:210–23. doi: 10.1016/j.ajhg.2009.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cantor RM, Lange K, Sinsheimer JS. Prioritizing GWAS results: A review of statistical methods and recommendations for their application. Am J Hum Genet. 2010;86:6–22. doi: 10.1016/j.ajhg.2009.11.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clayton D, Hills M. Statistical models in epidemiology. Oxford: Oxford University Press; 1993. [Google Scholar]
- Cochran BG. The combination of estimates from different experiments. Biometrics. 1954;10:101–29. [Google Scholar]
- Cox DR, Hinkley CV. Theoretical statistics. London: Chapman and Hall; 1979. [Google Scholar]
- de Bakker PI, Ferreira MA, Jia X, Neale BM, Raychaudhuri S, Voight BF. Practical aspects of imputation-driven meta-analysis of genome-wide association studies. Hum Mol Genet. 2008;17:R122–8. doi: 10.1093/hmg/ddn288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DerSimonian R, Laird N. Meta-analysis in clinical trials. Control Clin Trials. 1986;7:177–88. doi: 10.1016/0197-2456(86)90046-2. [DOI] [PubMed] [Google Scholar]
- Guan Y, Stephens M. Practical issues in imputation-based association mapping. PLoS Genet. 2008;4:e1000279. doi: 10.1371/journal.pgen.1000279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howie BN, Donnelly P, Marchini J. A flexible and accurate genotype imputation method for the next generation of genome-wide association studies. PLoS Genet. 2009;5:e1000529. doi: 10.1371/journal.pgen.1000529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu X, Pickering E, Liu YC, Hall S, Fournier H, Katz E, Dechairo B, John S, Van Eerdewegh P, Soares H Alzheimer's Disease Neuroimaging Initiative. Meta-analysis for genome-wide association study identifies multiple variants at the BIN1 locus associated with late-onset Alzheimer's disease. PLoS ONE. 2011;6:e16616. doi: 10.1371/journal.pone.0016616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- International HapMap Consortium. Frazer KA, Ballinger DG, Cox DR, Hinds DA, Stuve LL, Gibbs RA, Belmont JW, Boudreau A, Hardenbol P, Leal SM, Pasternak S, Wheeler DA, Willis TD, Yu F, Yang H, Zeng C, Gao Y, Hu H, Hu W, Li C, Lin W, Liu S, Pan H, Tang X, Wang J, Wang W, Yu J, Zhang B, Zhang Q, Zhao H, Zhao H, Zhou J, Gabriel SB, Barry R, Blumenstiel B, Camargo A, Defelice M, Faggart M, Goyette M, Gupta S, Moore J, Nguyen H, Onofrio RC, Parkin M, Roy J, Stahl E, Winchester E, Ziaugra L, Altshuler D, Shen Y, Yao Z, Huang W, Chu X, He Y, Jin L, Liu Y, Shen Y, Sun W, Wang H, Wang Y, Wang Y, Xiong X, Xu L, Waye MM, Tsui SK, Xue H, Wong JT, Galver LM, Fan JB, Gunderson K, Murray SS, Oliphant AR, Chee MS, Montpetit A, Chagnon F, Ferretti V, Leboeuf M, Olivier JF, Phillips MS, Roumy S, Sallée C, Verner A, Hudson TJ, Kwok PY, Cai D, Koboldt DC, Miller RD, Pawlikowska L, Taillon-Miller P, Xiao M, Tsui LC, Mak W, Song YQ, Tam PK, Nakamura Y, Kawaguchi T, Kitamoto T, Morizono T, Nagashima A, Ohnishi Y, Sekine A, Tanaka T, Tsunoda T, Deloukas P, Bird CP, Delgado M, Dermitzakis ET, Gwilliam R, Hunt S, Morrison J, Powell D, Stranger BE, Whittaker P, Bentley DR, Daly MJ, de Bakker PI, Barrett J, Chretien YR, Maller J, McCarroll S, Patterson N, Pe'er I, Price A, Purcell S, Richter DJ, Sabeti P, Saxena R, Schaffner SF, Sham PC, Varilly P, Altshuler D, Stein LD, Krishnan L, Smith AV, Tello-Ruiz MK, Thorisson GA, Chakravarti A, Chen PE, Cutler DJ, Kashuk CS, Lin S, Abecasis GR, Guan W, Li Y, Munro HM, Qin ZS, Thomas DJ, McVean G, Auton A, Bottolo L, Cardin N, Eyheramendy S, Freeman C, Marchini J, Myers S, Spencer C, Stephens M, Donnelly P, Cardon LR, Clarke G, Evans DM, Morris AP, Weir BS, Tsunoda T, Mullikin JC, Sherry ST, Feolo M, Skol A, Zhang H, Zeng C, Zhao H, Matsuda I, Fukushima Y, Macer DR, Suda E, Rotimi CN, Adebamowo CA, Ajayi I, Aniagwu T, Marshall PA, Nkwodimmah C, Royal CD, Leppert MF, Dixon M, Peiffer A, Qiu R, Kent A, Kato K, Niikawa N, Adewole IF, Knoppers BM, Foster MW, Clayton EW, Watkin J, Gibbs RA, Belmont JW, Muzny D, Nazareth L, Sodergren E, Weinstock GM, Wheeler DA, Yakub I, Gabriel SB, Onofrio RC, Richter DJ, Ziaugra L, Birren BW, Daly MJ, Altshuler D, Wilson RK, Fulton LL, Rogers J, Burton J, Carter NP, Clee CM, Griffiths M, Jones MC, McLay K, Plumb RW, Ross MT, Sims SK, Willey DL, Chen Z, Han H, Kang L, Godbout M, Wallenburg JC, L'Archevêque P, Bellemare G, Saeki K, Wang H, An D, Fu H, Li Q, Wang Z, Wang R, Holden AL, Brooks LD, McEwen JE, Guyer MS, Wang VO, Peterson JL, Shi M, Spiegel J, Sung LM, Zacharia LF, Collins FS, Kennedy K, Jamieson R, Stewart J. A second generation human haplotype map of over 3.1 million SNPs. Nature. 2007;449:851–61. doi: 10.1038/nature06258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- International Schizophrenia Consortium. Purcell SM, Wray NR, Stone JL, Visscher PM, O'Donovan MC, Sullivan PF, Sklar P. Common polygenic variation contributes to risk of schizophrenia and bipolar disorder. Nature. 2009;460:748–52. doi: 10.1038/nature08185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ioannidis JP. Non-replication and inconsistency in the genome-wide association setting. Hum Hered. 2007;64:203–13. doi: 10.1159/000103512. [DOI] [PubMed] [Google Scholar]
- Ioannidis JP, Patsopoulos NA, Evangelou E. Heterogeneity in meta-analyses of genome-wide association investigations. PLoS One. 2007;2:e841. doi: 10.1371/journal.pone.0000841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Abecasis GR. Rapid haplotype reconstruction and missing genotype inference. Am J Hum Genet. 2006;S79:2290. [Google Scholar]
- Lin DY, Sullivan PF. Meta-analysis of genome-wide association studies with overlapping subjects. Am J Hum Genet. 2009;85:862–72. doi: 10.1016/j.ajhg.2009.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin DY, Zeng D. Meta-analysis of genome-wide association studies: no efficiency gain in using individual participant data. Genet Epidemiol. 2010a;34:60–6. doi: 10.1002/gepi.20435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin DY, Zeng D. On the relative efficiency of using summary statistics versus individual-level data in meta-analysis. Biometrika. 2010b;97:321–32. doi: 10.1093/biomet/asq006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Louis TA. Finding the observed information matrix when using the EM algorithm. Jr Stat Soc. 1982;B44:226–33. [Google Scholar]
- Marchini J, Howie B, Myers S, McVean G, Donnelly P. A new multipoint method for genome-wide association studies by imputation of genotypes. Nat Genet. 2007;39:906–13. doi: 10.1038/ng2088. [DOI] [PubMed] [Google Scholar]
- McCullagh PJ, Nelder JA. Generalized linear models. 2nd. London: Chapman and Hall; 1989. [Google Scholar]
- Schaid DJ, Rowland CM, Tines DE, Jacobson RM, Poland GA. Score tests for association between traits and haplotypes when linkage phase is ambiguous. Am J Hum Genet. 2002;70:425–34. doi: 10.1086/338688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheet P, Stephens M. A fast and flexible statistical model for large-scale population genotype data: applications to inferring missing genotypes and haplotypic phase. Am J Hum Genet. 2006;78:629–44. doi: 10.1086/502802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scott LJ, Mohlke KL, Bonnycastle LL, Willer CJ, Li Y, Duren WL, Erdos MR, Stringham HM, Chines PS, Jackson AU, Prokunina-Olsson L, Ding CJ, Swift AJ, Narisu N, Hu T, Pruim R, Xiao R, Li XY, Conneely KN, Riebow NL, Sprau AG, Tong M, White PP, Hetrick KN, Barnhart MW, Bark CW, Goldstein JL, Watkins L, Xiang F, Saramies J, Buchanan TA, Watanabe RM, Valle TT, Kinnunen L, Abecasis GR, Pugh EW, Doheny KF, Bergman RN, Tuomilehto J, Collins FS, Boehnke M. A genome-wide association study of type 2 diabetes in Finns detects multiple susceptibility variants. Science. 2007;316:1341–5. doi: 10.1126/science.1142382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi J, Levinson DF, Duan J, Sanders AR, Zheng Y, Pe'er I, Dudbridge F, Holmans PA, Whittemore AS, Mowry BJ, Olincy A, Amin F, Cloninger CR, Silverman JM, Buccola NG, Byerley WF, Black DW, Crowe RR, Oksenberg JR, Mirel DB, Kendler KS, Freedman R, Gejman PV. Common variants on chromosome 6p22.1 are associated with schizophrenia. Nature. 2009;460:753–7. doi: 10.1038/nature08192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soranzo N, Rivadeneira F, Chinappen-Horsley U, Malkina I, Richards JB, Hammond N, Stolk L, Nica A, Inouye M, Hofman A, Stephens J, Wheeler E, Arp P, Gwilliam R, Jhamai PM, Potter S, Chaney A, Ghori MJ, Ravindrarajah R, Ermakov S, Estrada K, Pols HA, Williams FM, McArdle WL, van Meurs JB, Loos RJ, Dermitzakis ET, Ahmadi KR, Hart DJ, Ouwehand WH, Wareham NJ, Barroso I, Sandhu MS, Strachan DP, Livshits G, Spector TD, Uitterlinden AG, Deloukas P. Meta-analysis of genome-wide scans for human adult stature identifies novel Loci and associations with measures of skeletal frame size. PLoS Genet. 2009;5:e1000445. doi: 10.1371/journal.pgen.1000445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stefansson H, Ophoff RA, Steinberg S, Andreassen OA, Cichon S, Rujescu D, Werge T, Pietiläinen OP, Mors O, Mortensen PB, Sigurdsson E, Gustafsson O, Nyegaard M, Tuulio-Henriksson A, Ingason A, Hansen T, Suvisaari J, Lonnqvist J, Paunio T, Børglum AD, Hartmann A, Fink-Jensen A, Nordentoft M, Hougaard D, Norgaard-Pedersen B, Böttcher Y, Olesen J, Breuer R, Möller HJ, Giegling I, Rasmussen HB, Timm S, Mattheisen M, Bitter I, Réthelyi JM, Magnusdottir BB, Sigmundsson T, Olason P, Masson G, Gulcher JR, Haraldsson M, Fossdal R, Thorgeirsson TE, Thorsteinsdottir U, Ruggeri M, Tosato S, Franke B, Strengman E, Kiemeney LA, Genetic Risk and Outcome in Psychosis (GROUP) Melle I, Djurovic S, Abramova L, Kaleda V, Sanjuan J, de Frutos R, Bramon E, Vassos E, Fraser G, Ettinger U, Picchioni M, Walker N, Toulopoulou T, Need AC, Ge D, Yoon JL, Shianna KV, Freimer NB, Cantor RM, Murray R, Kong A, Golimbet V, Carracedo A, Arango C, Costas J, Jönsson EG, Terenius L, Agartz I, Petursson H, Nöthen MM, Rietschel M, Matthews PM, Muglia P, Peltonen L, St Clair D, Goldstein DB, Stefansson K, Collier DA. Common variants conferring risk of schizophrenia. Nature. 2009;460:744–7. doi: 10.1038/nature08186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanaka T, Scheet P, Giusti B, Bandinelli S, Piras MG, Usala G, Lai S, Mulas A, Corsi AM, Vestrini A, Sofi F, Gori AM, Abbate R, Guralnik J, Singleton A, Abecasis GR, Schlessinger D, Uda M, Ferrucci L. Genome-wide association study of vitamin B6, vitamin B12, folate, and homocysteine blood concentrations. Am J Hum Genet. 2009;84:477–82. doi: 10.1016/j.ajhg.2009.02.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willer C, Li Y, Abecasis G. METAL: fast and efficient meta-analysis of genomewide association scans. Bioinformatics. 2010;26:2190–1. doi: 10.1093/bioinformatics/btq340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaitlen N, Eskin E. Imputation aware meta-analysis of genome-wide association studies. Genet Epid. 2010;34:537–42. doi: 10.1002/gepi.20507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeggini E, Ioannidis JP. Meta-analysis in genome-wide association studies. Pharmacogenomics. 2009;10:191–201. doi: 10.2217/14622416.10.2.191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeggini E, Weedon MN, Lindgren CM, Frayling TM, Elliott KS, Lango H, Timpson NJ, Perry JR, Rayner NW, Freathy RM, Barrett JC, Shields B, Morris AP, Ellard S, Groves CJ, Harries LW, Marchini JL, Owen KR, Knight B, Cardon LR, Walker M, Hitman GA, Morris AD, Doney AS, Wellcome Trust Case Control Consortium (WTCCC) McCarthy MI, Hattersley AT. Replication of genome-wide association signals in UK samples reveals risk loci for type 2 diabetes. Science. 2007;316:1336–41. doi: 10.1126/science.1142364. [DOI] [PMC free article] [PubMed] [Google Scholar]


