Can the Focus of Attention Accommodate Multiple, Separate Items?

Abstract

Researchers of working memory currently debate capacity limits of the focus of attention, the proposed mental faculty in which items are most easily accessed. Cowan (1999) suggested that its capacity is about 4 chunks, whereas others have suggested that its capacity is only 1 chunk. Recently, Oberauer and Bialkova (2009) found evidence that 2 items could reside in the focus of attention, but only because they were combined into a single chunk. We modified their experimental procedure, which depends on a pattern of switch costs, to obtain a situation in which chunking was not likely to occur (i.e., each item remained a separate chunk), and still obtained results consistent with a capacity of at least 2 items. Therefore, either the focus of attention can hold multiple chunks, or the switch cost logic must be reconsidered.

Working memory is, according to theory, a system responsible for briefly storing and processing a subset of information present in one’s environment; presumably, the subset considered to be most important to meet one’s needs. A current debate in working memory research has centered upon how much information can be maintained briefly in the central part of a person’s mind at any given point in time; that is, in the focus of attention.

It is clear that there must be some limit in how many stimuli can be maintained at once (Miller, 1956). Based on the task, some environmental stimuli will stand out as more salient or higher priority than others. For example, when one drives a car, numerous visual stimuli (e.g., other cars, road signs) and auditory stimuli (e.g., ambulance sirens, GPS directions) compete for attention. The most relevant information must be added to working memory, which must be updated quickly as the environment changes. One must remember, for example, that the directions include turning right at the next intersection and then keeping left, whereas the most recent few turns already taken can now be forgotten without much consequence. Although there is thus little debate regarding the idea that multiple items can somehow be retained in working memory at the same time, what is still controversial is the question of how many of the retained items can be attended at any given time.

According to Cowan (1988, 1995, 2005), the focus of attention serves as a holding device within the working memory system in which several items can be maintained concurrently. Items maintained within the focus of attention presumably have a privileged status over other items in working memory. In particular, they not only are highly accessible, but also are in awareness and are protected from decay (e.g., Barrouillet, Portrat, & Camos, in press; Ricker & Cowan, 2010) and interference (e.g., Lewandowsky, Oberauer, & Brown, 2009).

Others disagree, however, suggesting instead that the focus of attention maintains only one item at a time (Garavan, 1998; McElree, 1998, 2001; Oberauer, 2002, 2005; Oberauer & Bialkova, 2009). Some researchers further propose that several other working memory items can be held in a capacity-limited region outside of the focus of attention (Allen, Baddeley, & Hitch, 2006; Oberauer, 2002, 2005). Further investigation of this controversial issue is important because it has consequences for our understanding of working memory in information processing. For example, forming a new integrated chunk in long-term memory from two or more previously separate items (e.g., upon first encountering the political term “blue dog”) or comparison of two or more items (e.g., the pitches of two tones) could occur by relating the items inside a multi-item focus of attention. In contast, if there is only a single-item focus, another, still-unexplored mechanism of new chunk formation would have to be proposed, whereby information inside the focus of attention affects information outside of the focus. It is the question of the size of the focus of attention that will be re-examined in the present article.

Some previous research reinforces our suggestion that capacity-limited storage may take place in the focus of attention. There is a tradeoff between vastly different types of items, such as colors and spoken words (Saults & Cowan, 2007) or colors and tones (Morey, Cowan, Morey, & Rouder, in press). Thus, there must exist some storage device that is not modality-specific but instead general, like the focus of attention (Cowan, 1988) or Baddeley’s episodic buffer (Baddeley, 2000, 2001). Between these two concepts, the notion that it is the focus of attention rather than a buffer per se that is responsible for general, amodal item storage is that there are tradeoffs between working memory of one sort and processing of a very different sort, such as the tradeoff between memory for colors and a speeded tone-identification task (Stevanovski & Jolicoeur, 2007) or between memory for spoken digits and a spatial choice reaction time task (Chen & Cowan, 2009a).

There are some theoretical details that must be specified in order to distinguish between single-item and multiple-item hypotheses about the focus of attention. If there were a focus of attention that could only hold one item at a time but rotated very rapidly from one item to the next, keeping several items active at once, it might be very difficult to distinguish between single-item and multiple item focus hypotheses (Cowan, in press). For example, Barrouillet and colleagues have proposed a rotating focus to keep memoranda active in complex working memory span tasks (Barrouillet, Bernardin, & Camos, 2004; Barrouillet, Bernardin, Portrat, Vergauwe, & Camos, 2007) but that process might be difficult to distinguish from a multiple-item focus, as Barrouillet et al. (in press) acknowledged. What is easier to distinguish from a multiple-item focus is a single-item focus that lingers on a particular item throughout a trial and in the period between trials, as many of the single-item theorists have proposed.

Our research follows up on a sophisticated study that has led to a single-item focus hypothesis (Oberauer & Bialkova, 2009). Like previous work in this area (Garavan, 1998; McElree, 1998, 2001; Oberauer, 2002, 2005), Oberauer and Bialkova made use of switch costs in response times that occur when the participant must switch between trials from one particular stimulus item to another. Oberauer and Bialkova provided considerable clarity to this area of research. They did find that at least two items could be in the focus of attention at once, but they found that result in a situation in which the two items appeared to be combined to form a single chunk. It is the generality of that finding that will be re-examined here; we suggest that at least two items can be held separately in the focus of attention, according to the logic established by Oberauer and Bialkova. To revisit this procedure, we will first discuss object switch costs in Oberauer’s research and their specific application in the study by Oberauer and Bialkova.

Object Switch Costs and the Focus of Attention

Support for a single-item focus of attention has been inferred from switch costs when a participant’s attention must shift between trials from one object to another (Oberauer, 2002, 2005). In one type of experiment showing the relevant pattern, for example, each trial included two lists of digits, displayed across the screen in different rows. The digits disappeared but were to be kept in memory. Then, on each trial, one digit was to be updated according to an arithmetic operation that was shown in the corresponding screen location. Both lists had to be remembered. Oberauer found one kind of disadvantage when the list to be updated was not the same from trial to trial, an effect termed a list-switch cost. Within the list to be updated, there was a reaction time (RT) disadvantage of about 300 ms when the item or object within the list that was to be updated switched from one trial to the next; this was the object-switch cost. This pattern of results, in particular the object-switch cost results, suggested that shifting attention to new items was hardly a rapid process.

On the basis of the pattern of two types of switch costs, Oberauer (2002, 2005) proposed a theoretical model that is like a working memory model originally proposed by Cowan, termed the embedded-processes model (Cowan, 1988, 1995, 1999). Cowan’s model included the activated portion of long-term memory and, within it, a focus of attention typically limited to three or four items. However, Oberauer’s model included a further level of subdivision. He suggested that there is a one-item focus of attention embedded in a direct-access region that was limited to about three to four items. The idea behind the one-item focus is that the object most recently accessed receives selective attention and is more readily accessible than other objects in working memory, reducing reaction time on the next trial if the same item or object must be accessed again. Meanwhile, the other objects in the currently-updated list remain in the region of direct access where, although not currently receiving attention, they can be attended in the very near future. In sum, Oberauer’s (2002, 2005) model differs importantly from that of Cowan (1988, 1999). Whereas Oberauer’s model includes a capacity-limited region and a focus of attention embedded within it, Cowan’s multi-item focus of attention and capacity-limited region are synonymous,.

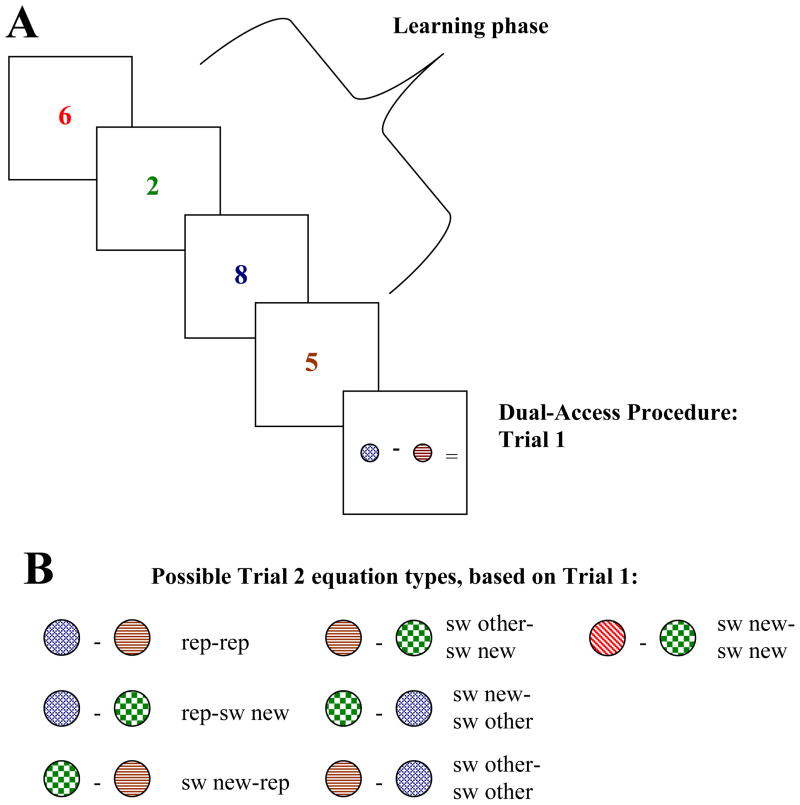
A key limitation in the support for Oberauer’s theoretical view was that the experimental procedure only required that one item per trial be accessed. To determine whether the focus of attention is in fact limited to a single item, cases in which participants are to access two or more items on the same trial also must be considered. Oberauer and Bialkova (2009) sought to resolve this issue in a study in which participants were to retrieve and use two items from memory on the same trial. The study was designed within a framework of theoretical possibilities including data patterns that could emerge if participants maintained two separate objects in the focus of attention, versus other data patterns that could emerge if participants maintained only one object in focus or combined the two objects to form a single chunk in the focus of attention. A description of the procedure of their first experiment, illustrated in Figure 1, clarifies their basic logic.

Figure 1.

Illustration of the methods of Oberauer and Bialkova (2009, Experiments 1–2). (A) Outline of the procedure on Trial 1 within a trial block. (B) Different potential equation types based on this particular example of Trial 1. Rep = repeated argument, sw other = switch to other argument, sw new = switch to new item color.

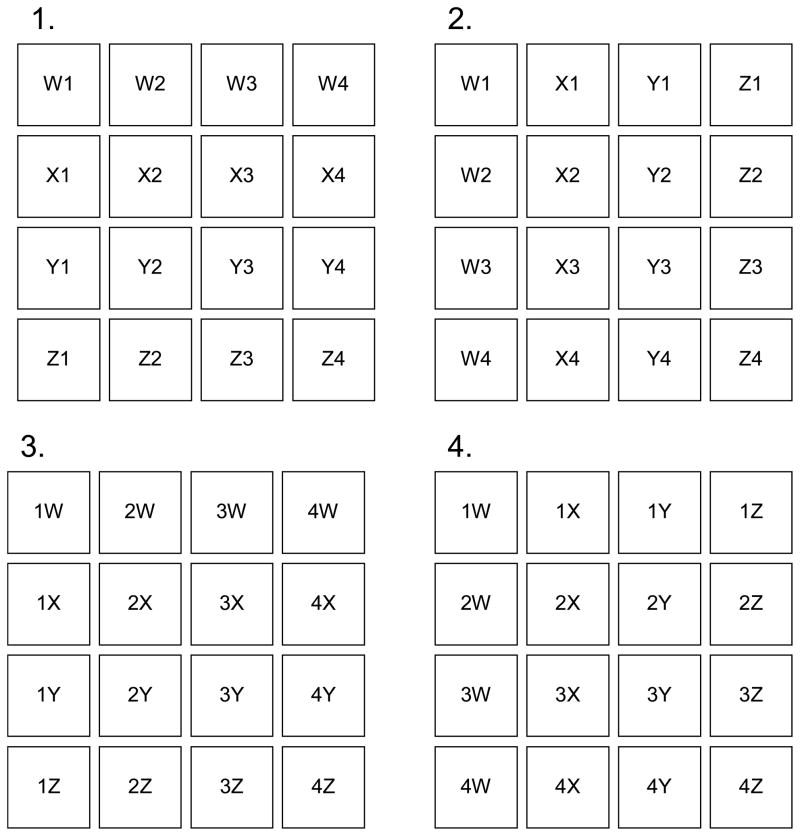
As shown in Figure 1A, Oberauer and Bialkova (2009, Experiment 1) began each block of trials with the presentation of a list of four digits, each printed in a different ink color (e.g., red, brown, green, or blue). During the learning phase, participants were to learn associations between 4 digits and the colors in which those digits were presented. Then they were to complete a series of mathematical equations involving these pairings; a critical, dual-access condition included two colored discs that represented the numbers shown previously. Here, to successfully answer the equation, participants were to recall the digits that were represented by the two colors on the screen. For example, if the digit 8 were presented in blue ink and the digit 5 were presented in brown ink, then shortly afterward the equation [(blue disc)−(brown disc) = ?] would warrant the answer 3, which participants entered via a keypress. The two colors in an equation were never the same as one another. Following 11 of these equations, a new block of trials began, with new color-digit pairings for participants to learn.

A critical manipulation in the dual-access trials was whether arguments within an equation switched to new colors or not, compared to the equation immediately prior. Using the example above, suppose BLUE - BROWN was the initial equation shown to participants. For the next equation, one of three possible things could happen to the first argument (i.e., blue): the color could be repeated again, the color could switch to what was the second argument’s color in the prior equation (i.e., brown), or the color could switch to a completely new color that was not shown in the previous equation (e.g., green). Likewise, the same possibilities could occur for the second color in the equation. Crossing both of these variables, but without allowing the two colors to be the same, resulted in seven different types of equations that could occur within a given trial (illustrated in Figure 1B).

The trial types were used in an ingenious manner to assess various alternative hypotheses about items in working memory. For the present purposes, the critical point involves trials like those in the experiment described above in which both colors are preserved from the previous trial, only one is preserved, or neither is preserved. (We need not consider cases in which colors switched places, as they do not apply to our experiment.) The key assumption on which their analyses were based was that objects (in this case, colors representing digits) must be retrieved into the focus of attention unless they are unchanged from the previous trial in the previous trial, in which case at least one of them may already be in focus. Oberauer and Bialkova (2009) proposed several ways that the focus of attention could access two items; we discuss two of these proposed patterns in detail, as they are critical to understand our current research. For the first possibility of interest, Oberauer and Bialkova considered patterns of response times for different trial types if the focus of attention were able to access two items separately. If this were the case, then there should be the most time savings when both colors are preserved from the previous trial due to repetition benefits (0-switch trials), fewer savings when only one item is repeated(1-switch trials), and no savings when neither is repeated (2-switch trials). The second proposal of interest to us was a focus of attention that was limited to a single chunk. In this case, two separate items must be bound to form a single chunk if they are to be accessed at once. Presumably a chunk must be retrieved as a unit, and changing even one portion of the chunk from the preceding trial means that a completely new chunk must be formed to form a response. Therefore, Oberauer and Bialkova proposed that for a single-chunk focus of attention, there would be time savings on 0-switch trials; however, response times for trials in which one item switched should not have any benefits when compared to trials in which 2 items switched (i.e., equivalent response times for 1-switch and 2-switch trials)..

Once response time data were obtained, Oberauer and Bialkova (2009) fit the results to each of their proposed hypotheses and patterns. For dual-access conditions, in which two items were to be accessed at once, actual response time patterns overwhelmingly fit the pattern for a focus of attention that was limited to a single chunk. To be more specific, there was no response time advantage for trials in which only one of the colors from the previous trial switched (i.e., 1-switch trials) compared to trials in which both colors from the previous trial changed to new colors (i.e., 2-switch trials).

We accept the findings of Oberauer and Bialkova (2009), but a critical issue remains. The two objects that were presented as the arguments within an equation on a given trial were highly interchangeable: in Experiments 1 and 2, both arguments were filled by colors representing digits, and that should encourage chunking them together. More important, each digit associated with a given stimulus was to be combined via an arithmetic equation, yielding a single, unified response. A similar manner of chunking also appears to have been encouraged by the arrangement of their third experiment, which involved the spatial locations of two digits. The implication is that the possibility that two items could remain separately in the focus of attention remains untested. The goal of the studies described below was to determine whether we could obtain a pattern of results that was discrepant with Oberauer and Bialkova’s results supporting a single-chunk focus of attention, and instead would indicate the presence of two chunks in the focus of attention according to their experimental assumptions. To do this, we developed a test situation in which chunking was not well supported. The current studies attempt to discourage participants from chunking, with Experiment 4 as an important exception, by having separate stimuli (colors versus shapes) refer to separate elements of the response (numbers versus letters). We discuss our general approach in greater detail below.

Note that, theoretically, a single-item focus of attention that circulates among objects rapidly enough becomes theoretically indistinguishable from a multi-item focus of attention. It is therefore important to emphasize that we naturally cannot address an infinite level of precision, but rather stay at the level of analysis that was articulated in the work of Oberauer and Bialkova (2009), which adhered to the thesis that working memory appears to include only a single chunk in the focus of attention during the carryover of information from one trial to the next. At that level, we find instead a multi-item focus.

The Present Approach

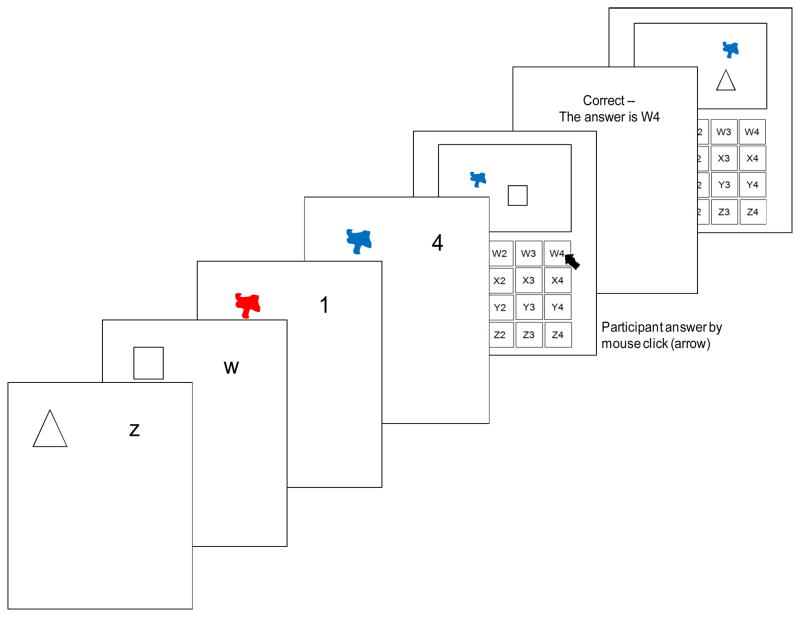
To test whether the focus of attention was able to hold two separate items at once, the experiments reported here involved a modification of the dual-access procedure utilized by Oberauer & Bialkova (2009). Specifically, the stimuli presented to participants, unlike the colored circles that were used in Oberauer and Bialkova’s study, did not share any features that would allow the objects to be interchanged from trial to trial. They made separate contributions to a compound response that was to be made. As a result, chunking should be minimized within this modified paradigm, shown in Figure 2.

Figure 2.

Illustration of the procedure in Experiment 1, including the learning phase procedure and the first two trials within an 11-trial block. In relation to the first trial, the second trial involves a shape change, while the color blob is repeated (i.e., shape switch trial). As can be seen in the figure, participants received feedback after each trial.

Two different associations were to be maintained in working memory: one between shapes and letters, and another between amorphous colored blobs and digits. As in Oberauer and Bialkova (2009), participants were presented with a total of four associations to learn (i.e., two shape-letter, two color blob-digit). Following this learning phase, participants completed a series of dual-access trials. On each trial within Experiment 1, a shape and a color blob simultaneously appeared. To ensure that they appeared as separate objects, the spatial relationship between the two objects was randomly varied from trial to trial. Below each shape-color blob pair was a grid of all possible combinations of corresponding letter-digit pair responses. Participants were instructed to use a mouse to click on the grid location that matched both the letter and digit that were associated with the pair above, as quickly as possible. The shape and color blob were presented as categorically different and shared no features, were not combined via any arithmetic operation, and randomly varied in their spatial relationship to each other. This should have provided participants with little encouragement to chunk the two objects into a single unit.

In the context of this task, the items that are being stored in the focus of attention are presumably bound representations, each consisting of a given stimulus and its associated response. The associative strength between stimulus and associate need not be bi-directional, as we always presented a colored and shape and required the digit-letter combined response. On the next trial, the savings for repeated features would come from the stimulus-response associations remaining in the focus of attention after the end of the trial, eliminating the need to retrieve those associations if the same stimulus features are presented on the following trial. To analyze response time data, we have adopted the assumptions of Oberauer and Bialkova (2009), in which capacity limits of the focus of attention are operationally defined by a pattern of response times across different feature switch conditions. As described in detail below, we are able to make similar, albeit simplified, predictions regarding switch cost patterns and how these relate to the size of the focus of attention in the present experiments. Following the first trial within a given block, shapes and color blobs could either be repeated, or could switch to the other items that had been learned in the initial learning phase. When all possibilities were crossed, this led to four different trial types for every trial in a series after the first: (1) neither object switched (i.e., both the shape and color from the previous trial were repeated), (2) shape switched, (3) color switched, or (4) both objects switched. Predictions regarding the relationship between response times and the four different trial types are as follows.

If the two items in the dual-access paradigm are combined to form a single chunk, response times should follow the pattern that Oberauer and Bialkova predicted for a single-chunk focus:

$$0-\mathit{switch}\mathit{trials}<1-\mathit{switch}\mathit{trials}(\text{i}.\text{e}.,\text{color}\text{switch}\text{or}\text{shape}\text{switch})=2-\mathit{switch}\mathit{trials}$$ (1)

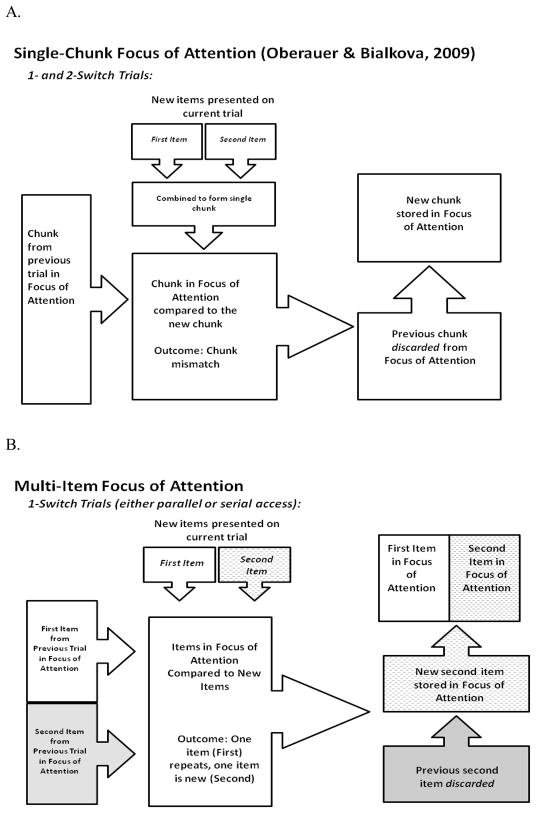
To provide further clarification, consider what potentially occurs on a trial if the focus of attention is limited to a single, multi-item chunk, illustrated in Figure 3A. As participants will need to access both shape and color in the near future, both items must be present in the focus of attention; it follows that shape and color must be bound together, as both items will be needed to make a response and the focus has a single-chunk limit. When a new trial begins, this previously-formed chunk must either be retained or discarded in favor of a new shape-color chunk. Participants are shown a new shape and color, which are bound into a chunk that does not yet have access to the focus of attention, but is present in working memory. This new chunk is compared to the previous trial’s chunk that currently occupies the focus of attention. When the new chunk matches the previous chunk, as it does in 0-switch trials, there is no need to discard the previous chunk. In contrast, in cases in which either one or both items change, there is a mismatch between the chunk formed on the previous trial and the new chunk. To make a correct response, the new chunk must replace the old one in the focus of attention, a time-consuming process.

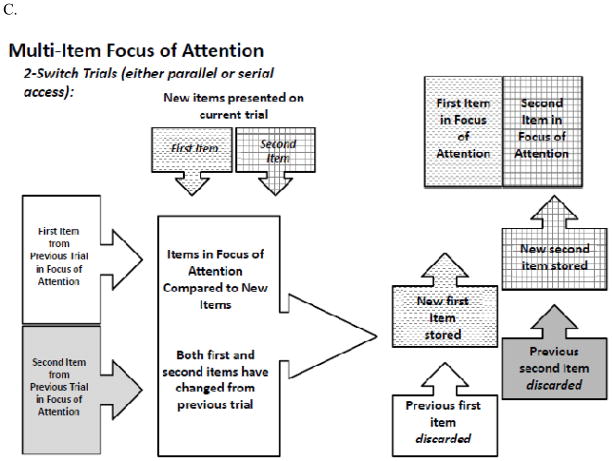
Figure 3.

Hypothesized processing for different kinds of attentional focus. (A) a single-chunk focus of attention (Oberauer & Bialkova, 2009); (B) a multi-item focus of attention for 1-switch trials; and (C) a multi-item focus of attention for 2-switch trials.

If the focus of attention can access the two objects separately and can access multiple, separate items, the response time pattern should be

$$0-\mathit{switch}\mathit{trials}<1-\mathit{switch}\mathit{trials}(\text{i}.\text{e}.,\text{color}\text{switch}\text{or}\text{shape}\text{switch})<2-\mathit{switch}\mathit{trials}$$ (2)

According to previous assumptions from Oberauer and Bialkova (2009), a switch to a new color blob or shape requires loading that given item into the focus. They can be loaded separately, and this should take more time to load two new items than to load a single color or shape. One-switch trials therefore may benefit from repeating a shape or color, compared to 2-switch trials.

Schematic diagrams of how multiple, separate items might be loaded into the focus of attention are illustrated in the latter portions of Figure 3. In cases in which one item from the previous trial switches and the other item repeats (i.e., 1-switch trials; see Figure 3B), items from the previous trial can be compared to the currently-presented shape and color. In contrast to a single-chunk focus of attention, having a partial repetition from the previous trial does not imply that all items from the previous trial must be discarded. Instead, the item that has been repeated from the previous trial remains in the focus and only the item that is no longer relevant to the current trial is discarded. Then the new item from the current trial can be uploaded into the focus of attention.

For cases in which both items from the previous trial switch, both of those items are replaced with the new items that must be uploaded into the focus of attention separately (Figure 3C). It is possible that participants engage in some combination of serial and parallel processes to load both items into the focus of attention during the dual-access task. The pattern described by Equation 2 should hold unless the two items are always loaded in a completely parallel and capacity-independent manner. Even if they are always loaded in parallel but with load times slowed by the concurrence, Equation 2 still applies. Mixture models of parallel and serial processing are permissible and should be studied in the future, but examining such mixture models is beyond the scope of the current research.

To reiterate, these predictions are based on patterns originally proposed and described by Oberauer and Bialkova (2009). We set out to test the predictions with the modified procedure described above because it does not support chunking, inasmuch as color and shape indicate separate components of a compound response. Our rationale was not that the use of two different features (color and shape) in itself would have prevented binding; indeed, a previous study demonstrated that two features, color and location or voice and tone, could be integrated in an updating type of task (Bao, Li, & Zhang, 2007). Nevetheless, we did not use colors for both stimulus elements like Oberauer and Bialkova did because it would have been difficult to assign two colors unambiguously to different response components.

Experiment 1

Method

Participants

Seventeen undergraduates at the University of Missouri (9 males, 8 females) participated in exchange for course credit. Of these participants, one male was excluded from further analysis because of color-blindness.

Design

Participants completed a block of practice trials and 24 blocks of test trials. Each block included an association learning phase followed by 11 trials, but the first trial per block could not include any kind of switch and was therefore not used. Color and shape were randomly selected on each trial from the learned set, so the proportions of trials in each condition were nearly, but not exactly, the same. Summed across participants, the proportions were: both repeated, 24.7%; color switch, 25.3%; shape switch, 25.1%; and both switch, 25.0%.

Apparatus, stimuli, and procedure

Participants were separately tested in quiet booths with computers. At the beginning of a trial block, the participant learned an association between each of two digits (randomly selected from the set 1 through 4) and a colored blob to be associated to each digit (randomly selected from the set red, blue, green, and brown). They also learned an association between each of two letters (randomly selected from the set w, x, y, and z) and an outlined, colorless shape to be associated to each letter (randomly selected from the set including a circle, triangle, square, and pentagon). As shown in Figure 2, the associations were presented one at a time. Participants were instructed to take as much time as they needed to learn each association before pressing the key causing the computer to proceed to the next association.

Once all four associations had been presented, participants began the dual-access task. At the top of the screen, an outlined box contained one shape and one colored blob that had been presented during the learning phase. Below the box was a 4×4 response grid that contained all possible combinations of letters and digits in a systematic arrangement as shown in Figure 2. The task was to use the computer mouse to select on each trial, as quickly as possible, the item in the response grid that corresponded to the displayed colored blob and outlined shape, based on the associations presented in the learning phase. Following the participant’s response, a feedback display was shown, indicating the response accuracy and the correct answer.

The outlined shapes and color blobs each were approximately 4 mm tall, both in the learning phase in which they appeared along with 4-mm-tall characters (letters or numbers), and in the dual-access phase. In the latter, the centers of these two objects in the aforementioned outlined box were never closer than 17.5 mm. They appeared at randomly-chosen locations within a box 86 mm wide and 74 mm tall, except that center of each object was never less than 8.5 mm away from the wall of this box. Below the box, the 4×4 response grid included each response possibility within a box 17.5 mm high. The rows corresponded to the letters w, x, y, and z and the columns corresponded to the numbers 1, 2, 3, and 4 in an organized fashion, such that each response box was labeled with a number and letter (e.g., x3). The viewing distance was approximately 50 cm. At this distance the outlined shapes and colored blobs each subtend about 0.46 degrees of visual angle.

Results

Proportion correct

Note that although we report the proportion correct to document performance fully, it is not of primary theoretical concern to us (and was not to Oberauer & Bialkova, 2009) except to eliminate RTs on error trials. Response errors could occur through a variety of mechanisms, and it is not possible to glean from the accuracy measure what information was carried over in the focus of attention from one trial to the next.

Participants were most accurate in trials in which neither shape nor color switched (M = .92, SEM = .01), followed by trials in which at least one item switched (one item switch: M = .86, SEM = .02; both items switch: M = .87, SEM = .02). A one-way, repeated measures ANOVA indicated that there was a significant effect of switch type, F(2, 32)=13.91, MSE=.02, η_p²=.45, p<.001. Post-hoc analysis via Newman-Keuls tests suggested that proportion correct was significantly higher in 0-switch trials than in the other switch conditions. The proportion correct for trials in which at least one item was switched (i.e., 1-switch and 2-switch trials) did not differ from each other.

Response time

In the analysis of reaction times, the same restrictions were followed as in the proportion correct but only response times for correct responses were included in the analysis. Furthermore, reaction times longer than 10 s were excluded as outliers. The trials eliminated as outliers amounted to an average of 1% of the otherwise usable trials, and no more than 2% in any one condition.

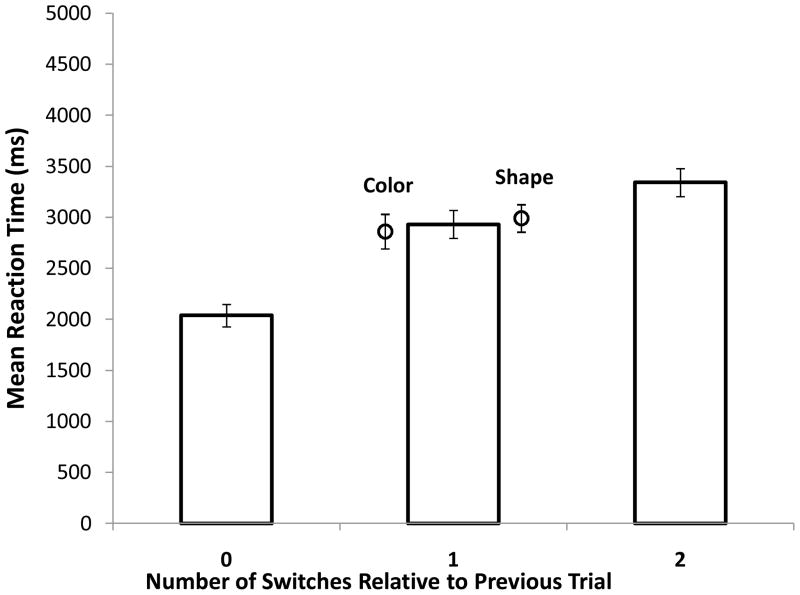
The results of the reaction time analysis are shown in Figure 4. There was again a significant effect in the one-way ANOVA, F(2,32)=76.78, MSE=7,547,475 η_p²=.83, p<.001. Participants were fastest for trials in which neither color nor shape switched (0-switch trials), followed by trials in which either color or shape switched (1-switch trials) or trials in which both items switched (2-switch trials). Most important, as illustrated in Figure 4, participants were significantly faster for trials in which one item switched compared to trials in which both switched. Post-hoc Newman-Keuls tests for this measure indicated that all conditions differed from one another significantly, p<.001 in all cases.. These results strongly suggest that, in line with the predictions in Equation 2, the response time cost for switching two items is larger than the cost associated with switching only one item.

Figure 4.

Patterns of response times across the number of switches from the previous trial in Experiment 1. Points are mean response times in the one-switch condition reported separately for color- and shape-switch trials, respectively. Error bars are standard errors of the mean.

We further examined the effect of trial block on response times to determine whether the pattern changed as participants became more familiar with the task. A repeated-measures ANOVA that included trial block (1–24) and switch condition as factors, showed a significant main effect of trial block on response time, F(23, 207) = 3.63, MSE = 3,936,747, η_p² = .29, p < .001. In general, response time decreased with learning, from a mean of 3904 ms in the first block of trials (SEM = 401.52) to 2496 ms in the final trial block (SEM = 139.37). The interaction between block and switch condition was not significant. Although participants were faster at responding as they became more familiar with the task, we found no evidence that the overall pattern of response times changed.

Discussion

Results from the first experiment suggest that switching two objects on a given trial compared to what had been presented in the previous trial led to a larger response time cost than when only one object had to be switched (either color or shape). These results presumably can occur only if the focus of attention can hold more than one item, in line with our predicted pattern above.

The present results stand in contrast to those obtained by Oberauer and Bialkova (2009), who found a response time cost associated with switching two items equivalent to the cost when only one item was switched. A reasonable interpretation is that the two objects appearing in a trial were chunked together in Oberauer and Bialkova’s study, but not in the present experiment.

Although the results from this experiment provide tentative support for a focus of attention that can hold multiple items concurrently, there is a remaining concern. Although the data pattern does not resemble what would be expected if the objects within a trial were chunked together, there is a logical way in which chunking could have occurred. Specifically, participants could have formed an additional association between the stimulus and the spatial location of the response on the grid, given that the configuration of responses never changed; this could potentially be done via motor learning, without any active retrieval of the associates paired with each stimulus. This situation differs from the one devised by Oberauer and Bialkova (2009) in which the arithmetic operations that participants were required to complete involved alternating between addition and subtraction. To reduce further the possibility that these associations could be formed, the second experiment included a slight modification of Experiment 1. In this experiment, characteristics of the response grid, in particular whether responses began with a letter or digit and the spatial location of each letter-digit pair, changed from trial to trial..

Experiment 2

Method

Participants

Twenty-seven University of Missouri undergraduates (12 males, 15 females) participated in exchange for course credit. They had not participated in the first experiment.

Apparatus, stimuli, and procedure

Our method was the same as in Experiment 1, save for the following modifications. There were 12 trials instead of 11 in each trial block to allow equal numbers of each of 4 response grids that were used on different trials (see Figure 5). The four configurations were the result of crossing two different factors: how the response was listed, and how rows and columns were organized. Responses were either listed as letter-first (e.g., W2), or as digit-first (e.g., 2W). Additionally, grids could have letters listed by row and numbers listed by column (as in Experiment 1), or these could be switched (letters by column, numbers by row). Trials alternated between these four grids in sequential fashion.

Figure 5.

Experiment 2 grid configurations. Each is formed by crossing item response (letter-digit or digit-letter) with the organization of responses on the grid, with letters held constant across rows and numbers held constant across columns, or vice versa.

Results

Proportion correct

As in Experiment 1, the inclusion of feedback ensured that participants performed the dual-access task with high accuracy. A one-way, repeated measures ANOVA indicated that there was a significant effect of the number of item switches, F(2,52)=6.83, MSE=.02, η_p²=.21, p<.01. As was found in the previous experiment, participants were most accurate in trials in which no items switched (M = .88, SEM = .02), followed by trials in which at least one item switched (one item switch: M = .84, SEM = .03; both items switch, M = .83, SEM = .04). Post-hoc Newman-Keuls tests showed that proportion correct was significantly higher in no-switch trials than in the other switch conditions, p < .01 in all cases; as before, the proportion correct for trials in which at least one item was switched (i.e., 1-switch and 2-switch trials) did not significantly differ from each other. Thus, any reaction time differences between trials in which at least one object switched cannot be attributed to a time-accuracy tradeoff.

Response times

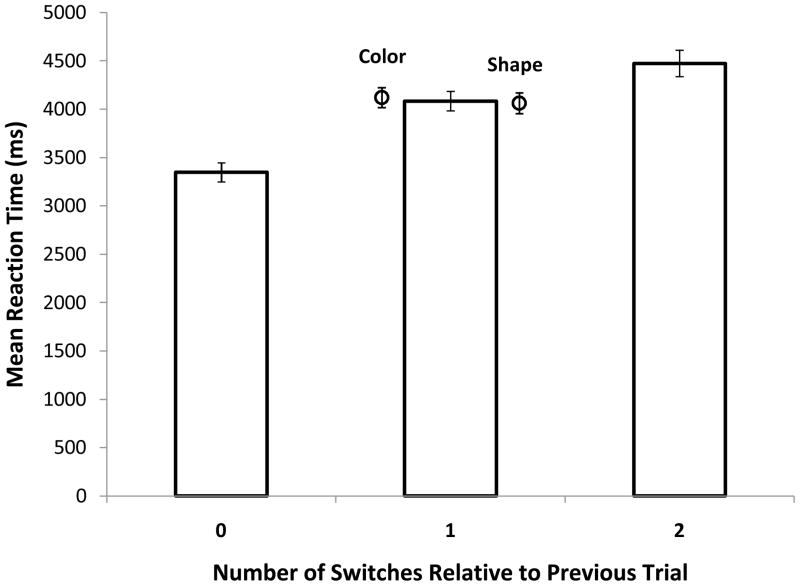
As in the previous experiment, only correct responses with reaction times lower than 10 s were included in the analyses. Trials that failed to meet these criteria comprised approximately 5% of all correct trials. The results of the reaction time analysis are shown in Figure 6. There was again a significant effect of number of item switches for a given trial in the one-way, repeated-measures ANOVA, F(2,52)= 102.54, MSE= 8,828,181, η_p²=.80, p<.001. As we found in Experiment 1, observed response times followed the pattern 0-switch trials < 1-switch trials < 2-switch trials, providing further support for multiple items in the focus of attention. Post-hoc Newman-Keuls tests showed that all conditions differed from each other (p < .001 in all cases)..

Figure 6.

Patterns of response times across number of switches from the previous trial in Experiment 2. Points are mean response times in the one-switch condition reported separately for color- and shape-switch trials, respectively. Error bars are standard errors of the mean.

As in our analyses of Experiment 1, we examined the effects of trial block and number of item switches on response times to determine whether the pattern of response times we observed above changed as participants familiarized themselves with the dual-access task. Using a repeated-measures ANOVA, we found a significant effect of trial block, F(23, 253) = 8.76, MSE = 11,711,620, η_p²=.44, p<.001. There was a general decrease in response time from the first trial block (M = 5191 ms, SEM = 273.98) to the final trial block (M = 3293, SEM = 209.61). The interaction between trial block and number of item switches, however, was not significant, F(46, 506) < 1, p =.71, suggesting that the general pattern we observed above did not change as participants became more familiar with the experimental paradigm.

Finally, to assess the effect of including a small modification (i.e., an alternating response grid) to our original procedure, we analyzed response time data from both Experiment 1 and Experiment 2 using a repeated-measures ANOVA. We observed a significant effect of experiment, F(1, 42) = 57.53, MSE = 44, 952,760, η_p²=.58, p<.001. Introducing an alternating grid significantly slowed participant responding, as RTs in Experiment 1 (M = 2770 ms, SEM = 123.79) were faster than RTs in Experiment 2 (M = 3969 ms, SEM = 98.22). There was also a significant effect of number of switches, F(2, 84) = 176.17, MSE = 15, 986, 590, η_p²=.81, p<.001. As in our previous analyses, we found the following pattern in response times: 0-switch trials < 1-switch trials < 2-switch trials. The interaction between experiment and number of feature switches was not significant, F(2, 84) = 1.08, p = .34. Although including an alternating grid in Experiment 2 slowed participant responses, we found no change in the pattern of RTs across switch conditions, providing further evidence that our findings from Experiment 1 were not due to the unchanging spatial locations of responses on the answer grid.

Discussion

The results from the second experiment closely replicated the findings from Experiment 1 even though there was no constant mapping from stimuli to responses. As before, these results indicate that, when chunking is precluded, the focus of attention is capable of concurrently holding more than one item.

Experiment 3

The purpose of the third experiment was to determine whether it would be possible to encourage chunking in one condition of our new procedure. If we could show that such a manipulation resulted in a pattern of RTs similar to what Oberauer and Bialkova (2009) obtained, and that the absence of the conditions encouraging chunking replicated our findings from Experiments 1–2, such a pattern of results would provide strong support for our assumption that our results so far have arisen through the absence of chunking. To this end, we presented the color and shape integrated into a single object in the testing phase. However, that testing phase was preceded by a training phase in which some stimuli were presented in an integrated form in consistent color-shape pairings (chunk training condition), whereas other stimuli were presented during training with color and shape separated, and with the pairing changing from one exposure to the next (no-chunk training condition).

A pilot experiment in which the method of Experiment 2 was modified, in that the color and shape were integrated into a single object in the testing phase (but with no special training of the objects), yielded results very similar to that experiment. Consequently, we were able to present an integrated color-shape object on each test trial of the present experiment, but now with training exposures for chunk and no-chunk conditions. We believed that this integrated presentation would make it easier to teach consistent color-shape chunks that could be used at test.

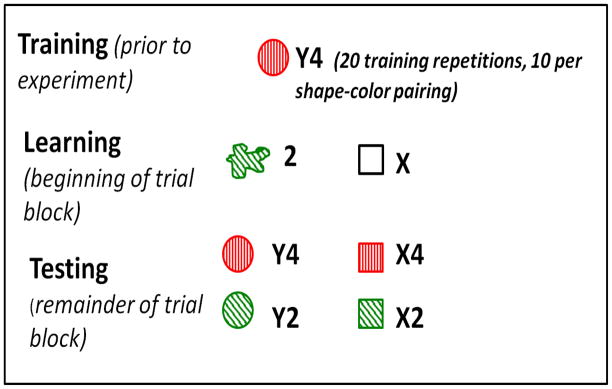
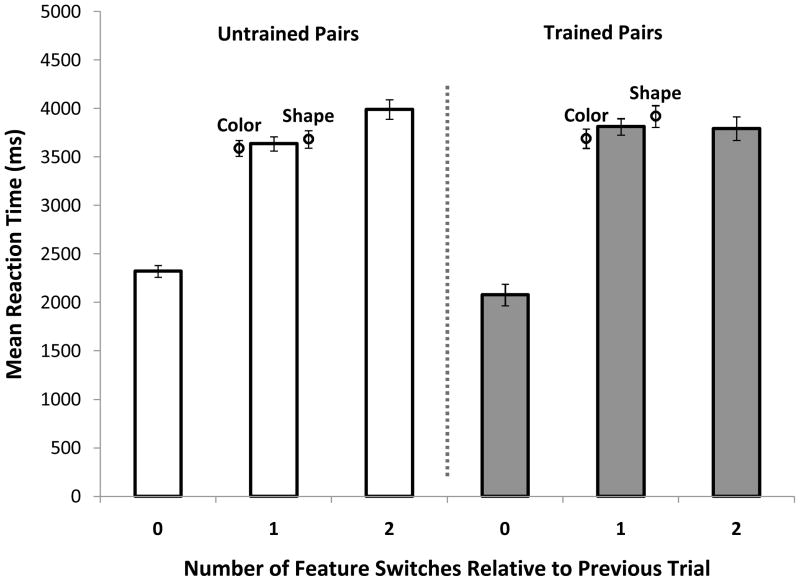
The method is illustrated in Figure 7. At the beginning of the study, participants learned two shape-color pairings that would be consistently used throughout the whole experiment. Once training concluded, in the context of the dual-access task, participants were presented with a shape and color that corresponded to a trained pairing, as well as a shape and color that had not been presented at training. In doing so, we were able to examine switch costs associated with switching from learned chunks versus unlearned shape-color pairings. Starting with a learned chunk on the previous trial, a switch of one element should produce responding no faster than a switch of both elements. In contrast, starting with an unlearned shape-color pairing should result in faster responding for one-element switches than for two-element switches. To discuss analyses that include trials referring back to the trained, integrated chunk as well as to unintegrated color and shape objects, in this experiment the term “feature switch” is used instead of the term “item switch” that was used in previous experiments.

Figure 7.

Illustration of the training procedure in Experiment 3. Prior to beginning the actual task, participants were trained to learn two shape-color pairs, along with their associated letter and digit (one trained pair out of two is shown). During the learning phase at the beginning of each block, participants were presented with a shape and color from a trained pair, as well as a new shape and color that had not been presented during training. At test, there were four possible shape-color combinations, one of which corresponded to a trained shape-color chunk.

Method

Participants

We increased the sample size relative to previous experiments because we needed to examine a more complex pattern of results within each participant. Forty-seven University of Missouri undergraduates (12 males, 35 females) participated in the experiment in exchange for psychology course credits. None of the participants had taken part in any of the previous studies.

During the test phase of the experiment, we wanted to make sure that participants sufficiently learned the trained pairs. In addition to feedback, we set a criterion for further data analysis. Any participant whose performance on the training phase was below 75% was excluded from further data analysis. On this basis, 4 participants (all of them female) were excluded from the experiment.

Apparatus, stimuli, and procedure

Participants were tested in a similar fashion to our previous studies described above, with some modifications to the general procedure. As discussed above, prior to the dual-access task, participants were presented with two shapes (paired with letters) and two colors (paired with numbers) that were randomly selected for each participant. As in the learning phase of the dual-access task, participants had as much time as needed to encode the stimuli and their corresponding associates. As in our previous experiments, stimuli were presented separately during the learning phase. Following this initial presentation, participants completed a training phase that encouraged the formation of two shape-color pairings using our answer grid display. Over the course of 20 trials, participants were shown one of two possible colored shapes at the top of the screen, and were to respond with the associated letter and digit; each shape-color pairing was consistently paired throughout training. Thus, if a participant saw that a circle was paired with the color red, the circle would never be paired with the other color presented in training. An example of this is shown in the top portion of Figure 7, in which one of two shape-color pairings is shown. Each shape-color pairing was randomly presented 10 times during the training phase. Similar to the answer grid portion of the dual-access task, participants always received feedback after making their response.

Following the pairs training, participants began the dual-access task. We included a critical manipulation at the beginning of each block, illustrated in the lower portion of Figure 7. As shown in the figure, participants were shown stimuli from one of the two trained pairs (here, the color red and a circle, and their associated memoranda); these stimuli were presented separately. The other shape and color (and their associates) were new (e.g., the color green and a square, also presented separately). As a result, one shape-color pairing out of all possible trial combinations corresponded to the learned pair (in Figure 7, the red circle); all other combinations were novel. Prior to beginning the answer grid portion of the task, participants were shown the trained shape-color pairings to serve as a reminder.

During the answer grid portion of our dual-access task, participants were shown one colored shape in the top portion of the screen, instead of a separate color and shape. Answer grids sequentially alternated between four different configurations as in Experiment 2. As in our previous studies, features randomly switched from the previous trial, with three different conditions that were possible: 0-switch trials (neither color nor shape switched), 1-switch trials (either color or shape switched), and 2-switch trials (color and shape switched). Additionally, given that one shape and one color had been part of a learned pair from the training phase, on some trials the original pairing that the participant had learned in training was presented at test; this occurred on 25.2% of all trials. We were interested in comparing response time patterns between those trials in which participants had to switch from that learned pairing versus trials in which participants were presented with a shape-color combination that had not been learned in prior training. Participants completed 26 blocks of trials, with 12 trials in each block. As in our previous studies, the first block was used for practice; data from the practice block were removed from our analyses.

Results

Proportion correct

We analyzed accuracy performance for the 43 participants who scored at least 75% correct during the training phase. We examined proportion correct for all trials, save for the first trial in each block, as no switch was possible for these trials. Results from a repeated-measures ANOVA indicated that participants were just as accurate when switching from a learned chunk as they were when switching from an unlearned pairing, F (1,42) < 1, p = .95. The number of feature switches, however, had a significant effect on accuracy, F (2, 84) = 26.34, MSE = .01, η_p²= .39, p<.001. Participants were most accurate for trials in which both color and shape repeated (M = .96, SEM = .01 ); accuracy declined with feature switches (1-switch trials: M = .88, SEM = .01; 2-switch trials: M = .87, SEM = .02). Newman-Keuls tests indicated that accuracy for trials in which color and shape repeated (i.e., 0-switch trials) were significantly different from 1-switch and 2-switch trials (p < .001 in all cases), which did not significantly differ from each other. Finally, the interaction between the presence of a trained pair and number of feature switches was not significant, F(2, 84) = 1.83, p = .17.

Response times

We examined response time patterns for 43 participants who scored at least 75% correct during the training phase. As mentioned above, we were interested in comparing trials in which participants switched from a trained shape-color pair to trials in which participants switched from any shape-color combination that had not been learned during training. If participants had encoded the trained shape-color pairing as a chunk, we expected response time patterns to be identical to the results of Oberauer and Bialkova (2009). In contrast to the predictions of a one-chunk focus of attention that we expected for trained pairings, we expected a replication of our previous results for those trials in which participants were presented with an untrained shape-color combination, as these had not been learned as chunks.

As in our previous experiments, we analyzed response times only for correct responses less than 10 s in duration; based on these criteria, 2% of all correct trials were removed from further analysis. Response time results are shown in Figure 8. Using a one-way ANOVA, we found no significant effect of whether the colored shape presented at test was trained or untrained, F(1, 42) = 1.906, p = .175. There was, however, a significant effect of the number of feature switches from the previous trial, F(2, 84) = 266.13, MSE = 7,464,298, η_p²= .864, p < .001.

Figure 8.

Patterns of response times across the different number of switches in Experiment 3, with separate panels for switches from trained or untrained stimuli. Points are mean response times in the one-switch condition for color- and shape-switch trials, respectively. Error bars are standard errors of the mean.

Most important, as shown in Figure 8, there was a small, significant interaction between these two effects, F(2, 84) = 6.40, MSE = 1,128,228, η_p²= .13, p < .05. Post hoc Newman-Keuls tests showed that for trials in which participants were to switch from shape-color combinations that had not been learned during training, the response time pattern was: 0-switch trials < 1-switch trials < 2-switch trials. For trials in which participants were to switch from a trained shape-color combination, the pattern was: 0-switch trials < 1-switch trials = 2-switch trials. Thus, for trials in which participants had presumably bound shape and color together to form a chunk, response time patterns conformed to the pattern originally reported by Oberauer and Bialkova (2009), in support of a single-chunk focus of attention. In contrast, for pairings that had not been learned, we replicated our previous results, providing further support for a multi-item focus of attention in the absence of chunking.

To confirm that the patterns we observed were different, we analyzed response time data for trained (i.e., chunked) and untrained pairs only for 1- and 2- switch trials, as it is the relationship between these two switch conditions that differentiates the multi-item focus RT pattern from the single-chunk focus pattern. Using a repeated-measures ANOVA, we found a pattern of results that was similar to our previous analysis. There was effect of number of feature switches, F(1, 42) = 6.81, MSE = 1, 220,293, η_p² = .14, p < .05. Response times for 1-switch trials were significantly faster than those for 2-switch trials (see Figure 8). There was no significant main effect of presence or absence of learning a shape-color pair as a chunk, F (1, 42) < 1, p = .88. However, as hoped, we did find a significant interaction between the two factors, F (1, 42) = 6.74, MSE = 1,480, 259, η_p² = .14, p < .05

An additional analysis using a repeated-measures ANOVA that included trial block and number of feature switches as factors suggested that response time was significantly influenced by trial block, F(24, 408) = 4.105, MSE = 5,602,727, η_p² = .194, p < .001. Participants made faster responses in later trial blocks than in early blocks, suggesting learning (first block: M = 3847 ms, SEM = 231.61; final (25th) block: M = 2704 ms, SEM = 162.12). The interaction between trial block and number of feature switches, however, was not significant, F(48, 816) = 1.07, p = .36. As we found in our previous experiments, the pattern of response times in relation to the number of feature switches did not change with learning.

Finally, given that this experiment provides the most comprehensive pattern of responses and was tested with a larger sample size than the other experiments, we performed analyses on individual participant RTs. We compared 1- versus 2-switch trials for trained and untrained pairs, which could reveal whether participants varied in the manner in which they loaded items into the focus of attention. Within each individual, a 1-tailed t test was used to compare 1- versus 2-switch trials for chunk-trained and untrained pairs. (It was an independent-sample t test because there could be no 1-to-1 correspondence between trials of the two types.) For untrained pairings, 33 out of 43 participants showed a pattern of means in the direction expected according to a multi-item focus, with RTs for 1-switch trials faster than for 2-switch trials ( a statistically significant effect with a one-tailed test within 15 participants). For trained pairs, in striking contrast, only 9 participants showed a pattern consistent with a multi-item focus of attention, with no significant differences in response times between 1- and 2-switch trials in any participant. It is clear from this examination of individual differences that when participants are not encouraged to chunk or bind stimuli together, a majority of participants show a response time pattern consistent with a multi-item focus of attention, whereas that did not occur when the previous trial involved a response to a color-shape pair that had become a trained chunk.

Discussion

The results of Experiment 3 provided a strong replication and extension of our previous results. Specifically, we found two differing response time patterns that were dependent upon whether participants had learned to associate a particular shape with a particular color. When participants were presented with a shape and color that had not been trained as a pairing, we replicated the results from our previous studies. Once again, we found faster responses for trials in which only one feature (either color or shape) switched than for trials in which both features switched; these results are in lines with Oberauer and Bialkova’s (2009) predictions for a focus of attention that can hold multiple items. However, when participants had previously been trained to pair a shape and a color together, the pattern changed. In this case, there was no additional response time cost for trials in which both features switched versus those in which only one feature switched. This pattern replicated previous findings from Oberauer and Bialkova in support of a single-chunk focus of attention. These results are most consistent with an interpretation in which the experimental procedure used by Oberauer and Bialkova may have strongly encouraged chunking.

Experiment 4

We believe that our findings from the previous studies show that the focus of attention is able to access multiple items. However, it is possible that we may have obtained faster response times on trials in which only one feature switched, compared to two feature switches, because of response-related priming. Specifically, in Experiments 1–3, if and only if a stimulus item repeated from one trial to the next, its response repeated as well, so those experiments provide no indication of which kind of repetition reduces reaction times. In Experiment 4, we modified our procedure to deconfound stimulus and response repetition, by having two shapes or colors be associated with the same letter or number for some of the stimuli.

Method

Participants

Twenty-nine University of Missouri undergraduates (12 males, 17 females) participated in the study in exchange for course credit. One female participant voluntarily withdrew from the study, and was excluded from further analysis. For two male participants the experimental program was aborted, and they too were excluded.

Stimuli, apparatus, and procedure

All stimuli and testing procedures used in this experiment were nearly identical to those used in Experiment 2, with two important exceptions. First, at the beginning of a block of trials, instead of being presented with two shapes and two colors, participants were shown three shapes and three colors as separate items, which were randomly selected. As a critical manipulation, two of the shapes that participants saw were associated with the same letter, and two of the colors were associated with the same number. Thus, even though 6 different stimuli were presented, there were only 4 possible responses (2 letters × 2 numbers) that could be made during the answer grid portion of the dual-access task. Second, during the answer grid portion of the task, shape and color were presented as an integrated object, instead of separate objects.

After participants had learned all 6 of the stimuli and their corresponding associates, they were presented with a colored shape at the top of the computer screen with the answer grid below where they could make their response. The answer grids sequentially alternated between four different configurations. As in previous studies, items switched from the previous trial, leading to four different possible trial types: both color and shape repeated from the previous trial, shape changed, color changed, or both shape and color changed. Of particular interest to us were trials in which either 1 or 2 items changed while the letter and digit did not (i.e., stimulus changes but response repeats). Participants completed 25 blocks of trials, with 12 trials per block¹. The first block was treated as a practice session, and data from this practice block was not used in data analysis.

Results

Proportion correct

The mean accuracy in each condition is shown with its standard error in Table 1. The analyses were focused on theoretical questions, including subsets of these conditions in order to dissociate different possible effects. One such analysis was an assessment of the effect of the number of stimulus switches (0, 1, or 2), which could be examined in a controlled fashion with the responses in each case unchanged from the previous trial (as shown in Table 1). According to our theoretical analysis, there should be an effect of stimulus switches because the focus of attention often contains the stimulus-response pairing for stimuli encountered on the previous trial.

Table 1.

Means and standard errors (in parentheses) for proportion correct across different combinations of feature switches and response switches in Experiment 4.

	0 Response Switches	1 Response Switch	2 Response Switches
0 Feature Switches	0.93 (.02)	--	--
1 Feature Switch	0.76 (.03)	0.73 (.04)	--
2 Feature Switches	0.73 (.04)	0.64 (.05)	0.63 (.05)

It is theoretically possible, however, that it was not the stimulus-response pairing that remained in the focus of attention but the response alone. In that case, there should be effects of the number of response switches with the number of stimulus switches held constant. As shown in Table 1, it was possible to examine this for trials with two stimulus switches, which could correspond to 0, 1, or 2 response switches.

As in previous experiments, we excluded those trials that were first in a block, as no possible item switch could occur. In the ANOVA for feature switches with no response switches (see Table 1), there was a significant effect of the number of feature switches, F(2, 50) = 26.55, MSE = .295, η_p²= .52, p < .001. Participants were most accurate for 0-switch trials, and were less accurate 1- and 2-switch trials, which did not differ significantly from each other according to Newman-Keuls tests.

To test the effect of number of response switches, it was possible to analyze accuracy for trials in which there were two feature switches (see Table 1). We found a small, significant effect of the number of response switches, F(2, 50) = 5.38, MSE = .079, η_p²= .18, p < .01. Participants were most accurate when no part of the response changed, with worse performance occurring for trials where either one or both components of the response changed. Post-hoc Newman-Keuls tests showed that 0-response-switch trials had higher accuracy than 1- or 2-response switch trials, which did not differ.

Response times

As in our previous studies, analyses of response times involved only correct trials that were less than 10 s. Approximately 4% of all correct trials were removed from further analysis based on this criterion. The analysis was otherwise constructed in the same way as for the proportion correct.

Just as for our analyses for proportion correct in this experiment, analyses of response time were based on the number of feature switches and response switches that occurred within the task. Means and standard errors for response times for all possible combinations of feature switch and response switch are presented in Table 2.

Table 2.

Means and standard errors (in parentheses) for response times across different combinations of feature switches and response switches in Experiment 4.

	0 Response Switches	1 Response Switch	2 Response Switches
0 Feature Switches	2496 ms (89)	--	--
1 Feature Switch	3798 ms (154)	4331 ms (129)	--
2 Feature Switches	4630 ms (267)	4840 ms (189)	4717 ms (221)

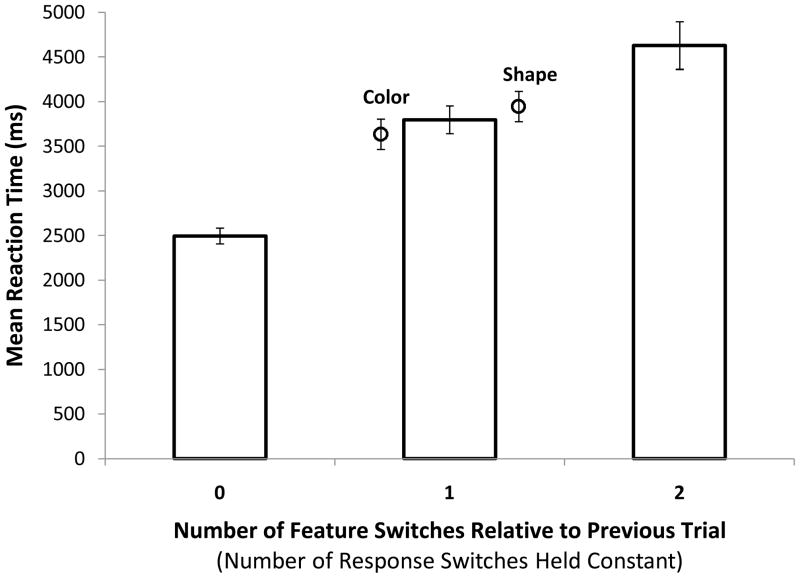
As in our analyses of proportion correct, we examined the effect of one factor (either feature or response switches) while holding the other factor constant. The number of response switches was held constant with no response switches, the only response condition in which all stimulus feature-switch conditions could be tested. There was a significant effect of number of stimulus feature switches, F(2, 50) = 58, MSE = 30, 079, 500, η_p²= .70, p < .001. Response times for feature-switch trials conformed to the expected pattern, 0-switch < 1-switch < 2-switch. These results were confirmed by Newman-Keuls tests, with all feature switch conditions significantly different from the others at the p < .001 level.

Conversely, to test the effect of number of response switches, we analyzed response times for trials in which there were two stimulus feature switches, as this was the only feature switch condition in which all possible response switches could occur. When the number of stimulus feature switches was held constant, there was no effect of number of response switches on RT, F(2, 50) < 1, p = .58. As Table 2 shows, RTs across response switch conditions were equivalent when two stimulus features switched, producing nonsignificant post-hoc Newman-Keuls test. This suggests that that the results we obtained in previous studies in support of a focus of attention that can maintain at least two separate items were not due to switching components of the response.

Discussion

The findings from Experiment 4 provide further clarification of response time patterns that support a multi-item focus of attention. We presented participants with two shapes that were associated with the same letter and two colors that were associated with the same digit. If our prior findings in support of a multi-item focus of attention were due to response priming, we should have found a significant effect of response switching when stimulus switches were held constant. In that case, it should have produced the now-familiar pattern: 0-switch < 1-switch < 2-switch. The results from this experiment, however, rule out this possibility. In concord with theory, when the number of response switches was held constant, we found a pattern of RTs across feature-switch conditions that corresponded to our previous results in support of a focus of attention that can hold at least two separate items. These results suggest that the replicated pattern of RTs we have reported were due to switches and repetitions in the encoded stimuli and, we believe, the bindings between the stimuli and associated memoranda, rather than the responses alone.

The results of this experiment are especially interesting in light of current interest in the binding between stimuli and responses in switch-time studies (e.g., Janczyk & Kunde, 2010). A theoretical analysis of the task demands of the present experiment might help to explain the results. It might be counterproductive to retain responses per se in the focus of attention. Too much response readiness can lead to errors in cases in which the new stimulus is inconsistent with the readied response (e.g., Gratton, Coles, Sirevaag, Eriksen, & Donchin, 1988). In contrast, keeping in the focus of attention a previous stimulus-response association is potentially less problematic because a simple match of the new stimulus with the contents of the focus of attention can be carried out to determine whether the stored information is useful or must be replaced, a process less likely to lead to response errors.

General Discussion

The concept of working memory was originally proposed over 40 years ago to explain how we are able to store and manipulate small amounts of task-relevant information over short periods of time (Baddeley & Hitch, 1974; Miller, Galanter, & Pribram, 1960). Yet, the nature of limits in working memory still has not been settled. One debate is whether the focus of attention holds multiple items at once (Cowan, 2001, 2005) or only one item at a time (e.g., Garavan, 1998; McElree, 2001; Oberauer, 2002). Oberauer and Bialkova (2009) suggested that the focus of attention could only hold a single chunk, though it could be formed from at least two items in combination that have become associated. The analysis of many cognitive tasks hinges on the focus of attention. For example, as mentioned above, combining two items to form a new chunk is a process that could occur in the focus of attention (Cowan, 1999, 2001, 2005) but, according to a 1-item focus, would somehow have to occur outside of the focus. The same issue arises when the task is to compare two items (e.g., “which is heavier, a grape or an orange?”)

The present research extended the experimental logic of Oberauer and Bialkova (2009) to a situation in which chunking was less natural, inasmuch as the two separate stimulus elements were mapped onto two separate elements of the response (Figure 2), rather than being integrated into a single response element such as an arithmetic sum as in Oberauer and Bialkova’s study (Figure 1). Our results suggest that multiple, separate items may be held in working memory concurrently. Specifically, the pattern of results was different from the ones based on either a one-item focus or a two-item, one-chunk focus. Instead, it was a pattern that Oberauer and Bialkova attributed to the retrieval of two items separately into the focus of attention, in a manner that is slower when two, as compared to one, of the items has switched from the previous trial. Below, we summarize the present findings and then discuss unresolved issues. Last, we explore some of the broader implications of our findings for cognitive psychology.

Summary of Findings

Oberauer and Bialkova (2009) found that when both items switched from one trial to the next (Figure 1), responses were no slower than when only one item switched; responses on both trial types were slower than when no items switched, presumably because both items were combined to forma single chunk. In our procedure that was substantially modified from Oberauer and Bialkova, we were able to minimize the formation of chunks within the task. To preclude chunk formation, we established two types of stimulus-response pairings (shape-letter and color-number) that had to be used separately rather than two stimuli contributing to a common response as in Oberauer and Bialkova’s study. Thus, we eliminated the main factor that we thought would have contributed to formation of a two-item chunk in their study.

In Experiments 2 through 5, we also used answer grid configurations that changed from trial to trial to prevent motor learning. The most important finding from Experiments 1 and 2 (seen in Figures 4 and 6) was that switching both the color and the shape from one trial to the next resulted in slower performance than switching either color or shape alone (i.e., the multi-chunk working memory pattern according to Oberauer and Bialkova).

Given that quite a bit was changed from the procedure of Oberauer and Bialkova (2009), one might worry that some unidentified difference between the procedures produced the differences between the patterns of results (equality versus inequality of one- versus two-switch reaction times). Providing further reassurance, though, in Experiment 3, participants were trained to bind a subset of stimuli into consistent shape-color pairings to create two-element chunks. Response time patterns showed the expected pattern. For shape-color pairings that were not seen during training, response times supported a multi-item focus of attention in which shape and color were separately stored, replicating our previous results. In contrast, response times for trained shape-color pairings showed a pattern essentially identical to the one reported by Oberauer and Bialkova, in support of a focus of attention limited to a single two-item chunk (Figure 8). These findings confirm that our procedure was logically comparable to that of Oberauer and Bialkova except that, in our procedure, two-item chunks were formed only in the presence of special training.

Results from Experiment 4 further distinguished between effects of stimulus repetition versus response repetition. Specifically, multiple shapes mapped onto the same letter responses and multiple colors mapped onto the same number responses. It was theoretically possible that what matters for response times is how many components of the responses remain the same from one trial to the next. Indeed, there was an overall benefit to response times when an element of the required response was unchanged. Nevertheless, response times for 2-switch trials were significantly longer than 1-switch trials no matter whether the corresponding response from the previous trial repeated or was new (Figure 9). This result shows that our pattern cannot be attributed to repetition priming of the responses, in which case there should be no difference between 1- and 2-switch trials when the responses do not change. Our results once again support a multi-item focus of attention, according to the experimental logic of Oberauer and Bialkova (2009).

Figure 9.

Patterns of response times across the different number of feature switches in Experiment 4 while the number of response switches are held constant (in this case, 0-response-switch trials). Points are mean response times in the one-switch condition for color- and shape-switch trials, respectively. Error bars are standard errors of the mean.

Unresolved Issues

Capacity of the focus of attention and levels of analysis

Our data cannot speak to all levels of analysis at once. It cannot address what might be called a microscopic level of analysis. In particular, a focus of attention that refreshed one item at a time, but rapidly rotated between items to be refreshed, could give rise to a system that would look a great deal like a multi-object focus of attention; it might be impossible to distinguish between the two on the basis of behavioral evidence. In the present procedure, the key finding that switching two items takes more time than switching one still could be explained by that kind of one-item focus, in that the process of switching could take additional time for each separate switch.

Our research is on a more macroscopic level of analysis. Oberauer and Bialkova (2009) showed that two items entered the focus of attention together only because they were combined into a single chunk. The implication was that there is no evidence for multiple separate chunks in the focus of attention concurrently. They articulated a pattern that would occur if multiple separate chunks (in this case, two 1-item chunks) did enter separately, and we obtained that pattern of results. Therefore, the best conclusion is that a multi-item focus hypothesis remains viable in light of our new results. These results, however, cannot rule out all versions of a one-item focus.

It is worth considering in detail other results that appear to support a one-item focus, inasmuch as they, too, might actually be expected on the basis of a multi-item focus. In their discussions of the time-based resource sharing model of working memory, Barrouillet and colleagues (Barrouillet et al., 2007; Barrouillet, Bernardin, & Camos, 2004; Barrouillet et al., in press) have suggested that the focus of attention must be limited to a single item. The finding underlying this suggestion was that working memory performance for a list of items depends closely upon the ratio of the time available to reactivate items through an attention-demanding refreshing process to the time taken up by distracting items; this relation holds across many presentation schedules and materials. It was proposed by the authors that there is decay of information when reactivation is impossible, and that decay and reactivation reach a balance in which some items can be preserved but others cannot. It was assumed that it is precisely because multiple items cannot be stored simultaneously in the focus of attention that focus must be circulated among items to cause memory reactivation.

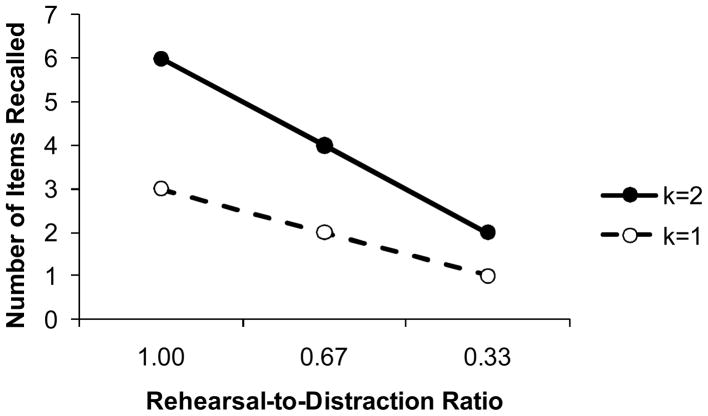
To predict a linear relationship between recalled items and time for refreshing traces, though, the focus of attention need not be limited to a single item, as Barrouillet et al. (in press) recently acknowledged. To see this, consider a simulation of memory with a simple set of rules in the spirit of Barrouillet et al: (1) The retention interval is divided into periods. (2) Any period can include either refreshment of items in memory, or distraction. (3) If memory capacity is k items, then k items can be loaded into working memory in each period of refreshment. (4) In order to do so, items must be dropped from the focus so that the sum of items in the focus of attention does not exceed k at any moment. (5) An item that has been dropped from the focus can persist in an activated form for 2 periods (as chosen here for convenience). On the third period, this item must be entered into the focus again or it will be lost from working memory. (6) At the time of recall, any item that is in the focus of attention, or was in it within the prior 2 periods, is recalled.

For example, suppose there is no distraction (a refreshment ratio of 1.0). Then with a 1-item focus of attention, it is possible for the participant to retain and refresh three items, a, b, and c, in a repeating loop, but no more. (If an Item d were added in the next period, it would be at the expense of letting Item a lapse from memory.) With a 2-item focus, the participant can refresh on successive periods Items ab, cd, and ef in a repeating loop; no more, or items would be lost. If there is a distraction period after every two refreshment periods (a ratio of .67), a 1-item focus is constrained to refreshing Items a and b so that each item can be repeated again after a distraction period without being lost. A 2-item focus is constrained to refreshing Items ab and cd but no more. Finally, if there are two distraction periods after each refreshment period (a ratio of .33), a 1-item focus is restricted to refreshing Item a only, because it must be refreshed after two successive distraction periods; and a 2-item focus is restricted to refreshing Items a and b only.

Figure 10 shows these theoretical results. This simple demonstration shows that the linear relations obtained by Barrouillet et al. (2004, 2007) need not indicate that the focus of attention can hold only one item at a time inasmuch as a linear function is obtained also with a two-item focus of attention, i.e., k=2 (and theoretically with any value of k).

Figure 10.

Theoretical model results from versions of the time-based resource sharing model (Barrouillet et al., in press) for working memory capacities of k=1 and k=2, assuming k items can be rehearsed concurrently. The graph shows the number of items recalled from a list when periods of distraction between list items are interpolated with periods of rehearsal, for 3 different rehearsal-to-distraction ratios,. The key point is that both functions are linear as expected in the theory.

McElree and colleagues have used a list probe recognition task to argue for a single-item focus that lingers on a single item during the response period, like the level of analysis that Oberauer and Bialkova (2009) evaluated (e.g., McElree & Dosher, 1989; McElree, 1998, 2001). Specifically, participants were presented with a tone that functioned as a cue to make a recognition response. As the time between the recognition probe and the tone varied, this permitted a tradeoff between speed and accuracy that allowed McElree and colleagues to obtain a time-course of retrieval for each list item. When these functions were examined, it was consistently found that the last item in a list had a faster retrieval rate than all other items; in contrast, the retrieval rates for all other items did not differ from each other. When participants were presented with lists that were blocked by category (3 exemplars within a set; McElree, 1998), the retrieval rate for all items in the list-final category was significantly faster than for any other set of category exemplars. Consequently, McElree (1998) concluded that the three items had been combined into a single chunk that could be held in a single-item focus of attention. This finding appears to corroborate the findings from Oberauer and Bialkova (2009).

McElree and Dosher (2001) have suggested that this capacity limit in the focus of attention may only apply to retrieval of lists, and not for simultaneous arrays of items such as those utilized in the present approach. Moreover, there are other potential explanations for the findings of McElree (1998) beyond a single-item focus of attention. First, the focus of attention may always hold a list-final item, in addition to a few other items from prior serial positions. Whereas the last item within a list will always be held within the focus, the probability that a particular list item from a non-final serial position will vary. The list-final item would have the greatest probability of entering the focus of attention. Second, faster retrieval rates for list-final items may not be due to processing within the focus of attention, but could instead be due to some other source that does not involve attention, such as the magnitude of lag between an item’s presentation and subsequent retrieval (cf., Oberauer, 2006).

Third, and finally, the evidence of McElree (1998) that three items in a row from the same semantic category are present within the focus of attention actually appears to involve three discrete items in the focus of attention, rather than one three-item chunk as was proposed. For some negative recognition probes, McElree used unstudied exemplars from semantic categories that were shown in the list (i.e., lures). To be able to reject these lures, participants would have to search each studied exemplar within a category and compare each to the lure; it would not be enough to reject the lure on the basis of semantic category. Because of the demands of the task, it is likely that participants had to store the three items separately within the focus, rather than as a single chunk. To be sure, a serial position function with multiple, successive 3-item scallops suggests that the items in the list were grouped according to semantic category; but according to the conventional meaning of a chunk as a strongly associated group of items (Cowan, 2001; Miller, 1956) if the three items in a triad truly had formed a single chunk, then performance should have been equally good for all three items in a chunk rather than the medial item being at a lower level of performance.

In sum, we believe that McElree’s behavioral evidence does not indicate that there is a one-item focus that must linger on a single item for a relatively long period of time, such as the period during which a response is made on a single trial.

A recent study by Oberauer and Bialkova (2011) further validates our conclusion, suggesting that a focus of attention that lingers on a single item or chunk may be untenable. Participants completed a task involving continuous updating of two different types of stimuli. Two different digits were presented along with trumpet and piano notes and were to be remembered. The one presented with a trumpet sound was then to be updated according to the pitch of a subsequent trumpet note (high, add 2; low, subtract 1); the other, according to the pitch of a subsequent piano note. Also, blue and red dots were to be moved in a grid according to the direction of corresponding arrows. In a critical dual-task condition, an instrumental note and an arrow were always presented concurrently. If the order of updating operations matched the order of initially presented information then chunks could be used (e.g., red dot with piano digit, blue dot with trumpet digit). The pattern of switch costs resembled our one-chunk results (Experiment 3) when chunks could be formed, but resembled our result suggesting two separate items in the focus concurrently (all our experiments) when the presentation discouraged chunking. Based on these findings, Oberauer and Bialkova (2011) concluded that the focus of attention can maintain at least two separate elements simultaneously, provided that the items are of different types to avoid interference. They made the observation that when items to be updated are similar in kind, a one-item focus may be implemented not because of a capacity limitation but to avoid confusion between the similar stimuli and responses (cf. Meyer & Kieras, 1997).

Studies such as ours only rule out a focus of attention that is limited to a single item or chunk if the focus either lingers on the most recent item presented or if it sluggishly cycles between to-be-remembered items (i.e., taking several seconds). If a single-item focus of attention could rapidly cycle between items, however, this would produce a pattern of results that would be indistinguishable from a multi-item focus that we propose. The recent neuroscientific literature might eventually help us decide between a multi-item focus and a rotating one-item focus though, at present, there are leads seeming to point in either direction. Here we attempt to reconcile these neuroscientific leads. Leaning toward a rapidly-rotating one-item focus, Lisman and Idiart (1995) proposed that refreshing may be enacted by oscillatory neuronal networks in the brain. The features of one item in working memory would be active at the same time (e.g., in the present context, triangle-z) followed by features of another item (in the present context, red-1) and so on. In this theory there is a repeating neural activity cycle within which all items must be active, and they cannot be active too close together or they will contaminate one another. Recently, Siegel, Warden, and Miller (2009) found a pattern of nerve cell activity in monkeys seeming to support this theory, with the patterns in the prefrontal cortex reflecting the sequential activation of patterns reflecting two items in working memory, one at a time within a repeating, 32-Hz cycle. That rate, seems far too fast for the circulating, strategic refreshment of items by attention as in the theory of Barrouillet et al. (in press) but they acknowledged that their findings involving the refreshment process are equally consistent with a single-or multi-item focus of attention, which in either case would shift from one subset of items to another to prevent decay (see Figure 10).

Recent neuroimaging studies have examined list item recognition and have suggested that there is a special status of the last list item, in that recognition of that item does not activate the hippocampus as earlier items do. Based on this evidence, it has been proposed that only the last list item is in the focus of attention, inasmuch as it does not require retrieval from memory, which typically activates the hippocampus (Nee & Jonides, 2011; Öztekin, Davachi, McElree, 2010). This would then reflect a one-item focus that does not rapidly rotate among items, at least in the list item recognition paradigm. Cowan (in press) raised several concerns regarding this line of evidence, however. First, the actual data suggested that not only the last item but also the first item in the list had a similar special status. Second, there has been no evidence that this special status is voluntary, as it should be if it reflects the focus of attention. Third, Cowan suggested the alternative hypothesis that the first and last items in the list do not show as much hippocampal activation because they are easier to bind to their context than the medial list items; binding items to context is another recently hypothesized function of the hippocampus (Baddeley, Allen, & Vargha-Khadem, 2010; Moses & Ryan, 2006).

Leaning toward a multi-item focus (e.g., as described by Cowan et al., 2005) is the recent neuroimaging research on the intraparietal sulcus (IPS). Todd and Marois (2004) showed that activity in the IPS increased with a visual memory load and, unlike other brain areas, reached an asymptote in activity as the memory load approached the participant’s capacity limit. Cowan et al. (in press) showed that the at least the left IPS cannot be considered a modality-specific visual storage area, inasmuch as the same area also stores acoustic-verbal materials and a combination of visual and verbal materials. Instead, it may reflect the contents of the focus of attention. Cowan reviewed considerable evidence of the attention-related function of the IPS. Importantly, Anderson, Ferguson, Lopez-Larson, and Yurgelun-Todd (2010) showed that the IPS includes maps to other cortical regions representing different kinds of input and that these maps can benefit from selective attention. One exciting possibility that remains to be tested is that different specific items in working memory activate different maps within the IPS, which would provide a spatial as opposed to temporal (e.g., Siegel et al., 2009) account of the attention-related storage function in working memory.

It is also possible that the temporal and spatial map mechanisms could work together. For example, a rotating pattern in the frontal cortex (Siegel et al., 2009) could activate an alternating pattern of neural maps within the IPS (Anderson et al., 2010), in which case it could be said that a focus of attention holding several items at once is maintained by an attentional refreshing process that quickly rotates among the items in the focus of attention.

In sum, we believe that the concept of a multi-item focus of attention holding items in a privileged state within working memory is made more plausible by our evidence, serving as a counter-weight to the implications of Oberauer and Bialkova (2009) that the focus of attention can include only one item at a time. Moreover, all available evidence seems to point either to a multi-item focus or to a rapidly-rotating one-item focus. Our data and some of the neurological evidence seem inconsistent with a one-item focus that always remains on a single item for hundreds of milliseconds or longer.

The detailed processes involved in switch costs

A second, related issue that our study cannot resolve is the exact processes involved in switch costs. In order for us to explain completely our pattern of results, we would have to explain why the cost of one switch compared to no switches is greater than the cost of two switches compared to one switch (Figures 4, 6, 8, & 9). There are many possible explanations and deciding among them is beyond the scope of the present article. One theoretical possibility is that a certain amount of time is needed to inhibit the solution on Trial n-1 before switching to the new element or elements, and/or to translate the new contents of the focus of attention into a new response. This extra processing would be needed even if the new response ultimately turned out to be the same as the previous one (as in the no-response-switch, 1- and 2-stimulus switch conditions of Experiment 5).

There is uncertainty regarding the processing involved in two-switch conditions. Recently, Oberauer and Bialkova (2011) obtained an underadditive interaction similar to ours. Specifically, the switch cost for trials where one item switched compared to trials where no item switched was larger than the resulting switch cost when trials with one and two item switches were compared. As such, they argued that two elements could be loaded into the focus of attention largely in parallel fashion, provided that the elements were of different types. If information about the two new items is indeed loaded into the focus of attention in parallel, the process could be either capacity-limited or capacity-unlimited. If it were capacity-limited, the results theoretically could be identical to what would be obtained if the items were loaded into the focus of attention in serial (cf. Townsend, 1976). Moreover, it is theoretically possible that the loading process would be serial on some trials and parallel on others, and mixture models are worth pursuing in future studies.

On the other hand, the absence of a difference between one- and two-item switch conditions in the data of Oberauer and Bialkova (2009) shows that the focus of attention need not always accommodate more than one chunk. Several investigators have suggested that the focus of attention can contract to include just a single item when appropriate according to the task, or expand to include several items when that is necessary (Cowan, 2005; McElree & Dosher, 2001; Verhaeghen, Cerella, & Basak, 2004). Providing a possible mechanism for this contraction and expansion of the focus of attention, Zhang and Luck (2008) suggested that, when the task-relevant items are fewer than working memory capacity, the available slots can double up on the items, improving the precision for each representation. Formation of a chunk when it is possible, as in the study of Oberauer and Bialkova, presumably would make the task less effortful than when two items must be loaded separately into the focus of attention.

The Oberauer and Bialkova (2009) models have built into them some constraints on the predictions, upon which we rely in finding support for a multi-item focus. In their 1-item focus models that they ruled out, they assumed that the two items within a trial were processed with a consistent order. A one-item focus of attention predicts no switch costs in our procedure under that assumption because there is always a within-trial switch from processing the first item to processing the second, and another switch from processing the second item to processing the next trial’s first item. However, single-item focus models with a variable order of processing of the two elements have not been explored to our knowledge.

Switch costs also may include additional processes besides shifting the focus of attention. For example, Janczyk and Kunde (2010) showed that switches in stimulus-response binding can contribute to switch costs. A recent study by Oberauer (2006) suggested that the accessibility of items in working memory, as measured by RT, differs depending upon the lag between the current trial and when it was last retrieved (i.e., lag effects) in addition to what happened in the prior trial relative to the current one (i.e., switch costs). Lag effects were given an interpretation that did not have to do with the nature of the focus of attention. There appears to be no airtight way, however, to rule out the possibility that switch costs are just the effects of lag=1 (i.e., the shortest possible period between the most recent presentation of a particular item and its presentation in the current trial). If that is the case, switch costs would not indicate the size of the focus of attention after all. Therefore, the interpretation of the present result must be tempered so that the proper conclusion is as follows: if switch costs indicate the size of the focus of attention in the manner outlined by Oberauer and Bialkova (2009), they are entirely consistent with the notion that at least two items can reside in that focus separately at the same time.

Aspects of RTs beyond switch times also may be relevant to the nature of the focus of attention. Verhaeghen and Basak (2005) proposed that a characteristic RT function should result if the focus of attention were limited to a single item. Specifically, one should see a step function, with the response time for Set Size 1 being significantly lower than those for larger set sizes. In contrast, there should be no significant differences in response times for any set size that is larger than 1. Examining response times in a modified N-back task, the results corresponded to this step function. This may suggest that, for those instances in which more than one object must be processed in working memory, the focus of attention will be required to switch. Processing more than one item was presumed to occur at a constant rate not dependent upon set size.

Additional research from Verhaeghen and colleagues, however, indicates that the focus of attention can hold multiple items at once. The step function described above was not always found using variations of the N-back task (Verhaeghen and Basak, 2005, Experiment 2; Zhang & Verhaeghen, 2009). Also, results from Verhaeghen et al. (2004) indicate that the focus of attention may expand to include multiple items through training. When participants received sufficient training, response times indicated that the focus of attention expanded to maintain up to four items at a time. The expansion of the focus of attention with practice is an idea that still is debated (Oberauer, 2006), and these training effects may be due to the long-term formation of multi-item chunks (e.g., Ericsson, Chase, & Falloon, 1980; Ericsson, Delaney, Weaver, & Mahadevan, 2004) instead of an alteration in the focus of attention. The results we have obtained cannot resolve this debate.

Implications for Cognitive Psychology

Given the key importance of the notion of the focus of attention as an information-holding device, the present results in favor of a multi-item focus have broad implications for the prioritization of certain methods in future studies. There appear to be two main theoretical camps regarding item limits in the focus of attention. Interestingly, experimental findings in support of a multi-item focus of attention typically emphasize the accuracy of recall or recognition. For example, a common measure used to estimate working memory capacity in change detection studies (e.g., Luck & Vogel, 1997) is k, which is calculated on the basis of hits and false alarms (Pashler, 1988; Cowan, 2001). In contrast, findings in support of a single-item focus often emphasize response times during recall or recognition (e.g., McElree, 1998, 2001; Oberauer, 2002; Oberauer & Bialkova, 2009). It is possible that these two different types of measures are capturing different properties of the focus of attention. Estimates of working memory capacity may tap structural, storage-related properties of the focus of attention; in contrast, studies that emphasize the speed of shifting the focus of attention (e.g., Barrouillet et al., 2007, in press) may capture its dynamic properties. Separating storage from processing and understanding the coordination of storage and processing, both with specific reference to the focus of attention, are important topics for future research.

Determining the capacity limits of the focus of attention also has important consequences for understanding information processing in working memory. For example, as we mentioned above, previous research has found an immediate memory limit of about three to four items when higher-order strategies are prevented. If it turns out that the focus of attention can hold multiple, separate items simultaneously, it is possible that the focus is synonymous with this capacity-limited region. As such, various cognitive operations in which multiple items must be consciously maintained (i.e., chunk formation) likely occurs inside the focus of attention, provided that capacity is not exceeded. In contrast, if the focus of attention is limited to a single item or chunk, it follows that the capacity-limited region is separate from the focus. As a consequence, cognitive operations must occur outside of the focus of attention, at least for a single-item focus that cannot rapidly rotate among multiple items. It has been proposed that information outside of the focus of attention is not item-limited, and can be subject to time-based decay and interference on the basis of similar features (e.g., Cowan, 1988, 1999, 2005); however, little else is known about the remaining contents of working memory and how these contents interact with the focus of attention. If we are able to gain a clearer understanding of how information is maintained and processed in the focus of attention, the potential to gain more understanding regarding information processing in working memory becomes greater as well.

In a larger sense, examining the limitations in the focus of attention has enormous implications for our understanding of how we attend to multiple pieces of information present in the environment. For example, consider when one must perform more than one task at the same time, as in divided attention tasks. If the focus of attention is only limited to a single item or chunk, a person engaging in two cognitive tasks at the same time would not actually be dividing attention between tasks; rather, attention could only shift between the two tasks, as a person could only process one task at a given time. On the other hand, if the focus of attention is able to accommodate multiple items at the same time, one is able to divide attention between the two tasks and can potentially perform both tasks at the same time, although shifting attention between tasks is also permissible. Understanding how the focus of attention is limited can clarify what it means to divide one’s attention between tasks, or whether it should instead be characterized as a shift in attention.

In addition to clarifying our understanding of attention, these findings also have important implications for studies involving select populations with reported deficits in working memory capacity. Previous studies have found that relative to healthy young adults, persons with schizophrenia (Gold et al., 2006), young children (Gilchrist, Cowan, & Naveh-Benjamin, 2009; Cowan, Morey, AuBuchon, Zwilling, & Gilchrist, 2010), and older adults (Naveh-Benjamin, Cowan, Kilb, & Chen, 2007; Gilchrist, Cowan, & Naveh-Benjamin, 2008) maintain fewer items in the focus of attention. Having a better understanding of the boundaries of the focus of attention, as well as the underlying processes that are the basis these limitations, should clarify why working memory capacity differs in these populations. A better understanding of these limitations also should help to explain individual differences in working memory capacity as a whole.

In navigating one’s environment, there are obvious limitations in terms of how many different stimuli a person can maintain and process for short periods of time. Because of these limitations, it has been proposed that we can selectively attend to a small number of items from the current environment and process or briefly store these items. The focus of attention has been proposed to meet this purpose; it is a mechanism that selectively attends to a small number of items, allowing for further processing and storage in the working memory system. Although it is clear that the focus of attention can only maintain a few items at a time, there has been disagreement regarding the number of items that can be maintained at once. In contrast to previous research that posits a focus of attention limited to a single chunk (e.g., Oberauer & Bialkova, 2009), results from the current studies suggest that the focus is able to hold at least two items at a time. Although much more work is needed, our findings provide additional clarification about item limits in the focus of attention, and point to future possibilities for gaining a clearer understanding of working memory and attention.