Informative Dorfman Screening

Summary

Since the early 1940s, group testing (pooled testing) has been used to reduce costs in a variety of applications, including infectious disease screening, drug discovery, and genetics. In such applications, the goal is often to classify individuals as positive or negative using initial group testing results and the subsequent process of decoding of positive pools. Many decoding algorithms have been proposed, but most fail to acknowledge, and to further exploit, the heterogeneous nature of the individuals being screened. In this paper, we use individuals’ risk probabilities to formulate new informative decoding algorithms which implement Dorfman retesting in a heterogeneous population. We introduce the concept of “thresholding” to classify individuals as “high” or “low risk,” so that separate, risk-specific algorithms may be used, while simultaneously identifying pool sizes that minimize the expected number of tests. When compared to competing algorithms which treat the population as homogeneous, we show that significant gains in testing efficiency can be realized with virtually no loss in screening accuracy. An important additional benefit is that our new procedures are easy to implement. We apply our methods to chlamydia and gonorrhea data collected recently in Nebraska as part of the Infertility Prevention Project.

1. Introduction

Chlamydia and gonorrhea are the two most common sexually transmitted diseases (STDs) in the United States. In addition to the 1.5 million new infections that are diagnosed annually, it has been estimated that an additional 2.1 million cases go unreported each year (Centers for Disease Control and Prevention, ^{CDC, 2009}). Both infections are usually asymptomatic, so positive individuals, perhaps unaware of their status, can spread the infections to others. Left untreated, both infections can lead to serious medical conditions, including pelvic inflammatory disease (PID), ectopic pregnancy, and sterility (Kacena et al., 1998a, 1998b). It also has been suggested that chlamydia and gonorrhea facilitate the transmission of other STDs, including HIV (Farley, Cohen, and Elkins, 2003).

Many countries have developed national programs to screen for chlamydia and gonorrhea infections. In the United States, one of the largest such programs is the Infertility Prevention Project (IPP), which is funded by the CDC. Since its origination in 1988, the primary goals of the IPP have been to screen for chlamydia and gonorrhea in high risk populations and to administer treatment to those who are infected. All 50 states participate in the IPP. The state of Nebraska does so through its Sexually Transmitted Diseases and Infertility Control Program. At clinic sites throughout the state, urine and swab specimens are collected on individuals. These individual specimens are then transported to the Nebraska Public Health Laboratory (NPHL) in Omaha for testing.

With increasing public health costs, our medical colleagues at the NPHL have expressed an interest in adopting group testing (pooled testing) for chlamydia and gonorrhea identification. Group testing dates back to Dorfman (1943), who proposed that it be used to screen World War II soldiers for syphilis. When testing for low prevalence diseases, pooling specimens (e.g., blood, urine, swabs, etc.) through group testing is a novel way to increase screening efficiency, and, when compared to individual testing, there is overwhelming evidence that group testing can maintain high levels of classification accuracy. Since Dorfman’s seminal work, group testing has been used to screen individuals for various STDs (see, e.g., Kacena et al., 1998a, 1998b; Mine et al., 2003; Pilcher et al., 2005) and also for other infectious agents including West Nile Virus (Alter, 2004) and the avian influenza virus H5N1 (Hourfar et al., 2007). In addition to blood/plasma donation screening in the United States and elsewhere (Tabor and Epstein, 2002; Mine et al., 2003), group testing has been utilized in screening individuals for drug use (Gastwirth and Johnson, 1994), in preventing the potential spread of bioterrorist agents (Schmidt et al., 2005), in genetics (Gastwirth, 2000), and in drug discovery (Xie et al., 2001; Remlinger et al., 2006).

The group testing literature contains a myriad of classification (decoding) algorithms which vary in their level of complexity. Kim et al. (2007) provide an excellent review of existing algorithms and derive their operating characteristics in the presence of testing error. In practice, testing errors (false positives/negatives) can occur when diagnostic tests do not have perfect sensitivity and specificity. Kim et al. (2007) consider array-based and hierarchical algorithms. Array testing involves placing individual specimens in a square or rectangular array and testing its rows and columns. These responses give information about the location of positive individuals, although further retesting is needed if there are ambiguities. A hierarchical algorithm involves retesting non-overlapping subsets of individuals from positive pools, possibly in multiple stages, until each individual is classified as positive or negative. Dorfman’s original procedure, where each individual is retested separately, is an example of a two-stage hierarchical algorithm. Higher-stage hierarchical algorithms often improve efficiency but are generally more difficult to implement. Likely because of its simplicity, Dorfman’s procedure is the most commonly used classification algorithm in practice.

Statistical research in the group testing classification problem has generally proceeded under the assumption that each individual has the same probability of infection; see, e.g., Kim et al. (2007). However, in most screening situations, including the Nebraska IPP, there are covariates available that offer information as to which individuals have a higher risk of infection. For example, it is well known that age, race, gender, socioeconomic status, and the number of sexual partners are excellent predictors of both chlamydia and gonorrhea positivity (CDC, 2009). Therefore, if the goal is to develop efficient screening protocols for the Nebraska IPP and elsewhere, one should exploit this available information.

Among all group testing algorithms in the literature, however, very few acknowledge population heterogeneity. Hwang (1975) generalized Dorfman’s original procedure to allow individuals to have different levels of risk and proposed an optimal grouping strategy that minimizes the number of tests needed to classify all individuals. Unfortunately, Hwang’s approach assumes that the probability of testing error is zero, which is unreasonable in the Nebraska IPP and in most screening applications involving human subjects. More recently, Bilder, Tebbs, and Chen (2010) have proposed a framework to incorporate covariate information using modifications of Sterrett’s (1957) algorithm. However, while the “informative retesting” procedures in Bilder et al. (2010) are effective at reducing the number of tests, Sterrett-type algorithms are inherently complex and may not be logistically feasible in some screening environments. This is especially true for the NPHL, where the use of complicated decoding algorithms could considerably lengthen the time needed to screen all individuals.

In this paper, we propose new hierarchical screening procedures that utilize Dorfman retesting in a heterogeneous population. Unlike Hwang’s approach, our algorithms allow for imperfect diagnostic testing, and when compared to the higher-stage Sterrett-type algorithms in Bilder et al. (2010), ours are easier to implement. In Section 2, we describe a general informative Dorfman algorithm that uses individual risk probabilities to assign individuals to pools, and we derive the operating characteristics of this algorithm in the presence of testing error. In Section 3, we propose three versions of this algorithm which incorporate two important criteria: the determination of optimal pool sizes and the use of risk thresholds (cutoffs) to classify subjects according to their level of risk. In Section 4, we provide simulation evidence to demonstrate the effectiveness of our new procedures, and, in Section 5, we illustrate their use with data from the Nebraska IPP. In Section 6, we provide a summary discussion.

2. Informative Dorfman Algorithm

2.1 Preliminaries

Suppose that N individuals are to be screened for the presence of a binary trait, such as chlamydia status, and denote by p_i the (true) probability of positivity for the ith individual ${\mathcal{I}}_i$, i = 1, 2, …, N. The true status of ${\mathcal{I}}_i$ is a binary random variable denoted by ${\tilde{g}}_i$, where $\mathrm{pr}({\tilde{g}}_i=1)=p_i$. We assume throughout that the statuses ${\tilde{g}}_i$ are independent random variables. To derive the operating characteristics of our algorithms, we initially assume that the true probabilities p_i are known (this assumption is relaxed later; see Section 5). We start by ordering the N individuals from low to high in terms of their risk probabilities, producing ${\mathcal{I}}_{\left(1\right)},{\mathcal{I}}_{\left(2\right)},\dots ,{\mathcal{I}}_{\left(N\right)}$ corresponding to $p_{\left(1\right)}\le p_{\left(2\right)}\le \cdots \le p_{\left(N\right)}$. Ordering the probabilities isolates those individuals who are at the highest risk for infection. This allows us to determine optimal pool sizes and formulate the use of thresholding; see Section 3.

Let c_j denote the pool size for the jth pool, j = 1, 2, …, J. Dorfman’s (1943) original strategy begins by assigning each individual, at random, to exactly one pool. Those pools which test negative are declared to contain all negative individuals and are not examined further. Positive pools are decoded by retesting each subject individually. Instead of random assignment, our Informative Dorfman (ID) algorithm specifies that individuals are assigned to pools based on their ordered risk probabilities. In particular, pool ${\mathcal{P}}_1$ consists of individuals ${\mathcal{I}}_{\left(1\right)},{\mathcal{I}}_{\left(2\right)},\dots ,{\mathcal{I}}_{\left(c_1\right)}$, pool ${\mathcal{P}}_2$ consists of individuals ${\mathcal{I}}_{(c_1+1)},{\mathcal{I}}_{(c_1+2)},\dots ,{\mathcal{I}}_{(c_1+c_2)}$, and so on; in general, pool ${\mathcal{P}}_j$ consists of the c_j lowest risk subjects which remain after constructing the first j − 1 pools; i.e., ${\mathcal{P}}_j=\{{\mathcal{I}}_{\left(i\right)}:i={\sum }_{j^{\prime }=1}^{j-1}{c}_{j^{\prime }}+k,k=1,2,\dots ,c_j\}$, for j = 2, 3, …, J. Positive pools are then decoded in the same way as in Dorfman’s (1943) algorithm.

2.2 Operating Characteristics

To streamline our notation, let ${\mathcal{I}}_{j\left(k\right)}$ denote the kth ordered individual in the jth pool and let p_j(k) denote the corresponding risk probability, for j = 1, 2, …, J and k = 1, 2, …, c_j. To derive the operating characteristics of ID, we assume that the test sensitivity S_e and specificity S_p are known constants which do not depend on c_j. Previous research has proceeded under this assumption (Vansteelandt, Goetghebeur, and Verstraeten, 2000; Kim et al., 2007; Kim and Hudgens, 2009), and numerous empirical studies have shown this to be reasonable for sensible values of c_j. For example, a number of chlamydia and gonorrhea studies have shown that assay tests based on nucleic acid technology (NAT) possess high sensitivity and specificity with negligible dilution effects for groups up to size c_j = 10 when pooling urine or swabs (Kacena et al., 1998a, 1998b; Butylkina et al., 2007; Shipitsyna et al., 2007). Similar findings have been documented for other infectious diseases when pooling blood or serum samples. For example, Mine et al. (2003) use c_j = 50 for hepatitis B/C screening in Japan. Pilcher et al. (2005) use pools of size c_j = 90 for HIV screening in North Carolina.

Let ${\tilde{G}}_j=1$ if the jth pool is truly positive; i.e., ${\mathcal{P}}_j$ contains at least one positive individual, ${\tilde{G}}_j=0$ otherwise, for j = 1, 2, …, J. Similarly, let G_j = 1 if ${\mathcal{P}}_j$ tests positive, G_j = 0 otherwise. Let the random variable T denote the total number of tests needed to decode all N individuals. For the ID algorithm, we show in Web Appendix A that

$$E\left(T\right)=J+\sum _{j=1}^J{c}_{j}I(c_j>1)\mathrm{pr}(G_j=1)$$

$$\mathrm{var}\left(T\right)=\sum _{j=1}^J{c}_j^{2}I(c_j>1)\mathrm{pr}(G_j=1)\mathrm{pr}(G_j=0),$$

where I(·) denotes the usual indicator function, $\mathrm{pr}(G_j=1)=S_e+(1-S_e-S_p){\prod }_{k=1}^{c_j}(1-p_{j\left(k\right)})$, and pr(G_j = 0) = 1 − pr(G_j = 1). In general, we refer to E(T) as the efficiency, as is common in the group testing literature.

The quality of a decoding algorithm is often measured through its efficiency. However, it is also important to characterize how well an algorithm correctly classifies individuals as being positive or negative. To explore this, $\mathrm{let}{\tilde{g}}_{j\left(k\right)}=1$, if the kth individual in the jth pool is truly positive, so that $\mathrm{pr}({\tilde{g}}_{j\left(k\right)}=1)=p_{j\left(k\right)}$, and $\mathrm{let}{\tilde{g}}_{j\left(k\right)}=0$, otherwise. We define the pooling sensitivity $P{S}_e^{{\mathcal{I}}_{j\left(k\right)}}$ and the pooling specificity $P{S}_p^{{\mathcal{I}}_{j\left(k\right)}}$ as

$$P{S}_e^{{\mathcal{I}}_{j\left(k\right)}}=\mathrm{pr}({\mathcal{I}}_{j\left(k\right)}\text{classified positive}\mid {\tilde{g}}_{j\left(k\right)}=1)$$

$$P{S}_p^{{\mathcal{I}}_{j\left(k\right)}}=\mathrm{pr}({\mathcal{I}}_{j\left(k\right)}\text{classified negative}\mid {\tilde{g}}_{j\left(k\right)}=0)$$

and derive expressions for $P{S}_e^{{\mathcal{I}}_{j\left(k\right)}}$ and $P{S}_p^{{\mathcal{I}}_{j\left(k\right)}}$ under ID when c_j > 1. Let g_j(k) = 1, if the kth individual in the jth pool tests positive, g_j(k) = 0, otherwise. As in Kim et al. (2007), we assume that diagnostic test results are independent, conditional on the true status of the pool (individual) being tested; see Litvak, Tu, and Pagano (1994) for discussion. This implies that the testing result for any pool (individual), given its true status, is independent of previous testing results. For ID, individual ${\mathcal{I}}_{j\left(k\right)}$ is classified as positive when its group test and its subsequent individual test are both positive. Therefore,

$$\begin{array}{cc}\hfill P{S}_e^{{\mathcal{I}}_{j\left(k\right)}}& =\mathrm{pr}(G_j=1,g_{j\left(k\right)}=1\mid {\tilde{g}}_{j\left(k\right)}=1)\hfill \\ \hfill & =\mathrm{pr}(G_j=1\mid {\tilde{g}}_{j\left(k\right)}=1)\mathrm{pr}(g_{j\left(k\right)}=1\mid G_j=1,{\tilde{g}}_{j\left(k\right)}=1)=S_e^2.\hfill \end{array}$$

This is identical to the pooling sensitivity of Dorfman’s strategy in a homogeneous population; see Kim et al. (2007). This equivalence would not result if an assay test’s performance was somehow related to an individual’s risk probability p_j(k). However, our medical colleagues have found no plausible reason for this to be true with any of the commonly used assays. To derive the pooling specificity $P{S}_p^{{\mathcal{I}}_{j\left(k\right)}}$, note that

$$P{S}_p^{{\mathcal{I}}_{j\left(k\right)}}=\mathrm{pr}(G_j=0\mid {\tilde{g}}_{j\left(k\right)}=0)+\mathrm{pr}(G_j=1,g_{j\left(k\right)}=0\mid {\tilde{g}}_{j\left(k\right)}=0).$$

From the Law of Total Probability, the first term

$$\begin{array}{cc}\hfill \mathrm{pr}(G_j=0\mid {\tilde{g}}_{j\left(k\right)}=0)& =\sum _{s=0}^1\mathrm{pr}(G_j=0\mid {\tilde{G}}_j=0)\mathrm{pr}({\tilde{G}}_j=s\mid {\tilde{g}}_{j\left(k\right)}=0)\hfill \\ \hfill & =(1-S_e)-(1-S_e-S_p)\prod _{k^{\prime }\in {\mathcal{A}}_j^{\left(k\right)}}(1-p_{j\left(k^{\prime }\right)}),\hfill \end{array}$$

where ${\mathcal{A}}_j^{\left(k\right)}=\{1,\dots ,k-1,k+1,\dots ,c_j\}$. Similarly, the second term

$$\begin{array}{cc}\hfill \mathrm{pr}(G_j=1,g_{j\left(k\right)}=0\mid {\tilde{g}}_{j\left(k\right)}=0)& =\mathrm{pr}(G_j=1\mid {\tilde{g}}_{j\left(k\right)}=0)\mathrm{pr}(g_{j\left(k\right)}=0\mid G_j=1,{\tilde{g}}_{j\left(k\right)}=0)\hfill \\ \hfill & =\sum _{s=0}^1\mathrm{pr}(G_j=1\mid {\tilde{G}}_j=s)\mathrm{pr}({\tilde{G}}_j=s\mid {\tilde{g}}_{j\left(k\right)}=0)\times S_p\hfill \\ \hfill & =S_e{S}_p+(1-S_e-S_p)S_p\prod _{k^{\prime }\in {\mathcal{A}}_j^{\left(k\right)}}(1-p_{j\left(k^{\prime }\right)}).\hfill \end{array}$$

Combining the terms and simplifying, we obtain

$$P{S}_p^{{\mathcal{I}}_{j\left(k\right)}}=1-(1-S_p)\left\{S_e+(1-S_e-S_p)\prod _{k^{\prime }\in {\mathcal{A}}_j^{\left(k\right)}}(1-p_{j\left(k^{\prime }\right)})\right\}.$$

Unlike the homogeneous case, $P{S}_p^{{\mathcal{I}}_{j\left(k\right)}}$ is potentially different for different individuals. When p_j(k) = p; i.e., each individual has the same probability of infection, our expression for $P{S}_p^{{\mathcal{I}}_{j\left(k\right)}}$ reduces to equation (7) in Kim et al. (2007), the pooling specificity for Dorfman retesting in a homogeneous population.

Two additional classification measures are commonly used in the group testing literature. The pooling positive predictive value, $PP{V}^{{\mathcal{I}}_{j\left(k\right)}}$, is the probability that the kth individual in the jth pool is truly positive, given that it is classified as positive. Similarly, the pooling negative predictive value, $NP{V}^{{\mathcal{I}}_{j\left(k\right)}}$, is the probability that the kth individual in the jth pool is truly negative, given that it is classified as negative. By Bayes Rule,

$$PP{V}^{{\mathcal{I}}_{j\left(k\right)}}=\mathrm{pr}({\tilde{g}}_{j\left(k\right)}=1\mid {\mathcal{I}}_{j\left(k\right)}\text{classified positive})=\frac{p_{j\left(k\right)}{S}_e^2}{p_{j\left(k\right)}{S}_e^2+(1-p_{j\left(k\right)})(1-P{S}_p^{{\mathcal{I}}_{j\left(k\right)}})}$$

$$NP{V}^{{\mathcal{I}}_{j\left(k\right)}}=\mathrm{pr}({\tilde{g}}_{j\left(k\right)}=0\mid {\mathcal{I}}_{j\left(k\right)}\text{classified negative})=\frac{(1-p_{j\left(k\right)})P{S}_p^{{\mathcal{I}}_{j\left(k\right)}}}{(1-p_{j\left(k\right)})P{S}_p^{{\mathcal{I}}_{j\left(k\right)}}+p_{j\left(k\right)}(1-S_e^2)}.$$

Like $P{S}_p^{{\mathcal{I}}_{j\left(k\right)}}$, these measures are individual-specific; thus, they can provide substantial information about the true statuses on a per-individual basis. On the other hand, treating the population as homogeneous provides constant values of PPV and NPV, offering no knowledge about which individuals are more likely to be misclassified. We would envision this additional per-individual information to be especially useful in developing informative back-end screening protocols (Gastwirth and Johnson, 1994; Johnson and Pearson, 1999), not only in chlamydia and gonorrhea surveillance, but also in blood screening, where Dorfman retesting is used extensively.

3. Optimized Informative Dorfman Procedures

Having developed the operating characteristics of ID, our goal is to now construct sets of heterogeneous pools to maximize testing efficiency; i.e., to minimize E(T). As stated in Section 1, Hwang (1975) finds the optimal solution to this problem when S_e = S_p = 1, a simpler and perhaps unrealistic setting. Because an extension of Hwang’s method to the imperfect testing case appears to be intractable, we propose three specific versions of ID which minimize E(T) subject to given pooling constraints. Our new algorithms are “greedy” in nature, forming optimal sets of pools in accordance with the specified constraints.

3.1 Optimal Dorfman

Consider using the ID algorithm with a common pool size c_j = c, for j = 1, 2, …, J (with c_J < c if N < cJ), and let T^(c) denote the number of tests needed to decode all N individuals when pools of size c are used. We call the ID procedure that uses c = c_opt, where

$$c_{opt}=\arg \underset{c\ge 1}{\min }\left\{J+cI(c>1)\sum _{j=1}^{J-1}\mathrm{pr}(G_j=1)+c_{J}I(c_J>1)\mathrm{pr}(G_J=1)\right\},$$

the Optimal Dorfman (OD) algorithm. In other words, OD is a special case of ID where the common pool size c = c_opt minimizes E(T^(c)). Computing c_opt can be done by performing a search over values of c deemed acceptable by the investigator. For example, if one is worried about dilution effects for pool sizes larger than M, say, the minimization procedure can be carried out over {c : c = 1, 2, …, M}. In the objective function above, we point out that J = [N/c], a function of c. If c = 1 (individual testing), then J = N.

3.2 Thresholding

The goal of OD is to maximize testing efficiency by identifying the best common size for all pools. We now consider a different approach to accomplish the same goal.

Suppose, hypothetically, that the N individuals to be screened are partitioned into the two distinct classes ${\mathcal{C}}_1=\{{\mathcal{I}}_i:{\tilde{g}}_i=0,i=1,2,\dots ,N\}$ and ${\mathcal{C}}_2=\{{\mathcal{I}}_i:{\tilde{g}}_i=1,i=1,2,\dots ,N\}$; that is, ${\mathcal{C}}_1\left({\mathcal{C}}_2\right)$ consists entirely of negative (positive) individuals. In the absence of testing error, the best possible decoding algorithm, in terms of minimizing E(T), would be to test all individuals in ${\mathcal{C}}_1$ in one pool and each individual in ${\mathcal{C}}_2$ separately. Of course, one never gets to construct this partition in practice; however, the salient point is that efficiency can always be increased if positive subjects are removed and are tested individually. With this in mind, suppose, more realistically, that one partitions the N individuals into the two classes ${\mathcal{C}}_1^{\ast }=\{{\mathcal{I}}_i:p_i\le p^{\ast },i=1,2,\dots ,N\}$ and ${\mathcal{C}}_2^{\ast }=\{{\mathcal{I}}_i:p_i>p^{\ast },i=1,2,\dots ,N\}$, where p* ∈ [0, 1] is a thresholding value; i.e., a value that distinguishes “low risk” individuals (in ${\mathcal{C}}_1^{\ast }$) from those that are “high risk” (in ${\mathcal{C}}_2^{\ast }$). By classifying individuals as high risk in ${\mathcal{C}}_2^{\ast }$ before testing begins, one is more likely to a priori isolate those who are positive. Our Optimal Dorfman with Threshold (TOD) procedure specifies that individuals in ${\mathcal{C}}_1^{\ast }$ are tested in pools of optimal equal size and that those in ${\mathcal{C}}_2^{\ast }$ are tested individually.

The threshold p* can be specified by the investigator; however, it is not necessary to do so, as our TOD algorithm identifies its optimal value. To explain this point, $T_{{\mathcal{P}}_j}$ denote the number of tests needed to decode the jth pool. When a common pool size is specified, say c₀, the per-pool efficiencies $E\left(T_{{\mathcal{P}}_j}\right)$ satisfy $E\left(T_{{\mathcal{P}}_J}\right)\ge E\left(T_{{\mathcal{P}}_{J-1}}\right)\ge \cdots \ge E\left(T_{{\mathcal{P}}_1}\right)$ whenever S_e + S_p ≥ 1; see Web Appendix B. Therefore, starting with the highest risk individuals, the TOD algorithm seeks to find the value of j, say j*, where $E\left(T_{{\mathcal{P}}_{j^{\ast }}}\right)\ge c_0$ and $E\left(T_{{\mathcal{P}}_{j^{\ast }-1}}\right)<c_0$. For j = j*, j* + 1, …, J (the high risk pools), the per-pool efficiency $E\left(T_{{\mathcal{P}}_j}\right)$ is larger than or equal to c₀; that is, it is more (as) costly to pool than (as) it is to screen individually. Subsequently, p* is taken to be ${\mathcal{p}}^{\ast }=\frac{1}{2}({\mathcal{p}}_{j^{\ast }-1\left(c_0\right)}+{\mathcal{p}}_{j^{\ast }\left(1\right)})$, the average of the risk probabilities for the highest risk subject in ${\mathcal{P}}_{j^{\ast }-1}$ and the lowest risk subject in ${\mathcal{P}}_{j^{\ast }}$. Subjects in pools ${\mathcal{P}}_{j^{\ast }},{\mathcal{P}}_{j^{\ast }+1},\dots ,{\mathcal{P}}_J$ are classified as “high risk,” placed into ${\mathcal{C}}_2^{\ast }$, and are tested individually. Subjects in pools ${\mathcal{P}}_1,{\mathcal{P}}_2,\dots ,{\mathcal{P}}_{j^{\ast }-1}$ are classified as “low risk,” placed into ${\mathcal{C}}_1^{\ast }$, and are decoded using OD with $c=c_{opt}\left({\mathcal{C}}_1^{\ast }\right)$, the optimal common pool size for those individuals in ${\mathcal{C}}_1^{\ast }$.

Small details regarding TOD warrant brief remarks. First, if N < c₀J, then the lowest risk pool ${\mathcal{P}}_1$ will contain c₁ < c₀ individuals, but the ordering $E\left(T_{{\mathcal{P}}_J}\right)\ge E\left(T_{{\mathcal{P}}_{J-1}}\right)\ge \cdots \ge E\left(T_{{\mathcal{P}}_1}\right)$ will still hold. Second, we have found through simulation that the choice of c₀ does not have a large effect on the efficiency of TOD. Generally, as c₀ increases, the number of individual tests from ${\mathcal{C}}_2^{\ast }$ also increases. However, this increase is typically offset by a fewer number of tests required to decode “low risk” individuals in ${\mathcal{C}}_1^{\ast }$. Third, if $E\left(T_{{\mathcal{P}}_j}\right)<c_0$ for all j = 1, 2, …, J, then TOD reduces to OD. Intuitively, this is more likely to occur when the overall prevalence is very low. On the other hand, if $E\left(T_{{\mathcal{P}}_j}\right)\ge c_0$ for all j = 1, 2, …, J, then one would classify all individuals as “high risk.” This rarely occurs when c₀ is chosen sensibly. We recommend choosing c₀ ≈ c_opt, the optimal pool size identified by OD for all N individuals.

3.3 Pool-Specific Optimal Dorfman

The OD and TOD algorithms share a common characteristic; namely, each uses a common pool size. OD uses a common size for all pools, while TOD uses a common pool size for all individuals who are “low risk.” Therefore, with regards to implementation, OD and TOD are simple procedures, requiring only individual testing and testing pools of common size (with the possible exception of one remainder pool). However, using a common pool size may not be the best way to exploit individual heterogeneity, especially if the individual probabilities exhibit a large amount of variability. With this in mind, we propose a final procedure that determines optimal sizes for each pool and call this the Pool-Specific Optimal Dorfman (PSOD) procedure. The idea behind PSOD is motivated by the fact that E(T) can be expressed as a sum of the efficiencies on a per-individual basis. If we can reduce the expected testing expenditure for each individual, we simultaneously reduce E(T).

Specifically, the goal of PSOD is to identify the pool sizes c_j, j = 1, 2, …, J, that minimize the expected per-individual testing expenditure on a pool by pool basis, starting with the lowest risk pool ${\mathcal{P}}_1$ and continuing until the highest risk pool ${\mathcal{P}}_J$ has been formed. To describe how PSOD determines the jth pool size c_j, $\mathrm{let}{N}_j^P$ denote the total number of individuals in the j − 1 lowest risk pools combined; i.e., $N_1^P=0$ and $N_j^P={\sum }_{j^{\prime }=1}^{j-1}{c}_{j^{\prime }}$, for j = 2, 3, …, J. $\mathrm{Let}{N}_j^R=N-N_j^P$ and define $T_{{\mathcal{P}}_j;c_j}$ to be the number of tests needed to decode ${\mathcal{P}}_j$, where ${\mathcal{P}}_j$ consists of the c_j lowest risk subjects remaining after ${\mathcal{P}}_1,{\mathcal{P}}_2,\dots ,{\mathcal{P}}_{j-1}$ have been formed. For Dorfman retesting, the expected per-individual testing expenditure is the same for each individual belonging to a common pool. Therefore, PSOD identifies $c_j^{\ast }=\arg {\min }_{1\le c_j\le N_j^R}\left\{c_j^{-1}E\left(T_{{\mathcal{P}}_j;c_j}\right)\right\}$, where

$$\begin{array}{cc}\hfill E\left(T_{{\mathcal{P}}_j;c_j}\right)& =1+c_{j}I(c_j>1)\mathrm{pr}(G_j=1)\hfill \\ \hfill & =1+c_{j}I(c_j>1)\left\{S_e+(1-S_e-S_p)\prod _{k=1}^{c_j}(1-p_{(N_j^P+k)})\right\},\hfill \end{array}$$

and defines $c_j=c_j^{\ast }$ as the optimal size for the jth pool. The full algorithm for PSOD is given in Web Appendix B.

Because individuals are ordered a priori in terms of their risk, the pool sizes c_j identified by PSOD, like those identified by Hwang’s method, are guaranteed to satisfy c₁ ≥ c₂ ≥ ⋯ ≥ c_J. This is a characteristic that makes PSOD and Hwang’s method attractive because higher risk pools should use smaller pool sizes. It is straightforward to amend PSOD to guard against excessively large pool sizes. One could simply minimize the expected per-individual testing expenditure $c_j^{-1}E\left(T_{{\mathcal{P}}_j;c_j}\right)$ over $\{c_j:c_j=1,2,\dots ,{\widehat{N}}_j^R\}$, where ${\widehat{N}}_j^R=\min \{N_j^R,M\}$ and M is the maximum allowable pool size. This guarantees that each pool will not contain more than M individuals. Hwang’s method can be amended similarly. It is important to note that even when S_e = S_p = 1, the situation in which Hwang’s solution is globally optimal, PSOD and Hwang’s method are different procedures, because PSOD is a greedy algorithm that makes pool size selections sequentially. Overall, PSOD and Hwang’s method do acknowledge heterogeneity more directly than OD or TOD. However, this also means that PSOD and Hwang’s method may be more difficult to implement, as different pool sizes are needed to complete the identification process.

4. Simulation Evidence

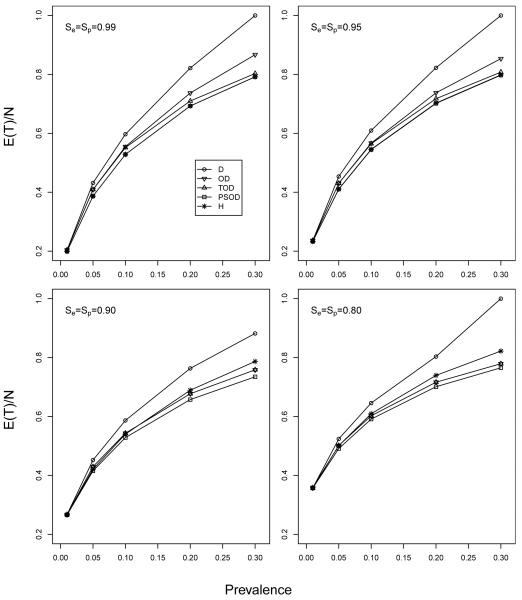
To assess the impact of incorporating heterogeneity, we first compare Dorfman’s original procedure (D), where individuals are assigned to pools at random, to OD, TOD, PSOD, and Hwang’s method (H). We generate true probabilities p_i, i = 1, 2, …, N, from a beta(1, θ) distribution; note that θ determines the mean prevalence, p = 1/(1 + θ), and the amount of heterogeneity in the population. We consider values of p = 0.0001, 0.0002, …, 0.0099 to investigate rare infections and also p = 0.01, 0.02, …, 0.50 to examine higher prevalence infections. Our decision to consider larger values of p may seem unsuited because group testing is typically used when the infection rate is small. However, as we demonstrate, the optimized Dorfman procedures consistently confer savings over individual testing even when p is large. We use values of S_e ∈ {0.80, 0.90, 0.91, …, 1} and S_p ∈ {0.80, 0.90, 0.95, 0.99, 1} and let the maximum allowable pool size M = 10, 20, or 30. Recall that using M = 10 is consistent with the chlamydia and gonorrhea screening literature; see Section 2. Also, recall that Hwang’s grouping method depends on neither S_e nor S_p.

Figure 1 displays a representative subset of the results; more extensive comparisons are in Web Appendix C. In Figure 1, we display the overall expected per-individual testing expenditure, E(T)/N, when M = 10 and N = 1000. For each (p, S_e, S_p) combination, OD, TOD, PSOD, and H use their own procedure-specific pool size(s). To ensure the fairest possible comparison, we use the optimal pool size for D throughout; i.e., the pool size c that minimizes the expected number of tests per pool, 1+c{S_e+(1−S_e−S_p)(1−p)^c}. The results in Figure 1, along with those in Web Appendix C, show that the gains in efficiency from OD, TOD, and PSOD (over D) are generally very small when p < 0.01 but increase notably as p increases. When p > 0.01, we have consistently seen that PSOD is more efficient than TOD, that TOD is more efficient than OD, and that OD remains more efficient than D as long as the prevalence is not too large (roughly p < 0.35; see Web Appendix C). Figure 1 also shows that PSOD and H are nearly identical when S_e and S_p are close to unity. However, for lower values of S_e and S_p, OD, TOD, and PSOD each can outperform H, especially when p is larger. For very large p, we have found that TOD, PSOD, and H each consistently outperform individual testing even when the prevalence is as high as 50%. This prevalence is likely not to be encountered when screening for sexually transmitted diseases, but it could be of interest in other applications where the use of pooling for identification has not been previously envisioned.

Figure 1.

Comparison of Dorfman algorithms. Expected per-individual efficiency, with M = 10 and N = 1000, for p = 0.01, 0.05, 0.10, 0.20, and 0.30. The optimal pool size for D has been used. A more comprehensive comparison among D, OD, TOD, PSOD, and H is in Web Appendix C.

Using the same values of p, S_e, S_p, and M, we also compare OD, TOD, and PSOD to noninformative array testing (A). Like Dorfman screening, A is a two-stage classification procedure; that is, rows and columns are tested initially followed by individual testing if needed. Higher stage procedures are included for comparison purposes in Section 5. The salient features of A were summarized in Section 1; we restrict attention to two-dimensional square arrays (Phatarfod and Sudbury, 1994; Kim et al., 2007; Hudgens and Kim, 2011) in the comparison. We make this comparison using the optimal array size for A; that is, for given values of p, S_e, and S_p, we compare OD, TOD, and PSOD with the c×c array procedure that minimizes the expected number of tests; see equation (13) in Kim et al. (2007).

Figure 2 shows how OD, TOD, and PSOD compare with A in terms of efficiency when M = 10 and N = 1000. For given values of p, S_e, and S_p, we first compute $E(T\mid \mathcal{D})-E(T\mid A)$, where $\mathcal{D}\in (\mathrm{OD},\mathrm{TOD},\mathrm{PSOD})$ and E(T|·) is the efficiency for a given procedure. Values of $E(T\mid \mathcal{D})-E(T\mid A)$ that are negative (positive) indicate that the informative Dorfman procedure $\mathcal{D}$ is more (less) efficient than A; this is represented in Figure 2 using dark (light) grey coloring. Heat maps of scaled values of $E(T\mid \mathcal{D})-E(T\mid A)$ are in Web Appendix C. From Figure 2, one sees that OD, TOD, and PSOD are all preferred to A, for nearly all (S_e, S_p) combinations, when the mean prevalence p is larger (e.g., p > 0.10). The optimized Dorfman procedures also outperform A for very small p when M = 10 is used as a maximum allowable pool size, although additional results in Web Appendix C show that A outperforms OD, TOD, and PSOD for most values of p < 0.08 (roughly) when larger arrays are allowed (e.g., M = 20, 30). Of course, as stated in Section 2, using larger pool sizes may not be possible with some diagnostic tests for fear of dilution effects. In addition, array testing generally requires more resources than Dorfman screening; this may make its use prohibitive in some screening applications (Westreich et al., 2008).

Figure 2.

Comparison of Dorfman algorithms (OD, TOD, and PSOD) with A when M = 10 and N = 1000. Top: OD versus A; Middle: TOD versus A; Bottom: PSOD versus A. Regions in dark grey denote those where the Dorfman procedures are more efficient. The optimal (square) array size for A has been used for each (p, S_e, S_p) configuration.

Finally, we have also compared D, OD, TOD, PSOD, H, and A in terms of the screening accuracy measures from Section 2. To summarize, when compared to D, there are no substantial changes in screening accuracy that arise from using our new informative Dorfman algorithms and H in realistic settings. Furthermore, in regions where A is more efficient, Dorfman procedures can improve overall pooling sensitivity and pooling negative predictive value. Complete details are given in Web Appendix C.

5. Nebraska IPP Data

We now apply our new Dorfman screening algorithms to chlamydia and gonorrhea data collected during 2008-2009 as part of the Nebraska IPP. For each infection, we create four strata by cross-classifying each individual according to gender and specimen type (swab/urine). A complete summary of the data, including the number of individuals screened per stratum, values of S_e and S_p (provided by the NPHL), and individual covariates, is given in Table 1. Across strata, there were 23,146 individuals screened in 2008 and 27,551 individuals screened in 2009. All individuals were screened for both infections. The NPHL estimates that individual swab (urine) tests cost about $11 ($16) each.

Table 1.

Nebraska IPP data summary. Numbers of individuals screened and overall prevalence levels are provided for years 2008 and 2009. The values of S_e and S_p are provided by the NPHL. The individual covariates available are age, gender, race, clinic type, location of clinic, reason for visit (family planning, prenatal, STD screening), symptoms, clinical observations (cervical friability, PID, cervicitis, urethritis), and risk history (multiple partners in last 90 days, new partner in last 90 days, contact to STD).

					Number screened		Mean prevalence
Infection	Gender	Specimen	Se	Sp	2008	2009	2008	2009
Chlamydia	Female	Urine	0.805	0.96	2338	4972	0.092	0.080
		Swab	0.928	0.96	14441	14530	0.072	0.069
	Male	Urine	0.930	0.95	3541	6139	0.077	0.081
		Swab	0.925	0.95	2826	1910	0.137	0.157
Gonorrhea	Female	Urine	0.849	0.98	2338	4972	0.024	0.017
		Swab	0.966	0.98	14441	14530	0.013	0.013
	Male	Urine	0.970	0.96	3541	6139	0.012	0.021
		Swab	0.985	0.96	2826	1910	0.068	0.070

Up until now, we have assumed that individuals’ risk probabilities are known. While this is not realistic, in most screening situations, investigators will often have access to data recorded from previous periods of screening. These data can be used to estimate the risk levels for new individuals to be screened. For example, in the Nebraska IPP, using a “training” data set is realistic, since testing is performed daily at the NPHL. For purposes of illustration, we treat the 23,146 individual diagnoses in 2008 and the individual covariates (see Table 1) as training data. For purposes of illustration, we fit a first-order logistic regression model using all of the available covariates for each infection and specimen type.

We regard the 2009 individual diagnoses as the true responses and, for OD, TOD, PSOD, and H, assign the 2009 individuals to pools based on their estimated probabilities ${\widehat{p}}_i$ from the 2008 model fits. For noninformative D (A), we assign the 2009 individuals to pools (arrays) chronologically based on the specimen arrival date using optimal pool (array) sizes determined from the 2008 estimated mean prevalence levels; see Table 1. A maximum pool size M = 10 is used for all procedures. Simulated pool diagnoses are then determined using the S_e and S_p levels in Table 1. For OD, TOD, PSOD, and H, we first create “blocks” of individuals of size N = 50, 100, and 200, ordered chronologically by the specimen arrival date; decoding is then completed within each block (the last block formed in 2009 is potentially of smaller size). We choose to implement retesting in this manner to acknowledge the sequential nature in which specimens are tested at the NPHL; it is not realistic to wait until all individual specimens from 2009 have been collected to start the screening process. Note that with noninformative D, the last pool formed is potentially of smaller size; for A, the last array formed is potentially smaller.

Table 2 displays the number of tests expended when screening individuals for chlamydia and gonorrhea in 2009. Because the 2009 diagnoses are simulated for each infection, we implement each procedure 1000 times for each gender-infection-specimen type configuration; values in Table 2 are averages over these 1000 simulations. First, the informative Dorfman procedures always provide a reduction in the number of tests when compared to the best noninformative D procedure, and this reduction can be substantial. For OD, TOD, PSOD, and H, it is difficult to identify a relationship between the blocking size (50, 100, 200) and efficiency, although this relationship likely depends on the order in which individual specimens arrive at the NPHL for testing. Second, although H is more efficient than PSOD in a small majority of the cases examined, the differences are often minor and could perhaps be explained by the fact that testing responses are simulated; recall also from Section 4 that PSOD and H are nearly identical for smaller prevalence levels. Not surprisingly, PSOD does outperform H for the lowest S_e cohort (female-chlamydia-urine). Finally, the informative Dorfman procedures perform on par with the best noninformative A procedure. OD, TOD, and PSOD are each more efficient (regardless of blocking size) in four of the eight gender-infection-specimen type strata; A is more efficient in three of the strata, and the remaining stratum (male-gonorrhea-urine) offers mixed results.

Table 2.

Nebraska IPP screening results for 2009. Mean number of tests, averaged over 1000 implementations, for the 8 strata created by infection, specimen type, and gender. Blocks of size N = 50, 100, and 200 are used for OD, TOD, PSOD, and H. Gender/specimen individual stratum counts and values of S_e and S_p are in Table 1. Optimal pool sizes for D and A have been used; see Web Appendix D.

			Male				Female
	Method		N = 50	N = 100	N = 200		N = 50	N = 100	N = 200
Chlamydia Urine	D	3417.3				2483.6
	OD		3301.6	3267.4	3271.5		2482.0	2469.4	2451.3
	TOD		3301.2	3267.6	3271.5		2482.6	2468.1	2453.1
	PSOD		3221.1	3210.4	3218.1		2458.7	2445.7	2434.5
	H		3218.3	3218.0	3240.8		2472.5	2450.7	2470.0
	A	3136.4				2124.6
Chlamydia Swab	D	1395.7				7354.9
	OD		1299.1	1295.3	1311.4		7214.6	7168.6	7189.1
	TOD		1290.8	1288.7	1301.2		7213.4	7167.8	7190.6
	PSOD		1308.4	1285.4	1316.3		7076.9	7107.6	7091.1
	H		1289.1	1303.5	1309.1		7035.3	7103.3	7054.2
	A	1385.4				6550.9
Gonorrhea Urine	D	1956.3				1225.2
	OD		1767.9	1771.4	1704.5		1200.5	1194.4	1178.6
	TOD		1768.6	1767.7	1704.7		1203.8	1197.6	1177.8
	PSOD		1716.7	1672.8	1624.8		1212.3	1176.9	1169.6
	H		1691.7	1681.0	1618.3		1170.4	1155.4	1176.5
	A	1630.5				1229.2
Gonorrhea Swab	D	1025.3				3401.8
	OD		829.4	811.4	806.3		3179.8	3279.1	3215.3
	TOD		787.6	812.8	816.9		3184.8	3279.0	3216.7
	PSOD		750.0	752.7	766.3		3189.4	3127.9	3125.9
	H		741.7	746.1	742.8		3128.7	3127.2	3108.5
	A	963.8				3467.2

Web Appendix D contains further analyses of the Nebraska IPP data, including a summary of the screening accuracy measures, histograms of the estimated individual probabilities in 2009, and additional comparisons which include three-stage halving and the best informative Sterrett procedure from Bilder et al. (2010). As expected, higher stage procedures can reduce the number of tests expended for the Nebraska IPP, but at the cost of increased complexity and, in some cases, screening accuracy.

6. Discussion

In this paper, we have proposed new Dorfman identification algorithms which use optimal pool sizes and thresholding in a heterogeneous population. Our informative algorithms account for imperfect diagnostic tests, compete strongly with other available screening procedures in terms of efficiency and accuracy, and preserve the simplicity of Dorfman retesting. To disseminate this work, we have written R programs to implement all of the algorithms in this paper. We are happy to provide these programs to those who request them.

We have illustrated the use of our new informative Dorfman procedures using chlamydia and gonorrhea data collected as part of the Nebraska IPP. We believe that our informative algorithms could also find successful application in blood and plasma donation screening, mainly because (noninformative) Dorfman retesting is already widely used to screen donations in the United States and elsewhere (Dodd, Notari, and Stramer, 2002; Tabor and Epstein, 2002; Mine et al., 2003; Seed, Kiely, and Keller, 2005). Our procedures are only minimally more involved than classical Dorfman retesting, and they can provide a substantial reduction in the number of tests without sacrificing classification accuracy. The development of enhanced back-end screening procedures is also possible as predictive probabilities can be estimated on a per-individual basis.

To implement any informative classification algorithm, it is necessary to estimate the levels of risk for individuals entering the screening procedure. In our collaboration with researchers from the NPHL and the American Red Cross (ARC), we have found that training data from past individuals are usually plentiful. For example, the NPHL screens around 25,000 individuals per year for chlamydia and gonorrhea, and the ARC screens about 6 million donations annually for a variety of infectious diseases (Zou et al., 2004). When training data are not available, one could use the regression methods of Vansteelandt et al. (2000) or Xie (2001) to estimate individual infection probabilities using responses from the initial pools, regroup individuals in positive pools based on these estimates, and then decode using our informative Dorfman techniques. We have found that this approach provides about the same level of benefit when compared to the results found in this paper. Of course, suitable diagnostics should always be performed to assess the fit of the model used to produce the risk estimates.

In closing, we believe that group testing in heterogeneous populations is a fertile area of research. We are currently developing informative extensions of the array testing procedures outlined in Kim et al. (2007) and the (hierarchical) halving algorithms proposed in Litvak et al. (1994). We also believe that developing informative procedures to screen for the presence of multiple infections simultaneously would be worthwhile.