Dynamics and control of state-dependent networks for probing genomic organization

Abstract

A state-dependent dynamic network is a collection of elements that interact through a network, whose geometry evolves as the state of the elements changes over time. The genome is an intriguing example of a state-dependent network, where chromosomal geometry directly relates to genomic activity, which in turn strongly correlates with geometry. Here we examine various aspects of a genomic state-dependent dynamic network. In particular, we elaborate on one of the important ramifications of viewing genomic networks as being state-dependent, namely, their controllability during processes of genomic reorganization such as in cell differentiation.

In recent years, network science has emerged as a powerful conceptual paradigm in the biological sciences. The reason for this is twofold. First, it has become vital to gain a deeper understanding of the role of interelemental interactions in the collective functionality of cellular organisms. It has also become increasingly clear that networked systems in biology often intricately evolve with multiple time scales, a property dictated by how the element or node dynamics intertwine with global network dynamics and functionality. A basic premise in network science is that the structure of the network (1, 2) influences the dynamical and functional properties exhibited at the system level. In this context, the relationship between higher levels of connectivity in the network and the convergence rate to certain biological equilibria or limit cycle can be examined.

Here, we highlight the elaborate connections between network structure and network function in the context of the genome. In particular, we examine, via empirical findings and abstraction-based models, the dynamics and control properties of chromosomal networks during cell differentiation. Structural reorganization in the nucleus during differentiation can be captured by considering the genome as a state-dependent dynamic network where evolving chromosomal geometry determines network structure. We hypothesize that a moment exists during terminal cell differentiation, perhaps coincident with cell cycle withdrawal, where the architecture and transcriptional networks undergo a unique change in their mutual relationships, to thus configure a developmentally informed “alignment.” Two models are used to describe the relationship between architecture and transcriptional networks. The first proposes that overall coregulated gene content (function) emerges according to overall chromosome associations (form) (Fig. 1A1). In other words the genome at the chromosomal level self-organizes to facilitate coordinated gene regulation during differentiation. Thus form precedes function. The second model proposes that the transcriptional network and coregulated genes precede and shape the architecture network, or that form follows function (Fig. 1A2). Under either model, commitment to terminal differentiation is associated with network alignment, and feedback between the two networks allows fine-tuning to achieve the optimal cell-specific network configurations (Fig. 1B).

Fig. 1.

Mechanics of cell specialization. (A1, A2, and B) The relationship between spatial (form) and transcriptional (function) networks over time during cell specialization. Alignment of the networks, where the architecture and transcriptional networks become mutually related. Prior to the aligned state, we propose two possible models: (A1) overall coregulated gene content emerges according to overall chromosome associations, or form precedes function, and (A2) the transcriptional network and coregulated genes precede and shape the architecture network, or form follows function. (B) After alignment, feedback between form and function networks allows fine-tuning to achieve optimal cell-specific network configurations.

We hypothesize that reorganization of chromosomal architecture minimizes the total information content or entropy. Transcription factories are an excellent example of this, as, in principle, they increase the degree of coordination of the transcription of gene (3). However, many questions remain, such as whether transcription factories are stable or whether they spontaneously and transiently self-organize, and whether developmental state influences the status and dynamics of transcription factories. Here, we provide an abstraction-based formalism, based on dynamic networks and their controllability properties, to shed light on the multifaceted aspects of nuclear organization underlying gene expression. We first expand upon the notion of dynamic state-dependent networks and their realizations in genomic organization. Subsequently, we examine the dynamics and control properties of such networks in the context of cell differentiation.

State-Dependent Networks

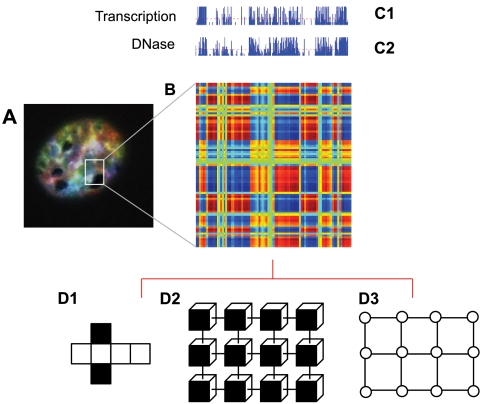
Consider the nucleus as a dynamical system composed of many interacting elements, among them networks having variable interactions with each other, for example, the networks of coregulated genes and chromosomal adjacencies (4). The emergent property of complex interactions among these elements defines the specific characteristics of an individual cell (4–6). Thus we describe the nucleus as self-organized because all interacting elements lead to a defined state, or signature, of that cell type (7). Networks within the nucleus could rewire in both space and time, if, for example, the mutual exchange of information between the coregulated gene network and the chromosomal interaction network changes (7). Viewing elements within the nucleus as networks allows assignment of quantifiable values such as intranuclear positions of chromsomes, and comparison of these values over time may then provide a framework for studying the process of differentiation as well as how nuclear organization generally affects the properties of a cell. Recently, a method called Hi-C was developed that probes the three-dimensional architecture of whole genomes by coupling cross-linking of chromosomal sites with massively parallel sequencing (8). Using Hi-C, spatial proximity maps of the human genome were constructed at a resolution of 0.1–1.0 megabase pairs in two human hematopoietic cell lines representing distinct hematopoietic lineages, one derived from B-lymphocytes and the other an erythroleukemia-derived line. These maps confirmed the presence of chromosome territories and the spatial proximity of small, gene-rich chromosomes (Fig. 2A). The maps also identified an additional level of genome organization that is characterized by the spatial segregation of open and closed chromatin to form two genome-wide compartments (Fig. 2B). Although compartment patterns in these two cell types were similar, many loci were discordant. Moreover, a strong correlation between the compartment pattern with transcription and chromatin accessibility was observed (Fig. 2 C1 and C2). These results demonstrate that open (euchromatin) and closed (heterochromatin) chromatin domains throughout the genome occupy different spatial compartments in the nucleus and that these patterns distinguish specific cell types or states.

Fig. 2.

The open and closed chromatin domains throughout the genome occupy different spatial compartments in the nucleus. (A) Image of an interphase nucleus labeled by spectral karyotyping (SKY). All chromosomes are labeled with a unique color to visualize their territories. Analysis of SKY data reveal spatial relationships between each pair of chromosomes. (B) Correlation map of a chromosome generated from Hi-C. A correlation matrix illustrates the correlation [range from 1 (blue) to +1 (red)] between the intrachromosomal interaction profiles of every pair of 1-Mb segments along each chromosome. (C1) The transcription profile along the chromosome. (C2) The open and closed chromatin profile along the chromosome (based on DNase I hypersensitivity). The two dominant proximity patterns, red and blue, correlate strongly with open and closed chromatin. (D1–D3) A state-dependent network representation of proximity patterns. The faces of each element are color-coded (D1); the elements can exchange information when the same color-coded sides are facing each other (D2); the interaction graph associated with D1 (D3).

To shed light on and formalize how chromosomal organization in the nucleus can lead to distinct functional and architecturally distinct networks, the notion of state-dependent networks becomes of particular significance. We thus start with a transparent example that abstracts the underlying phenomena—we use “cubes” instead of genes and chromosomes for this purpose. Here we highlight the ramifications of adopting such a point of view in the context of dynamics and control of genomic organization. Consider a set of cubes with color-coded faces that can rotate about their respective geometric centers. Let us assume that each color represents one type of modality for interaction with other elements in this system of cubes. Moreover, we assume that each pair can interact if the correct color sides are facing each other. As an example, when the elements are color-coded as in Fig. 2D1, we may require that they can interact only when the white or the black sides are facing each other. Hence for the arrangement in Fig. 2D2, we obtain the interaction graph of Fig. 2D3. Evidently, as the rotational states of these cubical elements evolve over time, we obtain a sequence of interaction graphs; in particular, we realize that the corresponding interaction graph is state-dependent and, in general, dynamic. Another example of a state-dependent graph, of particular relevance to our biological setting, is the distance-induced interaction model. In this framework, the interaction or coregulation among various parts of the genome is a function of their respective relative positions (see Fig. 2B). Naturally, as the configuration of these elements evolve in time, the underlying interaction network evolves in time as well, resulting in a dynamic proximity graph.

More generally, a state-dependent graph is a mapping, , from the system configuration space Q to the set of all labeled graphs on n vertices G(n); that is,

[1]

where specifies the edge–state-dependency set. We will subsequently denote 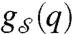by 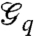to highlight the dependency of the resulting graph on the state q∈Q. It is assumed that the order of these graphs, n, is fixed. Their edge set, 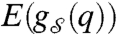, however, is a function of the state q. We now need to specify further how the state of the system dictates the existence of an edge between a pair of vertices in the state-dependent graph. This is achieved by considering the subset Q_ij⊆Q_i × Q_j, where Q_i and Q_j are the state spaces of nodes i and j, respectively, and requiring that 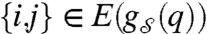if and only if (q_i,q_j)∈S_ij; we call S_ij the “edge states” of vertices i and j. If it is also assumed that the edge sets are such that (q_i,q_j)∈S_ij if and only if (q_j,q_i)∈S_ji for all i,j, then the resulting interaction graph is undirected; in general state dependency leads to a directed graph. The collections of edge states for all pairs of nodes in the network constitutes the edge–state-dependency set 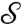in Eq. 1.

In the context of weighted graphs, an analogous point of view can be adopted in regard to the state dependency of the edge weights. For example, we can view the weight on the interaction link between nodes i and j as being inversely proportional to their distance, translating to a stronger interaction between the nodes that are geometrically closer.

Feedback and Control of State-Dependent Networks

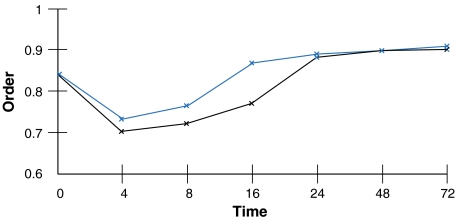
Previously we found that during differentiation of a hematopoietic progenitor into the erythroid or neutrophil lineages, the degree of intranuclear order changes, as captured by computing the total entropy in the system (7; see also Fig. 3). As the progenitor commits to either lineage, order decreases—entropy increases—to a minimum, which we define as the metastable state, then increases and eventually stabilizes at greater order than that of the original progenitor as terminal differentiation is achieved (Fig. 3). The metastable state is a necessary phase transition for advancement to a more highly ordered state that characterizes more advanced (committed) stages of cellular differentiation. This may be a general property of differentiation in other lineages as well, where cell-specific organization of the nucleus emerges from mutual interactions between gene coregulation and chromosomal architecture (Fig. 1B). As the nucleus “reorganizes,” loci containing up-regulated genes move from a repressive to an active nuclear compartment, whereas loci containing down-regulated genes move in the converse manner. Global reorganization of chromosome proximities also occurs during differentiation (3). However, it is unclear whether local changes in positioning, for example, looping of loci from chromosome territories, drive global reorganization on the whole chromosome level, or vice versa. The two models we discussed previously are compatible with this scheme. Specific acquired mutations could interfere with this process and direct cells down an alternative pathway, particularly if an additional perturbation were to occur in the metastable state. Bypassing network alignment may lead to an alternative quasistable, or less random, ordered state that might in some cases give rise to further mutations and emergence of almost any conceivable abnormal phenotype. We hypothesize that the intranuclear systems that are transitioning from a less-ordered state to a highly ordered state are losing controllability, or the ability to respond to specific external cues. A highly ordered system is generally less controllable than a disordered one (9). The notion that the metastable state is the most controllable one suggests the possibility that it is likely to be more responsive to therapeutic interventions.

Fig. 3.

Dynamics of order during cell specialization. When a progenitor commits to either the erythroid (black) or the neutrophil lineage (blue), there is a concomitant increase in order, eventually stabilizing at a level greater than that of the original multipotent progenitor (7).

In the context of state-dependent networks, consider the relative translational configuration of chromosome i with respect to chromosome j at time instance k, denoted by e_i(k). The configuration of the chromosomes induced a geometric network (either a weighted network or with the help of a threshold, a graph); this network will be referred to as the cell proximity network 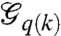, subsequently denoted by 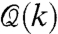. It is convenient to view this network as the structural organization of the cell. In view of our earlier discussion, we note that the cell proximity network is a state-dependent graph that is induced by the relative configurations of various chromosomes in the cell. Let 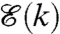denote, on the other hand, the gene regulatory network in the cell, which can be viewed as the functional organization of the cell. 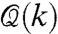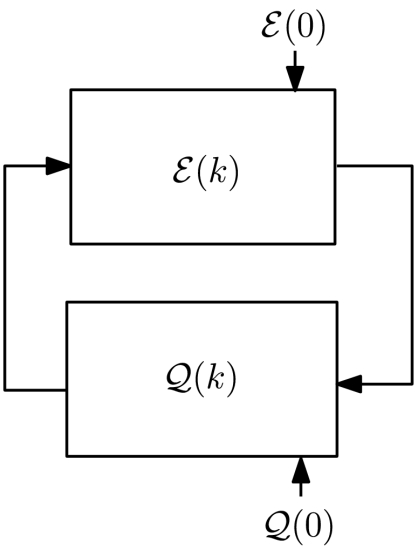Moreover, these two cell networks and 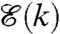are not only related, but are also highly correlated via feedback (Fig. 4).

Fig. 4.

Feedback between cell function and cell proximity network; the initial conditions 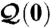and 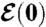are determined following an intricate alignment between form and function.

Introducing Control: MyoD and GATA1

Adopting the point of view of state-dependent networks, in conjunction with the premise that form and function of the cell are directly correlated, allows us to consider control mechanisms of the chromosomal network that derive the network geometry from an initial configuration toward a specific cell type. This is particularly exemplified by transcription factors that have broad influence on cell fate, such as MyoD. In addition to its role in myoblasts as a transcription factor regulating expression of skeletal muscle genes, MyoD can convert fibroblasts to skeletal muscle cells by activating the skeletal muscle differentiation program. Recent studies indicate that MyoD binds and induces histone modifications at tens of thousands of sites in the myoblast prior to transcription of most skeletal muscle genes, suggesting a potentially more global role in cell specification (10). Another “master regulator” is GATA-1, a zinc finger transcription factor essential to maintenance of the erythroid and megakaryocyte lineages (11). GATA-1 may have a global impact on nuclear organization by catalyzing interactions within and among the coregulated gene and chromosome topology networks. Cheng et al. have used ChiP-Seq methods to identify the spatial distribution of cis-regulatory elements targeted by GATA-1, and they determine criteria for distinguishing between target sites that promote activation versus repression of genes during erythroid development (12). The broad influence of these transcription factors provides a platform for understanding control over development of specific cell types. The proposed framework may also help identify previously uncharacterized master regulators that globally influence cell fate.

Embedding Dynamics and Control in State-Dependent Networks.

Viewing the network architecture dependent on the node dynamics allows for a more explicit reasoning about the dynamical properties of the network geometry itself, and via the feedback in Fig. 4, its function. In the special case where the interaction between a pair of nodes i and j is dictated by their geometric states q_i and q_j, the dynamics at the level of the state induces a corresponding dynamics at the network level, which in turn can further influence the evolution of the geometric states of the nodes. Representing the combined dynamics in continuous time assumes the form

[2]

where q(t) = [q₁(t)^T,⋯,q_n(t)^T]^T and 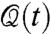represent, respectively, the geometric state of the genome and the cell proximity-induced interaction network, at time instance t. The exact form of functions f and g in Eq. 2 lead to distinct dynamical features for the evolution of the geometric state and interaction network, particularly in relation to time scales, decomposability, and state and network equilibria. Such state-dependent network models lead to a unique set of challenges to the field of genomics as well as systems and control research. In order to illustrate some of these challenges via a simple example, and highlight the utility of a control theoretic perspective on genomic organization, consider a state-dependent proximity network. Assume that the nodes in the network have adopted a diffusion-like interaction scheme for synchronization of their translational dynamics, which possibly after a coordinate transformation, has resulted in the perturbed diffusion dynamics on the interaction network,

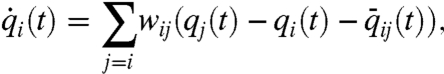where q_i(t) represents the translational coordinate of node i in the cell (with respect to some coordinate frame), which in turn evolves according to a local weighted gradient induced by the other nodes, including an offset induced by an ambient potential.*. This local interaction model leads to the collective dynamics of the form

[3]

where 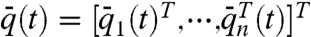, , 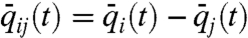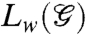is the weighted Laplacian of the network, I denotes the 3 × 3 identity matrix, and “⊗” is the matrix Kronecker product. This model has been extensively studied in recent years due to its ramification for distributed estimation and control (9). In order to examine the state-dependent extension of the above diffusion model, let 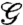denote the set of graphs of order n with vertex set V = {1,2,…,n} and edge set E = {ij|i = 1,2,…,n - 1,j = 2,…,n,i < j}, with the weighting function 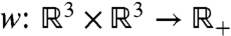, assigning to each edge ij a function of the distance between the two nodes i and j. Thus we have w_ij = w(q_i,q_j) = f(d_ij), where d_ij = ∥q_i - q_j∥ and 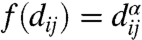for some α < 0. In this case, the interaction between a pair of nodes weakens as they drift apart. This dependency of the edge weights on the relative distances between the nodes is in direct correspondence with our earlier discussion on the role of genomic organization. In the setup of the dynamics (Eq. 3),

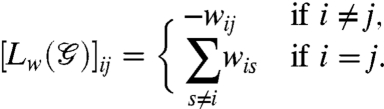Depending on the exact form of the edge-weight dependency, the dynamic network evolution has a distinct character. For example, the stability of the state as well and the network equilibria depend on the weighting functions, assigning how the edge weights depend on the state of the nodes. Moreover, the initial conditions for the geometric states are reflected in the resulting state equilibrium and by association in the network geometric and functional equilibria.

Control of State-Dependent Networks.

Consider now the “influenced version” of the diffusion dynamics over the network (Eq. 3), namely,

[4]

where u denotes an external influence on the network, the Diag(B_w) is a diagonal matrix with the vector B_w on its diagonal, and B_w indicates that the input matrix that might also be state-dependent. Within the context of this example, a few observations are pertinent: (i) whereas the state-independent diffusion dynamics over a connected network has a one-dimensional set of equilibria (namely, the translation of the span of the vector of all ones), the state-dependent dynamics might have multiple distinct equilibria as a function of the input u, (ii) the presence of an external influence can potentially drive the dynamics from one equilibria to the next, leading to a new network formation. In order to assess the network configuration that is more amenable to external influence, the notion of controllability Gramian becomes particularly useful and provides a direct connection with the role of network entropy in the metastable state of the cell discussed earlier (Fig. 3). Controllability Gramian for a network measures how controllable certain modes of the network are and which modal directions take less and more energy to be steered (Fig. 5). In the case where interaction between the nodes is inversely proportional to their distance, the closer the nodes come together, they have higher interaction with each other, and it is conceivable that the network becomes less controllable by an external signal such as MyoD (Fig. 6). Using linearization of the state-dependent network, the uncontrollability of the network can also be directly related to its network structure, in particular, to its symmetry. In general, symmetry in the network with respect to the external input leads to uncontrollable networks and singular controllability Gramians (Fig. 7 A and B). In the meantime, the controllability Gramian directly relates to how noise injected in the network maps to the state of the network and thus can be directly related to the network covariance and entropy. The general observation is that a higher degree of controllability relates to the determinant of the network covariance matrix—which in turn, translates to interpretation of network controllability in terms of the network entropy.

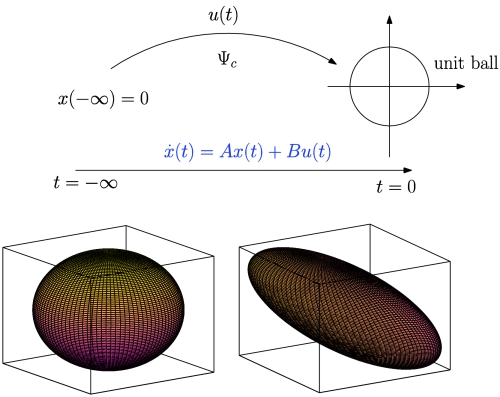
Fig. 5.

Controllability Gramian characterizes the minimum energy input to the linear system 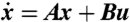that steers the initial zero state at infinite past to a point on the unit ball at t = 0 (Top). Moreover, this Gramian defines how inputs on the unit sphere (Bottom Left), such as noise or external signals, map to system states: Directions that are more controllable are characterized by elongated ellipsoidal axes, whereas the shortened axes are less controllable directions (Bottom Right).

Fig. 6.

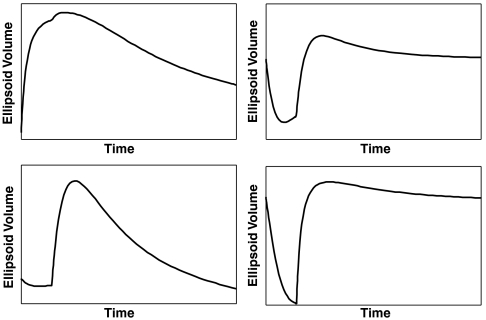
A control signal is introduced for a diffusion-like protocol on state-dependent weighted networks; the Euclidean distance matrices obtained from the experimental data are processed via a Euclidean embedding algorithm to obtain a realization for the network, which is then subjected to injected signal for the duration of 1 s. The controllability of the graph with respect to this input is then measured with respect to the two dominant directions over an interval. The network assumes a configuration that has a higher level of controllability with respect to the initial configuration, in direct correspondence with the metastable configuration during cell differentiation. Depending on the initial state of the nodes and their relative states with respect to the injected signal, the network’s controllability can assume distinct profiles: initial higher levels of controllability during the signal injection (Upper Left) as measured by the volume of the controllability ellipsoid in the two dominant directions, or initial lower levels of controllability followed by a higher level controllability (shown on the subsequent panels). The nonsmooth segment in each figure corresponds to the removal of injected signal.

Fig. 7.

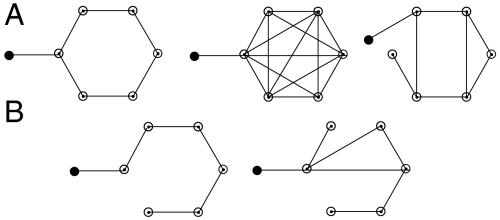
A network view of cellular reprogramming. Network diagrams A and B represent uncontrollable and controllable networks for the diffusion-like dynamics on graphs with one injected signal (black filled node).

Control from a Subset of Nodes.

Next, consider the controllability of the network in the neighborhood of the linearization point and the corresponding controllability Gramian structure. In this context one can examine local controllability of the state of the network from a small subset of nodes in the graph. It turns out that the structure of the network, as viewed from that node, has a direct implication for the system properties of the network, including its controllability. In our recent work, we have further refined the notion of symmetry to that of nodal domains, which refers to the partition of the network in terms of the signs of the entries of the eigenvectors of the combinatorial Laplacian (9). Nodal domains have historically been studied in the context of the Dirichlet problem and have been more recently tailored toward domains that are specified in terms of graphs (13).

Consider again the diffusion dynamics (Eq. 4) with augmented inputs, e.g., MyoD. Using this abstraction-based model, we can now characterize “most influential” external interactions with the network. That is, we are interested in identifying strategically optimal locations for the external input to exert influence, which in turn is highly dependent on the number of external signals and the structure of the network. For example, in the case of one external agent, it might be advantageous to locate this agent close to some “central” location in the network, where the distance (the number of edges) needed to be traversed in order to reach the farthest node, is minimum. However, in the case of two external signals, it is conceivable that their optimal placement would be at two peripheral locations in the network. This externally influenced diffusion dynamics (Eq. 4) that accepts inputs from external signals provides an ideal abstraction-based setting for a system-theoretic characterization of the influential location(s) in a genomic network. An instrumental construct for this purpose is the controllability Gramian. Consider a linear-time invariant model, with system and input matrices A and B, respectively, and a state denoted by x. Define the controllability operator 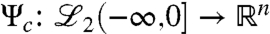by

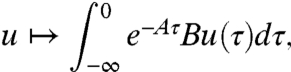which can be viewed as the response of the linear system with initial condition x(-∞) = 0 to an input 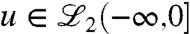; 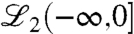denotes the space of square integrable functions with (-∞,0] as their domain. Given the initial condition x(0) with unit norm, it is now desired to find the smallest norm control input 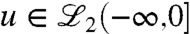that solves the functional equation Ψ_cu = x(0);^† that is, it is desired to find the minimum norm control that steers, respectively, and a state denoted by t = -∞ to the state x(0) on the unit circle at t = 0 (14, 15); see Fig. 5.

Standard arguments in linear systems theory then leads to two observations: assuming that the linear system is controllable, (i) the minimum norm control is parameterized by 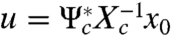( 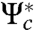is the adjoint of Ψ_c), with norm 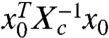, where X_c, the controllability Gramian, is the positive definite solution of the matrix equation

and (ii) the states reachable with control inputs with norms bounded by one are characterized by the ellipsoid 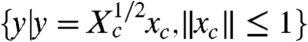, whose axes are the eigenvectors of the controllability Gramian X_c. In fact, if X_c has eigenvalues λ_i and λ_j such that λ_i≫λ_j, then there is more “stretching” in the direction of the normalized eigenvector corresponding to λ_i as compared with the normalized eigenvector corresponding to λ_j. That is, the ith direction is deemed “more controllable” than direction j.

The upshot of the aforementioned discussion is the following: The selection of the location for injecting steering signals in the network partitions the underlying network in Eq. 4, resulting in system and input matrices that, in turn, determine the controllability Gramian X_c. The controllability Gramian, on the other hand, characterizes which directions are more controllable than others. An influential location in the network is thus the node in the graph that leads to a controllability Gramian with a spectrum that stays away from the origin in the desirable directions. More precisely, suppose that in Eq. 4, we denote by 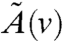and 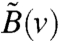the system and input matrices that are obtained when v is selected as the influenced node, and X_c(v) is the resulting controllability Gramian. Then the optimization problem

[5]

quantifies the most influential node in the network when measured with respect to providing most controllability in the ith direction. We note that the optimization problem (Eq. 5) can be extended to the case where more than one external signal (e.g., transcription factors) are presented to the network. Adopting this point of view for controlling cell organization provides a unifying perspective on cellular processes such as differentiation as well as a framework for more systematic reasoning on the role and efficiency of input signals in steering cell organization to particular network equilibria (Fig. 8). Furthermore, our methods may provide a means of evaluating and refining cell reprogramming strategies that rely on ectopic expression of transcription factors, such as derivation of iPS cells from a wide variety of differentiated cell types (16).

Fig. 8.

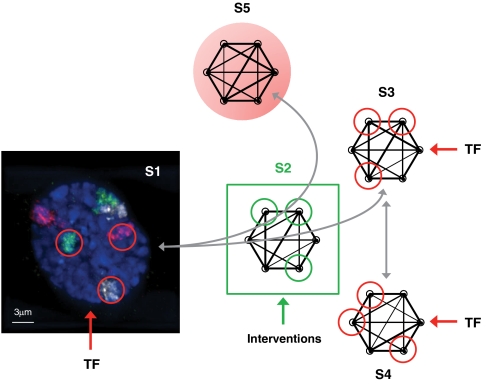
Control from a subset of nodes. With specific transcription factors (TF) as input signals, primary human fibroblasts (S1) transition to the metastable state (S2), where bifurcation takes place and two possible paths emerge. One leads to the normally specialized state (S3), and the other to an abnormally specialized state (S5). Under our hypothesis, interventions applied at S2 can influence the path taken. TF targeting a particular subset of nodes can also drive a transition from state S3 to another normally specialized state S4. The red and green circles denote the targeted nodes in each state.

Summary

The dynamics and control of state-dependent graphs provide the basis for our broad hypothesis that nuclear reorganization occurs at the time of cellular specification and both precedes and facilitates the orchestrated activation of transcriptional networks associated with subsequent cell differentiation. The processes of differentiation and reprogramming are intimately related, and therefore they may have similar, or at least mutually resonating, reception to control. Recent breakthroughs in reprogramming somatic cells back to an ES cell-like state using just four genes (16), as well as more direct reprogramming routes, for example, the overexpression of the master regulator MyoD (17) to generate myogenic cells or a combination of transcription factors to elicit neuronal differentiations (18), have all shown how cellular differentiation systems can be controllable at some early determinative step. Both of the foregoing strategies of reprogramming rely on expression of transcription factors to induce global changes, and it is likely that these changes are reflected in nuclear organization. From a control point of view, cellular reprogramming changes nuclear organization, thereby creating an environment that propels a system into a desired state. We have shown that control over systems can be acquired by altering nuclear organization. Our methods provide a means to identify critical subsets of nodes within state-dependent networks that lead to a specific specialized state through cellular differentiation. These nodes are highly relevant to mechanisms of reprogramming, or acquisition of control. Our modeling asserts that their defining characteristic will be that recreating their specific configuration in an alternative cell type will inevitably lead it to the specialized state of the original cell through the same or a highly similar differentiation pathway. Adopting such a state-dependent network point of view to genome organization would also provide a more systematic means of reasoning about therapeutic interventions for cell processes that have become “out of control” such as cancer.

Controllability of dynamic state-dependent networks provides an intriguing previously undescribed vista into steering complex and multifaceted interactions in the genome toward biologically desirable configurations. Network controllability can be formalized in various distinct forms. For example, in structural controllability (see, for example, ref. 19), the network is assumed to be controllable if arbitrary weights on certain permissible interaction links lead to a controllable configuration. As the dynamic and state-dependent nature of the chromosomal network requires reasoning on the “degree” of controllability in a setting where edges can appear or strengthen in a state-dependent dynamic manner, we have adopted the use of system-theoretic Gramians to examine and formalize network response and controllability properties. In the future, it will be important to examine the contribution of various notions of controllability for understanding distinct aspects of cell organization and differentiation, as well as the complementary means of viewing cell reorganization via local energy optimization principles and game theoretic network formation.

Our methodology also has applications for designing influence mechanisms, e.g., marketing strategies, on social networks. Moreover, in the case where a disease spreads over a network of interacting individuals and populations, our methodology can be used to design vaccination strategies to influence the progression of an infectious disease. In the context of engineering, the correspondence between the notions of network controllability and entropy has direct implications for designing robust robotic networks, for example, those that are less controllable (i.e., more secure) with respect to external perturbations.