Discovery of the recoverable high-pressure iron oxide Fe₄O₅

Abstract

Phases of the iron–oxygen binary system are significant to most scientific disciplines, directly affecting planetary evolution, life, and technology. Iron oxides have unique electronic properties and strongly interact with the environment, particularly through redox reactions. The iron–oxygen phase diagram therefore has been among the most thoroughly investigated, yet it still holds striking findings. Here, we report the discovery of an iron oxide with formula Fe₄O₅, synthesized at high pressure and temperature. The previously undescribed phase, stable from 5 to at least 30 GPa, is recoverable to ambient conditions. First-principles calculations confirm that the iron oxide here described is energetically more stable than FeO + Fe₃O₄ at pressure greater than 10 GPa. The calculated lattice constants, equation of states, and atomic coordinates are in excellent agreement with experimental data, confirming the synthesis of Fe₄O₅. Given the conditions of stability and its composition, Fe₄O₅ is a plausible accessory mineral of the Earth’s upper mantle. The phase has strong ferrimagnetic character comparable to magnetite. The ability to synthesize the material at accessible conditions and recover it at ambient conditions, along with its physical properties, suggests a potential interest in Fe₄O₅ for technological applications.

Iron oxides have a widespread occurrence, being composed of the two most abundant elements on Earth. They are the most common strong magnetic phases in nature and have vast technological uses including semiconductors, pigments, catalysts, and iron extraction (1). Iron oxides are also important biominerals and are used in biomedical applications (2). At ambient pressure, six crystalline forms of iron oxides exist, including wüstite FeO, magnetite Fe₃O₄, and four phases of Fe₂O₃ (1, 3–7 and references therein). The basic atomic arrangements of these phases are simple; however, they show extensive nonstoichiometry and complex defect structures (8, 9) that complicate the understanding and modeling of their properties. The possibility to host extensive amounts of defects explains their solid-state redox activity. For thousands of years iron oxides have attracted scientific curiosity and challenged the modeling of their physical and chemical properties, so it is compelling to report the discovery of a phase that is not simply a polymorph of known iron oxides, but a distinct compound with formula Fe₄O₅.

Synthesis and Structure of Fe₄O₅

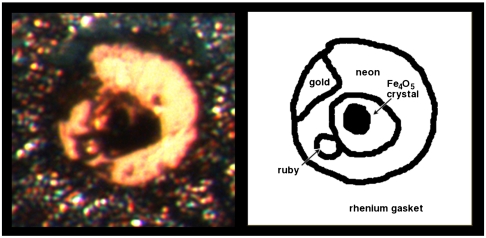
Fe₄O₅ was first synthesized in the diamond anvil cell from the breakdown products of siderite (FeCO₃) at about 10 GPa and 1,800 K. A spherical crystal of about 8 μm in diameter grew in less than a minute upon heating (Fig. 1). Diffraction patterns were collected at high pressure and ambient temperature using highly focused synchrotron X-rays. The single crystal diffraction pattern (Fig. S1) was indexed with an orthorhombic C-centered cell with a = 2.8430(7) Å, b = 9.700(8) Å, c = 12.29(6) Å. Structural solution and refinement converged to a structure isomorphic to CaFe₃O₅ (10), with space group Cmcm; therefore, we propose the crystal to be a distinct oxide of stoichiometry Fe₄O₅ (Table 1). Refined and ab initio calculated atomic coordinates at 10 GPa are in excellent agreement (Table 2); occupancies of all sites are full within uncertainty (about 5%), supporting the inferred stoichiometry. The atomic arrangement of Fe₄O₅ can be described as a stacking along the c axis of layers of edge-sharing FeO₆ octahedra and layers of face-sharing trigonal prisms, hosting Ca in the prototype phase (Fig. 2). There is close similarity between the structures of Fe₄O₅ and h-Fe₃O₄, the high-pressure polymorph of magnetite (11, 12). In the latter, edge-sharing octahedral layers are made of equivalent sites, whereas in the former two nonequivalent octahedral sites are arranged in a thicker layer. The similarity in the stacking perpendicular to the octahedral layers accounts for the similarity of two of the cell parameters of the two oxides; the thicker octahedral layer along the c axis in Fe₄O₅ accounts for a c-cell parameter that is about 3 Å longer than the analogous direction in h-Fe₃O₄.

Fig. 1.

The single crystal of Fe₄O₅ synthesized in the diamond anvil cell at high pressure after laser heating. The sample chamber, about 60 μm in diameter, viewed through a diamond anvil at 10 GPa and its sketch show the rounded opaque crystal of Fe₄O₅ grown in the heated area. The sample is well separated from the gasket, ruby, and the anvils by the inert neon medium.

Table 1.

Summary of instrumental parameters and refinement statistical parameters for the single crystal structural analysis

Beamline	13 IDD, GSECARS, APS, ANL
Wavelength, Å	0.3344
Pressure, GPa	10
Temperature, K	298
Composition	Fe4O5
Symmetry	orthorhombic, Cmcm
Lattice parameters a, b, c, Å	2.8430 (7), 9.700 (8), 12.29 (6)
Volume, Å3	339 (2)
Z	4
Rint	0.032
Refl. range	-2 ≤ h ≤ 2, -7 ≤ k ≤ 7, -2 ≤ l ≤ 4
θ range, °	3.5 ≤ θ ≤ 9.1
N. reflections	34
N. independent	20
N. I > 2σ(I)	20
Refinement	F2
R	0.050
wR2	0.134

Table 2.

Atomic fractional coordinates of Fe₄O₅

Atom	Wyckoff position	Method	x	y	z
Fe1	4a		0	0	0
Fe2	8f	SXD	0	0.2616(4)	0.1131(11)
		DFT	0	0.2623	0.1161
		XRPD	0	0.2657 (4)	0.1160 (3)
Fe3	4c	SXD	0	0.5048(6)	1/4
		DFT	0	0.4995	1/4
		XRPD	0	0.5038 (5)	1/4
O1	4c	SXD	0	0.158(3)	1/4
		DFT	0	0.1567	1/4
		XRPD	0	0.174 (2)	1/4
O2	8f	SXD	0	0.365(3)	0.55(1)
		DFT	0	0.3681	0.5375
		XRPD	0	0.3566 (12)	0.5389(10)
O3	8f	SXD	0	0.085 (3)	0.643 (9)
		DFT	0	0.0838	0.6422
		XRPD	0	0.090 (1)	0.6372 (9)

SXD, X-ray structural refinement of single-crystal (10 GPa); XRPD, powder diffraction data (10.5 GPa); DFT, ab initio calculation (10 GPa).

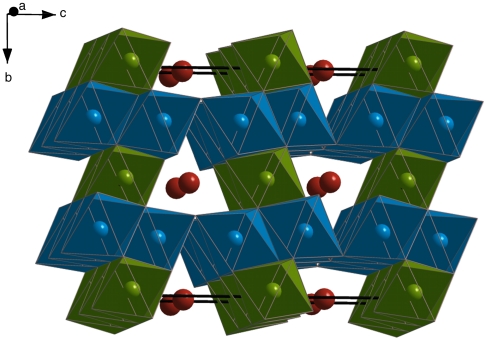
Fig. 2.

Structure of Fe₄O₅. Green and blue octahedra (sites Fe1 and Fe2, respectively) illustrate nonequivalent edge-sharing FeO₆ groups forming layers perpendicular to the c axis. Layers are alternated by channels where iron, represented as red spheres (Site Fe3), is arranged in larger triangular prisms sharing faces along the direction of the a axis.

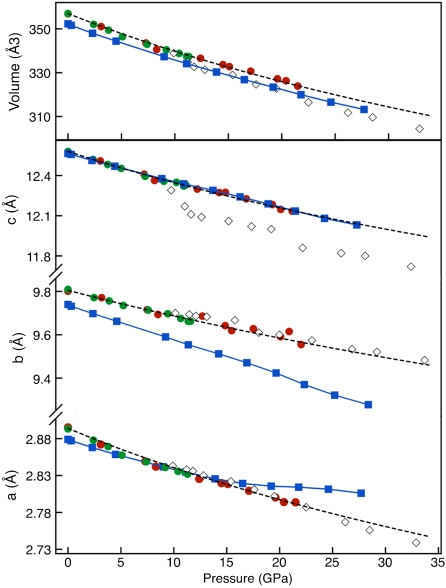
After synthesis and without further heating, the compressibility of the single crystal was measured up to 30 GPa (Fig. 3). The single crystal c lattice parameter shows a much greater decrease compared to powder diffraction data and first-principles calculations that are described later in this paper. We attribute this behavior to nonhydrostatic conditions developed as soon as pressure was increased after the synthesis. The single crystal grew at 10 GPa after the load was released from about 40 GPa. The sample chamber became very thin in the new compression cycle, because the gasket was deformed during the first compression and the crystal likely bridged the anvils. The single crystal c axis, nearly parallel to the load axis, shows therefore an apparent greater compressibility than in the powder samples.

Fig. 3.

Compressibility of Fe₄O₅. Pressure dependence of lattice parameters and volume of the unit cell. Data are from single crystal (open diamonds), two separate powder diffraction experiments (red and green circles), and from first-principles calculations (blue squares). Dashed black trends, interpolated from powder diffraction data, are reported as a visual aid. Standard deviations are smaller than the symbol sizes.

In order to explore the stability range of Fe₄O₅ in a pure Fe-O system, several syntheses were performed starting from mixtures of iron and Fe₃O₄ in appropriate proportions. Fe₄O₅ was readily synthesized at 10 and at 20 GPa, upon heating at 1,500–2,200 K. In most cases the high-pressure phase shows a rather coarse grain size (Fig. S2). Two samples were decompressed without further heating to ambient pressure. Remarkably, we found that Fe₄O₅ is a retrievable phase. One of the samples was heated during decompression; at about 5 GPa we observed its breakdown to magnetite and wüstite, showing that the observed phase has indeed intermediate composition between the two cubic oxides. The sample homogeneity and chemical gradients were monitored by collecting diffraction patterns in 2D grids across the sample area before and after most heating cycles. The analysis of individual patterns shows variable mixtures of fine unreacted material and more coarse high-pressure phases, not systematic chemical gradients. Because of the challenges in recovering and preparing the samples synthesized at high pressure as well as in measuring the Fe/O ratio, we could not independently determine the composition of the proposed phase. The bulk Fe/O ratio was, however, monitored from phase abundances determined by Rietveld refinement of the averaged patterns. Throughout the experiments the calculated Fe/O ratio shows random variations between 0.81 and 0.77, suggesting that no appreciable redox reaction occurred. Wide oscillation patterns were collected where Fe₄O₅ appeared to be the dominant phase and to have a finer size. The pattern of a fine grain powder collected at 10.5 GPa and that of a slightly textured sample collected at ambient pressure were selected for powder diffraction structural analysis (Fig. S3). Atomic fractional coordinates were refined for the pattern at 10.5 GPa; they were instead fixed to the values found for the single crystal in the analysis of the ambient conditions pattern. The Rietveld analysis converged with very satisfactory statistical parameters (Table S1) in both cases. Calculated atomic coordinates at 10.5 GPa are in good agreement with those from the refinement of the single crystal diffraction data and from first-principles calculations (Table 2).

Energetics and Stability of Fe₄O₅

To the best of our knowledge, Fe₄O₅ has not been previously described. Therefore, complementary first-principles calculations were carried out to examine the viability of Fe₄O₅ in terms of its energetics and phase stability under pressure. The enthalpies and volume-compression data of FeO, h-Fe₃O₄ [the high-pressure polymorph of magnetite (11, 12)] and Fe₄O₅ were calculated using an effective Hubbard parameter of U_eff = 2 eV for Fe-d electrons (see Materials and Methods, Fig. S4, and Table S2). The calculated lattice constants for Fe₄O₅ at 0 K and 0 GPa are a = 2.88 Å, b = 9.75 Å, c = 12.58 Å, in excellent agreement with the experimental values (Table S2). The calculated bulk moduli of FeO and h-Fe₃O₄ are 186.3 GPa and 184.4 GPa, respectively, in close agreement with previous studies (13, 14). The calculated bulk modulus of Fe₄O₅ is 185.7 GPa, in excellent agreement with the predicted value using Vegard’s law (ca. 0.5% deviation).

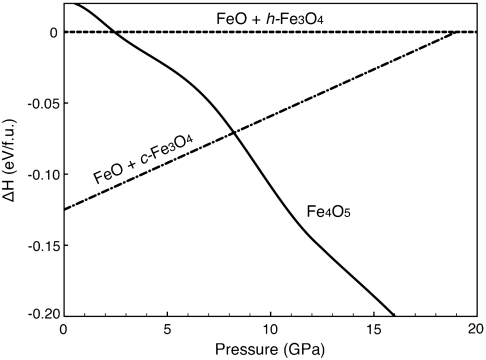
The enthalpy of Fe₄O₅ is computed and compared with the sum of the enthalpies of its possible breakdown products (FeO, cubic and orthorhombic Fe₃O₄, Fig. 4), revealing that Fe₄O₅ is about 0.096 eV less stable than h-Fe₃O₄ + FeO and about 0.783 eV less stable than c-Fe₃O₄ + FeO at 0 GPa. However, as pressure increases, Fe₄O₅ becomes energetically more favorable than the breakdown products (Fig. 4), providing complementary evidence that the synthesis of Fe₄O₅ is energetically plausible at high pressures. At 11 GPa, the average lengths of the Fe-O bonds are 1.944 Å (4a) and 2.076 Å (8f) in the octahedra and 2.089 Å (4c) in the trigonal prism. There is a significant charge transfer of about 1.6 e from Fe atoms to O atoms. Density functional calculations show that the proposed iron oxide is strongly ferrimagnetic (SI Text). The calculated lattice constants are a = 2.84 Å, b = 9.55 Å, and c = 12.34 Å at 11 GPa, close to experimental values. The structural changes of Fe₄O₅ under pressure can be closely followed by comparing the volume-compression data theoretically obtained from the first-principles calculations to the experimental data. In order to simulate the compression under hydrostatic conditions, all atoms and lattice constants were allowed to relax at each pressure point. The agreement between theory and experiment is remarkably good (cf. Fig. 3 and Table 2), providing a clear confirmation of Fe₄O₅. Nevertheless, further confirmation of its composition by direct methods will be pursued.

Fig. 4.

Enthalpies of Fe₄O₅ and of the plausible breakdown oxides FeO and h-Fe₃O₄. To examine the relative stability of Fe₄O₅ with respect to its possible breakdown products (FeO and Fe₃O₄ in the ambient and high-pressure structures), the enthalpy differences, ΔH^c = H(Fe₄O₅) - [H(FeO) + H(c-Fe₃O₄)] and ΔH^h = H(Fe₄O₅) - [H(FeO) + H(h-Fe₃O₄)], were calculated as a function of pressure. The solid, dashed, and dot-dashed lines represent the enthalpies of Fe₄O₅, ΔH^h (the reference), and ΔH^c, respectively. ΔH^c is extracted from the literature (15). The Fe₄O₅ structure is favored over the sum of breakdown products at 10 GPa.

Physics, Geophysics, Geochemistry, and Material Science Implications.

The stoichiometry of the phase here described falls within the most puzzling region of the Fe-O phase diagram, between wüstite and magnetite (7, 16–19). With increasing temperature, at ambient pressure, the Fe-O phase diagram at 44 at. % Fe shows coexistence of iron and magnetite up to about 900 K, wüstite and magnetite up to 1,700 K, magnetite and liquid up to 1,900 K, and liquid at higher temperature. Coexisting wüstite and magnetite exhibit extensive degrees of nonstoichiometry and complex defect structures, depending on the synthesis temperature and cooling path. The two cubic phases share the same oxygen array and can grow coherently (8, 20, 21), providing a nearly continuous range of structures with random defect distributions, clustered defects, and coherently grown distinct phases. The high-pressure behavior of the binary phase diagram is relatively unexplored. With the exception of the Fe-rich portion (22–24), relevant to planetary cores, only the polymorphism of known oxides is well investigated. Wüstite is stable to very high pressure and temperature (25), whereas magnetite undergoes a phase transition at about 10 GPa (26) into a nonrecoverable high-pressure phase having strong similarities with the phase presented in this work. Our experiment suggests that Fe₄O₅ is stable from about 5 GPa to at least 30 GPa. This phase, with lower symmetry, layered structure, and all six-coordinated iron, is favored over the largely nonstoichiometric framework structures hosting four- and six-coordinated iron, showing that pressure changes the character of atomic ordering of iron oxides in the most complex, intriguing region of the binary phase diagram.

Density functional theory (DFT) calculations show that Fe₄O₅ is ferrimagnetic. Although the high-pressure polymorph of magnetite is known to be a semiconductor (26, 27), a detailed account of the electronic structure of Fe₄O₅ is beyond the scope of this study and will be the subject of a forthcoming investigation along with experimental efforts. As in the isostructural calcium ferrite (28), electron delocalization is expected among the edge-sharing iron sites with short Fe-Fe distances (Fig. S5). Furthermore, in Fe₄O₅ strong interactions should be expected among the face-sharing Fe3 sites. Given its distinctive physical properties, the relatively low pressure of synthesis and its recoverability, Fe₄O₅ is a potentially interesting material for technological applications. The isomorphism with CaFe₃O₅ suggests that the doping with large cations is likely to decrease the synthesis pressure while concurrently affecting physical properties.

The stability of oxides in the deep Earth is a complex function of pressure, temperature, oxygen fugacity, bulk composition, and partitioning equilibria among coexisting minerals. It is therefore difficult to predict the occurrence of Fe₄O₅ in the deep interior without extensive investigations of systems with realistic composition. Nonetheless, it is important to note that Fe₄O₅, stable at the P-T conditions of the Earth’s upper and lower mantles, is more likely to occur than Fe₃O₄ from the viewpoint of oxygen fugacity given its more reduced composition. As geophysical research advances, the description of the Earth’s interior becomes increasingly complex, including structural, mineralogical, and chemical lateral heterogeneity. Oxygen fugacity and bulk chemical fluctuations might likely determine variations in the stabilities of accessory oxide minerals. The occurrence of mixtures of wüstite and ferrite inclusions in diamonds (29) provides direct evidence of the existence of compositions close to Fe₄O₅ in the Earth’s mantle. It follows that Fe₄O₅ is a plausible accessory phase of the Earth’s interior at least in locally Fe-rich portions at highly zoned shallow depths. Being isostructural with CaFe₃O₅, Fe₄O₅ and h-Fe₃O₄ would likely host significant substitutions of calcium and other large cations, not common in spinels and wüstite, representing a possible different scenario for the element partitioning of iron oxides at depth. It should be noted that the geophysical and geochemical importance of Fe₄O₅ goes beyond its occurrence or abundance, revising the iron–oxygen phase diagram, which is a fundamental reference for the thermodynamics and oxygen fugacity of the deep Earth.

As all oxides of elements of multiple closely accessible valence states, we expect Fe₄O₅ to show defect structures depending on pressure, temperature, and oxygen fugacity. In Fe₄O₅, in addition to vacancies and interstitials that are common in the cubic oxides, stacking disorder might occur. The Fe₄O₅ and h-Fe₃O₄ structures have similar trigonal-prism units that are intercalated by octahedral layers of different thickness, and therefore stacking disorder involving Fe₄O₅ and h-Fe₃O₄ octahedral layers is plausible. As the structures of iron oxides are common to many binary systems and complex solid solutions, we anticipate that a rich set of isostructural compounds and solid solutions with tunable properties may be synthesized.

Materials and Methods

The first experiment, where the single crystal of Fe₄O₅ was obtained, was performed using a crystal of siderite (FeCO₃) from Ivigtut, Greenland, as starting material. Several further syntheses were performed from mixtures of pure commercial magnetite and iron fine powders. Samples were loaded in diamond anvil cells along with the pressure gauges, e.g., gold (30) and a ruby sphere (31), and with Ne as a pressure medium. Ruby and gold were placed at the edge of the sample chamber; they were neither in contact with the sample nor were they heated. Experiments were conducted at the stations 13IDD, of GeoSoilEnviroCARS, Center for Advanced Radiation Sources, and 16IDB of High Pressure Collaborative Access Team, at the Advanced Photon Source, Argonne National Laboratory. Double-sided heating was performed with fiber lasers (32, 33). The structure was probed in situ with X-ray beams of 37 and 30 keV focused to 5 × 5 μm. Single crystal and powder diffraction patterns were collected with MAR165CCD detectors. Diffraction images were collected while the samples were rotated around the vertical axis by 30° to 70° according to the limitations imposed by the angular opening of the diamond anvil cell. GSE_ADA, RSV (34), Shelxl97 (35), FIT2D (36), General Structure Analysis System (GSAS) (37), and Endeavour (38) were used for data processing.

First-principles total energy calculations were performed using spin-polarized DFT as implemented in the Vienna ab initio simulation package (39). Structural and magnetic properties of Fe, FeO, h-Fe₃O₄, and Fe₄O₅ were calculated using the generalized gradient approximation (GGA) with the parameterization of Perdew and Wang (PW91) (40). The plane-wave cutoff energy for the electronic wave functions was set to 500 eV, ensuring the convergence of the total energy of the system to within 2 × 10^-6 eV/atom. A periodic unit cell containing four formula units was used in the calculations for FeO (B1), h-Fe₃O₄ (Cmcm), and Fe₄O₅ (Cmcm). The Brillouin zone was sampled using the Monkhorst–Pack special k-point scheme (41) with a 3 × 3 × 3 mesh for structural optimization and total energy calculations. In general, the PW91 functional tends to underestimate the lattice constants of iron and iron oxides; the GGA+U method was introduced in the total energy calculations (42). The resulting lattice constants of Fe and magnetite are close to the measured values when U_eff = 2 (SI Text).