ROS Initiated Oxidation of Dopamine under Oxidative Stress Conditions in Aqueous and Lipidic Environments

Abstract

Dopamine is known to be an efficient antioxidant and to protect neurocytes from oxidative stress by scavenging free radicals. In this work, we have carried out a systematic quantum chemistry and computational kinetics study on the reactivity of dopamine toward hydroxyl (•OH) and hydroperoxyl (•OOH) free radicals in aqueous and lipidic simulated biological environments, within the density functional theory framework. Rate constants and branching ratios for the different paths contributing to the overall reaction, at 298 K, are reported. For the reactivity of dopamine toward hydroxyl radicals, in water at physiological pH, the main mechanism of the reaction is proposed to be the sequential electron proton transfer (SEPT), whereas in the lipidic environment, hydrogen atom transfer (HAT) and radical adduct formation (RAF) pathways contribute almost equally to the total reaction rate. In both environments, dopamine reacts with hydroxyl radicals at a rate that is diffusion-controlled. Reaction with the hydroperoxyl radical is much slower and occurs only by abstraction of any of the phenolic hydrogens. The overall rate coefficients are predicted to be 2.23 × 10⁵ and 8.16 × 10⁵ M^–1 s^–1, in aqueous and lipidic environment, respectively, which makes dopamine a very good •OOH, and presumably •OOR, radical scavenger.

Introduction

Oxidative stress appears to be directly involved in the pathogenesis of several neurodegenerative disorders, including Alzheimer and Parkinson diseases.(1) Indeed, the brain is especially vulnerable to oxidative stress because of its high content of oxidizable substrates such as polyunsaturated fatty acids.(2) Also, the brain consumes about 20% of inhaled oxygen, and a large amount of reactive oxygen species (ROS) are believed to be produced in normal metabolic and physiologic processes.(3) External administration of antioxidants is usually not effective to prevent brain oxidative stress because of the presence of the blood brain barrier.(4)

Catecholamines (dopamine, norepinephrine, and epinephrine) constitute a class of chemical neurotransmitters that occupy key positions in the regulation of physiological processes and in the development of neurological, psychiatric, endocrine, and cardiovascular diseases. As such, these molecules and the neuronal and endocrine systems in which they are produced, continue to receive considerable research attention. These compounds are powerful electron and/or hydrogen donating antioxidants, the catechol moiety being one of the main structural features responsible for their antioxidant action.(5) In fact, the catechol structure is widely distributed in many naturally occurring antioxidants and it is known to play a role in scavenging ROS. There is strong evidence that the redox reactions of these neurotransmitters are involved in the first steps and in the progression of neurodegenerative diseases such as Parkinson’s disease.^6,7

Catecholamine neurotransmitters and related metabolites are expected to react with ROS under oxidative stress conditions,(8) and there exists a wealth of evidence demonstrating their neuroprotective effects. In addition, they have been recognized to quench electron mobility with the subsequent interruption of the free radical chain reaction.

Dopamine (DA) is an important endogenous catecholamine neurotransmitter that is present in high concentration in specific neurons in the central nervous system. Its concentration in the axon terminals of dopaminergic neurons is estimated at 47 mM.(9) In order to maintain its proper function, the brain requires a very delicate and precisely controlled DA environment; DA misregulation has been shown to alter development, movement, learning, and memory. The loss of dopaminergic neurons from the substantia nigra has devastating consequences. In fact, a significant reduction of dopaminergic neurons in this area can cause akinesia and tremors, both characteristic of Parkinson’s disease. Conversely, abnormally high amounts of DA can result in hyperkinesia, altered behavior, and delusions, as observed in schizophrenia.(10) DA has also been implicated in drug addiction, due to its role in reward-based learning.

On the other hand, the hydroxyl radical is an extremely reactive species that oxidizes cellular constituents via direct addition (e.g., ring-hydroxylation), hydrogen atom abstraction, and/or electron transfer. It is generated from H₂O₂ formed within the dopaminergic neurons during the oxidative deamination of dopamine by mitochondrial monoamine oxidase. The rate of H₂O₂ production follows neuronal activity. Consequently, it is important to understand the molecular mechanisms by which •OH radicals attack the dopamine molecule.

Many biologically relevant compounds exhibit second order •OH reaction rate constants of 10⁹–10¹⁰ M^–1 s^–l, which constitute essentially diffusion-limited reactivity.^11,12 It is generally believed that an indiscriminate attack on membranes, proteins, sulfhydryl groups, and other tissue constituents is a major reason for tissue damage during X-ray irradiation,(13) during exposure in vivo to •OH-generating cellular toxins,(14) or in the presence of OH-generating biochemical systems in vitro.(15) Previous studies have shown that •OH is responsible for the ring-hydroxylation of a variety of aromatic compounds including phenol and substituted phenols such as tyrosine.^16,17 OH has been found to damage DNA and particularly guanosine.(18)

Another important radical in biological media is the hydroperoxyl radical, •OOH, which is the protonated form of the superoxide radical anion, O₂^•–.(19) The protonation/deprotonation equilibrium exhibits a pK_a of 4.8. Consequently, only about 0.3% of any superoxide present in a typical cell is in the protonated form. However, O₂^•– is not a very reactive species, so the chemistry of superoxide in living systems is probably dominated by •OOH radical reactions.(19)

Dopamine is known to be an efficient antioxidant and to protect neurocytes from oxidative stress by scavenging free radicals.^20,21 Since dopamine may have neuroprotective effects in the brain, there is considerable theoretical and experimental interest for exploring dopamine reactivity toward free radicals.²²⁻²⁶ In the particular case of its •OH radical scavenging activity, it has been reported that its rate constant is 5.9 × 10⁹ M^–1 s^–1 at pH 4.7.(27) This value is close to the diffusion limit. However, there are no previous kinetic studies that allow one to assess the contribution of different pathways to the overall reactivity of dopamine toward •OH radicals, and to predict the proportion of the formed products. Several factors may also play a decisive role in dopamine reactivity: the presence of hydrogen bonding characteristics of the solvent,^28,29 or, in a biological context, solubility, and transport to specific tissues.(30)

In this work, we have carried out a systematic quantum chemistry and computational kinetics study on the mechanisms and kinetics of the •OH and •OOH-initiated oxidation of dopamine, in two model biological environments: water and pentylethanoate, at 298 K. Water, the biological solvent of choice and the most profuse constituent of living organisms, plays a particularly important role in biological processes. Pentylethanoate has been used to mimic a lipidic environment, in particular, cellular membranes. The hydroxyl radical (•OH) was chosen because it is the most electrophilic,(31) and reactive, of the oxygen-centered radicals, with a half-life of ∼10^–9 s.(32) We have also included the hydroperoxyl (•OOH) radical, which is a relatively slow-reacting species that is capable of diffusing to remote cellular locations,(33) with half-lives of the order of seconds.(34) Moreover, the behavior of •OOH is probably similar to the one of larger peroxyl radicals, RO₂•, which are abundant in biological systems. Thus, the studying of •OOH may yield insight on the reactions of other important radicals.

Computational Methodology

All electronic calculations were performed with the Gaussian 09 system of programs.(35) Geometry optimizations and frequency calculations have been carried out using the M05-2X functional(36) in conjunction with the 6-311++G(d,p) basis set. The M05-2X functional has been recommended for kinetic calculations by its developers,(36) and it has been successfully used by independent authors for that purpose.(37) Unrestricted calculations were used for open shell systems. Local minima and transition states were identified by the number of imaginary frequencies: local minima have only real frequencies, whereas transition states are identified by the presence of a single imaginary frequency that corresponds to the expected motion along the reaction coordinate. Relative energies are calculated with respect to the sum of the separated reactants. Zero-point energies (ZPE) and thermal corrections to the energy (TCE) at 298 K are included in the determination of energy barriers.

We have assumed that reactions take place according to the complex two-step typical mechanism of radical–molecule reactions,(38) in which the initial step leads to the formation of a prereactive complex (RC) that is in equilibrium with the reactants (R) and the second step is the formation of a transition state leading to the irreversible formation of the product.

Although gas-phase predictions can render fast and very accurate results for some chemical processes and molecular properties, there is a whole range of phenomena and molecular features that cannot be accurately addressed without including the effect of the solvent. Indeed the environment plays a vital role in biochemical phenomena, and it is essential to take into account its effect in the description of molecular biological systems and their properties. Thus, in this work, all structures involved in the studied reaction pathways are fully optimized in the solvent.

In this work, solvent effects are introduced with the SMD continuum model(39) using water and pentylethanoate as solvents, in order to mimic different cellular environments. Solvent cage effects have been included according to the corrections proposed by Okuno,(40) taking into account the free volume theory.(41) These corrections are in good agreement with those independently obtained by Ardura et al.(42) and have been successfully used by other authors.(43) The expression used to correct the Gibbs free energy is

where n represents the molecularity of the reaction. According to expression 1, the cage effects in solution cause ΔG to decrease by 2.54 kcal mol^–1 for bimolecular reactions, at 298.15 K. This correction is important because the packing effects of the solvent reduce the entropy loss associated with any chemical reaction whose molecularity is equal or larger than two.

Rate constants have been computed using conventional transition state Theory (TST)⁴⁴⁻⁴⁶ as implemented in TheRate program(47) at the Computational Science and Engineering Online Web site (www.cseo.net).(48) The energy values, partition functions and thermodynamic data were taken from the quantum-mechanical calculations.

where k_B and h are the Boltzman and Planck constants, ΔG^‡ is the Gibbs free energy of activation, σ represents the reaction path degeneracy, accounting for the number of equivalent reaction paths, and κ accounts for tunneling corrections. The latter are defined as the Boltzman average of the ratio of the quantum and the classical probabilities, and they were calculated using the zero-curvature tunneling (ZCT) method, using Eckart barrier.^49,50

For mechanisms involving single electron transfers (SET), the Marcus theory was used.^51,52 It relies on the transition state formalism, defining the SET activation barrier (ΔG_SET^‡) in terms of two thermodynamic parameters, the free energy of reaction (ΔG_SET) and the nuclear reorganization energy (λ)

The reorganization energy (λ) has been calculated as

where ΔE_SET has been calculated as the nonadiabatic energy difference between reactants and vertical products. This approach is similar to the one previously used by Nelsen and co-workers(53) for a large set of self-exchange reactions.

Some of the calculated rate constant (k) values are close to (or are, in fact) diffusion-limit rate constant. Accordingly, the apparent rate constant (k_app) cannot be directly obtained from TST calculations. In the present work the Collins–Kimball theory(54) is used to correct the rate constant, and k_app is calculated as

where k is the thermal rate constant, obtained from TST calculations and k_D is the steady-state Smoluchowski(55) rate constant for an irreversible bimolecular diffusion-controlled reaction

where R denotes the reaction distance, N_A is the Avogadro number, and D_AB is the mutual diffusion coefficient of the reactants A (free radical) and B (dopamine). D_AB has been calculated from D_A and D_B according to ref (56), and D_A and D_B have been estimated from the Stokes–Einstein approach(57)

where k_B is the Boltzmann constant, T is the temperature, η denotes the viscosity of the solvent, in our case water (η = 8.91 × 10^–4 Pa s) and pentylethanoate (η = 8.62 × 10^–4 Pa s), and a is the radius of the solute.

Dopamine is expected to exist in a protonated form in aqueous solution at pH below 8.(58) Since blood can be modeled basically as an aqueous solution at pH 7.4, full hydration and prevalence of the protonated form (DA⁺) is expected in biological environments, as shown in the predominance zones diagram in Scheme 1. The deprotonation sequence was established by Corona-Avendaño et al.(59) on the basis of the pK_a data reported by Sánchez-Rivera et al.,(60) using both quantum chemistry and NMR results. Conversely, in a non polar environment, dopamine exists mainly in the neutral form. In this work, the protonated form will be used to study the reactivity of dopamine toward free radicals in water, while the neutral form will be the reactant in pentylethanoate.

Scheme 1. Predominance Zones Diagram of Dopamine As a Function of pH.

Results and Discussion

Part 1. Dopamine Oxidation in Water

As mentioned before, dopamine is expected to exist in a protonated form in aqueous solution at pH below 8.^61,62 Since blood can be modeled basically as an aqueous solution at pH 7.4, the protonated form will be used to study the reactivity of dopamine toward free radicals in water.

First, we have performed a detailed conformational analysis of protonated dopamine (DA⁺) in water. In agreement with previous studies,(59) our results indicate that the antidistal conformer of DA⁺ has the lowest energy, while the coplanar α and β trans rotamers, although relatively stable, are more energetic.

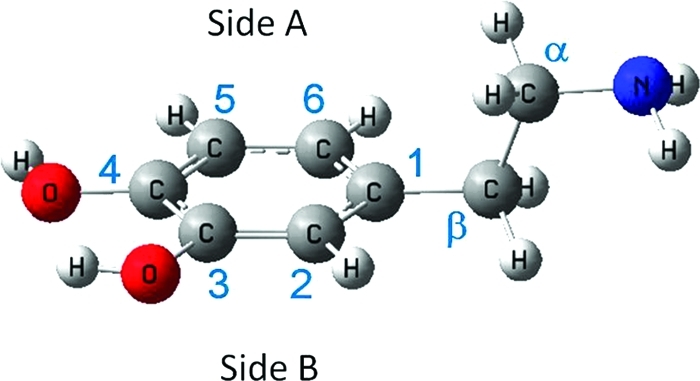
The optimized structure of protonated dopamine (DA⁺) is shown in Figure 1, where we have indicated the atomic numbering scheme. The molecule is not symmetrical with respect to the plane of the aromatic ring, and its two sides have to be differentiated in the reaction paths: sides A and B are shown in the figure.

Figure 1.

Optimized structure of protonated dopamine (DA⁺) in water.

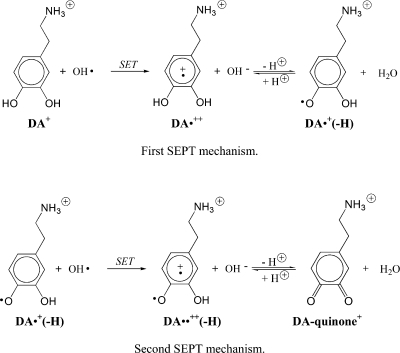
In an aqueous environment, a large number of possible reactions can occur, in principle, between (DA⁺) and free radicals. They can be grouped into two types of mechanisms: H-abstraction and radical addition (or radical adduct formation, RAF). However, H-abstraction can occur according to several different processes: direct hydrogen atom transfer (HAT), proton coupled electron transfer (PCET), or sequential electron–proton transfer (SEPT). In the particular case of the SEPT mechanism, the sequential transfer can take place in two different ways: (i) a single electron transfer (SET) process followed by deprotonation of the formed radical cation or (ii) a deprotonation followed by a SET process from the formed anion. Even though SEPT and PCET yield the same products as HAT, the influence of the solvent and of the nature of the reacting radical on their feasibility is expected to be different. While a SEPT mechanism is only possible in a polar environment that promotes solvation of the intermediate ionic species, the PCET mechanism may also be viable in a nonpolar medium since the charge separation is smaller than in SEPT.

All these channels could occur in parallel, but at different rates. One of the objectives of the present paper is to determine which mechanism has the fastest rate constant, in the reactions of dopamine with hydroxyl (•OH) and hydroperoxyl (•OOH) free radicals.

•OH Initiated Oxidation of Protonated Dopamine in Water

In the DA⁺ + •OH reaction in aqueous environment, we have considered the following H-abstraction and OH-addition pathways:

Hydroxyl radicals can abstract either the phenolic hydrogens attached to oxygens on carbons 3 and 4, or any of the aminoethyl chain hydrogens that are attached to the α and β carbons. H-abstraction from the charged amino group is highly improbable and has not been considered. Indeed, experimental results(63) show that glutathione, a molecule with two NH₃ groups analogous to the NH₃ group in dopamine, reacts with •OH by hydrogen abstraction from almost any of its carbon and sulfur atoms but not from NH₃.This unequivocally shows that NH₃, unlike NH₂ is not reactive trough radical reactions.

At this point we wish to emphasize the need to optimize stationary structures in the solvent, rather than performing single-point calculations at the gas phase geometries. In particular, in a polar solvent, the reaction involves a protonated form of dopamine, while in the gas phase only neutral dopamine exists. Thus, they cannot be compared.

In an aqueous environment, the H-abstraction from the phenolic groups is clearly barrierless, without a prereactive complex. However, using partial optimization with constrained O···H···OH bonds, we were able to obtain a structure that presents an imaginary frequency. The subsequent unfreezing of the two distances involved, followed by optimization to a saddle point, produces an increase of the H···OH distance, and a corresponding decrease of the imaginary frequency and of the gradient, leading to the separated reactants (see Figure S1 of the Supporting Information). A relaxed scan, obtained by decreasing the H···OH distance, produces an equivalent result: in this case, the energy decreases until the H atom is completely transferred. This means that the reaction is strictly diffusion-controlled; that is, every encounter results in a reaction. It is important to mention that when the •OH radical is relatively close to a phenolic H, the charge on the •OH radical oxygen atom is approximately −1.16, which is consistent with a PCET mechanism rather that a HAT mechanism. Charge separation between phenol and •OH is favored by the polar solvent. Direct HAT transition structures were also obtained for the phenolic hydrogens abstraction, but they are too high in energy to contribute to the rate constant (Figure S2). In these structures, the hydrogen atom that is being abstracted is located outside of the catechol ring symmetry plane. They are early transitions states, with rather long distances between the phenol O atoms and the radical.

Although both phenolic H-abstractions are PCET mechanisms, the corresponding rate constants are diffusion-controlled. The C3 and C4 radicals formed are very stable, presenting a large exergonicity (−37.95 and −38.91 kcal mol^–1, resvectively) relative to reactants. The interconversion reaction between product complexes PC-C3 and PC-C4 is a unimolecular process with a very small barrier (Figure 2), and its rate constant is expected to be close to the thermal rate of 5.79 × 10¹¹ s^–1. ΔG values are calculated relative to the PC-C3 product complex.

Figure 2.

Interconversion mechanism between product complexes PC-C3 and PC-C4. ΔG values are calculated relative to the PC-C3 product complex.

In the hydrogen atom transfer (HAT) pathways from α and β sites to the •OH radical, two weakly bound prereactive van der Waals complexes in the entry channel were identified, corresponding to both sides of the catechol plane (RC-A and RC-B). They are shown in Figure 2. In these structures the •OH hydrogen atom approaches the center of the ring, while its oxygen atom points at the side chain of dopamine. In RC-A, the •OH oxygen atom interacts with the Cα hydrogen atoms at a distance of 2.63 Å from the Hα-distal atoms, whereas in RC-B it interacts with the Cβ hydrogens, at 3.04 Å from the distal Hβ. They are practically the same, and in fact, it can be seen that, in an aqueous environment, they should be easily converted into each other by rotation of the side chain around the C1–Cβ axis.

Transition structures (TS) and product complexes (PC) for the α and β direct hydrogen atom transfer (HAT) reactions have been obtained. In these pathways, two possibilities arise due to different orientations with respect to the catechol OH groups (distal or proximal; see Figure 3). Abstractions of α hydrogen atoms come from RC-A, whereas those for β hydrogens initiate at RC-B. In TS-α, the OH hydrogen atom is oriented toward one of the catechol carbon atoms, while in TS-β, the •OH oxygen atom interacts with two catechol hydrogens. The presence of the amino group deactivates the α position, while the β hydrogens are favored. Cartesian coordinates of all the HAT transition structures in the protonated dopamine oxidation by •OH radicals in water are given in Table S1 of the Supporting Information.

Figure 3.

Prereactive complexes and transition structures in the α and β H-abstractions by •OH radical, in water. ΔG values at 298 K are indicated under each structure.

Relative electronic energies (including ZPE corrections) and Gibbs free energies calculated for the stationary points involved in the hydrogen atom transfer (HAT) by •OH radicals are reported in Table 1. In this table, relative energies are calculated relative to the separated reactants. ΔE₁ is the prereactive complex stabilization energy, which is calculated as ΔE₁ = E^RC – E^R; ΔE^‡ is the transition state energy, ΔE = E^TS – E^R; and ΔE is the reaction energy, ΔE = E^P – E^R. Analogously, ΔG₁ = G^RC– G^R, ΔG^‡ is the effective free energy of activation, ΔG = G^TS – G^R, and ΔG is the reaction free energy ΔG = G^P – G^R.

Table 1. Energies (Including ZPE) and Gibbs Free Energies at 298 K, in kcal mol^–1, in the HAT Hydrogen Abstractions by •OH Radicals, in Water.

path	ΔE1	ΔE‡	ΔE	ΔG1	ΔG‡	ΔG
solvent = water
Cα proximal	–2.68	3.65	–16.29	2.48	9.22	–19.74
Cα distal	–2.68	3.59	–15.97	2.48	9.51	–19.41
Cβ proximal	–2.71	0.93	–30.98	2.43	7.84	–33.73
Cβ distal	–2.71	0.86	–31.00	2.43	7.30	–33.71

All HAT reaction channels are found to be exothermic and exergonic. H-abstractions from α positions are less favored than from β positions, since the amino group is protonated, and therefore, the electron pair on the nitrogen atom does not activate the α site. Although barriers are larger, reaction energies and free energies are largest for abstraction from the phenolic groups because, in the product radicals, the unpaired electron is delocalized on the ring.

Rate constants for each HAT abstraction pathway have been calculated using eq 2, and are reported in Table 2. Transmission coefficients have been calculated at 298 K. Imaginary frequencies at the transition states are also indicated.

Table 2. Imaginary Frequencies (ν*, cm^–1) at the Transition States, Tunneling Coefficients (κ) at 298 K, TST Thermic (k^HAT, M^–1 s^–1) and Diffusion-Corrected Apparent (k_app^HAT, M^–1 s^–1) Rate Constants in the HAT Hydrogen Abstractions by •OH Radicals, in Water.

path	ν*	κ	kHAT	kappHAT
Cα proximal	–1594	14.99	3.97 × 108	2.99 × 108
Cα distal	–1647	15.83	2.56 × 108	2.12 × 108
Cβ proximal	–1125	3.39	9.22 × 108	5.25 × 108
Cβ distal	–1159	3.55	2.40 × 109	8.09 × 108

Two features of the barrier determine the extent of the tunneling factor: (i) the energy barrier, when the reactant complex is taken into account, and (ii) the barrier width, which is directly related to the imaginary frequency (ν*) associated to the transition vector. Tunneling corrections are considerably larger for Cα abstractions, due to tighter transition states.

When all the independent α and β HAT reaction paths are taken into account, it is possible to estimate the overall rate constant as the sum of all HAT individual rate constants. Thus, the overall diffusion-corrected apparent rate constant, k_app^HAT, in water is 1.84 × 10⁹ M^–1 s^–1, which is very close to the diffusion limit.

It is well-known that o-diphenolic (catecholic) compounds are oxidized to quinones via semiquinone formation, in two successive SEPT processes that eliminate protons from the phenolic groups.(64) In the SEPT mechanism, the sequential transfer can take place in two different ways: (i) a single electron transfer (SET) process followed by deprotonation of the formed radical cation or (ii) a deprotonation followed by a SET process from the formed anion. Since the polar environment is expected to promote solvation of the intermediate ionic species formed, the electron transfer process is expected to be favored.

The proposed two-step SEPT mechanism for dopamine oxidation is represented in Scheme 2.

Scheme 2. Proposed Two-Step SEPT Mechanism for Dopamine Oxidation in Water.

The reorganization energy (λ), the Gibbs free energy of activation (ΔG^‡), and the diffusion-corrected apparent rate constant (k_app^SET) of the initial single electron transfer between DA⁺ and •OH in Scheme 2 are reported in Table 3. ΔE^SET has been calculated as the nonadiabatic energy difference between reactants and vertical products, i.e., DA⁺ and OH^– in the geometries of DA⁺ and •OH. ΔG^‡ has been evaluated using the Marcus Theory. Since the subsequent proton transfer is known to be very fast, the SET and SEPT rate constants can be considered to bethe same. The diffusion rate constant k_D has been calculated according to eq 6 and is also included in this table for comparison. It is interesting to point out that, because the single electron transfer can occur when the reactants are at much larger distances than either in H-abstraction or •OH addition, the calculated diffusion limit for SET is larger. As expected, our calculations show that the SEPT process is diffusion-controlled.

Table 3. Reorganization Energy (λ, kcal mol^–1), Gibbs Free Energy of Activation (ΔG^‡, kcal mol^–1), Diffusion Rate Constant (k_D, M^–1 s^–1), SET Rate Constant (k^SET, M^–1 s^–1), and Diffusion-Corrected Apparent Rate Constant (k_app^SET, M^–1 s^–1) in the SET Mechanism, in Water .

λ	ΔG‡	kD	kSET	kappSET
12.96	2.95	8.16 × 109	4.26 × 1010	6.85 × 109

The phenolic group at the C4 position of the radical dication DA^•++ obtained via SET is relatively acid: its calculated pK_a is 7.49. Therefore, at physiological pH, an equilibrium exists between the radical dication and the radical deprotonated form, which is identical to the HAT and PCET product obtained in the C4 phenolic H-abstraction. Thus, the main product formed in the SEPT mechanism is the same as the ones obtained via HAT and PCET. Conversely, the radical obtained via H-abstraction from the phenolic groups is in equilibrium with the radical dication DA^•++ obtained via the SET mechanism. The equilibrium between the dication DA⁺⁺ and protonated dopamine depends on pH. Due to the small OH^– concentration, at neutral pH, DA^•++ is favored.

OH-addition to protonated dopamine also constitute important reaction channels that yield different ring-hydroxylated adducts. There are six possible addition centers, on carbons C1 to C6, and two possible pathways for each one, namely, from above (A) and below (B) the aromatic plane.

All reaction paths for addition of •OH to the carbon atoms in the aromatic ring of protonated dopamine have been characterized. The two sides of the molecule have been distinguished, and therefore twelve possible transition states have been obtained. Cartesian coordinates of all the RAF transition structures in the protonated dopamine oxidation by •OH radicals in water are given in Table S2 of the Supporting Information.

All additions occur in a similar way and destroy the aromaticity of the ring. The •OH radical oxygen atom approaches a carbon atom of the catechol ring. The transition vector in the transition states (TS) structures corresponds to the vertical movement of the OH group in the direction of the carbon site. The hydrogen atom or −OH groups attached to the carbon atom fold back slightly to accommodate the incoming •OH radical. All transition states are endergonic, and their ΔG^‡ values are much smaller than for HAT abstractions. In these TS, the distance between the •OH radical and the C atom ranges from 2.16 to 2.31 Å.

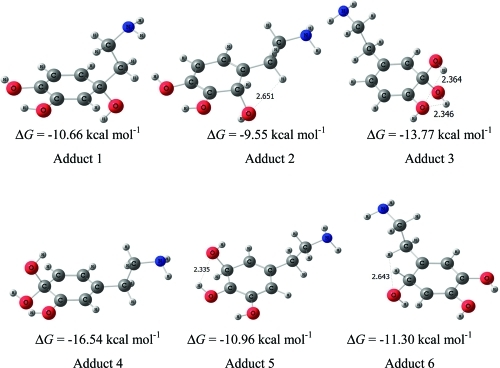
Only six adducts are formed, as the transitions states on both sides of the molecule yield the same final radical adduct. In each case, we are assuming that the most stable conformer between A and B adducts is the correct choice. Adducts are shown in Figure 4. Free energies ΔG^‡ and ΔG are given under each figure.

Figure 4.

Adducts structures in the RAF •OH-addition pathways, in water. ΔG values at 298 K are indicated under each structure.

Energies and free energies, relative to the separated reactants are given in Table 3 for all of the stationary points in the RAF pathways. All of the modeled •OH-addition channels are found to be thermodynamically feasible, with negative energy barriers. This is the typical behavior for electrophilic •OH-additions to an aromatic ring. The largest exergonicity also corresponds to •OH addition to sites 4 and 6.

Rate constants for addition pathways have been calculated at 298 K, and they are also reported in Table 4. All individual rate constants are diffusion controlled. For each carbon atom in the ring, the total addition rate constant is the sum of the rate constants for the attack on sides A and B. Then, it is possible to write the overall •OH-addition rate constant as the sum of the individual rate constants for each ring site. The calculated overall rate constant for the •OH radical addition to dopamine in water is 1.40 × 10¹⁰ M^–1 s^–1, which is larger than the diffusion limit for individual reaction channels.

Table 4. Relative Energies (Including ZPE), Gibbs Free Energies at 298 K, in kcal mol^–1, and TST Thermal (k^RAF, M^–1 s^–1) and Diffusion-Corrected Apparent (k_app^RAF, M^–1 s^–1) Rate Constants at 298 K, in the RAF •OH-Addition Reactions, in Water.

path	ΔE‡	ΔE	ΔG‡	ΔG	kRAF	kappRAF
solvent = water
C1 A	–0.33	–18.69	6.41	–11.62	3.04 × 109	8.706 × 108
C1 B	–1.91		4.70		5.45 × 1010	1.193 × 109
C2 A	–0.52	–16.51	4.99	–10.40	3.34 × 1010	1.177 × 109
C2 B	–1.31		4.92		3.76 × 1010	1.182 × 109
C3 A	–2.09	–22.21	5.02	–15.43	3.18 × 1010	1.175 × 109
C3 B	–2.10		4.83		4.38 × 1010	1.187 × 109
C4 A	–2.19	–22.00	4.32	–15.09	1.03 × 1011	1.206 × 109
C4 B	–2.96		2.49		2.27 × 1012	1.219 × 109
C5 A	–0.89	–17.24	5.38	–10.85	1.73 × 1010	1.140 × 109
C5 B	–0.79		4.92		3.76 × 1010	1.182 × 109
C6 A	–2.13	–18.01	4.02	–11.27	1.72 × 1011	1.211 × 109
C6 B	–2.36		3.57		3.67 × 1011	1.216 × 109

Overall Rate Constant in the •OH Initiated Oxidation of Protonated Dopamine in Water

The overall rate constant, which measures the rate of •OH disappearance, has been estimated by summing up the total rate coefficients calculated for all of the competing mechanisms

Each term includes all channels of the same type. Thus, the calculated overall diffusion-corrected apparent rate constant in the DA⁺ + •OH radical in aqueous solution is equal to 2.51 × 10¹⁰ M^–1 s^–1.

Direct reaction branching ratios (Γ), are computed as

and are reported in Table 5.

Table 5. Diffusion-Corrected Apparent Rate Constants, in M^–1 s^–1, and Direct Branching Ratios (Γ) in the DA⁺ + •OH Reaction in Water.

path	kapp	Γ, %
solvent = water
SEPT	6.85 × 109	27.3
PCET	2.44 × 109	9.7
HAT	1.84 × 109	7.3
RAF	1.40 × 1010	55.8

Since all mechanisms are diffusion-controlled, there might be a significant difference between the kinetic site reactivity and the products that are expected to prevail under equilibrium conditions. It can be seen that the C4 deprotonated DA⁺(-H)• is the only product that is obtained in the SEPT and PCET mechanisms, with the interconversion represented in Figure 2. Therefore, the total rate constant for the formation of DA⁺(-H)• is the sum of the individual rate constants for these pathways: 9.29 × 10⁹ M^–1 s^–1. This result is larger than any individual HAT or RAF rate constants, but lower than the sum of the HAT rate constants (which is the sum of four H-abstractions from α and β sites) and also much lower than the sum of the RAF rate constants (which is the sum of six adduct formation reactions, all with similar rate constants). This allows us to conclude that the main H-abstraction product, DA⁺(-H)•, is the major individual product obtained in the whole reaction, with a branching ratio of 37%, as calculated according to the branching ratios given in Table 5.

•OOH Initiated Oxidation of Protonated Dopamine in Water

As in the preceding section, in order to study the reactivity of protonated dopamine toward •OOH radicals in aqueous environment, we have considered all possible H-abstraction and RAF (•OOH addition) reaction pathways.

The thermochemical feasibility of the different mechanisms and channels of reaction was investigated first, since it determines the viability of chemical processes. The relative energies (ΔE) and Gibbs free energies of reaction (ΔG) for all of the studied channels are reported in Table S3 of the Supporting Information. Results are very different than the ones obtained with the •OH radical. In the present case, most reactions are endergonic, and only hydrogen abstractions from the phenolic groups are significanty exergonic. β-Hydrogen abstractions are also possible, though the corresponding ΔG values are almost zero. The difference in reactivity between •OH and •OOH radicals can be directly related to the electron-accepting character of the reacting radical, which is in turn related to the much stronger O–H bond energy in water, as compared with the one of hydrogen peroxide.

The reaction channels described above as endergonic or almost zero will not be considered in this work. Based on the Bell–Evans–Polanyi principle, they are not expected to occur at comparable rates. Moreover, they would be reversible, and therefore, the formed products would not be observed. Thus, in the following discussion, only C3 and C4 HAT hydrogen abstraction pathways will be studied in detail.

The prereactive complexes and transition states corresponding to the C3 and C4 phenolic H-abstraction pathways are shown in Figure 5. In the prereactive complexes, the terminal oxygen in the •OOH radical approaches either one of the phenolic hydrogen atoms. The •OOH radical is located in the plane of the catechol ring and forms a strong hydrogen bond with a phenolic group, and another interaction with a H atom of the ring. The transition state structures are approximately perpendicular to the catechol ring plane.

Figure 5.

Prereactive complexes and transition structures in the HAT H-abstractions by •OOH radical, in water. ΔG values at 298 K are indicated under each structure.

Energies and free energies, relative to the separated reactants, are given in Table 6 for all of the stationary points along the phenolic H-abstraction pathways. Reaction barriers are much higher than the ones of the corresponding •OH phenolic H-abstractions. Again, the C4 H-abstraction is favored over the C3 pathway.

Table 6. Relative Energies (Including ZPE) and Gibbs Free Energies at 298 K, in kcal mol^–1, in the Phenolic H-Abstractions by •OOH Radicals, in Water.

path	ΔE1	ΔE‡	ΔE	ΔG1	ΔG‡	ΔG
solvent = water
C3	–1.94	7.41	–5.48	5.12	16.16	–7.28
C4	–2.05	6.95	–5.98	5.42	15.17	–8.23

The values of the rate coefficients for the phenolic hydrogen abstractions are reported in Table 7. Since rates are much slower than diffusion, in this case, no diffusion correction is applied. Tunneling is very large, in agreement with the calculated large imaginary frequencies, an indication of a high and narrow barrier. This is typical of a relatively large O···H···O barrier due to hydrogen bonds present in the entrance and exit complexes.(65) Branching ratios (Γ) are also reported in Table 7.

Table 7. Imaginary Frequencies (ν*, cm^–1) at the Transition States, Tunneling Coefficients (κ), TST Thermal (k, M^–1 s^–1) Rate Constants, and Branching Ratios (Γ) at 298 K, and in the Phenolic H-Abstractions by •OOH Radicals, in Water.

path	ν*	κ	k	Γ, %
solvent = water
C3	–2113	144.2	3.10 × 104	∼14
C4	–2106	168.8	1.92 × 105	∼86

As discussed in the case of the corresponding reaction with an •OH radical, an interconversion is expected to occur between the C3 and C4 products, and only the latter should be formed to a significant extent. The predicted high selectivity of this reaction suggests that the product C4 radical formed should be an intermediate in the overall oxidation of dopamine by •OOH and similar radicals.

The rate constant for the SEPT mechanism has also been obtained. As in Table 4, k_D has been calculated using eq 5. ΔE^SET has been calculated as the nonadiabatic energy difference between reactants and vertical products, i.e., DA^•+ and OOH^– at the DA⁺ and •OOH geometries, respectively. In contrast to what was observed in the case of •OH, the calculated Gibbs free energy of activation (ΔG^‡) in the SEPT mechanism is 24.04 kcal mol^–1, which is much larger than in the phenolic H-abstraction. Thus, the resulting rate constant for this mechanism is totally negligible when compared to the one for phenolic hydrogen abstractions, and it can be ruled out.

The total rate coefficient for the DA⁺ + •OOH radical reaction in aqueous solution is calculated as the sum of the phenolic H-abstraction rate constants

This rate constant is a hundred thousand times smaller than the one for reaction of DA⁺ with an •OH radical, but it is still very fast. Moreover, since the •OOH half-life time is several orders larger(31) than the one of the •OH radical, these reactions should still contribute significantly to dopamine oxidation.

Part 2. Dopamine Oxidation in Pentylethanoate

In a nonpolar medium, dopamine exists mainly in its neutral form. Pentylethanoate was chosen as solvent to mimic a lipidic environment. Again, we have performed a complete conformational analysis of neutral dopamine structures. Our results indicate that the antidistal conformer has the lowest energy, in agreement with previous studies.(59) The optimized structure of neutral dopamine (DA) is shown in Figure 6, together with the atomic numbering. The molecule is not symmetrical with respect to the plane of the aromatic ring, and its two sides have to be differentiated in the reaction paths: sides A and B are shown on the figure.

Figure 6.

Optimized structure of neutral dopamine (DA) in pentylethanoate.

As in part I of this work, in order to study the global reactivity of neutral dopamine toward hydroxyl (•OH) and hydroperoxyl (•OOH) radicals in a lipidic environment, all possible reaction mechanisms have been studied in detail.

•OH Initiated Oxidation of Neutral Dopamine in Pentylethanoate

In the •OH initiated oxidation of dopamine in pentylethanoate, we have considered the following H-abstraction and OH-addition pathways:

Direct hydrogen atom transfer (HAT) mechanisms corresponding to phenolic and chain (α and β) H-abstraction by •OH radicals have been identified. However, in a nonpolar solvent, another pathway is possible, which corresponds to a H-abstraction from the amino −NH₂ group.

Prereactive complexes and transition state structures corresponding to the phenolic H-abstraction pathways, in pentylethanoate are shown in Figure 7. In the prereactive structures (RC-C3 and RC-C4), the •OH oxygen atom approaches the catechol plane in the direction of the phenolic hydrogen to be abstracted, at a distance of 1.934 Å. In the phenolic HAT transition state structures (Figure 7), the hydrogen atom that is being abstracted is located outside of the catechol ring symmetry plane. They are early transitions states, with rather long distances between the phenol O atoms and the radical. Their activation free energies are smaller than the corresponding ones in aqueous solution. While in water the transition state is less solvated than the individual reactants, in pentylethanoate the effect is less pronounced, because the solvent is less polar, in agreement with the “polar paradox”(66) that states that, for radical reactions, polar substances react faster in non polar solvents and viceversa.

Figure 7.

Prereactive complexes and transition structures in the phenolic H abstractions by •OH radicals, in pentylethanoate. ΔG values at 298 K are indicated under each structure.

Prereactive complexes and transition state structures in the α and β H-abstraction pathways, in pentylethanoate, are shown in Figure 8. For these pathways, two weakly bound prereactive van der Waals complexes in the entry channel were identified (RC-A and RC-B), on both sides of the catechol plane and with •OH pointing in the direction of the center of the ring. In RC-A, the •OH oxygen atom interacts with the Cα hydrogen atoms at a distance of 2.53 Å from the Hα-distal, while in RC-B it interacts with the Cβ hydrogens, at 2.87 Å from the distal Hβ.

Figure 8.

Prereactive complexes and transition structures in the α and β H-abstractions by •OH radical, in pentylethanoate. ΔG values at 298 K are indicated under each structure.

Prereactive complexes and transition state structures in the amino H-abstraction pathway, in pentylethanoate, are shown in Figure 9. In the prereactive complex (RC-NH₂), the H atom of the •OH radical approaches the nitrogen atom of the amino group of neutral dopamine, forming a strong hydrogen bond at a distance of 1.789 Å. RC-NH₂ is much more stable than any of the other prereactive complexes, and it even has a distinctly negative ΔG₁ value. The HAT transition structure arising from this prereactive complex occurs very early in the reaction, as observed in other hydrogen abstraction from amines.(67)

Figure 9.

Prereactive complex and transition structure in the •OH amino H-abstraction pathway, in pentylethanoate. ΔG values at 298 K are indicated under each structure.

Cartesian coordinates of all the HAT transition structures in the neutral dopamine oxidation by •OH radicals in pentylethanoate are given in Table S4 of the Supporting Information.

All relevant energy and free energy values for the HAT H-abstraction pathways in pentylethanoate are reported in Table 8. It can be seen that all of the hydrogen abstraction pathways are possible, moreover, their reaction free energies are even larger than in the case of protonated dopamine. In terms of reaction free energies, the phenolic H-abstractions are clearly favored, but all energy barriers are very low. In the gas phase, the reaction between OH radicals and neutral dopamine presents a 8.20 and 3.64 kcal mol^–1 barrier for the C3 and C4 H abstraction, respectively, and they are very different than the ones obtained in pentylethanoate. In pentylethanoate, the Cα distal transition state barrier is the lowest, both in terms of energy and free energy.

Table 8. Relative Energies (Including ZPE) and Gibbs Free Energies at 298 K, in kcal mol^–1, in the HAT Hydrogen Abstractions by •OH Radical, in Pentylethanoate.

path	ΔE1	E‡	ΔE	ΔG1	ΔG‡	ΔG
solvent = pentylethanoate
C3	–2.62	1.39	–38.26	1.76	7.72	–41.20
C4	–2.70	0.19	–39.27	1.63	6.32	–42.46
Cα proximal	–2.98	0.30	–27.02	2.16	6.19	–30.31
Cα distal	–2.98	–0.50	–27.02	2.16	5.22	–30.30
Cβ proximal	–3.13	0.84	–30.09	1.36	6.35	–33.61
Cβ distal	–3.13	1.03	–30.03	1.36	6.62	–33.90
C NH2	–7.13	0.33	–17.99	–2.30	6.17	–21.42

Rate constants and transmission coefficients for all HAT pathways in pentylethanoate have been calculated at 298 K. They are reported in Table 9. In agreement with the barrier values in the preceding table, abstraction of the hydrogen atom attached to Cα in a distal position presents the largest rate constant. Abstraction of the amino hydrogens is also very fast, and yields products that are definitely different than in water. Except for abstraction from C3, all other pathways have rate constants in the diffusion limit. Abstraction of β hydrogens is somewhat less favored than α hydrogens due the activation of the α position by the electronic pair on the nitrogen atom.

Table 9. Imaginary Frequencies (ν*, cm^–1) at the Transition States, Tunnelling Coefficients (κ), and TST Thermal (k^HAT, M^–1 s^–1) and Diffusion-Corrected Apparent (k_app^HAT, M^–1 s^–1) Rate Constants, at 298 K, in the HAT Hydrogen Abstractions by •OH Radical, in Pentylethanoate.

path	ν*	k	kHAT	kappHAT
solvent = pentylethanoate
C3	–844	2.22	7.35 × 108	4.59 × 108
C4	–1409	4.44	1.56 × 1010	1.13 × 109
Cα proximal	–1123	3.27	1.43 × 1010	1.12 × 109
Cα distal	–697	1.77	3.98 × 1010	1.18 × 109
Cβ proximal	–688	1.81	6.05 × 109	1.01 × 109
Cβ distal	–679	1.79	3.79 × 109	9.23 × 108
C NH2	–757	2.07	9.38 × 109	1.08 × 109

The overall diffusion-corrected HAT rate constant in the H-bstraction by •OH radical in pentylethanoate is 6.90 × 10⁹ M^–1 s^–1, which is larger than the estimated individual diffusion limiting rate constants calculated for this solvent according to eq 5.

All possible •OH additions to the carbon atoms in the aromatic ring of neutral dopamine in pentylethanoate have been also characterized. They are very similar to the ones calculated for protonated dopamine in water, and destroy the aromaticity of the ring. Cartesian coordinates of the twelve RAF transition structures in the neutral dopamine oxidation by •OH radicals in water are given in Table S5 of the Supporting Information. Their corresponding adducts are shown in Figure 10.

Figure 10.

Adducts structures in the RAF •OH-addition pathways, in pentylethanoate. ΔG values at 298 K are indicated under each structure.

Relative energies, Gibbs free energies and rate constants in the DA + •OH radical adduct formation pathways in pentylethanoate are reported in Table 10.

Table 10. Relative Energies (Including ZPE), Gibbs Free Energies at 298 K, in kcal mol^–1, and TST Thermal (k^RAF, M^–1 s^–1) and Diffusion-Corrected Apparent (k_app^RAF, M^–1 s^–1) Rate Constants at 298 K, in the RAF •OH-Addition Reactions in Pentylethanoate.

path	ΔE‡	ΔE	ΔG‡	ΔG	kRAF	kappRAF
solvent = pentylethanoate
C1 A	1.73	–17.67	8.60	–10.66	7.49 × 107	7.06 × 107
C1 B	0.14		6.72		1.79 × 109	7.25 × 108
C2 A	1.57	–16.30	7.82	–9.55	2.80 × 108	2.27 × 108
C2 B	0.29		6.42		2.97 × 109	8.65 × 108
C3 A	–0.14	–20.32	6.33	–13.77	3.46 × 109	9.02 × 108
C3 B	–0.16		5.88		7.39 × 109	1.05 × 109
C4 A	–2.96	–22.96	2.90	–16.54	1.13 × 1012	1.22 × 109
C4 B	–2.71		3.28		5.95 × 1011	1.22 × 109
C5 A	–0.43	–17.67	5.88	–10.96	7.39 × 109	1.05 × 109
C5 B	–0.42		5.74		9.36 × 109	1.08 × 109
C6 A	–0.26	–17.99	6.13	–11.30	4.85 × 109	9.75 × 108
C6 B	–3.15		1.76		7.74 × 1012	1.22 × 109

All addition pathways present negative reaction free energies at 298 K, the most favored one corresponding to addition to C4, followed by addition to C3. In both cases, the •OH radical adds to a carbon atom that already has an OH group, thus allowing for a stabilizing interaction in the adduct. However, by far, the smallest free energy barrier corresponds to addition to C6 from the B side: this reaction could promote the formation of the observed neurotoxic product, 6-hydroxydopamine.

Rate constants have been calculated at 298 K, and they are also reported in Table 10. In pentylethanoate, all OH-addition rate constants are very close, and they contribute about equally to the overall rate constant. The total OH-addition rate constant is 1.06 × 10¹⁰ M^–1 s^–1, which is larger than the individual diffusion limit rate constants.

Overall Rate Constant in the •OH Initiated Oxidation of Neutral Dopamine in Pentylethanoate

The total rate constant in the •OH initiated oxidation of neutral dopamine in pentylethanoate has been estimated by summing up the total diffusion-corrected rate coefficients calculated for all the HAT and RAF competing mechanisms:

This approach implies that, once the system engages a specific channel, it proceeds to completion, independently of the other pathways; that is, there is no mixing or crossover between different pathways. Thus, the calculated overall diffusion-corrected rate constant in the dopamine + •OH radical in pentylethanoate is equal to 1.75 × 10¹⁰ M^–1 s^–1.

The direct reaction branching ratios (Γ) are computed as

and are reported in Table 11.

Table 11. Diffusion-Corrected Apparent Rate Constants, in M^–1 s^–1, and Direct Branching Ratios (Γ) in the DA + •OH Reaction in Pentylethanoate.

path	kapp	Γ, %
solvent = pentylethanoate
HAT	6.90 × 109	39.4
RAF	1.06 × 1010	60.6

•OOH Initiated Oxidation of Neutral Dopamine in Pentylethanoate

For the reaction of neutral dopamine (DA) with •OOH radicals we have considered all possible H-abstraction and OH-addition pathways, according to following equations:

The relative energies (ΔE) and Gibbs free energies of reaction (ΔG) for all channels are reported in Table S6 of the Supporting Information. As in the case of reactions in water, it can be seen that most reactions are endergonic, and only hydrogen abstractions from the phenolic groups are exergonic. β-hydrogen abstractions are also possible, though the corresponding ΔG values are almost zero. Again, reaction channels described as endergonic or almost zero will not be considered in this work. Thus, in the following discussion, only C3 and C4 phenolic hydrogen abstraction pathways will be studied in detail.

Prereactive complexes and transition state structures in the HAT phenolic H abstraction reactions by •OOH radicals, in pentylethanoate, are shown in Figure 11. The geometrical features are similar to the ones obtained in water. Energies and free energies, relative to the separated reactants, are given in Table 12 for all stationary points along the phenolic H-abstraction pathways. As in an aqueous environment, the C4 pathway is favored over the C3 pathway. Values of the rate coefficients for the phenolic •OOH hydrogen abstractions in pentylethanoate are reported in Table 13, together with the direct branching ratios (Γ).

Figure 11.

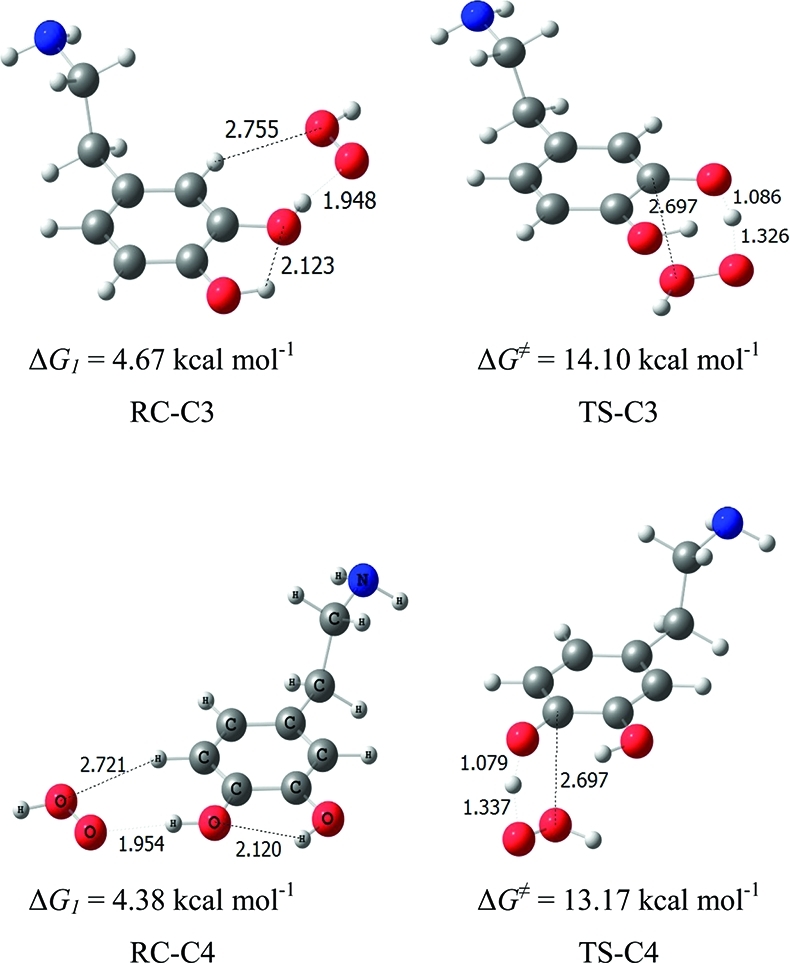
Prereactive complexes and transition structures in the phenolic H-abstractions by •OOH radicals, in pentylethanoate. ΔG values at 298 K are indicated under each structure.

Table 12. Relative Energies (Including ZPE) and Gibbs Free Energies at 298 K, in kcal mol^–1, in the Phenolic H Abstractions by •OOH Radical, in Pentylethanoate.

path	ΔE1	ΔE ddr	ΔE	ΔG1	ΔG‡	ΔG
solvent = pentylethanoate
C3	–2.19	6.51	–5.64	4.67	14.10	–7.81
C4	–2.21	5.93	–6.65	4.38	13.17	–9.07

Table 13. Imaginary Frequencies (ν*, cm^–1) at the Transition States, Tunneling Coefficients (κ), TST Thermal (k, M^–1 s^–1) Rate Constants, and Branching Ratios (Γ) at 298 K, in the Phenolic H-Abstractions by •OOH Radical, in Pentylethanoate.

path	ν*	κ	k	Γ, %
solvent = pentylethanoate
C3	–16.89	27.06	1.88 × 105	∼23
C4	–16.01	18.74	6.28 × 105	∼77

The total rate coefficient for the •OOH initiated oxidation of neutral dopamine in pentylethanoate is calculated as the sum of the phenolic H-abstractions

Conclusions

In this work, we have carried out a systematic study of the reactivity of dopamine toward hydroxyl (•OH) and hydroperoxyl (•OOH) radicals in aqueous and lipidic simulated environments, using density functional quantum chemistry and computational kinetics.

All possible mechanisms have been considered: hydrogen atom transfer (HAT), radical adduct formation (RAF), proton coupled electron transfer (PCET), and sequential electron proton transfer (SEPT). Rate constants have been calculated using Conventional Transition State Theory in conjunction with the Collins–Kimball theory. Branching ratios for the different paths contributing to the overall reaction, at 298 K, are reported.

It is important to note the importance of optimizing structures in the solvent, rather than performing single- point calculations at the gas phase geometries. However, while in the gas phase only neutral dopamine exists, the water reaction involves a protonated form of dopamine. Thus, they cannot be compared. When the structures are calculated in water, the phenolic H-abstraction channels are clearly barrierless.

For the global reactivity of dopamine toward •OH radicals in water at physiological pH, several mechanisms contribute to the overall rate constant in the following proportions: 27.3% for SEPT, 9.7% for PCET, 7.3% for all HAT channels, and 55.8% for all RAF. However, because HAT and RAF channels yield a variety of products, and SEPT and PCET yield the same C4 deprotonated DA⁺(-H)• product, the latter turns out to be the major reaction product, corresponding to about 36%.

As expected for polyphenols in water, the PCET H-abstraction is much faster than HAT; in the present case the SEPT mechanism leads to the same product and is even faster. In a lipidic environment, our results indicate that •OH will react with dopamine to generate a mixture of all the possible products.

The calculated overall diffusion-corrected rate constant for DA⁺ + •OH in an aqueous solution is equal to 2.51 × 10¹⁰ M^–1 s^–1, whereas the overall rate constant for DA + •OH in pentylethanoate is smaller, and equal to 1.75 × 10¹⁰ M^–1 s^–1. Moreover, it is clear that, independently of the cellular environment and the particular reaction path, dopamine always reacts with •OH radicals at a rate that is diffusion-controlled. This explains why dopamine is a very unselective but excellent scavenger of •OH radicals.

Regarding the efficiency of dopamine as an •OOH radicals scavenger, it is predicted to react with •OOH radicals about 3.6 imes faster in lipid media than in an aqueous solution. Since the solubility of dopamine is higher in polar than in nonpolar media, this ratio is in line with the previously proposed “polar paradox”.(66)

We find that abstraction from the phenolic groups is the only feasible •OOH reaction mechanism, regardless of the polarity of the environment. The total rate coefficients are predicted to be 2.23 × 10⁵ and 8.16 × 10⁵ M^–1 s^–1, in aqueous and lipid media, respectively, almost a hundred thousand times smaller than the ones for reactions of dopamine with •OH radicals, but still quite fast. Since the •OOH half-life time is several orders larger(31) than the one of the •OH radical, these reactions should contribute significantly to dopamine oxidation.

The •OOH scavenger activity of dopamine is predicted to be similar to that of carotenes, higher than that of allicin and much higher than that of melatonin. We can conclude that dopamine acts as a very efficient •OOH, and presumably •OOR radical scavenger.

It is important to notice that the mechanism of the oxidation of dopamine strongly depends on the nature of the radical and on the solvent. As previously reported for curcumin,(68) dopamine is capable of reacting with radicals according to almost any type of mechanism, depending on conditions. This seems to be the case for phenols in general. In contrast, this behavior is not possible for saturated antioxidants such as glutathione.(69)

In conclusion, this work provides new data on the global reactivity of dopamine toward endogenous free radicals under oxidative stress conditions. In particular, it gives information on dopamine oxidation pathways and predicts the proportion of the formed products in two types of model biological environment.

Supporting Information Available

Cartesian coordinates of stationary points. Relative energies (ΔE) and Gibbs free energies of reaction (ΔG). This material is available free of charge via the Internet at http://pubs.acs.org.