Abstract
Motivation: A number of computational methods have been proposed that predict protein–protein interactions (PPIs) based on protein sequence features. Since the number of potential non-interacting protein pairs (negative PPIs) is very high both in absolute terms and in comparison to that of interacting protein pairs (positive PPIs), computational prediction methods rely upon subsets of negative PPIs for training and validation. Hence, the need arises for subset sampling for negative PPIs.
Results: We clarify that there are two fundamentally different types of subset sampling for negative PPIs. One is subset sampling for cross-validated testing, where one desires unbiased subsets so that predictive performance estimated with them can be safely assumed to generalize to the population level. The other is subset sampling for training, where one desires the subsets that best train predictive algorithms, even if these subsets are biased. We show that confusion between these two fundamentally different types of subset sampling led one study recently published in Bioinformatics to the erroneous conclusion that predictive algorithms based on protein sequence features are hardly better than random in predicting PPIs. Rather, both protein sequence features and the ‘hubbiness’ of interacting proteins contribute to effective prediction of PPIs. We provide guidance for appropriate use of random versus balanced sampling.
Availability: The datasets used for this study are available at http://www.marcottelab.org/PPINegativeDataSampling.
Contact: yungki@mail.utexas.edu; marcotte@icmb.utexas.edu
Supplementary Information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
Protein–protein interactions (PPIs) underlie many processes essential to living organisms. Years of small-scale experimental work, along with genome-wide studies powered by high-throughput techniques (e.g. Gavin et al., 2006; Ito et al., 2001; Krogan et al., 2006; Tarassov et al., 2008; Uetz et al., 2000; Yu et al., 2008) have generated significant numbers of known PPIs, which provide a good foundation on which to learn protein sequence features that distinguish interacting protein pairs from non-interacting ones. In general, this has been a difficult and largely unsolved computational problem, exascerbated by strong biases in available datasets, including redundant interactions and skewed amino acid compositions in well-represented protein complexes (e.g. the ribosome). Nonethless, diverse computational methods have been developed that predict PPIs using protein sequence features (Ben-Hur and Noble, 2005; Bock and Gough, 2001; Chou and Cai, 2006; Gomez et al., 2003; Guo et al., 2008; Martin et al., 2005; Nanni and Lumini, 2006; Pitre et al., 2008; Roy et al., 2009; Shen et al., 2007; Sprinzak and Margalit, 2001; Yu et al., 2010a).
As with all computational prediction methods, improvements to datasets used for testing and training can strongly affect the quality of the predictions. It is thus critical that protein sequence feature-based PPI prediction methods be validated with appropriate positive and negative datasets. Since the numbers of high-confidence positive PPIs are still relatively modest, especially in comparison to the numbers of potential negative examples, most studies have used as much of the positive PPI data as possible. High-quality negative PPI data are equally important for learning and validation processes. Unfortunately, such data are not widely available, although a new database has begun to archive such data (Smialowski et al., 2010). Therefore, a typical strategy has been to employ protein pairs that are not previously known to interact as the set of negative PPIs. This is generally a reasonable assumption given that negative PPIs outnumber positive ones by a factor of hundreds to thousands.
More specifically, let us say that we have P protein pairs known to interact and the P protein pairs involve K different proteins. Then, there are K(K−1)/2 possible protein pairs. The P pairs known to interact serve as positive examples for predicting new interactions. The remaining N protein pairs, dominated by true negative interactions, are assumed not to interact (in general) and serve as negative examples, where N=K(K−1)/2− P. Usually, P≪N and P is of a manageable magnitude whereas N is not. For many algorithms, cross-validating predictive algorithms on the complete set of K(K−1)/2 protein pairs (consisting of P positive PPIs and N negative ones) is not feasible simply because it is too immense. Thus, sampling subsets, especially of negative PPIs, is routine practice.
Typically, one might want an unbiased subset of negative PPIs of size n, where n is of a manageable magnitude. Cross-validated test results on the set combining P positive PPIs and n negative ones are then assumed to generalize to the whole set of K(K−1)/2 protein pairs because the negative subset used for cross-validation is an unbiased representative of the N negative PPIs. This type of subset sampling—for cross-validated testing—aims to create unbiased subsets of negative PPIs such that predictive performance estimated with them can be safely assumed to generalize to the population level. Importantly, biased subsets of negative PPIs for cross-validation will likely fail to generalize to population levels, as has been previously demonstrated (Ben-Hur and Noble, 2006).
Negative PPI subsampling also arises in a second distinct context: let us assume that the size of our unbiased negative subset is 100 times larger than the set of positive PPIs (i.e. n=100P). (Note that this ratio of positive and negative PPIs is conservative for most organisms, but employing negative subsets of a size significantly greater than 100P is also not routinely feasible because of practical computational issues such as memory requirements and computation time.) In a typical cross-validated training approach, the training data would be highly skewed, with negative examples represented 100 times more than positive ones. Such high skew often adversely affects predictive algorithms, for example, leading to trivial predictions of all negatives that achieve 99% prediction accuracy. As algorithms such as support vector machines (SVMs) scale poorly with the amount of training data (Park, 2009), subset sampling of negative PPIs for the purposes of training—a distinct context from cross-validated testing—offers substantial advantages.
Clearly, the purpose of subset sampling for training differs from that of subset sampling for cross-validated testing. In subset sampling for cross-validation, one desires unbiased subsets representative of the overall population such that predictive performance estimated with them can be safely assumed to generalize to that population. In subset sampling for training, however, one is concerned about getting subsets most suitable for effective training of prediction algorithms. A lack of bias is the key to subset sampling for cross-validation whereas it may not be to subset sampling for training.
Traditionally, random sampling has been used for subset sampling for cross-validation, in which one randomly and uniformly samples negative PPIs. Recently, Yu et al. (2010b) argued against the suitability of random sampling. Instead, they proposed balanced sampling, in which the number of occurrences of a protein in the negative PPI subset is forced to match that in the positive PPI set. Using this approach, they concluded that PPI prediction algorithms employing protein sequence features perform hardly better than chance.
In this study, we demonstrate that balanced sampling for cross-validation generates highly biased negative subsets and that the predictive performance estimated with them does not generalize to populations. We demonstrate that, as a result, the predictive performances of PPIs estimated using balanced sampling are considerable underestimates, and the conclusions of Yu et al. (2010b) regarding PPI algorithm performance are invalid. Nonetheless, balanced sampling does offer advantages for the purposes of training, as we show with tests that isolate these distinct applications of sampling. In particular, we measure the relative contribution of representational bias of hub proteins in PPI sets to training, versus the contribution of protein sequence features themselves, and we show using balanced sampling that both contribute to effective PPI predictive performance. We conclude that protein sequence features are indeed informative for predicting PPIs, and we provide some guidance for implementing random versus balanced sampling in this context.
2 DATA AND METHODS
2.1 Datasets
Yeast PPI data were collected from the Saccharomyces cerevisiae core subset (‘Scere20080708.txt’) of the Database of Interacting Proteins (Salwinski et al., 2004). Human PPI data were collected from release 7 of the Human Protein Reference Database (Keshava Prasad et al., 2009). The PPI data were refined as follows: first, a non-redundant subset was generated at the sequence identity level of 40% by clustering analysis using the CD-HIT program (Li and Godzik, 2006). Second, proteins with lengths less than 50 amino acids were removed. These filters resulted in 3867 positive PPIs for yeast and 17 431 for human.
2.2 Cross-validation
For the algorithms employed in this study, a population-level cross-validation involving all relevant positive PPIs (e.g. 17 431 PPIs for human) was not computationally feasible. For this reason, we randomly chose three different independent sets of proteins of comparable sizes. For each set, the population was defined as all protein pairs in the set. For yeast, the sets involve approximately 1500 proteins with approximately 2900 positive and 1 119 000 negative PPIs. For human, the sets involve approximately 2000 proteins with approximately 5000 positive and 2 000 000 negative PPIs. For the population-level cross-validation results in Table 1, a 10-fold cross-validation was carried out. In each round of the 10-fold cross-validation, we had >300-fold more negative than positive examples in the training data. To generate a training set with reduced skew, random sampling was employed to sample a negative training subset of equal size to that of the unsampled positive training dataset (i.e. we used random sampling to sample subsets for training purposes). For the subset-based cross-validation results in Table 1, a given sampling technique was used to generate subsets for cross-validation. Then, the sampled negative subset was combined with positive PPI data for a 10-fold cross-validation. Each analysis in Table 1 includes 30 different test instances (3 independent protein sets × 10-fold cross-validation).
Table 1.
Similarity of random and balanced subsets with populations and comparison of population-level predictive performance with that estimated with sampled subsets
| Prediction algorithm | Yeast |
||
|---|---|---|---|
| Population | Random subsets | Balanced subsets | |
| M1 | 0.71 ± 0.02 | 0.70 ± 0.02 | 0.42 ± 0.02 |
| M2 | 0.67 ± 0.02 | 0.66 ± 0.02 | 0.52 ± 0.02 |
| M3 | 0.57 ± 0.01 | 0.57 ± 0.02 | 0.53 ± 0.02 |
| M4 | 0.71 ± 0.02 | 0.71 ± 0.02 | 0.62 ± 0.02 |
| Similarity to population | 0.00 ± 0.03 | −0.71 ± 0.01 | |
| Prediction algorithm | Human |
||
| Population | Random subsets | Balanced subsets | |
| M1 | 0.72 ± 0.01 | 0.72 ± 0.01 | 0.45 ± 0.01 |
| M2 | 0.67 ± 0.01 | 0.67 ± 0.01 | 0.49 ± 0.02 |
| M3 | 0.58 ± 0.01 | 0.58 ± 0.02 | 0.51 ± 0.02 |
| M4 | 0.72 ± 0.01 | 0.71 ± 0.01 | 0.63 ± 0.02 |
| Similarity to population | 0.02 ± 0.01 | −1.00 ± 0.00 | |
Similarity is reported in the form of the average correlation coefficient ± the standard deviation. Predictive performance is reported in the form of the average AUC ± the standard deviation.
Predictive performance was estimated by AUC [area under the ROC (receiver operating characteristic) curve] and recall–precision plots.
2.3 Method implementation
Four different protein sequence feature-based PPI prediction methods were used for the study:
M1: the signature product-based method proposed by Martin et al. (2005).
M2: the method developed by Guo et al. (2008). A feature vector of a protein sequence comprises its auto-correlation values of seven different physicochemical scales.
M3: the method introduced by Shen et al. (2007). In this method, a protein sequence is represented by a reduced set of amino acids. Then, the normalized counts of each possible conjoint triad become its feature vector.
M4: PIPE2 developed by Pitre et al. (2008). For a pair of proteins, PIPE2 looks for the co-occurrences of subsequences in protein pairs that are known to interact. PIPE2 does not require negative examples for its learning.
M1 and M3 were implemented using SVMlight as modified by Martin et al. (2005) and Joachims (1999). M2 was implemented by modifying the code of libsvm (Chang and Lin, 2011). M4 was implemented by downloading the source code of PIPE2 from the developers' website.
3 RESULTS AND DISCUSSION
3.1 The balanced sampling technique produces highly biased subsets
For a given set of positive PPIs, the space of negative PPIs is formed by pairing proteins appearing in the positive set and for which there is no interaction information yet. Thus, the number of times a protein appears in positive PPI data is inversely correlated with the number it appears in negative PPI data. The balanced sampling technique enforces the number of times a protein appears in positive PPI data to match that in negative PPI data. Hence, balanced sampling is guaranteed to produce biased subsets.
We first measured the extent of this bias by sampling negative subsets twice—once using the random sampling technique and the other time using the balanced sampling technique. The similarity between a sampled subset and the corresponding population was then measured as follows. A set of protein pairs (e.g. either sampled subsets or populations) was characterized by the frequencies of appearance of proteins in the set, as proposed by Yu et al. (2010b). The similarity between two sets of protein pairs was defined as the Pearson's correlation coefficient between their protein-appearance frequency vectors. The similarity of subsets sampled by the random sampling technique (random subsets) with corresponding populations was close to 0 for both yeast and human data (Table 1). Note that this similarity is not close to one because subsets are by definition much smaller than populations and thus many proteins present in populations are absent in subsets. In contrast, the similarity of subsets sampled by the balanced sampling technique (balanced subsets) with corresponding populations was close to −0.7 and −1.0 for the yeast and human data, respectively (Table 1). Thus, the balanced subsets have substantially greater bias, as expected.
Given this bias, we might expect that predictive performance estimated with balanced subsets would not generalize well to the population level. To directly address this issue, population-level predictive performance was obtained by performing cross-validation on the full set of protein pairs (see Section 2.2) and compared with predictive performance estimated with sampled subsets. Table 1 and Supplementary Figure S1 show that predictive performance estimated with random subsets agrees well with population-level predictive performance for four prominent PPI prediction algorithms (M1–M4). In contrast, there are significant differences between population-level predictive performances and those estimated with balanced subsets for all four methods. These differences are all both statistically significant (P<2×10−6) and large, and apply to both SVM-based (M1–M3) and non-SVM-based (M4) methods. Taken together, the analyses in Table 1 indicate that balanced sampling produces highly biased subsets of negative PPIs and predictive performance estimated with balanced subsets does not generalize to the population level.
While Yu et al. (2010b) also observed good and poor predictive performance with random and balanced subsets, respectively, this analysis clarifies that the predictive performance estimated with random subsets is the genuine one, demonstrating that poor predictive performance estimated with balanced subsets cannot be taken as evidence supporting that protein sequence features are hardly informative for predicting PPIs, because predictive performance estimated with balanced susbsets fails to generalize to the population level.
3.2 Cross-validated subset bias artificially deflates predictive performance
Table 1 suggests that there exists an anti-correlation between the degree of bias of the subset used for cross-validation and the estimated predictive performance. To test this, we generated subsets with intermediate levels of bias by randomly mixing random and balanced subsets at varying ratios, then estimated predictive performance as in Table 1. Table 2 shows that there is indeed a strong correlation between the lack of bias of the subset used for cross-validation—measured as the similarity of the sampled subset to the overall population—and the estimated predictive performance for all four methods. At least 80% of the variability in estimated predictive performance (in terms of AUC) can be explained by the degree of bias of the cross-validation subset. Thus, the poor predictive performance estimated with balanced subsets is explained by the strong bias inherent to balanced subsets.
Table 2.
Correlation between the lack of bias in the subset used for cross-validation and the estimated predictive performance
| Method | Yeast |
Human |
||
|---|---|---|---|---|
| Correlation coefficient | P-value | Correlation coefficient | P-value | |
| M1 | 0.98 | <2.0×10−39 | 0.98 | <6.0×10−41 |
| M2 | 0.98 | <3.0×10−43 | 0.98 | <2.0×10−41 |
| M3 | 0.90 | <5.0×10−22 | 0.98 | <4.0×10−40 |
| M4 | 0.96 | <2.0×10−32 | 0.97 | <2.0×10−35 |
The similarity of the subset used for cross-validation with the population was measure in Table 1 and correlated with estimated predictive performance. The more similar the subset to the population (i.e. the less biased the subset), the higher the predictive performance estimated.
3.3 Does representational bias-driven learning dominate over learning on protein sequence features in predicting PPIs?
Hub proteins in PPI networks are proteins that possess many interaction partners, a property that can lead to hubs dominating PPI prediction algorithms. In principle, the prediction score of a test pair of proteins may correlate with the number of appearances of the test proteins in the positive data, and anti-correlate with their appearances in the negative training data. Although part of a legitimate learning process, this representational bias-driven learning may dominate over learning on the protein sequence features themselves, and it was this possibility that inspired the balanced sampling technique, which specifically blocks representational bias-driven learning. Thus, although this sampling technique is not suitable for cross-validated estimates of prediction performance, as shown above, it has legitimate applications in a training context. We therefore asked if this approach was justified, by controlling for these two distinct sources of learning and thereby measuring the contributions of representational bias versus protein features to PPI predictions.
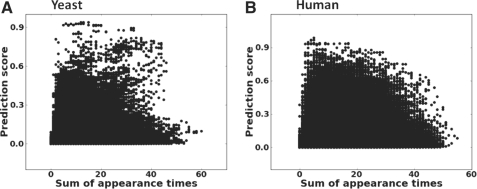
We estimated the overall contributions of representational bias-driven learning to the overall learning process as follows: For the yeast data in Table 1, the ratio between negative and positive PPIs was approximately 385, and that for the human data was approximately 395. The population-level predictive performances reported in Table 1 were obtained by using the random sampling technique to sample subsets for training as explained in Section 2.2 and thus are the results of the representational bias-driven learning combined with learning on protein sequence features. We thus compared these values with predictive performances obtained by using balanced subset sampling for training. Table 3 reports the results for M1 ~ M3 in terms of AUC. (M4 does not employ negative data for training, and thus cannot be assessed in this fashion. See below) For all three methods, excluding representational bias-driven learning significantly lowers predictive performance (all P<4×10−5), although to different degrees. As AUC values may be problematic if the two ROC curves cross (Hand, 2009), we also confirmed these results in terms of recall–precision plots (results not shown). In all but one case, the recall–precision plots also indicated that the exclusion of the representational bias-driven learning lowers predictive performance. For M4, we indirectly assessed the impact of representation bias-driven learning by plotting the numbers of times that test pair proteins appear in training data and their prediction scores (Fig. 1). It is apparent in the plots that test pairs that are more represented in training data do not necessarily get higher prediction scores that those that are not. Thus, it seems that the representation bias-driven learning does not play a dominant role in the predictive performance of M4.
Table 3.
A comparison of predictive performances obtained by using random sampling versus balanced sampling for training reveals that both protein representational biases and sequence features contribute to PPI predictions
| The subset sampling for training | Yeast |
Human |
||
|---|---|---|---|---|
| Random | Balanced | Random | Balanced | |
| M1 | 0.71 ± 0.02 | 0.65 ± 0.01 | 0.72 ± 0.01 | 0.63 ± 0.01 |
| M2 | 0.67 ± 0.02 | 0.60 ± 0.02 | 0.67 ± 0.01 | 0.57 ± 0.01 |
| M3 | 0.57 ± 0.01 | 0.55 ± 0.01 | 0.58 ± 0.01 | 0.54 ± 0.01 |
Fig. 1.
Plots of the numbers of times that test pair proteins appear in training data and their prediction scores for PIPE2.
Thus, we conclude that representational bias-driven learning contributes significantly to PPI predictions, at least for M1 ~ M3. Nonetheless, Table 3 shows that learning on protein sequence features alone still leads to predictive performance significantly better than random. Thus, both representational bias-driven learning and learning on protein sequence features significantly contribute to the overall learning for predicting PPIs.
4 CONCLUSION
In this study we clarified a critical distinction between subset sampling for algorithm training and for cross-validated estimates of predictive performance. We showed that a balanced sampling technique, recently proposed by Yu et al. (2010b) to prevent representational bias-driven learning of protein–protein interactions, is suitable for subset sampling during training but not for cross-validated testing, and that its use for cross-validation leads to significant underestimates of predictive performance and to erroneous conclusions regarding the value of protein sequence features for predicting PPIs. In contrast, when used only for training, use of the balanced sampling technique allows for estimates of the relative contributions of representational bias-driven learning as compared to learning based on protein sequence features. We observe both to contribute significantly to the prediction of PPIs.
Funding: National Institutes of Health (GM067779, GM088624, to E.M.); Welch (F1515) and Packard Foundations; and U.S. Army Research (58343-MA). Deutsche Forschungsgemeinschaft (DFG-Forschungsstipendium, to Y.P.).
Conflict of Interest: none declared.
REFERENCES
- Ben-Hur A, Noble WS. Kernel methods for predicting protein-protein interactions. Bioinformatics. 2005;21(Suppl. 1):i38–i46. doi: 10.1093/bioinformatics/bti1016. [DOI] [PubMed] [Google Scholar]
- Ben-Hur A, Noble WS. Choosing negative examples for the prediction of protein-protein interactions. BMC Bioinformatics. 2006;7(Suppl. 1):S2. doi: 10.1186/1471-2105-7-S1-S2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bock JR, Gough DA. Predicting protein–protein interactions from primary structure. Bioinformatics. 2001;17:455–460. doi: 10.1093/bioinformatics/17.5.455. [DOI] [PubMed] [Google Scholar]
- Chang C-C, Lin C-J. LIBSVM : a library for support vector machines. ACM TIST. 2011;2:1–27. [Google Scholar]
- Chou KC, Cai YD. Predicting protein-protein interactions from sequences in a hybridization space. J. Proteome Res. 2006;5:316–322. doi: 10.1021/pr050331g. [DOI] [PubMed] [Google Scholar]
- Gavin AC, et al. Proteome survey reveals modularity of the yeast cell machinery. Nature. 2006;440:631–636. doi: 10.1038/nature04532. [DOI] [PubMed] [Google Scholar]
- Gomez SM, et al. Learning to predict protein-protein interactions from protein sequences. Bioinformatics. 2003;19:1875–1881. doi: 10.1093/bioinformatics/btg352. [DOI] [PubMed] [Google Scholar]
- Guo Y, et al. Using support vector machine combined with auto covariance to predict protein-protein interactions from protein sequences. Nucleic Acids Res. 2008;36:3025–3030. doi: 10.1093/nar/gkn159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hand DJ. Measuring classifier performance: a coherent alternative to the area under the ROC curve. Mach. Learn. 2009;77:103–123. [Google Scholar]
- Ito T, et al. A comprehensive two-hybrid analysis to explore the yeast protein interactome. Proc. Natl Acad. Sci. USA. 2001;98:4569–4574. doi: 10.1073/pnas.061034498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joachims T. Making large-scale SVM learning practical. In: Schölkopf B, et al., editors. Advances in Kernel Methods - Support Vector Learning. Cambridge, MA: MIT-Press; 1999. pp. 41–56. [Google Scholar]
- Keshava Prasad TS, et al. Human Protein Reference Database—2009 update. Nucleic Acids Res. 2009;37:D767–D772. doi: 10.1093/nar/gkn892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krogan NJ, et al. Global landscape of protein complexes in the yeast Saccharomyces cerevisiae. Nature. 2006;440:637–643. doi: 10.1038/nature04670. [DOI] [PubMed] [Google Scholar]
- Li W, Godzik A. Cd-hit: a fast program for clustering and comparing large sets of protein or nucleotide sequences. Bioinformatics. 2006;22:1658–1659. doi: 10.1093/bioinformatics/btl158. [DOI] [PubMed] [Google Scholar]
- Martin S, et al. Predicting protein-protein interactions using signature products. Bioinformatics. 2005;21:218–226. doi: 10.1093/bioinformatics/bth483. [DOI] [PubMed] [Google Scholar]
- Nanni L, Lumini A. An ensemble of K-local hyperplanes for predicting protein-protein interactions. Bioinformatics. 2006;22:1207–1210. doi: 10.1093/bioinformatics/btl055. [DOI] [PubMed] [Google Scholar]
- Park Y. Critical assessment of sequence-based protein-protein interaction prediction methods that do not require homologous protein sequences. BMC Bioinformatics. 2009;10:419. doi: 10.1186/1471-2105-10-419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pitre S, et al. Global investigation of protein-protein interactions in yeast Saccharomyces cerevisiae using re-occurring short polypeptide sequences. Nucleic Acids Res. 2008;36:4286–4294. doi: 10.1093/nar/gkn390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy S, et al. Exploiting amino acid composition for predicting protein-protein interactions. PLoS One. 2009;4:e7813. doi: 10.1371/journal.pone.0007813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salwinski L, et al. The database of interacting proteins: 2004 update. Nucleic Acids Res. 2004;32:D449–D451. doi: 10.1093/nar/gkh086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen J, et al. Predicting protein-protein interactions based only on sequences information. Proc. Natl Acad. Sci. USA. 2007;104:4337–4341. doi: 10.1073/pnas.0607879104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smialowski P, et al. The Negatome database: a reference set of non-interacting protein pairs. Nucleic Acids Res. 2010;38:D540–D544. doi: 10.1093/nar/gkp1026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sprinzak E, Margalit H. Correlated sequence-signatures as markers of protein-protein interaction. J. Mol. Biol. 2001;311:681–692. doi: 10.1006/jmbi.2001.4920. [DOI] [PubMed] [Google Scholar]
- Tarassov K, et al. An in vivo map of the yeast protein interactome. Science. 2008;320:1465–1470. doi: 10.1126/science.1153878. [DOI] [PubMed] [Google Scholar]
- Uetz P, et al. A comprehensive analysis of protein-protein interactions in Saccharomyces cerevisiae. Nature. 2000;403:623–627. doi: 10.1038/35001009. [DOI] [PubMed] [Google Scholar]
- Yu CY, et al. Predicting protein-protein interactions in unbalanced data using the primary structure of proteins. BMC Bioinformatics. 2010a;11:167. doi: 10.1186/1471-2105-11-167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu H, et al. High-quality binary protein interaction map of the yeast interactome network. Science. 2008;322:104–110. doi: 10.1126/science.1158684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu J, et al. Simple sequence-based kernels do not predict protein-protein interactions. Bioinformatics. 2010b;26:2610–2614. doi: 10.1093/bioinformatics/btq483. [DOI] [PubMed] [Google Scholar]