Sparse non-negative generalized PCA with applications to metabolomics

Abstract

Motivation: Nuclear magnetic resonance (NMR) spectroscopy has been used to study mixtures of metabolites in biological samples. This technology produces a spectrum for each sample depicting the chemical shifts at which an unknown number of latent metabolites resonate. The interpretation of this data with common multivariate exploratory methods such as principal components analysis (PCA) is limited due to high-dimensionality, non-negativity of the underlying spectra and dependencies at adjacent chemical shifts.

Results: We develop a novel modification of PCA that is appropriate for analysis of NMR data, entitled Sparse Non-Negative Generalized PCA. This method yields interpretable principal components and loading vectors that select important features and directly account for both the non-negativity of the underlying spectra and dependencies at adjacent chemical shifts. Through the reanalysis of experimental NMR data on five purified neural cell types, we demonstrate the utility of our methods for dimension reduction, pattern recognition, sample exploration and feature selection. Our methods lead to the identification of novel metabolites that reflect the differences between these cell types.

Availability: www.stat.rice.edu/~gallen/software.html

Contact: gallen@rice.edu

Supplementary Information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Metabolomics, one of the newest fields within systems biology approaches to biomarker discovery in medicine, investigates an abundant pool of small molecules present in cells and tissues (Bollard et al., 2005; Hollywood et al., 2006; Holmes et al., 2008). One of the commonly used technologies for acquisition of this data is nuclear magnetic resonance (NMR) spectroscopy. It is a high-throughput technology for acquiring reproducible and resolved spectra that can be used to study the complete metabolic profile of a biological sample (Nicholson and Lindon, 2008). The spectra contain thousands of chemical resonances, which may belong to hundreds of metabolites (De Graaf, 2007). However, many metabolites resonate at multiple resonances and thus, unlike the typical DNA microarray data, different metabolite spectra overlap and introduce complexities that need to be addressed by signal processing and careful statistical analysis (Ebbels and Cavill, 2009; Weljie et al., 2006).

As understanding relationships between the set of biological samples and the underlying spectra is a challenge, principal components analysis (PCA) is commonly used for both dimension reduction and pattern recognition with NMR data (Coen et al., 2008; Dunn et al., 2005; Goodacre et al., 2004; Maletić-Savatić et al., 2008; Weckwerth and Morgenthal, 2005). In high-dimensional settings, however, it is well known that PCA can perform poorly due to the large number of irrelevant variables (Johnstone and Lu, 2009). Hence, many have proposed to incorporate sparsity into the principal component directions, thus selecting important features (Johnstone and Lu, 2009; Jolliffe et al., 2003; Shen and Huang, 2008; Zou et al., 2006). Non-negativity of the matrix factors, or principal component directions, has also been proposed in a number of settings to improve interpretability of the factors (Lee and Seung, 1999; Sajda et al., 2004). Several recent papers have combined these concepts to encourage both sparsity and non-negativity into the model (Hoyer, 2004; Kim and Park, 2007; Zass and Shashua, 2007).

In this article, we make the following statistical contributions: (i) propose a framework for incorporating sparsity, known structural dependencies and non-negativity into the principal component (PC) loadings and (ii) develop a fast, computationally efficient algorithm to compute these in high-dimensional settings. This work is presented in Section 2. Then, in Section 3, we evaluate the performance of our methods on real NMR data. We also demonstrate how to interpret the PC loadings to understand important biological patterns and identify candidate metabolites. In Section 4, we conclude with a summary of the implications of our work and future areas of research.

2 METHODS

We introduce a framework for PCA that incorporates structural dependencies, sparsity and non-negativity to better understand relationships between the samples and recognize patterns among the variables.

2.1 Review: generalized PCA

Recently, Allen et al. (2011) introduced a new matrix decomposition, the Generalized Least Squares Matrix Decomposition (GMD), and showed how this decomposition can be used to generalized PCA by directly incorporating known structural information or dependencies. Here, we review the Generalized PCA (GPCA) problem and specifically discuss its utility in the context of spectroscopy data.

We observe data, X∈ℜ^n×p, for n samples and p variables that has previously been normalized. (With NMR data, this includes baseline correction, normalizing by the integral of the spectrum and standardizing the variables at each ppm.) Let R∈ℜ^p×p be a positive semi-definite matrix called the quadratic operator that captures the noise structure in the data. Then, GPCA seeks the linear combination of variables maximizing the sample variance in the inner product space induced by R:

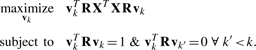(1)

The k-th GPC is z_k=XR v_k. If R=I, then we have the standard PCA optimization problem. Additionally, Allen et al. (2011) have shown that an extension of the power method for computing eigenvectors can be used to calculate these GPCs.

GPCA can be used to directly account for dependencies between adjacent variables in the spectra. The quadratic operator, R, behaves like an inverse covariance matrix of multivariate normal data (Allen et al., 2011). We can let R encode the inverse covariance of dependencies or structure in the data that do not contribute, and are independent of the signal of interest. The resulting GPCA solution can be interpreted as a decomposition of the covariance given by: Cov(X)=VD² V^T+R⁻¹, where D² is diagonal with entries, d²_k=v_k^T RX^T XR v_k. With NMR spectroscopy, variables at adjacent chemical shifts are strongly positively correlated. These dependencies, however, do not contribute to the biological signal, or the peaks and groups of peaks that vary across the samples. Thus, letting R encode these dependencies between adjacent chemical shifts, allows GPCA to ignore the biologically irrelevant structure and estimate more of the biologically relevant variability.

2.1.1 Kernel smoothers as quadratic operators

To this end, we employ kernel smoothers that are a function of the distance between the variables. Take the p×p distance matrix, D, where D_ij is the pair-wise distance between variables i and j. Then, the quadratic operator R can be taken as R_ij=k(D_ij, γ) where k() is a kernel and γ is the smoothing parameter. Standard kernels used in local linear regression, such as the Gaussian kernel, 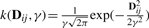, can be employed. If γ=10, for example, then elements in the kernel smoother are weighted according to a normal distribution with a SD of 10 distance units apart. For NMR data, the GPCA loading vectors multiply the data through a range of adjacent chemical shifts weighted by the kernel smoother. Thus, we directly account for dependencies between neighboring variables.

2.2 Sparse non-negative GPCA

While GPCA directly accounts for biologically irrelevant structure in NMR data, the problems of high dimensionality and the non-negativity of the spectra are left unsolved. To this end, we introduce Sparse Non-Negative GPCA, which gives interpretable PCA direction vectors by incorporating feature selection through sparsity and by constraining the loadings to be non-negative.

2.2.1 Problem and solution

We introduce the single-factor sparse non-negative GPCA optimization problem. Let u∈ℜⁿ, λ≥0, and R and v as defined previously, and consider the following:

(2)

The PCA loading vectors, v_k are constrained to be non-negative, and sparsity is encouraged via the ℓ₁-norm or lasso penalty on the loadings (Tibshirani, 1996). Here, λ is a penalty parameter controlling the amount of sparsity.

This simple criterion for the single-factor sparse non-negative GPCA is related to many existing approaches to sparse PCA and non-negative PCA. First, if λ=0, the non-negativity constraint is removed, and the remaining inequalities hold with equality, Equation (2) is equivalent to the GPCA or GMD optimization problem (Allen et al., 2011). This is related to the Lagrangian form of the sparse PCA approach in Witten et al. (2009), and is also a constrained version of the regression-based sparse PCA approach of Shen and Huang (2008). This single factor problem, however, differs from the multicomponent problem for sparse non-negative PCA of Zass and Shashua (2007). Also, notice that we do not require subsequent direction vectors to be orthogonal. Many have noted that orthogonality of sparse PCA factors is unwarranted and hence is often not imposed (Journée et al., 2010; Shen and Huang, 2008; Zou et al., 2006).

Our single-factor approach has many advantages. Notice that the problem is biconcave, meaning that it is concave in v with u fixed and in u with v fixed. This leads to a simple maximization strategy that is guaranteed to increase the objective and converge to a local maximum: alternate maximizing with respect to u and v. These coordinate-wise maximization problems turn out to have a simple solution:

Proposition 1. —

Let be the minimizer of the following:

(3)

Then, the coordinate updates, u^* and v^*, maximizing the single-factor sparse non-negative GPCA problem, (2), are given by:

(All proofs are given in the Supplementary Materials).

The solution to the single-factor sparse non-negative GPCA problem, (2), can be obtained by solving a simple lasso penalized non-negative regression problem. This non-negative regression problem in turn can be solved via a fast coordinate descent algorithm:

Proposition 2. —

The solution to (3) can be obtained via coordinate descent with updates: , where R_rj denotes the row elements of column j of R and ()₊ denotes the positive part.

This coordinate descent approach is related to the fast shooting algorithms of Friedman et al. (2010), and the speed can be further improved by employing active set learning and warm starts. We note that this algorithmic approach is a major improvement in terms of computational efficiency over the least angle-based approach to the non-negative lasso of Renard et al. (2008).

2.2.2 Algorithm

We have presented an optimization problem and solution to the single-factor sparse non-negative GPCA problem, and we are also interested in extracting multiple components. Then, we employ a greedy approach to estimating multiple components that is closely related to the power method algorithm for computing eigenvectors. This algorithm is summarized in Algorithm 1.

The sparse non-negative GPCA algorithm begins with the standardized data and computes the first component by solving the single-factor problem via coordinate descent. Subsequent components are calculated by solving the single-factor problem for the residual where the previously computed outer product has been removed. Each component is calculated in a greedy manner and is hence conditional on the previously estimated components. Thus, the components are not necessarily ordered in terms of the amount of variance they explain. This approach is common among existing methods for sparse PCA (Allen et al., 2011; Lee et al., 2010; Shen and Huang, 2008; Witten et al., 2009; Zou et al., 2006). As the dominant operation in our algorithm is solving a non-negative lasso problem, the computational complexity is O(n³). While traditional PCA methods may be faster to compute, our algorithm requires comparable computational time to existing sparse and/or non-negative PCA methods (Shen and Huang, 2008; Zass and Shashua, 2007).

2.2.3 Selecting regularization parameters

The amount of sparsity in the GPCA loading vectors, v, is controlled by the regularization parameter, λ. We seek a data-driven mechanism for selecting the amount of sparsity in each of the components. To this end, we employ the λ value that minimizes the following Bayesian Information Criterion (BIC) for each factor, v_k: 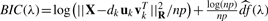. Here, 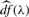denotes the degrees of freedom associated with the value of λ. For the non-negative lasso, 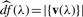, that is the number of non-zero elements of v. This follows from a result of Tibshirani and Taylor (2011). The criterion can be derived from considering each update in the power method algorithm as a generalized least squares problem with unknown variance (Allen et al., 2011; Lee et al., 2010). While other methods such as cross-validation may be employed to find the optimal regularization parameter, minimizing the BIC is computationally more efficient and leads to greater flexibility to select differing penalty parameters for each component.

2.2.4 Amount of variance explained

When using PCA methods for dimension reduction and exploratory analysis, the amount of variance explained by each principal component is an important measure to consider. As our GPCA and sparse non-negative GPCA methods incorporate structural information through the quadratic operator, R, the formulas for calculating the variance explained by each component are altered.

Proposition 3. —

1. The proportion of variance explained by the k-th GPC is v_k^T RX^T XR v_k / tr(XRX^T).

2. Define V_k=[v₁,… v_k] and X_k=XRV_k (V_k^T RV_k)⁻¹ V_k^T. Then, the cumulative proportion of variance explained by the k-th sparse non-negative GPC is tr(X_k RX_k^T) / tr(XRX^T).

Note that the proportion of variance explained by individual sparse non-negative GPCs can be found by taking the differences of the cumulative proportion explained. Thus, the proportion of variance explained by our methods can be interpreted as the ratio of the R-norm projected sample variance of the k-th linear projection relative to the total variance of the data in the R-norm. Notice that as the sparse non-negative GPCA factors are not constrained to be orthogonal, the sample variance explained must be adjusted for possible correlations among the factors as discussed in Shen and Huang (2008). Given these results, we can compare our methods to traditional PCA and sparse PCA methods in terms of the variance explained and dimension reduction.

3 RESULTS

We evaluate the utility of GPCA and Sparse Non-Negative GPCA for metabolomics through comparisons on real NMR data. (Simulation studies are given in the Supplementary Materials.) We use a dataset with 27 samples acquired by in vitro 1D H-NMR on five neural cell types: neurons, neural stem cells, microglia, astrocytes and oligodendrocytes (Manganas et al., 2007). [For methodology used on cell culturing, see Manganas et al. (2007)] The data are preprocessed in the traditional manner (Dunn et al., 2005): after acquisition, functional spectra is discretized by binning variables into bins of size 0.04 ppms yielding a total of 2394 variables. For each sample, the spectra are baseline corrected and normalized to their integral. Before applying multivariate techniques, the variables are standardized to have mean zero and variance one. While typically PCA is applied to unsupervised or unlabeled data, we apply our methods to this labeled data so that we may test their performance in terms of sample exploration, dimension reduction, pattern recognition and feature selection when the biological relationships between samples clear.

We compare our GPCA method to traditional PCA and our sparse non-negative GPCA method to sparse non-negative PCA. The later is implemented via Algorithm 1 by setting R=I. The BIC method is used to select penalty parameters for both sparse PCA methods and the first 15 PCs are calculated for all methods. For the GPCA methods, the quadratic operator, R, was taken to be a Gaussian kernel smoother with smoothing parameter, γ=20. Five possible values of γ were considered, γ=5, 10, 15, 20, 25, with γ chosen to explain the most sample variance.

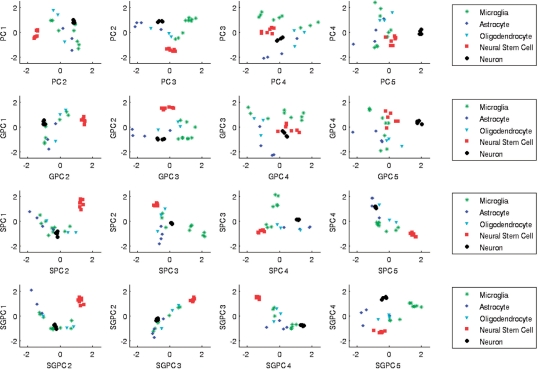
In Figure 1, we compare scatter plots of the normalized sample PCs for the four methods. Notice that the scatterplots of all methods exhibit clustering of the neuron and neural stem cell samples, while the other cell types are more scattered. Sparse methods and especially sparse non-negative GPCA, however, cluster the remaining cell types better, illustrating the utility of incorporating sparsity in high-dimensional data analysis.

Fig. 1.

Scatter plots of normalized sample PCs for the neural cell types data. Results from PCA, GPCA, Sparse Non-Negative PCA (SPCA) and Sparse Non-Negative GPCA (SGPCA) are compared for the five neural cell types. Sparse methods (bottom rows) demonstrate clearer separation of samples from different cell types.

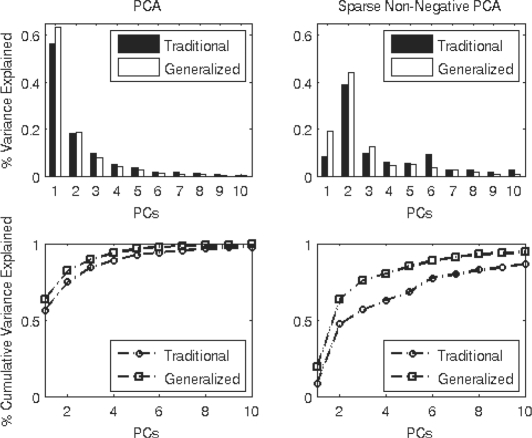
Next, we compare the methods in terms of dimension reduction in Figure 2. As sparse PCA methods naturally explain less sample variance than PCA methods, we compare the two sets of methods separately. Also note that as sparse PCA methods calculate components in a greedy manner, they are not necessarily ordered in terms of how much variance they explain. Overall, by incorporating the known structure of spectroscopy data into the PCA problem, the GPCA methods explain a larger portion of the sample variance. Thus, the reduction of dimensions for GPCA methods is greater. This behavior is especially pronounced for the sparse non-negative methods where seven PCs explain over 90% of the variance for sparse non-negative GPCA, while 15 PCs are needed to explain the same amount of variance for sparse non-negative PCA. Thus, sparse non-negative GPCA provides over 50% more dimension reduction than sparse non-negative PCA. GPCA methods demonstrate a clear advantage over traditional PCA methods in terms of variance explained and dimension reduction.

Fig. 2.

Amount of variance explained by the PCs for the five neural cell type data. Comparison of the percentage of variance explained by individual PCs (top panel) and cumulative percentage of variance explained (bottom) between PCA and GPCA (left), and sparse non-negative PCA and sparse non-negative GPCA (right). GPCA methods explain larger proportions of the sample variance.

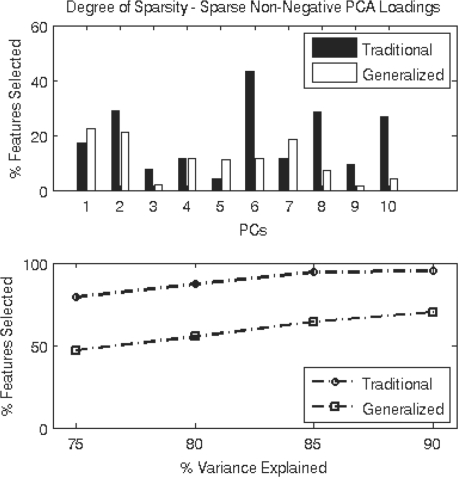
A major motivation of our work is to incorporate feature selection into the traditional PCA framework and assess its utility for NMR data. We compare the degree of sparsity seen in the PCs for the sparse non-negative PCA and GPCA methods in Figure 3. By directly accounting for the dependencies at adjacent chemical shifts, sparse non-negative GPCA gives a greater degree of sparsity, yielding a more parsimonious model. The GPCA method also explains more of the variance in the data with fewer features selected, an important attribute. Greater sparsity means that one needs to consider fewer peaks when explaining the patterns in the data. Also, a parsimonious PC loading vector indicates that more irrelevant variables have been discarded from the model. As sparse non-negative PCA does not incorporate structural information, many more variables are selected as the method tries to explain both the dependencies between neighboring chemical shifts and the biological variation. By directly accounting for these spatial dependencies, however, sparse non-negative GPCA is free to select features that explain the biological variation in the samples. Overall, these results indicate that sparse non-negative GPCA outperforms PCA, GPCA and sparse non-negative PCA in terms of sample exploration, dimension reduction and feature selection.

Fig. 3.

Proportion of features selected on the five neural cell types data by sparse non-negative PCA and GPCA for individual PCs (top) and by the cumulative PCs (bottom). Sparse non-negative GPCA explains more of the sample variance with fewer features selected.

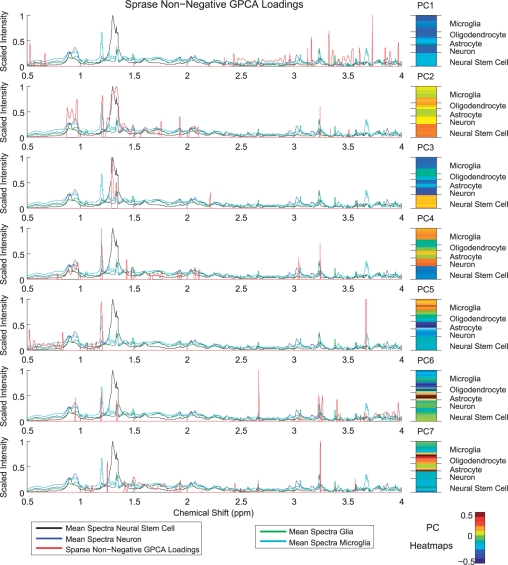
Sparse non-negative GPCA can be used to understand important biological patterns in the NMR data. Figure 4 gives the sparse non-negative GPCA loadings for the first seven sparse non-negative GPCs which explain over 90% of the variance in the data. Along with these loadings, we give heatmaps of the sample PCs to show how each of the samples contribute to the patterns seen in the loading vectors. The loading vectors are scaled and superimposed on the mean spectra from neurons, neural stem cells, microglia and ‘glia’, which includes astrocytes and oligodendrocytes. (Plots of the loading vectors for PCA, GPCA and sparse non-negative PCA are given in the Supplementary Materials.)

Fig. 4.

Sparse non-negative GPCA loadings and sample PC heatmaps for the first seven PCs, which explain over 90% of the sample variance. Scaled PC loadings are superimposed on the average scaled spectra of neural stem cells, neurons, microglia and ‘Glia’, which includes oligodendrocytes and astrocytes. Sparse non-negative GPCA loadings reveal important patterns across the samples and spikes in the loadings denote the location of peaks that vary greatly across the samples. For example, PC3 exhibits peaks that have higher intensities in neural stem cells, while the peaks selected by PC5 have higher concentrations in microglia.

By constraining the PC loading vectors to be non-negative, interpretation of the relationships between the features selected and the samples is made simpler. Spikes selected in the loading vectors indicate peaks that vary greatly across the samples. The positive sample PCs or scores (shown in the heatmaps of Fig. 4) have higher intensities at the peaks selected by the associated loading vector. The groups of spikes selected by each loading vector then indicate an important metabolic pattern that is up- or downregulated in each sample as revealed by the sample PCs. These metabolic patterns will consist of both metabolites that resonate at multiple peaks and also metabolites belonging to the same pathway. Thus, further testing of the peaks selected by our methods should be done to resolve the specific metabolites responsible for the metabolic pattern identified.

Considering the first loading vector, the features selected are at chemical shifts where there are few peaks. This occurs as the first direction vector accounts for the baseline height difference between the samples due to normalization to the integral. This behavior is observed also in the first loading vector for the three competing methods (shown in the Supplementary Materials). Loading vectors two and three denote peaks that have higher concentrations in neural stem cells. Loading vector four exhibits a pattern of peaks that are upregulated in neurons and microglia, while the peaks selected in loading vectors five have higher intensities in microglia. Peaks in loading vectors six and seven denote metabolites that are upregulated in astrocytes and both oligodendrocytes and astrocytes, respectively.

In Table 1, we give the locations of important selected peaks in parts per million, the cell types in which these peaks exhibited the highest intensities, as well as metabolites that have previously been identified at these peak locations. A previous analysis of this data using traditional PCA methods identified the peaks at 1.28, 2.02 and 3.23 ppm as higher in neural stem cells, neurons, and astrocytes, respectively (Manganas et al., 2007). Our methods however, identify several other novel biomarkers, especially for microglia. In future work, we will identify candidate metabolites for the novel biomarkers in Table 1 via public databases such as BioMagResBank (BMRB) (Ulrich et al., 2008), metabolite identification models (Crockford et al., 2005; Zheng et al., 2011) and spike-in experiments. Thus, our results are consistent with the existing literature, andt also identify novel biomarkers for consideration.

Table 1.

Locations in parts per million (ppm) of the most important peaks identified by the first seven sparse non-negative GPCA loadings

Peak location (ppm)	Cell types	Metabolites
0.96	Neuron, microglia
1.19	Microglia, neuron
1.28	Neural stem cell, ogliodendrocyte	Lipid moiety
1.48	Ogliodendrocyte
2.02	Neuron	NAA
2.65	Astrocyte
3.01	Neuron
3.04	Ogliodendrocyte	Creatine
3.23	Ogliodendrocyte, neuron, astrocyte	Choline
3.43	Ogliodendrocyte
3.66	Microglia

Boldfaced locations denote peaks with especially strong signals as indicated by the loading vectors. Information on which cell types exhibited the highest intensity as well as metabolites that have previously been identified at the locations is also given.

These results demonstrate the many advantages of using sparse non-negative GPCA for NMR spectroscopy. Not only does our method exhibit greater dimension reduction, better clustering of samples according to biological relationships and provide more feature selection than competing methods, but also yields easily interpretable results that lead to understanding of important biological patterns in the spectra.

4 DISCUSSION

We have presented a framework for incorporating structural dependencies, sparsity and non-negativity into PCA. By comparing our techniques to traditional PCA methods on real NMR data, we have demonstrated the many advantages of our methods. Future areas of research are to extend our framework to supervised multivariate analysis techniques such as partial least squares and linear discriminant to better classify NMR samples.

While we have demonstrated our methods on 1D H-NMR spectroscopy, our approach can be applied to many other high-throughput metabolomics technologies. Mass spectrometry and other spectroscopy techniques also produce a spectrum of non-negative variables. Additionally, many researchers employ multidimensional spectroscopy to further identify metabolites in a sample (De Graaf, 2007). In this data, each sample consists of a matrix of spectroscopy variables. Sparse non-negative GPCA can be applied to this multidimensional data in a straightforward manner by vectorizing the matrix of variables and employing a 2D kernel smoother over the lattice of variables. As a future area of research, one can also extend our methods to tensors or higher order PCA to find patterns and achieve dimension reduction for this multidimensional metabolomics data.

In addition to metabolomics data, our methods are general and hence applicable to a variety of other structured biomedical data. As the dependencies of the noise must be known to construct the quadratic operator, our methods can be used to find patterns in data where these noise dependencies are well established. Possible further applications of our methods then include copy number variation and methylation data in which variables strongly depend on known chromosomal location, and microscopy, neuroimaging and other bio-medical imaging data in which pixels are spatially correlated with adjacent pixels.

In conclusion, we have developed a novel modification of PCA particularly suited to the challenges associated with analyzing NMR data. While our methods show numerous advantages in the analysis of metabolomics data, there are still many open research problems and potential extensions related to our work.